Effect of Surface Groove Structure on the Aerodynamics of Soccer Balls
Abstract
1. Introduction
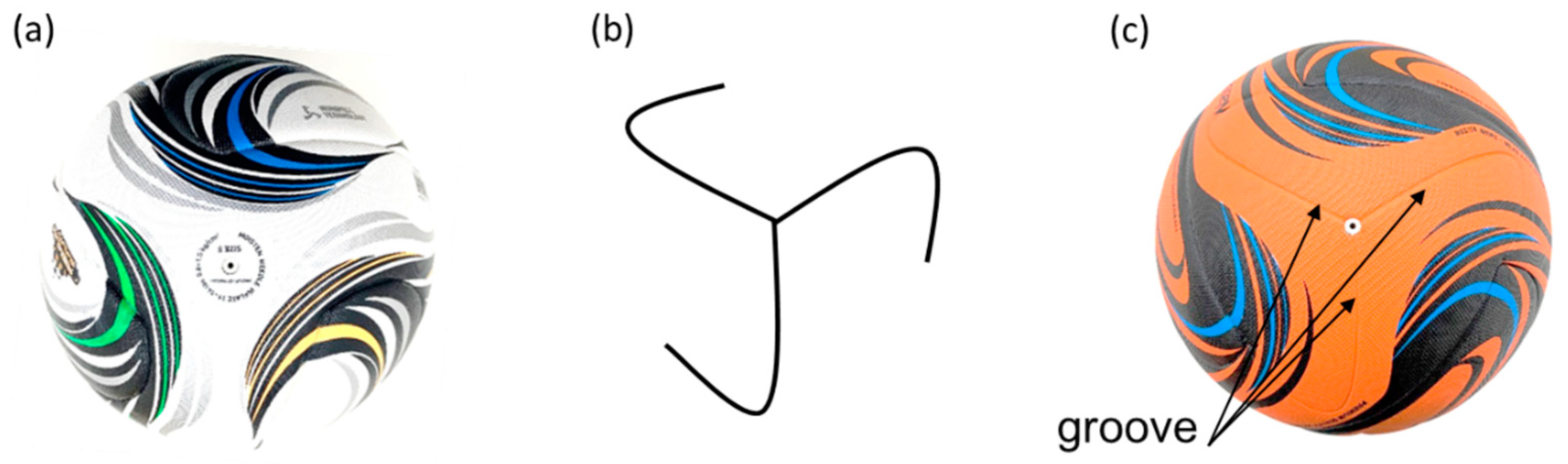
2. Methods
Wind-Tunnel Experiment
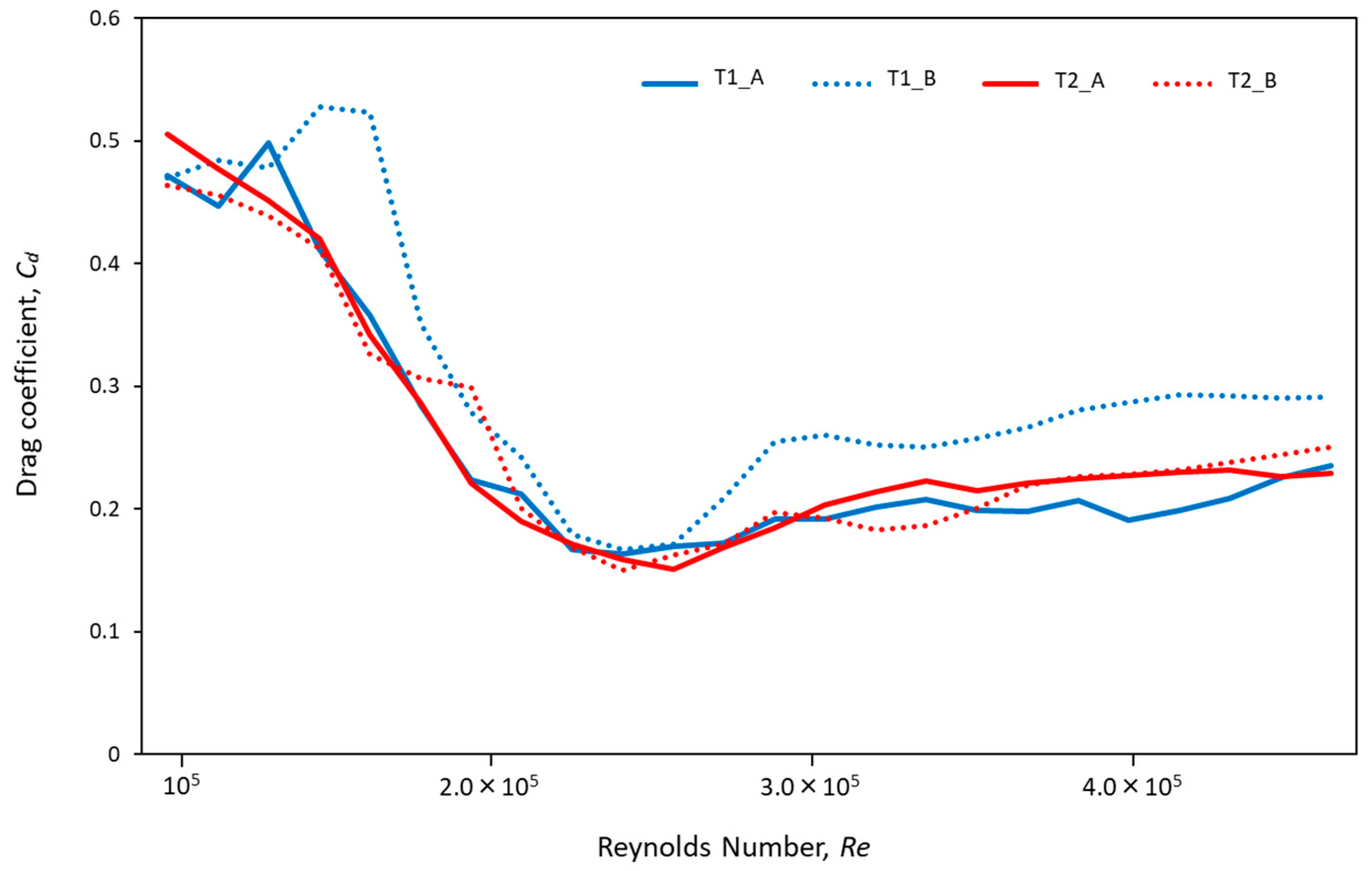
3. Results and Discussion
3.1. Drag Coefficient Variation by Ball Type
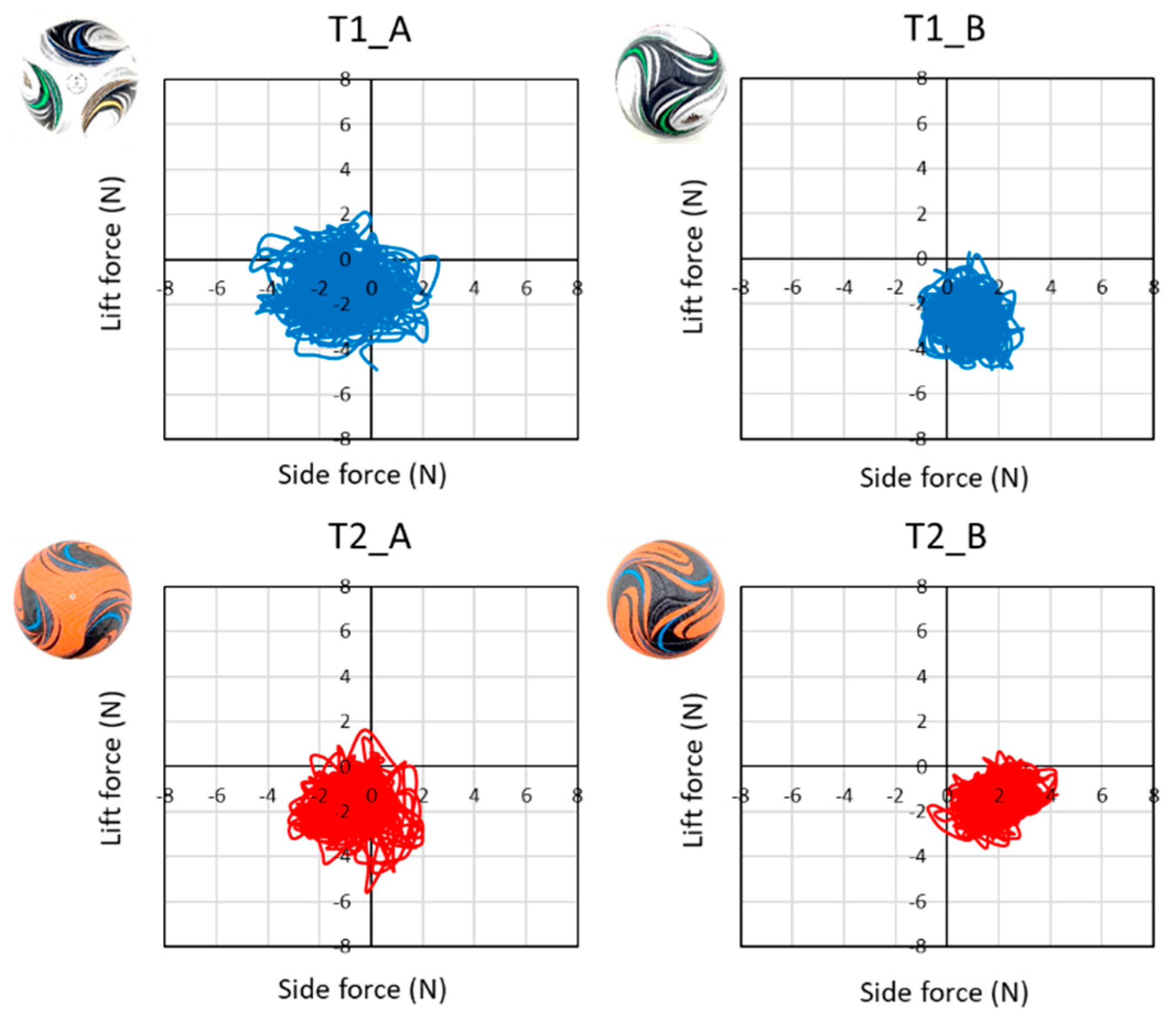
3.2. Changes in the in Lift and Side Forces over Time
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Naito, K.; Hong, S.; Koido, M.; Nakayama, M.; Sakamoto, K.; Asai, T. Effect of seam characteristics on critical Reynolds number in footballs. Mech. Eng. J. 2018, 5, 17-00369. [Google Scholar] [CrossRef]
- Hong, S.; Asai, T. Effect of panel shape of soccer ball on its flight characteristics. Sci. Rep. 2014, 4, 5068. [Google Scholar] [CrossRef] [PubMed]
- Goff, J.E.; Hong, S.; Asai, T. Aerodynamic and surface comparisons between Telstar 18 and Brazuca. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2018, 232, 342–348. [Google Scholar] [CrossRef]
- Goff, J.E.; Asai, T.; Hong, S. A comparison of Jabulani and Brazuca non-spin aerodynamics. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2014, 228, 188–194. [Google Scholar] [CrossRef]
- Hong, S.; Asai, T.; Seo, K. Visualization of air flow around soccer ball using a particle image velocimetry. Sci. Rep. 2015, 5, 15108. [Google Scholar] [CrossRef] [PubMed]
- Goff, J.E.; Hong, S.; Asai, T. Effect of a soccer ball’s seam geometry on its aerodynamics and trajectory. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2019, 234, 19–29. [Google Scholar] [CrossRef]
- Passmore, M.A.; Rogers, D.; Tuplin, S.; Harland, A.; Lucas, T.; Holmes, C. The aerodynamic performance of a range of FIFA-approved footballs. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2011, 226, 61–70. [Google Scholar] [CrossRef]
- Aoki, K.; Muto, K.; Okanaga, H. Aerodynamic characteristics and flow pattern of a golf ball with rotation. Procedia Eng. 2010, 2, 2431–2436. [Google Scholar] [CrossRef]
- Djamovski, V.; Rosette, P.; Chowdhury, H.; Alam, F.; Steiner, T. A comparative study of rugby ball aerodynamics. Procedia Eng. 2012, 34, 74–79. [Google Scholar] [CrossRef][Green Version]
- Price, D.S.; Jones, R.; Harland, A.R. Computational modelling of manually stitched soccer balls. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2006, 220, 259–268. [Google Scholar] [CrossRef]
- Asai, T.; Ito, S.; Seo, K.; Hitotsubashi, A. Fundamental aerodynamics of a new volleyball. Sports Technol. 2010, 3, 235–239. [Google Scholar] [CrossRef]
- Hong, S.; Weon, B.M.; Nakanishi, Y.; Kimachi, K.; Seo, K.; Asai, T. Aerodynamic effects of a panel orientation in volleyball float serve. In Proceedings of the 2018 International Society of Biomechanics in Sports, Auckland, New Zealand, 10–14 September 2018; pp. 1–4. [Google Scholar]
- Hong, S.; Asai, T.; Weon, B.M. Surface patterns for drag modification in volleyballs. Appl. Sci. 2019, 9, 4007. [Google Scholar] [CrossRef]
- Asai, T.; Nakanishi, Y.; Akiyama, N.; Hong, S. Flow Visualization of Spinning and Nonspinning Soccer Balls Using Computational Fluid Dynamics. Appl. Sci. 2020, 10, 4543. [Google Scholar] [CrossRef]
- Thomson, J.J. The dynamics of a golf ball. Nature 1910, 85, 2151–2157. [Google Scholar]
- Mehta, R.D.; Bentley, K.; Proudlove, M.; Varty, P. Factors affecting cricket ball swing. Nature 1983, 303, 787–788. [Google Scholar] [CrossRef]
- Hong, S.; Asai, T. Aerodynamic effects of dimples on soccer ball surfaces. Heliyon 2017, 3, e00432. [Google Scholar] [CrossRef] [PubMed]
- Naruo, T.; Mizota, T. The influence of golf ball dimples on aerodynamic characteristics. Procedia Eng. 2014, 72, 780–785. [Google Scholar] [CrossRef]
- Chen, H. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept. Phys. Rev. E 1998, 58, 3955–3963. [Google Scholar] [CrossRef]



| Type | T1_A | T1_B | T2_A | T2_B | ||||
|---|---|---|---|---|---|---|---|---|
| Side Force | Lift Force | Side Force | Lift Force | Side Force | Lift Force | Side Force | Lift Force | |
| Mean | −1.10 | −1.38 | 0.77 | −2.69 | −0.83 | −1.74 | 1.85 | −1.50 |
| SD | 1.23 | 1.05 | 0.70 | 0.80 | 0.92 | 0.88 | 0.74 | 0.70 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.; Asai, T. Effect of Surface Groove Structure on the Aerodynamics of Soccer Balls. Appl. Sci. 2020, 10, 5877. https://doi.org/10.3390/app10175877
Hong S, Asai T. Effect of Surface Groove Structure on the Aerodynamics of Soccer Balls. Applied Sciences. 2020; 10(17):5877. https://doi.org/10.3390/app10175877
Chicago/Turabian StyleHong, Sungchan, and Takeshi Asai. 2020. "Effect of Surface Groove Structure on the Aerodynamics of Soccer Balls" Applied Sciences 10, no. 17: 5877. https://doi.org/10.3390/app10175877
APA StyleHong, S., & Asai, T. (2020). Effect of Surface Groove Structure on the Aerodynamics of Soccer Balls. Applied Sciences, 10(17), 5877. https://doi.org/10.3390/app10175877






