Destruction of Fibroadenomas Using Photothermal Heating of Fe3O4 Nanoparticles: Experiments and Models
Abstract
1. Introduction
2. Results
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Experiments
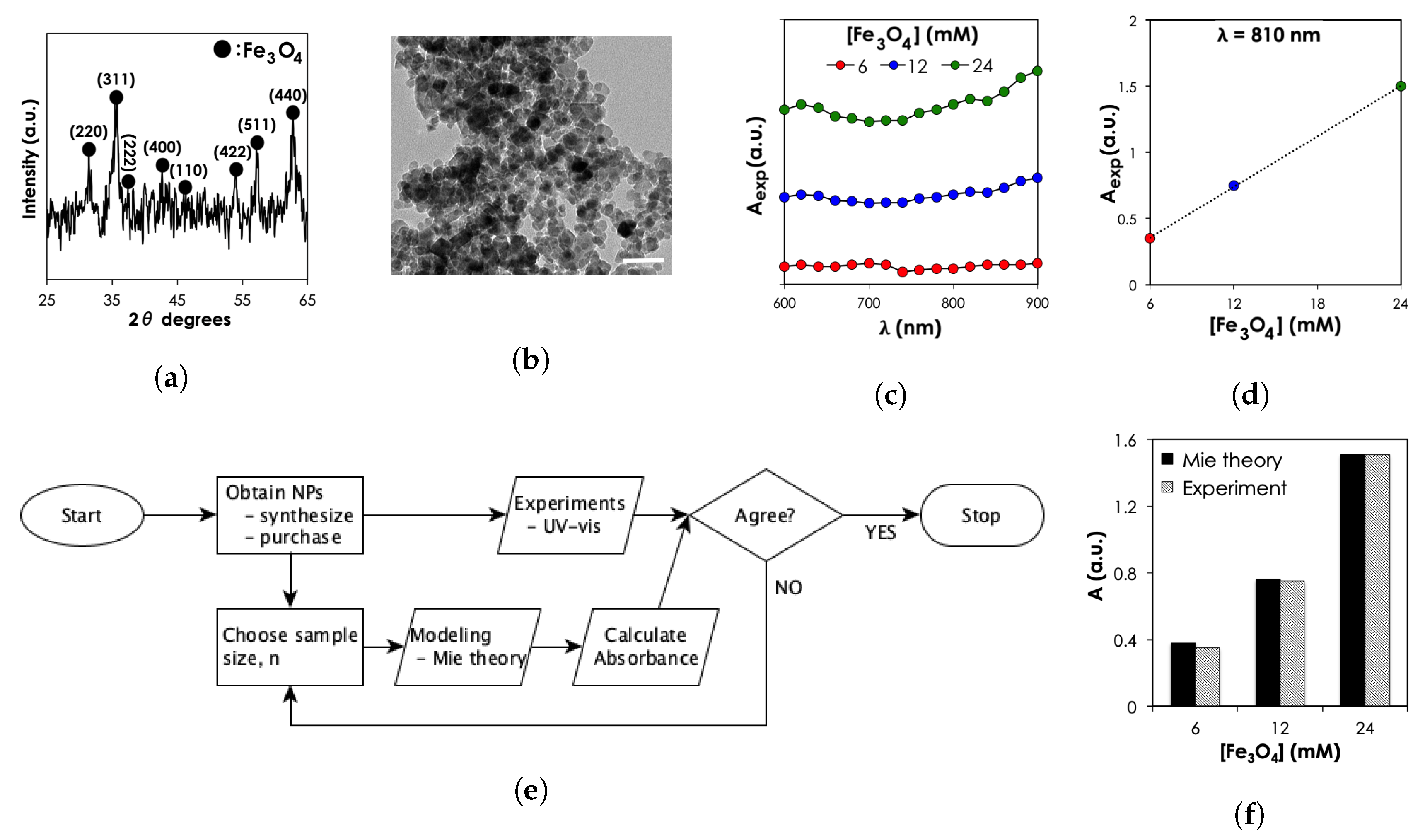
4.2.1. MNP Characterization
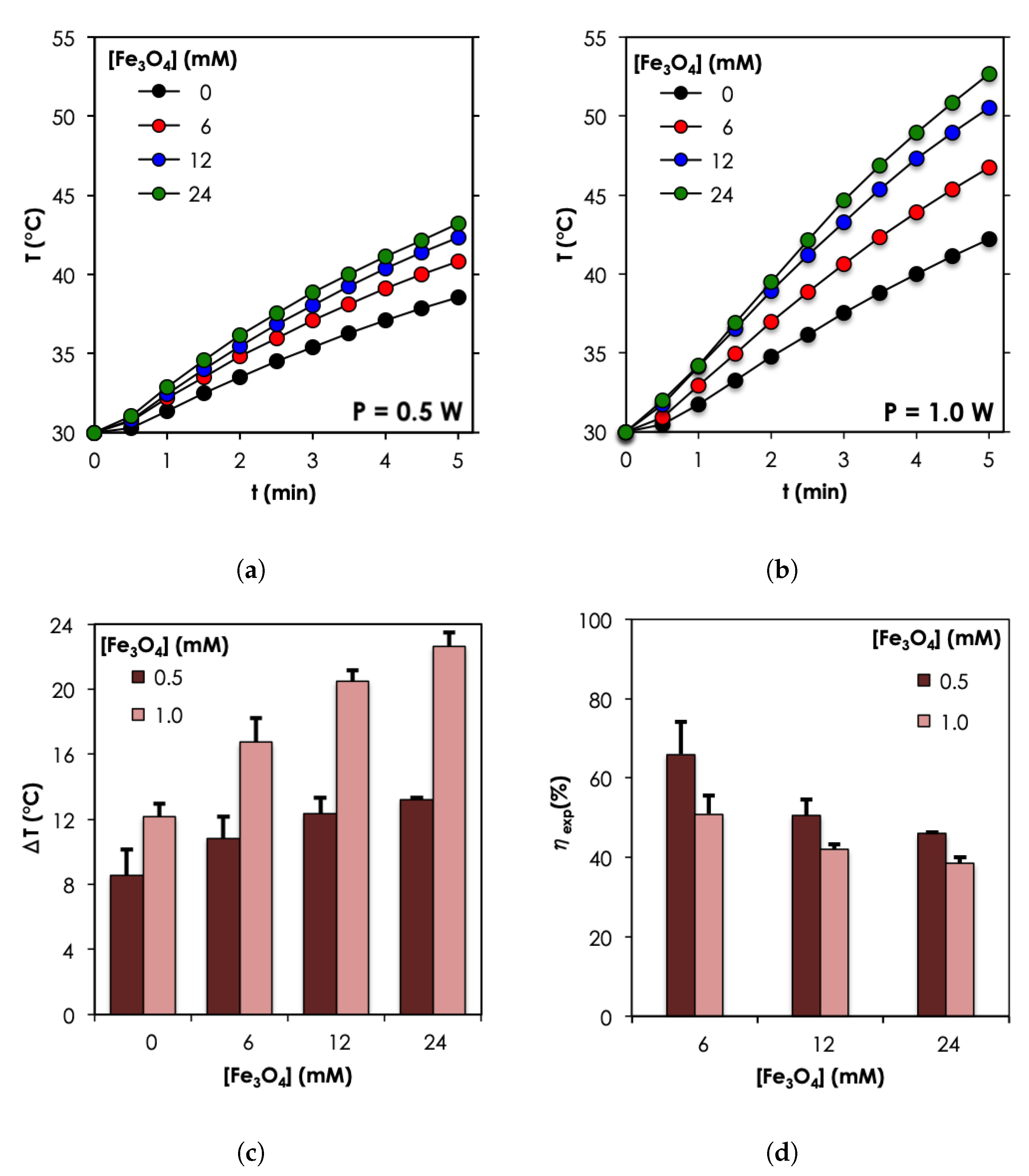
4.2.2. Photothermal Measurement in Water
4.3. Models
4.3.1. Optical Properties Predictions
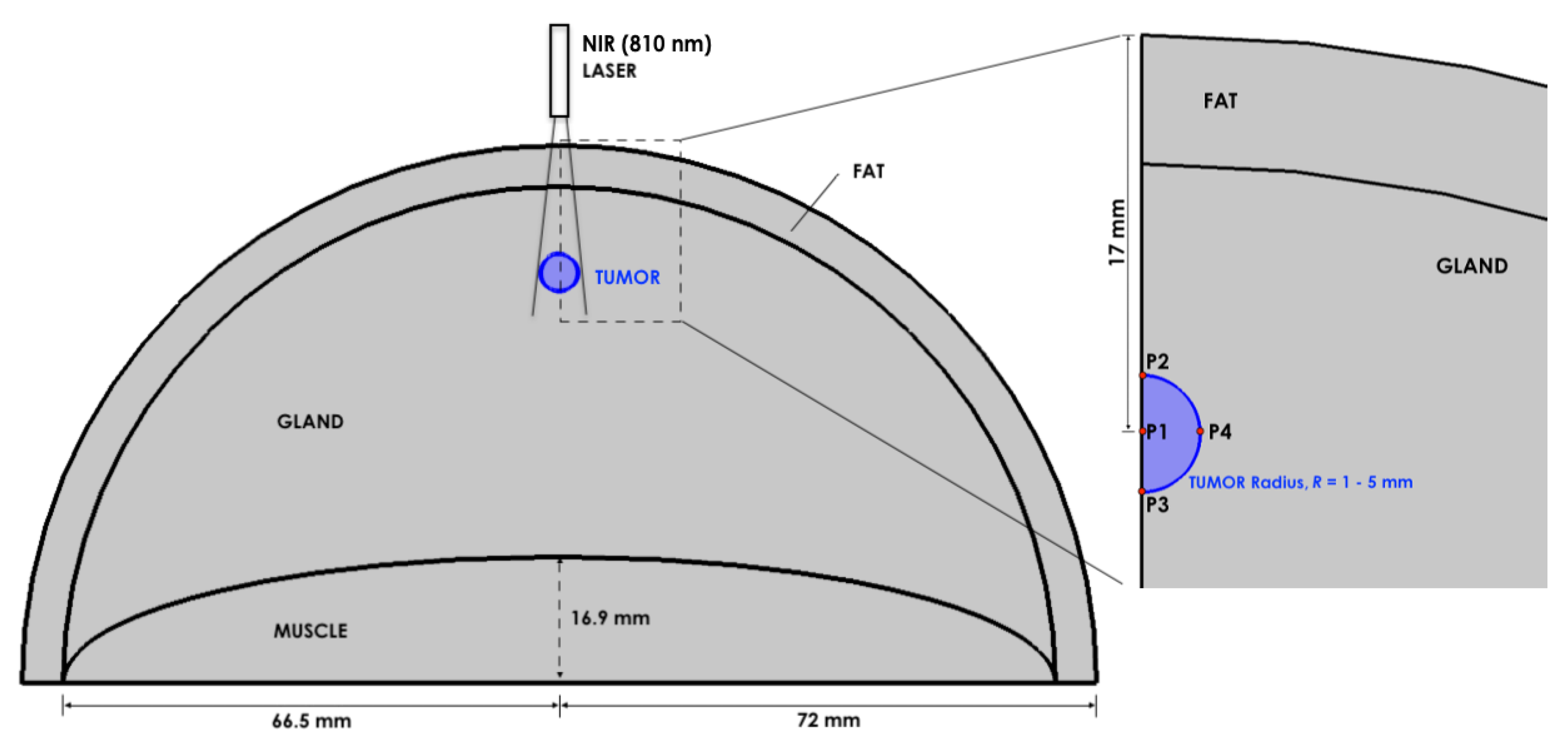
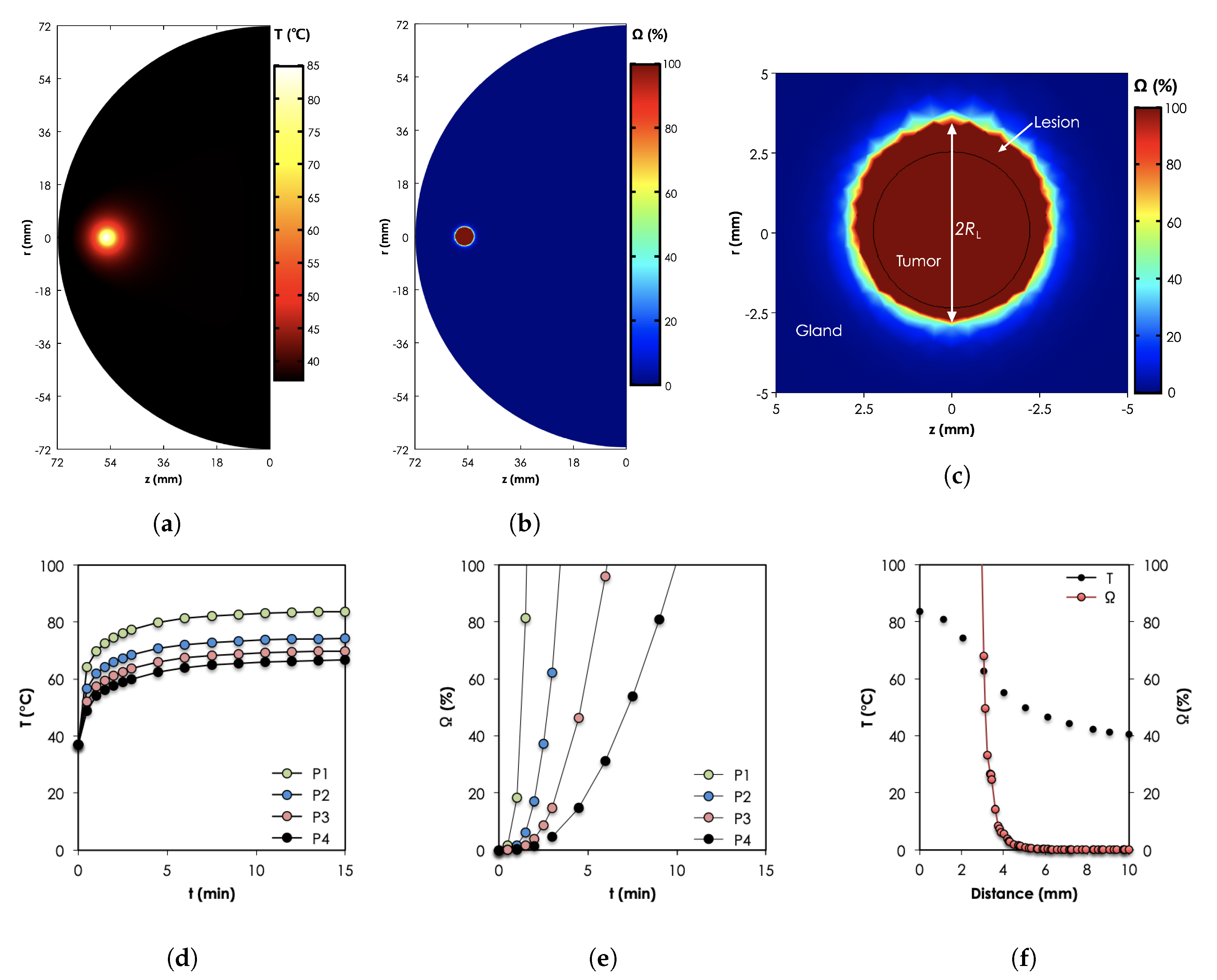
4.3.2. In-Vivo Predictions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guray, M.; Sahin, A.A. Benign Breast Diseases: Classification, Diagnosis, and Management. Oncologist 2006, 11, 435–449. [Google Scholar] [CrossRef] [PubMed]
- Chinyama, C.N. Benign Breast Diseases: Radiology-Pathology-Risk Assessment, 2nd ed.; Springer: Berlin, Germany, 2014; p. 9. [Google Scholar]
- Santen, R.J.; Mansel, R. Benign breast disorders. N. Engl. J. Med. 2005, 353, 275–285. [Google Scholar] [CrossRef] [PubMed]
- El-Wakeel, H.; Umpleby, H.C. Systematic review of fibroadenoma as a risk factor for breast cancer. Breast (Edinb. Scotl.) 2003, 12, 302–307. [Google Scholar] [CrossRef]
- Cerrato, F.; Labow, B.I. Diagnosis and management of fibroadenomas in the adolescent breast. Semin. Plast. Surg. 2013, 27, 23–25. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.S.; McGrath, M.H. Management of benign tumors of the adolescent breast. Plast. Reconstr. Surg. 2007, 120, 13e–19e. [Google Scholar] [CrossRef]
- Derkyi-Kwarteng, L.; Brown, A.A.; Derkyi-Kwarteng, A.; Gyan, E.; Akakpo, K.P.; Abraham, A. Benign Proliferative Breast Disease: A Histopathological Review of Cases at Korle Bu Teaching Hospital. J. Adv. Med. Med. Res. 2019, 31, 1–5. [Google Scholar] [CrossRef]
- Bewtra, C. Fibroadenoma in women in Ghana. Pan Africa Med. J. 2009, 2, 11. [Google Scholar] [CrossRef]
- Oluwole, S.F.; Freeman, H.P. Analysis of benign breast lesions in blacks. Am. J. Surg. 1979, 137, 786–789. [Google Scholar] [CrossRef]
- Newman, L.A. Breast cancer in African-American women. Oncologist 2005, 10, 1–14. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, F. Minimally-invasive thermal ablation of early-stage breast cancer: A systemic review. Eur. J. Surg. Oncol. 2010, 36, 1149–1155. [Google Scholar] [CrossRef]
- Ezer, S.S.; Oguzkurt, P.; Ince, E.; Temiz, A.; Bolat, F.A.; Hicsonmez, A. Surgical Treatment of the Solid Breast Masses in Female Adolescents. J. Pediatr. Adolesc. Gynecol. 2013, 26, 31–35. [Google Scholar] [CrossRef]
- Dyrstad, S.W.; Yan, Y.; Fowler, A.M.; Colditz, G.A. Breast cancer risk associated with benign breast disease: Systematic review and meta-analysis. Breast Cancer Res. Treat. 2015, 149, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Lakoma, A.; Kim, E.S. Minimally invasive surgical management of benign breast lesions. Gland Surg. 2014, 3, 142–148. [Google Scholar] [PubMed]
- Ashikbayeva, Z.; Tosi, D.; Balmassov, D.; Schena, E.; Saccomandi, P.; Inglezakis, V. Application of Nanoparticles and Nanomaterials in Thermal Ablation Therapy of Cancer. Nanomaterials 2019, 9, 1195. [Google Scholar] [CrossRef] [PubMed]
- Maier-Hauff, K.; Ulrich, F.; Nestler, D.; Niehoff, H.; Wust, P.; Thiesen, B.; Orawa, H.; Budach, V.; Jordan, A. Efficacy and Safety of Intratumoral Thermotherapy Using Magnetic Iron-Oxide Nanoparticles Combined with External Beam Radiotherapy on Patients with Recurrent Glioblastoma Multiforme. J. Neuro-Oncol. 2011, 103, 317–324. [Google Scholar] [CrossRef]
- Johannsen, M.; Thiesen, B.; Wust, P.; Jordan, A. Magnetic Nanoparticle Hyperthermia for Prostate Cancer. Int. J. Hyperthermia 2010, 26, 790–795. [Google Scholar] [CrossRef]
- Chu, M.; Shao, Y.; Peng, J.; Dai, X.; Li, H.; Wu, Q.; Shi, D. Near-infrared laser light mediated cancer therapy by photothermal effect of Fe3O4 magnetic nanoparticles. Biomaterials 2013, 34, 4078–4088. [Google Scholar] [CrossRef]
- Espinosa, A.; Di Corato, R.; Kolosnjaj-Tabi, J.-T.; Flaud, P.; Pellegrino, T.; Wilhelm, C. Duality of Iron Oxide Nanoparticles in Cancer Therapy: Amplification of Heating Efficiency by Magnetic Hyperthermia and Photothermal Bimodal Treatment. ACS Nano 2016, 10, 2436–2446. [Google Scholar] [CrossRef]
- Maltzahn, G.V.; Park, J.-H.; Agrawal, A.; Bandaru, N.K.; Das, S.K.; Sailor, M.J.; Bhatia, S.N. Computationally guided photothermal tumor therapy using long-circulating gold nanorod antennas. Cancer Res. 2009, 69, 3892–3900. [Google Scholar] [CrossRef]
- Bagley, A.F.; Hill, S.; Rogers, G.S.; Bhatia, S.N. Plasmonic Photothermal Heating of Intraperitoneal Tumors through the Use of an Implanted Near-Infrared Source. ACS Nano 2013, 7, 8089–8097. [Google Scholar] [CrossRef]
- Morozov, K.I.; Lebedev, A.V. The effect of magneto-dipole interactions on the magnetization curves of ferrocolloids. J. Magn. Magn. Mater. 1990, 85, 51–53. [Google Scholar] [CrossRef]
- Pshenichnikov, A.; Lebedev, A.; Ivanov, A.O. Dynamics of Magnetic Fluids in Crossed DC and AC Magnetic Fields. Nanomaterials 2019, 9, 1711. [Google Scholar] [CrossRef]
- Tang, J.; Myers, M.; Bosnick, A.; Brus, L.E. Magnetite Fe3O4 Nanocrystals: Spectroscopic Observation of Aqueous Oxidation Kinetics. J. Phys. Chem. B 2003, 107, 7501–7506. [Google Scholar] [CrossRef]
- Shen, S.; Kong, F.; Guo, X.; Wu, L.; Shen, H.; Xie, M.; Wang, X.; Jin, Y.; Ge, Y. Cmcts Stabilized Fe3O4 Particles with Extremely Low Toxicity as Highly Efficient near-Infrared Photothermal Agents for in Vivo Tumor Ablation. Nanoscale 2013, 5, 8056–8066. [Google Scholar] [CrossRef] [PubMed]
- Pan, P.; Lin, Y.; Gan, Z.; Luo, X.; Zhou, W.; Zhang, N. Magnetic field enhanced photothermal effect of Fe3O4 nanoparticles. J. Appl. Phys. 2018, 123, 115115. [Google Scholar] [CrossRef]
- Wong, K.V.; Castillo, M.J. Heat transfer mechanisms and clustering in Nanofluids. Adv. Mech. Eng. 2010, 2010, 795478. [Google Scholar] [CrossRef]
- Chen, H.; Shao, L.; Ming, T.; Sun, Z.; Zhao, C.; Yang, B.; Wang, J. Understanding the photothermal conversion efficiency of gold nanocrystals. Small 2010, 6, 2272–2280. [Google Scholar] [CrossRef]
- Kim, A.D. Transport theory for light propagation in biological tissue. J. Opt. Soc. Am. A 2004, 21, 820–827. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Wahab, A.A.; Salim, M.I.M.; Ahamat, M.A.; Manaf, N.A.; Yunus, J.; Lai, K.W. Thermal distribution analysis of three-dimensional tumor-embedded breast models with different breast density compositions. Med. Biol. Eng. Comput. 2016, 54, 1363–1373. [Google Scholar] [CrossRef]
- Balleyguier, C.; Bidault, F.; Mathieu, M.C.; Ayadi, S.; Couanet, D.; Sigal, R. BIRADSTM mammography: Exercises. Eur. J. Radiol. 2007, 61, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Paruch, M. Mathematical Modeling of Breast Tumor Destruction Using Fast Heating during Radiofrequency Ablation. Materials 2020, 13, 136. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, Y.; Verhey, J.F. A finite element method model to simulate laser interstitial thermo therapy in anatomical inhomogeneous regions. Biomed. Eng. OnLine 2005, 4, 2. [Google Scholar] [CrossRef]
- Sarkar, S.; Gurjarpadhye, A.A.; Rylander, C.G.; Rylander, M.N. Optical properties of breast tumor phantoms containing carbon nanotubes and nanohorns. J. Biomed. Opt. 2011, 16, 051304. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Dehghani, H.; Brooksby, B.A.; Pogue, B.W.; Paulsen, K.D. Effects of refractive index on near-infrared tomography of the breast. Appl. Opt. 2005, 44, 1870–1878. [Google Scholar] [CrossRef] [PubMed]
- Dewhirst, M.; Stauffer, P.R.; Das, S.; Craciunescu, O.I.; Vujaskovic, Z. Clinical Radiation Oncology, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 21. [Google Scholar]
- Sundeep, S.; Repaka, R. Parametric sensitivity analysis of critical factors affecting the thermal damage during RFA of breast tumor. Int. J. Therm. Sci. 2018, 124, 366–374. [Google Scholar]
- Goldberg, S.N.; Gazelle, G.S.; Compton, C.C.; Mueller, P.R.; Tanabe, K.K. Treatment of intrahepatic malignancy with radiofrequency ablation: Radiologic-pathologic correlation. Cancer 2000, 88, 2452–2463. [Google Scholar] [CrossRef]
- Zevas, N.T.; Kuwayama, A. Pathological characteristics of experimental thermal lesions: Comparison of induction heating and radiofrequency electrocoagulation. J. Neurosurg. 1972, 37, 418–422. [Google Scholar] [CrossRef]
- Bloom, K.J.; Dowlat, K.; Assad, L. Pathologic changes after interstitial laser therapy of infiltrating breast carcinoma. Am. J. Surg. 2001, 182, 384–388. [Google Scholar] [CrossRef]
- Dowlatshahi, K.; Fan, M.; Gould, V.E.; Bloom, K.J.; Ali, A. Stereotactically guided laser therapy of occult breast tumors: Work-in-progress report. Arch. Surg. 2000, 135, 1345–1352. [Google Scholar] [CrossRef]
- Wilhelm, S.; Tavares, A.J.; Dai, Q.; Ohta, S.; Audet, J.; Dvorak, H.F.; Chan, W.C.W. Analysis of nanoparticle delivery to tumours. Nat. Rev. Mater. 2016, 1, 1–12. [Google Scholar] [CrossRef]
- Kannadorai, R.K.; Liu, Q. Optimization in interstitial plasmonic photothermal therapy for treatment planning. Med. Phys. 2013, 40, 103301. [Google Scholar] [CrossRef] [PubMed]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering by a Sphere. In Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 2008; pp. 83–129. [Google Scholar]
- Qin, Z.; Wanf, Y.; Randrianalisoa, J.; Raesi, V.; Chan, W.C.W.; Lipiński, W.; Bischof, J.C. Quantitative Comparison of Photothermal Heat Generation between Gold Nanospheres ad Nanorods. Sci. Rep. 2016, 6, 29836. [Google Scholar] [CrossRef]
- Popescu, R.C.; Andronescu, E.; Vasile, B.S. Recent Advances in Magnetite Nanoparticle Functionalization for Nanomedicine. Nanomaterials 2019, 9, 1791. [Google Scholar] [CrossRef]
- Soenen, S.J.; Parak, W.J.; Rejman, J.; Manshian, B. Intra Cellular Stability of Inorganic Nanoparticles: Effects on Cytotoxicity, Particle Functionality, and Biomedical Applications. Chem. Rev. 2015, 115, 2109–2135. [Google Scholar] [CrossRef]
- Debye, P. Der Lichtdruck auf Kugeln von beliebigem Material. Ann. Phys. 1909, 335, 57–136. [Google Scholar] [CrossRef]
- Wiscombe, W.J. Mie Scattering Calculations: Advances in Technique and Fast, Vector-speed Computer Codes (No. NCAR/TN-140+STR); University Corporation for Atmospheric Research: Boulder, CO, USA, 1979. [Google Scholar]
- Complex Refractive Index for Fe3O4. Available online: https://refractiveindex.info/?shelf=main&book=Fe3O4&page=Querry (accessed on 15 January 2020).
- Rylander, M.N.; Feng, Y.; Bass, J.; Diller, K.R. Heat shock protein expression and damage optimization for laser therapy design. Lasers Surg. Med. 2007, 39, 734–746. [Google Scholar] [CrossRef]
- Duck, F.A. Physical Properties of Tissue: A Comprehensive Reference Book; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
(°C) | mm | mm | mm | |||
|---|---|---|---|---|---|---|
(×1014/mL) | (mm3) | N () (×1014/mL) | (mm3) | N () (×1014/mL) | (mm3) | |
| 70 | (5.68%) | 2.95 (0.89) | (0.06%) | 20.94 (1.71) | (0.002%) | 44.00 (2.19) |
| 85 | (8.17%) | 15.30 (1.54) | (0.09%) | 128.45 (3.13) | (0.003%) | 347.17 (4.36) |
| 100 | (10.6%) | 24.43 (1.80) | (0.13%) | 256.20 (3.94) | (0.004%) | 998.31 (6.20) |
| Tissue | Coefficients, (m) | Refractive Index, (1) | |
|---|---|---|---|
| Absorption, | Reduced Scattering, | n | |
| Fat [35] | 3 | 950 | 1.455 |
| Gland [35] | 6 | 1100 | 1.4 |
| Muscle [34] | 23 | 130 | 1.37 |
| Tumor [36] | 7 | 1400 | 1.37 |
| Tissue | Specific Capacity Heat | Thermal Conductivity | Density | Metabolic Heat | Blood Perfusion |
|---|---|---|---|---|---|
| c [J (kg K)] | [W (mK)] | [kg m] | [W m] | [s] | |
| Fat | 2348 | 0.21 | 911 | 400 | 0.0002 |
| Gland | 2960 | 0.48 | 1041 | 700 | 0.0005 |
| Muscle | 3421 | 0.48 | 1090 | 700 | 0.0008 |
| Tumor | 3770 | 0.48 | 1050 | 8720 | 0.0001 |
| Blood | 3617 | - | 1050 | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeboah, I.B.; Hatekah, S.W.K.; Konku-Asase, Y.K.; Yaya, A.; Kan-Dapaah, K. Destruction of Fibroadenomas Using Photothermal Heating of Fe3O4 Nanoparticles: Experiments and Models. Appl. Sci. 2020, 10, 5844. https://doi.org/10.3390/app10175844
Yeboah IB, Hatekah SWK, Konku-Asase YK, Yaya A, Kan-Dapaah K. Destruction of Fibroadenomas Using Photothermal Heating of Fe3O4 Nanoparticles: Experiments and Models. Applied Sciences. 2020; 10(17):5844. https://doi.org/10.3390/app10175844
Chicago/Turabian StyleYeboah, Ivan B., Selassie Wonder King Hatekah, Yvonne Kafui Konku-Asase, Abu Yaya, and Kwabena Kan-Dapaah. 2020. "Destruction of Fibroadenomas Using Photothermal Heating of Fe3O4 Nanoparticles: Experiments and Models" Applied Sciences 10, no. 17: 5844. https://doi.org/10.3390/app10175844
APA StyleYeboah, I. B., Hatekah, S. W. K., Konku-Asase, Y. K., Yaya, A., & Kan-Dapaah, K. (2020). Destruction of Fibroadenomas Using Photothermal Heating of Fe3O4 Nanoparticles: Experiments and Models. Applied Sciences, 10(17), 5844. https://doi.org/10.3390/app10175844





