Abstract
The incorporation of Si16 nanoclusters into the pores of pillared graphene on the base of single-walled carbon nanotubes (SWCNTs) significantly improved its properties as anode material of Li-ion batteries. Quantum-chemical calculation of the silicon-filled pillared graphene efficiency found (I) the optimal mass fraction of silicon (Si)providing maximum anode capacity; (II) the optimal Li: C and Li: Si ratios, when a smaller number of C and Si atoms captured more amount of Li ions; and (III) the conditions of the most energetically favorable delithiation process. For 2D-pillared graphene with a sheet spacing of 2–3 nm and SWCNTs distance of ~5 nm the best silicon concentration in pores was ~13–18 wt.%. In this case the value of achieved capacity exceeded the graphite anode one by 400%. Increasing of silicon mass fraction to 35–44% or more leads to a decrease in the anode capacity and to a risk of pillared graphene destruction. It is predicted that this study will provide useful information for the design of hybrid silicon-carbon anodes for efficient next-generation Li-ion batteries.
1. Introduction
Silicon-based materials are considered as one of the most potential anode materials for LIB because of their high theoretical capacity of 4200 mAh∙g−1, for Li4.4Si [1,2,3,4,5,6,7,8,9,10]. There are various types of Li-Si intermetallic states. Each of the Li-Si phases has a corresponding capacity, for example, Li1.71Si (1632 mAh∙g−1), Li2.33Si (2224 mAh∙g−1), Li3.25Si (3100 mAh∙g−1). The applicability of particular intermetallic Li-Si states as a LIB anode is determined by the smallest volume change during the lithiation/delithiation process [11]. The phases Li1.71Si, Li2.33Si, Li3.25Si are applicable to both the crystalline and amorphous forms of silicon (monocrystalline and polycrystalline). In amorphous form, silicon can also form other intermetallic states, such as Li3.38Si [12]. The disadvantage of the silicon anode material is its instability caused by significant change in volume that mayincrease to 300% during the process of lithiation/delithiation. This leads to mechanical destruction, and consequently, to a decrease in capacity, electrical conductivity, and to the formation of SEI—solid electrolyte interphase [13,14,15]. This problem can be solved by application of the so-called buffer electroconductive frame that can ensure the stability of the anode material volume. At the same time the buffer frame must have high mechanical strength, low resistivity, scalability, and high porosity [16,17,18,19,20]. As a material for such buffer frame it can be used a pillared graphene—hybrid carbon material on the base of monolayer graphene covalently bonded to vertically oriented SWCNTs [21,22,23,24,25,26,27,28]. A particular feature of the pillared graphene atomic structure is high porosity. The pillared graphene has a highly developed surface that allows to fill its pores with atoms of various chemical elements. It is already used for storing atomic gases and lithium ions [29] and serves as the basis for effective gas filter membranes [30,31]. The theoretical study of pillared graphene as anode material is required for the search of an effective silicon concentration in pores.
This work is devoted to a quantum-chemical study of the lithiation/delithiation process in films of pillared graphene filled with silicon clusters in order to evaluate the effectiveness of its application as a buffer frame of LIB anode material.
2. Materials and Methods
To form stable, energy-efficient atomic supercells of 2D pillared graphene without and with silicon clusters in its pores, the SCC-DFTB (the self-consistent charge density functional tight-binding) method was applied [32]. This method allows calculating the energy and electronic characteristics of structures with supercells consisting of several hundred and even thousands of atoms. This method has been successfully implemented in the software packages dftb+ [33] and Kvazar-Mizar [34].
For quantum-chemical study of the lithiation process, molecular dynamics (MD) with the reactive force-field ReaxFF [12] was implemented in the LAMMPS program [35]. Previously, this force field was successfully applied to establish the relationship between the LIB durability and the rate of lithiation/delithiation in the LIB with anode material on the base of silicon, silicon dioxide, and alumina [36,37,38]. The modified ReaxFF force field [39] allowedto describe the mechanism of Li ions interaction in ideal and defective carbon materials. Also, simulation of the lithiation process of Si and Si-C materials by the modified ReaxFF force field made possible the design of the new anode material with the capacity of 1345 mAh∙g−1 [40]. The application of this force field was caused by the large number of atoms in the supercell and by the necessity in molecular dynamics. The limitation of the SCC DFTB method and the ReaxFF force field is absent of parameterizations for wide group of atoms, but at the present time this problem is being actively solved [41,42,43]. In this work, the time step was 0.5 fs, the temperature of 300 K was maintained by a Nose-Hoover thermostat with a damping parameter of 0.01 fs−1.
For simulation of delithiation process and for evaluation of its efficiency, the profile of the potential barrier of lithium atom elimination from the carbon frame and silicon clusters was calculated. It also allowed to find the binding energy. It was realized by the high-precision DFT method in the Quantum Espresso 6.5 software package [44]. Since the DFT method is the most resource-consuming and calculation by this method is limited by a hundred of atoms, we used only parts of the considered supercells. In the frame of DFT, the BFGS method (Broyden-Fletcher-Goldfarb-Shanno) and the 25 × 25 × 1 Monkhorst–Pack sampling was applied.
3. Results and Discussion
3.1. Atomistic Models
The atomistic model of pillared graphene represents two sheets of monolayer graphene with SWCNTs (9,9) of 1.2 nm in diameter between them. These tubes were chosen for two reasons: (1) The tubes of this diameter are being synthesized most often; (2) earlier it was shown that the pillared graphene with tubes (9,9) is the most energetically favorable [45]. Two models that differ in the height of the tubes were built (Figure 1). Figure 1a,b shows the supercells of the model I containing 2760 atoms, Figure 1c shows the supercell of model II with 2976 atoms. The translation vectors of the supercells were 49.3 Å in the X direction and 42.6 Å in the Y direction. During the building of the pillared grapheme supercell the nanotube with open edges was chemically bonded to the graphene sheet that had the cut hole corresponding to the diameter of the attached CNT. The resulting structure matched with experimental data on pillared graphene [46]. The heat of formation of the pillared grapheme supercells was 1.2–142 kcal∙mol−1·atom regardless of the CNTs length. Six pairs of penta/heptagons, as well as three octagons, were formed in the graphene–SWCNT contact region.
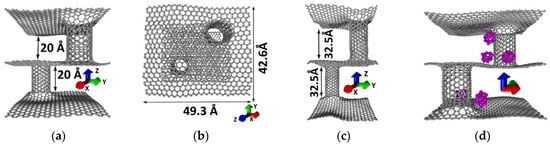
Figure 1.
Pillared graphene: (a) supercell of model I—with short tube; (b) view from above; (c) supercell of model II—with long tube; (d) supercell of model I with silicon clusters Si16 (purple color).
Further, the pores of the pillared graphene were filled with Si16 clusters. As was shown earlier, these clusters had the highest stability among silicon ones [47,48]. Such anode samples have been already synthesized in the world. For example in [46] real samples of carbon–silicon composite on the base of monolayer pillared graphene were obtained by the method of single-stage chemical vapor deposition (CVD) with the incorporation of precursor gases mixture (H2, C2H4). The layer of amorphous silicon was added to already grown 3D-carbon nanostructure by deposition and evaporation.The pores of pillared graphene were filled with Si16 clusters randomly with the condition that the distance between the clusters and pillared graphene would be at least 3.5–3.6 Å. The number of clusters varied from 5 to 59. After optimization of the supercell with silicon the distance between the carbon framework and silicon clusters was ~3.3 Å. Here, the clusters changed their position in the pores. The clusters are located homogeneously, partially “stuck” at the area of the junction between SWCNTs and graphene near non-hexagonal elements, while the rest was “stuck” at the walls of SWCNTs. There are no clusters inside the tubes. Encapsulation of silicon clusters inside tubes is energetically unfavorable; therefore, filling was observed only in the pores of pillared graphene. Figure 1d shows the supercell with five silicon clusters.
3.2. Lithiation
Evaluation of the anode efficiency is related to its capacity and the formation of the SEI layer. This work does not discuss the formation of the SEI layer, however, in the experimental works [46,49], where similar topologies of carbon and carbon-silicon anodes were studied, the formation of an SEI layer was observed in the first charge/discharge cycles. During subsequent cycling the anode capacity is reduced by 8% (10 cycles for the carbon-silicon anode) and by 0.74% (5 cycles for the carbon anode). We assume that the formation of the SEI layer at the interface of the studied anode will have a similar character because of the similarity of the anode material. To evaluate the efficiency of the anode material (excluding the SEI) we have successively performed numerical experiments on the lithiation of the composite with various amounts of silicon clusters in the pores of the pillared graphene. To find the optimal concentration of the silicon mass fraction in the LIB anode material, which would ensure the maximum capacity, we considered the filling of the carbon frame with Si16 clusters in amount of 5 to 59. For the model I (Figure 1a), this filling corresponded to the range 6.34–44.5wt.% silicon of the total mass, for model II (Figure 1c)—to the range of 5.9–42.6 wt.%. Each numerical experiment of lithiation with a different mass fraction of silicon in the composite was performed according to the following algorithm. At the first stage, the composite with a certain number of silicon clusters was completely filled with positively charged lithium ions according to the rule—the distance between the framework and the neighboring lithium ion should be at least 3.2Å.By the LAMMPS software package we removed one electron from lithium atoms to form lithium ions. The required number of electrons was transferred to the carbon-silicon frame so that the total charge was zero. In the second step the supercell was optimized by the molecular dynamics method. At the third stage, the capacity of the composite was calculated. The capacity was calculated based on the amount of lithium ions that interact with silicon and carbon. Further, according to the Faraday principle [50], the capacities of Li-Si and Li-C were calculated separately, and then their capacities were summed on the basis of their mass fractions. This approach was applied in [12], where it was studied the intercalation of lithium into a layer of silicon and silicon oxide “wrapped” in a carbon framework that could retain the silicon volume.
The following electrochemical reactions in the anode were studied:
Figure 2a demonstrates the first step of the algorithm at the example of model I, where there are only five silicon clusters of Si16 in the composite pores (purple color) and the entire free space of the pores is filled with lithium ions (green color). The number of lithium ions incorporated into the cell was corresponded to maximal Li-Si and Li-C bond to assess the capacity of the anode. A numerical experiment in this case showed that lithium ions “settled” on the carbon frame and on the silicon atoms. Here, the carbon frame demonstrated mechanical stability, while silicon clusters did not. Si16 clusters lost their initial shape and, in some cases, lost their chemical bond with the carbon framework. When the chemical bond is lost, there is no electronic contact either, this is due to the low concentration of silicon clusters. Figure 2b clearly shows that a layer or several layers of lithium have been appeared between silicon and carbon. In this case, the capacity was 1378.6 mAh∙g−1 that exceeds such value for the graphite anode (372 mAh∙g−1) [51].
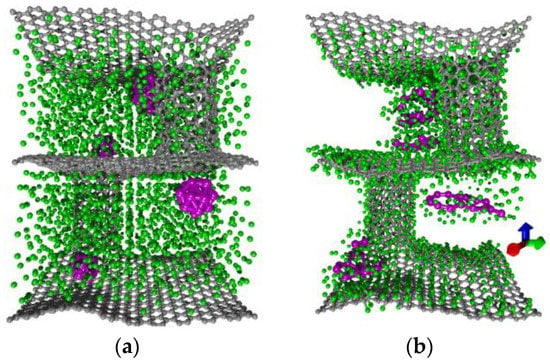
Figure 2.
Lithiation of anode material on the example of model I with five Si16 clusters: (a) initial configuration; (b) result of numerical simulation.
Some other cases of filling composite pores with silicon clusters are shown in Figure 3. There are atomic structures of model I with 18 Si16 clusters (Figure 3a), 36 Si16 clusters (Figure 3b), and 59 Si16 clusters (Figure 3c) obtained by numerical simulation of supercells lithiation. It is clearly seen that when the filling of pores with silicon reached maximum, the carbon frame was strongly deformed, but did not destruct. On the base of numerical simulation we can conclude that the maximum mass fraction of silicon has been reached. At the same time, the carbon frame seemed to “compensate” the dramatic increase in the volume of the anode material. A further increase in the mass fraction of silicon would inevitably lead to the destruction of the carbon frame and to an uncontrolled increase in the volume of the anode material. For the case (c) of Figure 3 the lithium ions covered only the surface of the silicon clusters. Clusters that fill all the pores of the carbon frame prevented intercalation of lithium ions.
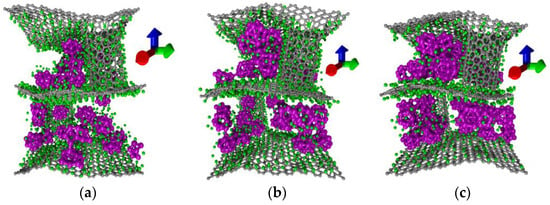
Figure 3.
Lithiation of anode material on the example of model I with: (a) with 18 clusters of Si16; (b) with 36 clusters of Si16; (c) with 59 clusters of Si16.
Detailed data on all numerical experiments for model I with different mass fractions of silicon are presented in Table 1 that shows the number of lithium ions and silicon atoms, Si16 clusters, the mass fraction of silicon, and such important parameters for the anode material as the ratio between lithium, carbon, and silicon atoms, as well as the capacity of the anode. The Li:C and Li:Si ratios show how lithium was distributed on the surfaces of the carbon frame pores and the silicon clusters. For model 1, the maximum number of lithium ions intercalated when the pores contain 5, 8, 11 silicon clusters. The coordination ratio was 1:2, i.e., every 2 carbon atoms imbibes 1 ion of lithium on average. As the mass fraction of silicon increases, this ratio changes for the worse. Two lithium ions can only bind to 5 carbon atoms, and in the case of a maximum concentration of silicon, they can bind only to 9 carbon atoms. A similar situation was observed for silicon. Maximum lithium adsorption, when each silicon atom imbibes 4 lithium ions, occurred only when amount of Si clusters was 5 and 8. In this case, the clusters had the largest surface for contact with lithium. As the mass fraction of silicon increased, the cluster structure was transformed and the surface in contact with lithium decreased. From Table 1 it is seen that at 13–20 wt.% each silicon atom imbibed 2 lithium ions, at 32.8 wt.%—only one lithium ion, and then less than one. Analyzing the simultaneous changes in the Li:C and Li:Si ratios with an increase in the mass fraction of silicon, we can already assume that composites with a silicon fraction of ~6–20 wt.% is the most effective. Note that the rest of the lithium ions, which are not adsorbed on either carbon or silicon, filled the free volume of pores. On the other hand, another important indicator of performance is capacity. As mentioned above, the anode capacity was calculated according to the Faraday principle. For example, for the case of 9.8 wt.% (1403.4 mAh∙g−1, model I), the capacity of Li-Si was ~2724.5 mAh∙g−1, but we had 9.8% of that capacity, that is, 267 mAh∙g−1. Pillared graphene contributed most of the capacity (~1136.4 mAh∙g−1). It is known that the theoretical capacities of graphene and CNTs are the same and equal to 1116 mAh∙g−1 [52], respectively, pillared graphene of any form and topology must have the same capacity. In our work, we obtained a pure pillared graphene capacity of about 1136.4mAh∙g−1 (1.88% error with a theoretical capacity). Numerical experiments found that for the model I the biggest capacity values were reached at 9.8–13 wt.% of silicon, and maximum capacity equaled to 1507.7 mAh∙g−1 (Table 1). The smallest capacity value of 922.4 mAh∙g−1 was found in the case of the maximum concentration of silicon—44.5 wt.%. Indeed, this capacity value is even less than the capacity of pristine graphene. It can be explained by the fact that a large amount of silicon “screens” lithium, whose ions can be intercalated only on the surface of silicon clusters and on some free areas of pillared graphene (Figure 3c). Comparison with other types of carbon frameworks based on graphene and CNT shows the advantages of using a pillared graphene as an anode material due to mechanical strength and porosity of the atomic mesh. For example, [12] specified the capacity value equal to 1147 mAh∙g−1 for the case of a cell with a wrapped graphene sheet. During intercalation of lithium ions, the graphene sheet opened under the action of silicon that increased its volume. Application of large-diameter CNT as a frame with silicon located inside the tube resulted the capacity at the level of 1374 mAh∙g−1.

Table 1.
Parameters of model I as the battery anode material.
As the Table 1, Table 2 provides detailed information for models II with different mass fraction of silicon. Reasoning similarly to model I, we can conclude that composites with the silicon fraction of ~9–18.4 wt.% would be the most effective. In this range, the simultaneous change in the Li:C and Li:Si ratios provides the biggest capture of lithium ions by carbon and silicon atoms. The optimal mass fraction of silicon is ~12–18.4 wt.%, since the maximum capacity values were observed in this case. Figure 4 shows the change in the capacity of a battery based on the composite versus the mass fraction of silicon. The optimal mass fraction of silicon for both models of the composite was in the range of 12–18 wt.%. It can be seen from the graphs in Figure 4 that when the mass fraction of silicon reaches 30wt.% and continues to increase, the capacity begins to decrease rapidly that drops battery efficiency. It is also confirmed by the data in the table for the Li:C and Li:Si ratios. Mass fraction of ~30 wt.% is critical; in this case the number of imbibed lithium ions by carbon and silicon sharply decreases.

Table 2.
Parameters of model II as the battery anode material.
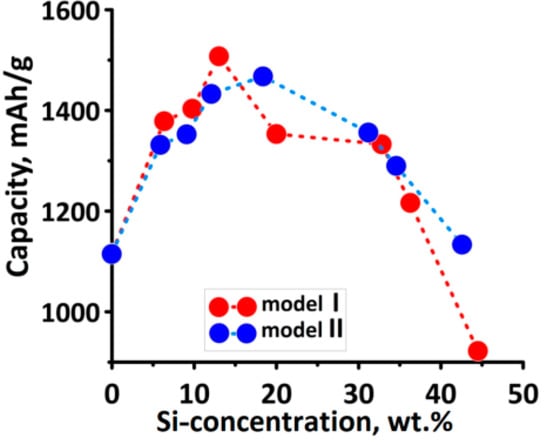
Figure 4.
Change of the capacity vs. the concentration of silicon in the anode.
3.3. Delithiation
The study of the delithiation process was focused on the determination of the binding energy between the lithium ion and the components of the anode material composite. Therefore, we calculated the profiles of the potential barrier for the detachment of the lithium ion via high-precision DFT method. Since the supercell of the composite contained several hundred atoms, it was built several cells containing a single lithium ion and a fragment of the composite: graphene, nanotube (9,9), and a silicon cluster. During the interaction between a lithium ion and a composite fragment the equilibrium structure of such compound was revealed by optimization of the supercell atomic structure. For the graphene–Li cell, the Monkhorst–Pack partition was 25×25×1, for the SWCNT-cell—1×1×65 and for the Si-Li cell—10×10×10. Then the lithium ion was moved away from the composite fragment to the distance of 10 Å with a step of 0.5 Å. At each step the cell energy and the binding energy between lithium and each of the composite fragments were calculated. Figure 5 shows the graphs of binding energy. Thee limination of the Li atom from the outer surface of the nanotube required the least amount of energy, about 0.544 eV, while the lithium ion interacted with three atoms of the tube. These results correspond to [53] where the binding energy between tube (9,9) and lithium ion was in the range of 0.5–0.6 eV. The binding energy of lithium and graphene was bigger and equaled to 1.09 eV, while the lithium ion interacted with six graphene atoms. This value is equal to twice the value of the binding energy between lithium and the SWCNT. The highest binding energy was found for the interaction of lithium with silicon and silicon clusters: for Li-Si and Li-Si16 compounds it was equaled to 1.78 eV and 1.92 eV, respectively. The obtained results are in good agreement with the works [54,55]. Thus, the most energy-consuming process is the elimination of lithium from silicon structures.
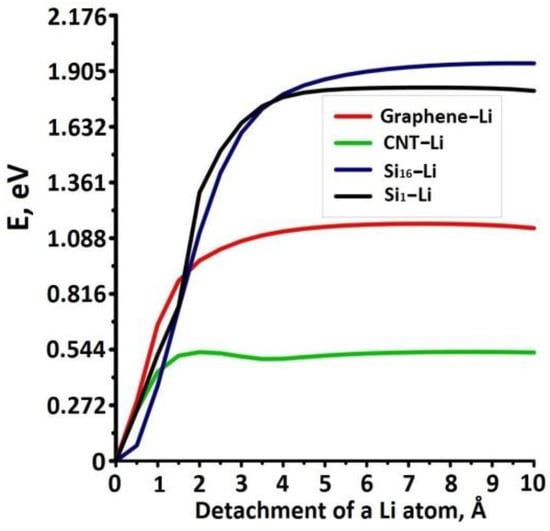
Figure 5.
Binding energy if Li atom with components of the anode material.
4. Conclusions
Quantum-chemical calculation search of the most effective anode material on the base of silicon-filled pillared graphene was performed. The search was carried out of several positions: (I) the optimal mass fraction of silicon (Si) providing maximum anode capacity, (II) the optimal Li:C and Li:Si ratios, when a smaller number of C and Si atoms imbibed more amount of Li ions, and (III) the conditions of the most energetically favorable delithiation process. It was found that for 2D-pillared graphene with sheets distance of 2–3 nm and step between SWCNTs ~5 nm the optimal concentration of silicon in the composite’s pores was ~13–18 wt.%. Under such conditions the achieved capacity was ~1500 mAh∙g−1. For such a small mass fraction of silicon, the amount of lithium intercalated into silicon was ~27% of the lithium captured by the carbon cage for model I and ~45% for model II.
In general, according to our calculations, an increase in the volume of pillared grapheme pores did not lead to an improvement in the quality of the anode material. For the first model with short SWCNT, the maximum capacity was 10% higher in comparison to the second model with long SWCNT. The first model is also supported by the significantly lower mass fraction of silicon (13 wt.%) and the small fraction of the imbibed lithium ions. This is very important for the process of delithiation, since, as was shown Section 3.3, the most energy-consuming is the detachment of lithium from silicon, and the most favorable is the detachment from the SWCNT. Successful elimination of the largest number of lithium ions from the anode material will ensure the battery′s durability and a large number of charging/discharging cycles. The advantages of the first model are explained by the fact that the main role in lithiation process is played by the surface rather than by the volume of pillared grapheme pores, as for any porous material.
The capacity of the considered in this paper anode material is higher by 400% in comparison to the widely used graphite anode. This allows to predict great prospects for the application of the anode material based on the composite of pillared graphene and silicon in modern and future batteries.
Author Contributions
Conceptualization, O.E.G.; methodology, O.E.G.; funding acquisition, D.A.K.; investigation, O.E.G., D.A.K.; writing—original draft preparation, D.A.K.; writing—review and editing, O.E.G.; supervision, O.E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the RFBR grant (project No. 19-32-90160).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, G.; Xu, B.; Shi, J.; Wu, M.; Su, H.; Ouyang, C.Y. New insights into Li diffusion in Li-Si alloy for Si anode materials: Role of Si microstructure. Nanoscale 2019, 11, 14042–14049. [Google Scholar] [CrossRef] [PubMed]
- Dash, R.; Pannala, S. RETRACTED ARTICLE: Theoretical Limits of Energy Density in Silicon-Carbon Composite Anode Based Lithium Ion Batteries. Sci. Rep. 2016, 6, 27449. [Google Scholar] [CrossRef] [PubMed]
- Nazir, A.; Le, H.T.T.; Min, C.-W.; Kasbe, A.; Kim, J.; Jin, C.-S.; Park, C.-J. Coupling of conductive Ni3(2,3,6,7,10,11-hexaiminotriphenylene)2 metal-organic framework with silicon nanoparticles for use in high-capacity lithium-ion batteries. Nanoscale 2019, 12, 1629–1642. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; Lu, L.; Wu, B.; Fan, X.; Yang, Y.; Li, J.; Lin, Y.; Li, Y.; Huang, Z.; Lu, J. Dramatic improvement enabled by incorporating thermal conductive TiN into Si-based anodes for lithium ion batteries. Energy Storage Mater. 2019, 29, 367–376. [Google Scholar] [CrossRef]
- Hosoya, K.; Kamidaira, T.; Tsuda, T.; Imanishi, A.; Haruta, M.; Doi, T.; Inaba, M.; Kuwabata, S. Lithium-Ion Battery Performance Enhanced by Combination of Si Thin Flake Anode and Binary Ionic Liquid System. Adv. Mater. 2020, 1, 625–631. [Google Scholar] [CrossRef]
- Tong, L.; Wang, P.; Fang, W.; Guo, X.; Bao, W.; Yang, Y.; Shen, S.; Qiu, F. Interface engineering of silicon/carbon thin film anode for high-rate lithium-ion batteries. ACS Appl. Mater. Interfaces 2020, 12, 29242–29252. [Google Scholar] [CrossRef]
- Hapuarachchi, S.N.S.; Wasalathilake, K.; Siriwardena, D.P.; Nerkar, J.; Chen, H.; Zhang, S.; Liu, Y.; Zheng, J.; Golberg, D.; O’Mullane, A.; et al. Interfacial Engineering with Liquid Metal for Si-based Hybrid Electrodes in Lithium Ion Batteries. ACS Appl. Energy Mater. 2020, 3, 5147–5152. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Ivanichkina, K.A.; Katin, K.P.; Maslov, M.M. Computer Test of a Modified Silicene/Graphite Anode for Lithium-Ion Batteries. ACS Omega 2020, 5, 13207–13218. [Google Scholar] [CrossRef]
- Yan, M.-Y.; Li, G.; Zhang, J.; Tian, Y.-F.; Yin, Y.-X.; Zhang, C.-J.; Jiang, K.-C.; Xu, Q.; Li, H.-L.; Guo, Y.-G. Enabling SiOx/C Anode with High Initial Coulombic Efficiency through a Chemical Pre-Lithiation Strategy for High Energy Density Lithium-Ion Batteries. ACS Appl. Mater. Interfaces 2020, 12, 27202–27209. [Google Scholar] [CrossRef]
- Yin, Y.; Arca, E.; Wang, L.; Yang, G.; Schnabel, M.; Cao, L.; Xiao, C.; Zhou, H.; Liu, P.; Nanda, J.; et al. Non-Passivated Silicon Anode Surface. ACS Appl. Mater. Interfaces 2020, 12, 26593–26600. [Google Scholar] [CrossRef]
- Dimov, N.; Fukuda, K.; Umeno, T.; Kugino, S.; Yoshio, M. Characterization of carbon-coated silicon. Power Sour. 2003, 114, 88–95. [Google Scholar] [CrossRef]
- Yeo, B.C.; Jung, H.; Lee, H.W.; Yun, K.-S.; Kim, H.; Lee, K.-R.; Han, S.S. Atomistic Simulation Protocol for Improved Design of Si–O–C Hybrid Nanostructures as Li-Ion Battery Anodes: ReaxFF Reactive Force Field. J. Phys. Chem. C 2017, 121, 23268–23275. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Wang, D. Si/TiSi2 Heteronanostructures as High-capacity Anode Material for Li Ion Batteries. Nano Lett. 2010, 10, 860–863. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Kong, X.; Usman, I.; Xie, X.; Liang, S.; Cao, G.; Pan, A. Rational design of Pea-pod structure of SiOx/C in carbon nanofibers as high-performance anode for lithium ion batteries. Inorg. Chem. Front. 2020, 7, 1762–1769. [Google Scholar] [CrossRef]
- Ma, D.; Cao, Z.; Hu, A. Si-Based Anode Materials for Li-Ion Batteries: A Mini Review. Nano-Micro Lett. 2014, 6, 347–358. [Google Scholar] [CrossRef]
- Xie, C.; Xu, Q.; Sari, H.M.K.; Li, X. Elastic buffer structured Si/C microsphere anodes via polymerization-induced colloid aggregation. Chem. Commun. 2020, 56, 6770–6773. [Google Scholar] [CrossRef]
- Zhang, W.; Fang, S.; Wang, N.; Zhang, J.; Shi, B.; Yu, Z.; Yang, J. A compact silicon–carbon composite with an embedded structure for high cycling coulombic efficiency anode materials in lithium-ion batteries. Inorg. Chem. Front. 2020, 7, 2487–2496. [Google Scholar] [CrossRef]
- Kim, S.; Yoo, H.; Kim, H. Chemically anchored two-dimensional-SiOx/zero-dimensional-MoO2 nanocomposites for high-capacity lithium storage materials. RSC Adv. 2020, 10, 21375–21381. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Yu, Q.; Liu, Z.; Yu, C.; Wu, L.; Zhou, L.; Liqiang, M. Polydopamine Sacrificial Layer Mediated SiOx/C@C Yolk@Shell Structure for Durable Lithium Storage. Mater. Chem. Front. 2020, 4, 1656–1663. [Google Scholar] [CrossRef]
- Su, W.; Wan, R.; Liang, Y.; Zuo, Y.; Tang, Y. A Novel 3D Porous Pseudographite/Si/Ni Composite Anode Materials Fabricated by a Facile method. Dalton Trans. 2020, 49, 7166–7173. [Google Scholar] [CrossRef]
- Yang, X.; Yu, D.; Cao, B.; To, A.C. Ultrahigh Thermal Rectification in Pillared Graphene Structure with Carbon Nanotube–Graphene Intramolecular Junctions. ACS Appl. Mater. Interfaces 2017, 9, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Banda, H.; Périé, S.; Daffos, B.; Taberna, P.-L.; Dubois, L.; Crosnier, O.; Simon, P.; Lee, D.; Paepe, G.-D.; Duclairoir, F. Sparsely Pillared Graphene Materials for High Performance Supercapacitors: Improving Ion Transport and Storage Capacity. ACS Nano 2019, 13, 1443–1453. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Zhong, Y.; Zhang, X.; He, Y.; Wang, G. Percolating Film of Pillared Graphene Layer Integrated with Silver Nanowire Network for Transparent and Flexible Supercapacitors. Langmuir 2018, 34, 15245–15252. [Google Scholar] [CrossRef]
- Bi, L.; Yin, J.; Huang, X.; Wang, Y.; Yang, Z. Graphene pillared with hybrid fullerene and nanotube as a novel 3D framework for hydrogen storage: A DFT and GCMC study. Int. J. Hydrogen Energy 2020, 45, 17637–17648. [Google Scholar] [CrossRef]
- Mert, H.; Deniz, C.U.; Baykasoglu, C. Monte Carlo simulations of hydrogen adsorption in fullerene pillared graphenenanocomposites. Mol. Simul. 2020, 46, 650–659. [Google Scholar] [CrossRef]
- Duan, K.; Li, Y.; Li, L.; Hu, Y.; Wang, X. Pillared graphene as excellent reinforcement for polymer-based nanocomposites. Mater. Des. 2018, 147, 11–18. [Google Scholar] [CrossRef]
- Wang, C.-H.; Fang, T.-H.; Sun, W.-L. Mechanical properties of pillared-graphene nanostructures using molecular dynamics simulations. J. Phys. D Appl. Phys. 2014, 47, 405302. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Shmygin, D.S.; Zhang, G.; Glukhova, O.E. Controlling the electronic properties of 2D/3D pillared graphene and glass-like carbon via metal atom doping. Nanoscale 2019, 11, 16414–16427. [Google Scholar] [CrossRef]
- Dimitrakakis, G.K.; Tylianakis, E.; Froudakis, G.E. Pillared Graphene: A New 3-D Network Nanostructure for Enhanced Hydrogen Storage. Nano Lett. 2008, 8, 3166–3170. [Google Scholar] [CrossRef]
- Wesołowski, R.P.; Terzyk, A.P. Pillared graphene as a gas separation membrane. Phys. Chem. Chem. Phys. 2011, 13, 17027–17029. [Google Scholar] [CrossRef]
- Wesołowski, R.P.; Terzyk, A.P. Dynamics of effusive and diffusive gas separation on pillared graphene. Phys. Chem. Chem. Phys. 2016, 18, 17018–17023. [Google Scholar] [CrossRef] [PubMed]
- Aradi, B.; Hourahine, B.; Frauenheim, T. DFTB+, a Sparse Matrix-Based Implementation of the DFTB Method. J. Phys. Chem. A 2007, 111, 5678–5684. [Google Scholar] [CrossRef] [PubMed]
- DFTB+. Available online: https://www.dftbplus.org/ (accessed on 21 July 2020).
- Glukhova, O.E. Molecular Dynamics as the Tool for Investigation of Carbon Nanostructures Properties. In Thermal Transport in Carbon-Based Nanomaterials, 1st ed.; Zhang, G., Ed.; Elsevier: Oxford, UK, 2017; pp. 267–289. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.-M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. npj Comput. Mater. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Sun, Q.; Lu, K.; Kubo, M.; Xu, J. Development of a Transferable ReaxFF Parameter Set for Carbon- and Silicon-Based Solid Systems. J. Phys. Chem. C 2020, 124, 10007–10015. [Google Scholar] [CrossRef]
- Hong, S.; van Duin, A.C.T. Atomistic-Scale Analysis of Carbon Coating and Its Effect on the Oxidation of Aluminum Nanoparticles by ReaxFF-Molecular Dynamics Simulations. J. Phys. Chem. C 2016, 120, 9464–9474. [Google Scholar] [CrossRef]
- Raju, M.; Ganesh, P.; Kent, P.R.C.; van Duin, A.C.T. Reactive Force Field Study of Li/C Systems for Electrical Energy Storage. J. Chem. Theory Comput. 2015, 11, 2156–2166. [Google Scholar] [CrossRef]
- Wasalathilake, K.; Hapuarachchi, S.; Zhao, Y.; Fernando, J.F.S.; Chen, H.; Nerkar, J.; Golberg, D.; Zhang, S.; Yan, C. Unveiling the Working Mechanism of Graphene Bubble Film/Silicon Composite Anodes in Li-Ion Batteries: From Experiment to Modelling. ACS Appl. Energy Mater. 2020, 3, 521–531. [Google Scholar] [CrossRef]
- Li, Y.; Qi, Y. Transferable Self-Consistent Charge Density Functional Tight-Binding Parameters for Li–Metal and Li-Ions in Inorganic Compounds and Organic Solvents. J. Phys. Chem. C 2018, 122, 10755–10764. [Google Scholar] [CrossRef]
- Oliveira, A.F.; Philipsen, P.; Heine, T. DFTB Parameters for the Periodic Table, Part 2: Energies and Energy Gradients from Hydrogen to Calcium. J. Chem. Theory Comput. 2015, 11, 5209–5218. [Google Scholar] [CrossRef]
- Shin, Y.K.; Sengul, M.Y.; Jonayat, A.S.M.; Lee, W.; Gomez, E.D.; Randall, C.A.; van Duin, A.C.T. Development of a ReaxFF reactive force field for lithium ion conducting solid electrolyte Li1+xAlxTi2−x(PO4)3 (LATP). Phys. Chem. Chem. Phys. 2018, 20, 22134–22147. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; BuongiornoNardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Slepchenkov, M.M.; Shmygin, D.S.; Zhang, G.; Glukhova, O.E. Controlling anisotropic electrical conductivity in porous graphene-nanotube thin films. Carbon 2020, 165, 139–149. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, L.; Zhang, C.; Casillas, G.; Sun, Z.; Yan, Z.; Ruan, G.; Peng, Z.; Raji, A.R.O.; Kittrell, C.; et al. A seamless three dimensional carbon nanotube graphene hybrid material. Nat. Commun. 2012, 3, 1–7. [Google Scholar] [CrossRef]
- Mahtout, S.; Belkhir, M.A. Structural, magnetic and electronic properties of Fe encapsulated by silicon clusters. Phys. Lett. A 2006, 360, 384–389. [Google Scholar] [CrossRef]
- Mahtout, S. Effect of Iron Atoms on the Properties οf Silicon Cage Clusters. Acta Phys. Pol. A 2013, 124, 688–694. [Google Scholar] [CrossRef]
- Wang, W.; Ruiz, I.; Ozkan, M.; Ozkan, C.S. Pillared graphene and silicon nanocomposite architecture for anodes of lithium ion batteries. In Proceedings of theSPIE NanoScience + Engineering 2014, San Diego, CA, USA, 17–21 August 2014. [Google Scholar]
- Wang, W.; Ruiz, I.; Guo, S.; Favors, Z.; Bay, H.H.; Ozkan, M.; Ozkan, C.S. Hybrid carbon nanotube and graphene nanostructures for lithium ion battery anodes. Nano Energy 2014, 3, 113–118. [Google Scholar] [CrossRef]
- Li, J.; Tritsaris, G.A.; Zhang, X.; Shi, B.; Yang, C.; Liu, S.; Yang, J.; Xu, L.; Yang, J.; Pan, F.; et al. Monolayer honeycomb borophene: A promising anode material with a record capacity for lithium-ion and sodium-ion batteries. J. Electrochem. Soc. 2020, 167, 090527. [Google Scholar] [CrossRef]
- Tritsaris, G.A.; Kaxiras, E.; Meng, S.; Wang, E. Adsorption and Diffusion of Lithium on Layered Silicon for Li-Ion Storage. Nano Lett. 2013, 13, 2258–2263. [Google Scholar] [CrossRef]
- Xiao, J.; Xu, W.; Wang, D.; Choi, D.; Wang, W.; Li, X.; Graff, G.L.; Liu, J.; Zhang, J.-G. Stabilization of Silicon Anode for Li-Ion Batteries. J. Electrochem. Soc. 2010, 157, A1047. [Google Scholar] [CrossRef]
- Yang, G.; Fan, X.; Liang, Z.; Xu, Q.; Zheng, W. Density functional theory study of Li binding to graphene. RSC Adv. 2016, 6, 26540–26545. [Google Scholar] [CrossRef]
- Liu, Y.; Yukawa, H.; Morinaga, M. First-principles study on lithium absorption in carbon nanotubes. Comput. Mater. Sci. 2004, 30, 50–56. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).