Failure Warning at the End of Service-Life of Lead–Acid Batteries for Backup Applications
Abstract
Featured Application
Abstract
1. Introduction
2. Linear Superposition-Voltage Aging Model
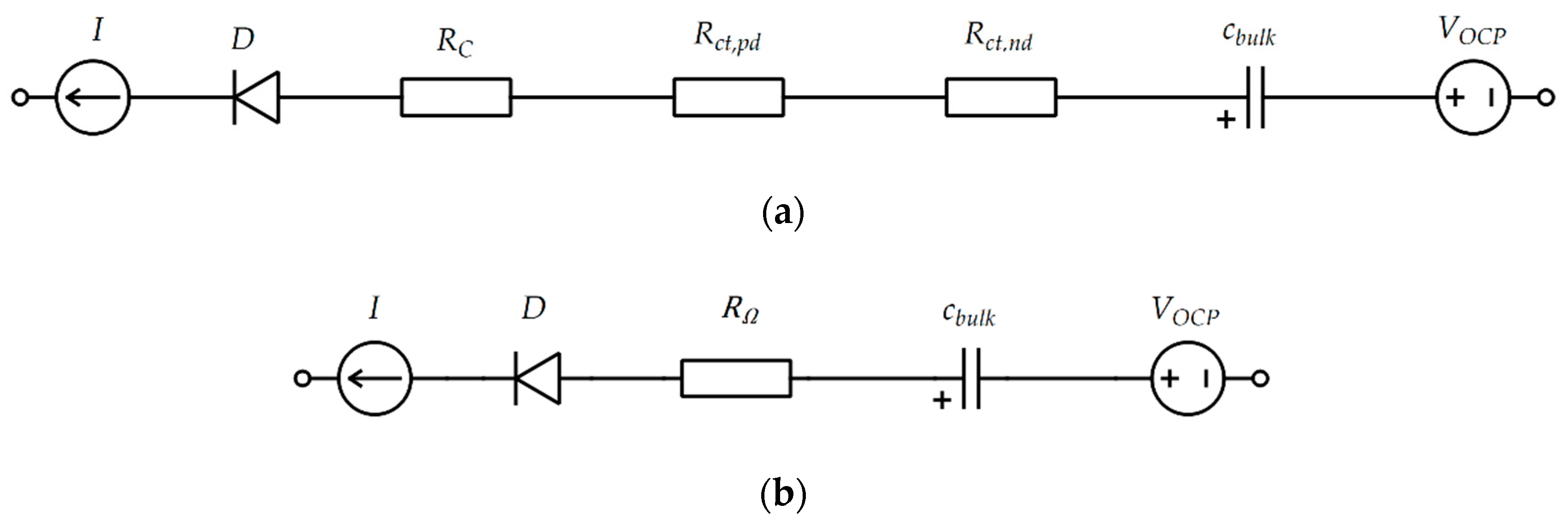
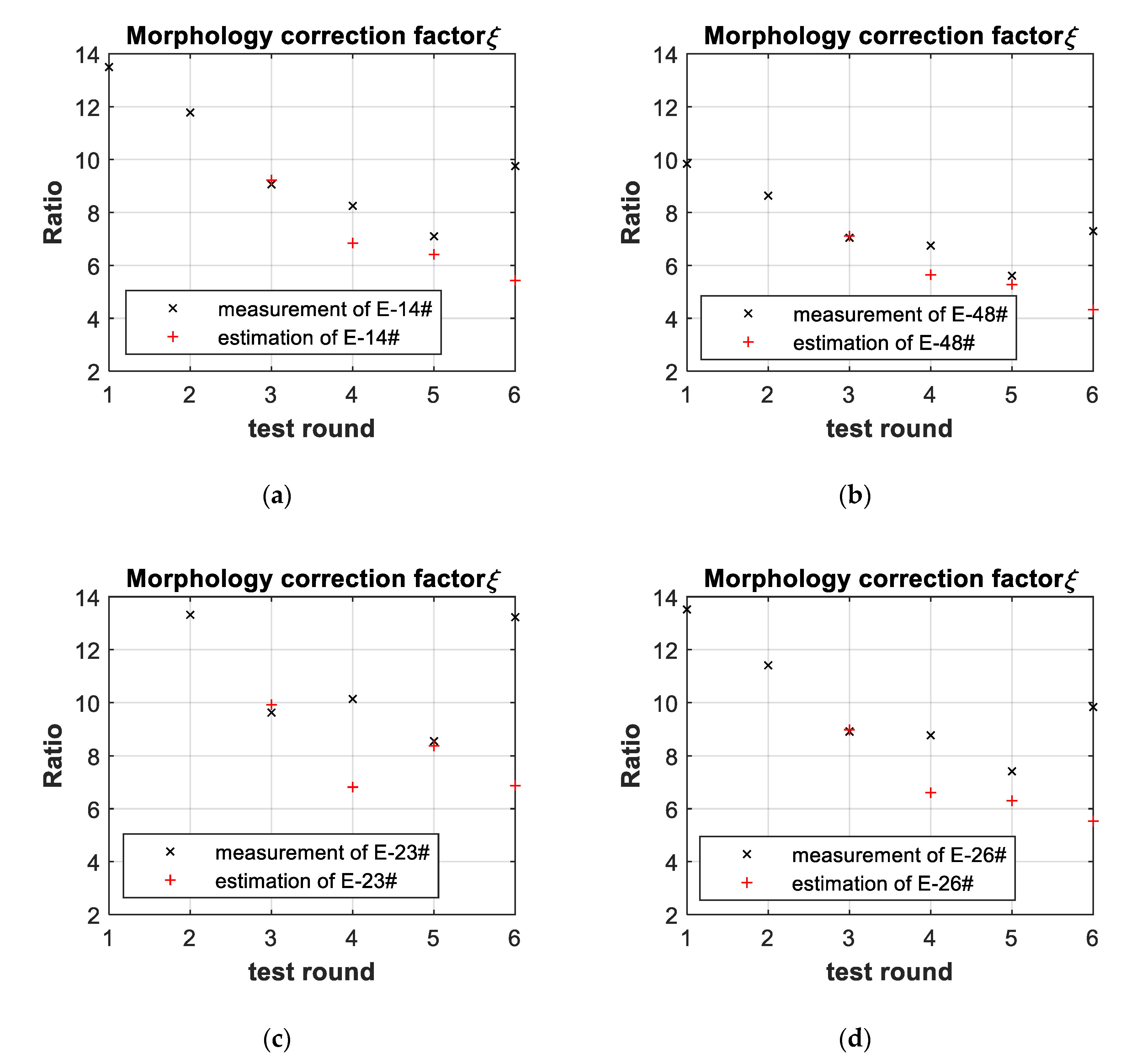
2.1. Morphology Correction Factor of Battery Internal Resistance
2.2. Analysis of Deep-Discharge Curve by Linear Superposition
2.3. Interactive Analysis of Internal Resistance of Discontinuous Current
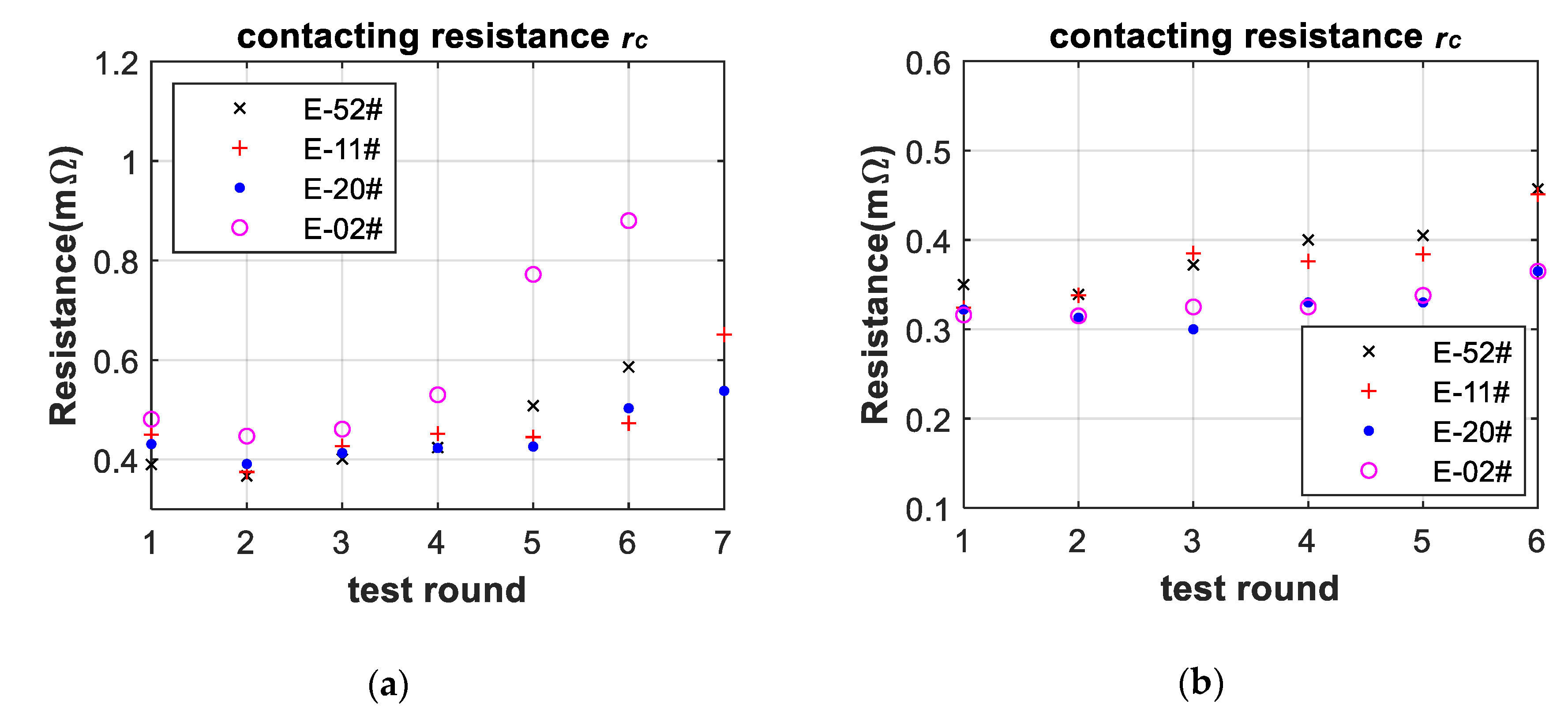
2.4. Linear Aging Filter of Internal Resistance Based on Contacting Resistance of EIS
2.5. Linear Aging Filter of Parameters to Counter Hysteresis
2.6. Linear Aging Model of Quantity of Remaining Useful Capacity
3. Results and Discussion
3.1. Accelerated Aging Experiments
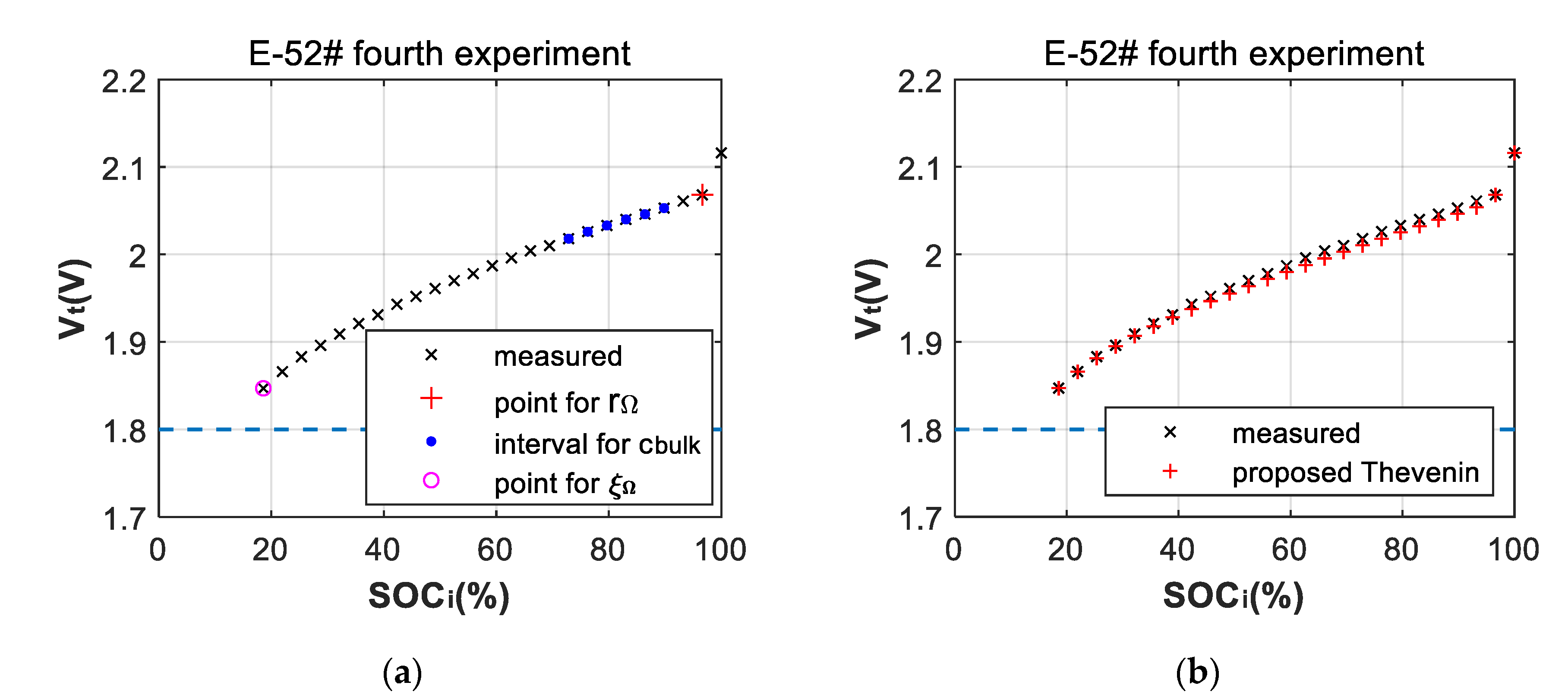
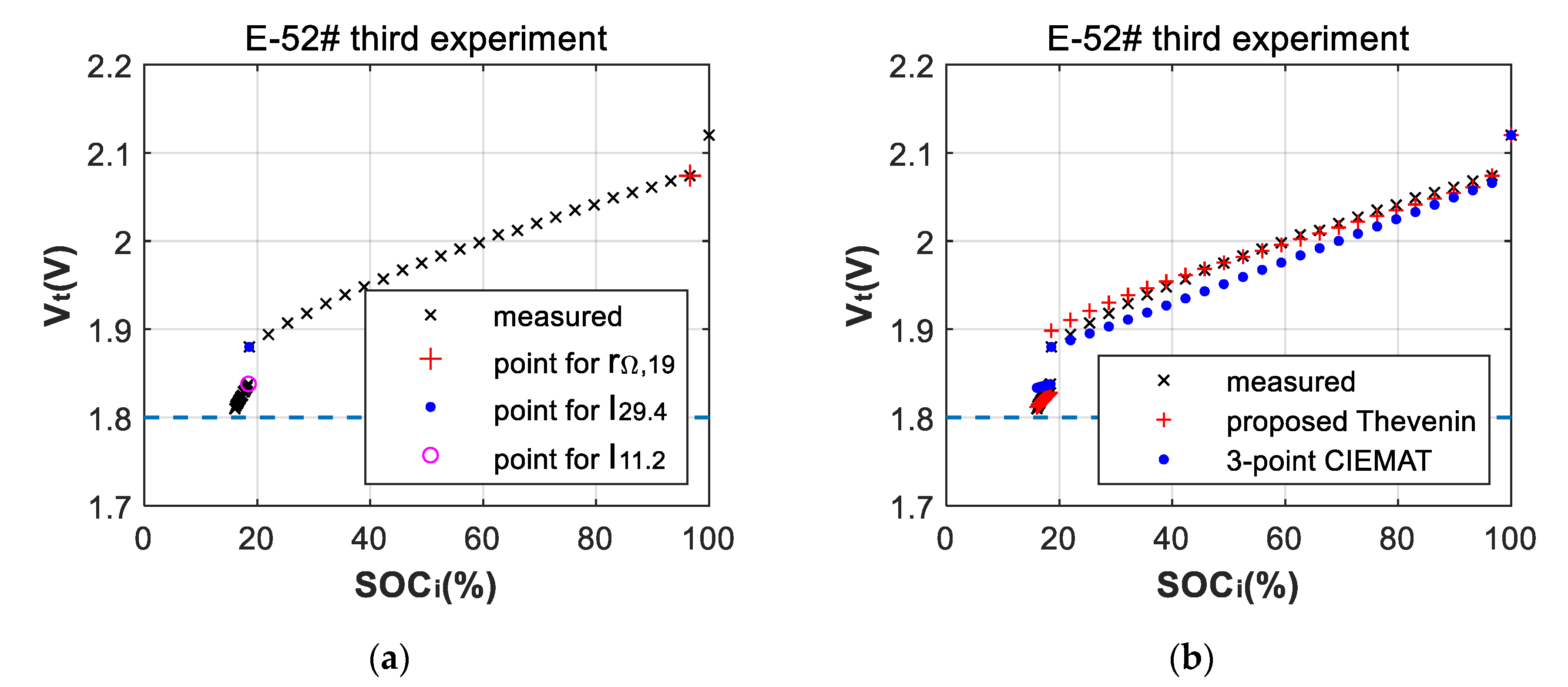
3.2. Fitting Errors of Deep-Discharge Curves of 70 °C Aging Experiments
3.3. Battery-Failure Warning Results of the Proposed Linear Aging Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Item | Elements | Physical Meanings |
|---|---|---|
| 1 | Initial voltage of electrolyte bulk capacitor | |
| 2 | Electrolyte bulk capacitor | |
| 3 | Charge-transfer resistances of discharging of positive electrode | |
| 4 | Charge-transfer resistances of discharging of negative electrode | |
| 5 | EUC | Electrode utilization coefficient |
| 6 | Morphology correction factor | |
| 7 | SOC | State of charge |
| 8 | Capacity of discharging | |
| 9 | Rated design capacity (560 Ah) | |
| 10 | Charge-transfer resistances of the full state of charge of positive electrode | |
| 11 | Charge-transfer resistances of the full state of charge of negative electrode | |
| 12 | Contacting resistance | |
| 13 | Battery internal resistance | |
| 14 | Discharging surface area | |
| 15 | Electrode surface area | |
| 16 | Contacting resistance of the full state of charge | |
| 17 | Internal resistance of the full state of charge | |
| 18 | Morphology correction factor of internal resistance | |
| 19 | Terminal voltage of | |
| 20 | Discharging current | |
| 21 | Morphology correction factor of positive electrode | |
| 22 | Morphology correction factor of negative electrode | |
| 23 | Electrode utilization coefficient of | |
| 24 | Terminal voltage approaching to the end of voltage (1.80 v) | |
| 25 | Initial time moment of deep-discharge | |
| 26 | Terminal voltage of the beginning of deep-discharge | |
| 27 | Electrode utilization coefficient of the beginning of discharge | |
| 28 | Electrode utilization coefficient as equal as 0.1 | |
| 29 | Electrode utilization coefficient as equal as 0.3 | |
| 30 | Internal resistance related to 19 a discharge current | |
| 31 | Internal resistance related to 50 a discharge current | |
| 32 | Temperature variation | |
| 33 | Current for discharging rated battery capacity (560 Ah) for 10 h | |
| 34 | Capacity of discharging under | |
| 35 | 50-A current for discharging rated battery capacity (560 Ah) for 11.2 h | |
| 36 | 19-A current for discharging rated battery capacity (560 Ah) for 29.4 h | |
| 37 | Capacity of discharging under | |
| 38 | Limit Capacity when the discharge Current tends to zero | |
| 39 | Parameters of CIEMAT model | |
| 40 | Parameters of CIEMAT model | |
| 41 | Parameters of CIEMAT model | |
| 42 | Capacity of discharging before current discontinuous | |
| 43 | Capacity of discharging after current discontinuous | |
| 44 | Ratio between contacting and internal resistances at k-round aging test | |
| 45 | Contacting resistance of EIS at k-round aging test. | |
| 46 | Internal resistance of deep-discharge at k-round aging test | |
| 47 | estimation of internal resistance of deep-discharge after k-round aging test | |
| 48 | Estimation of ratio after k-round deep-discharge | |
| 49 | Error covariance of estimation at k-round aging test | |
| 50 | Covariance matrix of measurement errors | |
| 51 | Transformation matrix between measurement and state vector | |
| 52 | Kalman gain at k-round aging test | |
| 53 | Expected value of variable | |
| 54 | Error covariance for updated estimation at k-round aging test | |
| 55 | Incremental contacting resistance between k-round and (k-1)-round aging test | |
| 56 | State transition matrix | |
| 57 | Prediction of internal resistance at k-round EIS sampling | |
| 58 | Prediction of ratio at k-round EIS sampling | |
| 59 | Measured parameters (, , ) at k-round aging test | |
| 60 | Aging rates adjusted according to parameters’ highest value | |
| 61 | Aging rates adjusted according to parameters’ last value | |
| 62 | Parameters’ historical highest value | |
| 63 | Aging rates of the parameters | |
| 64 | Covariance matrix of measurement errors of the parameter | |
| 65 | Transformation matrix between measurement and state vector of the parameter | |
| 66 | State transition matrix of the parameter | |
| 67 | Estimation of the parameter after k-round deep-discharge | |
| 68 | Prediction of aging parameter of k-round aging test | |
| 69 | Prediction of aging rates of parameters of k-round aging test | |
| 70 | Estimation of aging rates of parameters after k-round aging test | |
| 71 | Electrode utilization coefficient corresponding to the end of terminal voltage (1.80 v) at k-round aging test |
References
- Ballantyne, A.D.; Hallett, J.P.; Riley, D.J.; Shah, N.; Payne, D.J. Lead acid battery recycling for the twenty-first century. R. Soc. Open Sci. 2018, 5, 171368. [Google Scholar] [CrossRef]
- Matteson, S.; Williams, E. Residual learning rates in lead-acid batteries: Effects on emerging technologies. Energy Policy 2015, 85, 71–79. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Du, X.Y.; Salman, M. Battery state estimation with a self-evolving electrochemical ageing model. Int. J. Electr. Power Energy Syst. 2017, 85, 178–189. [Google Scholar] [CrossRef]
- Lyu, C.; Lai, Q.Z.; Ge, T.F.; Yu, H.H.; Wang, L.X.; Ma, N. A Lead-acid battery’s remaining useful life prediction by using electrochemical model in the particle filtering framework. Energy 2017, 120, 975–984. [Google Scholar] [CrossRef]
- Ren, D.S.; Lu, L.G.; Shen, P.; Feng, X.N.; Han, X.B.; Ouyang, M.G. Battery remaining discharge energy estimation based on prediction of future operating conditions. J. Energy Storage 2019, 25, 100836. [Google Scholar] [CrossRef]
- Lu, J.D.; Wei, L.F.; Pour, M.M.; Mekonnen, Y.; Sarwat, A.I. Modeling discharge characteristics for predicting battery remaining life. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Chicago, IL, USA, 22–24 June 2017. [Google Scholar] [CrossRef]
- Shepherd, C.M. Design of primary and secondary cells: II. An equation describing battery discharge. J. Electrochem. Soc. 1965, 112, 657–664. [Google Scholar] [CrossRef]
- Copetti, J.B.; Chenlo, F. Lead/acid batteries for photovoltaic applications. test results and modeling. J. Power Sour. 1994, 47, 109–118. [Google Scholar] [CrossRef]
- Achaibou, N.; Haddadi, M.; Malek, A. Modeling of lead acid batteries in PV Systems. Energy Procedia 2012, 18, 538–544. [Google Scholar] [CrossRef]
- Achaibou, N.; Haddadi, M.; Malek, A. Lead acid batteries simulation including experimental validation. J. Power Sour. 2008, 185, 1484–1491. [Google Scholar] [CrossRef]
- Degla, A.; Chikh, M.; Chouder, A.; Bouchafaa, F. Comparison study and parameter identification of three battery models for an off-grid photovoltaic system. Int. J. Green Energy 2019, 16, 299–308. [Google Scholar] [CrossRef]
- Blaifi, S.; Moulahoum, S.; Colak, I.; Merrouche, W. An enhanced dynamic model of battery using genetic algorithm suitable for photovoltaic applications. Appl. Energy 2016, 169, 888–898. [Google Scholar] [CrossRef]
- Thirugnanam, K.; Joy, T.P.E.R.; Singh, M.; Kumar, P. Mathematical modeling of Li-Ion battery using genetic algorithm approach for V2G applications. IEEE Trans. Energy Convers. 2014, 29, 332–343. [Google Scholar] [CrossRef]
- Haddad, R.J.; El-Shahat, A.; Kalaani, Y. Lead acid battery modeling for PV applications. J. Electr. Eng. 2015, 15, 17–24. [Google Scholar]
- Burgess, W.L. An analysis of float service life test data of VRLA batteries. J. Power Sour. 1998, 75, 28–35. [Google Scholar] [CrossRef]
- Burgess, W.L. Valve regulated lead acid battery float service life estimation using a Kalman Filter. J. Power Sour. 2009, 191, 16–21. [Google Scholar] [CrossRef]
- Sauer, D.U.; Wenzl, H. Comparison of different approaches for lifetime prediction of electrochemical systems—Using lead-acid batteries as example. J. Power Sour. 2008, 176, 534–546. [Google Scholar] [CrossRef]
- Schiffer, J.; Sauer, D.U.; Bindner, H.; Cronin, T.; Lundsager, P.; Kaiser, R. Model prediction for ranking lead-acid batteries according to expected lifetime in renewable energy systems and autonomous power-supply systems. J. Power Sour. 2007, 168, 66–78. [Google Scholar] [CrossRef]
- Pilatowicz, G.; Budde-Meiwes, H.; Schulte, D.; Kowal, J.; Zhang, Y.; Du, X.; Salman, M.; Gonzales, D.; Alden, J.; Sauer, D.U. Simulation of SLI lead-acid batteries for SoC, aging and cranking capability prediction in automotive applications. J. Electrochem. Soc. 2012, 159, A1410–A1419. [Google Scholar] [CrossRef]
- Franke, M.; Kowal, J. Empirical sulfation model for valve-regulated lead-acid batteries under cycling operation. J. Power Sour. 2018, 380, 76–82. [Google Scholar] [CrossRef]
- Bashir, N.; Sardar, H.S.; Nasir, M.; Hassan, N.U.; Khan, H.A. Lifetime maximization of lead-acid batteries in small scale UPS and distributed generation systems. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar] [CrossRef]
- Kwiecien, M.; Huck, M.; Badeda, J.; Zorer, C.; Komut, K.; Yu, Q.; Sauer, D.U. Variation of impedance in lead-acid batteries in the presence of acid stratification. Appl. Sci. 2018, 8, 1018. [Google Scholar] [CrossRef]
- Kwiecien, M.; Badeda, J.; Huck, M.; Komut, K.; Duman, D.; Sauer, D.U. Determination of SoH of lead-acid batteries by electrochemical impedance spectroscopy. Appl. Sci. 2018, 8, 873. [Google Scholar] [CrossRef]
- Qahouq, J.A.A.; Xia, Z.Y. Single-perturbation-cycle online battery impedance spectrum measurement method with closed-loop control of power converter. IEEE Trans. Ind. Electr. 2017, 64, 7019–7029. [Google Scholar] [CrossRef]
- Lee, Y.D.; Park, S.Y.; Han, S.B. Online embedded impedance measurement using high-power battery charger. IEEE Trans. Ind. Appl. 2015, 51, 498–508. [Google Scholar] [CrossRef]
- Son, J.B.; Zhou, S.Y.; Sankavaram, C.; Du, X.Y.; Zhang, Y.L. Remaining useful life prediction based on noisy condition monitoring signals using constrained Kalman Filter. Reliab. Eng. Syst. Saf. 2016, 152, 38–50. [Google Scholar] [CrossRef]
- Bhalaji, N.; Rimi, C. Remaining Useful Life (RUL) estimation of lead acid battery using bayesian approach. J. Electr. Eng. Autom. 2020, 2, 25–34. [Google Scholar] [CrossRef]
- Nazghelichi, T.; Torabi, F.; Esfahanian, V. Non-dimensional analysis of electrochemical governing equations of lead-acid batteries. J. Energy Storage 2020, 27, 101120. [Google Scholar] [CrossRef]
- Lopez, B.D.; Lujano-Rojas, J.M.; Bernal-Agustin, J.L. Comparison of different lead–acid battery lifetime prediction models for use in simulation of stand-alone photovoltaic systems. Appl. Energy 2014, 115, 242–253. [Google Scholar] [CrossRef]
- Tiedemann, W. Forty years of porous electrode theory with battery applications. ECS Trans. 2008, 16, 23–37. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Porous-electrode theory with battery applications. AlChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef]
- Srinivasan, V.; Wang, G.Q.; Wang, C.Y. mathematical modeling of current-interrupt and pulse operation of valve-regulated lead acid cells. J. Electrochem. Soc. 2003, 150, A316–A325. [Google Scholar] [CrossRef]
- Berndt, D.; Teutsch, U. Float charging of valve-regulated lead-acid batteries: A balancing act between secondary reactions. J. Electrochem. Soc. 1996, 143, 790. [Google Scholar] [CrossRef]
- Karden, E. Using Low-Frequency Impedance Spectroscopy for Characterization, Monitoring, and Modeling of Industrial Batteries. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, December 2001; pp. 13–24. [Google Scholar]
- Shi, Y. Modeling, Real-Time Degradation Identification, and Remediation of Pb-acid Batteries. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, December 2013; p. 73. [Google Scholar]
- Wang, W.B.; Yao, W.X.; Chen, W.; Chen, D.; Lu, Z.Y. characteristic charge transfer resistance of electrodes on lead-acid batteries. J. Electrochem. Soc. 2020, 167, 040515. [Google Scholar] [CrossRef]
- Brik, K.; Ammar, F.B. Causal tree analysis of depth degradation of the lead acid battery. J. Power Sour. 2013, 228, 39–46. [Google Scholar] [CrossRef]
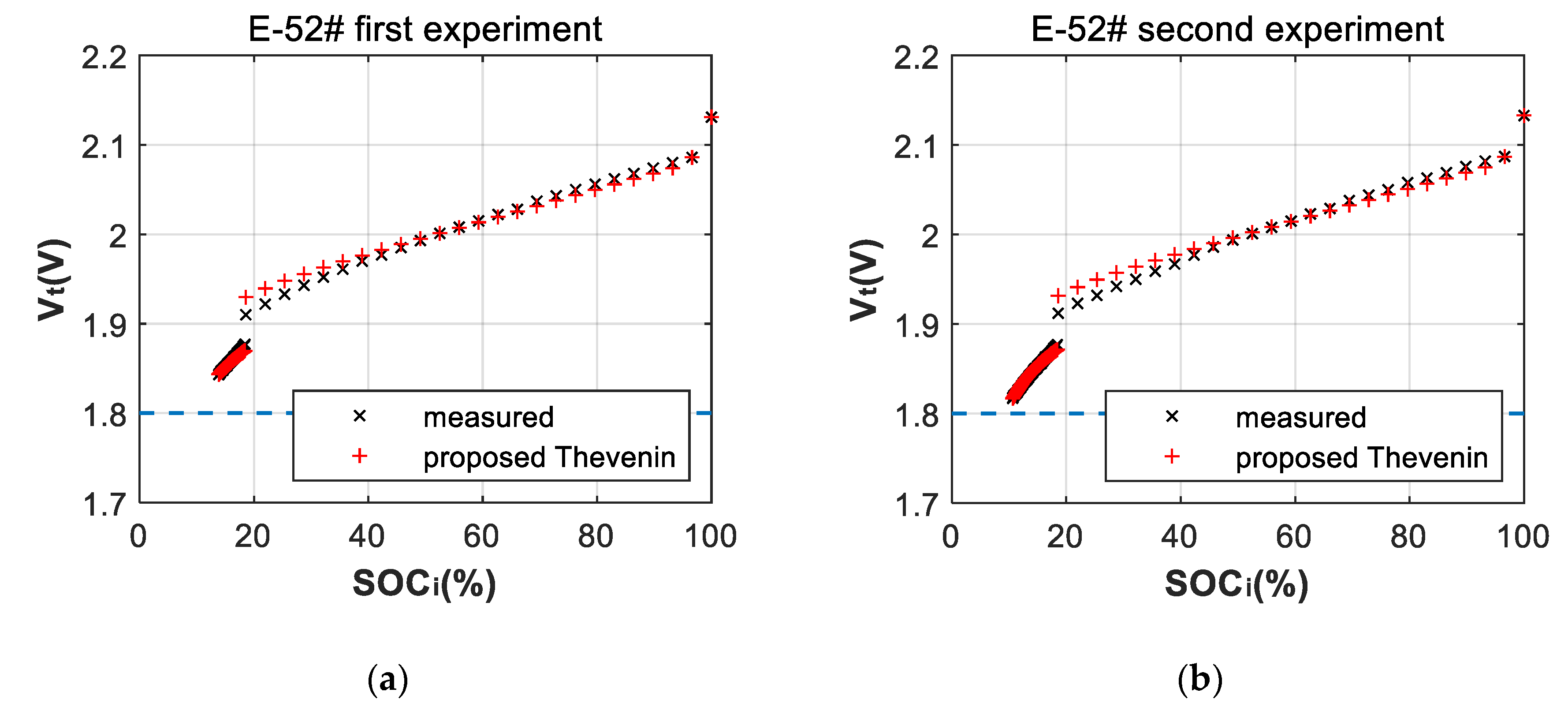
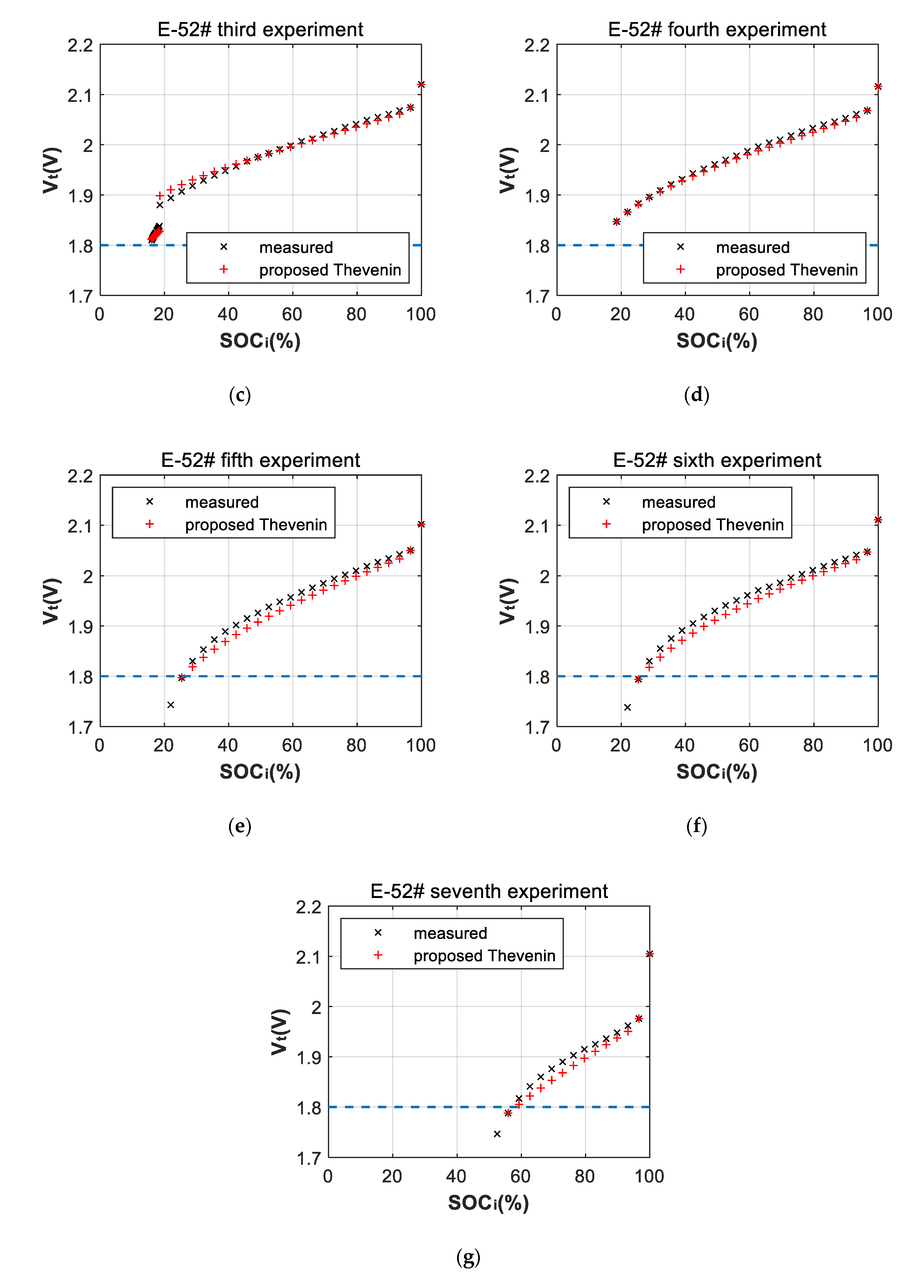

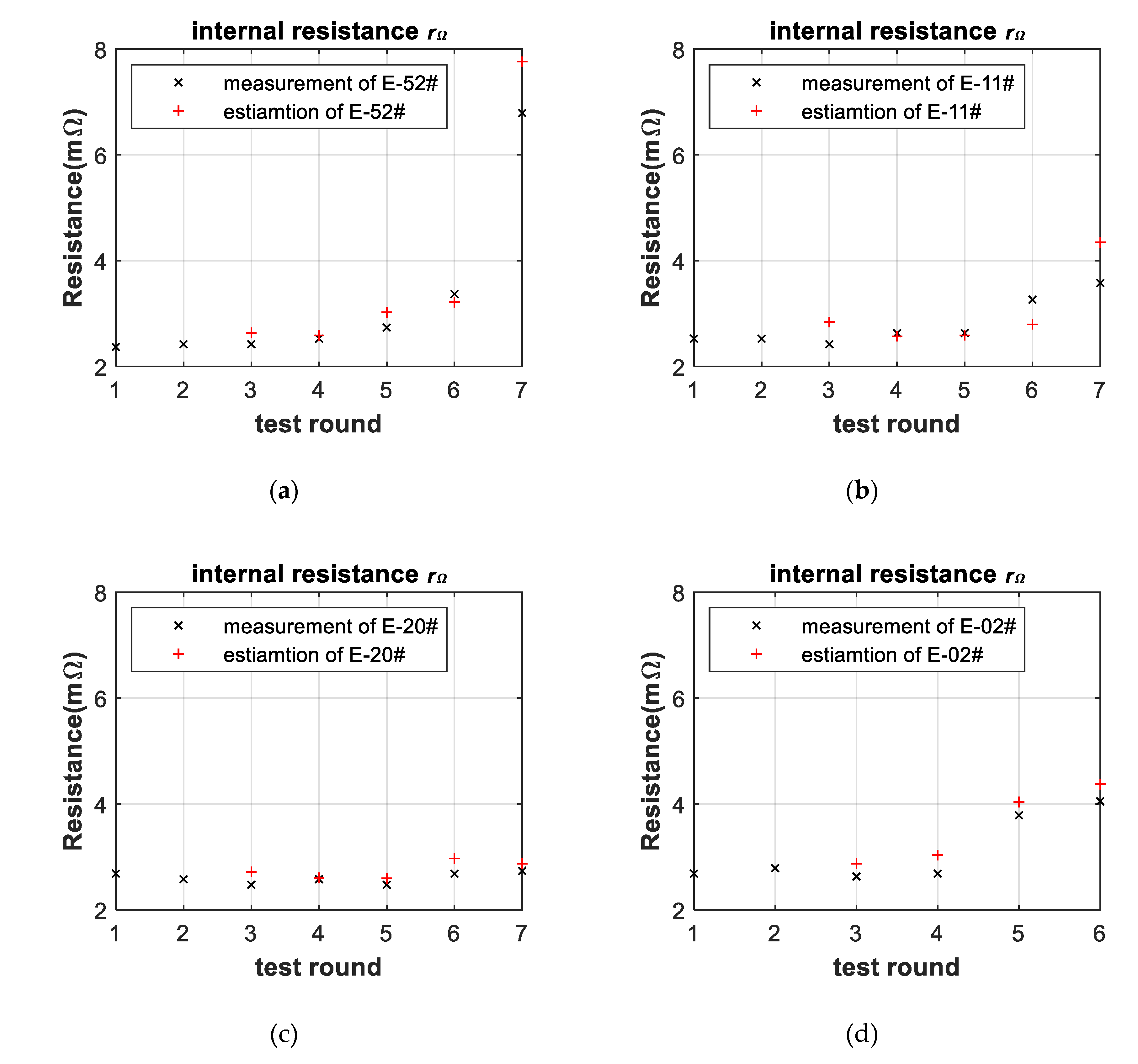
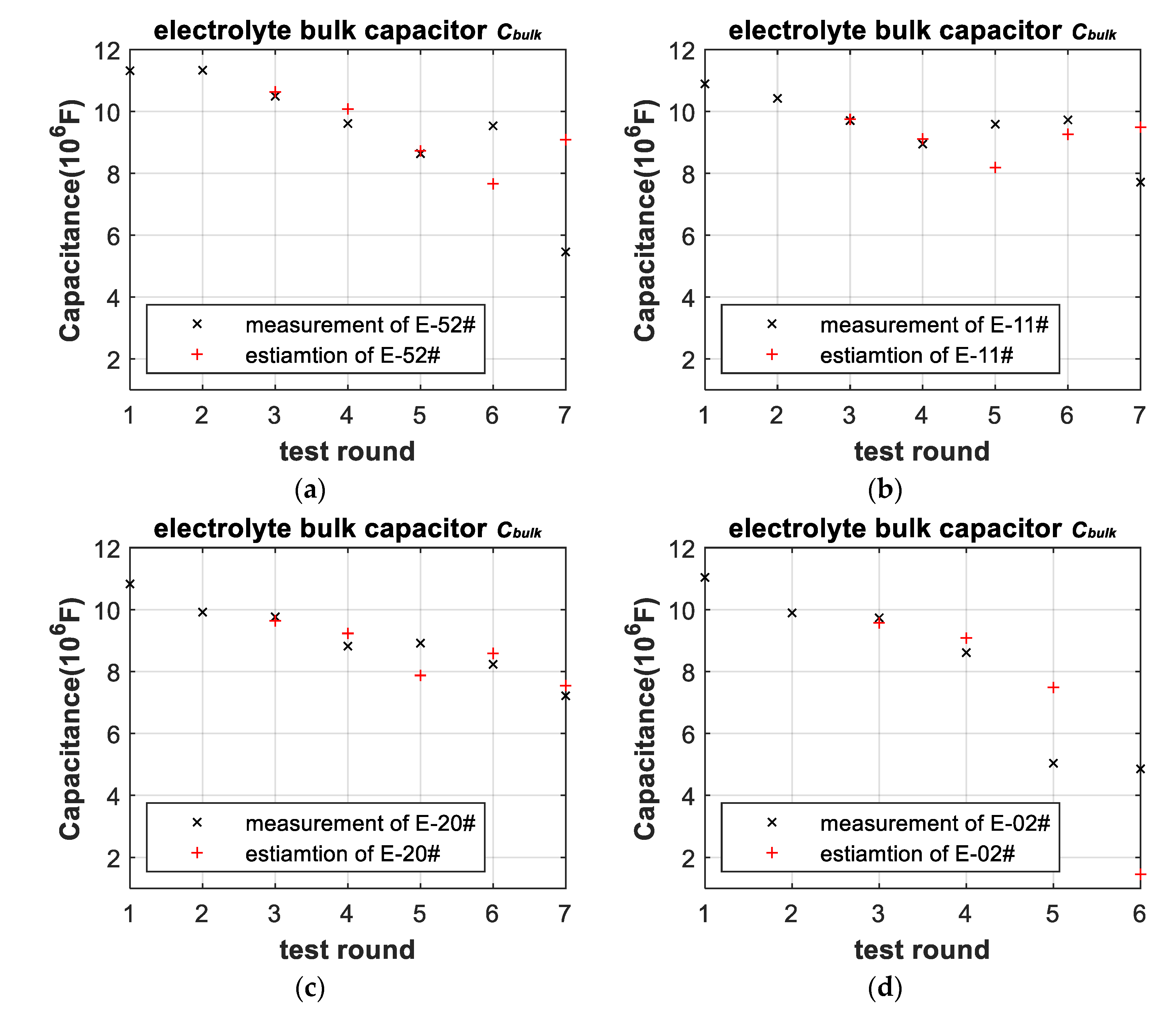
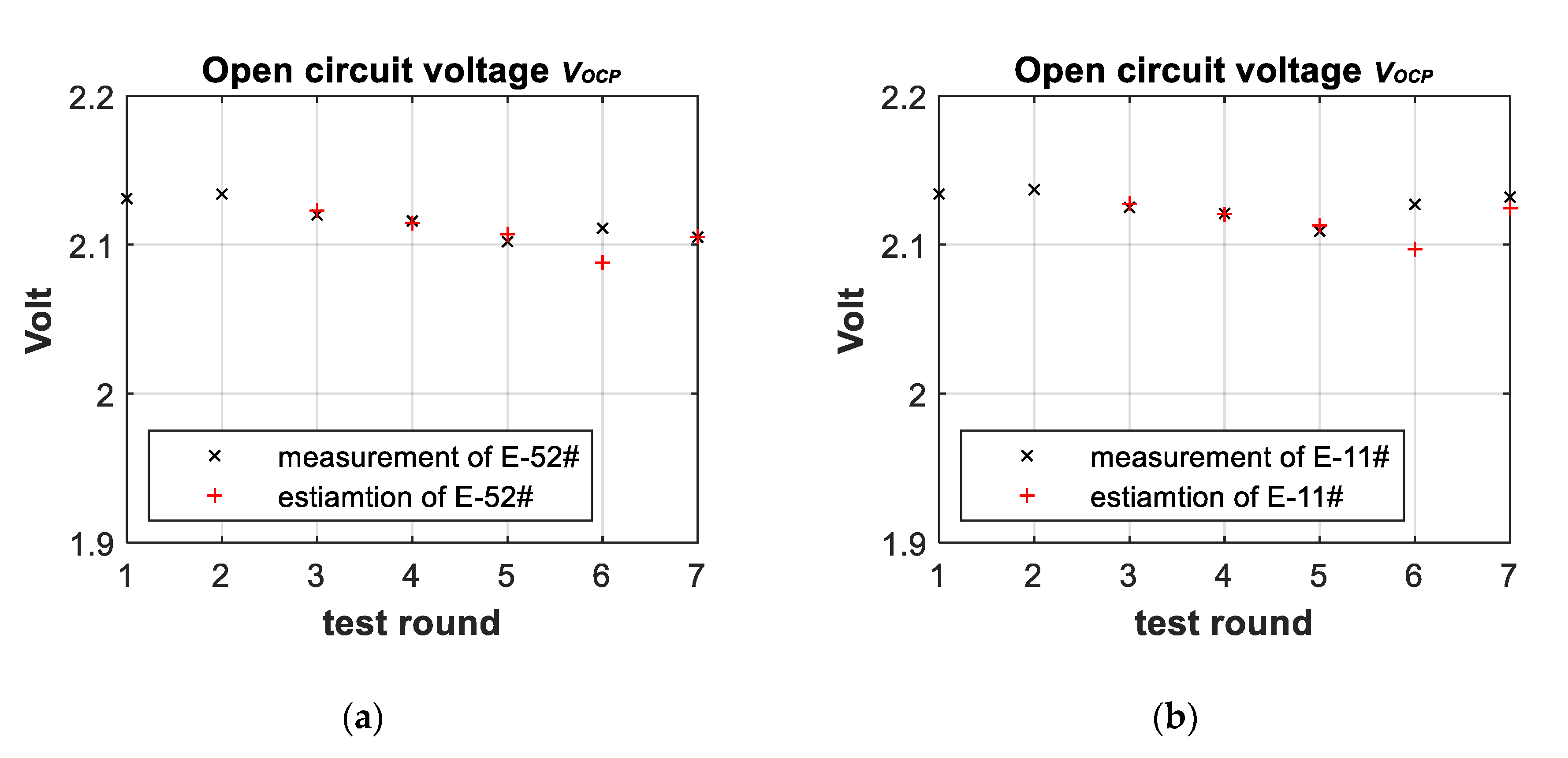
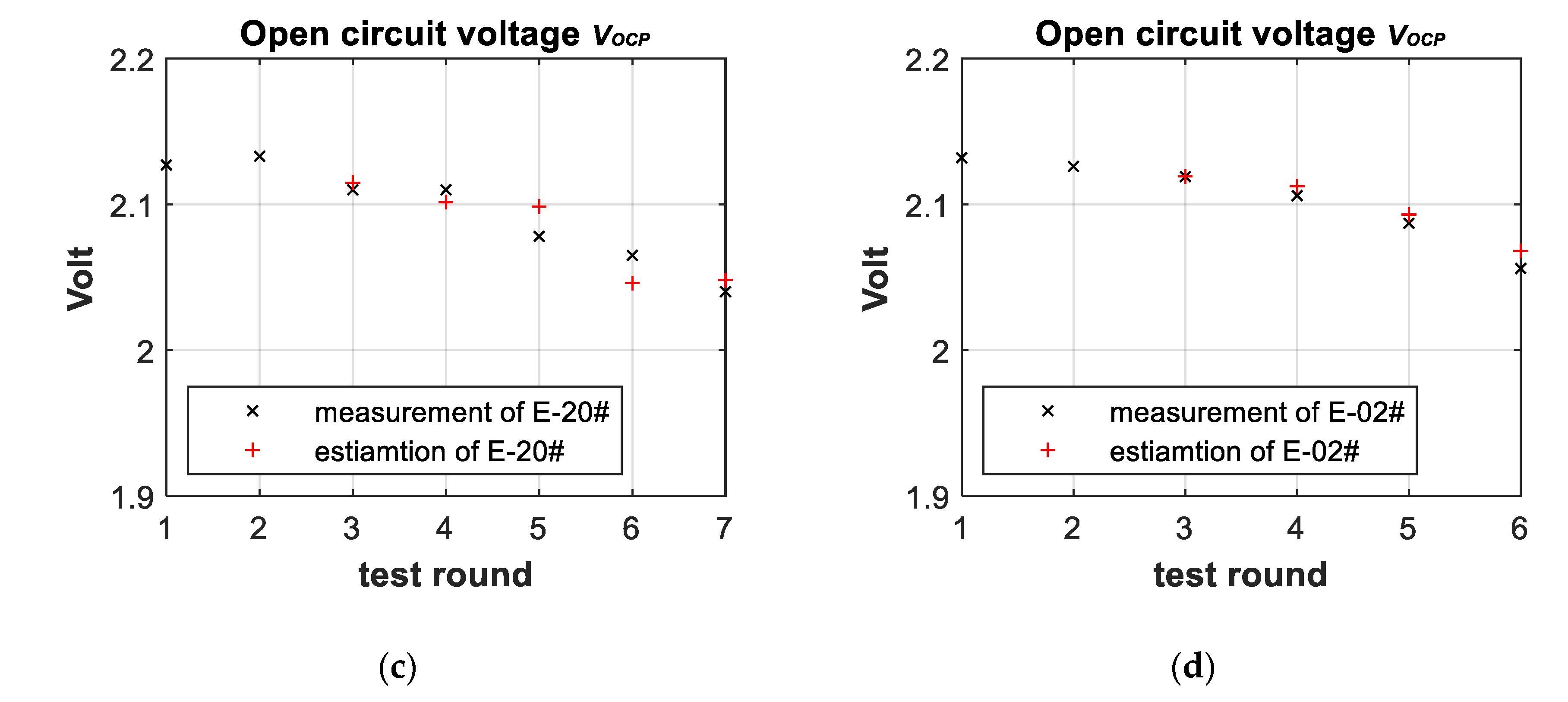
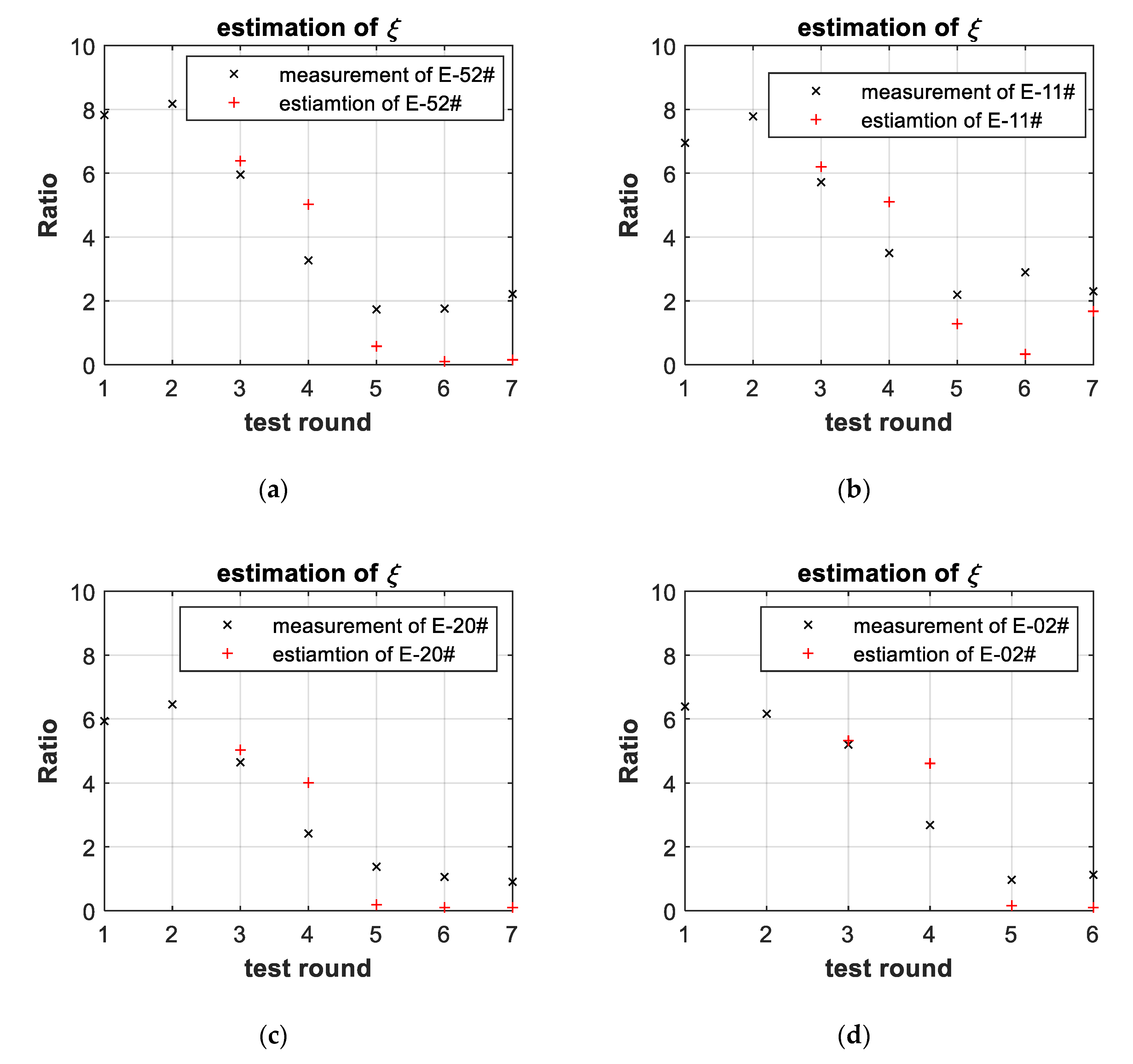
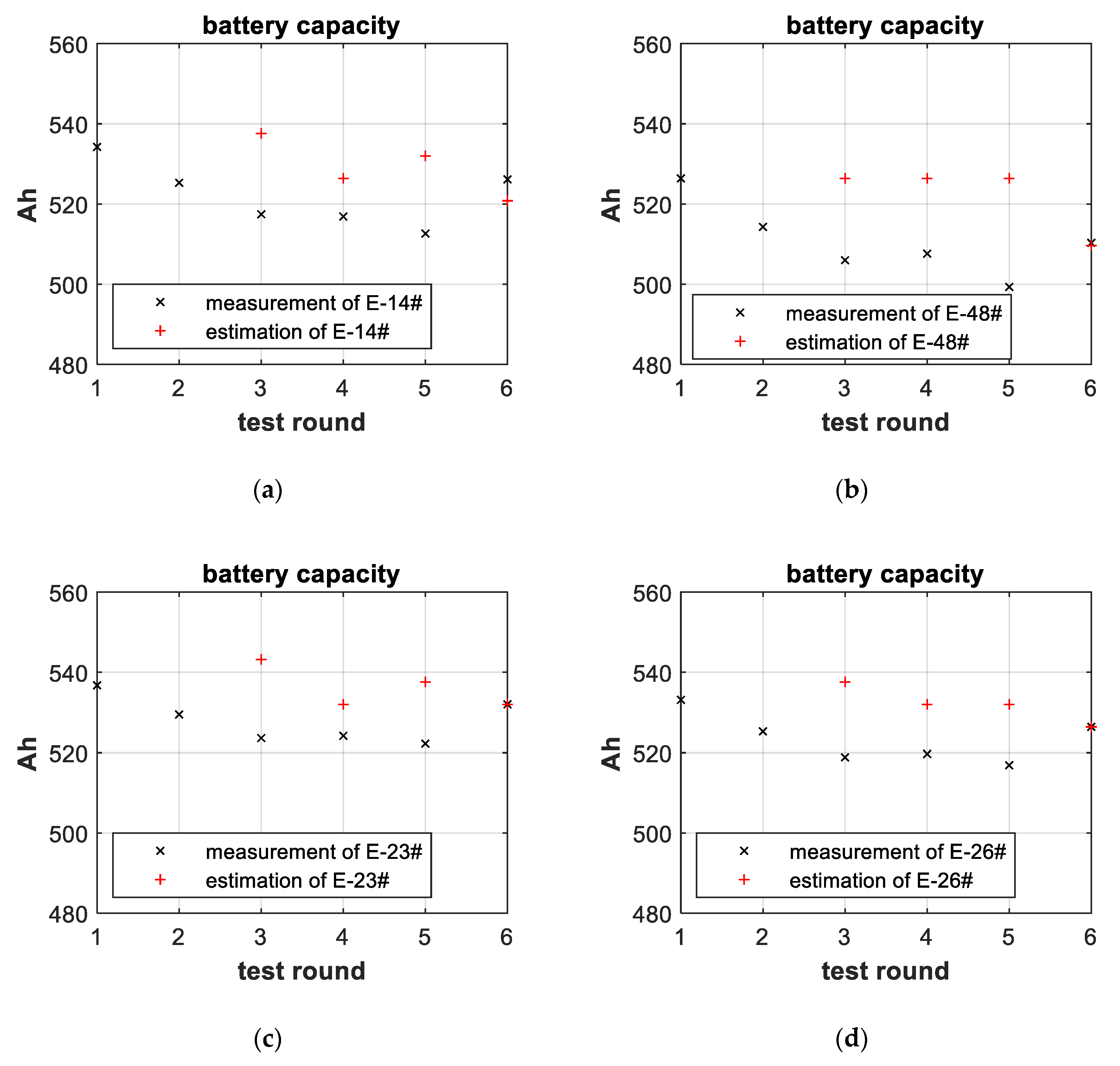
| Cell | |||
|---|---|---|---|
| E-52# 01st | 0.9976 | −0.0004 | 0.0059 |
| E-52# 02nd | 0.9977 | 0.0010 | 0.0058 |
| E-52# 03rd | 0.9971 | −0.0006 | 0.0073 |
| E-52# 04th | 0.9992 | −0.0049 | 0.0058 |
| E-52# 05th | 0.9974 | −0.0128 | 0.0141 |
| E-52# 06th | 0.9975 | −0.0129 | 0.0142 |
| E-52# 07th | 0.9956 | −0.0131 | 0.0154 |
| E-11# 01st | 0.9977 | −0.0019 | 0.0065 |
| E-11# 02nd | 0.9981 | −0.0028 | 0.0062 |
| E-11# 03rd | 0.9983 | −0.0031 | 0.0067 |
| E-11# 04th | 0.9992 | −0.0062 | 0.0068 |
| E-11# 05th | 0.9992 | −0.0077 | 0.0082 |
| E-11# 06th | 0.9994 | −0.0048 | 0.0057 |
| E-11# 07th | 0.9985 | −0.0109 | 0.0119 |
| E-20# 01st | 0.9974 | −0.0037 | 0.0084 |
| E-20# 02nd | 0.9956 | 0.0032 | 0.0117 |
| E-20# 03rd | 0.9975 | 0.0059 | 0.0134 |
| E-20# 04th | 0.9984 | −0.0096 | 0.0105 |
| E-20# 05th | 0.9953 | −0.0144 | 0.0160 |
| E-20# 06th | 0.9895 | −0.0206 | 0.0234 |
| E-20# 07th | 0.9854 | −0.0219 | 0.0251 |
| E-02# 01st | 0.9974 | −0.0026 | 0.0077 |
| E-02# 02nd | 0.9950 | 0.0068 | 0.0159 |
| E-02# 03rd | 0.9980 | 0.0051 | 0.0120 |
| E-02# 04th | 0.9986 | −0.0100 | 0.0109 |
| E-02# 05th | 0.9848 | −0.0233 | 0.0271 |
| E-02# 06th | 0.9857 | −0.0209 | 0.0247 |
| Cell | ||
|---|---|---|
| E-52# | 0.28 × 10−3 | 0.47 × 10−3 |
| E-11# | 0.12 × 10−3 | 0.45 × 10−3 |
| E-20# | 0.16 × 10−3 | 0.19 × 10−3 |
| E-02# | 0.29 × 10−3 | 0.30 × 10−3 |
| Cell | ||
|---|---|---|
| E-14# | 10.93 | 15.01 |
| E-48# | 16.40 | 19.40 |
| E-23# | 10.71 | 13.07 |
| E-26# | 11.55 | 13.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Yao, W.; Chen, W.; Chen, D.; Lu, Z. Failure Warning at the End of Service-Life of Lead–Acid Batteries for Backup Applications. Appl. Sci. 2020, 10, 5760. https://doi.org/10.3390/app10175760
Wang W, Yao W, Chen W, Chen D, Lu Z. Failure Warning at the End of Service-Life of Lead–Acid Batteries for Backup Applications. Applied Sciences. 2020; 10(17):5760. https://doi.org/10.3390/app10175760
Chicago/Turabian StyleWang, Wubin, Wenxi Yao, Wei Chen, Dong Chen, and Zhengyu Lu. 2020. "Failure Warning at the End of Service-Life of Lead–Acid Batteries for Backup Applications" Applied Sciences 10, no. 17: 5760. https://doi.org/10.3390/app10175760
APA StyleWang, W., Yao, W., Chen, W., Chen, D., & Lu, Z. (2020). Failure Warning at the End of Service-Life of Lead–Acid Batteries for Backup Applications. Applied Sciences, 10(17), 5760. https://doi.org/10.3390/app10175760





