1. Introduction
On board all operative ships, internal combustion engines (ICEs) are installed with the function of both propulsion engines and auxiliaries in electric energy generators. Specifically in large ships, ICEs are mainly 2-stroke and 4-stroke turbocharged diesel engines. Two-stroke engines are used exclusively for the propulsion of merchant ships such as very large container ships, tankers, and ro-ro due to the required great power. Moreover, the layout of the general arrangements of these types of ships does not create particular constraints on the installation of these mammoth-sized engines. On the other hand, 4-stroke engines, coupled with suitable generators, are used for the production of electric energy practically on board all ships. Moreover, thanks to the high specific power, they are mainly employed in the propulsion of ferries, naval ships (up to frigates), pleasure crafts, fishing vessels, and support vessels for offshore operations. It is still worth underlining that 4-stroke engines are also used in passenger ship gensets, which, as known, adopt an electric propulsion system.
For both types of engines, the power they can deliver ranges from 10 to 100 MW; therefore, they must be fed with low-cost fuels that make the shipping of goods and passengers profitable for shipowners. In fact, as reported in [
1], global shipping is responsible for moving about 90% of the world trade, while cruise ships in 2017 allowed nearly 25 million of passengers to sail the oceans. These significant results were obtained thanks to the great flexibility offered by shipping and the low cost per ton transported of this mode of transportation. Despite maritime transport still being the most fuel-efficient means of good transit, it should be noted that ships have, as mentioned before, big ICEs installed on board; as a consequence, shipping greatly contributes to the emission of air pollutants (PM, SO
X, NO
X), sea pollutants (noise, thermal, discharges), and greenhouse gases (GHG).
To be honest, in order to reduce all forms of pollution from ships, since 1973, the International Maritime Organization (IMO) has already issued a whole series of regulations. Moreover, the IMO has drawn up a roadmap for reducing emissions from ships in order to provide shipowners and shipbuilders with a clear long-term strategy to guide their research and development activities. With particular reference to air emissions, in 2006, MARPOL Annex 6 [
2] was issued introducing the definition of Emission Control Areas, which are the areas of the planet with precise limits of air pollutant from ships allowed. Given the size of the world fleet and the partially retroactive effect of these regulations, several steps and implementation dates have been identified. On the same occasion, the compulsory adoption of the Ship Energy-Efficiency Management Plan (SEEMP) was introduced in order to limit waste as much as possible. Subsequently, IMO also ruled in favor of reducing GHG emissions [
3], setting the 50% reduction of CO
2 produced by ships as a target in 2050 compared to that produced in 2011 (year of entry into force of [
2]).
On this premise, from 2006 onwards, countless studies have been carried out to evaluate reliable, economic, and efficient technological solutions capable of achieving these objectives. In particular, three solutions have been identified [
4]: reducing the hull resistance; increasing the overall efficiency of the propulsion and power generation systems; and using alternative fuels with low or zero pollutant contents. It is easy to understand that the first strategy is really effective if applied on the construction of new ships, while the other two ones have found multiple applications also in the retrofitting of existing ships. In particular, the use of Liquefied Natural Gas (LNG) as a fuel is now a consolidated reality; additionally, many studies are being carried out in order to evaluate the use of other fuels such as hydrogen, methanol, and ammonia [
5,
6,
7]. However, given the effectiveness of the application of exhaust gas treatment systems such as SCR (Selective Catalytic Reduction) and Scrubber, the main energy source in marine industry is still Heavy Fuel Oil (HFO). In reality, this choice is also a consequence of the fact that shipowners must guarantee an adequate return on investment, and the major contributors in the life cycle cost of a ship are precisely maintenance and fuel. Therefore, HFO is preferred because besides having the lowest cost among fuels, it is very available on the market, has a low sulfur content variant, and has a consolidated and branched distribution network. However, it should also be noted that the standards currently achieved by the main marine diesel engine manufacturers ensure that the conventional marine turbocharged diesel engines (TDEs) have the potential to further reduce their fuel consumption and their emissions, improving their energy efficiency.
Therefore, monitoring and setting the performance of TDEs is vital: indeed, the efficiency of any onboard machinery is directly related to its performance in order to get an efficient combustion. Shipowners know very well that ensuring an efficient combustion reduces not only pollutant emissions but also fuel and maintenance costs. Conventionally, there are several ways to monitor the performance of a TDE: measuring the peak pressure by mechanical peak pressure gauge; indicator card measurement; digital pressure monitoring; intelligent combustion monitoring; monitoring of engine control parameters; engine parameters; log book monitoring; and engine emission evaluation. All these techniques, which are actually very effective, currently have the limit of providing for the offline processing of the data obtained in the monitoring and subsequent adjustment of the engine. However, numerous studies [
8,
9,
10,
11,
12] have demonstrated the possibility of simulating engine operation with remarkable precision.
The adoption of the Industry 4.0 paradigm by engine manufacturers has led the development of a new generation of products equipped with advanced automation systems [
13]. These automation systems are made up of a dense network of sensors that allows the detection of performance data of the TDEs and a series of actuators that are able to adjust the functional parameters of most of the auxiliary devices, in order to make the TDE always work at a maximum of its possibilities. Unfortunately, the common current practice foresees that, especially when new TDEs are installed, the manufacturer controls the monitoring functions, and the data collected are exploited only for diagnostic and maintenance purposes.
In this paper, a software tool that is capable of processing the in-live performance of TDEs is described. In particular, with reference to the main international standards, the tool instantly processes the data collected by the network of sensors installed on board, obtaining the engine performance data in-live and allowing the dynamic optimization of TDE operation. Particular attention was paid to writing the routine for the evaluation of air polluting emissions, because the latter can be significantly reduced in the first instance by acting on the combustion parameters and subsequently on the actuators that regulate the operation of both the SCR and Scrubber. Given the importance of determining the emissions, the tool calculates them by using two methods, the Air Nozzle and the Carbon Balance methods, both widely described below.
2. Rule Framework
Regarding the software’s mathematical steps required for the in-live performance evaluation, the following regulations have been analyzed:
Regulation ISO 5167-1:2003 [
14]. In this document, the Technical Committee establishes the general principles for methods of measurement and computation of the flowrate of fluid flowing in a conduit by means of pressure differential devices. Thus, Regulation ISO 5167-3:2003 [
15] provides the procedure for the evaluation of the incoming air mass flowrate to the compressor
by means of an Air Nozzle. Via the calculation of an ideal air mass flow through an Air Nozzle with Bernoulli’s equation and the implementation of discharge coefficient
and expansion coefficient ϵ, the real air mass flow can be rated;
Resolution MEPC.177 (58) (NOx Technical Code 2008) [
16]. This technical code, besides providing mandatory procedures for the testing, survey, and certification of marine diesel engines, gives a method to estimate exhaust mass flowrate
by means of Carbon Balance. The method is demonstrated in ISO 8178-1 [
17] through the equivalence between carbon entering the engine versus carbon leaving the engine;
Regulation ISO 8217:2010 [
18]. Within this regulation, standard values for fuels (in terms of density, viscosity, flash point, and much more) are provided. These are used if correct values from tests on in-use fuels are not available;
CIMAC Number 27|2007 [
19]. The overall efficiency of a turbocharger
can be evaluated by using the general formula provided in this document. Anyway, some manufactures (ABB and Mitsubishi) allow using simplified formulas, derived from the general one, which are reported in manufacturer’s technical notes;
Resolution MEPC.176(58)|2008 [
20]. For air pollution emission in atmosphere (in terms principally of nitrogen oxides NO
X and sulfur oxides SO
X emissions), the worldwide thresholds are fixed in this International Convention. This resolution embeds the previous 1997 Protocol that sets limits on sulfur oxide and nitrogen oxide emissions from ship exhausts and prohibits deliberate emissions of ozone-depleting substances. As regards the European Union, the Directive EU 2016/802 [
21], commonly known as “EU Sulphur Directive”, concerning the maximum amount of sulfur dioxide emissions in the atmosphere, and the Regulation C(2016)8381 [
22], concerning the general and technical requirements for emission limits and type approval for non-road ICEs, are issued.
3. Tool Description
3.1. General Principles
The software described in this paper was developed using as environment LABVIEW (Laboratory of Virtual Instrumentation and Engineering Workbench), which is system engineering software for applications that requires tests, measurements, and control. The programming language is called Graphic Language (G-Language) and differs from the traditional ones because the syntax is not written but graphic. This language is able to perform multithreading spontaneously without explicit control from the programmer; consequently, it is an excellent tool for handling all the processes in parallel. In order to define a digital configuration environment that is capable of perfectly adapting to the real on-board configuration, the number of independent choices to perform is very high. As a result, the software requires several processes.
The calculation procedure of the performance values starts with the evaluation of the incoming air mass flowrate to the engine .
This quantity, expressed in , is evaluated through two different procedures:
by means of the evaluation of incoming air mass flow to the compressor , which is measured if the Air Nozzle is installed;
by means of the evaluation of exhaust gas mass flow , calculated using the Carbon Balance method if CO2, CO and THC (Total HydroCarbon) detectors are present.
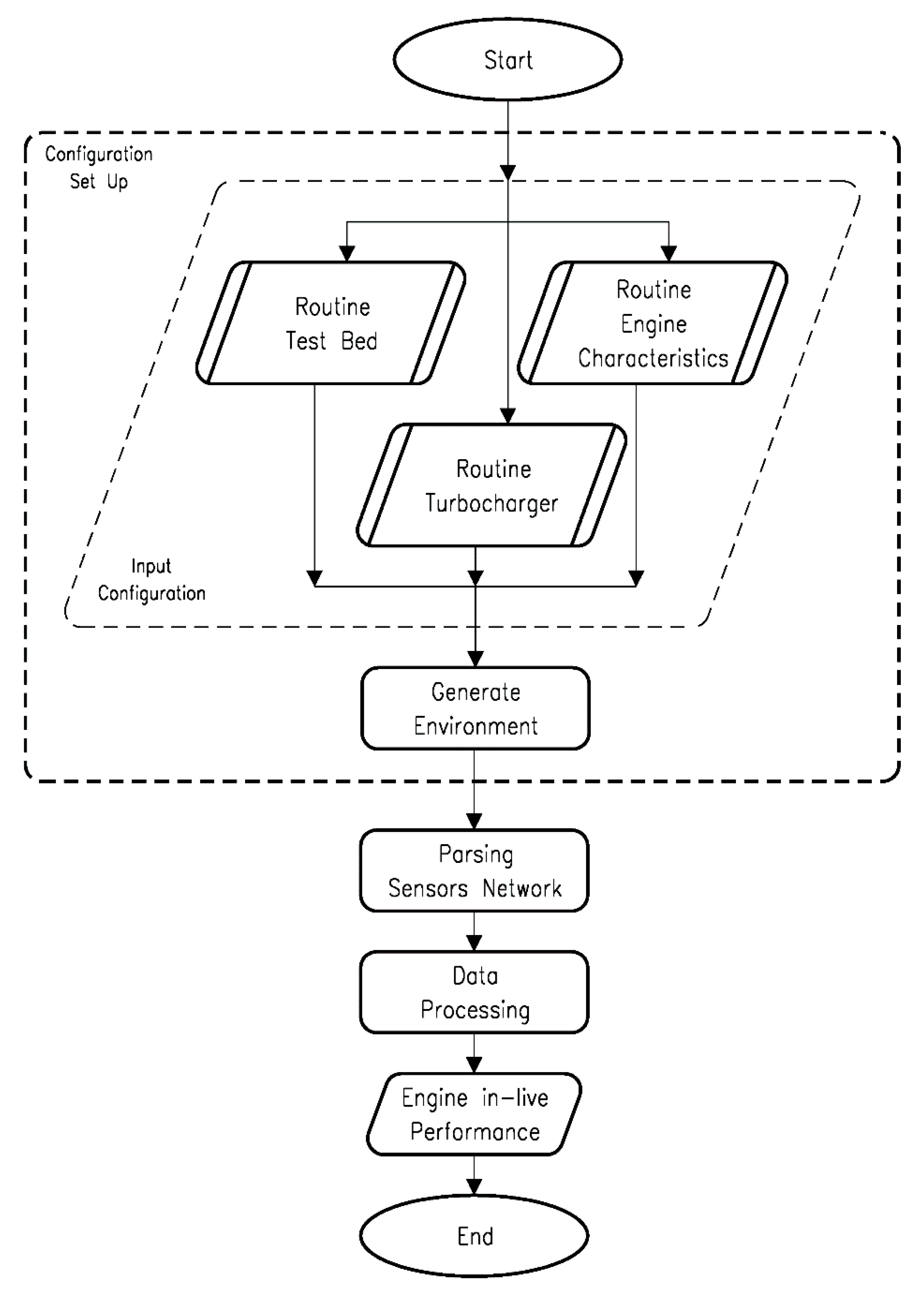
As regards the logical functioning of the software, four consequential phases can be identified (
Figure 1).
During the first phase of Configuration Set Up, the software requires the user to make all the choices previously mentioned in order to generate a Set Up Environment. The latter will be used to communicate to the actual engine of the software, which is called Main, the calculations to perform and the constants and variables necessary for them; furthermore, it provides an association between the variables and the sensors detected in the network.
The next phase requires running the parsing—that is, the association between the variables used in the Calculation Routine and the numerical values (i.e., the physical sensors) detected in the Sensor Network (SN). The user has to perform this phase manually every time.
Once the parsing is completed, the software starts with the Data Processing phase. The Main determines the calculations to perform and the input to use, which is based on available in-use configuration information, manually inserted constant values, and variables collected by the SN. Indeed, the analysis of both classic bibliography and the Rules in Performance Calculation area allowed identifying the functions required to define the interest value in Performance Evaluation. A huge number of them can be calculated only if the Border Conditions provided by the Set Up Environment are fulfilled; otherwise, the software does not perform the calculation of those functions and proceeds to verify all the others.
The last phase concerns the real calculation and the in-live visualization of the performance through a continuous update of the input values detected by the SN.
3.2. Configuration Set Up
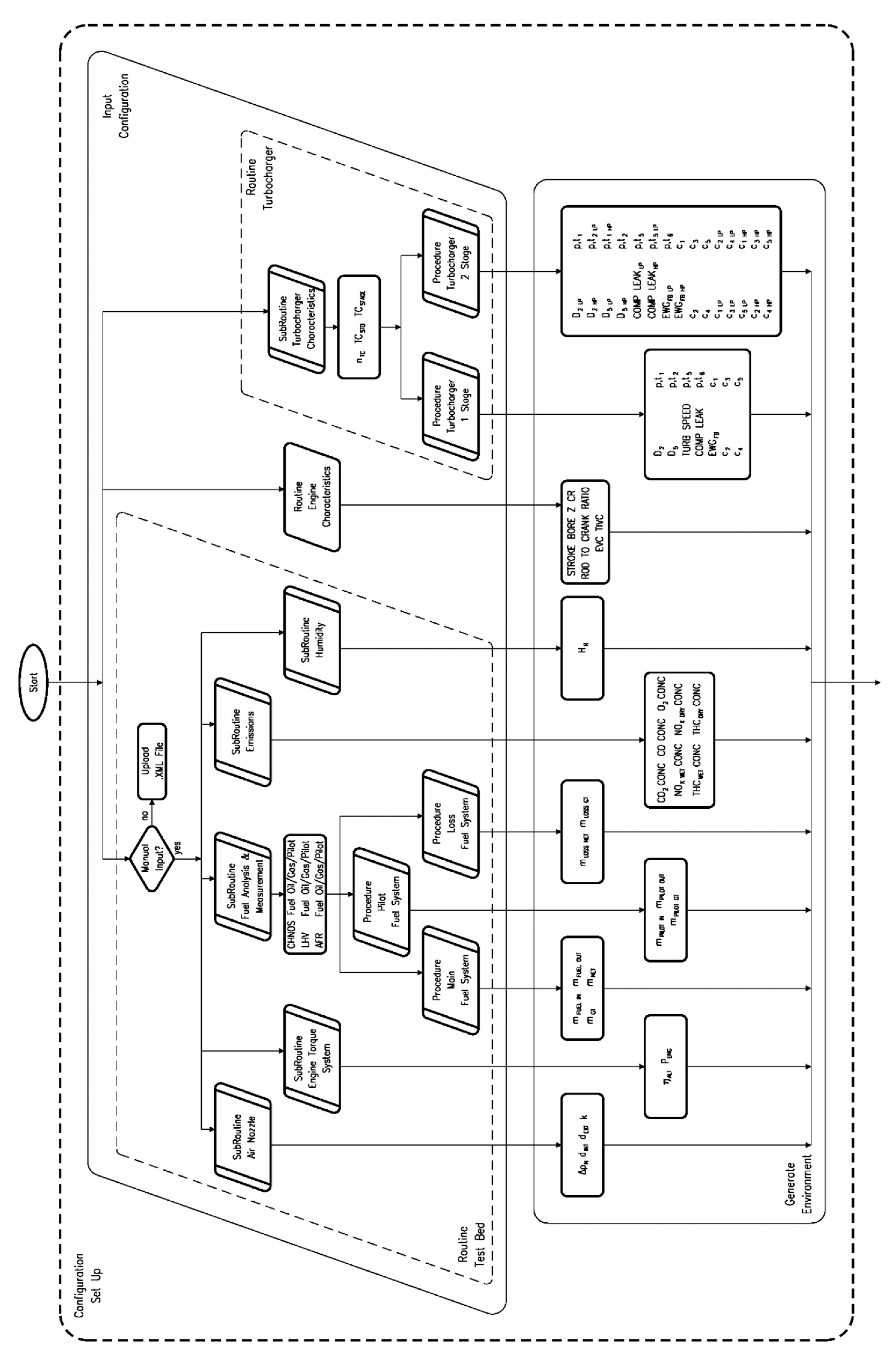
As regards to Configuration Set Up phase (
Figure 2), three principal Routines can be defined. Each of them refers to an .xml database file that is able to contain all the choices made in that specific Routine by the user during the Input Configuration phase (if saved). These databases will be used to speed up the future operations of the Configuration Set Up. The Routines are the following ones:
Routine Test Bed: routine used to insert all the information concerning the Test Bed instrumentation installed; it is composed of five SubRoutines: SubRoutine Air Nozzle, SubRoutine Engine Torque System, SubRoutine Fuel Analysis and Measurement, SubRoutine Emissions, and SubRoutine Humidity.
Furthermore, the SubRoutine Fuel Analysis and Measurement refers to its own .xml database file, containing the chemical characteristics of the fuel used by the engine. In this way, the opportunity of monitoring the variation in terms of carbon, hydrogen, nitrogen, oxygen, and sulfur concentration of a fuel compared to another one is provided.
Routine Engine Characteristic: routine used to insert all the information concerning the engine;
Routine Turbocharger: routine used to insert all the information concerning the turbocharger.
With these Routines, the user must make a series of choices necessary to define a Set Up Environment that is able to identify uniquely both the sensors and instrumentations list installed and the Border Conditions required for the determination of computability of the following mathematical functions.
Among the choices, the user has also to answer about the presence on the SN of every sensor. If the sensor is not online, then the software requires manually inserting a constant value; otherwise, the variable name becomes available in the parsing phase for the matching with the relevant sensor.
3.3. Output
The Routines allow the calculation of several outputs: in particular, the following quantities, summarized in
Table 1, represent the most important parameters for Performance Evaluation.
Turbocharger efficiencies in terms of compressor efficiency
, turbine efficiency
, and overall efficiency
can be determined by both formulations contained in the literature (e.g., CIMAC [
19]) and formulations recommended by manufacturer (e.g. ABB and Mitsubishi).
The compressor pressure ratio (total to total) , turbine pressure ratio (total to partial) , and corrected turbocharger speed represent the inputs for the most common in-use compressor and turbine maps. Indeed, the implementation of in-live visualization of the operating point of the compressor and the turbine inside the relative map is still under study.
The Brake Specific Fuel Consumption (evaluated for each contribution of fuel, corrected for (ISO Lower Heating Value) of the fuel in use and total) and the Effective Compression Ratio are necessary to evaluate the engine consumption and its thermal efficiency.
Eventually, the main parameters for Performance Evaluation are NO
X, CO, CO
2, THC, O
2, and SO
2 concentrations, which are expressed in
. This unit of measurement is very important because is the one used to verify the compliance with the standards regarding air pollution established by MARPOL 2017 [
2].
Once these outputs have been calculated, to optimize the TDE’s functioning (in terms of both increasing turbocharger efficiency and decreasing fuel consumption and emissions, given in g/kWh), the engine automation, in the forthcoming future, will be directly connected with the tool by means of a dedicated Programmable Logic Controller (PLC). Thus, through the automatic modification of some electromechanical processes (such as wastegate opening and inlet and exhaust valve closure), the self-acting improving of Performance values will be achieved.
4. Tool Application to Evaluate Pollutant Emissions
For marine engines, pollution production is strictly related to their working. Indeed, pollutant substances such as NOX, CO, CO2, THC, O2, and SO2 are a natural consequence of the combustion process. However, their production can be mitigated through more efficient and high-performing engines and combustion process. In this regard, the use of a lower quantity of fuel, without affecting the output power, is one of the first measures to apply. Furthermore, also a cleaner combustion process ensures a significant reduction of pollutant emissions. As a result, in order to achieve the best performance from a TDE, it’s fundamental to keep a continuous monitoring and control of the engine while running.
As regards the paper’s subject, the evaluation of emissions will be thoroughly examined hereafter in terms of both the formulation’s explanation and Emission Routine’s logic. As a reference for the thermodynamic quantities, the WIT (Wärtsilä Italia) Convention (in
Appendix A) is used.
To define the polluting values in terms of , the exhaust mass flowrate must be calculated. As mentioned above, two methods have been identified:
By means of the Air Nozzle approach, from which the incoming air mass flowrate to the compressor can be measured, and then the exhaust mass flowrate can be calculated by simple mathematical steps; and
By means of the Carbon Balance method, from which the exhaust mass flowrate can be directly evaluated.
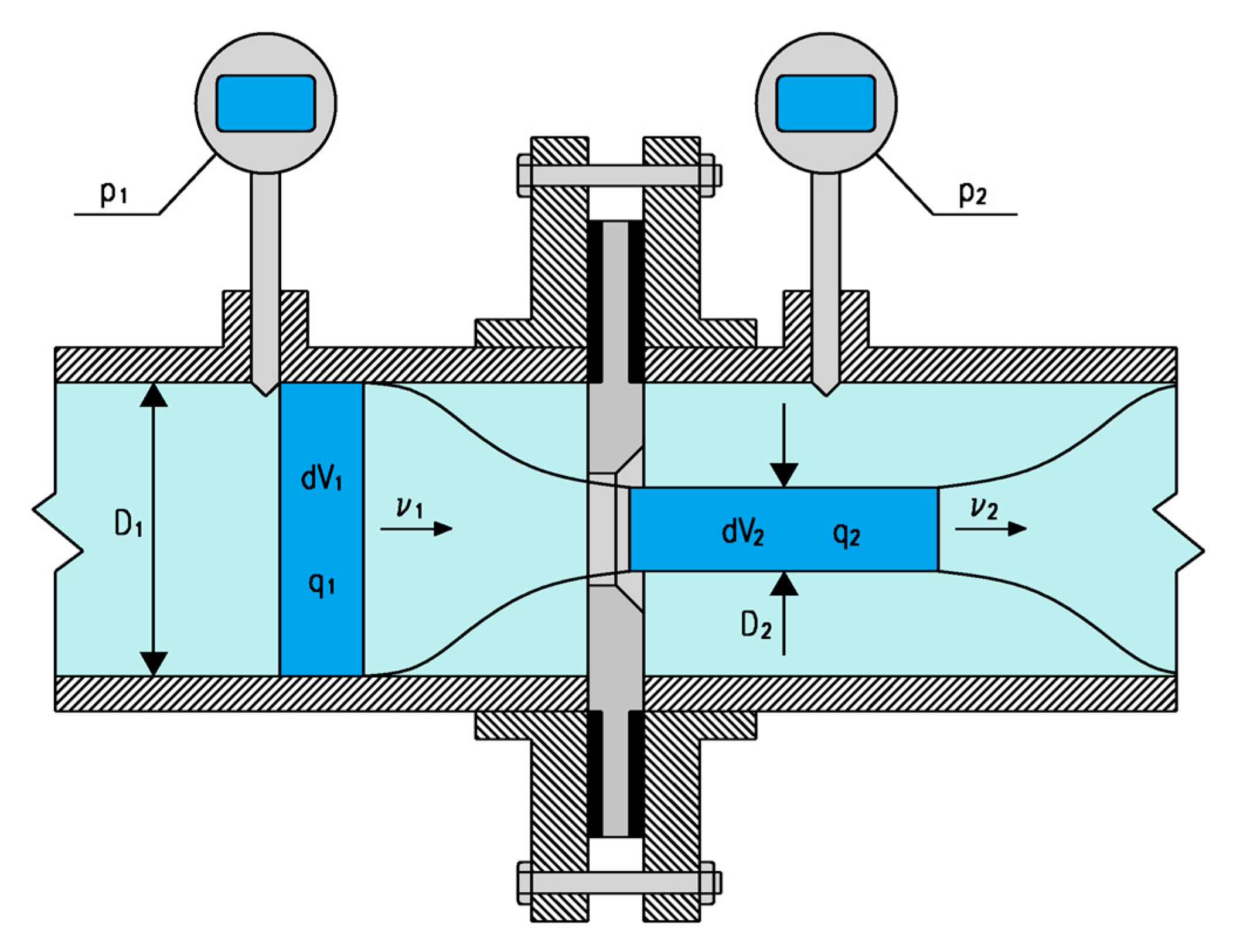
4.1. Air Nozzle Approach
The Air Nozzle is a device consisting of a convergent inlet connected to a cylindrical section installed at the compressor inlet. The reference Regulation regarding the Air Nozzle approach is the above-mentioned ISO 5167-3:2003 [
15].
In this approach, the formula for the air flowrate calculation is the same for both two-stroke and four-stroke engines. It derives from the Bernoulli’s equation for ideal fluids passing through a section shrinkage (
Figure 3). Indeed, for incompressible fluids, the following equation is valid:
in which subscripts “1” and “2” mark the fluid situation before/upstream and after/downstream the shrinkage, respectively. In both cases, the fluid situation must be measured at a point at which the flow can be considered stationary.
The continuity equation gives the following equation:
where:
Eventually, through the following equations, the ideal mass flowrate
can be calculated:
in which
is the density of the fluid.
The previous equations allowed calculating the ideal flowrate
. For the real flowrate, the following two coefficients are necessary:
Coefficient of discharge (non-dimensional coefficient): it takes into account friction, viscosity, and turbulence effects;
Expansion factor (non-dimensional coefficient): it takes into account fluid compressibility.
4.1.1. Coefficient of Discharge Calculation
The coefficient of discharge
can be calculated through formulations based on the following equations:
The formula for calculating
depends on the type of the Air Nozzle [
15]. In particular, we have the following different formulations:
Eventually, the formula for calculating the real mass flowrate
is the following:
in which
is defined as the flow shrinkage coefficient
(non-dimensional).
4.1.2. Expansion Factor calculation
In order to take into account the fluid compressibility, the expansion factor
must be introduced as follows:
where:
4.1.3. Real Flowrate Calculation
The previous equations can be combined to obtain the formulation for calculating the air flowrate as follows
:
in which:
is the Air Nozzle coefficient;
is the air density, equal to , where ;
is the orifice plate differential pressure. Usually, values are between and .
In order to take into account the measurement units used for
, it is necessary to introduce a small change in the previous formula as follows:
Eventually, it is worth noting that the air flowrate that effectively reaches the engine is lower, due to compressor losses. Moreover, a situation with multiple inlets to the turbocharger (
) could be the real one. As a result, the following equation is the most correct one to evaluate the real air flowrate
:
in which
represents the air loss within the compressor seal. Its approximated value is usually equal to 1.5%.
Finally, the exhaust mass flowrate
can be calculated as follows:
where
the total brake-specific fuel consumption, which is defined below. Indeed, for the flow equivalence principle, the exhaust mass flowrate is equal to the air mass flowrate plus the burnt-fuel flowrate.
4.2. Carbon Balance Method
The Carbon Balance method allows calculating the exhaust flowrate by means of the concentration of some components of the exhaust gases and the fuel concentration and consumption. The approach is regulated within the revision of MEPC (Marine Environment Protection Committee) Resolution 176(58)|2008 [
20], of the NOx Technical Code 2008 [
16] and partially within the EU 2016/802 [
21].
In order to apply this method, both fuel analyses and sensors able to evaluate exhaust gases and calculate engine consumptions are necessary.
In the following sections, thermodynamics quantities will be distinguished on the basis of their water content in two categories: wet and dry quantities. This is important because some sensors could be damaged while measuring quantities (e.g., oxygen detectors).
Another important necessary distinction is related to dual-fuel engines: indeed, for some quantities, the fuel gas duration injection will be reported. In particular, a fuel gas duration injection < 1 µs implies an engine working with fuel oil; in such a way, the transition between fuel and gas will not be considered.
4.2.1. Demonstration of the Carbon Balance Method
The basic assumption of the Carbon Balance method implies that the exhaust gas components are in the form of CO, CO
2, and HC (HydroCarbon). Consequently, the flowrate of wet exhaust gases is defined by the following equation [
16]:
This formula is based on the principle for which the carbon-inlet quantity is equal to the carbon-outlet quantity: Carbon in = Carbon out. The following sections will clearly define the meaning of the two quantities.
Carbon in
The carbon-inlet quantity is calculated through the following formula:
where
is the net fuel flowrate and
is the carbon content in the fuel mixture, which is calculated as follows:
in which:
where:
is the net fuel flowrate;
is the fuel flowrate, losses included;
is the mass of fuel lost;
is the engine power;
is the losses measurement time.
is the brake-specific pilot fuel consumption, which is calculated with the following formula:
in which is the pilot fuel flowrate and is the engine power.
: fuel gas carbon content;
brake-specific fuel gas consumption, equal to where is the gas flowrate and is the engine power.
is the total brake-specific fuel consumption, which is calculated through the following formulae:
Carbon out
The carbon-outlet quantity is calculated through the following formula:
in which:
is the relative carbon mass;
and are the substances flowrate emissions;
and are the molar masses of pollutant.
Emissions can be calculated through the following general equation:
where
is the molar mass and the molar volume of pollutant CO
2, CO, or HC, respectively. It is worth noting that the molar mass/molar volume ratio of a pollutant is equal to its density, as shown below:
As a result, by substituting the density in the carbon out formulation, the following equation is obtained:
Exhaust gas density calculation
The exhaust gas density is equal to the ratio between mass flowrate
and volumetric flowrate
:
The volumetric flowrate
can be calculated by summing up the volumetric flowrate of all the exhaust gas components; however, since they are dependent mainly on CO, CO
2, and HC content, the formula can be simplified as follows:
The last expression of
implies that the exhaust gas volumetric flowrate is calculated by taking into account also the water content (i.e., it is a wet quantity). To obtain the dry exhaust gas volumetric flowrate, the water contribution
must be deducted as follows:
The volumetric flowrate for CO and HC can be evaluated through the single components concentrations as follows:
On the other hand, as regards the volumetric flowrate for H
2O and CO
2, the following formulae must be used:
These equations are based on the principle for which water and carbon dioxide are contained also in the combustion air; therefore, to consider it, a first addend, whose factors are described below, is necessary:
is the wet mass flowrate of the combustion air;
are the concentration of water and carbon dioxide in the combustion air, respectively;
4.2.2. Carbon Balance Quantities
The quantities in the Carbon Balance method are the following:
fuel flowrate;
emission carbon factor. It is a coefficient that allows converting activity data into GHG emissions and is calculated as follows:
where the dry quantities are the
[%] (concentration of CO
2 in the ambient air),
(concentration of CO
2 and CO in the exhaust gas, respectively), while
(concentration of HC in the exhaust gas) is a wet quantity. Since the carbon dioxide can be found in larger quantities than the other components, it is usually measured in percentage;
: absolute moisture in the aspiration air, defined as the ratio between steam density and dry air density at the same temperature;
carbon content in the fuel mixture;
hydrogen content in the fuel mixture;
fuel dry specific constant for exhaust gases, calculated as follows:
The basic assumption of the Carbon Balance method is flawed: indeed, since it considers only the emissions based on carbon (CO, CO2 and HC), it eliminates all the other components based on nitrogen and oxygen (e.g., nitrogen oxides NOX and the oxygen itself). Consequently, corrective coefficients able to consider all the other fuel components are necessary:
4.3. Emissions Calculation
The values of pollutant concentration measured by the emission sensors are the basis for the calculation of emissions, which are calculated through the following formula:
Here, two new quantities are introduced:
dry to wet coefficient, used to convert a dry quantity to a wet one by means of the following formulation provided in [
16]:
component specific factor, equal to the ratio between gas component density (
Table 2) and exhaust gas density. The NO
X Technical Code [
16] provides specific tables containing
values (
Table 3).
Formula (32) for the calculation of emissions is applicable to all the pollutant emissions except for nitrogen oxides, due to their dependency on ambient air conditions. A coefficient that takes into account ambient air temperature and moisture is introduced as follows:
where
is the nominal air receiver temperature. The coefficient
applies to the moisture range
.
As a result, the NO
X emissions can be calculated as dry quantities with the formula:
The emissions calculated as wet quantities can be obtained omitting the coefficient in the previous Formula (35).
4.4. Emission SubRoutine
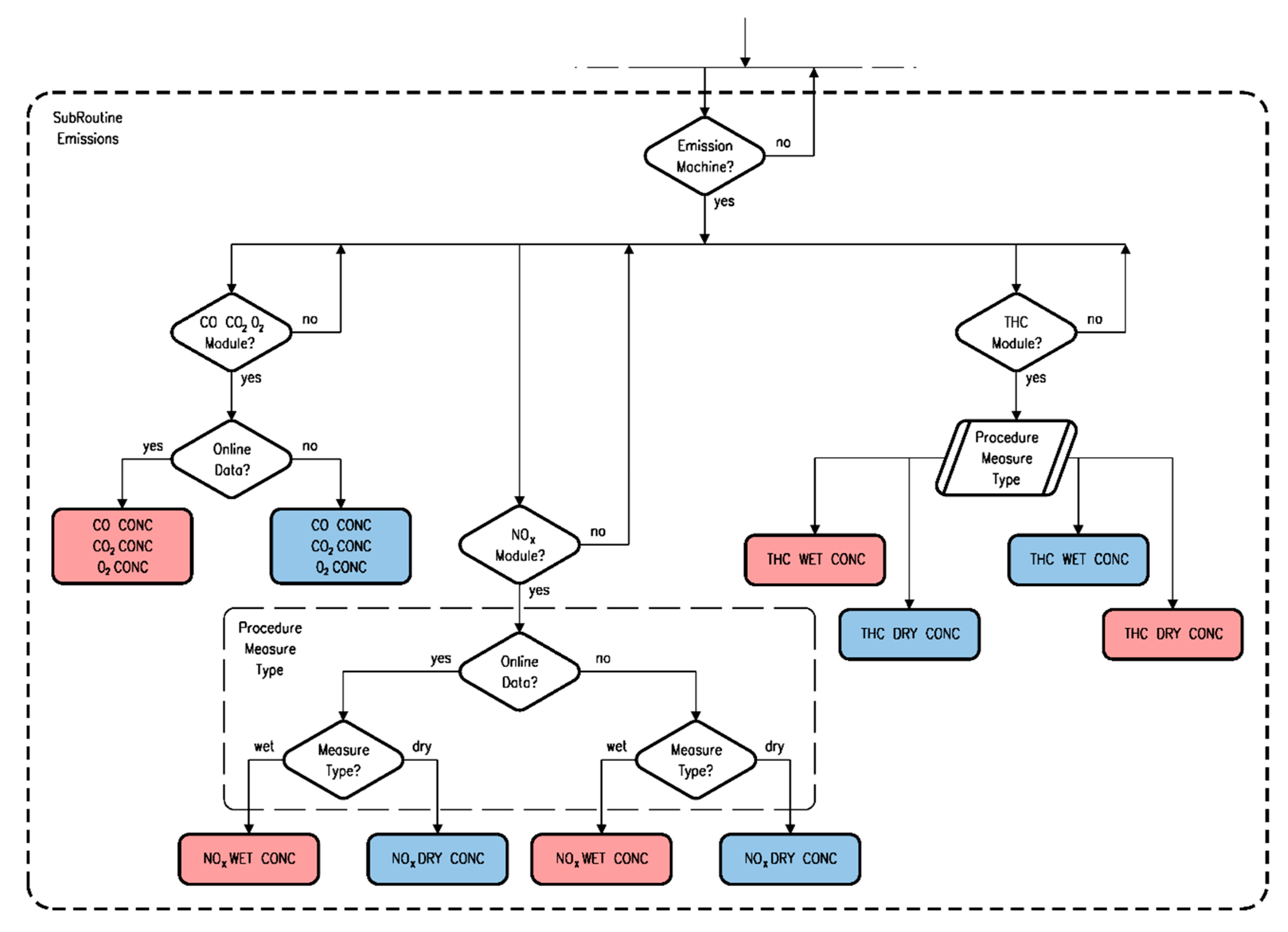
The Emission SubRoutine (
Figure 4) is the part of the code dedicated to managing the user’s choices in terms of modules for emissions detection within the Test Bed. The current analyses have identified three modules for the emissions detection:
CO/CO2/O2 module;
NOX module;
THC module.
As mentioned previously, in this Routine, the user is called to answer the presence of every above-listed module in the SN (in
Figure 4, the red boxes represent Online data, which are available for the parsing, while the blue ones represent Offline data, to insert as a constant value).
Finally, as regards the NOX and THC modules, the user is called to answer another important question about the method used for acquiring emissions values. Indeed, the measurement of these pollutants can be performed either with or without the water contribution; in the first case, the software refers to wet measurements, whereas in the second one, the software refers to dry measurements. For practical purposes, the main difference between these two cases lies in the coefficient that is present or not in Formula (32).
5. Tool–First Validation
In order to make a first validation about the correct working of the software, a comparison between the results obtained from both the tool and the WIT offline procedure, based on the same engine configuration, has been carried out.
The configuration used for this comparison (
Table 4) is about a Test Bed with an in-line four-stroke engine W6L50DF, a two-stage ABB turbocharger and, as equipment, an Air Nozzle and emission machine with all the pollution detection modules.
The analyzed operating point is at 110% of the engine nominal load in only gas mode.
To perform this comparison, the pilot contribution to the combustion and the nitrogen and oxygen values in the fuel gas were not considered due to their negligible values.
Once the Set Up Environment has been properly generated (
Table 5) and the parsing has been performed, the software determined which functions had to be calculated, verifying whether the Border Conditions were fulfilled or not. On the basis of the selected engine configuration, the software established 111 calculable functions out of 584.
Table 6,
Table 7 and
Table 8 presents the output of the first validation of the tool determined by both Air Nozzle and Carbon Balance methods, compared with the same features evaluated by the WIT offline procedure.
The root mean square error of all features evaluated with the tool and the WIT offline procedure is equal to 1.46%, which is a more than acceptable result given the extent of the analyzed quantities.
6. Conclusions
The paper presents a tool for the evaluation of the performance in-live of turbocharged diesel engines for marine application. The tool has been developed in G-Language within the LABVIEW environment; its management is very simple and rapid, even if it requires many formulas in order to reliably describe the thermodynamic phenomena resulting from supercharged combustion inside the engine. One of the main challenges fought has concerned a process of synthesis and selection of the input variables, which are in large part to be acquired from the network of sensors installed on the engine. In order to fully describe the engine performance, 584 different formulas were used in the different routines and subroutines. In the present work, the routine for evaluating air pollutant emissions in terms of NOX, SOX, COX and HC has been completely described. In particular, the two methods that are used (i.e., the Air Nozzle approach and Carbon Balance approach) have been thoroughly presented.
The great novelty offered by this tool is the ability of processing all the data detected by the sensor network in-live in order to monitor and dynamically optimize the TDEs’ operation, whereas the common practice involves the collection of performance data and then their off-line processing. The connection between the presented tool and the automation of the TDEs is currently under development. In this way, the software, in the forthcoming future, will be able to automatically act on the electromechanical processes of TDEs from the perspective of Performance improvement. All this has been made possible thanks to the commitment of the engine manufacturers in the implementation of the principles of Industry 4.0. In particular, in order to offer the market increasingly cheaper products (in terms of fuel consumption) and maintenance costs, the new engines are equipped with a dense network of sensors that is capable of measuring all the quantities related to the definition of the engine performance. The processing of this large amount of in-live data and the further connection with the various actuators able to perform all the adjustments on the engine makes the TDEs of the latest generation very competitive. In recent years, the competition among the various global marine engine manufactures is in fact being fought not only from an economic point of view, but also in the continuous research for new technological solutions that are capable of satisfying all the international regulations issued in order to preserve the global environment.
In order to reduce the release of polluting substances into the atmosphere, many new technologies have been invented and applied in ship propulsion systems. The use of alternative fuels to HFO has been studied, and eventually, LNG can be considered a valid option (even if in this specific case, the bunkering logistics network is not adequately functional at a global level). Hydrogen and ammonia seem very promising, but currently, there is no availability of the large quantities needed to refuel ships and the cost is orders of magnitude greater than that of HFO; moreover, ship propulsion systems would become even more complex than they are.
In this scenario, shipowners need to make adequate profits in order to be able to carry out their service continuously. They cannot operate their ships unless they comply with the international regulations in force. Therefore, the use of the tool described in this paper will certainly benefit them because TDEs working near the efficiency peak will reduce fuel consumption and maintenance, reducing the periods of inactivity of the ship. Future developments of this work (already under consideration) will concern the live visualization of the operating point of the compressor and the turbine within the relative map and the addition of further components for the detection of PM and lightning. Furthermore, the software will be equipped with a digital twin routine: by comparing the real behavior of the engine with the expected one, it will be possible to predictively identify any wear and tear of components inside the engine and set an artificial intelligence to autonomously modify the operating parameters with a view to optimizing consumption, performance, energy, and maintenance.
Author Contributions
Conceptualization, M.D. and V.B.; methodology, M.D. and V.B.; software, M.D.; validation, M.D. and S.B.; formal analysis, M.D. and S.B.; investigation, M.D.; resources, A.M.; data curation, M.D.; writing—original draft preparation, M.D. and S.B.; writing—review and editing, A.M. and V.B.; visualization, M.D., S.B., A.M. and V.B.; supervision, A.M. and V.B.; project administration, V.B.; funding acquisition, A.M. and V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by 2014–2020 Interreg V-A, Italy-Croatia CBC Programme, by means of the 2017 Standard call research project “METRO—Maritime Environment-friendly TRanspOrt systems”, Priority Axis: Maritime transport.
Acknowledgments
The authors gratefully acknowledge Wärtsilä Italia S.p.a. for the high skilled technical support received in order to carry out the studies described in this work.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Incoming air mass flowrate to the compressor [kg/s] |
| Discharge coefficient |
| Expansion coefficient |
| Exhaust gas mass flowrate [kg/s] |
| Incoming air mass flowrate to the engine [kg/s] |
| Compressor efficiency [%] |
| Turbine efficiency [%] |
| Overall efficiency of turbocharger [%] |
| Compressor pressure ratio |
| Turbine pressure ratio |
| Corrected turbocharger speed [rpm] |
| Brake-Specific Fuel Consumption [g/kWh] |
| ISO correction Brake-Specific Fuel Consumption [g/kWh] |
| Total Brake-Specific Fuel Consumption [g/kWh] |
| Ideal mass flowrate [kg/s] |
| Section diameters ratio |
| Reynolds number for shrinkage |
| Real mass flowrate [kg/s] |
| Flow shrinkage coefficient |
| Pressure ratio |
| Adiabatic expansion coefficient |
| Air Nozzle coefficient [m2] |
| Air density [kg/m3] |
| Orifice plate differential pressure [mbar] |
| Air Nozzle incoming mass flowrate to the compressor [kg/s] |
| Air loss within the compressor seal [%] |
| Number of turbochargers |
| Engine power [kW] |
| Carbon-inlet quantity [kg/h] |
| Net fuel flowrate [kg/h] |
| Carbon content in fuel mixture [% mass] |
| Carbon content in the primary fuel [% mass] |
| Brake-Specific Fuel Consumption minus losses [g/kWh] |
| Fuel flowrate, losses included [kg/h] |
| Mass of fuel lost [g] |
| Losses measurement time [min] |
| Pilot Brake-Specific Fuel Consumption [g/kWh] |
| Pilot fuel flowrate [g/h] |
| Fuel gas carbon content [% mass] |
| Brake-Specific Fuel gas Consumption [g/kWh] |
| Fuel gas flowrate [kg/h] |
| Carbon-outlet quantity [kg/h] |
| Carbon relative atomic mass [g] |
| Pollutant emissions [g/h] |
| Pollutant molar mass [g/mol] |
| Pollutant molar volume [m3/mol] |
| Pollutant concentration |
| Exhaust gas density [kg/m3] |
| Wet exhaust gas volumetric flowrate [m3/h] |
| Dry exhaust gas volumetric flowrate [m3/h] |
| Wet mass flowrate of combustion air [kg/h] |
| Water content in combustion air [% mass] |
| Carbon dioxide content in combustion air [% mass] |
| Water density [kg/m3] |
| Carbon dioxide density [kg/m3] |
| Emission carbon factor |
| Absolute moisture in aspiration air |
| Hydrogen content in fuel mixture [% mass] |
| Fuel dry specific constant for exhaust gas |
| Nitrogen content in fuel mixture [% mass] |
| Oxygen content in fuel mixture [% mass] |
| Dry to wet coefficient |
| Component specific factor |
| Ambient-air temperature and moisture coefficient |
| Air receiver temperature [°C] |
Abbreviations
| ABB | Asea Brown Boveri |
| CIMAC | International Council on Combustion Engines |
| CO | Carbon Monoxide |
| CO2 | Carbon Dioxide |
| ECR | Effective Compression Ratio |
| EU | European Union |
| GHG | GreenHouse Gases |
| HC | HydroCarbon |
| HFO | Heavy Fuel Oil |
| ICE | Internal Combustion Engine |
| IMO | International Maritime Organization |
| ISO | International Organization for Standardization |
| LABVIEW | Laboratory of Virtual Instrumentation and Engineering Workbench |
| LHVISO | ISO Lower Heating Value |
| LNG | Liquefied Natural Gas |
| MARPOL | International Convention for the Prevention of Marine Pollution |
| MEPC | Marine Environment Protection Committee |
| NOX | Nitrogen Oxides |
| O2 | Oxygen |
| PLC | Programmable Logic Controller |
| SCR | Selective Catalytic Reduction |
| SEEMP | Ship Energy Efficiency Management Plan |
| SN | Sensor Network |
| SO2 | Sulphur Dioxides |
| TC | Turbocharger |
| TDE | Turbocharged Diesel Engine |
| THC | Total HydroCarbon |
| WIT | Wärtsilä Italia |
Appendix A
In the paper, the following WIT Convention is used to standardize the terms/words related to thermodynamic quantities (i.e., pressure and temperature [°C]) within performance documents. It was chosen for the following reasons:
The WIT standard simplifies reading formulae in internal documentation;
On test engines, the sensors for thermodynamic quantities (e.g., pressure gauges and thermocouples) are installed on the basis of the WIT convention, and then additional calculations are not necessary;
The WIT standard does not distinguish between four-stroke and two-stroke engines. The only difference in terms of number of sensors refers to single-stage and double-stage cases.
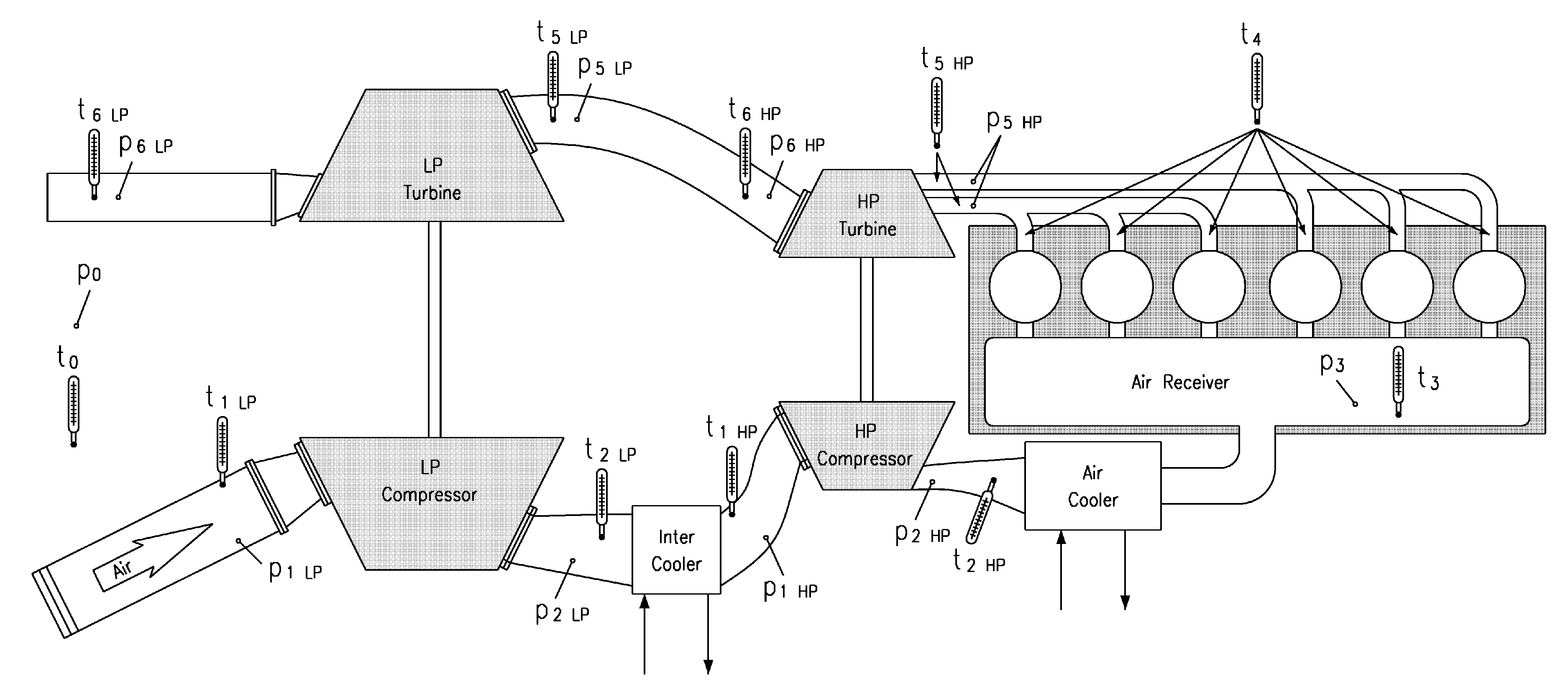
Single-stage case
As regards the single-stage case (single turbocharger), with reference to
Figure A1, the WIT convention is the following:
Subscript “0” marks all the room/atmospheric/ambient-condition quantities;
Subscript “1” marks all the compressor-inlet quantities;
Subscript “2” marks all the compressor-outlet quantities;
Subscript “3” marks all the air-receiver quantities;
Subscript “4” marks the exhaust-gas manifold temperature, calculated as the average of all the exhaust-gas manifold temperatures (each single temperature is marked through an additional subscript that specifies the cylinder number). It is worth noting that the exhaust-gas pressure is not calculated due to its significant fluctuation;
Subscript “5” marks all the turbine-inlet quantities. It is worth noting that, in this case, the pressure value is stationary and can be measured;
Subscript “6” marks all the turbine-outlet quantities.
Figure A1.
WIT convention: single-stage case.
Figure A1.
WIT convention: single-stage case.
As regards measurement units, the WIT uses the following:
Room/atmospheric pressure [mbar];
Compressor-inlet pressure [mbar];
Compressor-outlet pressure [bar];
Receiver pressure [bar];
Turbine-inlet pressure [bar];
Turbine-outlet pressure [bar];
Temperatures [°C].
The standard for measurement units simplifies the measurement process of quantities, but it also has some disadvantages. Indeed, since the SI unit for pressure is Pascal [Pa] and for temperature is Kelvin [K], proper transformations are needed.
Double-stage case
As regards the double-stage case (two turbochargers in series), the WIT convention is the following, and it is sketched in
Figure A2:
Subscript “0” marks all the room/atmospheric/ambient-condition quantities;
Subscript “1LP” marks all the low-pressure compressor-inlet quantities;
Subscript “2LP” marks all the low-pressure compressor-outlet quantities;
Subscript “1HP” marks all the high-pressure compressor-inlet quantities;
Subscript “2HP” marks all the high-pressure compressor-outlet quantities;
Subscript “3” marks all the air-receiver quantities;
Subscript “4” marks the exhaust-gas manifold temperature, calculated as the average of all the exhaust-gas manifold temperatures;
Subscript “5HP” marks all the high-pressure turbine-inlet quantities;
Subscript “6HP” marks all the high-pressure turbine-outlet quantities;
Subscript “5LP” marks all the low-pressure turbine-inlet quantities;
Subscript “6LP” marks all the low-pressure turbine-outlet quantities.
Figure A2.
WIT convention: Double-stage case.
Figure A2.
WIT convention: Double-stage case.
As regards measurement units, the WIT uses the following:
Room/atmospheric pressure [mbar];
Compressor-inlet pressure and [mbar];
Compressor-outlet pressure and [bar];
Receiver pressure [bar];
High-pressure turbine-inlet pressure [bar];
High-pressure turbine-outlet pressure , low-pressure turbine-inlet pressure and low-pressure turbine-outlet pressure [bar];
Temperatures [°C].
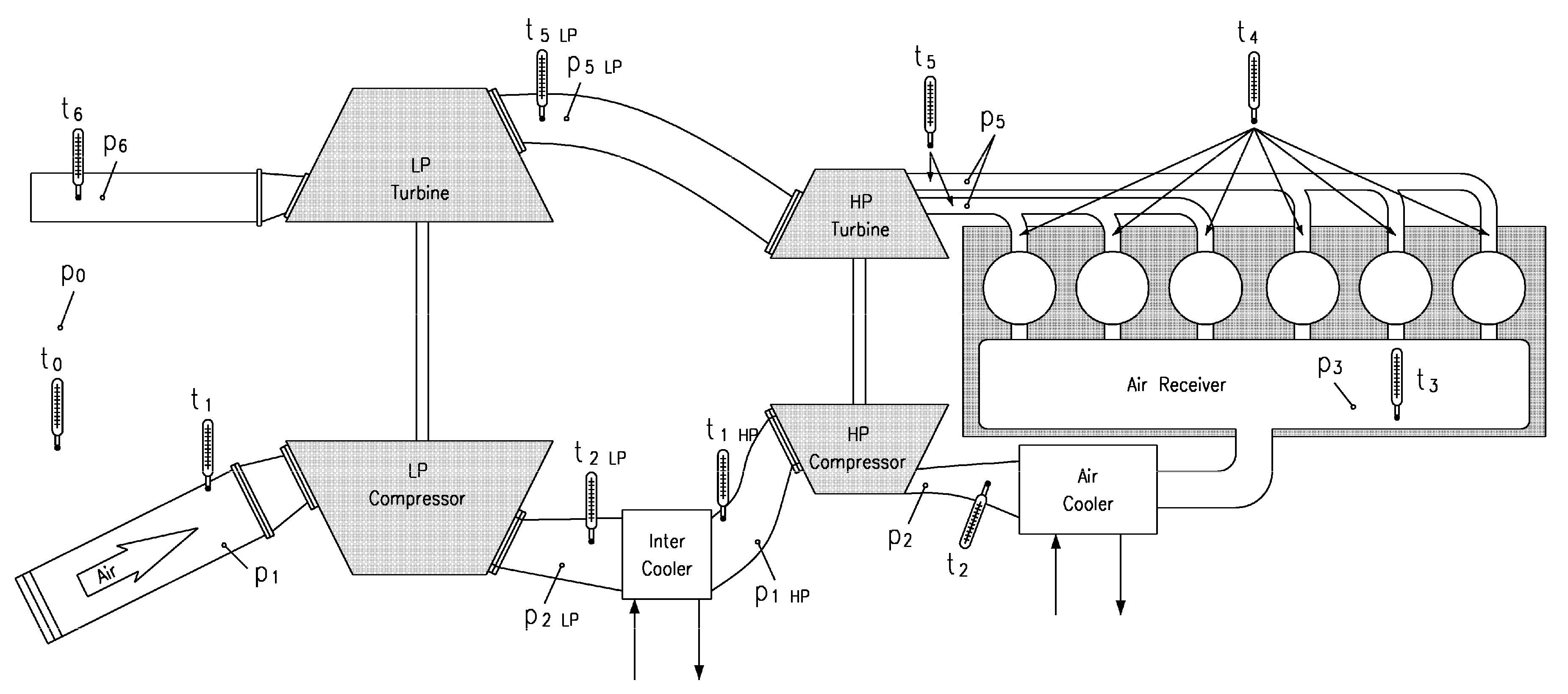
In order to simplify calculations, the previous convention was slightly modified, in particular with reference to inlet and outlet quantities. Indeed, the double-stage case can be equated to a single-stage case having the following characteristics:
Compressor inlet = low-pressure compressor inlet;
Compressor outlet = high-pressure compressor outlet;
Turbine inlet = high-pressure turbine inlet;
Turbine outlet = low-pressure turbine outlet.
In addition, thermodynamic quantities regarding the high-pressure turbine outlet and the low-pressure turbine inlet can be simplified. Since these values are very similar, they are considered equal and marked with the subscript “5LP” (the subscript of low-pressure turbine-inlet quantities).
In conclusion, the modified WIT convention for double-stage cases is presented in
Figure A3.
Figure A3.
Modified WIT convention: Double-stage case.
Figure A3.
Modified WIT convention: Double-stage case.
References
- Brenna, M.; Bucci, V.; Falvo, M.C.; Foiadelli, F.; Ruvio, A.; Sulligoi, G.; Vicenzutti, A. A review on energy efficiency in three transportation sectors: Railways, electrical vehicles and marine. Energies 2020, 13, 2378. [Google Scholar] [CrossRef]
- International Maritime Organization. International Convention for the Prevention of Pollution from Ships-MARPOL 2017 Consolidated Edition. Available online: http://www.imo.org/en/Publications/Documents/Supplements%20and%20CDs/English/QQE520E_022019.pdf (accessed on 14 February 2020).
- International Maritime Organization. Third IMO Greenhouse Gas Study. Available online: http://www.imo.org/en/OurWork/Environment/PollutionPrevention/AirPollution/Documents/Third%20Greenhouse%20Gas%20Study/GHG3%20Executive%20Summary.pdf (accessed on 14 February 2020).
- Altosole, M.; Benvenuto, G.; Campora, U.; Laviola, M.; Zaccone, R. Simulation and performance comparison between diesel and natural gas engines for marine applications. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 690–704. [Google Scholar]
- Taccani, R.; Ustolin, F.; Zuliani, N.; Pinamonti, P.; Pietra, A. Fuel Cells and Shipping Emissions Mitigation, Technology and Science for Ships of the Future. Proceedings of NAV 2018: 19th International Conference on Ship & Maritime Research, Trieste, Italy, 20–22 June 2018; pp. 885–892. [Google Scholar]
- Kim, K.; Roh, G.; Kim, W.; Chun, K. A preliminary study on an alternative ship propulsion system fueled by ammonia: Environmental and economic assessments. J. Mar. Sci. Eng. 2020, 8, 183. [Google Scholar] [CrossRef]
- Brynolf, S.; Fridell, E.; Andersson, K. Environmental assessment of marine fuels: Liquefied natural gas, liquefied biogas, methanol and bio-methanol. J. Clean. Prod. 2014, 74, 86–95. [Google Scholar] [CrossRef]
- Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. Optimising design and power management in energy-efficient marine vessel power systems: A literature review. J. Mar. Eng. Technol. 2019, 18, 92–101. [Google Scholar] [CrossRef]
- Muše, A.; Jurić, Z.; Račić, N.; Radica, G. Modelling, performance improvement and emission reduction of large two-stroke diesel engine using multi-zone combustion model. J. Therm. Anal. Calorim. 2020, 141, 337–350. [Google Scholar]
- Stoumpos, S.; Theotokatos, G.; Mavrelos, C.; Boulougouris, E. Towards marine dual fuel engines digital twins-integrated modelling of thermodynamic processes and control system functions. J. Mar. Sci. Eng. 2020, 8, 200. [Google Scholar] [CrossRef]
- Ntonas, K.; Aretakis, N.; Roumeliotis, I.; Pariotis, E.; Paraskevopoulos, Y.; Zannis, T. Integrated simulation framework for assessing turbocharger fault effects on diesel-engine performance and operability. J. Energy Eng. 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Altosole, M.; Campora, U.; Figari, M.; Laviola, M.; Martelli, M. A diesel engine modelling approach for ship propulsion real-time simulators. J. Mar. Sci. Eng. 2019, 7, 138. [Google Scholar] [CrossRef]
- Aiello, G.; Giallanza, A.; Vacante, S.; Fasoli, S.; Mascarella, G. Propulsion monitoring system for digitized ship management: Preliminary results from a case study. Procedia Manuf. 2020, 42, 16–23. [Google Scholar] [CrossRef]
- ISO 5167-1:2003. In Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full-Part 1: General Principles and Requirements; International Organization for Standardization (ISO): Geneva, Switzerland, 2003.
- ISO 5167-3:2003. In Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full-Part 3: Nozzles and Venturi Nozzles; International Organization for Standardization (ISO): Geneva, Switzerland, 2003.
- Marine Environment Protection Committee. Amendments to the Technical Code on Control of Emission of Nitrogen Oxides from Marine Diesel Engines (NOx Technical Code 2008). Resolution MEPC 177(58). Available online: http://www.imo.org/en/KnowledgeCentre/IndexofIMOResolutions/Marine-Environment-Protection-Committee-(MEPC)/Documents/MEPC.177(58).pdf#search=Amendments%20to%20the%20technical%20code%20on%20control%20of%20emission%20of%20Nitrogen%20Oxides%20from%20marine%20Diesel%20Engines%20%28NOx%20Technical%20Code%202008%29%2E%20Resolution%20MEPC%20177%2858%29 (accessed on 14 February 2020).
- ISO 8178-1:1996. In Reciprocating Internal Combustion Engines—Exhaust Emission Measurement—Part 1: Test-Bed Measurement of Gaseous and Particulate Exhaust Emissions; International Organization for Standardization (ISO): Geneva, Switzerland, 1996.
- ISO 8217-4:2010. In Petroleum Products—Fuel (Class F). Specification of Marine Fuels; International Organization for Standardization (ISO): Geneva, Switzerland, 2010.
- International Council of Combustion Engines. Turbocharging Efficiency. Definitions and Guidelines for Measurement and Calculation. Available online: https://www.cimac.com/cms/upload/Publication_Press/Recommendations/Recommendation_27_rev_081007.pdf (accessed on 14 February 2020).
- Marine Environment Protection Committee. Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ship, 1973, as Modified by the Protocol of 1978 Relating Thereto. Resolution MEPC 176(58) 2008. Available online: http://www.imo.org/en/OurWork/Environment/PollutionPrevention/AirPollution/Documents/176(58).pdf#search=176%2058 (accessed on 14 February 2020).
- European Commision. Directive (EU) 2016/802 of the European Parliament and of the Council of 11 May 2016 Relating to a Reduction in the Sulphur Content of Certain Liquid Fuels. EU 2016/802. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1597385743484&uri=CELEX:32016L0802 (accessed on 14 February 2020).
- European Commission. Annex 7: Technical and General Requirements Relating to Emission Limits and Type-Approval for Internal Combustion Engines for Non-Road Mobile Machinery C(2016)-8381. Available online: https://ec.europa.eu/transparency/regdoc/rep/3/2016/EN/C-2016-8381-F1-EN-ANNEX-1-PART-1.PDF (accessed on 14 February 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).