A Clustering-Based Bubble Method for Generating High-Quality Tetrahedral Meshes of Geological Models

Abstract

High-quality mesh generation is critical in the finite element analysis of displacements and stabilities of geological bodies. In this paper, we propose a clustering-based bubble method for generating high-quality tetrahedral meshes of geological models. The proposed bubble method is conducted based on the spatial distribution of the point set of given surface meshes using the clustering method. First, the inputted geological models consisting of triangulated surface meshes are divided into several parts based on spatial distribution of point set, which can be used for the determination of the positions and radii of initial bubbles. Second, a procedure based on distance of nearby bubbles is used to obtain the initial size of bubbles. Third, by enforcing the forces acting on bubbles, all bubbles inside the 3D domain reach an equilibrium state by the motion control equations. Finally, the center nodes of the bubbles can form a high-quality node distribution in the domain, and then the required tetrahedral mesh is generated. Comparative benchmarks are presented to demonstrate that the proposed method is capable of generating highly well-shaped tetrahedral meshes of geological models.

1. Introduction

Numeral simulation has been applied to solve many problems in various fields, and mesh generation always is a vital topic in finite element analysis. Among the mesh generation algorithms, Delaunay triangulation [1,2,3,4], the advancing front technique [5], the mapping method [6] have been widely developed and applied due to the high quality of the generated mesh and easy implementation of the algorithms. Many researchers have focused on tetrahedral mesh generation methods [7,8]. For example, Meng [9,10] proposed a novel link-Delaunay-triangulation method to achieve geometric and topological consistency. Indirect methods [11,12] were proposed to convert Delaunay triangular meshes into quadrilateral meshes by combining adjacent pairs of triangles. Constrained triangulated surfaces can be used to mesh a three-dimensional geological model by using a series of tetrahedral meshes [13,14]. Other methods [15,16] for generating three-dimensional meshes were also proposed.

Moreover, Shimada et al. [17] and Yamakawa [18] first proposed the bubble method for mesh generation of the non-manifold geometry. This method generates point sets and the Delaunay triangulation technique is used for mesh generation. Yokoyama [19] proposed an algorithm for three-dimensional bubble mesh generation. In this method, many points were inserted by the mapping-based method. Zhang [20] used bubble method to discretize two-parameter surfaces into a high-quality mesh. Guo [21,22] proposed a fast local mesh generation algorithm based on the node-set generated by this method and proposed a subdivided dynamic bubble system to shorten the calculation time. Wang [23] presented an automatic triangular mesh generation method, based on bubble dynamics simulation and a modified Delaunay method to generate high-quality mesh on complex surfaces efficiently. Jeong-Hun Kim [24] implemented bubble method for adaptive mesh generation in two and three dimensions.

The geological model is a three-dimensional model representing the ground surface, strata, and faults, which consists of multiple geological blocks describing the structure and geometry of the stratum. Each block in the model has a different shape. The thin layer and the fault are very flat geometry, and the thick layer is a very thick geometry. Therefore, when the geological model is transformed into a numerical model, the geological model needs to be divided into the high-quality mesh to meet a balance between calculation accuracy and efficiency.

In this paper, we propose a clustering-based bubble method for generating high-quality tetrahedral meshes of geological models. The proposed bubble method is conducted based on the spatial distribution of point set of given surface meshes using the clustering method. There are four main procedures in the method. First, the inputted geological models consisting of triangulated surface meshes are divided into several parts based on spatial distribution of point set, which can be used for the determination of the positions and radii of initial points. Second, a procedure based on distance of nearby bubbles is used to obtain the initial size of bubbles. Third, by enforcing the forces acting on bubbles, all bubbles inside the 3D domain reach an equilibrium state by the motion control equations. Finally, the center node of the bubble can form a high-quality node distribution in the domain, and then the required tetrahedral mesh is generated.

The novelty of the proposed method can be explained as follows. As mentioned above, most of the above bubble methods focus on two-dimensional cases and three-dimensional parameter surface. However, since geological structures and conditions are generally quite complex, a three-dimensional geological model cannot be well represented by parametric surfaces but can be well represented of triangulated surfaces. The proposed bubble method is specifically proposed to generate the high-quality meshes of geological models consisting of triangulated meshes.

The main contributions of this paper can be summarized as follows.

(1)

We apply the clustering algorithm based on the spatial distribution to divide the surface points for determining the initial bubbles.

(2)

A procedure based on the distance of nearby bubbles to determine the initial size of bubbles.

(3)

We evaluate the quality of the tetrahedral mesh in the geological model using three indicators.

The structure of this paper is organized as follows. Section 1 introduces related research about mesh generation for surfaces and three-dimensional domains. Section 2 introduces the background of bubble meshing method. Section 3 introduces the method for geological model discretization based on the physical analogy between nodes and bubbles. In Section 4, mesh quality indices are introduced to evaluate the resultant meshes and applications to demonstrate the effectiveness are provided. In Section 5, the advantages and shortcomings are analyzed. Finally, the presented work is concluded in Section 6.

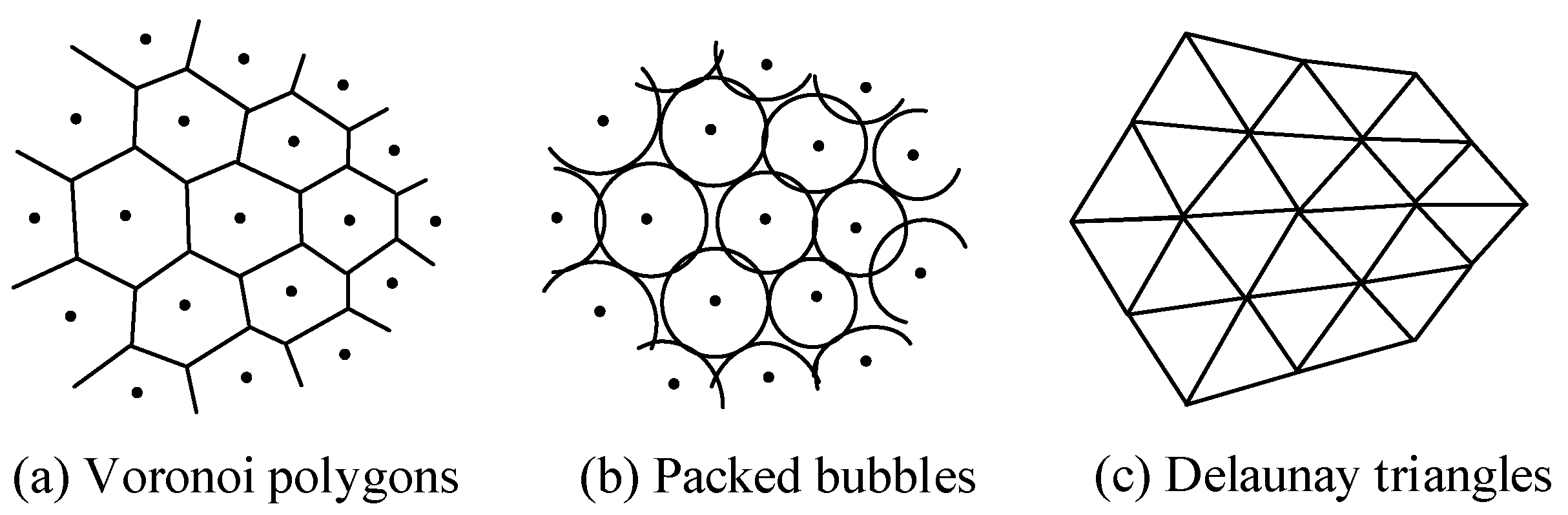
2. Brief Introduction to the Original Bubble Meshing Method

The original bubble meshing method is proposed by Shimada et al. [17]. Bubble meshing is based on the observation that the shape of a bubble simulates a Voronoi diagram, where a set of Delaunay triangles and tetrahedrons are created by connecting the centers of the bubble, see Figure 1. In order to obtain a close bubble distribution, a physical relaxation method with a controlled force is introduced. Given the geometric domain and spacing function, all bubbles inside the 3D domain will reach equilibrium through the force acting on the bubbles. When the bubbles fill the domain, connecting the center of the bubble to form a triangle and a tetrahedron. During adaptive filling, the mesh relaxation process reduces the number of badly shaped triangles.

2.1. Initial Bubble Placement

It is critical to obtain a good initial bubble configuration before physically-based relaxation. A bubble placement method based on hierarchical spatial subdivision was proposed for general node spacing. Bubbles are packed on all vertices (0-cells) in the non-manifold model, see Figure 2b. All curves are filled in with bubbles (l-cells), see Figure 2c. Bubbles are packed on all surfaces (2-cells), see Figure 2d. And all volumes (3-cells) are filled in with bubbles, see Figure 2e.

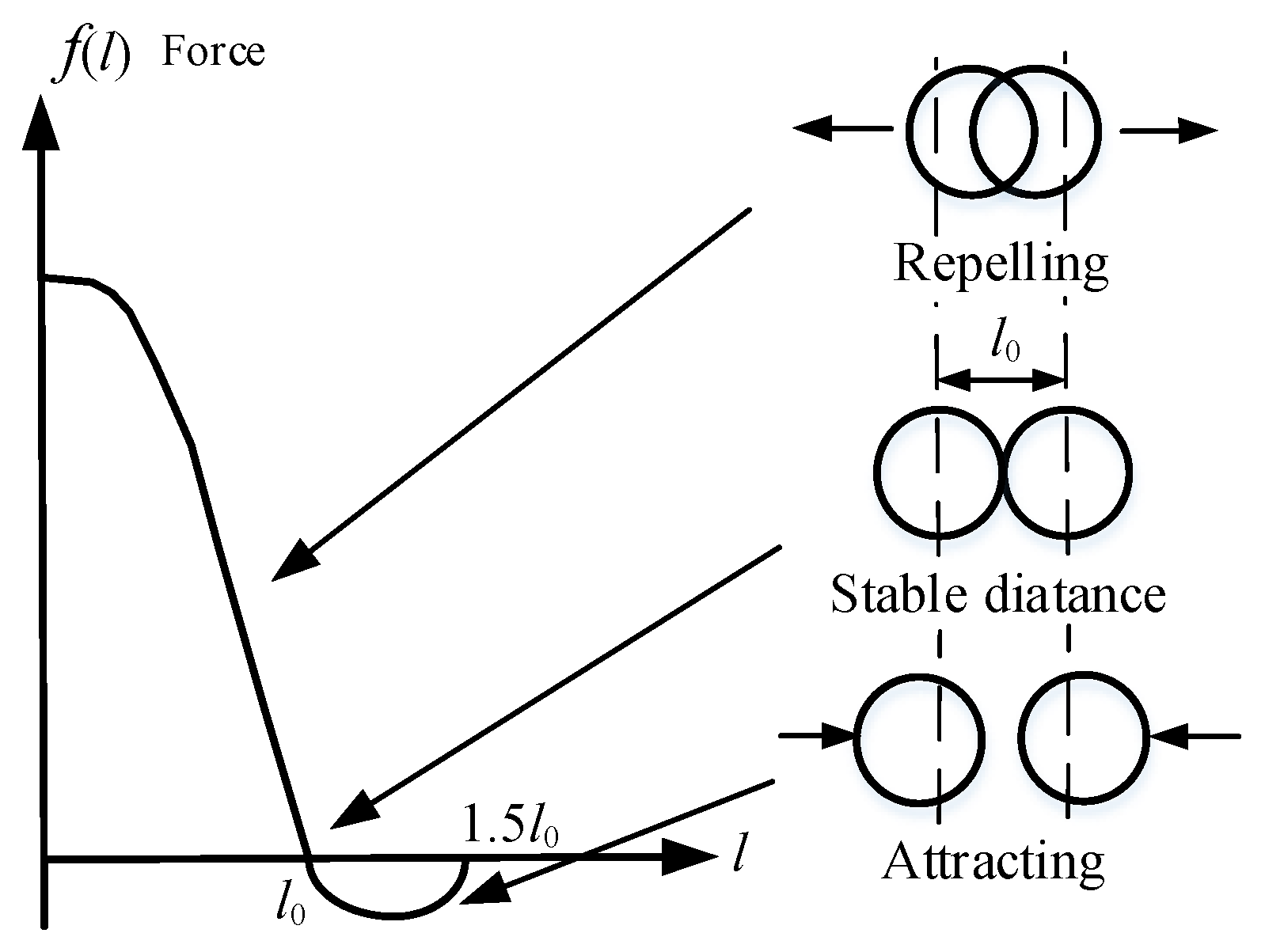
2.2. Interaction Forces

For any two bubbles i and j, the stable distance l${}_0$ is calculated as the sum of the radii of the bubbles. And defining an interaction force f for any two bubbles such that the forces are repulsive when two bubbles are located closer than l${}_0$. And the forces are attractive with the distance apart than l${}_0$, see Figure 3. The approximation force is set to the following Equation (1):

$$\begin{array}{cc}\hfill f& \left(l\right)=\left\{\begin{array}{cc}a{l}^3+b{l}^2+cl+d,\hfill & 0<l<l_0\hfill \\ 0,\hfill & 1.5l_0<l\hfill \end{array}\right.\hfill \\ \hfill f& \left(l_0\right)=f\left(1.5l_0\right)=0,f^{\prime }\left(0\right)=0,f^{\prime }\left(l_0\right)=-k_0.\hfill \end{array}$$

(1)

where k${}_0$ represents the corresponding linear spring constant at the stabilized distance l${}_0$. l is the distance of two adjacent bubbles.

2.3. Physically-Based Relaxation

The equation of motion of the ith bubble is written as follows:

$$m_i\frac{d^2{x}_i\left(t\right)}{d{t}^2}+c_i\frac{d{x}_i\left(t\right)}{dt}=f_i\left(t\right)(i=1,2,\cdots ,n)$$

(2)

where m${}_i$ is the mass, c${}_i$ is the viscosity coefficient, x${}_i$ is the position of ith bubble, and n is the number of bubbles. Given the initial positions of the bubbles, the differential equations are integrated through time at each time step with the standard fourth-order Runge-Kutta method.

2.4. Adaptive Population Control

In order to determine whether a bubble should be deleted or reserved, the overlapping ratio for the ith bubble is defined:

$${\alpha }_i=\frac{2}{d{x}_i}{\sum }_{j=0}^n(d{x}_i+\frac{2d{x}_j}{2}-l_{ij})$$

(3)

where dx${}_i$ is the radius of the ith bubble, dx${}_j$ is the radius of the jth adjacent bubble, and n is the number of adjacent bubbles. l${}_{ij}$ is the distance of ith bubble and jth bubble.

For the ideal situation, the standard overlapping ratio of a bubble on an edge, on a face and in a volume are 2, 6 and 12. One or more bubbles must be added near the bubble with a small ratio and the bubble must be deleted with too large ratio.

3. The Proposed Clustering-Based Bubble Meshing Method

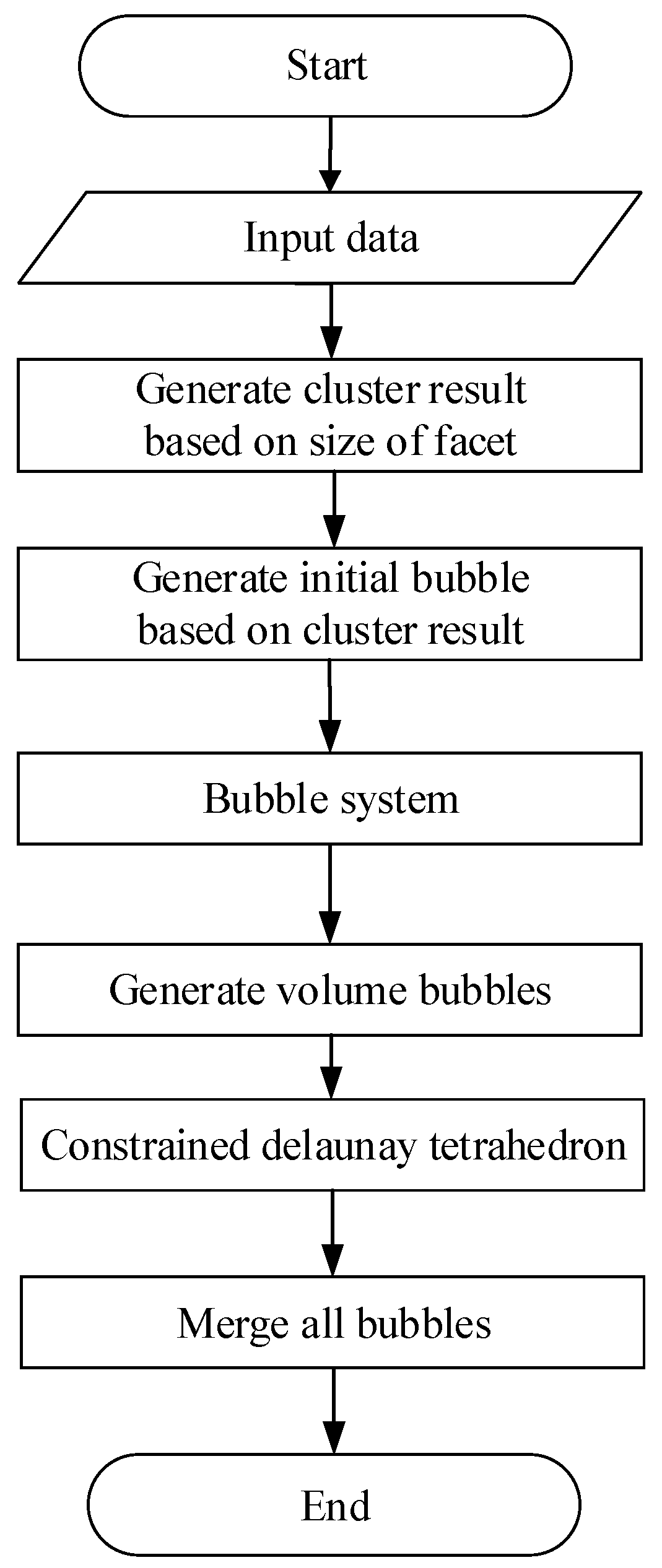
3.1. Overview

The proposed bubble method is devoted to tetrahedral mesh generation of a geological model consisting of several geological bodies, see Figure 4. The geological model is typically composed of several strata, each one represents a geological body. Figure 5 shows workflow of the proposed method for a three-dimensional model. Surface vertices in Figure 5a will become bubbles with the radii in Figure 5b. These vertices will be divided into several parts based on spatial distribution in Figure 5c, which can be used for placement of the position and determination of radius of initial points as shown in Figure 5d. Next, the force acting on the bubbles is introduced, and all bubbles in the 3D domain will reach equilibrium by the motion control equation. Then the Constrained Delaunay Triangulation is used for the mesh generation by as shown in Figure 5e. Finally, all topologically consistent meshes will be merged to obtain the target computational mesh model, see Figure 5f.

3.2. Procedures of the Proposed Bubble Method

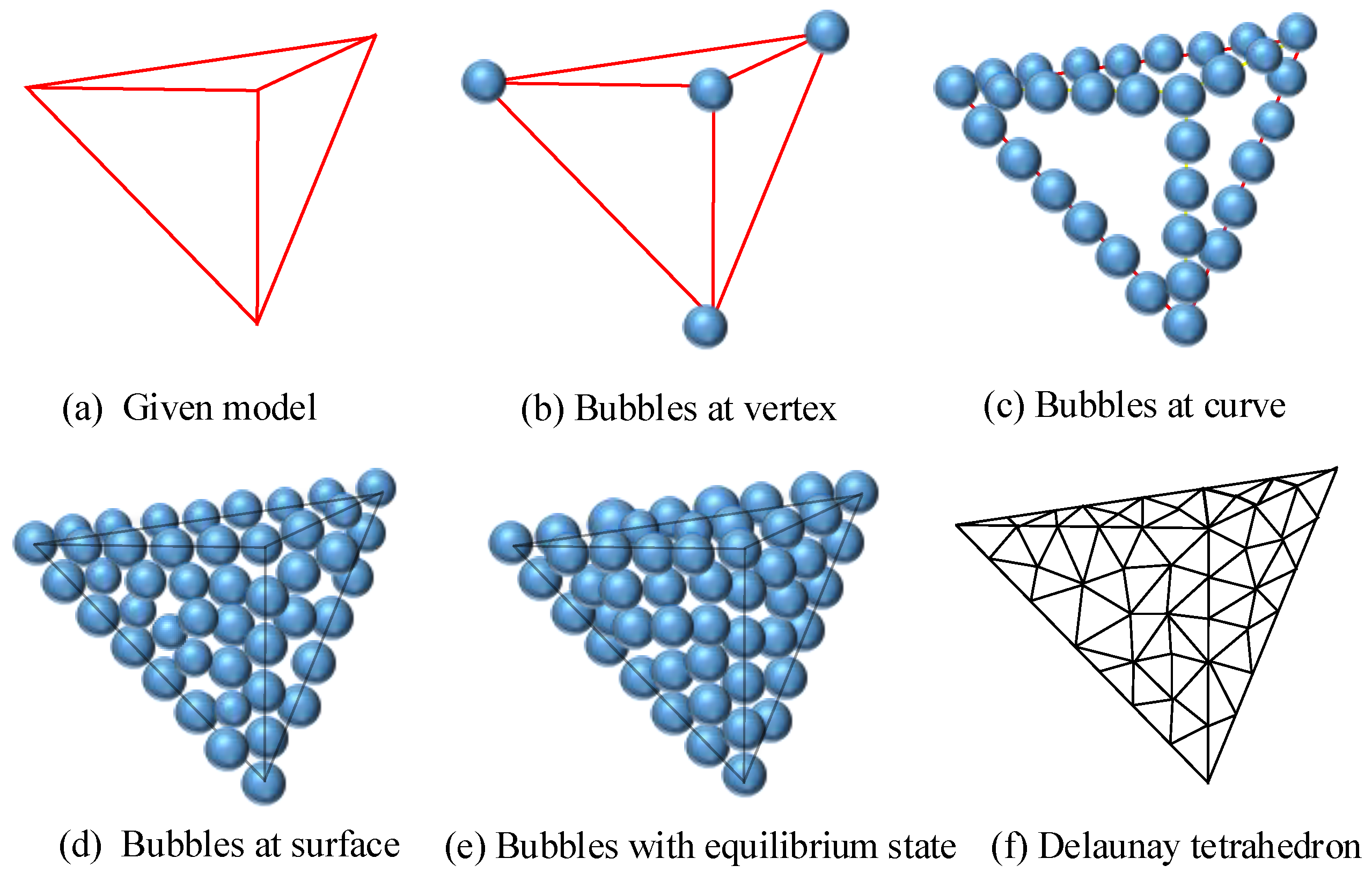
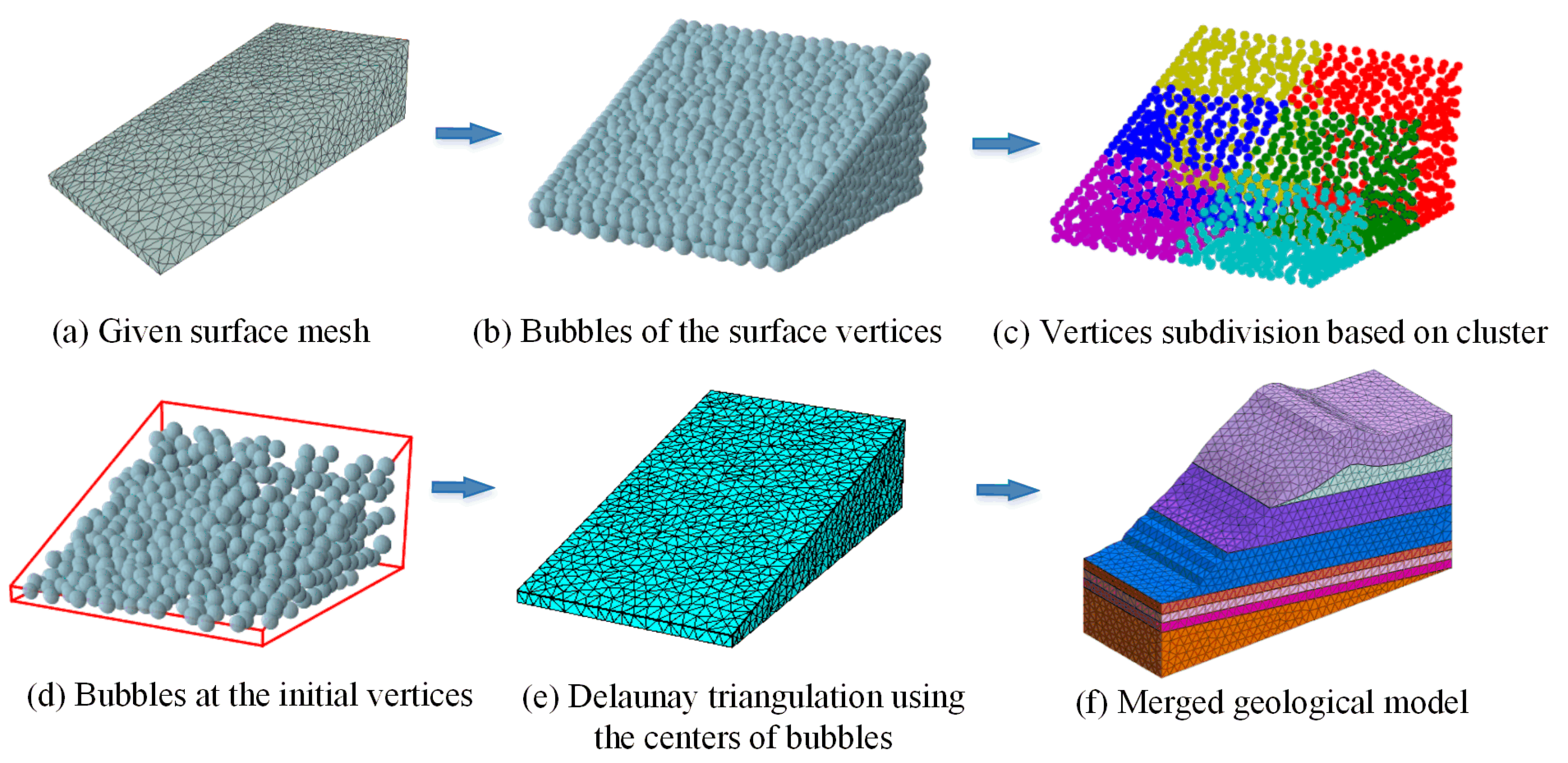
3.2.1. Procedure 1: Inputted Geological Model

Conventional input information includes the geometric boundary of the given solution area, which can be described by the planar straight line graph. And the parametric surface will be meshed by mapping method. However, geological structures and conditions are generally quite complex so that it cannot be well represented by parametric surfaces but can be well represented of triangulated surfaces. And the mesh generation of shared faces between adjacent bodies must be consistent for the aim of topological consistency. Thus, it needs to input object file format to control the surface mesh and promise the topologically consistent in this method, see Figure 5a.

For the generation of the high-quality mesh according to the surface mesh, we implement the clustering algorithm to divide surface points. Cluster analysis [25,26] is a multivariate statistical analysis method. The basic principle is: investigate m data points in m-dimensional space, define the distance between points and points of a certain character, set m data points to form n types ($n\le m$), and then combine the two types with the smallest distance into one Class, and recalculate the distance between classes.

This paper uses the K-means clustering method [27] for the classification of the surface vertices. First, each surface vertice become a bubble with a radius, which is the half of average of the distances of all points incident to this point, see Figure 5b. Then according to the geometric distance distribution of spatial relationships, surface points are divided into several groups, see Figure 5c. The most optimal number of groups in surface points we can obtain based on the Sum of the Squared Errors index (SSE), Calinski-Harabaz index (CH) [28] and Silhouette index [29]. The larger CH value and the Silhouette value, the smaller the SSE value, then select the corresponding number of clusters as the optimal number.

3.2.2. Procedure 2: Initial Bubble Placement

Initial positions and radii of bubbles are essential for the procedure of iteration in this method because a good initial position can reduce the convergence time of the relaxation. We devised an initial bubble determination combining the box technique with the result of clustering in Section 3.2.1. This method subdivides the inputted domain by using the groups of points based on the clustering result. Bounding boxes of points are created in each group. Then the bounding box is divided into several boxes. The length of the boxes is half of the sum of maximum and minimum length of surface bubbles.

It is also important to determine suitable initial radii of bubbles for the high quality of mesh efficiently in three-dimensional domains. A procedure based on the distance of nearby bubbles to obtain the initial size of bubbles. First, the initial radius will be given the value of half of the sum of max and min radii of surface bubbles. If the sum of the radius of the initial point and the nearby point is 1.5 times smaller than the distance between the two points, this adjacent point is called the weight point. The weighted point will affect the determination of the initial point radius. Then the closer the surface vertices, the greater the weight for the bubble near the surface, see Equation (4). Our experience has shown that the proposed method leads to better shapes of initial mesh.

$$\begin{array}{cc}\hfill & {\lambda }_i=\frac{1/ri}{{\sum }_{i=1}^{n}1/ri}\hfill \\ \hfill & R_i={\sum }_{i=1}^n{\lambda }_i\ast r_i\hfill \end{array}$$

(4)

where r${}_i$ is the radius of weight point, $\lambda$${}_i$ is the weight of the weight bubble, n is the number of weight points, R${}_i$ is the computed radii by its neighboring bubbles.

We construct initial conditions including the clustering of point set of given surface meshes and generating initial internal bubbles. First, we adopt internal clustering validation measures [26,30] to evaluate the clustering validation of initial bubble of given surface vertices. In general, CH value [31] and Silhouette value [26] correspond to the same optimal number with the small the SSE value. The result of clustering is relatively reasonable. Second, each group of vertices based on clustering results is divided several boxes for initial bubble placement, the distance of the bubbles within the range of force. Therefore, process of iteration is easier to converge and the initial conditions are relatively good.

3.2.3. Procedure 3: Equation of Motion Control

The motion of the bubbles is controlled by the center and radius in an analysis domain, wherein bubbles ultimately have a smooth dense and reach relatively stabilized position. Two kinds of forces act on the bubbles. One is an interaction force [17] that is non-linear and works within a specified distance of two adjacent bubbles. The other force is the viscous damping force [18] of the system to ensure the bubble system converges to a stable state. The following equation is considered in the bubble method:

$$m_i\frac{d^2{x}_i\left(t\right)}{d{t}^2}+c_i\frac{d{x}_i\left(t\right)}{dt}=f_i\left(t\right)(i=1,2,\cdots ,n)$$

(5)

where m${}_i$ is the mass, c${}_i$ is the viscosity coefficient, x${}_i$ is the position of bubble i, and f${}_i$ is the resultant force, which depends on the center position and the distance between this bubble and neighboring bubbles. And n is the number of bubbles.

For any two neighboring bubbles, the interaction force [32] can be set to:

$$f\left(w\right)=\left\{\begin{array}{cc}k(1.25w^3-2.375w^2+1.125),\hfill & 0<w<1.5\hfill \\ 0,\hfill & 1.5<w\hfill \end{array}\right.$$

(6)

where w is denoted the ratio of the real distance and the desired distance of two bubbles i and j. The desired distance is the sum of radius i and j. And k is a constant.

Euler predictor-correction method is used for solving Equation (5). The current position of the bubbles is the initial position, and the initial velocity is zero. In addition, the surface points are fixed at the process of simulation. Some internal nodes moved outside the domain must be pulled into the domain during simulation.

The stability [33] for motion control means that the bubbles must eventually reach its equilibrium state. And the selection of physical parameters [34], the non-linear interaction forces [35] and the node constrain decide [17] the stability. The physical parameters [34] based on the original bubble meshing method can make the bubble motion obtain more stability and strike a quick response for bubble system. Viscous damping is introduced to consume motion energy of system and eventually become a static system. The interaction force is small where two bubbles are extremely close. This can prevent the force from increasing infinitely large and ensure the numerical stability of motion control. The force only works when two bubbles are within a specified distance and adjacent to each other. The force used for motion control is not linear so that the gradual distribution of bubbles can also be obtained by the magnitude and the range of the forces. Meanwhile, bubbles can not be allowed to move out the domain and the movement of bubbles must be corrected in each iteration so that all bubbles are exactly located inside the target geometries interior. The result shows the robustness and stability of motion control.

3.2.4. Procedure 4: Adaptive Population Control

The number of bubbles is the key factor for obtaining a high quality of mesh for the proposed method presented in the previous section. The overlap ratio [33,35] is introduced to control the number of bubbles adaptively for avoiding the overfitting. This metric checks a local bubble population, deletes excess bubbles that obviously overlap with neighboring bubbles, and adds bubbles around bubbles with significant gaps. The method is capable of removing from over-populated areas and adding bubbles in under-populated areas in each iteration. The overlap ratio is defined as:

$${\alpha }_i=\frac{1}{r_i}{\sum }_{j=0}^n(2r_i+r_j-l_{ij})$$

(7)

where r${}_i$ and r${}_j$ are the radii of bubbles i and j, respectively. l${}_{ij}$ denotes the distance of bubbles i and j, and n is the number of bubbles associated with bubble i. Shimada [17] believed that the standard overlap ratio of bubbles on a surface or in the internal domain are 6 and 12, respectively, which form an optimal mesh in the three-dimensional domains. Consequently, bubbles with large overlap ratio will be removed, while new bubbles will be added around those with small overlap ratio. In the present study, ten to fourteen bubbles are preserved in the domain. Our result reveals that bubble population may be controlled automatically when bubbles reach stabilized position. Finally, a set of nodes with the well-shape is obtained.

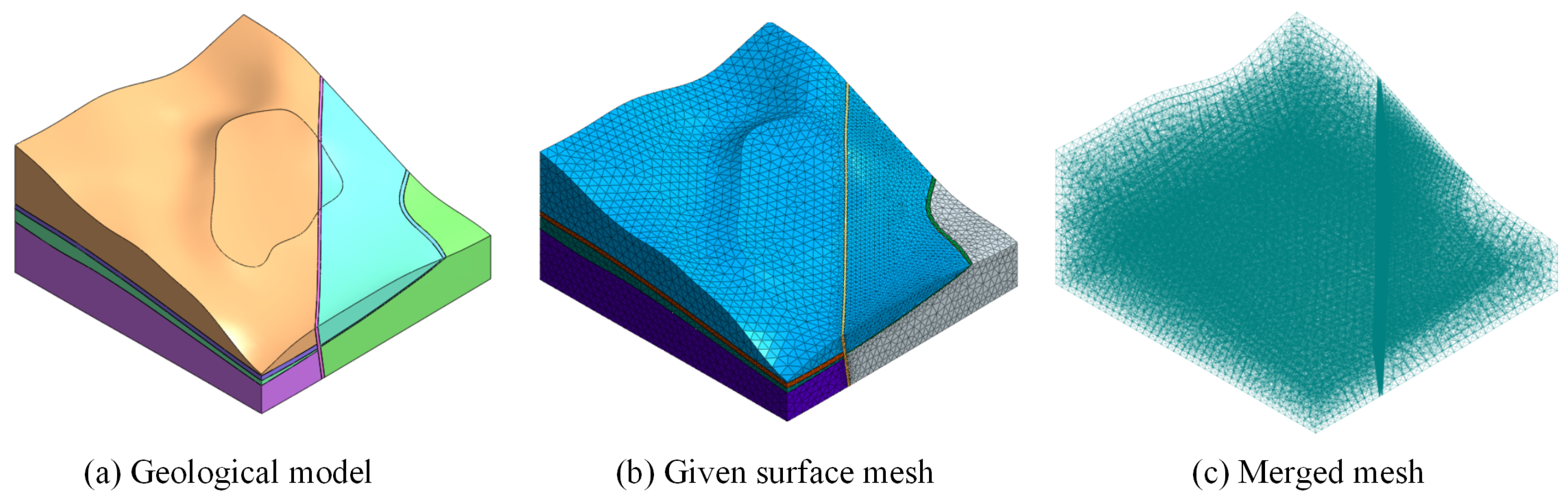
3.2.5. Procedure 5: Obtaining the Final Mesh Model by Merging

For each geological body, a surface mesh with an interior node-set can be generated and Constrained Delaunay Triangulation algorithm is used for the tetrahedral mesh generation by merging the center of bubbles. MeshCleaner [36] is a program that contributes to merge topologically consistent mesh for each geological bodies to obtain the target computational mesh model.

4. Results

To comparatively evaluate the effectiveness of the proposed clustering-based bubble method, it is applied to generate the tetrahedral mesh of a geological model in Shanxi Province; and then the generated tetrahedral mesh is compared with that generated by using the package TetGen [37,38].

TetGen [37,38] is a tetrahedral mesh generator and aims at scientific experiments and engineering applications. It will generate an adaptive tetrahedral mesh based on the input mesh size function and can be used as an independent program or embedded in other software as a component. This model is composed of eight geological bodies. There are two thin layers and a fault in this model. For this kind of geological model, different mesh sizes for different subdomains based on the surface mesh can generally better fulfill the engineering requirements. The mesh generated by our method can be seen in Figure 6.

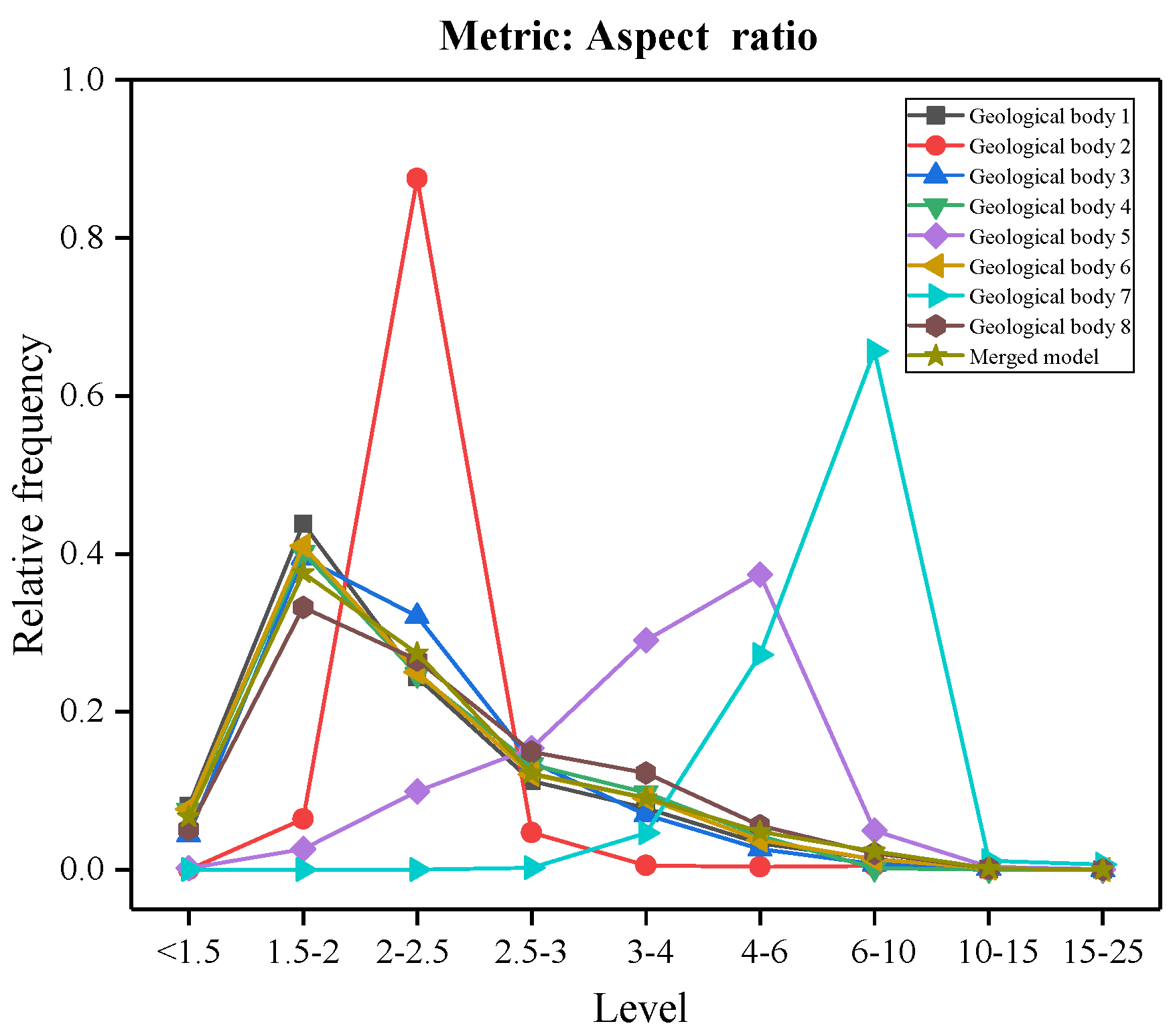
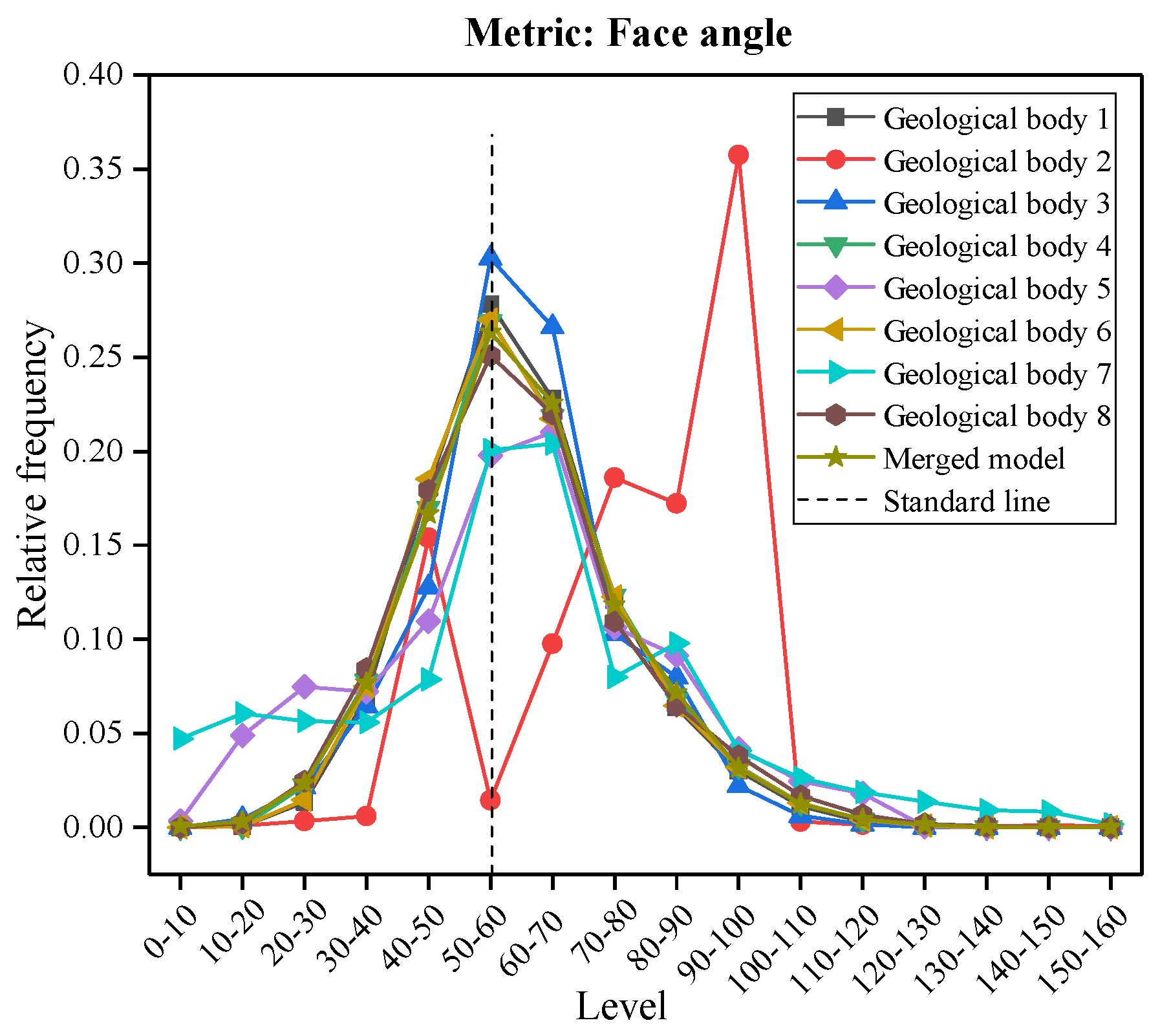
4.1. Mesh Quality Metrics

Many mesh quality metrics have been proposed from a different angle. In this paper, we use aspect radio, facet angle, and dihedral angle to evaluate the quality of the mesh.

The aspect ratio of tetrahedral mesh is the ratio of the longest edge length to the shortest height.

$$A_{ratio}=L_{max}/h_{min}$$

(8)

where A${}_{ratio}$ represents the aspect ratio, l${}_{max}$ is the longest edge length and h${}_{min}$ is the shortest height. The aspect ratio of an ideal tetrahedral element is 0.81. In general, elements with an aspect ratio exceeding 10 should not exceed 10%. Elements with values greater than 40 should be carefully checked to determine their location and whether the stresses generated in these areas are meaningful.

The face angle is the angle between any two sides of a triangular element. The face angle of an ideal tetrahedral element is 60°.

Each of the six sides of the tetrahedron is surrounded by two faces. The dihedral angle between two faces of a given edge is the intersection of the two faces and a plane perpendicular to the side angle. The dihedral angle of an ideal tetrahedral element is 70.53°.

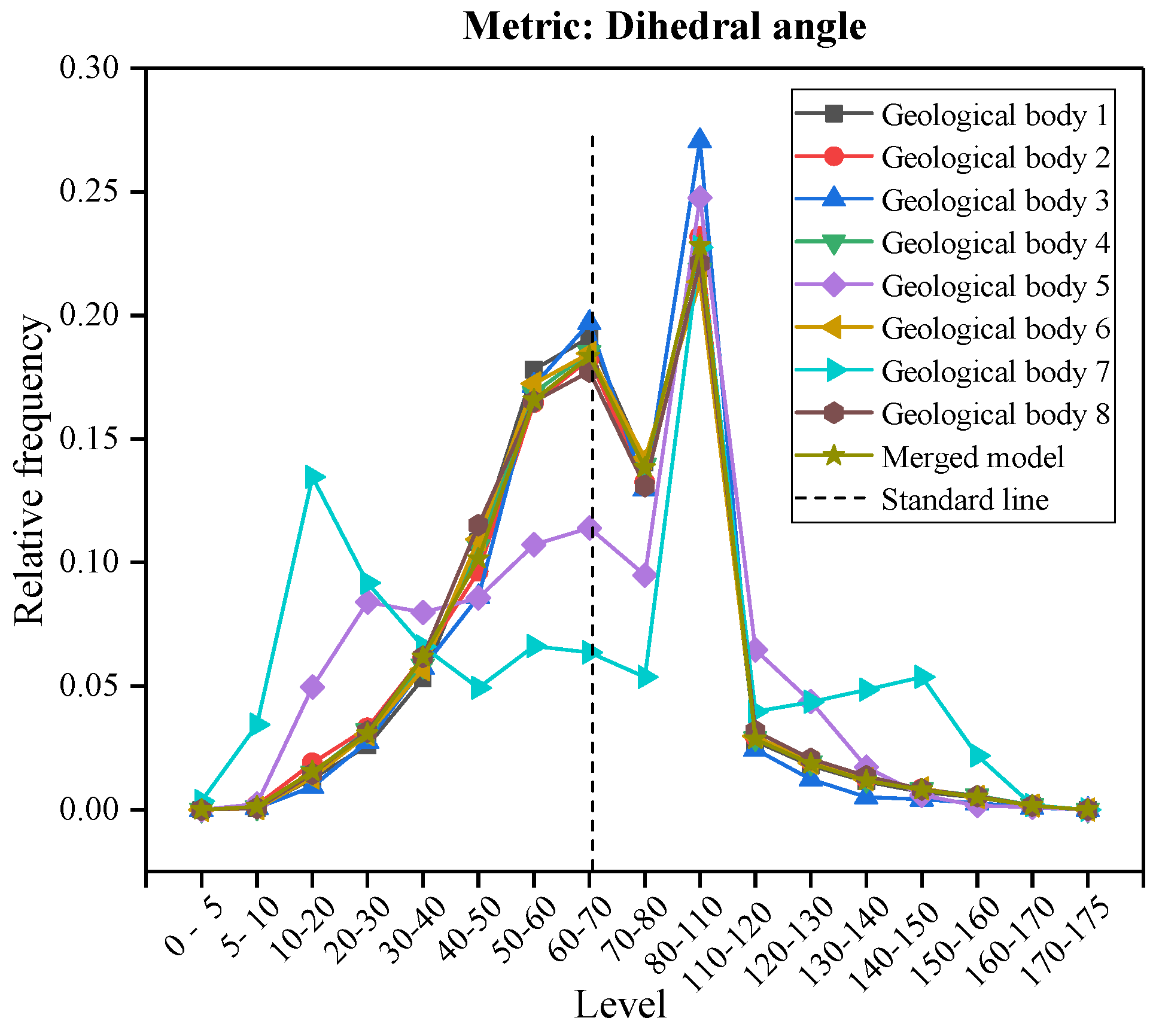
4.2. Statistics of the Mesh Quality

The overall quality of the merged mesh and the mesh of each geological body is showed as follows. In general, it can be seen that the overall quality of the mesh generated by the bubble meshing method is higher. Thin layer and fault are often long and narrow geometries so that the peak of aspect ratio is diffident. There are three curves that represent geological thin layer and fault, thus the peaks of aspect ratio are inconsistent in Figure 7.

The face angle distribution is mostly between 40°∼70°, and the peak is between 50°∼60°, which means the high quality in Figure 8. Similarly, the peak of distribution of thin layer focused on 90°∼100°. The dihedral angle peak value is distributed between 80°∼110°, the mesh distribution of each geological body and complete mesh is basically the same in Figure 9, which means that the overall quality of the mesh is good. The above three comparison results show that the distribution of thin layers and fault is different from other geological bodies. While the distribution of the overall mesh is not affected and the result suggests the mesh quality is still better.

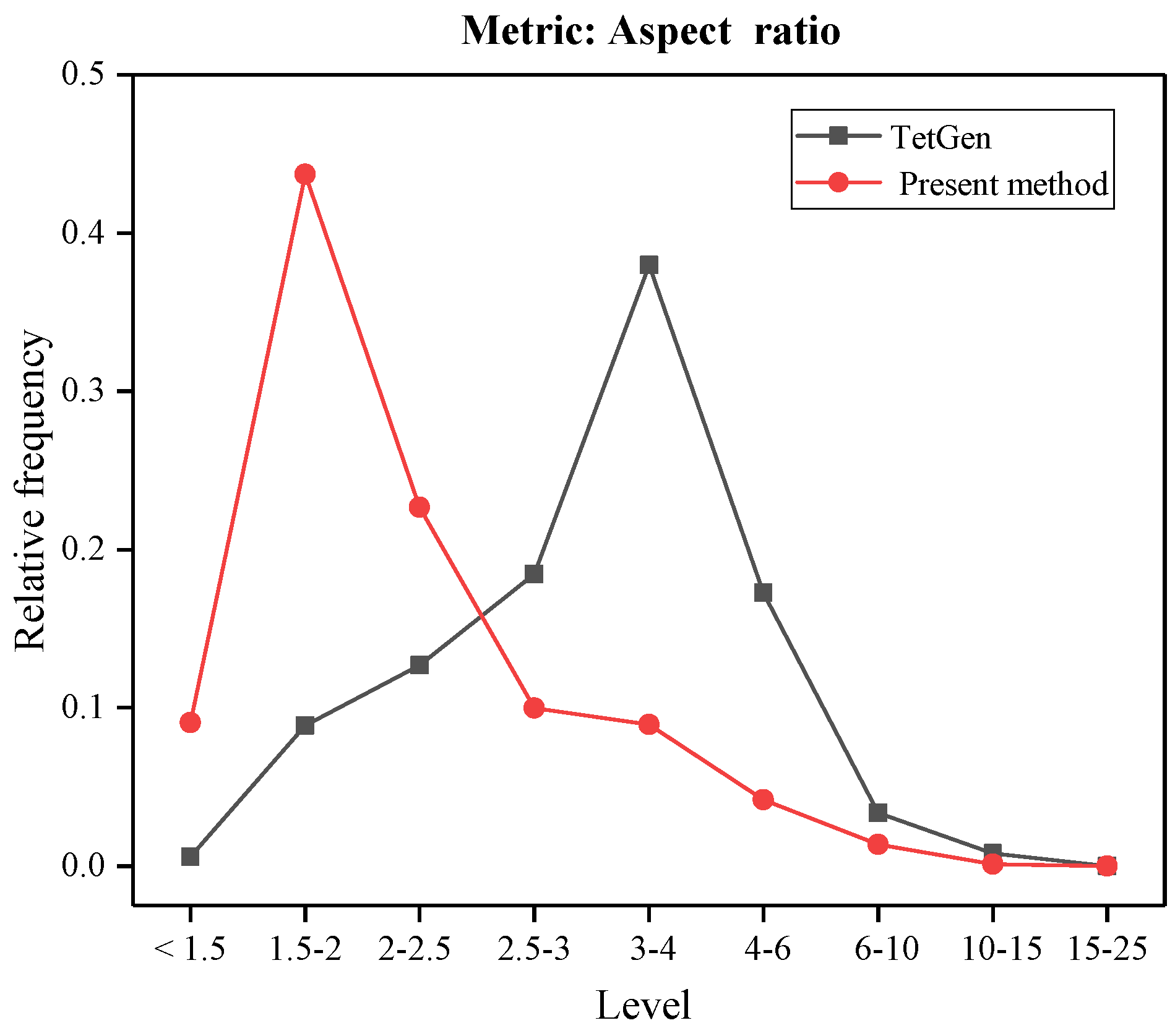
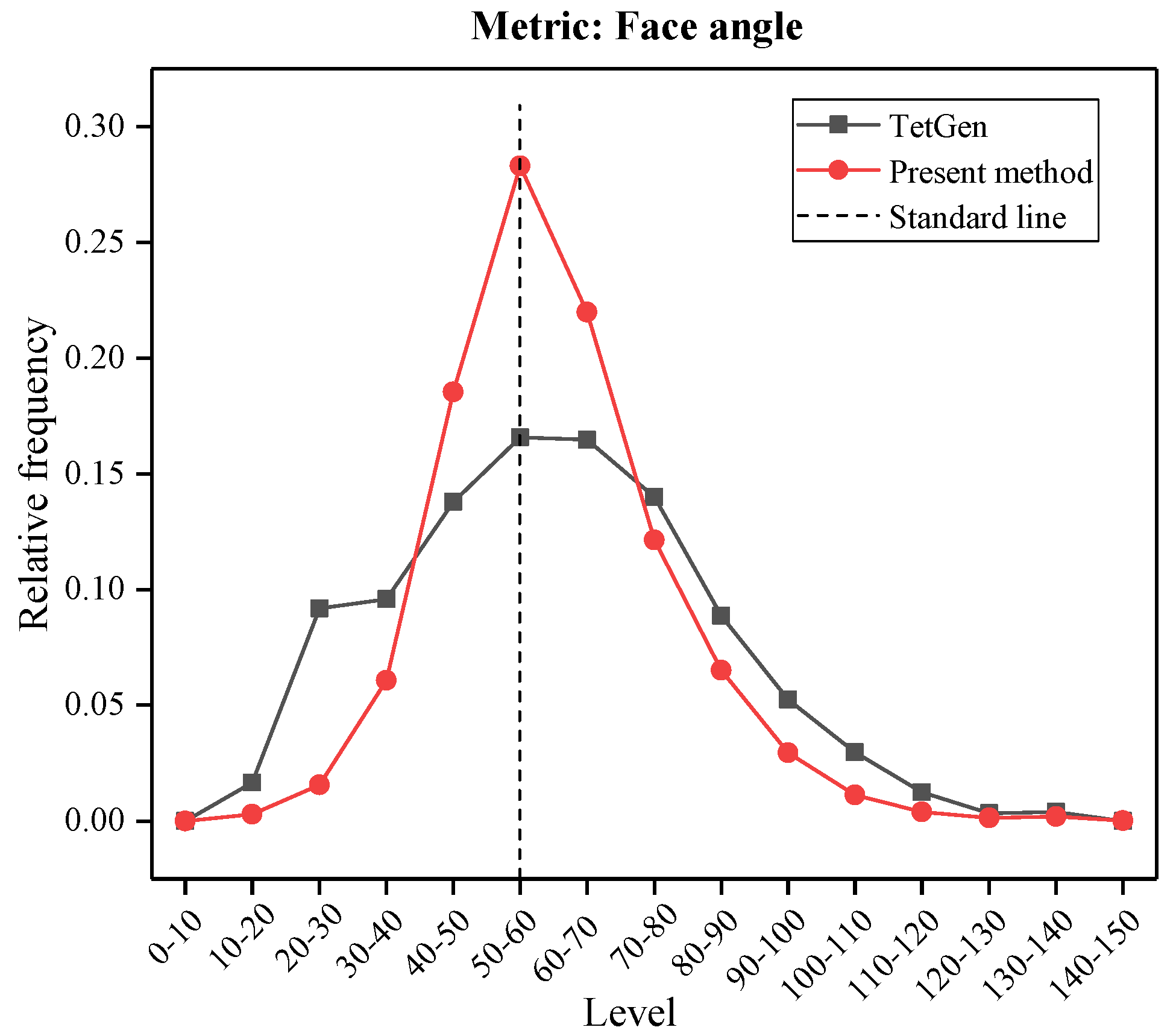
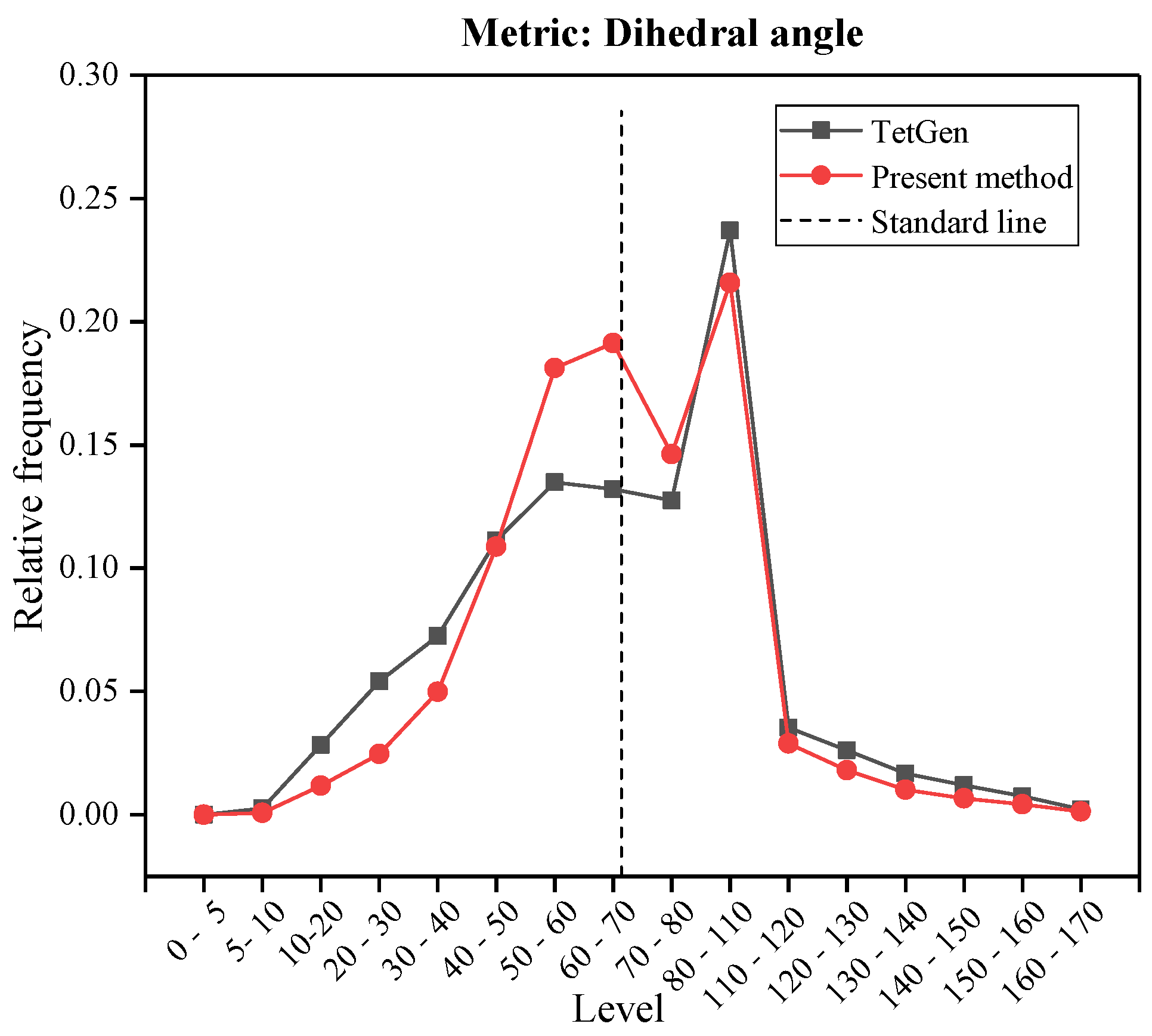
4.3. Comparative Analysis of Mesh Quality

We use TetGen’s default commands to generate the mesh for comparison. The comparative result of mesh quality generated by proposed method and TetGen is as follows. The mesh generated by the bubble vertices has a smaller proportion of mesh with a larger aspect ratio, and the peak value is 1.5∼2. The peak value of the mesh generated by the TetGen is 3∼4 in Figure 10. The distribution of bubble mesh about face angle is more concentrated between 40°∼70°, and the mesh generated by TetGen is distributed between 30°∼80° in Figure 11. The triangle elements indicate the bubble mesh is of higher quality. The distribution of the dihedral angle of the bubble vertices is concentrated on 40°∼70° and TetGen’s is 50°∼80° in Figure 12. From the above three comparison results, the distribution of the face angle is more concentrated on 50°∼70° and the dihedral angle is focused on 80°∼110°. The aspect ratio is smaller which suggests the quality of mesh by proposed method is better.

5. Discussion

5.1. Applicability, Advantage and Shortcomings of the Proposed Method

In this paper, we propose a clustering-based bubble method for generating high-quality tetrahedral meshes of geological models. The proposed method is not application-specific and can deal with generic and complex geological models. Starting data are several triangulated surface meshes of geological bodies which are topologically consistent and merged to obtain the target computational mesh model [36]. The method is not limited to meshing of provided geological model; and it is designed to apply clustering algorithm [25,26] to process inputted surface meshes of any 3D geological bodies with quite complex structures and conditions. This method can generate high-quality mesh and has high calculation accuracy. In summary, this method requires less manual intervention and is more applicable to a variety of complex geological models.

The generated high-quality mesh models can be used in the numerical modeling and prevention of common geo-hazards [39,40], such as landslide [41] and debris flow [42]. And high-quality mesh is critical in the simulation analysis. This method focuses on high-quality mesh generation of geological models, especially complex models containing faults and thin layers. Each geological bodies can be discretized into tetrahedral meshes easily and quickly. The target computational mesh model will be used for analysis of displacements and stabilities of geological bodies.

This method is more appropriate than those currently incorporated in digital terrain models [43,44]. Digital terrain model (DTM) is to represent the spatial distribution of actual terrain features in digital form. While the geological models not only need the information of ground surface but also consist of multiple geological blocks describing the structure and geometry of the stratum under the ground surface. Numerical modeling [39] of the stability and failure of soil and rock masses (for example, the numerical simulation and modeling of landslides) is the final aim of mesh generation of geological model, which be used for the analysis of displacements and stabilities [41] of geological bodies. Digital terrain model can be represented as a raster or as a vector-based triangular irregular network (TIN) for large areas, and the mesh quality is rough so that the triangulated surface mesh is not suitable for the numerical simulation. While our method can generate high-quality meshes for each geological bodies, which are used for numerical simulation reliably [42].

The measurement comprises three aspects of mesh quality. These metrics are mainly used to determine the quality based on the degree and edge length of elements. As shown in Section 4, the quality of tetrahedral meshes is generally quite good. Smooth distributions are visible for the above three metrics, which implies a large proportion of high-quality tetrahedral meshes in terms of numerical accuracy.

Tetrahedral meshes with different mesh sizes can be generated in different subdomains, while there is also a shortcoming for the developed bubble meshing. The bubble radius will be determined by the initial surface bubble, and the process of bubble placement is executed automatically based on the given surface mesh. High-quality mesh will be generated for the geological model. However, if certain geological bodies need to be divide into more denser mesh, mesh refinement will be used for fulfilling requirement.

5.2. Outlook and Future Work

The bubble meshing process is executed serially and geological bodies are meshed one after another. When model consists of many geological bodies, the generation of large scale tetrahedral meshes will lead to increased calculation time and a decreased computational efficiency. In the future, we plan to develop a parallel version of the proposed method for complex geological models. Moreover, the interaction force between any bubbles is so short-range force such that the method can be achieved with parallelism. In that version, the mesh generation time will also be significantly reduced because the bubble mesh generation has the features of parallelism.

6. Conclusions

In this paper, we have proposed the bubble method based on spatial distribution of point set of given surface mesh using the clustering algorithm. The inputted geological models consisting of triangulated surface meshes have been divided into several parts based on spatial distribution of point set, which can be used for determination of the positions and radii of initial bubbles. And a procedure based on distance of nearby bubbles has been used to obtain the initial size of bubbles. This method can generate high-quality mesh for three-dimension geological model with several geological bodies, giving it wide adaptability. Moreover, the final mesh can be used for numerical simulation directly. Comparative results have been presented to demonstrate the effectiveness and advantage of the proposed method.