Edge-Event-Triggered Synchronization for Multi-Agent Systems with Nonlinear Controller Outputs
Abstract
:1. Introduction
- The proposed event- and self-triggered policies take the effects of controller output nonlinearities into account, not only including controllers’ inherent nonlinear properties, but also the signal distortion caused by network data transmission. In comparison with edge-based distributed event-triggered control in [39,40,41,42,43,45,46,47,54,55], our policies consider non-ideal digital signal transmission in actual application scenarios, paving the way for digital applications of distributed sampled-data control.
- The proposed event- and self-triggered schemes have trade-offs in the scheduling of system resources. The event-triggered policy does not require digital signal transmission between neighboring individuals but requires all sensors to continuously obtain edge state information to evaluate triggering conditions and implement intermittent controller updates. The proposed self-triggered policy avoids continuous acquisition of edge state information and requires a small amount of information transmission between neighboring individuals. The trade-off between these two policies is also suitable for scenarios with different levels of resource schedulability. Furthermore, in comparison with the previous distributed self-triggered approaches [34,39,41,42,46,47,52], the interactive control inputs in our algorithm are quantized information, which is a more efficient solution for saving communication bandwidth.
2. Preliminaries and Problem Formulation
2.1. Preliminaries on Graph Theory
2.2. Problem Formulation
- P1.
- if and only if .
- P2.
- .
- P3.
- with the positive scalars .
- .
- .
- .
3. Edge-Event-Triggered Policy
4. Edge-Self-Triggered Policy
| Algorithm 1: Edge-Self-Triggered Control Algorithm |
| Step 1: Set the algorithm execution time . At initial time , let , , and . Let ; update ; compute and by (24) and (25); compute maximum allowable value by (26) such that . Step 2: When , check the events related to agents , ; perform the following steps: – If any agent updated before , let ; recompute and by (24) and (25), such that ; – If there is no agent updated before , the event related to agent , occurs at ; let ; update the event instant ; let ; update ; let ; compute and by (24) and (25); compute maximum allowable value by (26) such that . Step 3: When , jump out of Algorithm 1. |
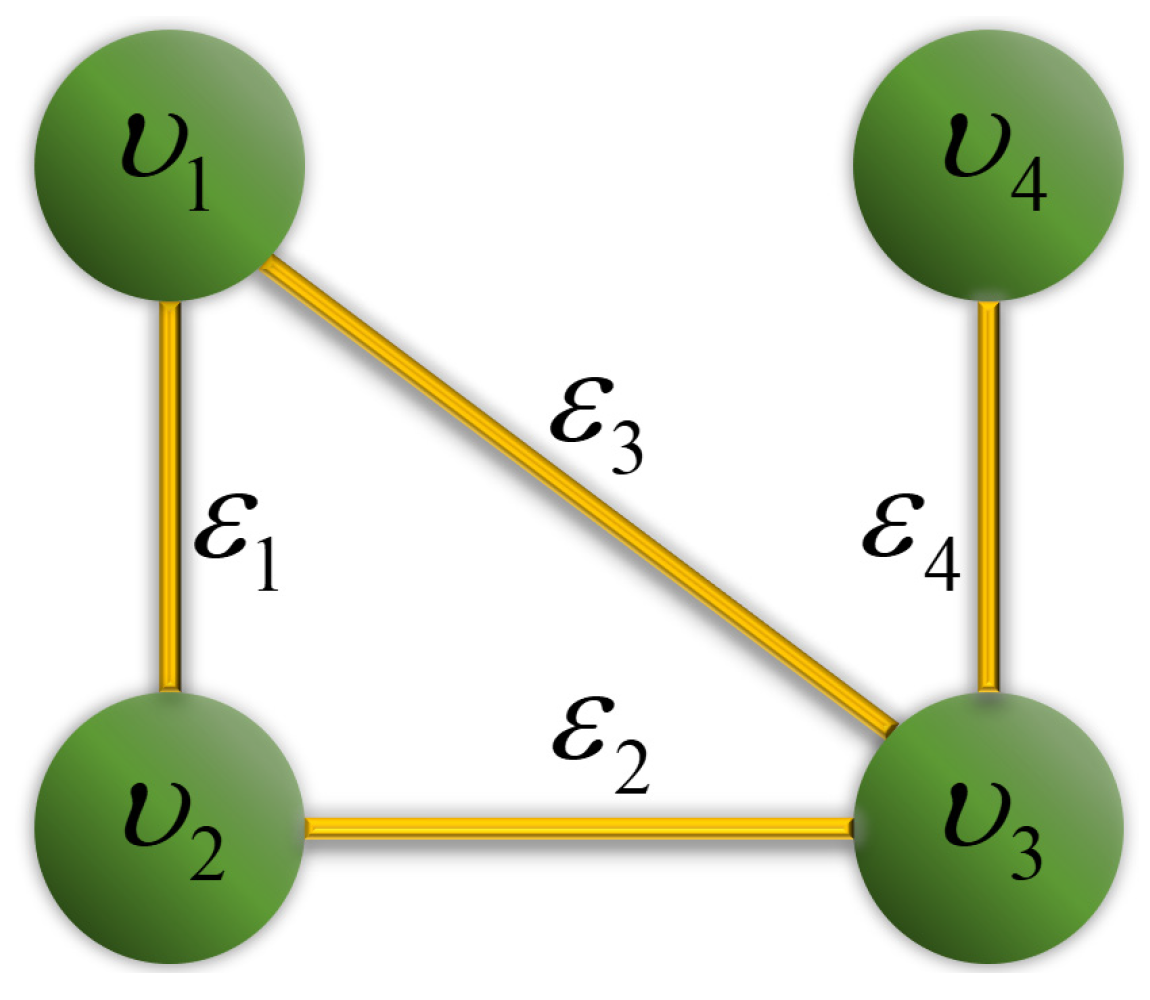
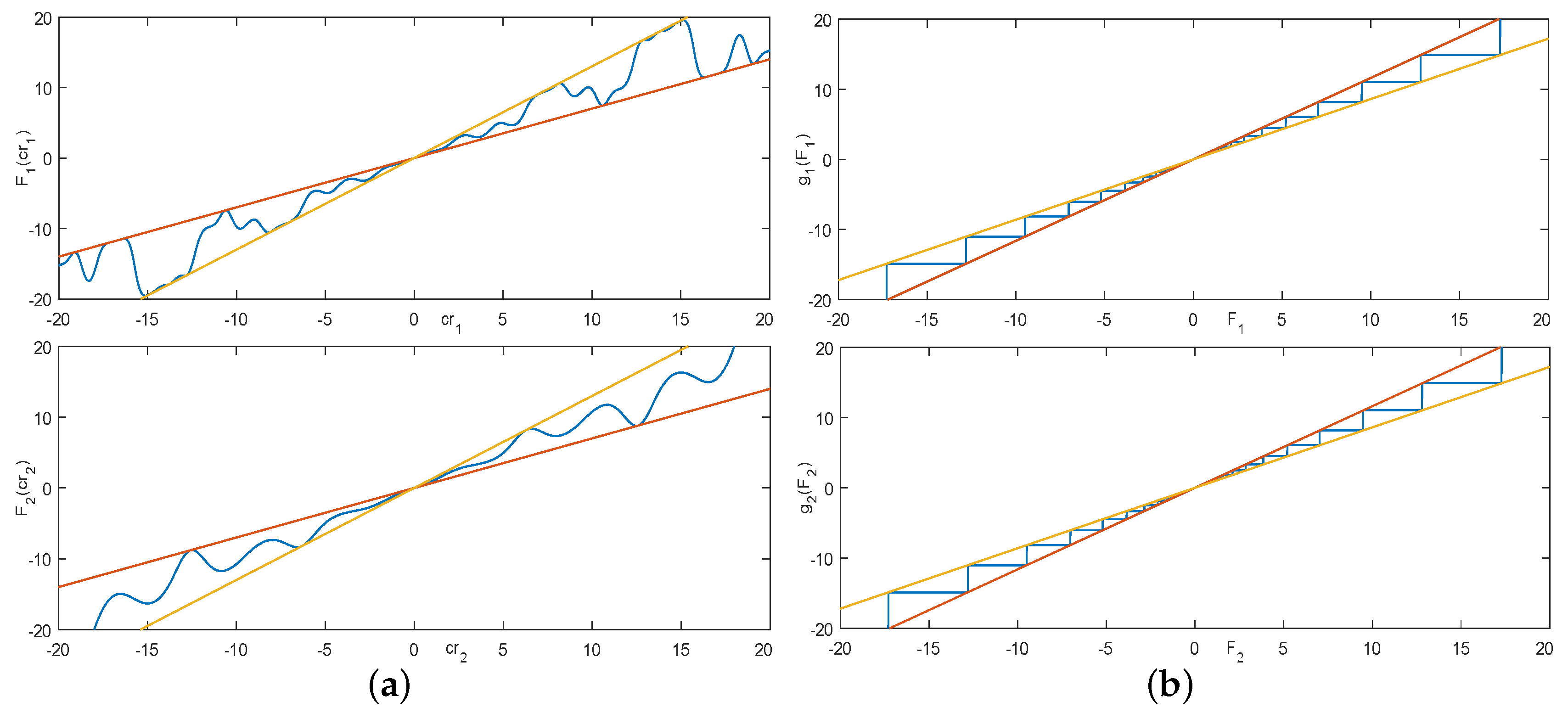
5. Simulations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Inform. 2012, 9, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Gao, H. A sufficient condition for convergence of sampled-data consensus for double-integrator dynamics with nonuniform and time-varying communication delays. IEEE Trans. Autom. Control 2012, 57, 2417–2422. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Jing, G.; Zheng, Y.; Wang, L. Consensus of multiagent systems with distance-dependent communication networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2712–2726. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Ma, J.; Wang, L. Consensus of hybrid multi-agent systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1359–1365. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Wang, J. Fully Distributed Fault-Tolerant Consensus Protocols for Lipschitz Nonlinear Multi-Agent Systems. IEEE Access 2018, 6, 17313–17325. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, L.; Yu, J. Adaptive Finite-Time Consensus Tracking for Nonstrict Feedback Nonlinear Multi-Agent Systems with Unknown Control Directions. IEEE Access 2019, 7, 155262–155269. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, G.; Zheng, W.X.; Kang, Y. Adaptive sliding mode consensus tracking for second-order nonlinear multiagent systems with actuator faults. IEEE Trans. Cybern. 2018, 49, 1605–1615. [Google Scholar] [CrossRef]
- Qin, J.; Li, M.; Shi, Y.; Ma, Q.; Zheng, W.X. Optimal synchronization control of multiagent systems with input saturation via off-policy reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 85–96. [Google Scholar] [CrossRef]
- Ren, C.; Shi, Z.; Du, T. Distributed Observer-Based Leader-Following Consensus Control for Second-Order Stochastic Multi-Agent Systems. IEEE Access 2018, 6, 20077–20084. [Google Scholar] [CrossRef]
- Wei, B.; Xiao, F. Distributed Consensus Control of Linear Multiagent Systems with Adaptive Nonlinear Couplings. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- He, L.; Zhang, J.; Hou, Y.; Liang, X.; Bai, P. Time-Varying Formation Control for Second-Order Discrete-Time Multi-Agent Systems with Directed Topology and Communication Delay. IEEE Access 2019, 7, 33517–33527. [Google Scholar] [CrossRef]
- Ma, J.; Ye, M.; Zheng, Y.; Zhu, Y. Consensus analysis of hybrid multiagent systems: A game-theoretic approach. Int. J. Robust Nonlinear Control 2019, 29, 1840–1853. [Google Scholar] [CrossRef]
- Wei, B.; Xiao, F.; Shi, Y. Fully distributed synchronization of dynamic networked systems with adaptive nonlinear couplings. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, G.; Zheng, W.X.; Kang, Y. Neural network-based adaptive consensus control for a class of nonaffine nonlinear multiagent systems with actuator faults. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3633–3644. [Google Scholar] [CrossRef]
- Fu, W.; Qin, J.; Shi, Y.; Zheng, W.X.; Kang, Y. Resilient Consensus of Discrete-Time Complex Cyber-Physical Networks under Deception Attacks. IEEE Trans. Ind. Inform. 2020, 16, 4868–4877. [Google Scholar] [CrossRef]
- Wei, B.; Xiao, F.; Shi, Y. Synchronization in kuramoto oscillator networks with sampled-data updating law. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Qin, J.; Ma, Q.; Yu, X.; Wang, L. On Synchronization of Dynamical Systems over Directed Switching Topologies: An Algebraic and Geometric Perspective. IEEE Trans. Autom. Control 2020. [Google Scholar] [CrossRef] [Green Version]
- Åström, K.J.; Bernhardsson, B. Comparison of periodic and event based sampling for first-order stochastic systems. IFAC Proc. Vol. 1999, 32, 5006–5011. [Google Scholar] [CrossRef] [Green Version]
- Velasco, M.; Fuertes, J.; Marti, P. The self triggered task model for real-time control systems. In Proceedings of the Work-in-Progress Session of the 24th IEEE Real-Time Systems Symposium (RTSS03), Cancun, Mexico, 3–5 December 2003; Volume 384. [Google Scholar]
- Miskowicz, M. Send-on-delta concept: An event-based data reporting strategy. Sensors 2006, 6, 49–63. [Google Scholar] [CrossRef] [Green Version]
- Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef] [Green Version]
- Miskowicz, M. Event-Based Control and Signal Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Pan, L.; Lu, Q.; Yin, K.; Zhang, B. Signal source localization of multiple robots using an event-triggered communication scheme. Appl. Sci. 2018, 8, 977. [Google Scholar] [CrossRef] [Green Version]
- Theodosis, D.; Dimarogonas, D.V. Event-Triggered Control of Nonlinear Systems with Updating Threshold. IEEE Control Syst. Lett. 2019, 3, 655–660. [Google Scholar] [CrossRef]
- Zhu, C.; Li, C.; Chen, X.; Zhang, K.; Xin, X.; Wei, H. Event-Triggered Adaptive Fault Tolerant Control for a Class of Uncertain Nonlinear Systems. Entropy 2020, 22, 598. [Google Scholar] [CrossRef]
- Pérez-Torres, R.; Torres-Huitzil, C.; Galeana-Zapién, H. A Cognitive-Inspired Event-Based Control for Power-Aware Human Mobility Analysis in IoT Devices. Sensors 2019, 19, 832. [Google Scholar] [CrossRef] [Green Version]
- Thakur, S.S.; Abdul, S.S.; Chiu, H.Y.S.; Roy, R.B.; Huang, P.Y.; Malwade, S.; Nursetyo, A.A.; Li, Y.C.J. Artificial-intelligence-based prediction of clinical events among hemodialysis patients using non-contact sensor data. Sensors 2018, 18, 2833. [Google Scholar] [CrossRef] [Green Version]
- Socas, R.; Dormido, R.; Dormido, S. New control paradigms for resources saving: An approach for mobile robots navigation. Sensors 2018, 18, 281. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Lu, Q.; Hu, Y. Event-based communication and finite-time consensus control of mobile sensor networks for environmental monitoring. Sensors 2018, 18, 2547. [Google Scholar] [CrossRef] [Green Version]
- Zietkiewicz, J.; Horla, D.; Owczarkowski, A. Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event-and Self-Triggered Control Approaches. Robotics 2018, 7, 77. [Google Scholar] [CrossRef] [Green Version]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
- Seyboth, G.S.; Dimarogonas, D.V.; Johansson, K.H. Event-based broadcasting for multi-agent average consensus. Automatica 2013, 49, 245–252. [Google Scholar] [CrossRef]
- Guo, M.; Dimarogonas, D.V. Nonlinear consensus via continuous, sampled, and aperiodic updates. Int. J. Control 2013, 86, 567–578. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J. Distributed event-triggered control of multiagent systems with general linear dynamics. J. Control Sci. Eng. 2014, 2014, 698546. [Google Scholar] [CrossRef] [Green Version]
- Nowzari, C.; Cortés, J. Distributed event-triggered coordination for average consensus on weight-balanced digraphs. Automatica 2016, 68, 237–244. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Jiang, Z.P. Event-based leader-following consensus of multi-agent systems with input time delay. IEEE Trans. Autom. Control 2015, 60, 1362–1367. [Google Scholar] [CrossRef]
- Liuzza, D.; Dimarogonas, D.V.; Di Bernardo, M.; Johansson, K.H. Distributed model based event-triggered control for synchronization of multi-agent systems. Automatica 2016, 73, 1–7. [Google Scholar] [CrossRef] [Green Version]
- De Persis, C.; Postoyan, R. A Lyapunov redesign of coordination algorithms for cyber-physical systems. IEEE Trans. Autom. Control 2016, 62, 808–823. [Google Scholar] [CrossRef] [Green Version]
- Adaldo, A.; Liuzza, D.; Dimarogonas, D.V.; Johansson, K.H. Cloud-Supported Formation Control of Second-Order Multiagent Systems. IEEE Trans. Control Netw. Syst. 2017, 5, 1563–1574. [Google Scholar] [CrossRef]
- Xiao, F.; Shi, Y.; Ren, W. Robustness analysis of asynchronous sampled-data multiagent networks with time-varying delays. IEEE Trans. Autom. Control 2017, 63, 2145–2152. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Tian, D.; Hu, J. Event-Triggered Cooperative Output Regulation for Heterogeneous Multi-Agent Systems with an Uncertain Leader. IEEE Access 2019, 7, 174270–174279. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Yan, J.; Guan, X. Event-Triggered Consensus Control for Second-Order Multi-Agent Systems with/without Input Time Delay. IEEE Access 2019, 7, 156993–157002. [Google Scholar] [CrossRef]
- Hu, W.; Yang, C.; Huang, T.; Gui, W. A distributed dynamic event-triggered control approach to consensus of linear multiagent systems with directed networks. IEEE Trans. Cybern. 2018, 63, 2145–2152. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huang, N.; Anderson, B.D.; Duan, Z. Event-Based Multiagent Consensus Control: Zeno-Free Triggering via Signals. IEEE Trans. Cybern. 2018, 50, 284–296. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.W.; Lei, Y.; Bian, T.; Guan, Z.H. Distributed control of nonlinear multiagent systems with unknown and nonidentical control directions via event-triggered communication. IEEE Trans. Cybern. 2020, 50, 1820–1832. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Nguyen, T.B.; Hong, S.K. Dynamic Event-Triggered Time-Varying Formation Control of Second-Order Dynamic Agents: Application to Multiple QuadcoptersSystems. Appl. Sci. 2020, 10, 2814. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.H.; Xu, M.; Ge, M.F.; Ding, T.F.; Qi, F.; Li, M. Distributed Event-Based Control of Hierarchical Leader-Follower Networks with Time-Varying Layer-To-Layer Delays. Energies 2020, 13, 1808. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Kong, Z.; Ding, L. Flocking of Multi-Agent System with Nonlinear Dynamics via Distributed Event-Triggered Control. Appl. Sci. 2019, 9, 1336. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Liu, L.; Feng, G. An event-triggered control approach to cooperative output regulation of heterogeneous multi-agent systems. IFAC-PapersOnLine 2016, 49, 564–569. [Google Scholar] [CrossRef]
- Li, H.; Chen, G.; Huang, T.; Zhu, W.; Xiao, L. Event-triggered consensus in nonlinear multi-agent systems with nonlinear dynamics and directed network topology. Neurocomputing 2016, 185, 105–112. [Google Scholar] [CrossRef]
- Li, Z.; Yan, J.; Yu, W.; Qiu, J. Event-Triggered Control for a Class of Nonlinear Multiagent Systems with Directed Graph. IEEE Trans. Syst. Man Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Li, Z.; Yan, J.; Yu, W.; Qiu, J. Adaptive Event-Triggered Control for Unknown Second-Order Nonlinear Multiagent Systems. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef] [PubMed]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]


| Agents | Total Numbers | Average Time Intervals | ||||
|---|---|---|---|---|---|---|
| The edge-event-triggered policy | 35 | 35 | 23 | 20 | 113 | 0.354 |
| The edge-self-triggered policy | 71 | 97 | 145 | 48 | 361 | 0.111 |
| System Resources | Sampling Times | Communication Times | Controller Update Times |
|---|---|---|---|
| The edge-event-triggered policy | Continuous | 0 | 113 |
| The edge-self-triggered policy | 361 | 361 | 361 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Dai, M.-Z.; Zhang, C.; Wu, J. Edge-Event-Triggered Synchronization for Multi-Agent Systems with Nonlinear Controller Outputs. Appl. Sci. 2020, 10, 5250. https://doi.org/10.3390/app10155250
Liu J, Dai M-Z, Zhang C, Wu J. Edge-Event-Triggered Synchronization for Multi-Agent Systems with Nonlinear Controller Outputs. Applied Sciences. 2020; 10(15):5250. https://doi.org/10.3390/app10155250
Chicago/Turabian StyleLiu, Jie, Ming-Zhe Dai, Chengxi Zhang, and Jin Wu. 2020. "Edge-Event-Triggered Synchronization for Multi-Agent Systems with Nonlinear Controller Outputs" Applied Sciences 10, no. 15: 5250. https://doi.org/10.3390/app10155250
APA StyleLiu, J., Dai, M.-Z., Zhang, C., & Wu, J. (2020). Edge-Event-Triggered Synchronization for Multi-Agent Systems with Nonlinear Controller Outputs. Applied Sciences, 10(15), 5250. https://doi.org/10.3390/app10155250







