A Multicriteria Motion Planning Approach for Combining Smoothness and Speed in Collaborative Assembly Systems
Abstract
1. Introduction
- There is experimental evidence that suggests that humans adopt minimum jerk movements [15,16,17], and thus, these can be perceived as predictable and familiar by a person that interacts with the robot. In [18], the impact of different industrial robot motion profiles was investigated in a cooperative human-robot interaction (HRI) task showing that minimum jerk trajectories significantly reduce the heart rate in humans, thus suggesting an improvement of robot acceptance and a reduction of the psychological stress;
- For a given execution time, minimum jerk motions could require higher speeds than trapezoidal speed profiles. To make the motion feasible for the robot and for the safety requirement, an upper bound value of velocity has to be set, and a linear scaling of the trajectory penalizes this kind of trajectory in terms of execution time much more than it does for trapezoidal speed profiles;
- Large deviations from the straight lines that join consecutive via-points may occur. The magnitude of such deviations is not predictable and may create unexpected deviations from the intended path between via-points, forcing the user to define additional via-points to possibly limit this problem.
2. Optimal Trajectory Formulation
2.1. General Problem Formulation
2.2. The Variational Formalism
2.3. Final Formulation
3. Implementation
- calculation of the family of trajectories dependent on the weighting factor ;
- multi-criteria optimization finding the optimal time interval and selection of the weighting factor ;
- trajectory feasibility verification and possible scaling.
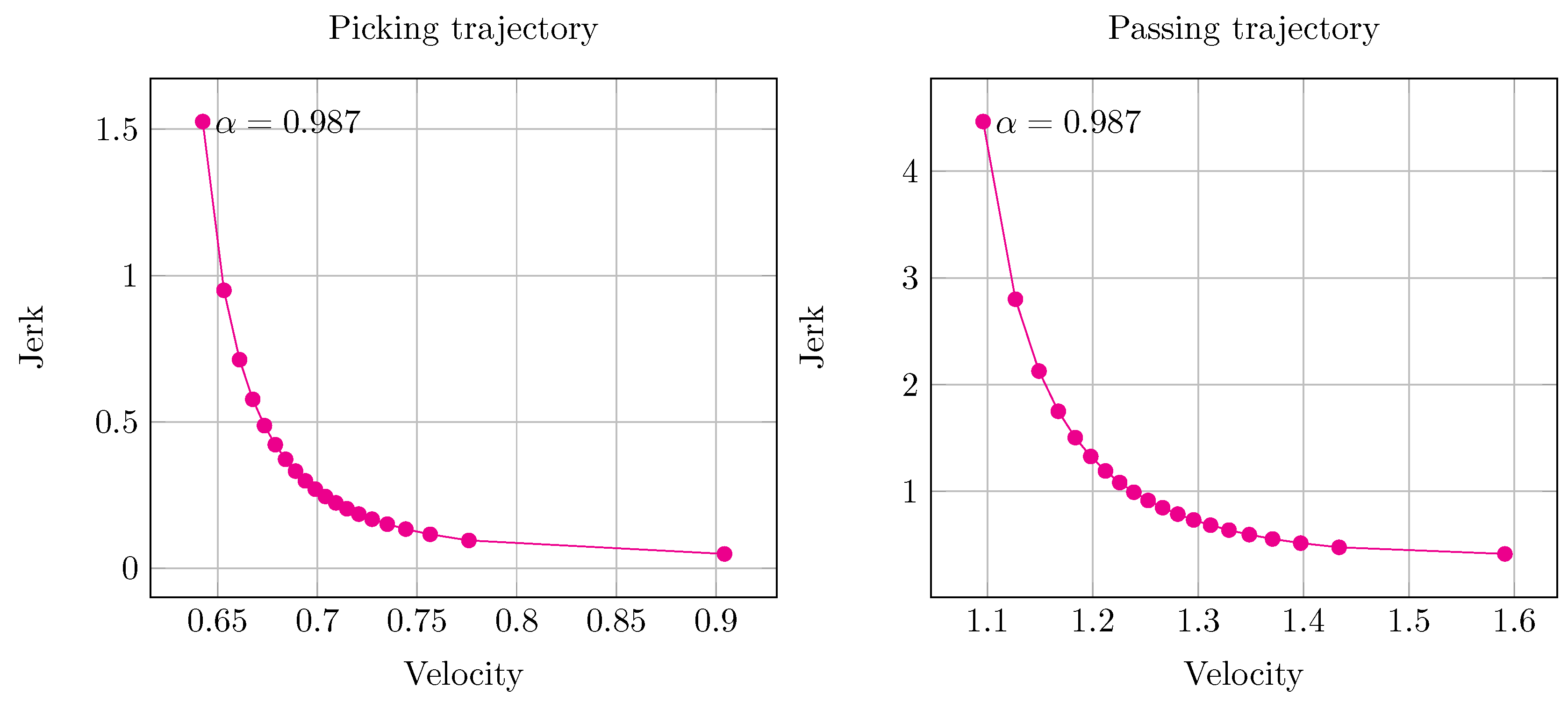
3.1. Multi-Criteria Optimization and Pareto Front
3.2. Feasibility of the Motion
3.3. Implemented Procedure
- User: definition of the trajectory via-points and desired execution time.
- Robot controller: computation of the optimal solutions and generation of the Pareto front chart.
- User: selection of the desired trajectory choosing the proper value of from the Pareto front chart.
- Robot controller: Evaluation of the trajectory feasibility and, if needed, linear scaling of it.
- Robot controller: Execution of the trajectory according to the starting command given by the user.
4. Experimental Validation of the Method
4.1. Experimental Setup
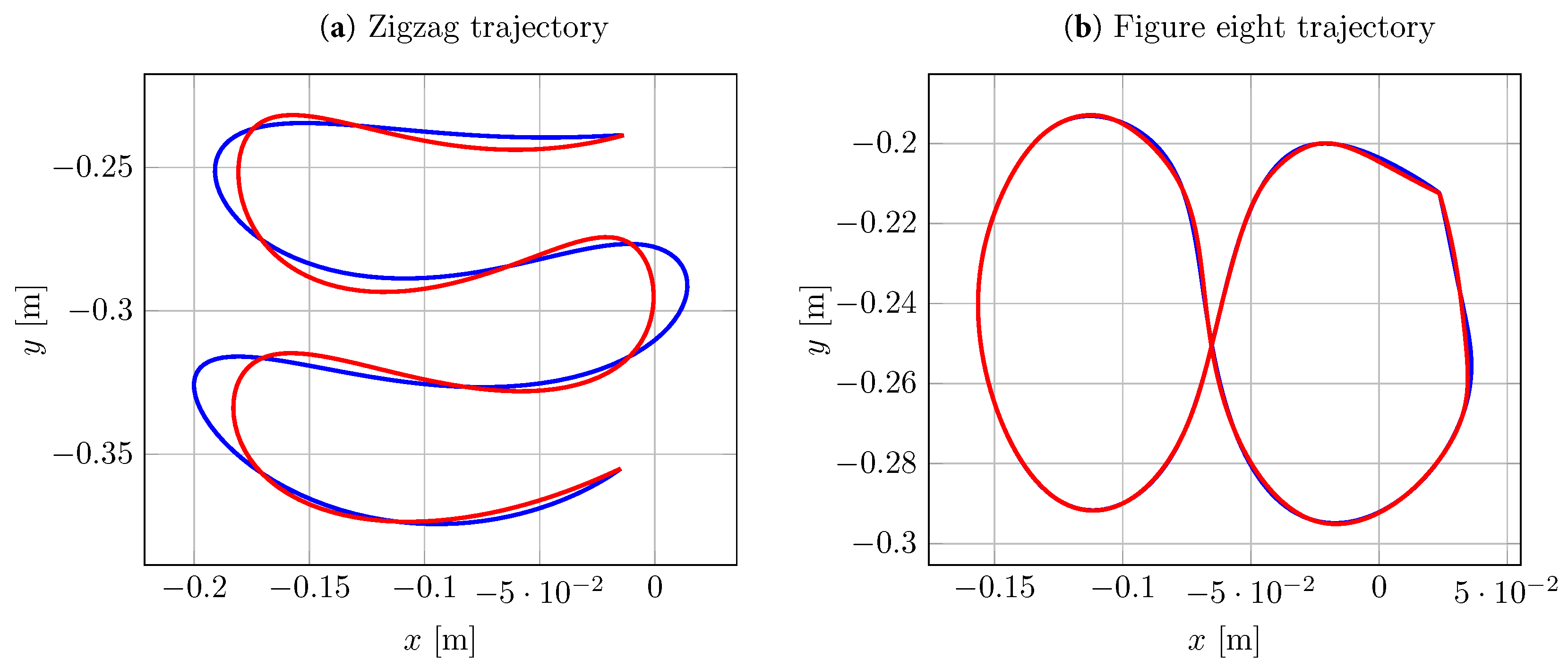
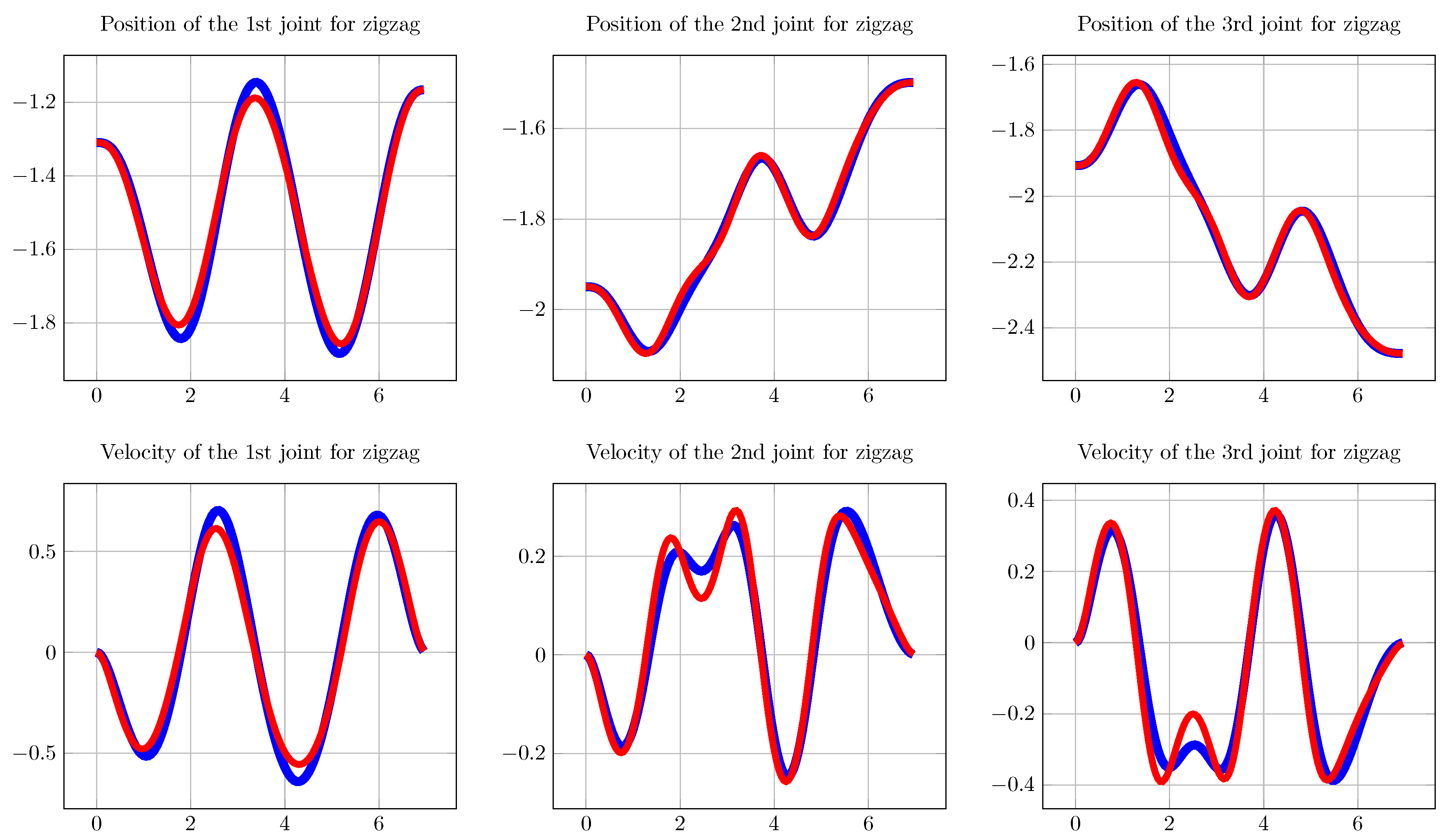
4.2. Trajectories Chosen for Numerical and Experimental Comparison
4.2.1. Benchmark Trajectories
4.2.2. Collaborative Trajectory
4.3. Results
4.3.1. Benchmark Trajectories
4.3.2. Collaborative Trajectory
- a trapezoidal velocity profile generated by the robot’s controller;
- a min-jerk trajectory computed considering ;
- a minimum arc-length trajectory computed considering .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rojas, R.A.; Rauch, E.; Vidoni, R.; Matt, D.T. Enabling Connectivity of Cyber-Physical Production Systems: A Conceptual Framework. Procedia Manuf. 2017, 11, 822–829. [Google Scholar] [CrossRef]
- Robots and Robotic Devices—Safety Requirements for Industrial Robots—Part 1: Robots; Standard; International Organization for Standardization: Geneva, Switzerland, 2011.
- Robots and Robotic Devices—Safety Requirements for Industrial Robots—Part 2: Robot Systems and Integration; Standard; International Organization for Standardization: Geneva, Switzerland, 2011.
- Robots, U. User Manual UR3/CB3 Original Instructions; Technical Report; Universal Robots: Odense, Denmark, 2017. [Google Scholar]
- ABB. Operatingmanual IRB 14000; Technical Report; ABB: Zürich, Switzerland, 2018. [Google Scholar]
- Gualtieri, L.; Rauch, E.; Vidoni, R.; Matt, D.T. An evaluation methodology for the conversion of manual assembly systems into human-robot collaborative workcells. Procedia Manuf. 2019, 38, 358–366. [Google Scholar] [CrossRef]
- Gualtieri, L.; Palomba, I.; Merati, F.A.; Rauch, E.; Vidoni, R. Design of Human-Centered Collaborative Assembly Workstations for the Improvement of Operators’ Physical Ergonomics and Production Efficiency: A Case Study. Sustainability 2020, 12, 3606. [Google Scholar] [CrossRef]
- Gualtieri, L.; Rauch, E.; Vidoni, R. Emerging Research Fields in Safety and Ergonomics in Industrial Collaborative Robotics: A Systematic Literature Review. Robot. Comput.-Integr. Manuf. 2020, 67, 101998. [Google Scholar] [CrossRef]
- Or, C.K.; Duffy, V.G.; Cheung, C.C. Perception of safe robot idle time in virtual reality and real industrial environments. Int. J. Ind. Ergon. 2009, 39, 807–812. [Google Scholar] [CrossRef]
- Arai, T.; Kato, R.; Fujita, M. Assessment of operator stress induced by robot collaboration in assembly. CIRP Ann. 2010, 59, 5–8. [Google Scholar] [CrossRef]
- Lasota, P.A.; Shah, J.A. Analyzing the effects of human-aware motion planning on close-proximity human–robot collaboration. Hum. Factors 2015, 57, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Kokabe, M.; Shibata, S.; Yamamoto, T. Modeling of handling motion reflecting emotional state and its application to robots. In Proceedings of the SICE Annual Conference, Tokyo, Japan, 20–22 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 495–501. [Google Scholar]
- Robots and Robotic Devices—Collaborative Robots; Technical Specification; International Organization for Standardization: Geneva, Switzerland, 2016.
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Trajectory planning in robotics. Math. Comput. Sci. 2012, 6, 269–279. [Google Scholar] [CrossRef]
- Flash, T.; Hogan, N. The coordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef] [PubMed]
- Meirovitch, Y.; Bennequin, D.; Flash, T. Geometrical invariance and smoothness maximization for task-space movement generation. IEEE Trans. Robot. 2016, 32, 837–853. [Google Scholar] [CrossRef]
- Oguz, O.S.; Zhou, Z.; Glasauer, S.; Wollherr, D. An Inverse Optimal Control Approach to Explain Human Arm Reaching Control Based on Multiple Internal Models. Sci. Rep. 2018, 8, 5583. [Google Scholar] [CrossRef] [PubMed]
- Kühnlenz, B.; Kühnlenz, K. Reduction of Heart Rate by Robot Trajectory Profiles in Cooperative HRI. In Proceedings of the ISR 2016: 47st International Symposium on Robotics, Munich, Germany, 21–22 June 2016; VDE: Frankfurt, Germany, 2016; pp. 1–6. [Google Scholar]
- Gasparetto, A.; Zanotto, V. A new method for smooth trajectory planning of robot manipulators. Mech. Mach. Theory 2007, 42, 455–471. [Google Scholar] [CrossRef]
- Gasparetto, A.; Lanzutti, A.; Vidoni, R.; Zanotto, V. Validation of minimum time-jerk algorithms for trajectory planning of industrial robots. J. Mech. Robot. 2011, 3. [Google Scholar] [CrossRef]
- Kyriakopoulos, K.J.; Saridis, G.N. Minimum jerk path generation. In Proceedings of the International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 24–29 April 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 364–369. [Google Scholar]
- Boscariol, P.; Gasparetto, A.; Vidoni, R. Planning continuous-jerk trajectories for industrial manipulators. In Engineering Systems Design and Analysis; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 3, pp. 127–136. [Google Scholar]
- Piazzi, A.; Visioli, A. Global minimum jerk trajectory planning of robot manipulators. IEEE Trans. Ind. Electron. 2000, 47, 140–149. [Google Scholar] [CrossRef]
- Bianco, C.G.L. Minimum-jerk velocity planning for mobile robot applications. IEEE Trans. Robot. 2013, 29, 1317–1326. [Google Scholar] [CrossRef]
- Rojas, R.A.; Garcia, M.A.R.; Wehrle, E.; Vidoni, R. A Variational Approach to Minimum-Jerk Trajectories for Psychological Safety in Collaborative Assembly Stations. IEEE Robot. Autom. Lett. 2019, 4, 823–829. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Giaquinta, M.; Hildebrandt, S. Calculus of Variations II; Springer Science & Business Media: Berlin, Germany, 2013; Volume 311. [Google Scholar]
- Van Brunt, B. The Calculus of Variations; Universitext, Springer: New York, NY, USA, 2006. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C.; Villagómez Velázquez, H. Elementary Differential Equations and Boundary Value Problems. Ecuaciones Diferenciales y Problemas con Valores en la Frontera; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Dai, Y.H.; Schittkowski, K. A sequential quadratic programming algorithm with non-monotone line search. Pac. J. Optim. 2008, 4, 335–351. [Google Scholar]
- Lacevic, B.; Rocco, P. Kinetostatic danger field-a novel safety assessment for human-robot interaction. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2169–2174. [Google Scholar]
- Gualtieri, L.; Rojas, R.; Carabin, G.; Palomba, I.; Rauch, E.; Vidoni, R.; Matt, D.T. Advanced automation for SMEs in the I4. 0 revolution: Engineering education and employees training in the smart mini factory laboratory. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1111–1115. [Google Scholar]
- Rojas, R.A.; Rauch, E.; Dallasega, P.; Matt, D.T. Safe Human-Machine Centered Design of an Assembly Station in a Learning Factory Environment. In Proceedings of the 8th International Conference on Industrial Engineering and Operations Management, Bandung, Indonesia, 6–8 March 2018. [Google Scholar]





| Body Region | Speed Limit (mm/s) |
|---|---|
| Upper arms and elbow joints | 330 |
| Lower arms and wrist joints | 360 |
| (a) Zigzag path. | ||||||
| J 1 | J 2 | J 3 | J 4 | J 5 | J 6 | |
| −1.30 | −1.94 | −1.90 | −0.82 | 1.64 | −9.20 | |
| −1.74 | −2.09 | −1.66 | −0.96 | 1.65 | −9.64 | |
| −1.76 | −1.96 | −1.86 | −0.89 | 1.65 | −9.65 | |
| −1.26 | −1.81 | −2.10 | −0.76 | 1.64 | −9.15 | |
| −1.21 | −1.66 | −2.30 | −0.71 | 1.64 | −9.10 | |
| −1.79 | −1.83 | −2.04 | −0.83 | 1.65 | −9.68 | |
| −1.83 | −1.73 | −2.19 | −0.80 | 1.65 | −9.73 | |
| −1.16 | −1.49 | −2.47 | −0.69 | 1.64 | −9.05 | |
| (b) Figure-eight path. | ||||||
| J 1 | J 2 | J 3 | J 4 | J 5 | J 6 | |
| −1.16 | −1.49 | −2.47 | −0.69 | 1.64 | −9.05 | |
| −1.02 | −1.57 | −2.29 | −0.84 | 1.56 | −8.89 | |
| −1.13 | −1.65 | −2.21 | −0.84 | 1.56 | −9.00 | |
| −1.26 | −1.68 | −2.18 | −0.84 | 1.56 | −9.14 | |
| −1.35 | −1.61 | −2.26 | −0.83 | 1.56 | −9.23 | |
| −1.37 | −1.50 | −2.37 | −0.83 | 1.56 | −9.25 | |
| −1.39 | −1.35 | −2.49 | −0.86 | 1.56 | −9.26 | |
| −1.51 | −1.32 | −2.51 | −0.87 | 1.55 | −9.39 | |
| −1.66 | −1.42 | −2.44 | −0.84 | 1.55 | −9.54 | |
| −1.72 | −1.53 | −2.35 | −0.82 | 1.55 | −9.60 | |
| −1.73 | −1.66 | −2.22 | −0.82 | 1.55 | −9.62 | |
| −1.68 | −1.74 | −2.12 | −0.84 | 1.55 | −9.57 | |
| −1.61 | −1.77 | −2.09 | −0.84 | 1.55 | −9.50 | |
| −1.51 | −1.74 | −2.13 | −0.84 | 1.55 | −9.41 | |
| −1.42 | −1.65 | −2.25 | −0.82 | 1.55 | −9.32 | |
| −1.34 | −1.50 | −2.40 | −0.82 | 1.55 | −9.24 | |
| −1.23 | −1.32 | −2.53 | −0.86 | 1.56 | −9.14 | |
| −1.05 | −1.21 | −2.59 | −0.91 | 1.56 | −8.95 | |
| −0.90 | −1.30 | −2.54 | −0.87 | 1.56 | −8.81 | |
| (a) Picking trajectory. | ||||||
| J 1 | J 2 | J 3 | J 4 | J 5 | J 6 | |
| −1.60 | −1.90 | −1.76 | −2.57 | −1.55 | 0.00 | |
| −0.96 | −1.96 | −1.76 | −2.58 | −1.74 | 0.00 | |
| 0.78 | −2.23 | −1.95 | −2.09 | −2.36 | 0.00 | |
| 0.81 | −2.24 | −1.93 | −2.10 | −2.32 | 0.00 | |
| 0.87 | −2.26 | −1.87 | −2.14 | −2.27 | 0.00 | |
| 0.92 | −2.29 | −1.80 | −2.18 | −2.22 | 0.00 | |
| (b) Passing trajectory. | ||||||
| J 1 | J 2 | J 3 | J 4 | J 5 | J 6 | |
| 0.92 | −2.29 | −1.80 | −2.18 | −2.22 | 0.00 | |
| 0.92 | −2.23 | −1.79 | −2.25 | −2.22 | 0.00 | |
| 0.92 | −2.19 | −1.78 | −2.30 | −2.22 | 0.00 | |
| 0.92 | −2.15 | −1.77 | −2.36 | −2.45 | 0.00 | |
| 0.69 | −2.04 | −1.97 | −2.26 | −1.55 | 0.00 | |
| −0.77 | −1.90 | −1.78 | −2.57 | −1.55 | 0.00 | |
| −1.60 | −1.90 | −1.75 | −2.57 | −1.55 | 0.00 | |
| (rad/s) | (m/s) | |
|---|---|---|
| Trapezoidal speed profile | 1.267 | 0.397 |
| 1.245 | 0.366 | |
| 0.844 | 0.245 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojas, R.A.; Wehrle, E.; Vidoni, R. A Multicriteria Motion Planning Approach for Combining Smoothness and Speed in Collaborative Assembly Systems. Appl. Sci. 2020, 10, 5086. https://doi.org/10.3390/app10155086
Rojas RA, Wehrle E, Vidoni R. A Multicriteria Motion Planning Approach for Combining Smoothness and Speed in Collaborative Assembly Systems. Applied Sciences. 2020; 10(15):5086. https://doi.org/10.3390/app10155086
Chicago/Turabian StyleRojas, Rafael A., Erich Wehrle, and Renato Vidoni. 2020. "A Multicriteria Motion Planning Approach for Combining Smoothness and Speed in Collaborative Assembly Systems" Applied Sciences 10, no. 15: 5086. https://doi.org/10.3390/app10155086
APA StyleRojas, R. A., Wehrle, E., & Vidoni, R. (2020). A Multicriteria Motion Planning Approach for Combining Smoothness and Speed in Collaborative Assembly Systems. Applied Sciences, 10(15), 5086. https://doi.org/10.3390/app10155086







