3-D Integral Formulation for Thin Electromagnetic Shells Coupled with an External Circuit
Abstract
1. Introduction
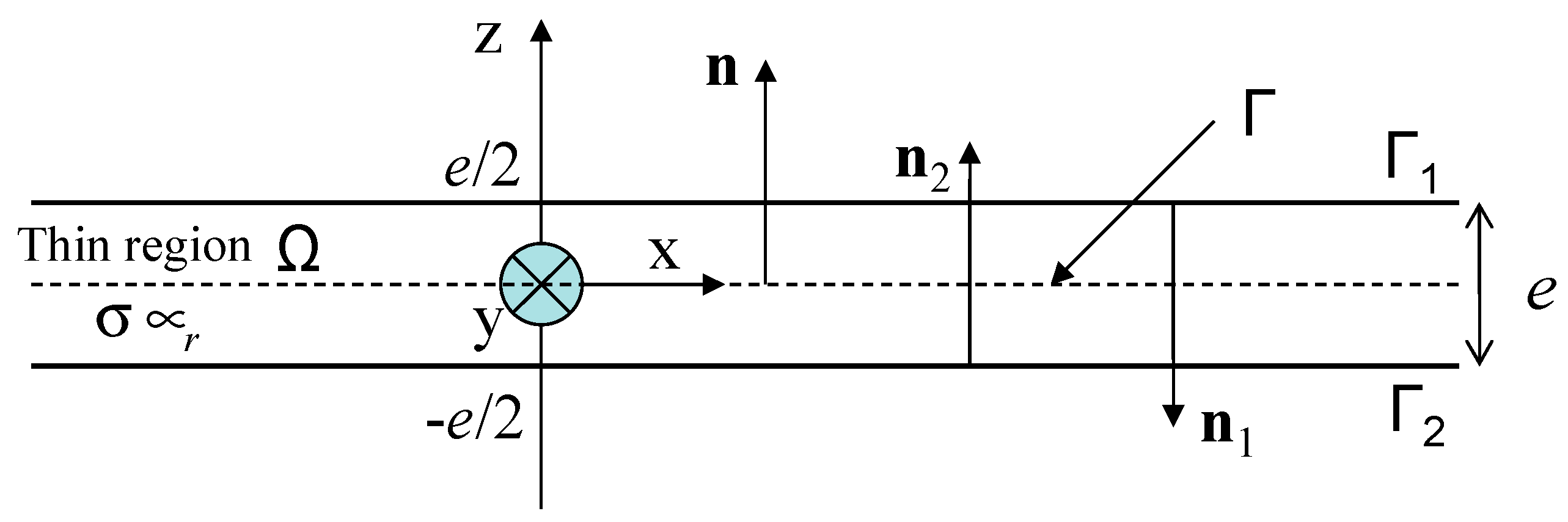
2. Thin Shell Equation
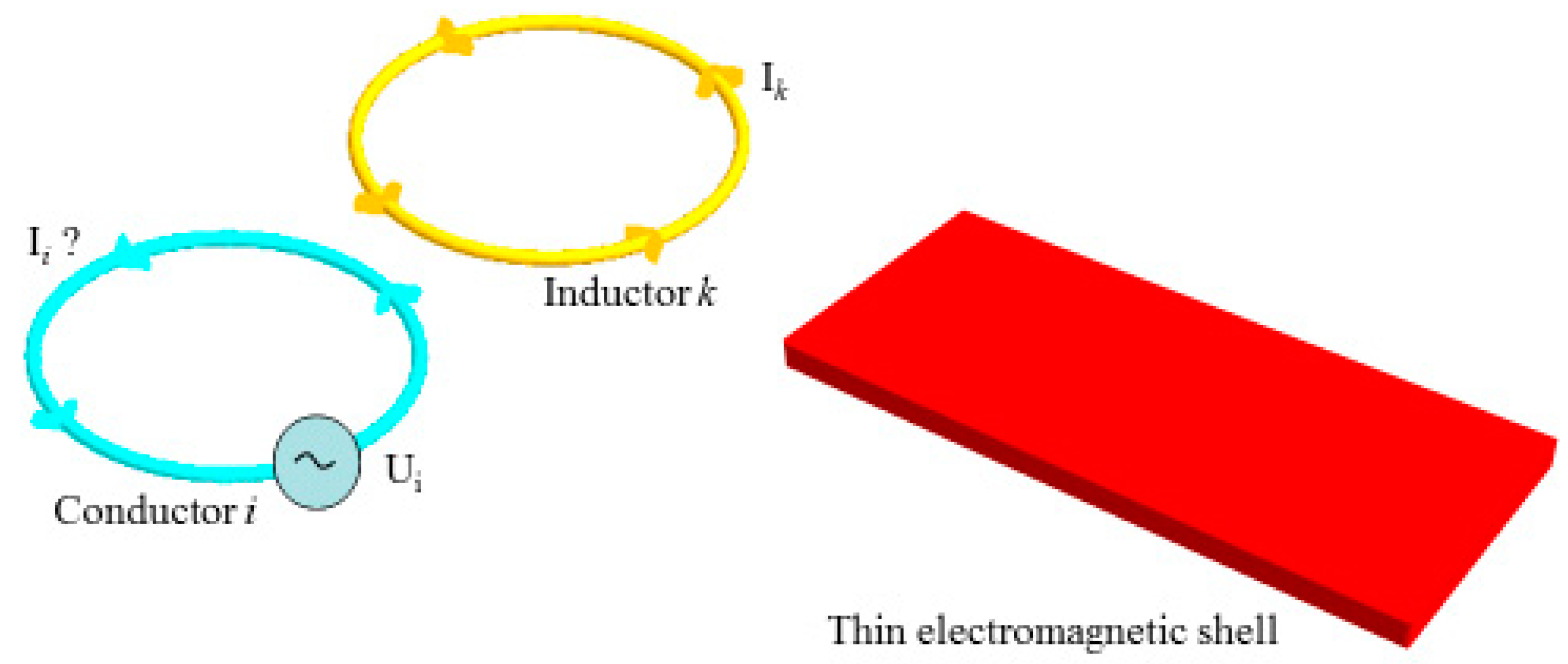
3. Conductor System Modelling
4. Coupling Thin Shell with Circuit Equation
4.1. Influence of the Conductor Current on the Thin Region
4.2. Influence of Thin Shell Magnetization on the Conductor
4.3. Influence of Thin Shell Eddy Current on the Conductor
4.4. Final System of Equations
5. Numerical Examples
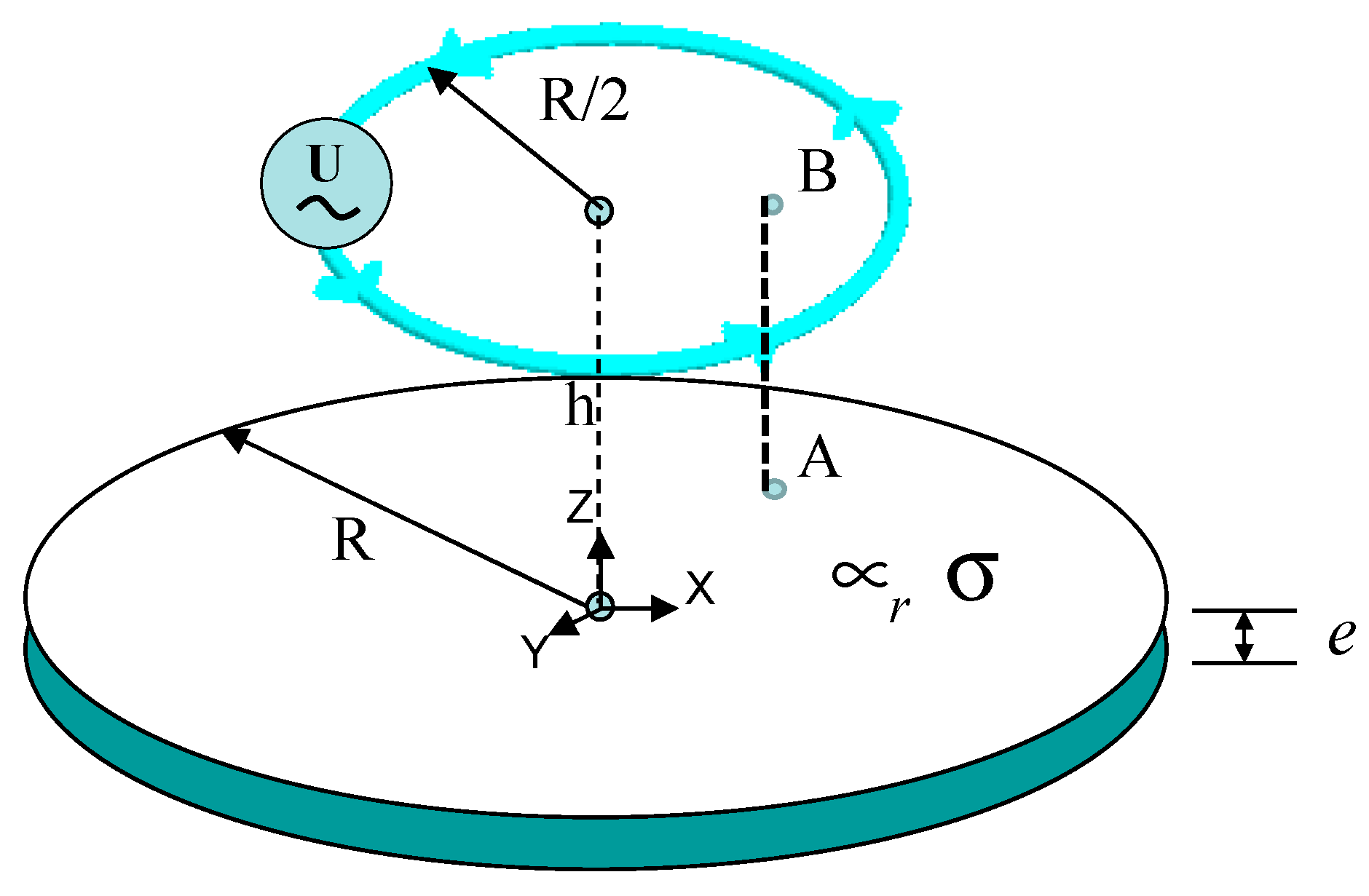
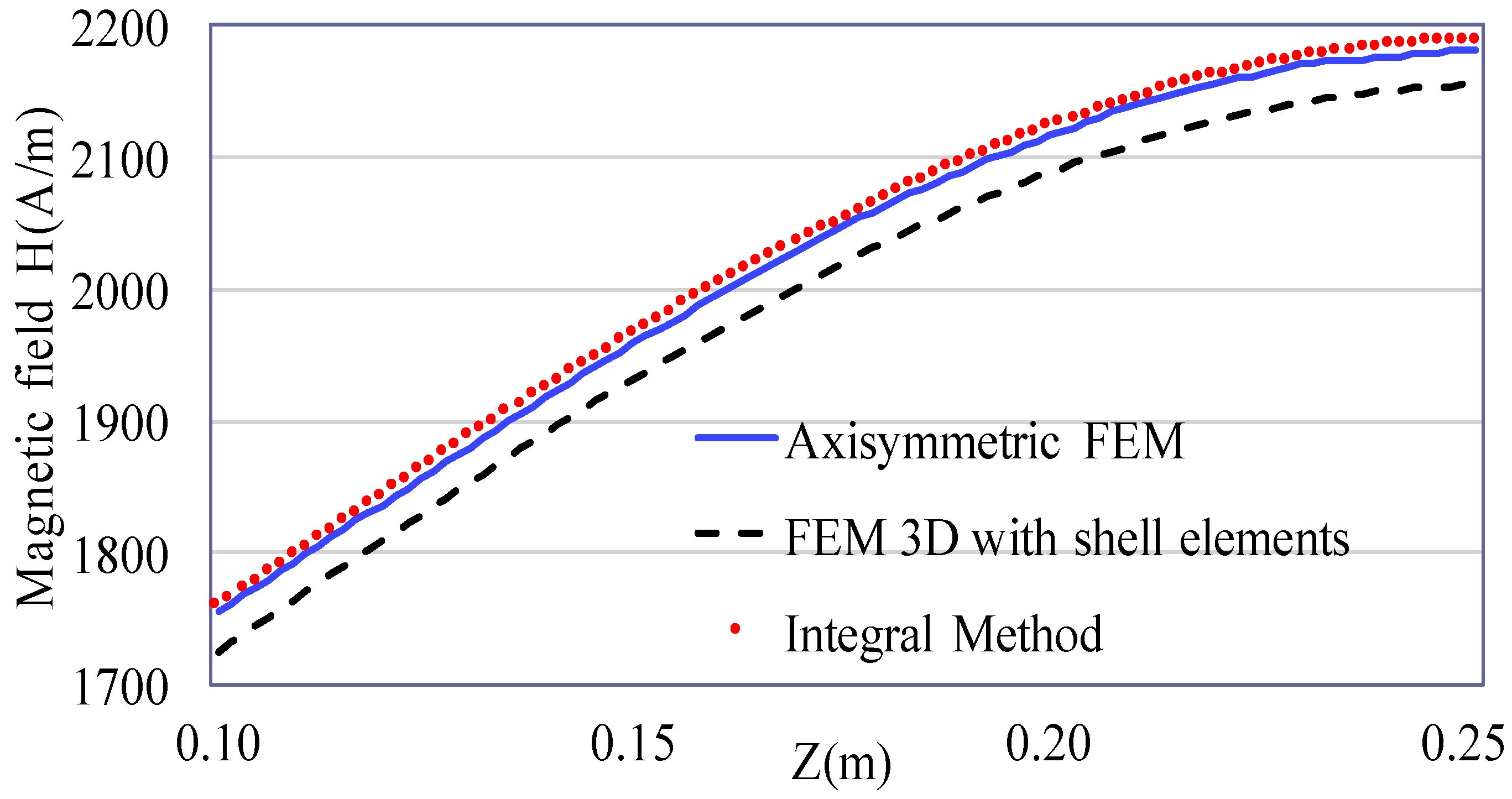
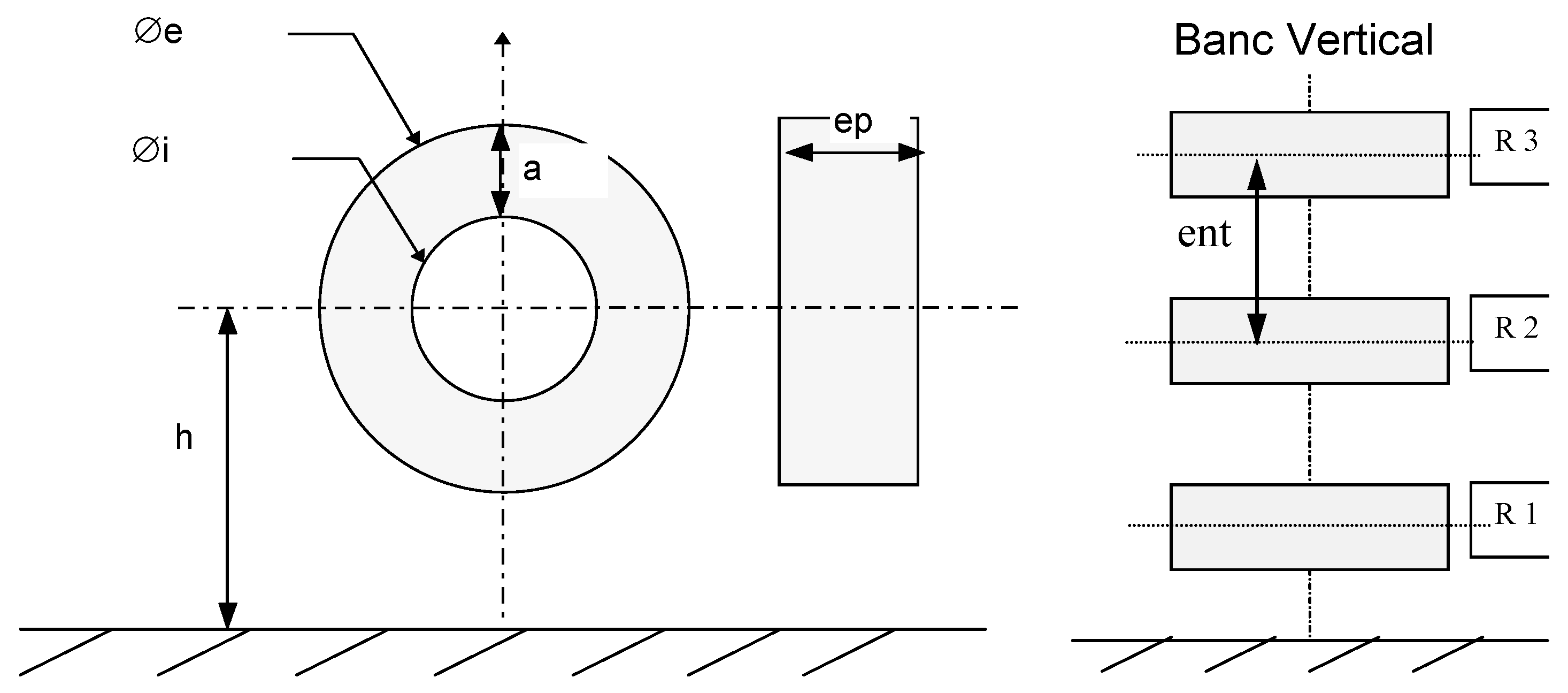
5.1. Validation Through an Academic Example
- –
- Thin disk:
- ○
- Electrical conductivity σdisk = 6 × 107 S/m
- ○
- Permeability μr = 200
- ○
- R = 1 m, e = 50 mm
- ○
- The skin depth δ = 1.45 mm is smaller than the disk’s thickness
- –
- Conductor:
- ○
- Electrical conductivity σ conductor = 5.79 × 107 S/m
- ○
- h = R/4 = 0.25 m
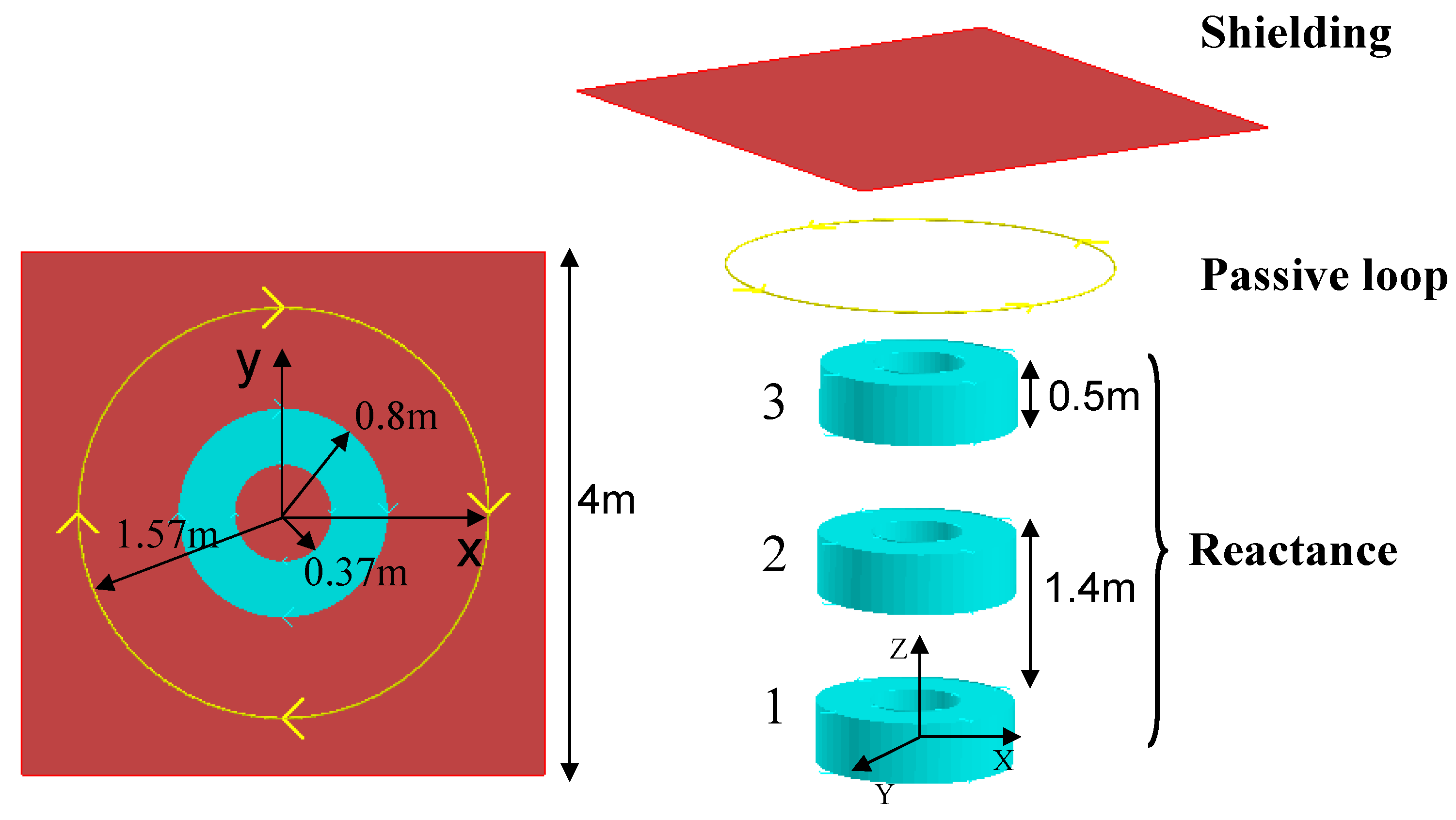
5.2. A Pratical Device Example
- –
- Outside diameter: ∅e = 1.6 m
- –
- Inside diameter: ∅i = 0.74 m
- –
- Winding thickness: ep = 0.5 m
- –
- Center distance: Ent = 1.4 m
- –
- Passive loop:
- ○
- Permeability μr = 1,
- ○
- Electrical conductivity σ = 3.03 × 107 S/m
- ○
- Section radius rs = 9.25 mm
- ○
- Zloop = 3.85 m
- –
- Shielding:
- ○
- Permeability μr = 20,000,
- ○
- Electrical conductivity σ = 2.2 × 106 S/m
- ○
- Thickness = 3.5 mm
- ○
- Zshielding = 5.15 m
- ○
- The skin depth δ = 0.339mm is thinner than the shielding’s thickness.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| FVM | Finite Volume Method |
| BEM | Boundary Elements method |
| MoM | Methods of Moments |
| PEEC | Partial Element Equivalent Circuit |
References
- Salon, S.; Chari, M.V.K. Numerical Methods in Electromagnetism; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Meunier, G. The Finite Element Method for Electromagnetic Modeling; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Krähenbühl, L.; Muller, D. Thin Layers in electrical engineering. Example of Shell Models in Analyzing Eddy-Currents by Boundary and Finite Element Methods. IEEE Trans. Magn. 1993, 29, 1450–1455. [Google Scholar] [CrossRef]
- Igarashi, H.; Kost, A.; Honma, T. A Three-Dimensional Analysis of Magnetic Fields around a Thin Magnetic Conductive Layer Using Vector Potential. IEEE Trans. Magn. 1998, 34, 2539–2542. [Google Scholar] [CrossRef]
- Guérin, C.; Meunier, G. 3-D Magnetic Scalar Potential Finite Element Formulation for Conducting Shells Coupled with an External Circuit. IEEE Trans. Magn. 2012, 48, 323–326. [Google Scholar] [CrossRef]
- Dang, Q.V.; Dular, P.; Sabariego, R.V.; Krahenbuhl, L.; Geuzaine, C. Subproblem Approach for Thin Shell Dual Finite Element Formulations. IEEE Trans. Magn. 2012, 48, 407–410. [Google Scholar] [CrossRef][Green Version]
- Hoer, C.; Love, C. Exact Inductance Equations for Rectangular Conductors with Applications to More Complicated Geometries. J. Res. Natl. Bur. Stand.-C. Eng. Instrum. 1965, 69C, 127–137. [Google Scholar] [CrossRef]
- Ruehli, A.E. Equivalent circuit models for three dimensional multiconductor systems. IEEE Trans. Microw. Theory Tech. 1974, 22, 216–221. [Google Scholar] [CrossRef]
- Clavel, E.; Roudet, J.; Foggia, A. Electrical modeling of transformer connecting bars. IEEE Trans. Magn. 2002, 38, 1378–1382. [Google Scholar] [CrossRef]
- Chadebec, O.; Coulomb, J.-L.; Janet, F. A review of Magnetostatic Moment Method. IEEE Trans. Magn. 2006, 42, 515–520. [Google Scholar] [CrossRef]
- Le-Duc, T.; Chadebec, O.; Guichon, J.M.; Meunier, G. Coupling between partial element equivalent circuit method and an integro-differential approach for solving electromagnetics problems. IET Sci. Meas. Technol. 2012, 6, 394–397. [Google Scholar] [CrossRef]
- Ishibashi, K.; Andjelic, Z.; Pusch, D. Nonlinear Eddy Current Analysis by BEM Minimum Order Formulation. IEEE Trans. on Magn. 2010, 46, 3085–3088. [Google Scholar] [CrossRef]
- Ishibashi, K.; Andjelic, Z.; Takahashi, Y.; Takamatsu, T.; Tsuzaki, K.; Wakao, S.; Fujiwara, K.; Ishihara, Y. Ishihara. Some Treatments of Fictitious Volume Charges in Nonlinear Magnetostatic Analysis by BIE. IEEE Trans. Magn. 2012, 48, 463–466. [Google Scholar] [CrossRef]
- Bettini, P.; Passarotto, M.; Specogna, R. Coupling Volume and Surface Integral Formulations for Eddy-Current Problems on General Meshes. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Le-Duc, T.; Meunier, G.; Chadebec, O.; Guichon, J.M. A New Integral Formulation for Eddy Current Computation in Thin Conductive Shells. IEEE Trans. Magn. 2012, 48, 427–430. [Google Scholar] [CrossRef][Green Version]
- Le-Duc, T.; Meunier, G.; Chadebec, O.; Guichon, J.M.; Bastos, J.P.A. General integral formulation for the 3D thin shell modelling. IEEE Trans. Magn. 2013, 49, 1989–1992. [Google Scholar] [CrossRef]
- De Camillis, L.; Ferranti, F.; Antonini, G.; Vande Ginste, D.; De Zutter, D. Parameterized Partial Element Equivalent Circuit Method for Sensitivity Analysis of Multiport Systems. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 248–255. [Google Scholar] [CrossRef][Green Version]
- Meunier, G.; Guichon, J.M.; Chadebec, O.; Bannwarth, B.; Krähenbühl, L.; Guérin, C. Unstructured–PEEC Method for Thin Electromagnetic Media. IEEE Trans. Magn. 2020, 56, 1–5. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Guichon, J.M.; Chadebec, O.; Meunier, G.; Vincent, B. An independent loops search algorithm for solving inductive PEEC large problems. Prog. Electromagn. Res. M. 2012, 23, 53–63. [Google Scholar] [CrossRef][Green Version]
- Lombardi, L.; Romano, D.; Antonini, G. Efficient Numerical Computation of Full-Wave Partial Elements Modeling Magnetic Materials in the PEEC Method. IEEE Trans. Microw. Theory Tech. 2020, 68, 915–925. [Google Scholar] [CrossRef]
- Ferranti, F.; Nakhla, M.S.; Antonini, G.; Dhaene, T.; Knockaert, L.; Ruehli, A.E. Multipoint full-wave model order reduction for delayed PEEC models with large delays. IEEE Trans. Electromagn. Compat. 2011, 53, 959–967. [Google Scholar] [CrossRef]
- Ishida, K.; Itaya, T.; Tanaka, A.; Takehira, N. Mutual inductance of arbitrary-shaped coils using shape functions. IET Sci. Meas. Technol. 2019, 13, 1085–1091. [Google Scholar] [CrossRef]
- Babic, S.I.; Akyel, C. New analytic-numerical solutions for the mutual inductance of two coaxial circular coils with rectangular cross section in air. IEEE Trans. Magn. 2006, 42, 1661–1669. [Google Scholar] [CrossRef]
- Antonini, G.; Sabatini, M.; Miscione, G. PEEC modeling of linear magnetic materials. IEEE Int. Symp. Electromagn. Compat. 2006, 1, 93–98. [Google Scholar]
- Carpentier, A.; Chadebec, O.; Galopin, N.; Meunier, G.; Bannwarth, B. Resolution of Nonlinear Magnetostatic Problems with a Volume Integral Method Using the Magnetic Scalar Potential. IEEE Trans. Magn. 2013, 49, 1685–1688. [Google Scholar] [CrossRef]
- Abakar, A.; Meunier, G.; Coulomb, J.L.; Zgainski, F.X. 3D Modeling of Shielding Structures Made by Conductors and Thin Plates. IEEE Trans. Magn. 2000, 36, 790–794. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Guichon, J.M.; Chadebec, O.; Labie, P.; Coulomb, J.L. Ships Magnetic Anomaly Computation with Integral Equation and Fast Multipole Method. IEEE Trans. Magn. 2011, 47, 1414–1417. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Duc, T.L.; Tran, T.S.; Guichon, J.M.; Chadebec, O.; Meunier, G. Adaptive Multipoint Model Order Reduction Scheme for Large-Scale Inductive PEEC Circuits. IEEE Trans. Electromagn. Compat. 2017, 59, 1143–1151. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Le Duc, T.; Tran, S.T.; Guichon, J.M.; Chadebec, O.; Sykulski, J. Circuit realization method for reduced order inductive PEEC modeling circuits. Compel. Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1203–1217. [Google Scholar] [CrossRef]

| FEM Axisymmetric | |||
| Number of elements | 15,000 | 30,000 | 55,000 |
| Current values (A) | 1905.95 − j493.12 | 1905.78 − j492.87 | 1905.75 − j492.86 |
| FEM 3D with shell elements | |||
| Number of elements | 130,000 | 500,000 | 950,000 |
| Current values (A) | 1866.75 − j460.52 | 1841.78 − j505.48 | 1839.23 − j509.75 |
| Integral method | |||
| Number of elements | 300 | 800 | 1000 |
| Current values (A) | 1908.21 − j495.44 | 1907.85 − j495.37 | 1907.76 − j495.35 |
| FEM 3D with Shell Elements | |||
| Number of elements | 450,000 | 800,000 | 1,100,000 |
| Current values (A) | 619.14 + j1946.05 | 602.72 + j1878.72 | 606.87 + j1870.24 |
| Integral method | |||
| Number of elements | 430 | 850 | 1020 |
| Current values (A) | 615.21 + j1742.30 | 619.86 + j1745.98 | 621.38 + j1746.60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le-Duc, T.; Meunier, G. 3-D Integral Formulation for Thin Electromagnetic Shells Coupled with an External Circuit. Appl. Sci. 2020, 10, 4284. https://doi.org/10.3390/app10124284
Le-Duc T, Meunier G. 3-D Integral Formulation for Thin Electromagnetic Shells Coupled with an External Circuit. Applied Sciences. 2020; 10(12):4284. https://doi.org/10.3390/app10124284
Chicago/Turabian StyleLe-Duc, Tung, and Gerard Meunier. 2020. "3-D Integral Formulation for Thin Electromagnetic Shells Coupled with an External Circuit" Applied Sciences 10, no. 12: 4284. https://doi.org/10.3390/app10124284
APA StyleLe-Duc, T., & Meunier, G. (2020). 3-D Integral Formulation for Thin Electromagnetic Shells Coupled with an External Circuit. Applied Sciences, 10(12), 4284. https://doi.org/10.3390/app10124284






