Application of Deep Reinforcement Learning in Traffic Signal Control: An Overview and Impact of Open Traffic Data
Abstract
1. Introduction
2. Reinforcement Learning
2.1. Drawbacks of Reinforcement Learning
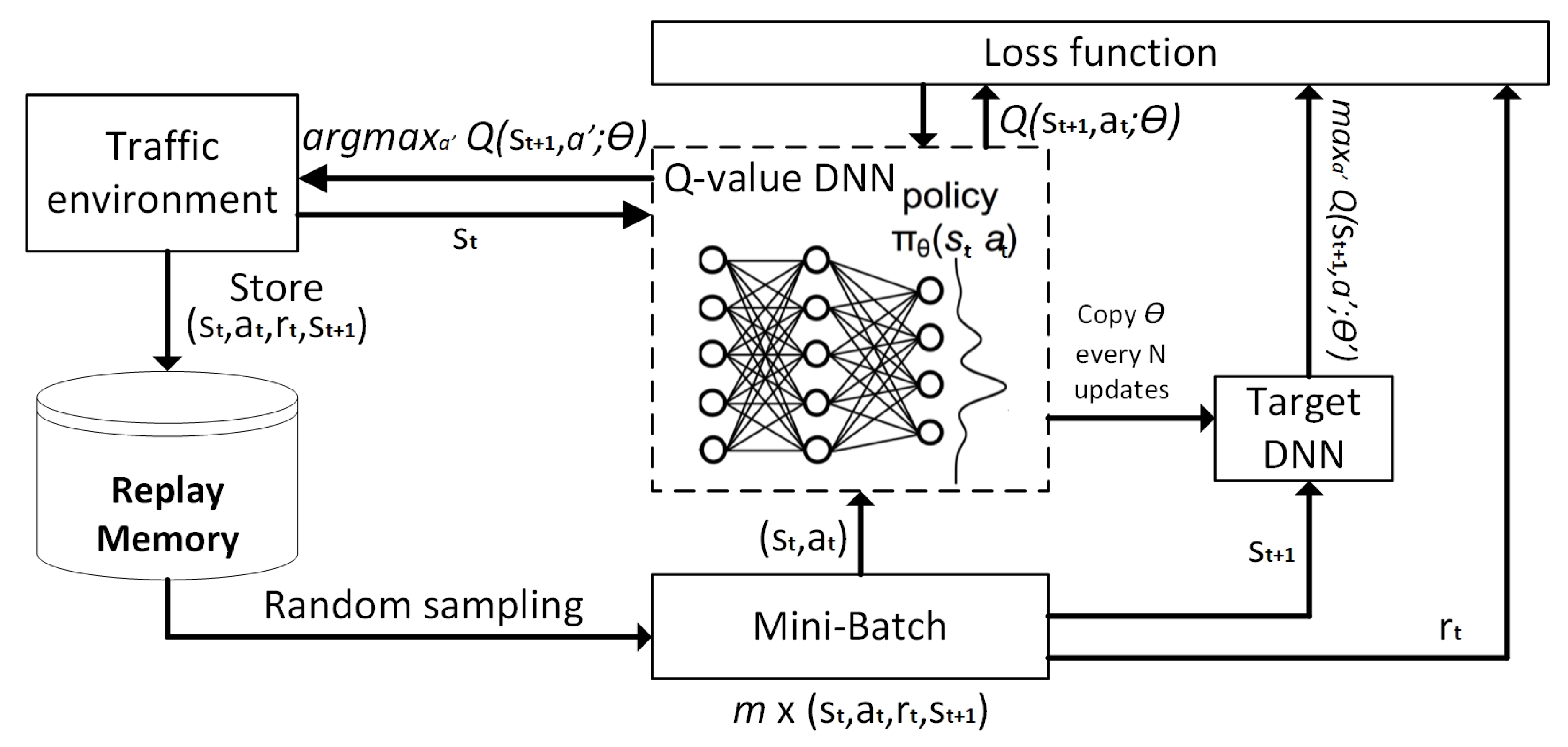
2.2. General Deep Reinforcement Learning
2.3. Advanced Approaches for Deep Reinforcement Learning
- Prioritized Experience Memory (PER) allows the RL based agent to consider state–action transitions with the different frequency that they are experienced [25]. It increases the replay probability of samples stored in RM that have a high Temporal-Difference (TD) error, and therefore possible high impact on learning convergence. The TD error is computed based on the difference between the current and targeted Q-values. Mentioned prioritization can lead to a loss of diversity. This problem can be alleviated by introducing the stochastic prioritization, and biased outputs can be corrected by importance sampling, as described in [26].
- Dueling Deep Q-Networks (DDQN) represents the special architecture of DNN models used in DQL. The Q-value is estimated according to the value of the current state and each action’s advantage of taking this action a in state s. The value of state is the overall expected reward in the case of taking probabilistic action in the future steps. Advantage, denoted by , is computed for all possible actions in accordance with the given state and with the main task to describe how important particular action is to the value function compared to the other actions. The final Q-value is computed by summing the value V, and advantage A. The dueling architecture is able to improve the performance of DQL as it can be seen in the following studies [5,27].
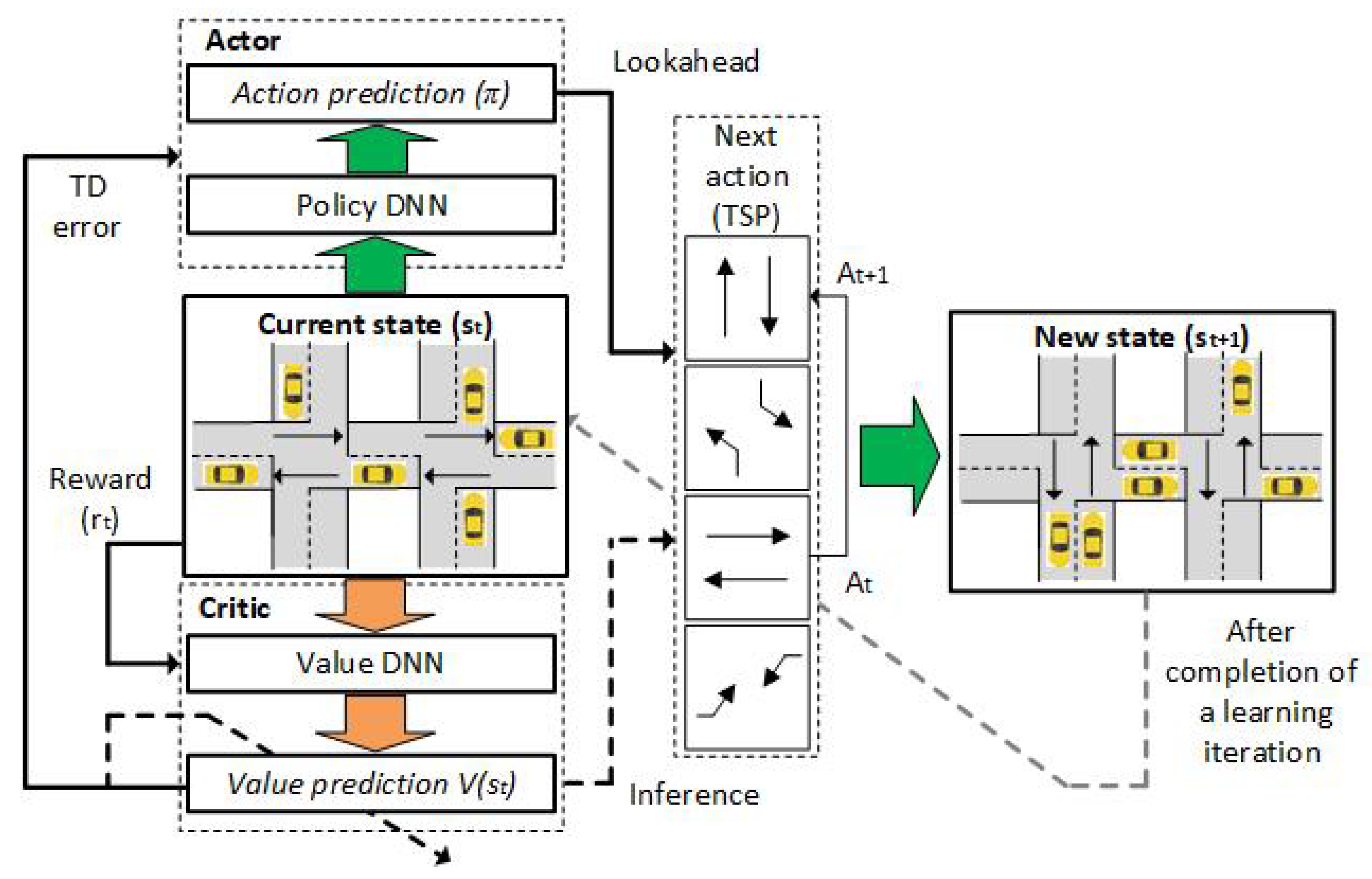
- Asynchronous Advantage Actor–Critic (A3C) approach is based on the central agent with global DNN model parameters. Its workers are copies of the Actor part of this agent; thus, this approach does not use ER since it requires a lot of memory. In A3C, there is only one Critic that learns the value function while multiple copies of actors are learned in parallel as his workers. Each worker in the A3C framework is executing in parallel in different instances and each of them is periodically asynchronously synced with the global DNN model. Due to independent exchange data between workers and the global parameters, there can be an issue related to the policy inconsistency among some workers.
- Advantage Actor–Critic (A2C) approach implements the coordinator module between workers and global DNN model parameters, which waits for all workers to finish their segment of experience before updating the global DNN model. This approach enables all workers to synchronously start with the same policy. In A2C, all workers are the same and they have the same set of weights since all workers are updated at the same time. This approach requires several versions of the environment that must be executed in parallel. Additionally, one worker should be assigned for each of them. Since the traffic flows are described by complex spatiotemporal datasets there is a danger that MDP may become non-stationary if the agent only knows the current state [9]. Furthermore, it is infeasible to input all historical inputs to A2C so it is common to include LSTM layers in its DNN models, which maintains hidden states in order to memorize short history [29]. Such a setup of A2C approach makes its learning process more cohesive and faster.
3. Adaptive Traffic Light Signal Control Based on DRL
Traffic Signal Control on a Larger Scale
4. Design of the DRL Algorithm for the Traffic Signal Control
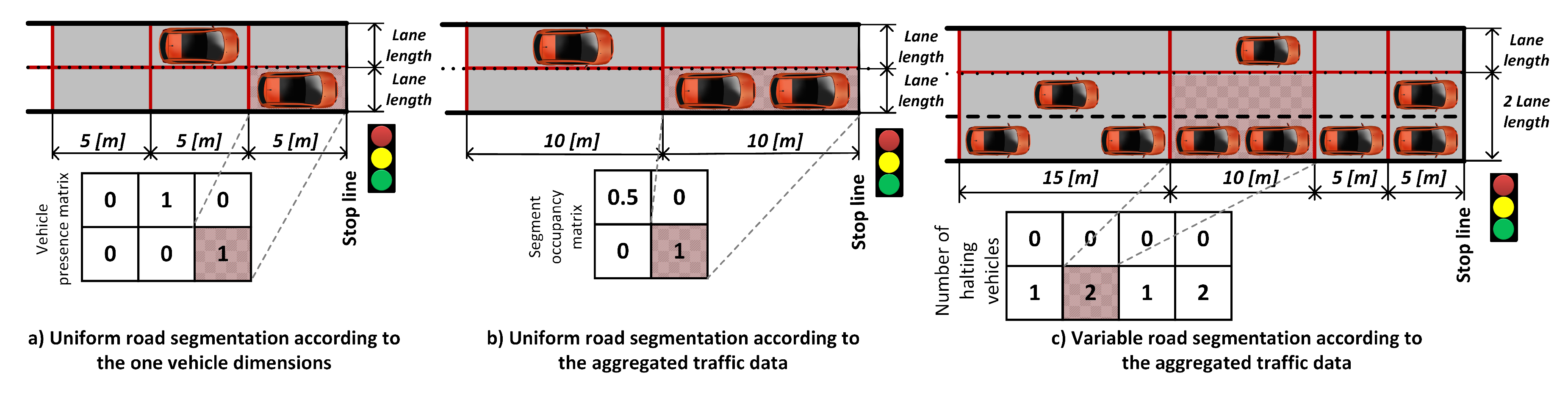
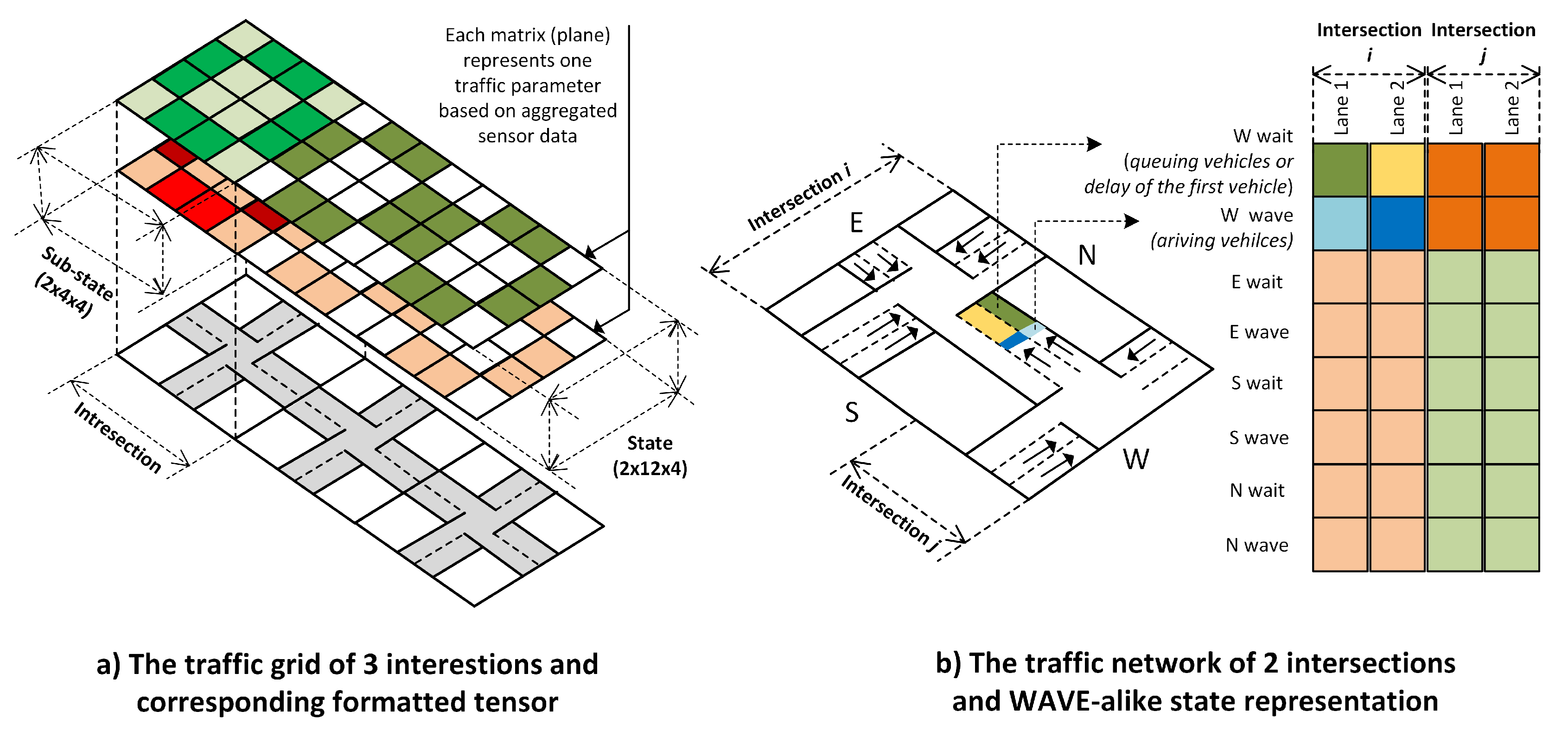
4.1. State Representation
4.2. Action Representation
4.3. Reward Function
5. Open Traffic Data Framework in the Context of Deep Learning
6. Discussion
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Benuwa, B.; Zhan, Y.; Ghansah, B.; Wornyo, D.; Banaseka, F. A Review of Deep Machine Learning. Int. J. Eng. Res. Afr. 2016, 24, 124–136. [Google Scholar] [CrossRef]
- Yau, K.L.A.; Qadir, J.; Khoo, H.L.; Ling, M.H.; Komisarczuk, P. A Survey on Reinforcement Learning Models and Algorithms for Traffic Signal Control. ACM Comput. Surv. 2017, 50. [Google Scholar] [CrossRef]
- Rohunen, A.; Markkula, J.; Heikkilä, M.; Heikkilä, J. Open Traffic Data for Future Service Innovation: Addressing the Privacy Challenges of Driving Data. J. Theor. Appl. Electron. Commer. Res. 2014, 9, 71–89. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Schukat, M.; Howley, E. Traffic light control using deep policy-gradient and value-function-based reinforcement learning. Iet Intell. Transp. Syst. 2017, 11, 417–423. [Google Scholar] [CrossRef]
- Liang, X.; Du, X.; Wang, G.; Han, Z. A Deep Reinforcement Learning Network for Traffic Light Cycle Control. IEEE Trans. Veh. Technol. 2019, 68, 1243–1253. [Google Scholar] [CrossRef]
- Li, Y. Deep Reinforcement Learning: An Overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Chin, Y.K.; Kow, W.Y.; Khong, W.L.; Tan, M.K.; Teo, K.T.K. Q-Learning Traffic Signal Optimization within Multiple Intersections Traffic Network. In Proceedings of the 2012 Sixth UKSim/AMSS European Symposium on Computer Modeling and Simulation, Valetta, Malta, 14–16 November 2012; pp. 343–348. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-Agent Deep Reinforcement Learning for Large-scale Traffic Signal Control. In IEEE Transactions on Intelligent Transportation Systems; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Williams, R.J. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Belletti, F.; Haziza, D.; Gomes, G.; Bayen, A.M. Expert Level Control of Ramp Metering Based on Multi-Task Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1198–1207. [Google Scholar] [CrossRef]
- Kušić, K.; Ivanjko, E.; Gregurić, M. A Comparison of Different State Representations for Reinforcement Learning Based Variable Speed Limit Control. In Proceedings of the 2018 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shabestary, S.M.A.; Abdulhai, B. Deep Learning vs. Discrete Reinforcement Learning for Adaptive Traffic Signal Control. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 286–293. [Google Scholar] [CrossRef]
- Li, L.; Lv, Y.; Wang, F. Traffic signal timing via deep reinforcement learning. Ieee/Caa J. Autom. Sin. 2016, 3, 247–254. [Google Scholar] [CrossRef]
- Kiran, B.R.; Thomas, D.M.; Parakkal, R. An Overview of Deep Learning Based Methods for Unsupervised and Semi-Supervised Anomaly Detection in Videos. J. Imaging 2018, 4, 36. [Google Scholar] [CrossRef]
- Genders, W.; Razavi, S.N. Using a Deep Reinforcement Learning Agent for Traffic Signal Control. arXiv 2016, arXiv:1611.01142. [Google Scholar]
- Yang, S.; Yang, B.; Wong, H.S.; Kang, Z. Cooperative traffic signal control using Multi-step return and Off-policy Asynchronous Advantage Actor–Critic Graph algorithm. Knowl.-Based Syst. 2019, 183, 104855. [Google Scholar] [CrossRef]
- Lin, Y.; Dai, X.; Li, L.; Wang, F. An Efficient Deep Reinforcement Learning Model for Urban Traffic Control. arXiv 2018, arXiv:1808.01876. [Google Scholar]
- Bhagat, S.; Banerjee, H.; Ho Tse, Z.T.; Ren, H. Deep Reinforcement Learning for Soft, Flexible Robots: Brief Review with Impending Challenges. Robotics 2019, 8, 4. [Google Scholar] [CrossRef]
- Casas, N. Deep Deterministic Policy Gradient for Urban Traffic Light Control. arXiv 2017, arXiv:1703.09035. [Google Scholar]
- Gao, J.; Shen, Y.; Liu, J.; Ito, M.; Shiratori, N. Adaptive Traffic Signal Control: Deep Reinforcement Learning Algorithm with Experience Replay and Target Network. arXiv 2017, arXiv:1705.02755. [Google Scholar]
- Ge, H.; Song, Y.; Wu, C.; Ren, J.; Tan, G. Cooperative Deep Q-Learning With Q-Value Transfer for Multi-Intersection Signal Control. IEEE Access 2019, 7, 40797–40809. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Savarese, P. On the Convergence of AdaBound and its Connection to SGD. arXiv 2019, arXiv:1908.04457. [Google Scholar]
- Calvo, J.A.; Dusparic, I. Heterogeneous Multi-Agent Deep Reinforcement Learning for Traffic Lights Control. In Proceedings of the Irish Conference on Artificial Intelligence and Cognitive Science (AICS), Dublin, Ireland, 6–7 December 2018. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Wang, Z.; de Freitas, N.; Lanctot, M. Dueling Network Architectures for Deep Reinforcement Learning. arXiv 2015, arXiv:1511.06581. [Google Scholar]
- Aslani, M.; Mesgari, S.; Wiering, M. Adaptive traffic signal control with actor-critic methods in a real-world traffic network with different traffic disruption events. Transp. Res. Part Emerg. Technol. 2017, 85, 732–752. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Kalweit, G.; Huegle, M.; Boedecker, J. Off-policy Multi-step Q-learning. arXiv 2019, arXiv:1909.13518. [Google Scholar]
- Asis, K.D.; Hernandez-Garcia, J.F.; Holland, G.Z.; Sutton, R.S. Multi-step Reinforcement Learning: A Unifying Algorithm. arXiv 2017, arXiv:1703.01327. [Google Scholar]
- Such, F.P.; Madhavan, V.; Conti, E.; Lehman, J.; Stanley, K.O.; Clune, J. Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning. arXiv 2017, arXiv:1712.06567. [Google Scholar]
- Wu, Y.; Tan, H.; Jiang, Z.; Ran, B. ES-CTC: A Deep Neuroevolution Model for Cooperative Intelligent Freeway Traffic Control. arXiv 2019, arXiv:1905.04083. [Google Scholar]
- Tan, T.; Bao, F.; Deng, Y.; Jin, A.; Dai, Q.; Wang, J. Cooperative Deep Reinforcement Learning for Large-Scale Traffic Grid Signal Control. IEEE Trans. Cybern. 2019, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, X.; Liang, H.; Liu, Y. A Review of the Self-Adaptive Traffic Signal Control System Based on Future Traffic Environment. J. Adv. Transp. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Zheng, G.; Zang, X.; Xu, N.; Wei, H.; Yu, Z.; Gayah, V.V.; Xu, K.; Li, Z. Diagnosing Reinforcement Learning for Traffic Signal Control. arXiv 2019, arXiv:1905.04716. [Google Scholar]
- Zhang, R.; Ishikawa, A.; Wang, W.; Striner, B.; Tonguz, O.K. Using Reinforcement Learning With Partial Vehicle Detection for Intelligent Traffic Signal Control. In IEEE Transactions on Intelligent Transportation Systems; IEEE: Piscataway, NJ, USA, 2020; pp. 1–12. [Google Scholar]
- Parasumanna Gokulan, B.; German, X.; Srinivasan, D. Urban traffic signal control using reinforcement learning agents. Intell. Transp. Syst. IET 2010, 4, 177–188. [Google Scholar] [CrossRef]
- Bazzan, A.L.C. Opportunities for multiagent systems and multiagent reinforcement learning in traffic control. Auton. Agents Multi-Agent Syst. 2008, 18, 342–375. [Google Scholar] [CrossRef]
- Dusparic, I.; Monteil, J.; Cahill, V. Towards autonomic urban traffic control with collaborative multi-policy reinforcement learning. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 2065–2070. [Google Scholar]
- Srinivasan, D.; Choy, M.C.; Cheu, R.L. Neural Networks for Real-Time Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2006, 7, 261–272. [Google Scholar] [CrossRef]
- Bakker, B.; Whiteson, S.; Kester, L.; Groen, F.C.A. Traffic Light Control by Multiagent Reinforcement Learning Systems. In Interactive Collaborative Information Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 475–510. [Google Scholar] [CrossRef]
- Van der Pol, E.; Oliehoek, F.A. Coordinated Deep Reinforcement Learners for Traffic Light Control. In Proceedings of the NIPS’16 Workshop on Learning, Inference and Control of Multi-Agent Systems, Barcelona, Spain, 9 December 2016. [Google Scholar]
- Foerster, J.; Nardelli, N.; Farquhar, G.; Afouras, T.; Torr, P.H.S.; Kohli, P.; Whiteson, S. Stabilising Experience Replay for Deep Multi-Agent Reinforcement Learning. arXiv 2017, arXiv:1702.08887. [Google Scholar]
- Wang, S.; Xie, X.; Huang, K.; Zeng, J.; Cai, Z. Deep Reinforcement Learning-Based Traffic Signal Control Using High-Resolution Event-Based Data. Entropy 2019, 21, 744. [Google Scholar] [CrossRef]
- Zambrano-Martinez, J.L.; Calafate, C.T.; Soler, D.; Cano, J.C. Towards Realistic Urban Traffic Experiments Using DFROUTER: Heuristic, Validation and Extensions. Sensors 2017, 17, 2921. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Jeong, O. Cooperative Traffic Signal Control with Traffic Flow Prediction in Multi-Intersection. Sensors 2019, 20, 137. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Ishikawa, A.; Wang, W.; Striner, B.; Tonguz, O. Intelligent traffic signal control: Using reinforcement learning with partial detection. arXiv 2018, arXiv:1807.01628. [Google Scholar] [CrossRef]
- Liang, X.; Du, X.; Wang, G.; Han, Z. Deep Reinforcement Learning for Traffic Light Control in Vehicular Networks. arXiv 2018, arXiv:1803.11115. [Google Scholar]
- Vidali, A.; Crociani, L.; Vizzari, G.; Bandini, S. A Deep Reinforcement Learning Approach to Adaptive Traffic Lights Management. In Proceedings of the WOA, Parma, Italy, 26 June 2019. [Google Scholar]
- Gu, J.; Fang, Y.; Sheng, Z.; Wen, P. Double Deep Q-Network with a Dual-Agent for Traffic Signal Control. Appl. Sci. 2020, 10, 1622. [Google Scholar] [CrossRef]
- Vujić, M.; Mandzuka, S.; Gregurić, M. Pilot Implementation of Public Transport Priority in The City of Zagreb. Promet-Traffic Transp. 2015, 27, 257–265. [Google Scholar] [CrossRef]
- Touhbi, S.; Babram, M.A.; Nguyen-Huu, T.; Marilleau, N.; Hbid, M.L.; Cambier, C.; Stinckwich, S. Adaptive Traffic Signal Control: Exploring Reward Definition for Reinforcement Learning. Procedia Comput. Sci. 2017, 109, 513–520. [Google Scholar] [CrossRef]
- Liu, M.; Deng, J.; Deng, U.; Ming, X.; Northeastern, X.Z.; Wang, W. Cooperative Deep Reinforcement Learning for Traffic Signal Control. In Proceedings of the UrbComp 2017: The 6th International Workshop on Urban Computing, Halifax, NS, Canada, 14 August 2017. [Google Scholar]
- Kastrinaki, V.; Zervakis, M.; Kalaitzakis, K. A survey of video processing techniques for traffic applications. Image Vis. Comput. 2003, 21, 359–381. [Google Scholar] [CrossRef]
- Ferdowsi, A.; Challita, U.; Saad, W. Deep Learning for Reliable Mobile Edge Analytics in Intelligent Transportation Systems. arXiv 2017, arXiv:1712.04135. [Google Scholar] [CrossRef]
- Grondman, I.; Busoniu, L.; Lopes, G.A.D.; Babuska, R. A Survey of Actor–Critic Reinforcement Learning: Standard and Natural Policy Gradients. IEEE Trans. Syst. Man Cybern. Part (Appl. Rev.) 2012, 42, 1291–1307. [Google Scholar] [CrossRef]
- Khamis, M.A.; Gomaa, W. Enhanced multiagent multi-objective reinforcement learning for urban traffic light control. In Proceedings of the 11th International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 12 December 2012; Volume 1, pp. 586–591. [Google Scholar]
- Chen, Y.-Y.; Lv, Y.; Li, Z.; Wang, F. Long short-term memory model for traffic congestion prediction with online open data. In Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 4 November 2016; pp. 132–137. [Google Scholar]
- Yisheng, L.; Duan, Y.; Kang, W.; Li, Z. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Tan, H.; Feng, G.; Feng, J.; Wang, W.; Zhang, Y.J.; Li, F. A tensor-based method for missing traffic data completion. Transp. Res. Part Emerg. Technol. 2013, 28, 15–27. [Google Scholar] [CrossRef]
- Nguyen, H.; Kieu, M.; Wen, T.; Cai, C. Deep learning methods in transportation domain: A review. IET Intell. Transp. Syst. 2018, 12. [Google Scholar] [CrossRef]
- Janssen, M.; Charalabidis, Y.; Zuiderwijk, A. Benefits, Adoption Barriers and Myths of Open Data and Open Government. Inf. Syst. Manag. 2012, 29, 258–268. [Google Scholar] [CrossRef]


| Paper | Year | DRL Method | Number of Intersections | Compared Against | Control Strategy | Improvements |
|---|---|---|---|---|---|---|
| [17] | 2019 | Regional A3C + PER | 42 | Hierarchical MARL, Rainbow DQL, Decentralized multi-agents | Acyclic TSP selection and TSP duration omputation | 8.78% lower Average Delay |
| [9] | 2019 | Stabilised IA2C | 30 | IA2C, IQL-LR, IQL-DNN | Acyclic TSPs with fixed duration | 63.7% lower Average Delay |
| [34] | 2019 | Hierarchical regional A2C | 24 | Regional DRL | Acyclic TSPs with fixed duration | 44.8% lower Waiting time |
| [46] | 2019 | 3DQN + PER | 1 | Actuated and fixed time controller | Acyclic TSPs with fixed duration | 10.1% lower Average Delay |
| [18] | 2018 | ResNet based A2C | 9 | Actuated controller | Cyclic fixed TSP switch | 16% lower Waiting time |
| [20] | 2017 | DDPG | 43 | Q-learning algorithm | Cyclic TSPs with computed duration | No data |
| [21] | 2017 | DDQN + ER | 1 | LQF, fixed time controller | Cyclic TSPs with fixed duration | 47% lower Overall Delay |
| [16] | 2016 | DDQN + ER | 1 | STSCA | Acyclic TSPs with intermediate TSPs | 82% lower Overall Delay |
| [14] | 2016 | DeepSAE + RL | 1 | Q-learning algorithm | Two TSPs with dynamic duration | 14% lower Overall Delay |
| DRL Method/Year | DNN Configuration | DNN Parameters | Optimization Algorithm | ER/ Batch Size | Learning Episodes |
|---|---|---|---|---|---|
| Regional A3C + PER 2019 [17]; | Single A3C CNN (1: 3×Conv, 2: 1×FC, 3: 2×LSTM ) | 1: (32, 4×4, 2) (64, 2×2, 1) (128, 2×2, 1) 2: 128 3: (128, 128) | AdaBound | 50.000 TS /32 | 1 Million TS; |
| Stabilised IA2C 2019 [9]; | Single A2C 3 inputs per 1×FC, 1×LSTM | 1 input 128 2 input 32 3 inputs 64 LSTM: 64; | Orthogonal initializer, RMSprop as gradient optimiser | 1000 TS /20; | 1400 episodes (1 episode is 720 TS); |
| Hierarchical regional A2C 2019 [34]; | Regional A2C agents: 2×(3×MLP+ReLU) Global layer: 1×FC+ReLU | Agent: Critic net: (300, 200, 200) Actor net: (200, 200, 100) | Adam | - /64 | 250 episodes (1 episode is 1000 TS); |
| 3DQN + PER 2019 [46]; | Dueling CNN: 3×Conv 2×FC | 1: (32, 3×15, 3,1) 2: (64, 2×2, 2) 3: (128, 2×2, 1) FCs (464, 64) | Adam | 100.000 TS /32; | 1000 episodes |
| ResNet based A2C 2018 [18]; | Single A2C DNN, 4×ResNet Blocks (2×Conv, 2×BN, ReLU) Actor and Critic each: (1×Conv, 1×BN, 2×FC) | Filters for Conv in ResNet (32, 64, 128, 256) | Adam | - /64x× (16 agents) | 50 episodes (1 episode is 3600 TS) |
| DPG 2017 [20] | (4×FC+LeakyReLU, 1×BN+ReLU Gaussian Noise) (4×FC+Leaky ReLU) | Critic: (4×nd + np, 1×nd) Actor: (2×nd + np, 1×np, 1×nd) | Adam | - /- | 1000 episodes |
| DQN + ER 2017 [21]; | Each input 2×Conv merged with 2×FC; | 1: (16, 4×4, 2) 2: (32, 2×2, 2) 3: 128, 4: 64 | RMSprop | 200 episodes /32 | 2000 episodes |
| DQN + ER 2017 [16]; | 2×Conv + 2×FC; | 1: (16, 4×4, 2) 2: (32, 2×2, 2) 3: 128, 4: 64 | RMSprop | 111 simulations /16 | 100 simulations (1 simulation is 4500 TS) |
| DeepSAE + RL 2016 [14] | 4 layer SAE | (32, 16, 4, 2) | SGD | - /- | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gregurić, M.; Vujić, M.; Alexopoulos, C.; Miletić, M. Application of Deep Reinforcement Learning in Traffic Signal Control: An Overview and Impact of Open Traffic Data. Appl. Sci. 2020, 10, 4011. https://doi.org/10.3390/app10114011
Gregurić M, Vujić M, Alexopoulos C, Miletić M. Application of Deep Reinforcement Learning in Traffic Signal Control: An Overview and Impact of Open Traffic Data. Applied Sciences. 2020; 10(11):4011. https://doi.org/10.3390/app10114011
Chicago/Turabian StyleGregurić, Martin, Miroslav Vujić, Charalampos Alexopoulos, and Mladen Miletić. 2020. "Application of Deep Reinforcement Learning in Traffic Signal Control: An Overview and Impact of Open Traffic Data" Applied Sciences 10, no. 11: 4011. https://doi.org/10.3390/app10114011
APA StyleGregurić, M., Vujić, M., Alexopoulos, C., & Miletić, M. (2020). Application of Deep Reinforcement Learning in Traffic Signal Control: An Overview and Impact of Open Traffic Data. Applied Sciences, 10(11), 4011. https://doi.org/10.3390/app10114011








