Weighted Constraint Iterative Algorithm for Phase Hologram Generation

Featured Application

Phase hologram and diffractive optics element optimization with effective convergence and quality reconstruction.

Abstract

A weighted constraint iterative algorithm is presented to calculate phase holograms with quality reconstruction. The image plane is partitioned into two regions where different constraint strategies are implemented during the iteration process. In the image plane, the signal region is constrained directly according to the amplitude distribution of the target image based on an adaptive strategy, whereas the non-signal region is constrained indirectly by total energy control of the hologram plane based on the energy conservation principle. The weighted constraint strategy can improve the reconstruction quality of the phase holograms by broadening the optimizing space of the iterative algorithm, leading to effective convergence of the iteration process. Finally, numerical and optical experiments have been performed to validate the feasibility of our method.

1. Introduction

Computer-generated holograms (CGHs) can reconstruct the whole optical wave field of the synthetic object beam, which leads a wide range of applications, including beam shaping, holographic displays, optical encryption and atom trapping [1,2,3,4,5]. Commercial spatial light modulators (SLMs) provide an effective way to dynamically upload CGHs, whereas complex modulation is difficult to directly realize on a single SLM. Compared to amplitude SLMs, multilevel-phase SLMs can reconstruct optical wave fields with higher efficiency and no conjugate image. Therefore, phase holograms are preferable in the applications where optical efficiency and compact configuration are demanded [6,7].

In order to improve the reconstruction qualities of phase holograms, various non-iterative methods have been proposed to calculate phase holograms [8,9,10,11,12,13,14,15,16,17]. A straightforward solution is to transform a complex amplitude distribution into a phase distribution. The double-phase method was proposed to decompose the complex value into two phase values, which were then used to encode the complex wave fields into phase distributions with the help of a low-pass filter in the Fourier plane [8,9,10]. The space-bandwidth product was not efficiently utilized in this method due to the decomposition operation of each complex value. The error diffusion method was introduced to transform a complex hologram to a phase hologram by diffusing the residual errors to adjacent sampling points [11,12]. However, the optical efficiency would be affected by this method. Recently, some researchers have attempted to impose a designed phase mask to target images for improving the reconstruction quality of phase holograms, such as random phase-free, periodic patterned phase masks, gradient-limited random phase and optimized phase modulation methods [13,14,15,16,17]. These methods possess the merit of low computation load; whereas the generalization of these methods would be affected due to the lack of further optimization.

Iterative algorithms can optimize the phase profile of the hologram according to target images, which are widely used for designing phase holograms [18]. Iterative algorithms try to optimize the phase profile for improving the reconstruction quality by utilization of phase freedom in the image plane. The majority of iterative algorithms were developed on the basis of the error-reduction (ER) algorithm, which is also referred to as the Gerchberg–Saxton (GS) algorithm [19,20,21]. The GS algorithm has the property of non-increasing error under increasing quantity of iterations, leading effective convergence of the iteration process. Input–output algorithms were introduced to speed up convergence by introducing feedback calculation during the iterations [22,23,24]. However, the GS algorithm and input–output algorithms often stagnate into the local minimum. Instead of imposing amplitude constraint to the entire image plane, some iterative algorithms have been proposed to improve reconstruction quality by introducing amplitude freedom into the image plane [25,26,27,28]. In these methods, the image plane was partitioned into a signal region and non-signal region, and only the amplitude distribution of the signal region was directly constrained. Recently, double-constraint iterative algorithms were introduced to suppress the speckle noise, in which the desired amplitude and smooth phase distribution were constrained in the signal region during the iteration process [29,30]. These methods improve the reconstruction quality of the signal region by relaxing the amplitude constraint of the non-signal region. However, the reconstruction in the non-signal region would be less controlled, causing severe noise and low optical efficiency. Although the noise in the non-signal region could be reduced by introducing a noise suppression parameter [26], it would sacrifice the optimization space of the iterative algorithm and degrade the reconstruction quality in the signal region. It is difficult to obtain a satisfactory reconstruction while maintaining a high optical efficiency in these methods. In addition, the noise suppression parameter should be chosen manually, and the optimal value is dependent on different target images, which would be inconvenient when generating phase holograms with different target images. In our previous work [31], the noise in the non-signal region was suppressed by controlling the total energy in the hologram plane, and the amplitude distribution of the signal region was constrained by a two-step constraint strategy. This method can effectively reduce the noise in the non-signal region; however, the amplitude constraint strategy in the signal region is not stable and might degrade the convergence of the iteration process.

In this study, a weighted constraint iterative algorithm (WCIA) is presented to calculate phase holograms with quality reconstruction and effective convergence. Specifically, the image plane is partitioned into signal region and non-signal region according to the amplitude distribution of the target image. The signal region is the area where the signal pattern is located, and the non-signal region is the area where there is no designed signal. Different constraint strategies are addressed on the corresponding regions during the iteration process. The amplitude distribution of the signal region is constrained directly according to the target image using an adaptive over-compensation method, which can change the constraint parameter in the image plane with the iteration progress for effective and fast convergence. The non-signal region is constrained indirectly by total energy control in the hologram plane based on the energy conservation principle rather than directly introducing a noise suppression parameter. Our proposed method can provide quality reconstruction of phase holograms by broadening the optimizing space of the iterative algorithm, and the weighted constraint strategy also provides overall and effective constraints in the image plane with effective convergence.

2. Method

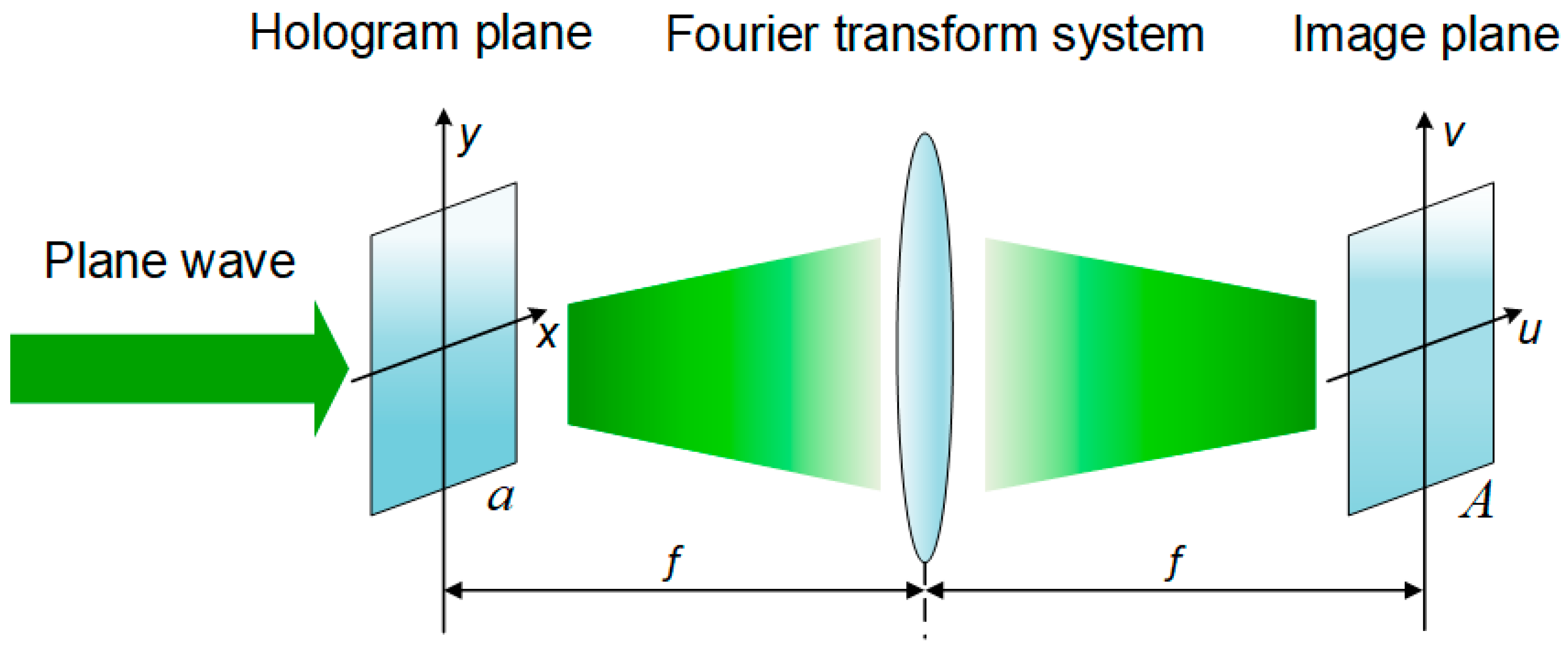
An iterative optimization algorithm is an effective technique to design a phase hologram for converting the incident plane wave in the hologram plane into the target intensity distribution in the image plane. In this work, we focus on the generation of Fourier phase holograms, and an optical Fourier transform system is shown as Figure 1. The hologram plane is located in the front focal plane of the Fourier lens, and the image plane is located in the back focal plane of the Fourier lens. The incident plane wave in the hologram plane is modulated by the phase hologram and then converted into the target intensity distribution in the image plane by the optical Fourier transform system. A conventional iterative algorithm, such as the GS algorithm, is a stable algorithm to design phase holograms. However, the GS algorithm gives the same weight to all sampling points in the image plane, leading a slow and stagnant convergence.

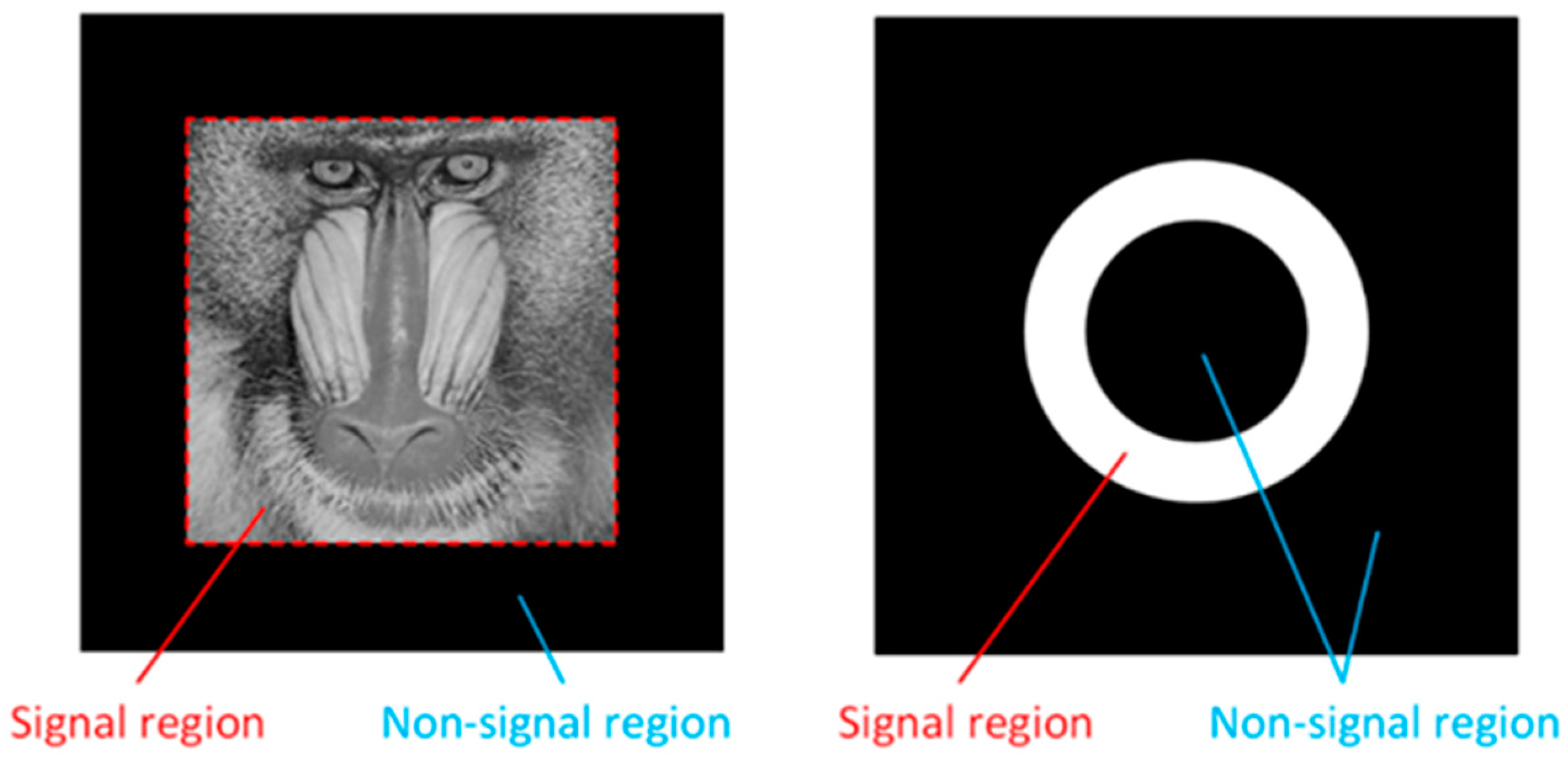
Our method would effectively improve the visual quality of the reconstructed image by addressing different constraint strategies at the corresponding regions in the image plane. The image plane is partitioned into two regions according to the amplitude distribution of the target image. The signal region is the area where the signal pattern is located, and the non-signal region is the area where there is no designed signal. Figure 2 illustrates two typical examples of the target images. The left one is a grayscale image where the non-signal region is set at the surrounding area. The right one shows a target image where the signal region is located in the annulus with uniform intensity, which is often used in beam shaping applications. In this case, the signal region is not rectangular, and the non-signal region is set at the black area which is separated by the annulus.

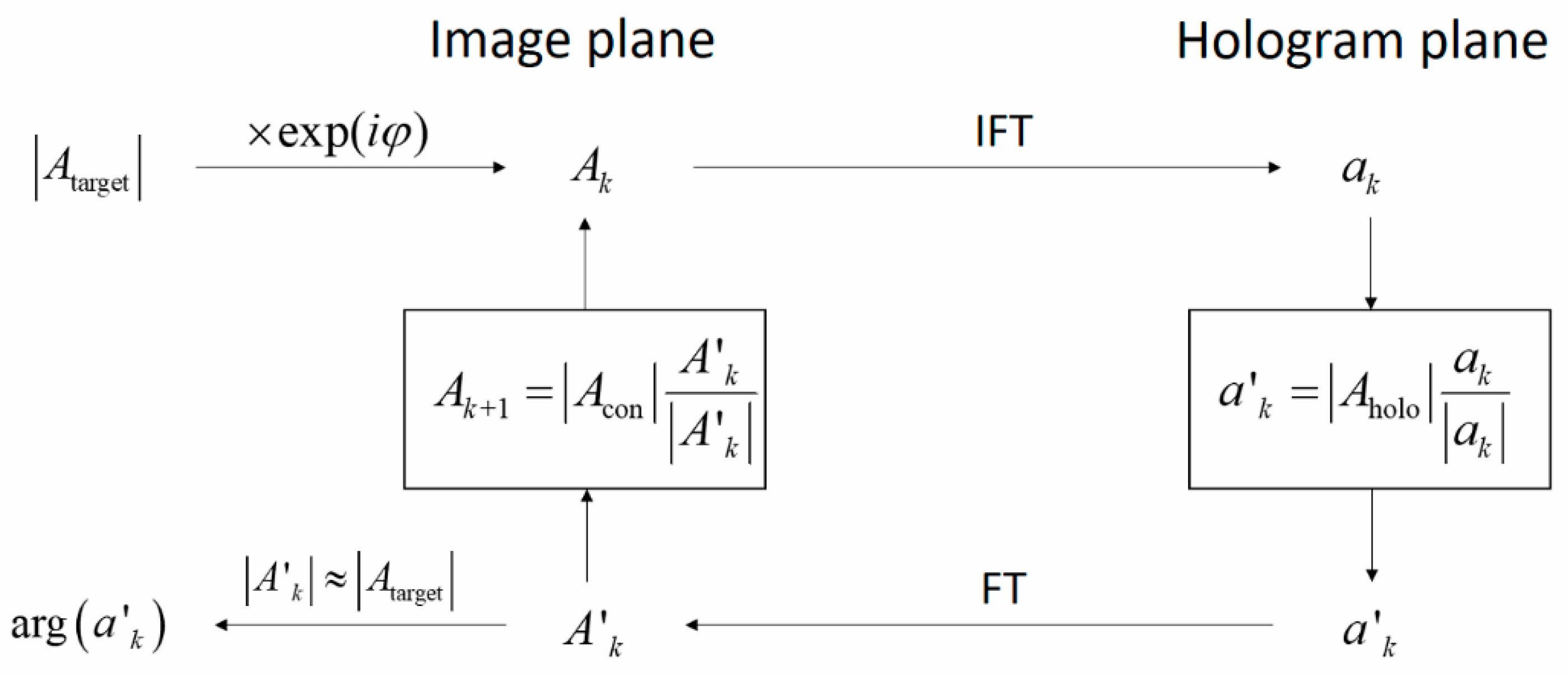
The working principle of our proposed algorithm is shown in Figure 3. The initial random phase φ is applied to the target image as A₀ = |A_target|exp(iφ), where |A_target| is the amplitude distribution of the target image, and the resulting complex amplitude A₀ is set as the initial input of the iteration process. Complex amplitude a_k in the hologram plane is calculated by the inverse Fourier transform of the input complex amplitude A_k in the image plane. Then, the phase hologram a’_k is generated from the complex amplitude a_k after a phase extraction and amplitude regularization. Subsequently, the reconstructed complex amplitude distribution A’_k in the image plane is calculated by the Fourier transform of the phase hologram a’_k. The input complex amplitude A_k+1 for the next iteration is generated after the amplitude constraint in the image plane. In the amplitude constraint of the image plane, only the amplitude distribution of the signal region is constrained using an adaptive over-compensation method. The over-compensation method is always utilized to speed up the convergence of the iteration process [23]. However, the convergence of the conventional over-compensation method would be easily degraded if used alone. Here, we modify the over-compensation method by introducing adaptive parameters which can change with the iteration progress. During the iteration process, the enforced amplitude constraint for the next iteration in the image plane is

$$\left|A_{\mathrm{con}}\right|=\{\begin{array}{ccc}\left|A_k\right|{\left(\left|A_{\mathrm{target}}\right|/\left|A{\prime }_k\right|\right)}^{{\beta }_k}& ,& (u,v)\in S\\ \left|A{\prime }_k\right|& ,& (u,v)\notin S\end{array}$$

(1)

where |A_k| is the amplitude distribution of the input in kth iteration, |A’_k| is the amplitude distribution of the reconstructed image in kth iteration, (u, v) are the coordinates in the image plane, and S denotes the signal region. Adaptive parameters β_k are used here to enhance convergence of the iterative algorithm. In the numerical calculation, a small number ~10⁻¹⁰ should be added on |A’_k| for avoiding the division by zero in the amplitude constraint of the signal region.

The amplitude constraint strategy in the image plane improves the reconstruction quality in the signal region by relaxing the amplitude constraint in the non-signal region. The enforced amplitude constraint changes during the iteration process, so that the difference between |A_k+1| and |A’_k| is reduced. In this way, when the complex amplitude a_k+1 in the hologram plane is calculated by the inverse Fourier transform of the image plane, it has better amplitude uniformity than the previous iteration, which helps to improve the reconstruction quality. Furthermore, the amplitude distribution of the signal region is constrained by the adaptive over-compensation method. From Equation (1), we can see that in kth iteration that if amplitude distribution |A’_k| at some pixels of the signal region is smaller than the target amplitude |A_target|, the enforced amplitude |A_con| at the corresponding pixels will be enlarged in (k + 1)th iteration, which helps to enlarge the amplitude |A’_k+1| at the corresponding pixels and make it closer to the target amplitude. After several iterations, the difference between the amplitude distribution of the reconstructed image and the amplitude distribution of the target image is reduced. It should be noted that the convergence of the conventional over-compensation method would be easily degraded if it is used alone to design phase holograms [23]. Hence, it is always used as a final step to optimize further results obtained by some stable iterative algorithms, such as the GS algorithm. Here, we modify the conventional over-compensation method by introducing adaptive parameters β_k into the iteration process. The adaptive parameters β_k are given by

$${\beta }_k=\sqrt{{\beta }_{k-1}}$$

(2)

where the initial value β₀ is a small number, ~10⁻⁸. β_k would increase and approach to one after a certain number of iterations. When β_k is relatively small, the constraint strategy in the signal region is similar to the GS algorithm so that the convergence of the iteration process is effective and stable. After several iterations, β_k would be close to one, then the constraint strategy in the signal region is similar to the conventional over-compensation method, and a further optimized result can be obtained.

In order to suppress the noise in the non-signal region, total energy in the hologram plane is controlled based on the energy conservation principle. In the Fourier transform system, the energy in the image plane is equal to the energy in the hologram plane:

$${\displaystyle \iint {\left|A{\prime }_k(u,v)\right|}^{2}dudv}={{\displaystyle \iint \left|A_{\mathrm{holo}}(x,y)\right|}}^{2}dxdy$$

(3)

By controlling the total energy in the hologram plane, the total energy in the image plane is constrained. During the iteration process, the amplitude of the incident plane wave in the hologram plane is calculated as:

$$E_{\mathrm{target}}={\displaystyle \iint {\left|A_{\mathrm{target}}(u,v)\right|}^{2}dudv}$$

(4)

$$E_{\mathrm{holo}}=E_{\mathrm{target}}$$

(5)

$$\left|A_{\mathrm{holo}}\right|=\sqrt{\frac{E_{\mathrm{holo}}}{H}}$$

(6)

where E_target represents the total energy of the target image, E_holo represents the total energy in the hologram plane, H is the area of the hologram, and |A_holo| is the enforced amplitude constraint in the hologram plane. During the iterations, the amplitude of the incident plane wave in the hologram plane is replaced by |A_holo|. According to Equations (3)–(6), the following formula can be deduced:

$${\displaystyle \iint {\left|A{\prime }_k(u,v)\right|}^{2}dudv}={\displaystyle \iint {\left|A_{\mathrm{target}}(u,v)\right|}^{2}dudv}$$

(7)

In this way, the total energy in the image plane is constrained indirectly by controlling the total energy in the hologram plane. Meanwhile, the amplitude distribution of the signal region is constrained directly during the iteration process. Through the iterations, more and more energy is gathered in the signal region so that the noise of the non-signal region is suppressed effectively. The above operation provides a larger optimization space of the algorithm than introducing the noise suppression parameter to directly constrain the non-signal region [26] while maintaining overall and effective constraint in the image plane.

3. Reconstruction Results

To validate the feasibility of the WCIA, numerical simulation is performed. The measures of root-mean-square error (RMSE) and structural similarity index measure (SSIM) are used to evaluate the reconstruction quality objectively. The RMSE is calculated as follows:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \sum _P{\left({\left|A{\prime }_k\right|}^2-{\left|A_{\mathrm{target}}\right|}^2\right)}^2}/{\displaystyle \sum _P{\left({\left|A_{\mathrm{target}}\right|}^2\right)}^2}}$$

(8)

where P represents the pixel in the reconstructed image. The RMSE indicates how well the reconstructed image agrees with the target one. The SSIM is another well-known evaluation function and is given by

$$\mathrm{SSIM}=\frac{(2{\mu }_t{\mu }_r+c_1)\cdot (2{\sigma }_{t,r}+c_2)}{({\mu }_t^2+{\mu }_r^2+c_1)\cdot ({\sigma }_t^2+{\sigma }_r^2+c_2)}$$

(9)

where μ_r and μ_t are the mean values of the reconstructed and target images, σ_r and σ_t are the standard deviations of the reconstructed and target images, σ_t,r is the covariance between the reconstructed image and target image, and c₁ and c₂ are constants used here to avoid the division by zero.

The performances of the WCIA and GS algorithms are compared. During calculation, a “baboon” image (from USC-SIPI image database) with the dimensions of 600 × 600 was set as the signal region, and the sampling numbers of the image plane were 1000 × 1000, as shown in Figure 4a. The number of iterations was set as 100. The reconstruction results are shown in Figure 4b,c. The RMSEs and the SSIMs are plotted in Figure 4d,e, respectively. Figure 4b shows that the image reconstructed by the GS algorithm is degraded by the noise. Figure 4c shows that the image was precisely reconstructed by WCIA, and the noise in the non-signal region was effectively suppressed at the same time. From Figure 4d, it can be seen that the convergence rate of WCIA is faster than the GS algorithm during the iteration process. Figure 4e shows that the SSIMs of the reconstructed image with WCIA approach to nearly one after 20 iterations. The reconstruction results confirm that the weighted constraint strategy can improve the reconstruction quality in the signal region and maintains overall and effective constraint on the image plane.

To further confirm that the weighted constraint strategy can effectively suppress the noise in the non-signal region with the iteration progress, the efficiency of reconstructions under different numbers of iterations was calculated. The measure of efficiency η is used here to evaluate the performance of the noise suppression, which is defined as the ratio of energy in the signal region compared to the total image plane. The results are shown in Figure 5. It can be seen that the noise in the non-signal region can be effectively suppressed during the iteration process based on the weighted constraint strategy.

Qualitative comparisons for more gray images are given in Figure 6 for evaluating our proposed algorithm. The resolution of the test images is 1000 × 1000. The number of iterations was set as 100 for both the GS algorithm and WCIA. This shows that our proposed algorithm produces superior reconstruction quality and outperforms the GS algorithm across all these test images.

Some typical patterns that are often used in beam shaping were also used as the target images to illustrate the effectiveness of WCIA. Figure 7 shows the reconstruction results of these test images with GS and WCIA. The sampling numbers of the images are 800 × 800, and the iteration number was set as 100. From the reconstruction results, it can clearly be seen that WCIA can effectively suppress noise while improving the reconstruction quality for these images compared to the GS algorithm.

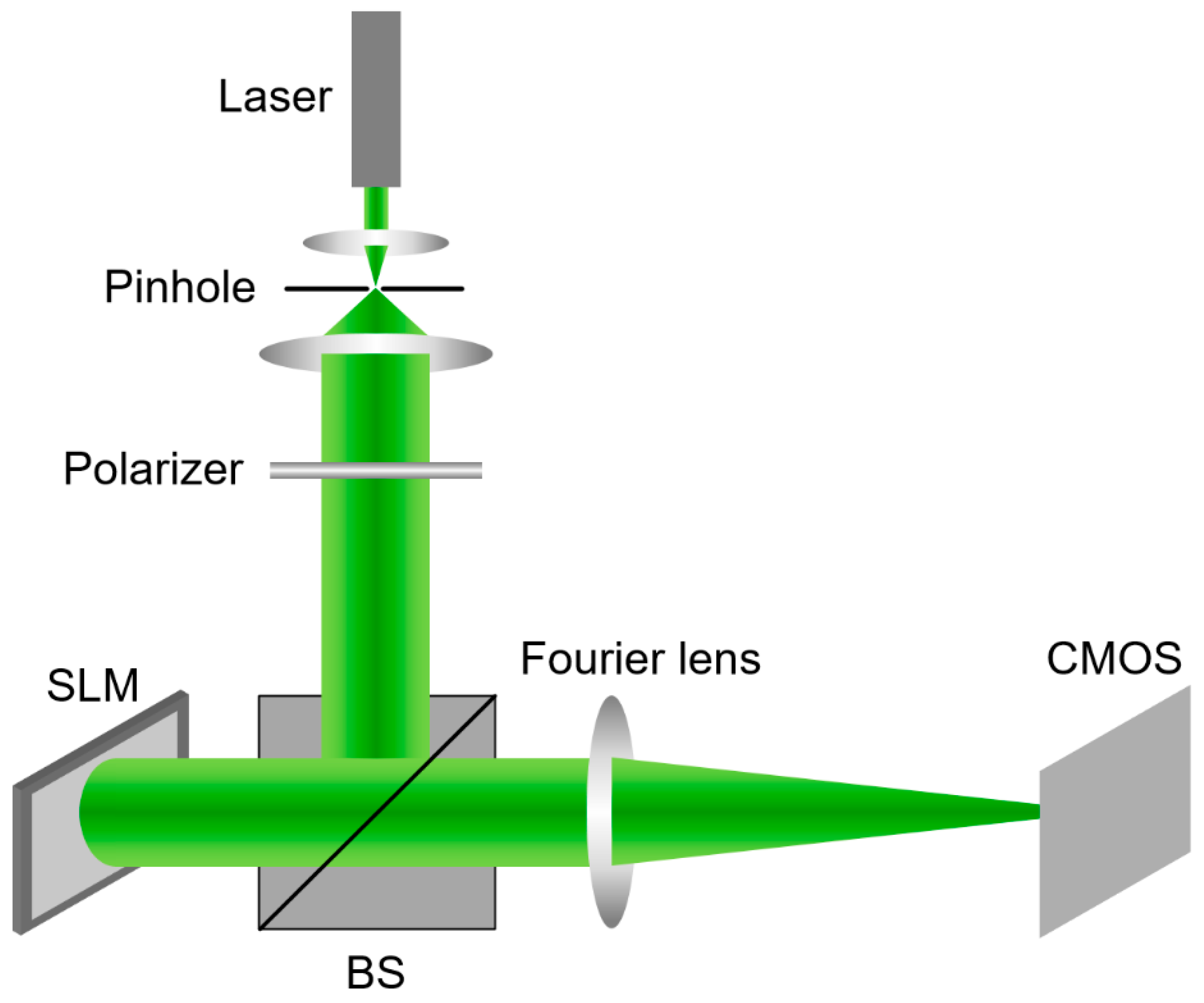
To further validate the feasibility of our proposed algorithm, optical experiments were also performed. The experimental setup is shown in Figure 8. The wavelength of the laser beam was 532 nm. The laser beam was collimated and polarized to achieve a uniform plane wave illumination. In the experiment, we used Holoeye GAEA-2 256 gray-scale level Phase-only SLM. The pixel pitch of the SLM was 3.74 μm, and the pixel resolution was 3840 × 2160. The focal length of the Fourier lens was 200 mm. The reconstructed images were located in the back focal plane of the Fourier lens and were captured directly by a sensor. A linear phase was added on the calculated hologram to separate the reconstructed image from the zero-order noise of SLM [32].

The optical reconstruction results of gray test images with GS algorithm and WCIA are shown in Figure 9. To capture the entire image on the sensor, the resolution of the signal region was set as 960 × 540. The iteration number was set as 100. Although the reconstructions were affected by the systematic noise, it can be seen that better image quality and more details can be optically reconstructed with our proposed method.

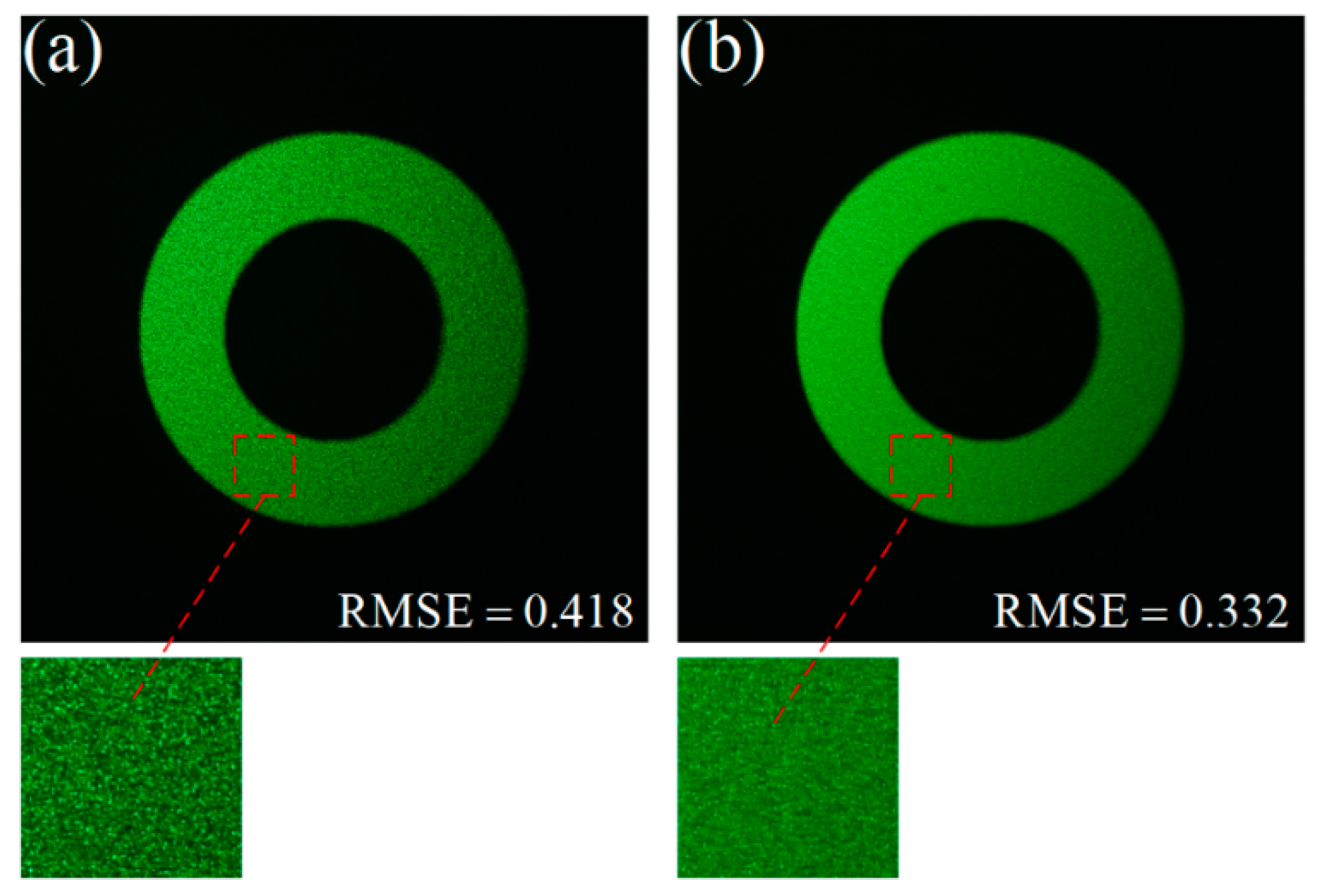
A binary ring pattern was also set as the test image to evaluate the optical reconstruction performance of WCIA. In order to avoid the effect of the systematic noise, the time-average method [33] by uploading five sequential holograms obtained with different initial random phase was used here for both these methods. The RMSEs of optical reconstructed images were calculated to compare WCIA with the GS algorithm. Figure 10 shows the optical reconstruction results. To calculate the RMSEs, the same part of the signal region was set as the measured raw data, which is circled by a red rectangle. The measured raw data were transformed into a gray image and then used to calculate the RMSEs. It can be seen that the reconstructed image with WCIA is of lower error.

4. Conclusions

In conclusion, we propose a weighted constraint iterative algorithm for generating phase holograms with quality reconstruction. Different constraint strategies are addressed in the corresponding areas during the iteration process. The signal region is constrained directly based on an adaptive strategy, whereas the other part of the image plane is constrained indirectly by total energy control in the hologram plane. The proposed algorithm can improve reconstruction quality by broadening the search space for optimizing the phase distribution. Our method can provide quality reconstructions of phase holograms while maintaining overall and effective constraint in the image plane. Although this method is based on the Fourier transform, it can be extended to the Fresnel region and can also be used in holographic displays, beam shaping and optical trapping.