Empirical Modeling of Liquefied Nitrogen Cooling Impact during Machining Inconel 718
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup Description
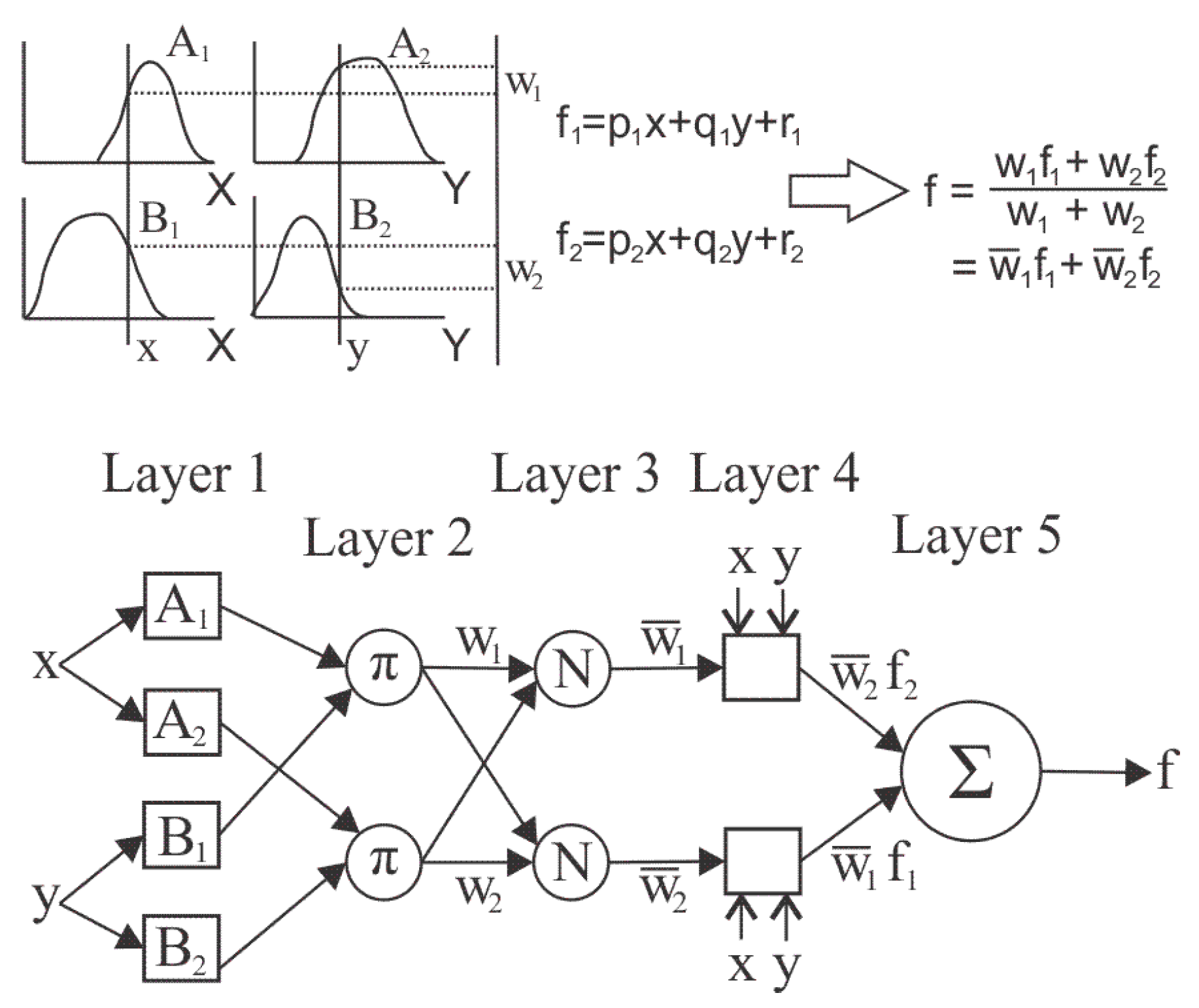
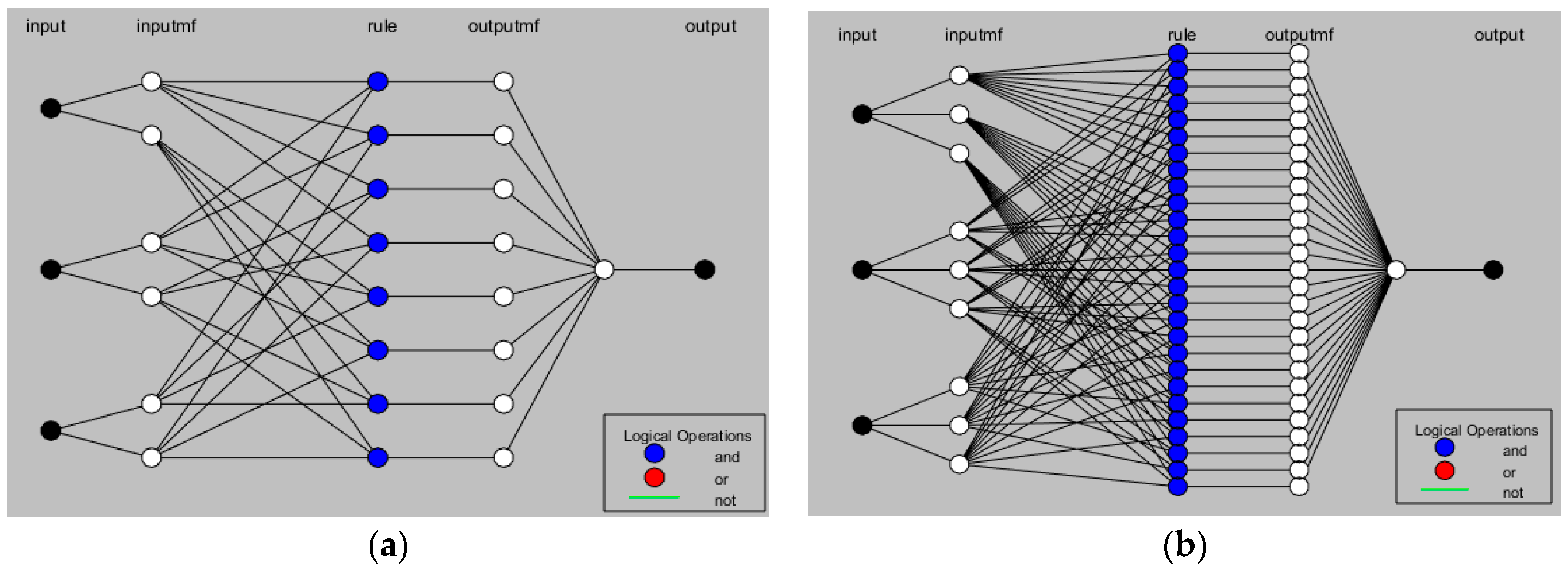
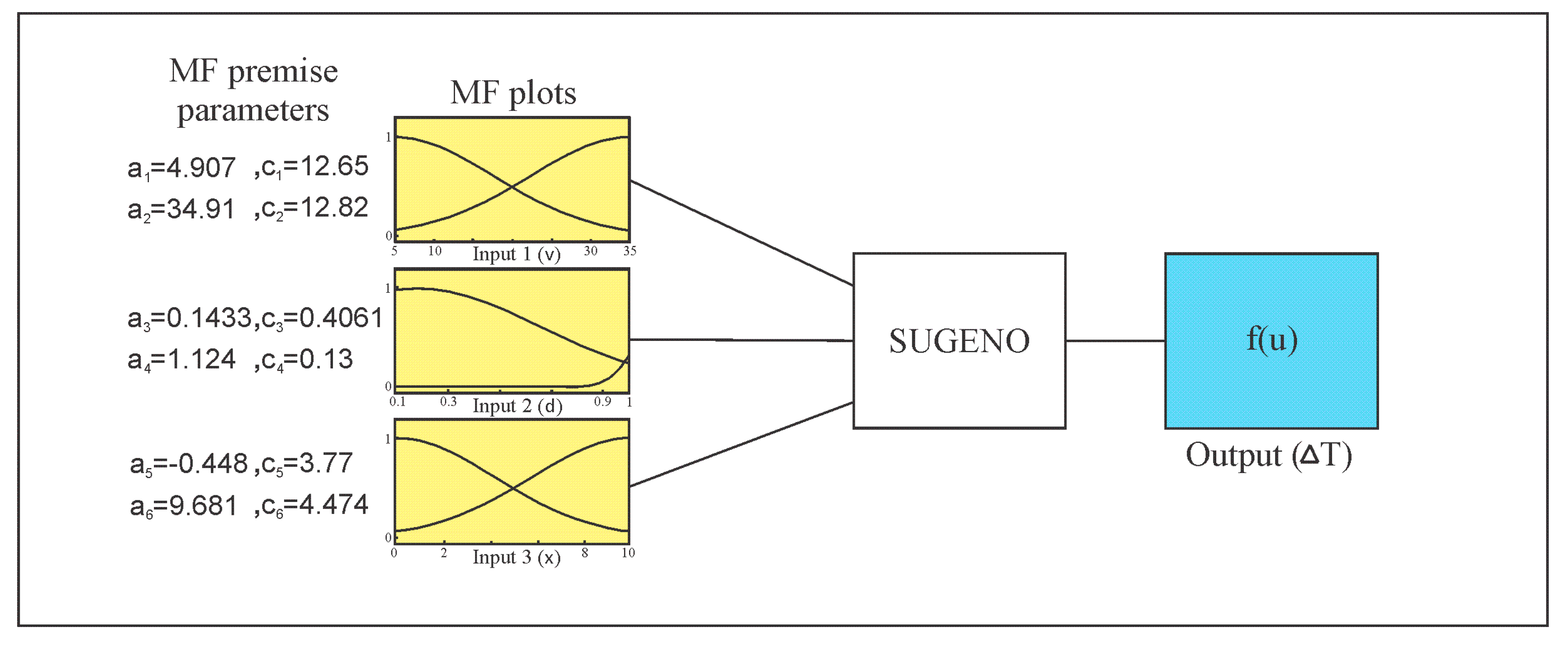
2.2. The Empirical Model—Adaptive Neuro-Fuzzy Inference System (ANFIS)
- Rule 1: if is and is , then .
- Rule 2: if is and is , then .
- and are the inputs,
- and are the membership functions (MF),
- is the output, and
- , and are the linear design parameters (consequent parameters), determined during the training process [16].
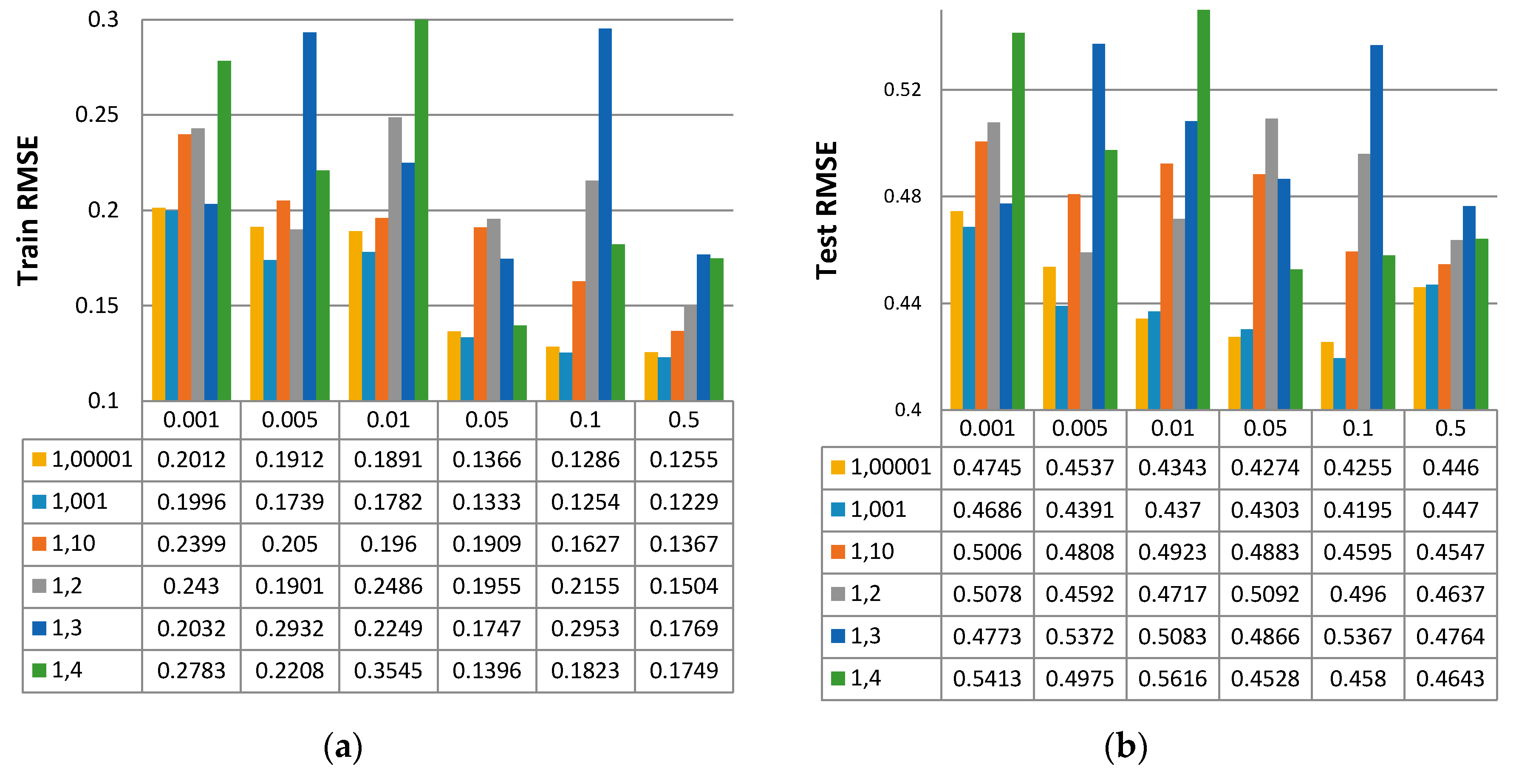
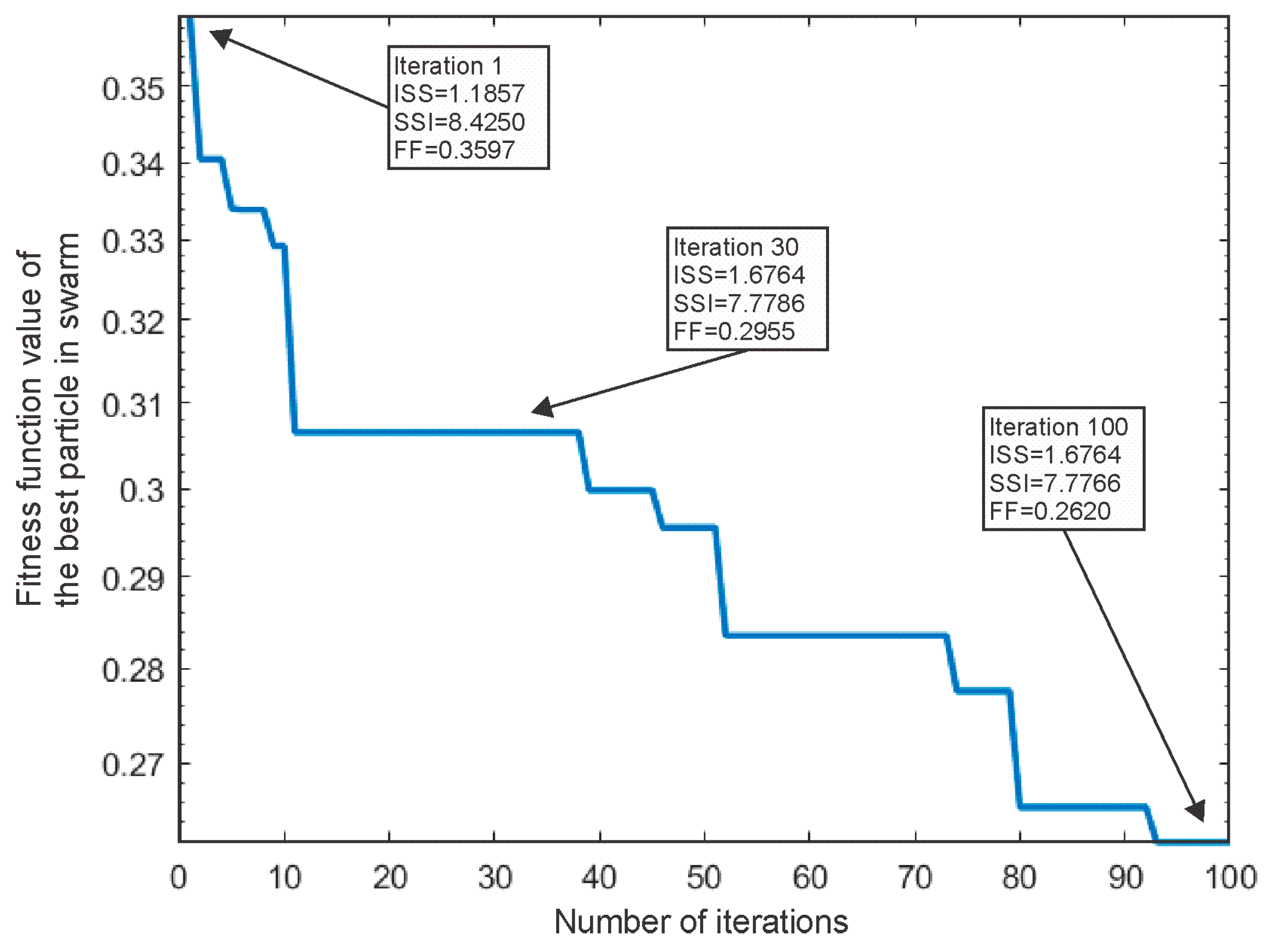
2.3. Particle Swarm Optimization
- subscript represents the current particle,
- is the current iteration,
- w is the inertia weight coefficient,
- and are the acceleration coefficients, and
- and () represent random number generators.
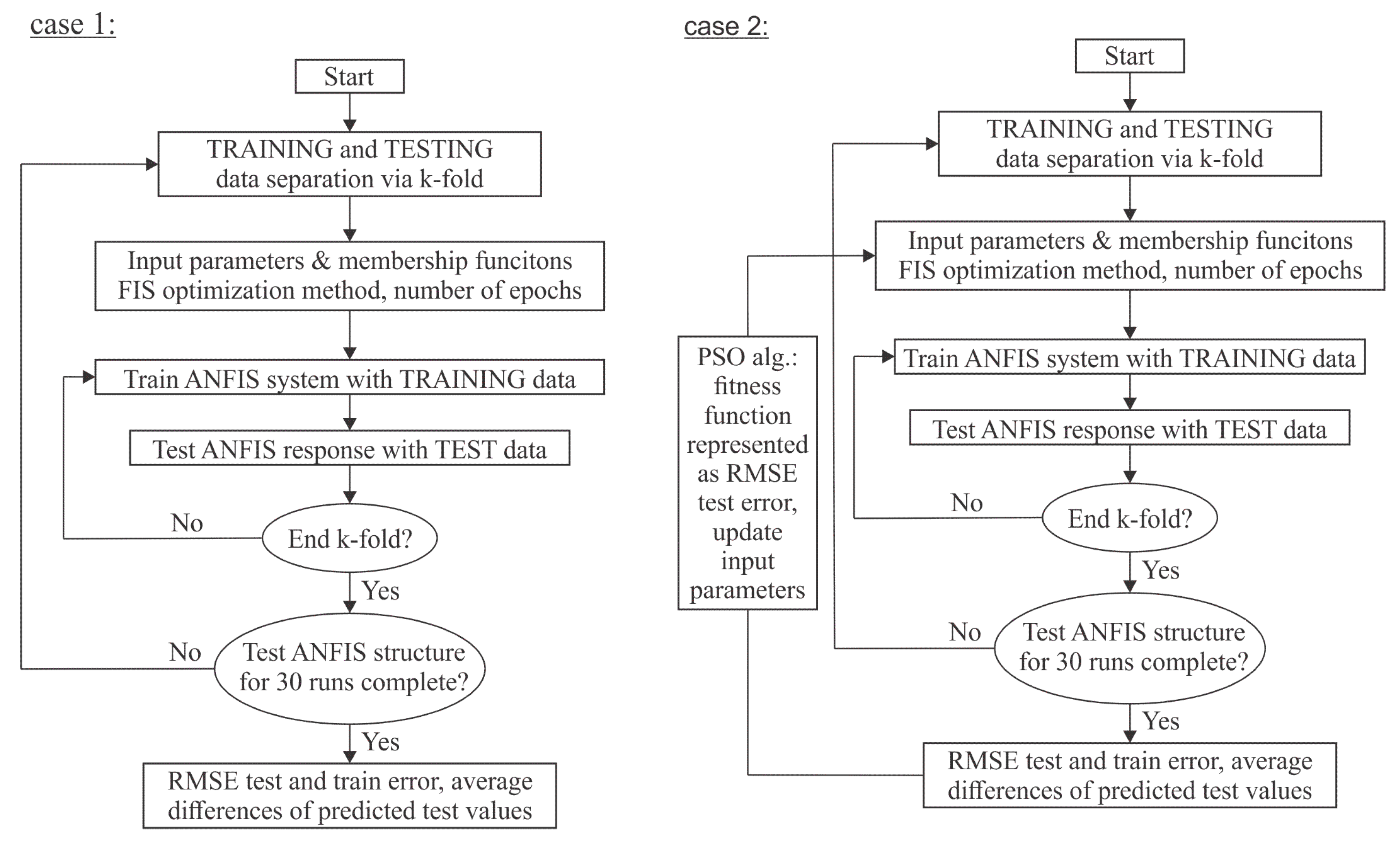
2.4. Workflow and Validation
3. Results and Discussion
3.1. Case 1
3.2. Case 2
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Quantity | Unit | Description |
| vc | [m/min] | Velocity of cutting |
| Ra | [µm] | Average surface roughness |
| dn | [mm] | Nozzle internal diameter |
| Tt | [°C] | Thermocouple working temperature |
| p | [Pa] | Pressure |
| T | [°C] | Temperature |
| v | [m/min] | Velocity of the nozzle |
| d | [mm] | Depth |
| x | [mm] | Distance |
| ΔT | [K] | Temperature difference |
References
- Pusavec, F.; Courbon, C.; Rech, J.; Kopac, J.; Jawahir, I. Importance of the Nitrogen Phase on the Cryogenic Machining Performance. In Proceedings of the ASME International Manufacturing Science and Engineering Conference, Detroit, MI, USA, 9–13 June 2014. [Google Scholar]
- Pusavec, F.; Hamdi, H.; Kopac, J.; Jawahir, I.S. Surface integrity in cryogenic machining of nickel based Alloy—Inconel 718. J. Mater. Process. Technol. 2011, 211, 773–783. [Google Scholar] [CrossRef]
- Pusavec, F.; Deshpande, A.; Yang, S.; M′Saoubi, R.; Kopac, J.; Dillon, O.J.; Jawahir, I. Sustainable machining of high temperature Nickel Alloy—Inconel 718: Part 1—Predictive Performance Models. J. Clean. Prod. 2014, 81, 255–269. [Google Scholar] [CrossRef]
- Yildiz, Y.; Nalbant, M. A Review of Cryogenic Cooling in Machining Processes. Int. J. Mach. Tools Manuf. 2008, 48, 947–964. [Google Scholar] [CrossRef]
- Mozammel, M.; Dhar, N.R. Response surface and neural network based predictive models of cutting temperature in hard turning. J. Adv. Res. 2016, 7, 1035–1044. [Google Scholar]
- Chinchanikar, S.; Choudhury, S. Machining of hardened steel—Experimental investigations, performance modeling and cooling techniques: A review. J. Mach. Tools Manuf. 2015, 89, 95–109. [Google Scholar] [CrossRef]
- Ezugwu, E.O.; Fadare, D.A.; Bonney, J.; Da Silva, R.B.; Sales, W.F. Modelling the correlation between cutting and process parameters in high-speed machining of Inconel 718 Alloy using an artificial neural network. Int. J. Mach. Tools Manuf. 2005, 45, 1375–1385. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yuan, D.-J.; Xu, Y.-S. Optimization of EPB shield performance with adaptive neuro-fuzzy inference system and genetic algorithm. Appl. Sci. 2019, 9, 780. [Google Scholar] [CrossRef] [Green Version]
- Elbaz, K.; Shen, S.-L.; Yin, Z.; Zhou, A. Prediction Model of shield performance during tunneling with AI via incorporating improved PSO into ANFIS. IEEE Access 2020, 8, 39659–39671. [Google Scholar] [CrossRef]
- Hriberšek, M.; Šajn, V.; Pušavec, F.; Rech, J.; Kopac, J. The procedure of solving the inverse problem for determining surface heat transfer coefficient between liquified Nitrogen and Inconel 718 Workpiece in Cryogenic Machining. J. Mech. Eng. 2016, 62, 331–339. [Google Scholar] [CrossRef]
- Suparta, W.; Alhasa, K.M. Modeling of Tropospheric Delays Using ANFIS; Cham Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Simeunovic, N.; Kamenko, I.; Bugarski, V.; Jovanovic, M.; Lalic, B. Improving workforce scheduling using artificial neural networks model. APEM J. 2017, 12, 337–352. [Google Scholar] [CrossRef]
- Klancnik, S.; Begic-Hajdarevic, D.; Paulic, M.; Ficko, M.; Cekic, A.; Cohodar, M. Prediction of laser cut quality for Tungsten Alloy. Using the neural network method. J. Mech. Eng. 2015, 61, 714–720. [Google Scholar]
- Senthilkumar, N.; Sudha, J.; Muthukumar, V. A grey-fuzzy approach for optimizing machining parameters and the approach angle in turning AISI 1045 Steel. APEM J. 2015, 10, 195–208. [Google Scholar] [CrossRef]
- Jang, J.-R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Al-Hmouz, A.; Shen, J.; Al-Hmouz, R.; Yan, J. Modeling and simulation of an adaptive neuro-fuzzy inference system (ANFIS) for mobile learning. IEEE Educ. Soc. 2011, 5, 226–237. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Cheng, Q.; Zhan, C.; Liu, Z.; Zhao, Y.; Gu, P. Sensitivity-based multidisciplinary optimal design of a hydrostatic rotary table with particle swarm optimization. J. Mech. Eng. 2015, 61, 432–447. [Google Scholar] [CrossRef]
- Hrelja, M.; Klancnik, S.; Irgolic, T.; Paulic, M.; Balic, J.; Brezocnik, M. Turning Parameters Optimization Using Particle Swarm Optimization. In Proceedings of the 24th DAAAM International Symposium on Intelligent Manufacturing and Automation, Zadar, Croatia, 23–26 October 2013; Volume 69, pp. 670–677. [Google Scholar]
- Clerc, M.; Kennedy, J.; Kennedy, J. The Particle Swarm—Explosion, stability and convergence in a multi-dimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef] [Green Version]



| n | v [m/min] | d [mm] | x [mm] | ΔT [K] |
|---|---|---|---|---|
| 1 | 5 | 0.1 | 5 | 3.2517 |
| 2 | 10 | 2.3180 | ||
| 3 | 5 | 0.5 | 0 | 5.7544 |
| 4 | 5 | 2.2840 | ||
| 5 | 10 | 1.8445 | ||
| 6 | 5 | 1 | 0 | 3.3258 |
| 7 | 5 | 1.9913 | ||
| 8 | 10 | 1.4317 | ||
| 9 | 15 | 0.1 | 0 | 1.9796 |
| 10 | 5 | 1.2245 | ||
| 11 | 10 | 0.9354 | ||
| 12 | 15 | 0.5 | 0 | 2.1012 |
| 13 | 5 | 0.8687 | ||
| 14 | 10 | 0.7829 | ||
| 15 | 15 | 1 | 0 | 0.0872 |
| 16 | 5 | 0.0754 | ||
| 17 | 10 | 0.0485 | ||
| 18 | 25 | 0.1 | 0 | 1.3235 |
| 19 | 5 | 0.8455 | ||
| 20 | 10 | 0.5057 | ||
| 21 | 25 | 0.5 | 0 | 1.2517 |
| 22 | 5 | 1.1352 | ||
| 23 | 10 | 0.3763 | ||
| 24 | 25 | 1 | 0 | 0.0687 |
| 25 | 5 | 0.1148 | ||
| 26 | 10 | 0.1193 | ||
| 27 | 35 | 0.1 | 0 | 0.3686 |
| 28 | 5 | 0.2779 | ||
| 29 | 10 | 0.3592 | ||
| 30 | 35 | 0.5 | 0 | 0.2790 |
| 31 | 5 | 0.3057 | ||
| 32 | 10 | 0.3448 | ||
| 33 | 35 | 1 | 0 | 0.2546 |
| 34 | 5 | 0.2446 | ||
| 35 | 10 | 0.3993 |
| ANFIS Information | ||||
|---|---|---|---|---|
| Learning method | hybrid | hybrid | Back-propagation | Back-propagation |
| Output MF | linear | linear | linear | linear |
| Number of MF per input | 2 | 3 | 2 | 3 |
| Number of nodes | 34 | 78 | 34 | 78 |
| Number of linear parameters | 32 | 108 | 32 | 108 |
| Number of nonlinear parameters | 18 | 27 | 18 | 27 |
| Number of fuzzy rules | 8 | 27 | 8 | 27 |
| Training RMSE | 0.0603 | 8.37 × 10−7 | 0.1643 | 0.1769 |
| Test RMSE | 0.8125 | 0.8594 | 0.3450 | 0.5507 |
| Training R2 | 0.9985 | 1.000 | 0.9855 | 0.9549 |
| Test R2 | 0.6775 | 0.4051 | 0.6917 | 0.4870 |
| Time (sec) | 8.04 | 42.85 | 7.60 | 36.44 |
| [m/min] | [mm] | [mm] | |||
|---|---|---|---|---|---|
| 5 | 0.1 | 5 | 3.2517 | 2.2990 | 2.7937 |
| 10 | 2.3180 | 2.6407 | 2.4037 | ||
| 0.5 | 0 | 5.7544 | 3.1399 | 3.2125 | |
| 5 | 2.2840 | 3.0916 | 3.1094 | ||
| 10 | 1.8445 | 1.9927 | 1.3562 | ||
| 1 | 0 | 3.3258 | 2.2173 | 1.9850 | |
| 5 | 1.9913 | 1.5084 | 2.1284 | ||
| 10 | 1.4317 | 1.0998 | 1.4480 | ||
| 15 | 0.1 | 0 | 1.9796 | 2.2419 | 2.1050 |
| 5 | 1.2245 | 0.9262 | 1.0530 | ||
| 10 | 0.9354 | 0.6331 | 1.0758 | ||
| 0.5 | 0 | 2.1012 | 1.9184 | 2.3156 | |
| 5 | 0.8687 | 1.3459 | 1.1354 | ||
| 10 | 0.7829 | 0.6331 | 0.8089 | ||
| 1 | 0 | 0.0872 | 0.0352 | 0.1320 | |
| 5 | 0.0754 | 0.0227 | 0.0314 | ||
| 10 | 0.0485 | 0.0617 | 0.0547 | ||
| 25 | 0.1 | 0 | 1.3235 | 1.2691 | 1.4158 |
| 5 | 0.8455 | 0.1928 | 0.8042 | ||
| 10 | 0.5057 | 0.4781 | 0.5750 | ||
| 0.5 | 0 | 1.2517 | 1.0434 | 1.3065 | |
| 5 | 1.1352 | 0.5572 | 0.6713 | ||
| 10 | 0.3763 | 0.7014 | 0.6201 | ||
| 1 | 0 | 0.0687 | 0.1075 | 0.0682 | |
| 5 | 0.1148 | 0.1483 | 0.2113 | ||
| 10 | 0.1193 | 0.1975 | 0.2759 | ||
| 35 | 0.1 | 0 | 0.3686 | 0.1927 | 0.3734 |
| 5 | 0.2779 | 0.5793 | 0.4713 | ||
| 10 | 0.3592 | 0.2636 | 0.3178 | ||
| 0.5 | 0 | 0.2790 | 0.4457 | 0.4316 | |
| 5 | 0.3057 | 0.4535 | 0.5660 | ||
| 10 | 0.3448 | 0.1845 | 0.3113 | ||
| 1 | 0 | 0.2546 | 0.1296 | 0.2175 | |
| 5 | 0.2446 | 0.3129 | 0.3007 | ||
| 10 | 0.3993 | 0.1667 | 0.2239 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hribersek, M.; Berus, L.; Pusavec, F.; Klancnik, S. Empirical Modeling of Liquefied Nitrogen Cooling Impact during Machining Inconel 718. Appl. Sci. 2020, 10, 3603. https://doi.org/10.3390/app10103603
Hribersek M, Berus L, Pusavec F, Klancnik S. Empirical Modeling of Liquefied Nitrogen Cooling Impact during Machining Inconel 718. Applied Sciences. 2020; 10(10):3603. https://doi.org/10.3390/app10103603
Chicago/Turabian StyleHribersek, Matija, Lucijano Berus, Franci Pusavec, and Simon Klancnik. 2020. "Empirical Modeling of Liquefied Nitrogen Cooling Impact during Machining Inconel 718" Applied Sciences 10, no. 10: 3603. https://doi.org/10.3390/app10103603
APA StyleHribersek, M., Berus, L., Pusavec, F., & Klancnik, S. (2020). Empirical Modeling of Liquefied Nitrogen Cooling Impact during Machining Inconel 718. Applied Sciences, 10(10), 3603. https://doi.org/10.3390/app10103603






