Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach
Abstract
:1. Introduction
2. Fuzzy Preliminaries
3. Adaptive Robust Control Design
3.1. Fuzzy Dynamic Modeling of Delta Robot
3.2. Deign of Adaptive Robust Control for Delta Robot
4. Optimal Design for Delta Robot
4.1. Design of Fuzzy Performance Index
4.2. Solution of the Optimization Problem
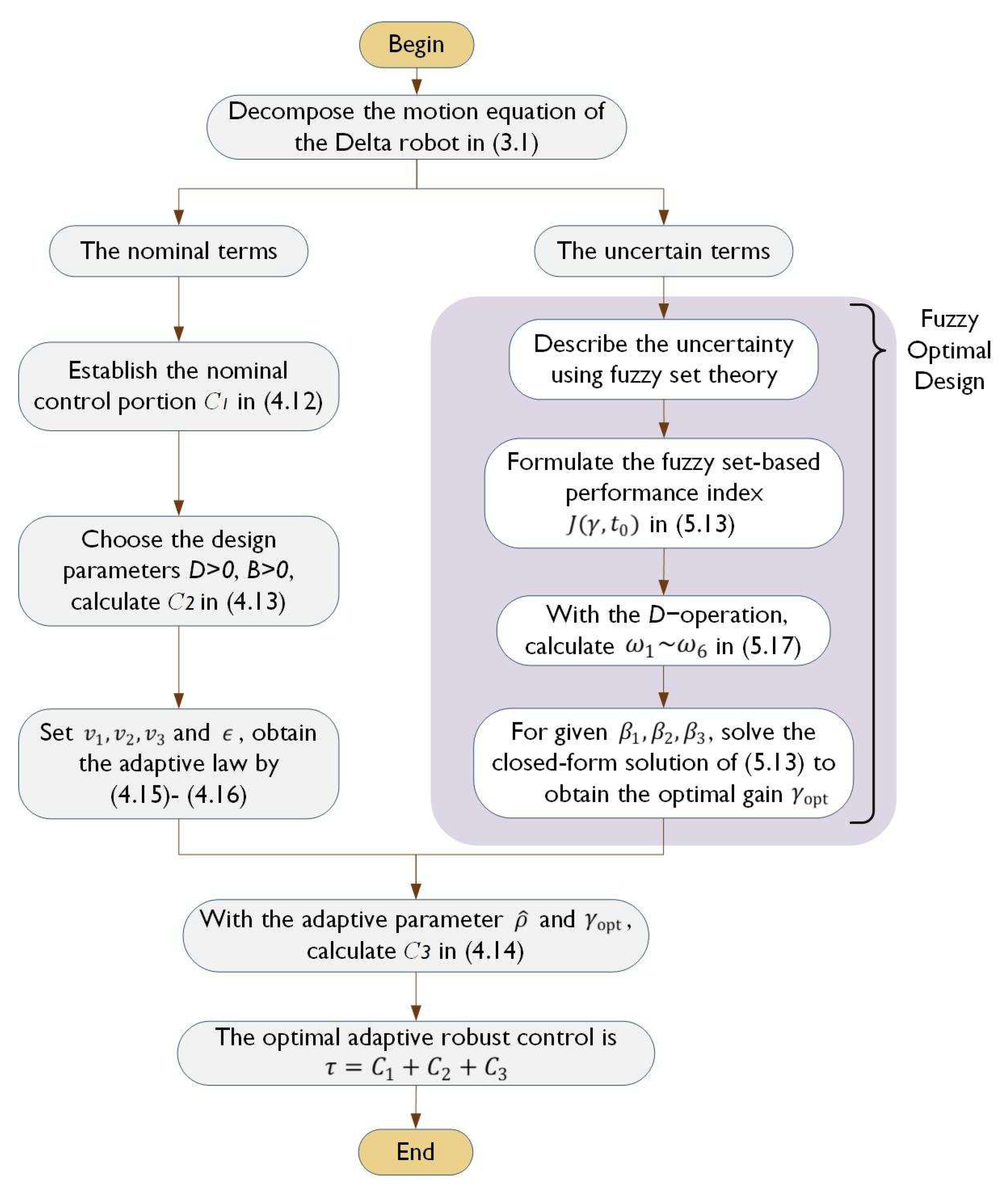
4.3. Optimal Design Procedure
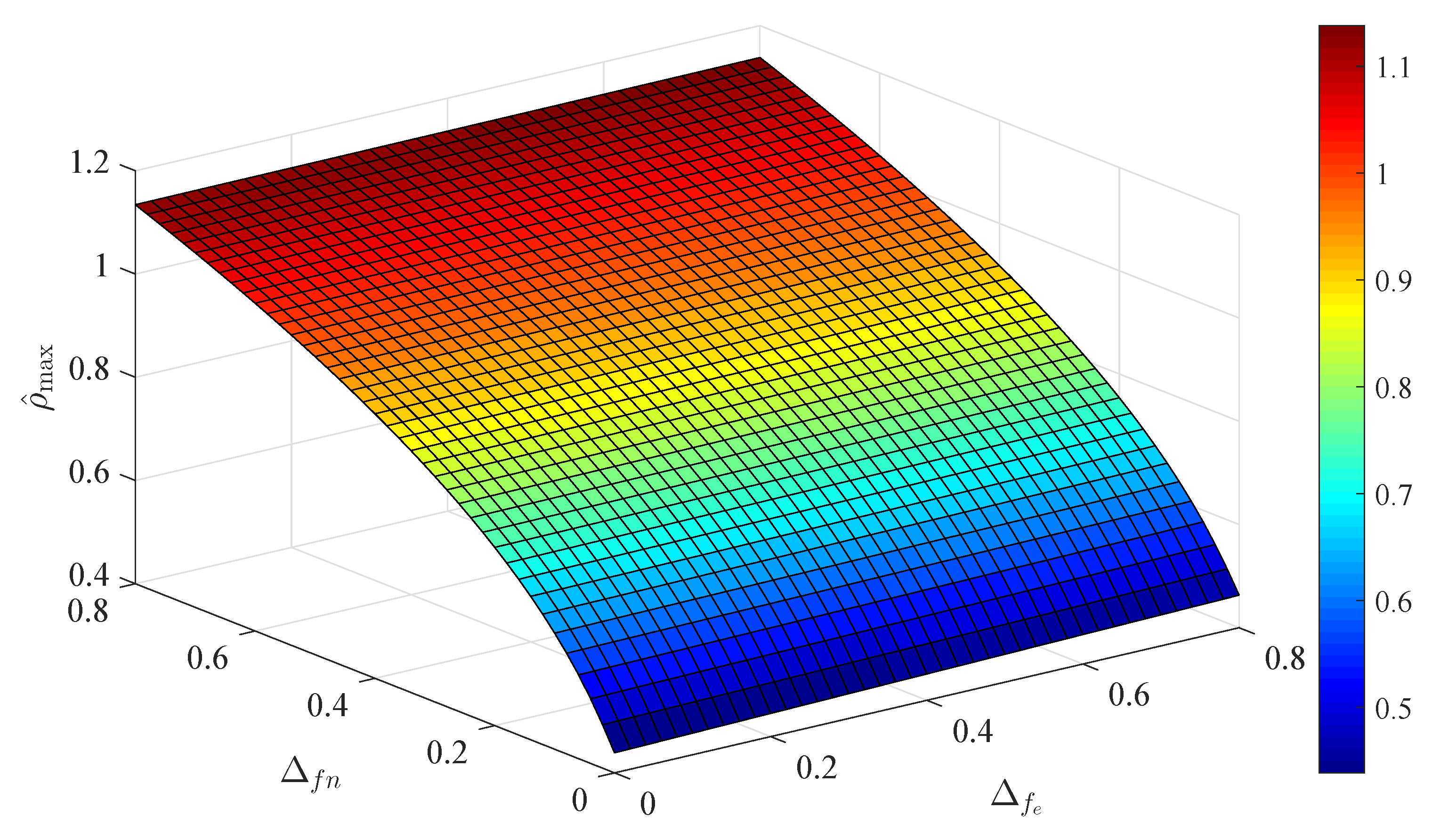
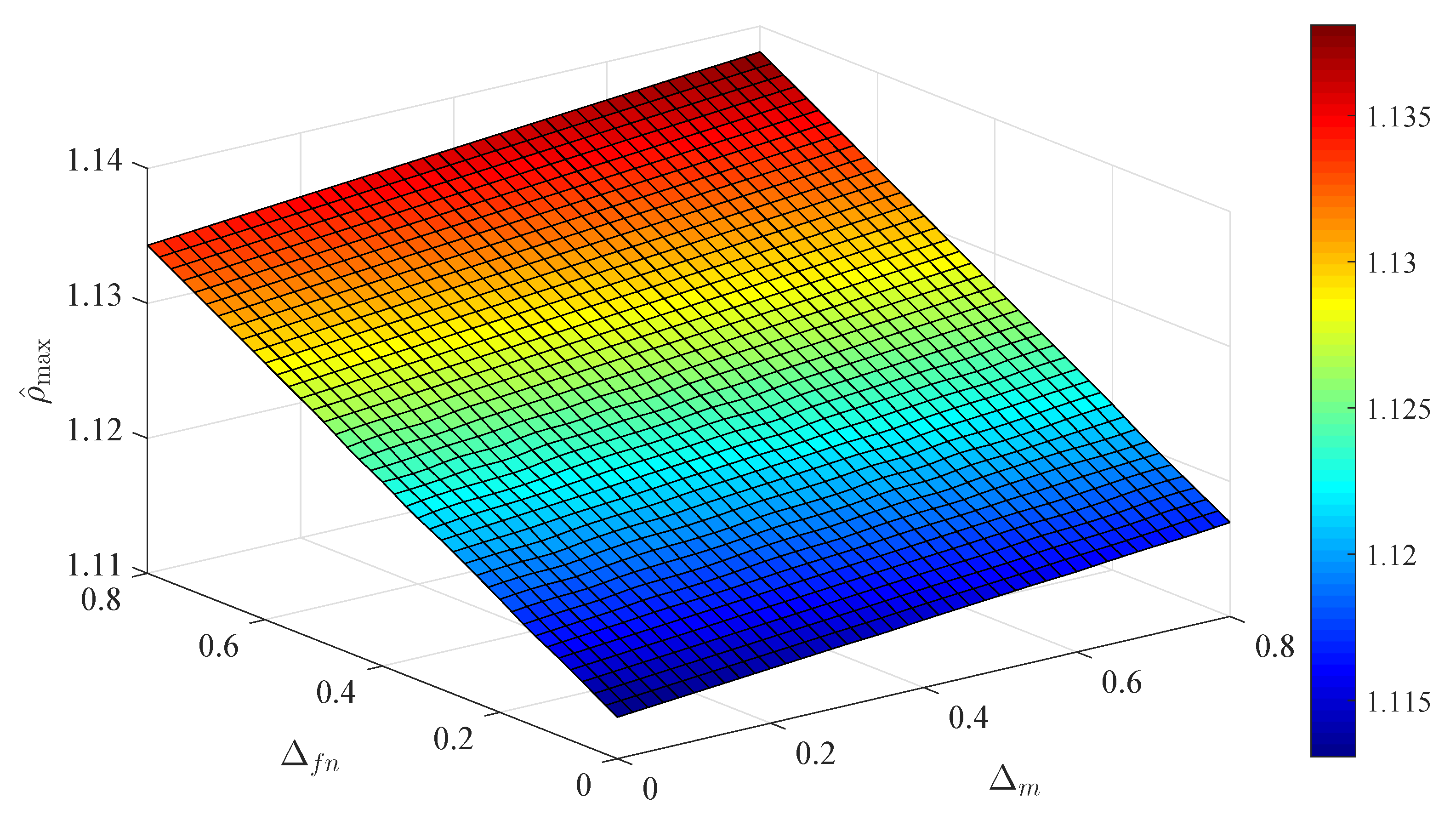
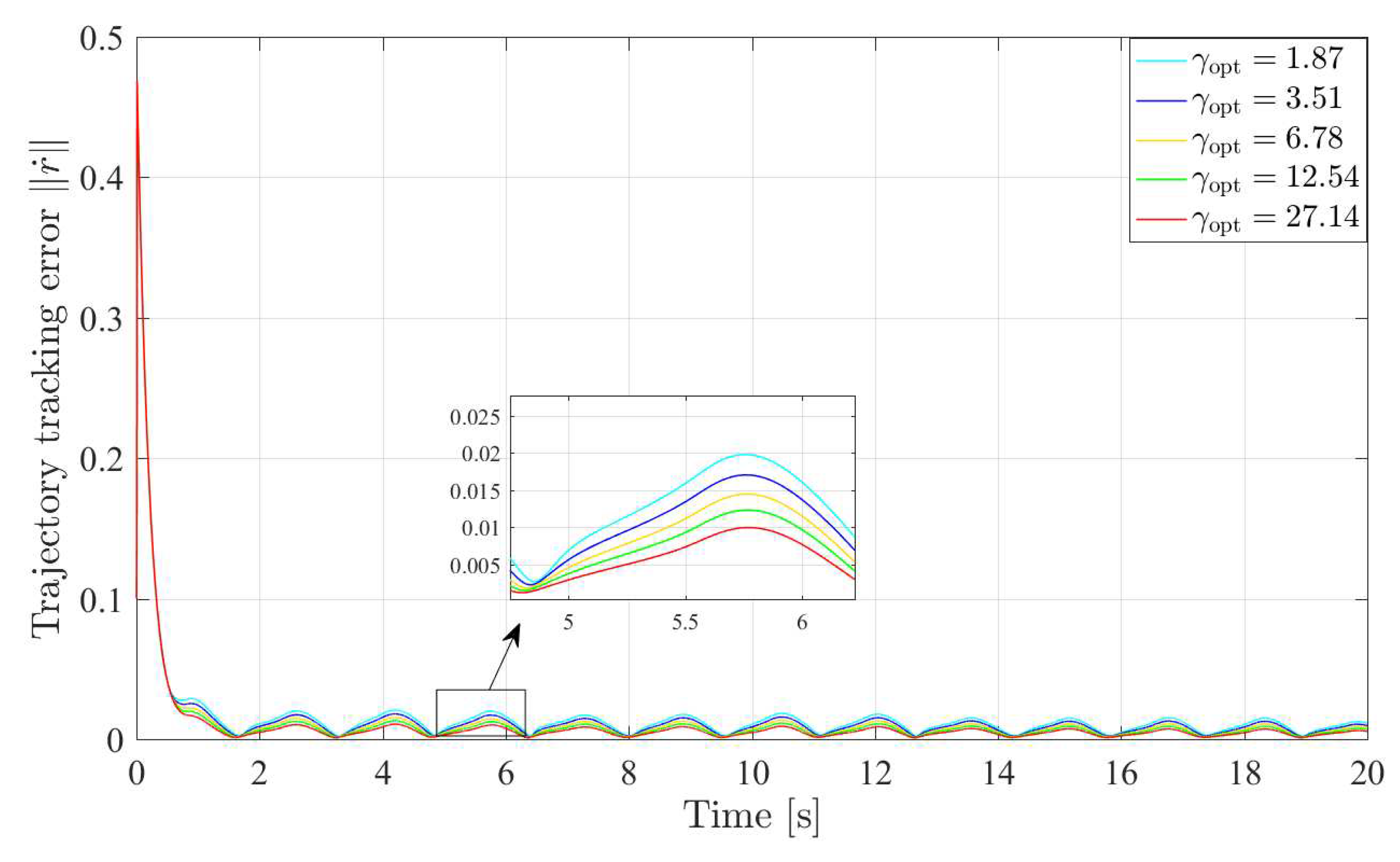
5. Simulations and Discussion
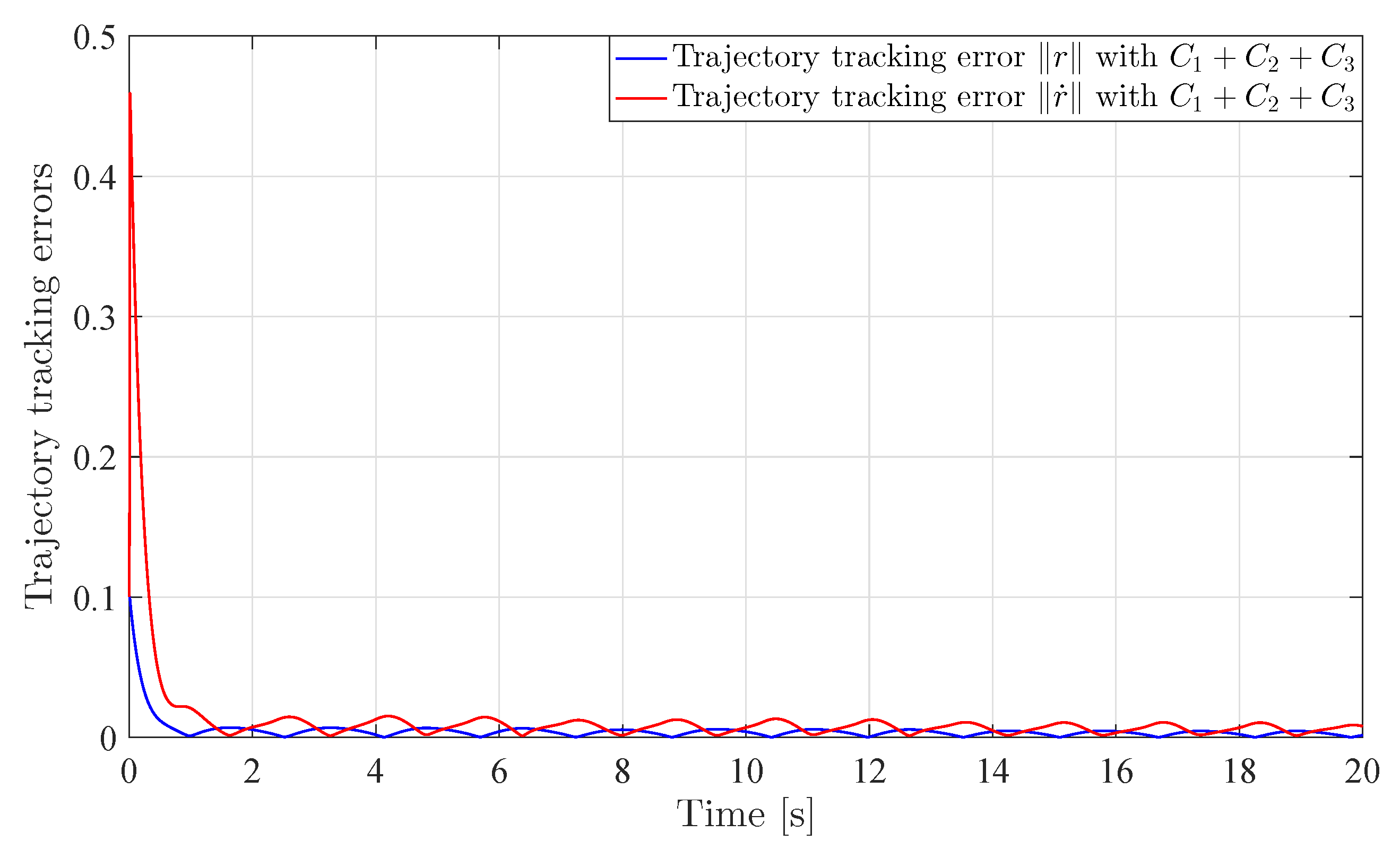
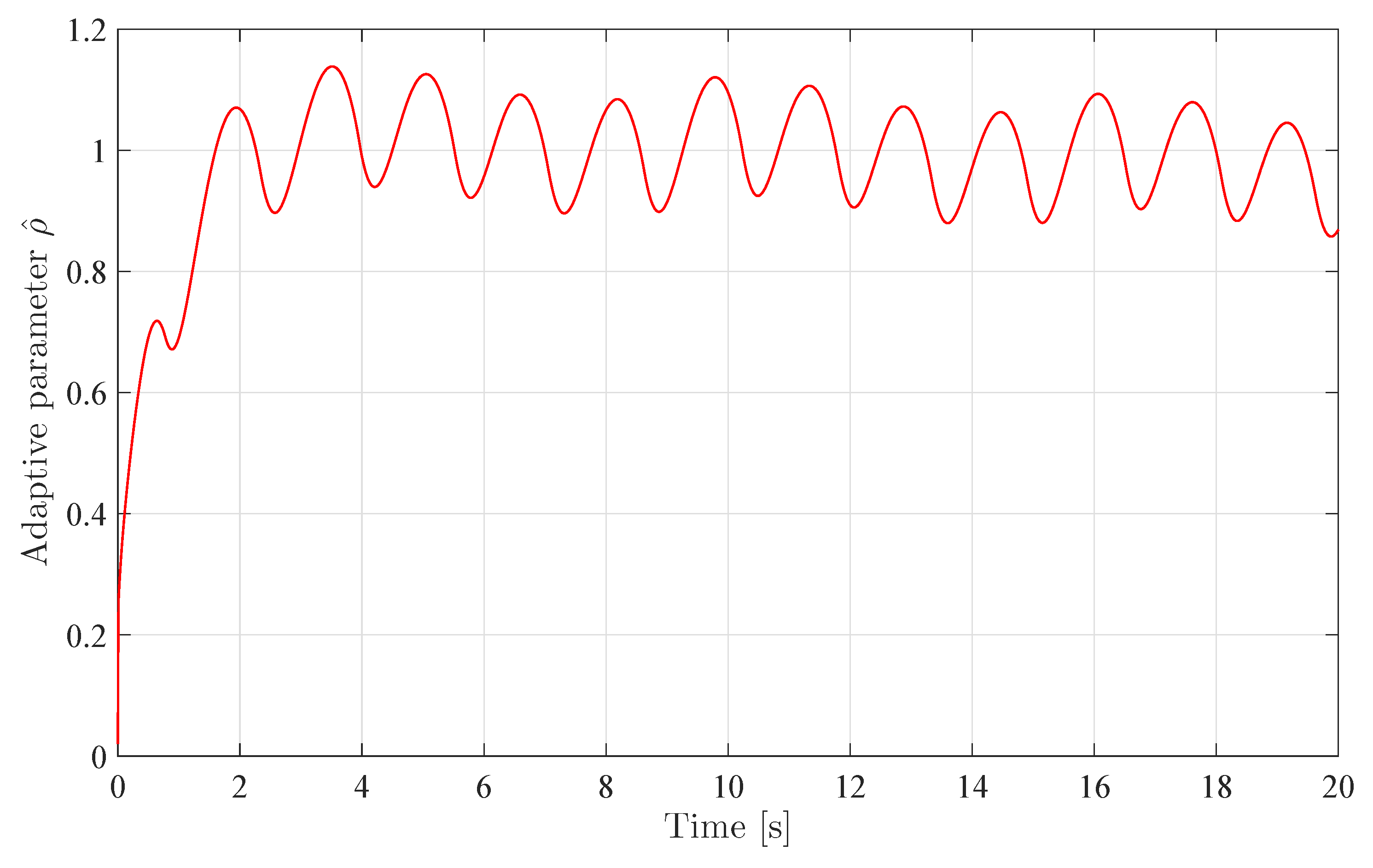
5.1. Simulations
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Borchert, G.; Battistelli, M.; Runge, G.; Raatz, A. Analysis of the mass distribution of a functionally extended delta robot. Robot. Comput.-Integr. Manuf. 2015, 31, 111–120. [Google Scholar] [CrossRef]
- Correa, J.E.; Toombs, J.; Toombs, N.; Ferreira, P.M. Laminated micro-machine: design and fabrication of a flexure-based delta robot. J. Manuf. Process. 2016, 31, 370–375. [Google Scholar] [CrossRef] [Green Version]
- Coronado, E.; Maya, M.; Cardenas, A.; Guarneros, O.; Piovesan, D. Vision-based control of a delta parallel robot via linear camera-space manipulation. J. Intell. Robot. Syst. 2017, 85, 93–106. [Google Scholar] [CrossRef]
- Bekelis, K.; Radwan, T.A.; Desai, A.; Roberts, D.W. Frameless robotically targeted stereotactic brain biopsy: feasibility, diagnostic yield, and safety. J. Neurosurg. 2012, 116, 1002–1006. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Wang, X.; Wu, F.; Chen, X.; Wang, C.; Shen, G. Development and validation of a surgical training simulator with haptic feedback for learning bone-sawing skill. J. Biomed. Inform. 2014, 48, 122–129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, X.; Feng, Z.; Liu, C.; Ren, X. A geometric method for kinematics of Delta robot and its path tracking control. In Proceedings of the International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 22–25 October 2014. [Google Scholar]
- Kelaiaia, R. Improving the pose accuracy of the Delta robot in machining operations. Int. J. Adv. Manuf. Technol. 2017, 91, 2205–2215. [Google Scholar] [CrossRef]
- Morocho, D.; Anita, S.; Celi, R.; Loza, D.; Mariela, P. Study, design and construction of a 3D printer implemented through a delta robot. In Proceedings of the CHILEAN Conference on Electronics Engineering, Information and Communication Technologies, Santiago De Chile, Chile, 28–30 October 2015. [Google Scholar]
- He, K.; Yang, Z.; Bai, Y.; Long, J.; Li, C. Intelligent fault diagnosis of delta 3D printers using attitude sensors based on support vector machines. Sensors 2018, 18, 1298. [Google Scholar] [CrossRef] [Green Version]
- Bengoa, P.; Zubizarreta, A.; Cabanes, I.; Mancisidor, A.; Pinto, C.; Mata, S. Virtual sensor for kinematic estimation of flexible links in parallel robots. Sensors 2017, 17, 1934. [Google Scholar] [CrossRef] [Green Version]
- Shang, D.; Li, Y.; Liu, Y.; Cui, S. Research on the motion error analysis and compensation strategy of the Delta robot. Mathematics 2019, 7, 411. [Google Scholar] [CrossRef] [Green Version]
- Lee, L.-W.; Chiang, H.-H.; Li, I.-H. Development and control of a pneumatic-actuator 3-DOF translational parallel manipulator with robot vision. Sensors 2019, 19, 1459. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Su, T. Quintic pythagorean-hodograph curves based trajectory planning for Delta robot with a prescribed geometrical constraint. Appl. Sci. 2019, 9, 4491. [Google Scholar] [CrossRef] [Green Version]
- Rachedi, M.; Bouri, M.; Hemici, B. Design of an H∞ controller for the Delta robot: experimental results. Adv. Robot. 2015, 29, 1–17. [Google Scholar] [CrossRef]
- Angel, L.; Viola, J. Fractional order PID for tracking control of a parallel robotic manipulator type delta. ISA Trans. 2018, 79, 1–17. [Google Scholar] [CrossRef]
- Mario, R.; Hebertt, S.; Alberto, L.; Alejandro, R. Active disturbance rejection control applied to a Delta parallel robot in trajectory tracking tasks. Asian J. Control 2015, 17, 636–647. [Google Scholar]
- Castañeda, L.A.; Luviano-Juárez, A.; Chairez, I. Robust trajectory tracking of a Delta tobot through adaptive active disturbance rejection control. IEEE Trans. Control Syst. Technol. 2015, 23, 1387–1398. [Google Scholar] [CrossRef]
- Natal, G.S.; Chemori, A.; Pierrot, F. Nonlinear control of parallel manipulators for very high accelerations without velocity measurement: stability analysis and experiments on Par2 parallel manipulator. Robotica 2016, 34, 43–70. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Wu, J.; Mei, J. Motor-mechanism dynamic model based neural network optimized computed torque control of a high speed parallel manipulator. Mechatronics 2007, 17, 381–390. [Google Scholar] [CrossRef]
- Linda, O.; Manic, M. Uncertainty-robust design of interval type-2 fuzzy logic controller for Delta parallel robot. IEEE Trans. Ind. Inform. 2011, 7, 661–670. [Google Scholar] [CrossRef]
- Lu, X.; Liu, M.; Liu, J. Design and optimization of interval type-2 fuzzy logic controller for Delta parallel robot trajectory control. Int. J. Fuzzy Syst. 2017, 19, 190–206. [Google Scholar] [CrossRef]
- Zhai, D.; Liu, X.; Xi, C.; Wang, H. Adaptive reliable H∞ control for a class of T-S fuzzy systems with stochastic actuator failures. IEEE Access 2017, 5, 22750–22759. [Google Scholar] [CrossRef]
- Wang, M.; Paulson, J.A.; Yan, H.; Shi, H. An adaptive model predictive control strategy for nonlinear distributed parameter systems using the type-2 takagi-sugeno model. Int. J. Fuzzy Syst. 2016, 18, 792–805. [Google Scholar] [CrossRef]
- Phu, D.X.; Choi, S.-B. A new adaptive fuzzy PID controller based on riccati-like equation with application to vibration control of vehicle seat suspension. Appl. Sci. 2019, 9, 4540. [Google Scholar] [CrossRef] [Green Version]
- Ghavidel, H.F.; Kalat, A.A. Robust control for MIMO hybrid dynamical system of underwater vehicles by composite adaptive fuzzy estimation of uncertainties. Nonlinear Dyn. 2017, 89, 1–19. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhu, Y.; Yang, T. Robust decentralized static output-feedback control design for large-scale nonlinear systems using takagi-sugeno fuzzy models. IEEE Access 2016, 4, 8250–8263. [Google Scholar] [CrossRef]
- Tai, K.; El-Sayed, A.-R.; Biglarbegian, M.; Gonzalez, C.I.; Castillo, O.; Mahmud, S. Review of recent type-2 fuzzy controller applications. Algorithms 2016, 9, 39. [Google Scholar] [CrossRef] [Green Version]
- Le Thi Thuy, N.; Nguyen Trong, T. The multitasking system of swarm robot based on null-space-behavioral control combined with fuzzy logic. Micromachines 2017, 8, 357. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. The birth and evolution of fuzzy logic. Int. J. Gen. Syst. 1990, 17, 95–105. [Google Scholar] [CrossRef]
- Han, J.; Chen, Y.H.; Zhao, X.; Dong, F. Optimal design for robust control of uncertain flexible joint manipulators: a fuzzy dynamical system approach. Int. J. Control 2017, 91, 937–951. [Google Scholar] [CrossRef]
- Rey, L.; Clavel, R. The Delta Parallel Robot. In Advanced Manufacturing; Boër, C.R., Molinari-Tosatti, L., Smith, K.S., Eds.; Springer: London, UK, 1999; pp. 401–417. [Google Scholar]
- Hui, J.; Pan, M.; Zhao, R.; Luo, L.; Wu, L. The closed-form motion equation of redundant actuation parallel robot with joint friction: an application of the Udwadia-Kalaba approach. Nonlinear Dyn. 2018, 93, 689–703. [Google Scholar] [CrossRef]
- Zhao, R.; Chen, Y.H.; Wu, L.; Pan, M. Robust trajectory tracking control for uncertain mechanical systems: Servo constraint-following and adaptation mechanism. Int. J. Control 2018. [Google Scholar] [CrossRef]
- Chen, Y.H.; Leitmann, G.; Chen, J.S. Robust control for rigid serial manipulators: A general setting. In Proceedings of the 1998 American Control Conference, Philadelphia, PA, USA, 26 June 1998. [Google Scholar]
- Chen, Y.H. A new approach to the control design of fuzzy dynamical systems. J. Dyn. Syst. Meas. Control 2011, 133, 061019. [Google Scholar] [CrossRef]
- Chen, Y.H.; Zhang, X. Adaptive robust approximate constraint-following control for mechanical systems. J. Frankl. Inst. 2010, 347, 69–86. [Google Scholar] [CrossRef]
- Batschelet, E. Ordinary Differential Equations. In Introduction to Mathematics for Life Scientists; Springer Study Edition; Springer: Berlin, Germany, 1979; pp. 334–380. [Google Scholar]
- Chen, Y.H. Performance analysis of controlled uncertain systems. Dynam. Control 1996, 6, 131–142. [Google Scholar] [CrossRef]
- Xu, J.; Fang, H.; Zhou, T.; Chen, Y.H.; Guo, H.; Zeng, F. Optimal robust position control with input shaping for flexible solar array drive system: A fuzzy-set theoretic approach. Int. Trans. Fuzzy Syst. 2019, 27, 1807–1817. [Google Scholar] [CrossRef]
- Bede, L.; Rudas, I.J.; Fodor, J. Friction model by using fuzzy differential equations. In Proceedings of the 12th International Fuzzy Systems Association World Congress, Cancun, Mexico, 18–21 June 2007. [Google Scholar]
- Hanss, M. Applied Fuzzy Arithmetic: An Introduction with Engineering Applications; Springer Study Edition; Springer: Berlin/Heidelberg, Germany, 2005; pp. 141–231. [Google Scholar]
- Romano, D.; Bloemberg, J.; Tannous, M.; Stefanini, C. Impact of aging and cognitive mechanisms on high-speed motor activation patterns: evidence from an orthoptera-robot interaction. IEEE Trans. Med. Robot. Bionics 2020, 14, 1–7. [Google Scholar] [CrossRef]
- Santer, R.D.; Rind, F.C.; Stafford, R.; Simmons, P.J. Role of an identified looming-sensitive neuron in triggering a flying locust’s escape. J. Neurophysiol. 2006, 95, 3391–3400. [Google Scholar] [CrossRef]
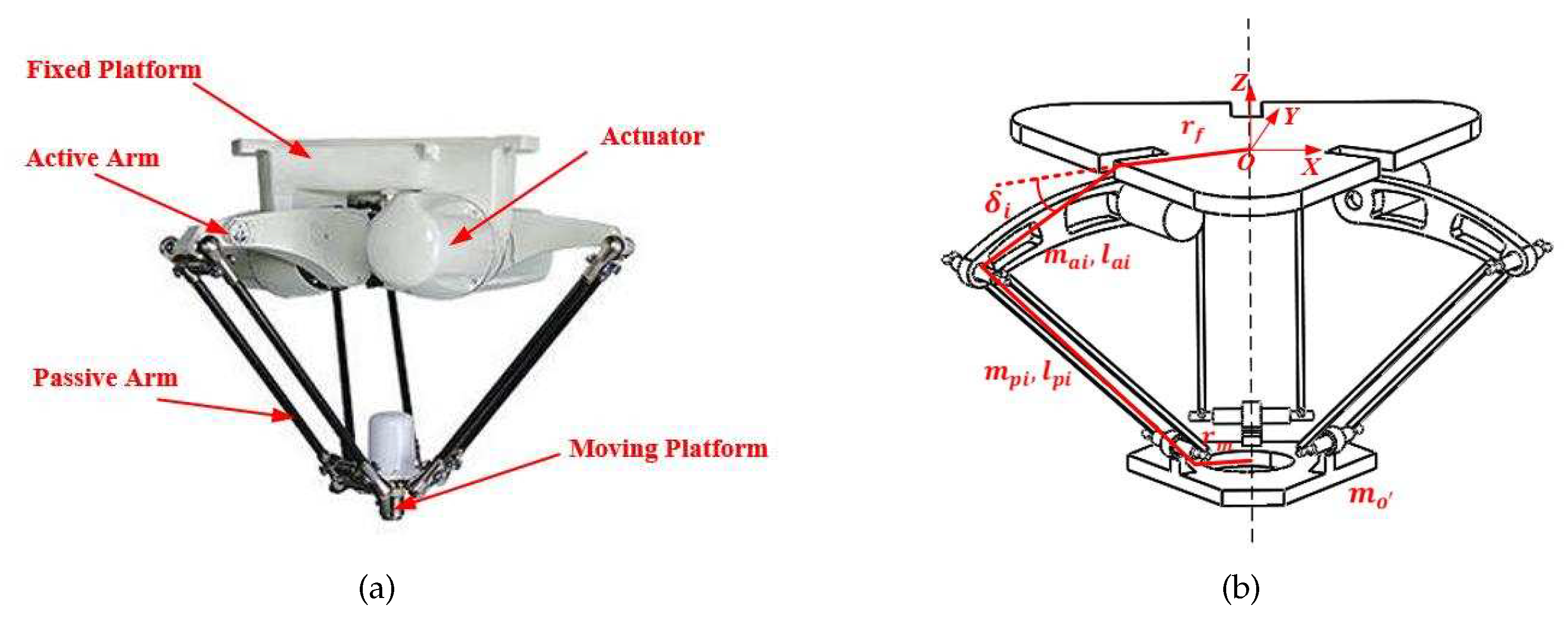





| Description | Notation | Units |
|---|---|---|
| Angle of the i-th active joint | rad | |
| Length of the i-th active arm | m | |
| Length of the i-th passive arm | m | |
| Radius of the fixed platform | m | |
| Radius of the moving platform | m | |
| Mass of the i-th active arm | kg | |
| Mass of the i-th passive arm | kg | |
| Mass of the moving platform | kg |
| (, , ) | ||
|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhao, R.; Li, Y.; Chen, Y.-H. Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach. Appl. Sci. 2020, 10, 3472. https://doi.org/10.3390/app10103472
Wu L, Zhao R, Li Y, Chen Y-H. Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach. Applied Sciences. 2020; 10(10):3472. https://doi.org/10.3390/app10103472
Chicago/Turabian StyleWu, Linlin, Ruiying Zhao, Yuyu Li, and Ye-Hwa Chen. 2020. "Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach" Applied Sciences 10, no. 10: 3472. https://doi.org/10.3390/app10103472
APA StyleWu, L., Zhao, R., Li, Y., & Chen, Y.-H. (2020). Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach. Applied Sciences, 10(10), 3472. https://doi.org/10.3390/app10103472






