Optical Soliton Solutions of the Cubic-Quartic Nonlinear Schrödinger and Resonant Nonlinear Schrödinger Equation with the Parabolic Law
Abstract
Featured Application
Abstract
1. Introduction
2. Instructions for the Methods
3. Application to the Expansion Method
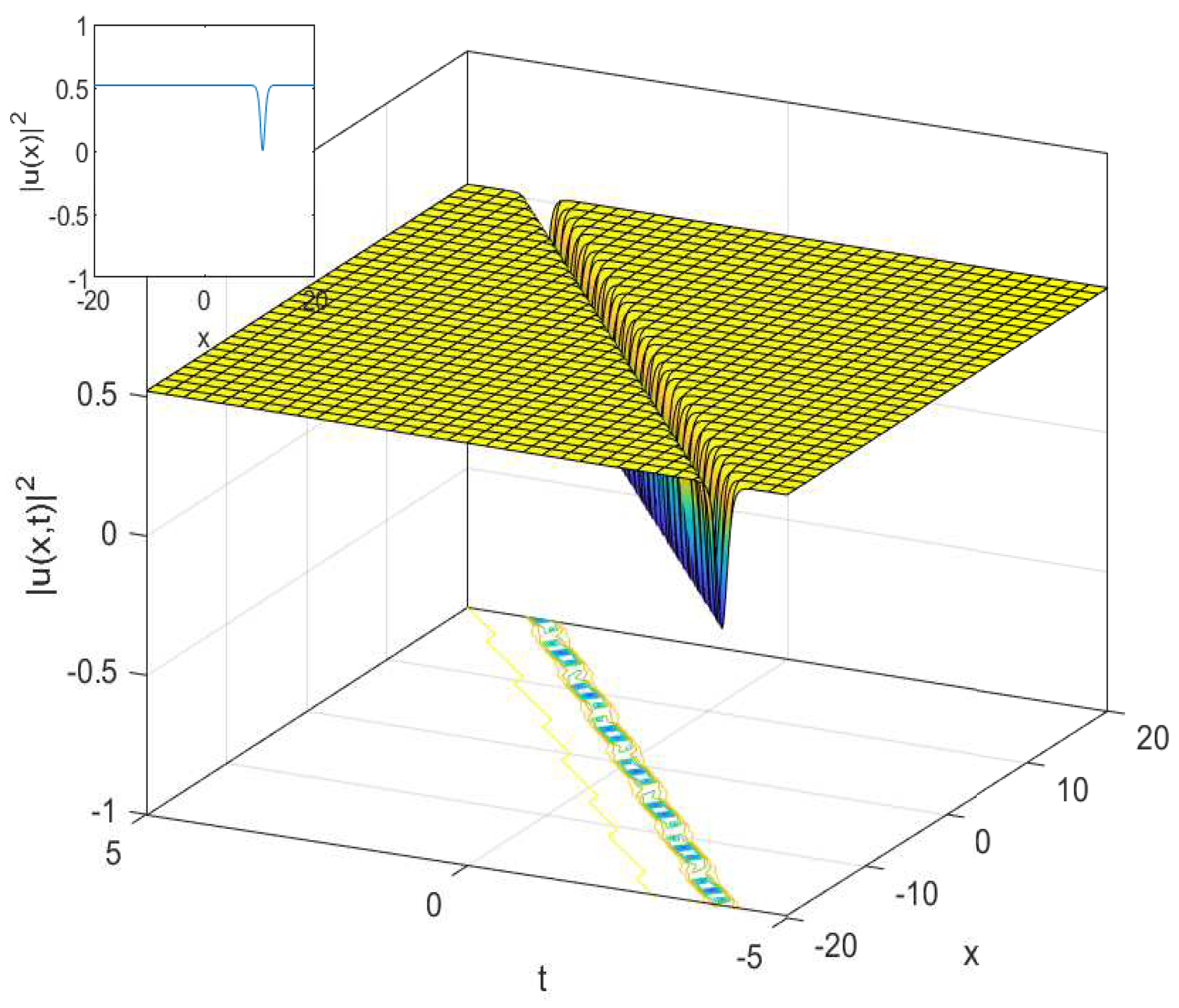
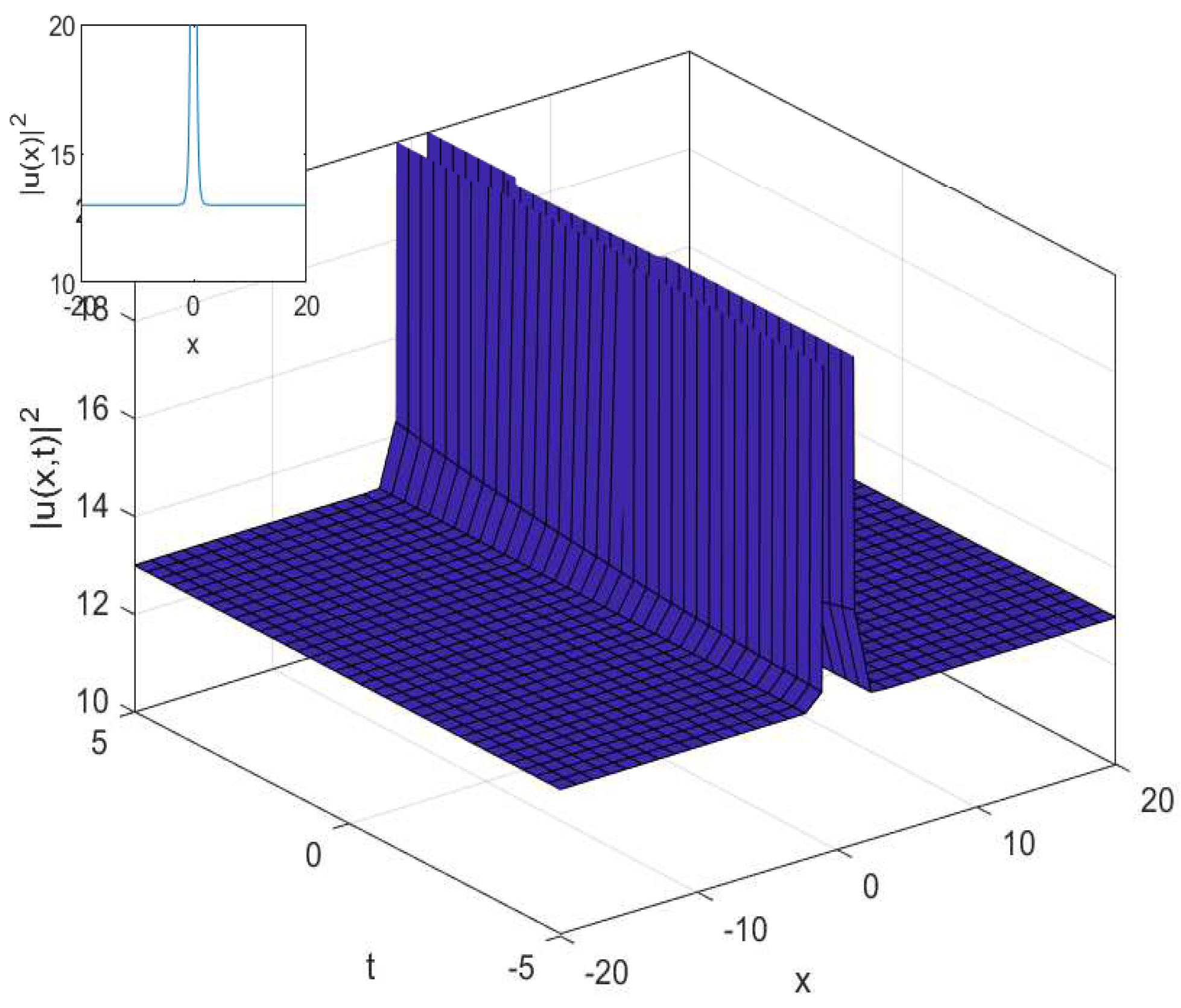
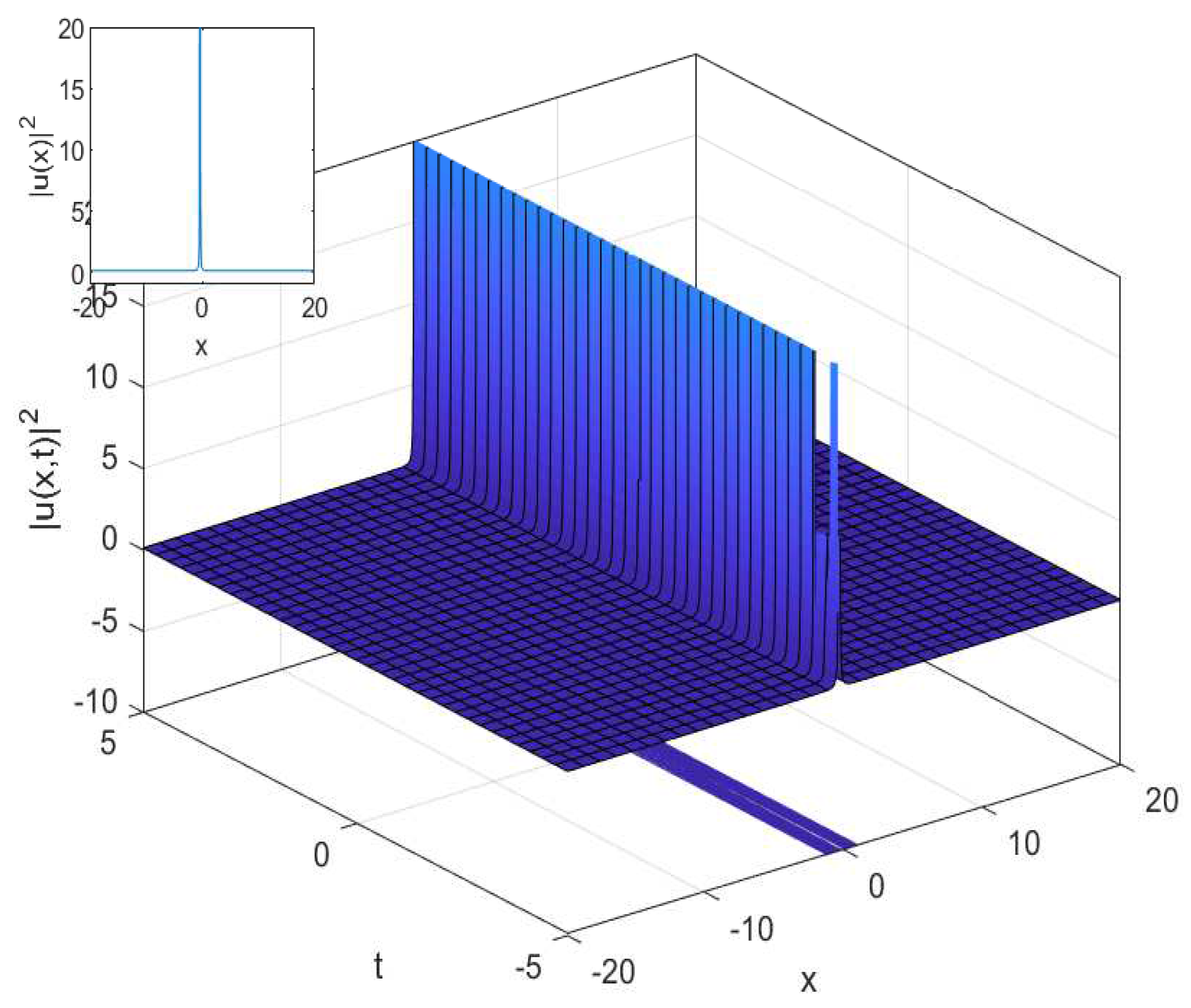
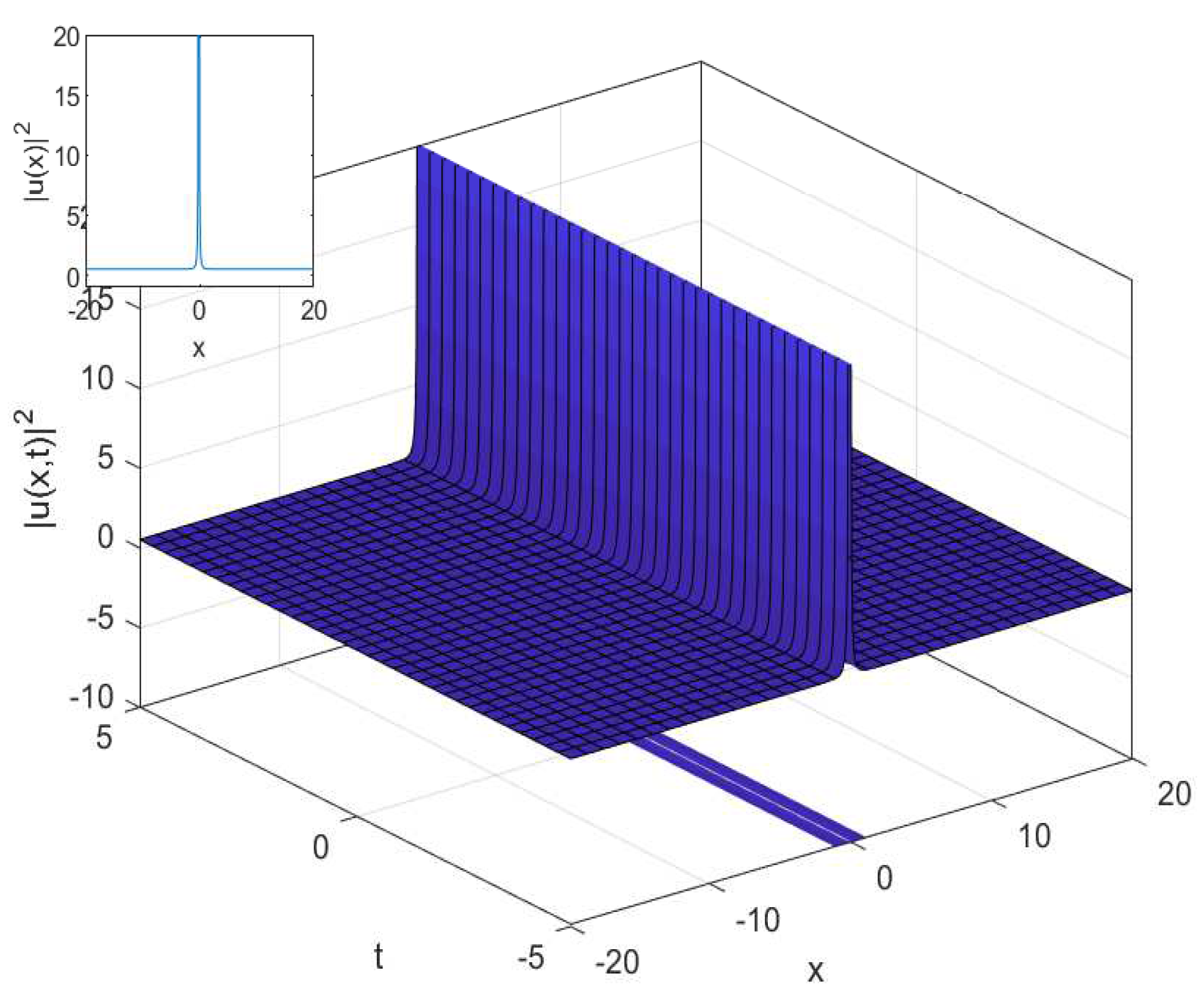
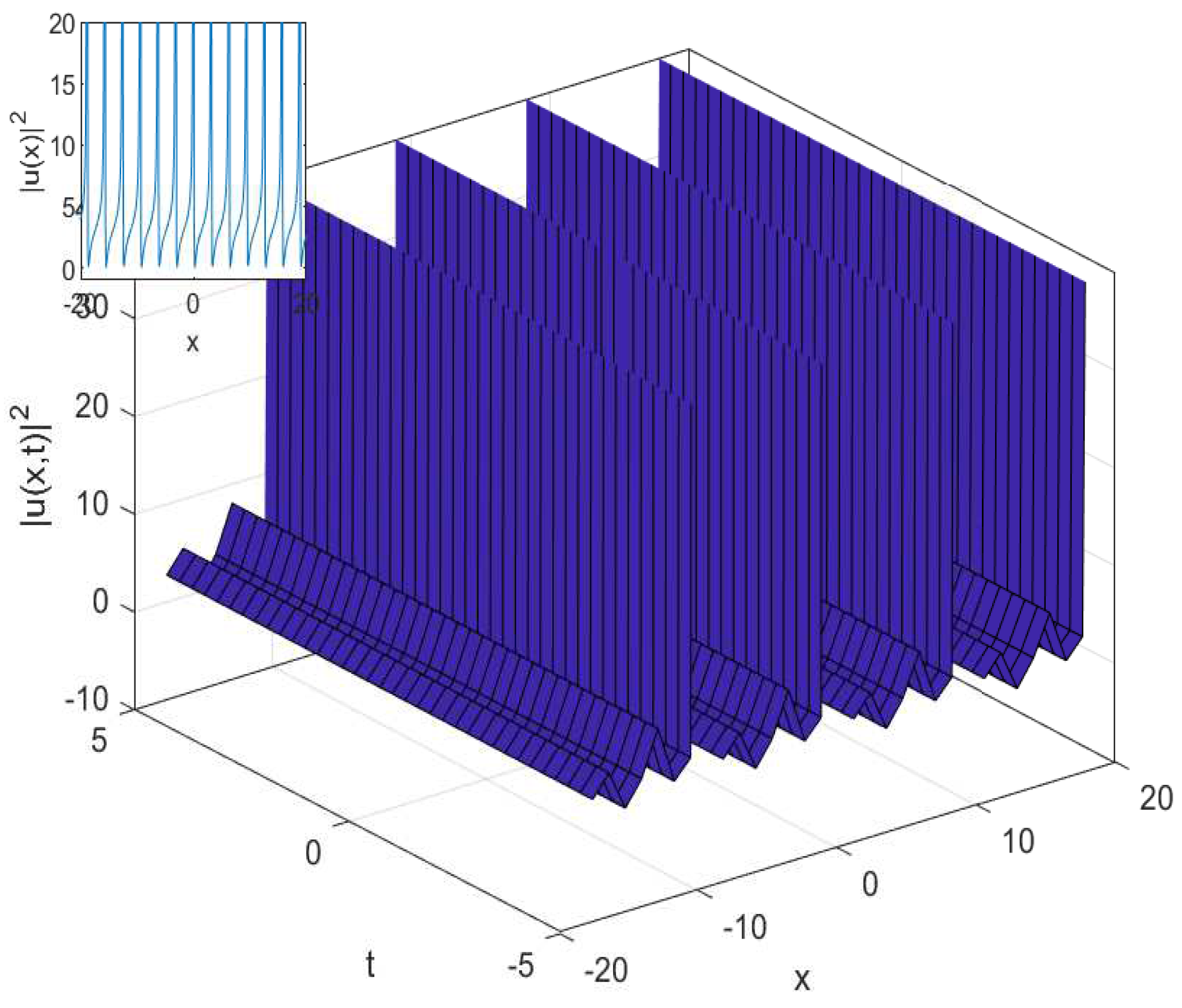
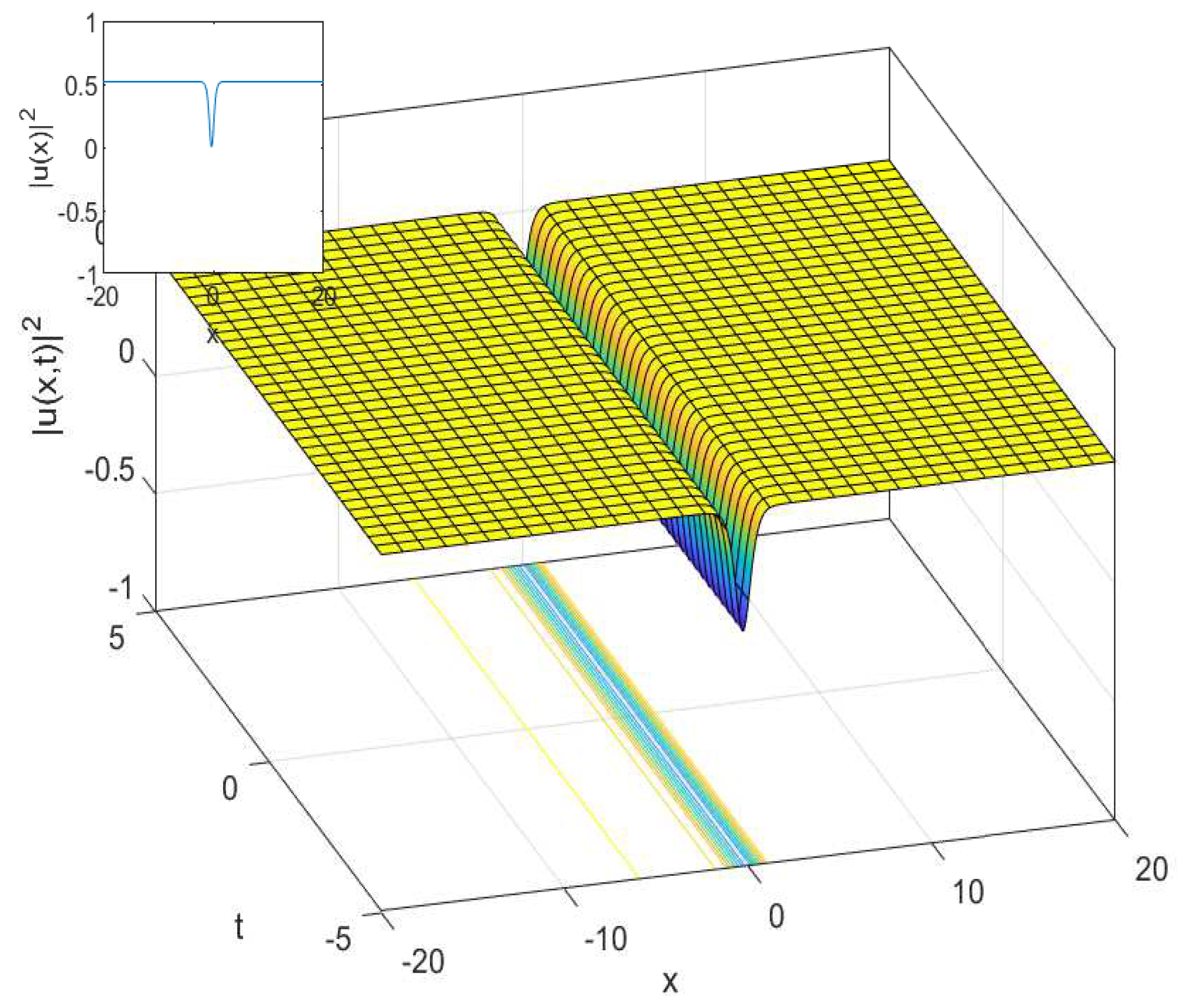
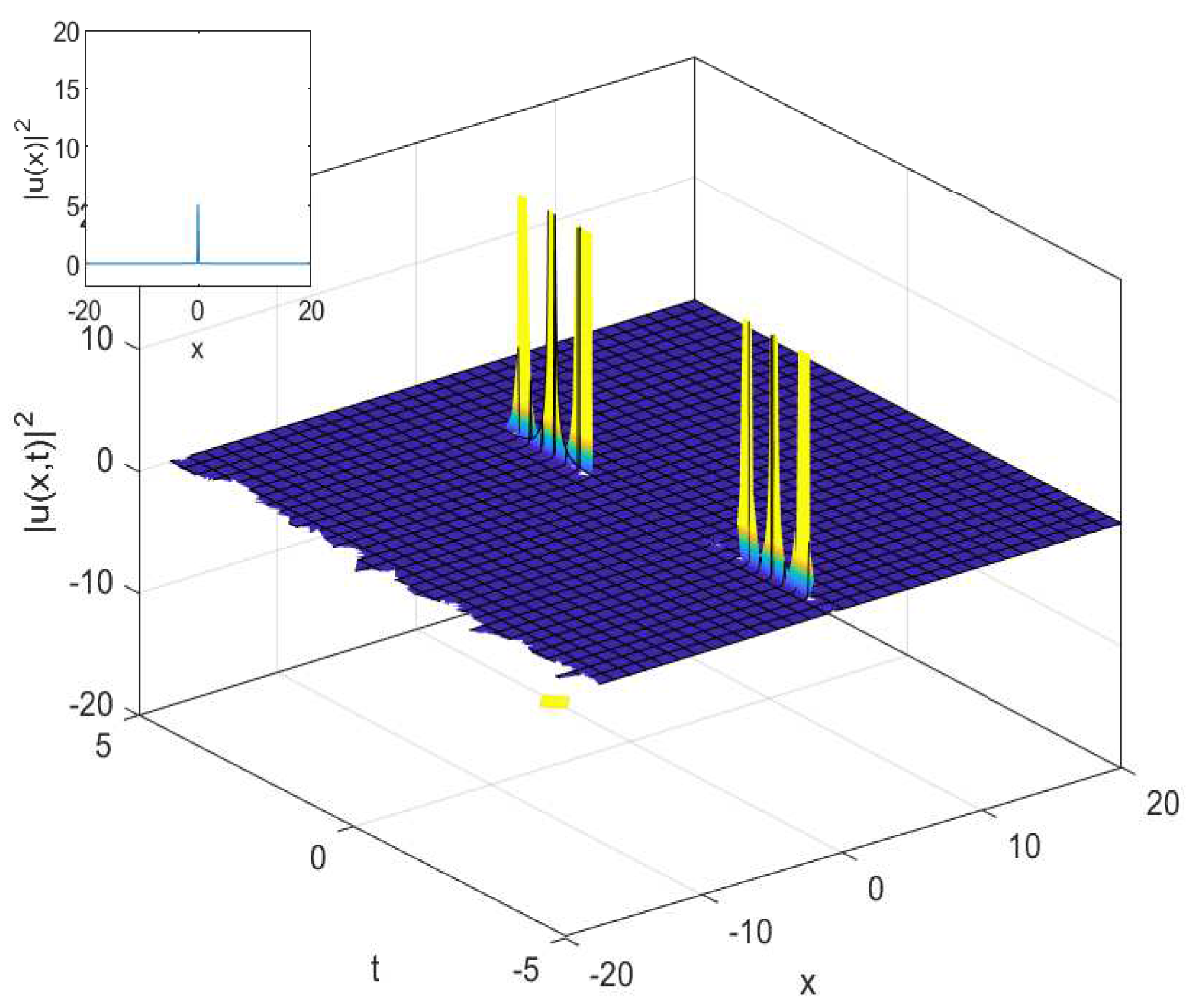
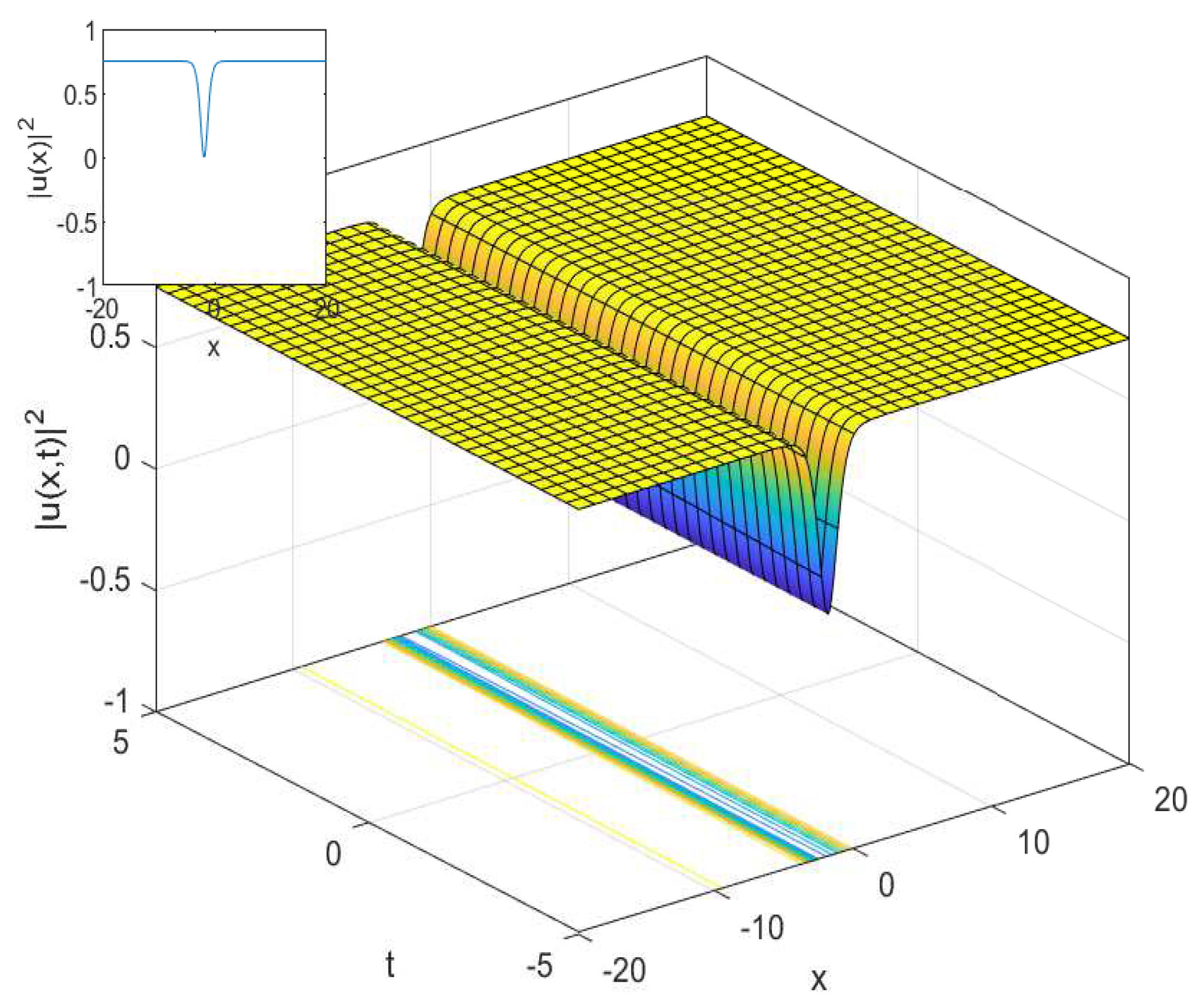
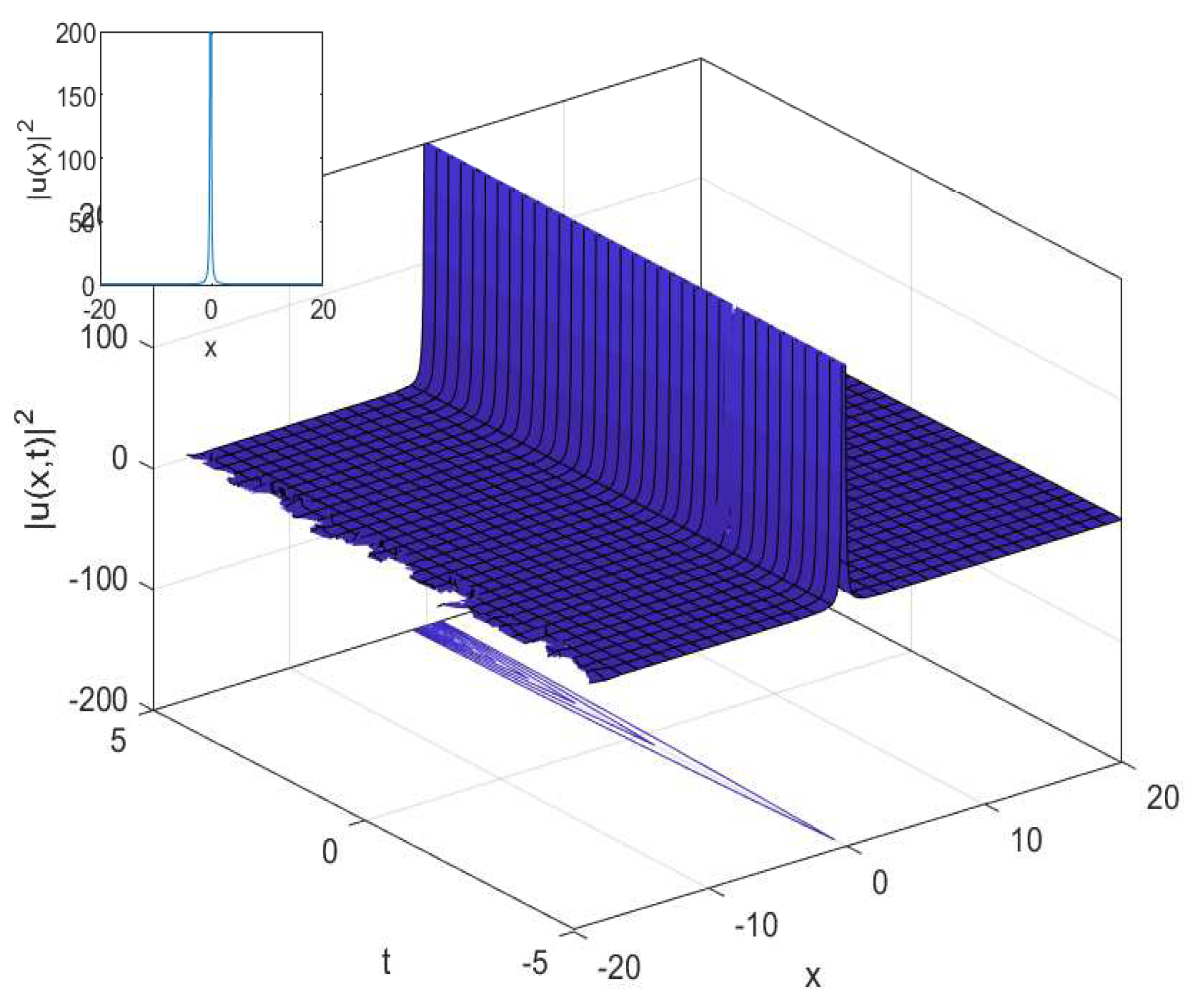
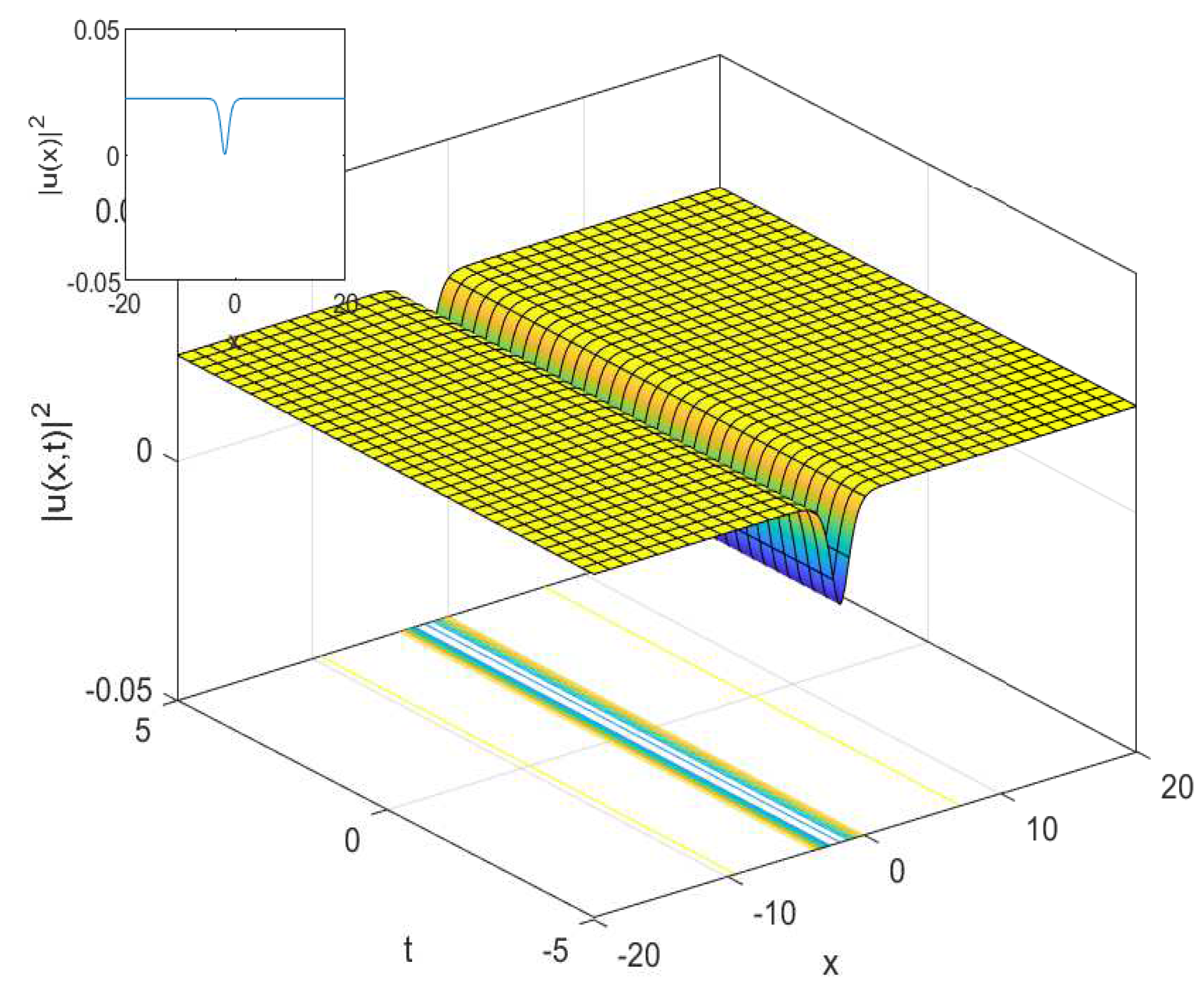
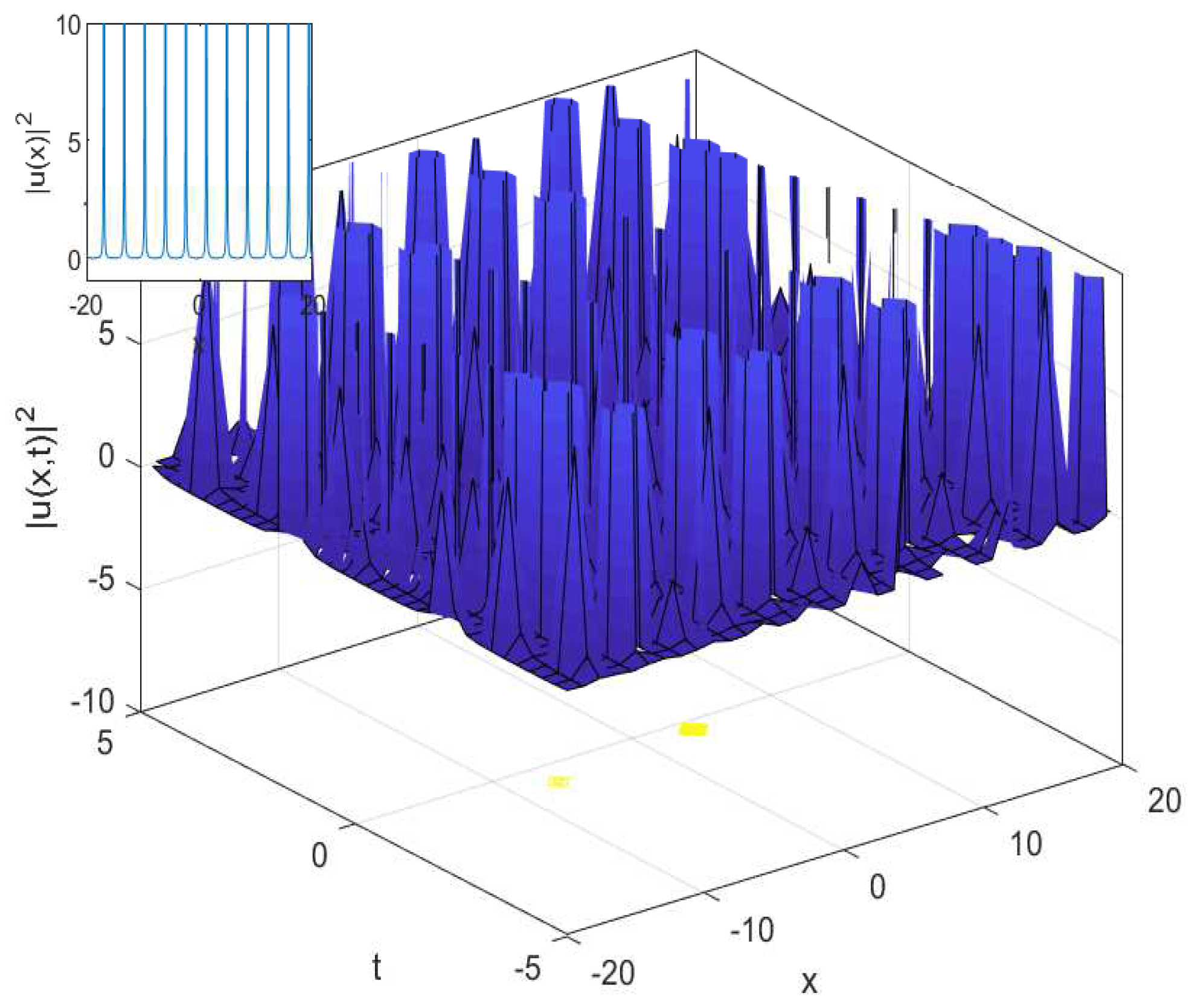
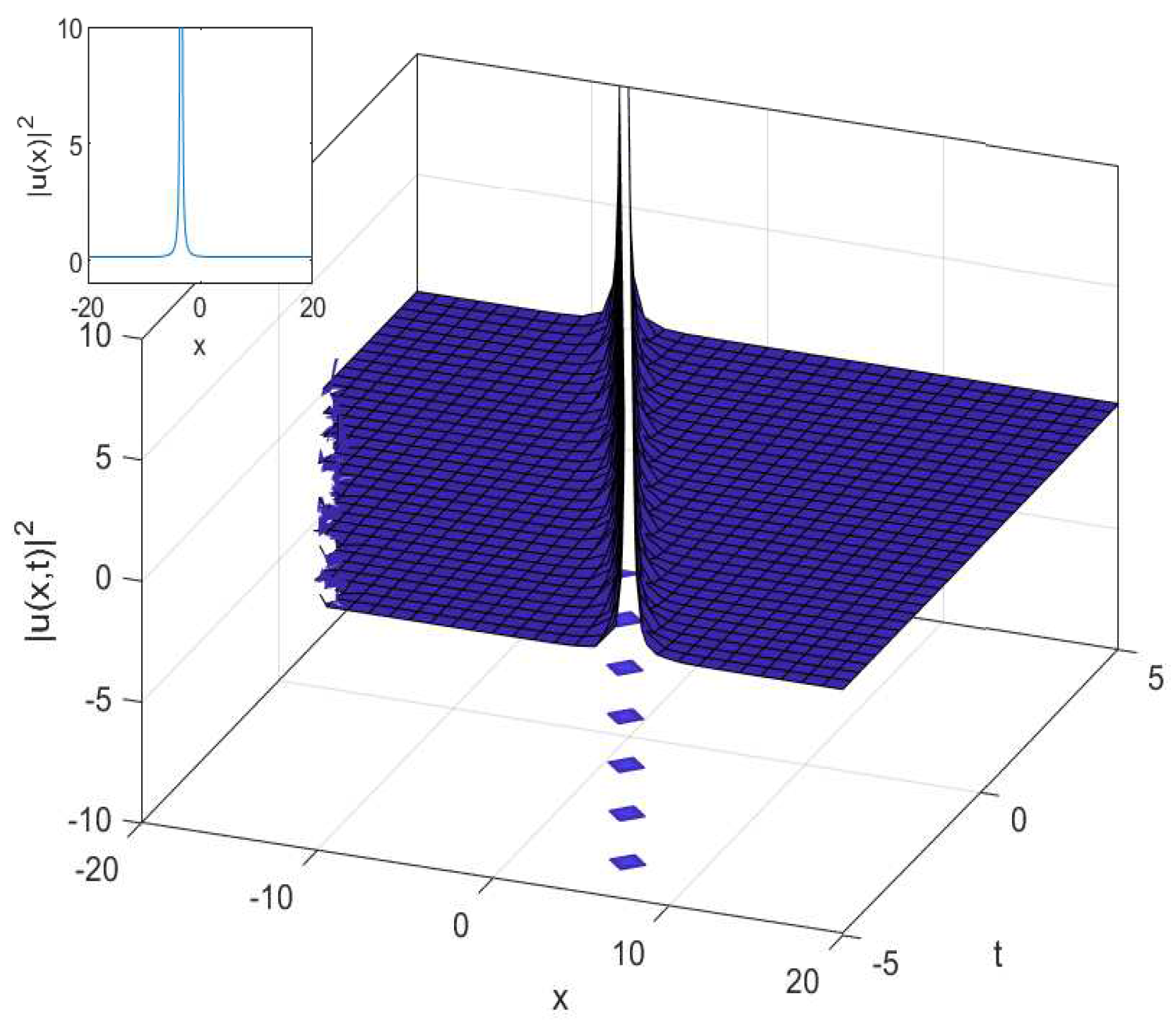
3.1. The Cubic-Quartic Nonlinear Schrödinger Equation
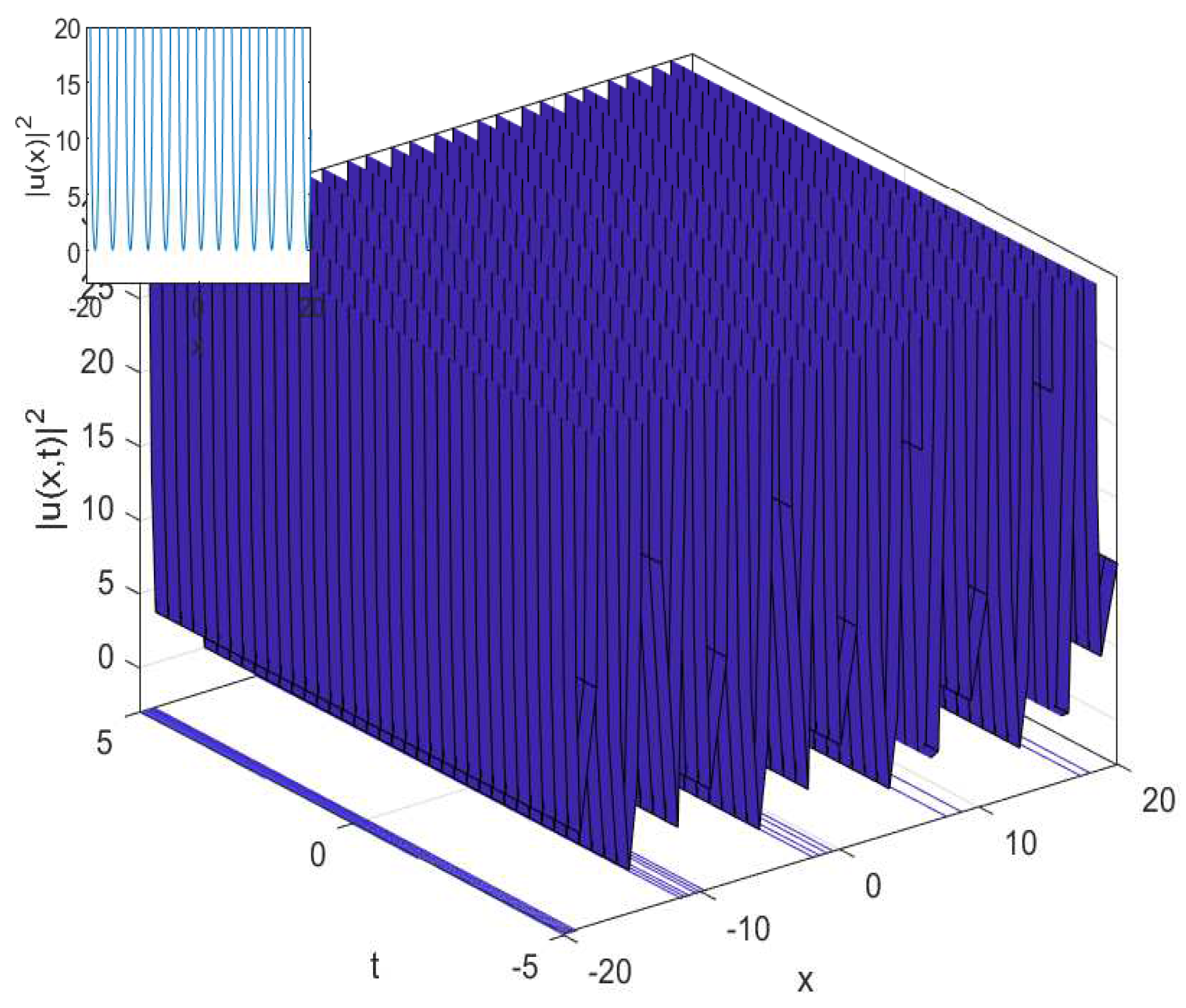
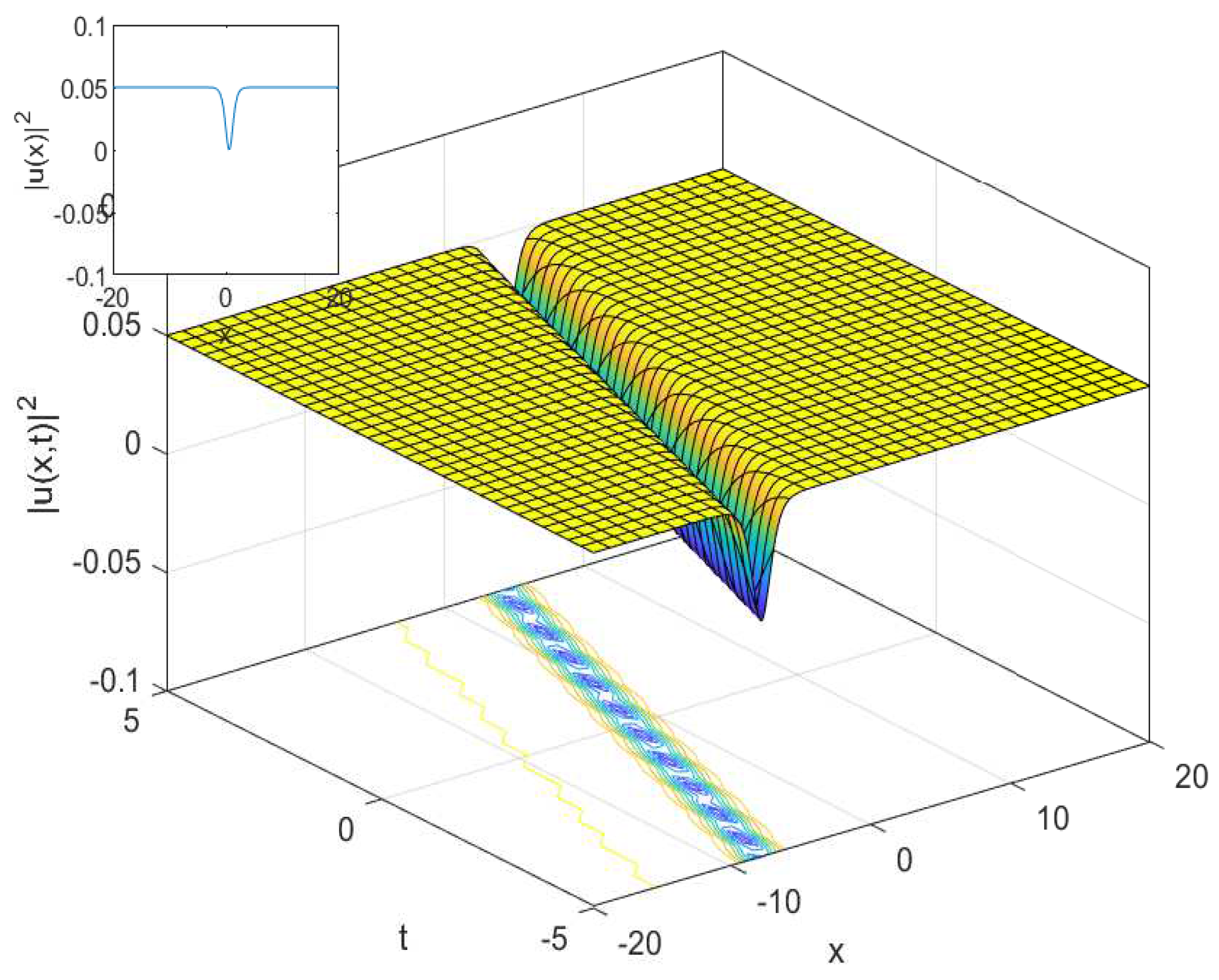
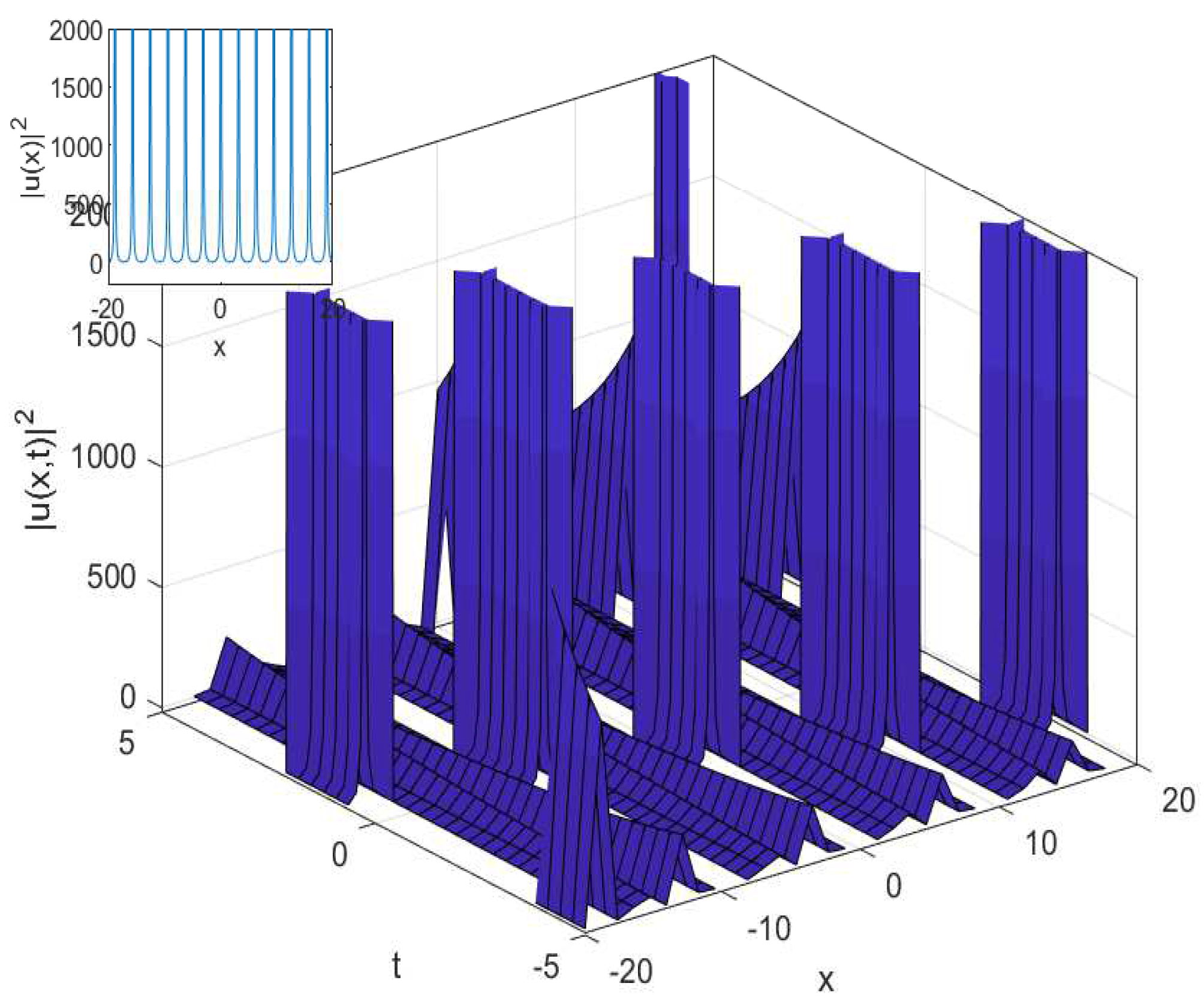
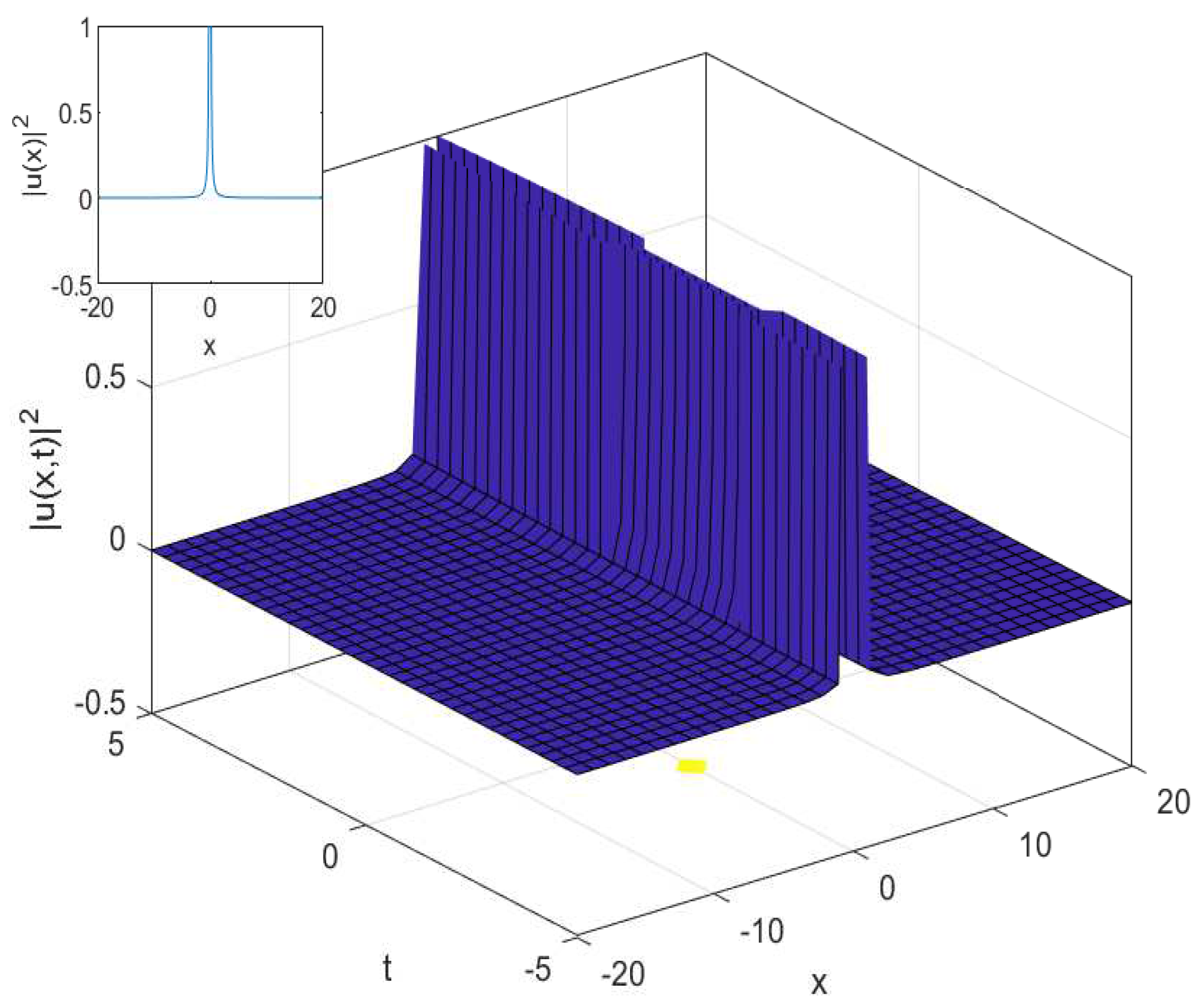
3.2. The Cubic-Quartic Resonant Nonlinear Schrödinger Equation
4. Application to the Expansion Method
4.1. The Cubic-Quartic Nonlinear Schrödinger Equation
4.2. The Cubic-Quartic Resonant Nonlinear Schrödinger Equation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NLPDE | Nonlinear partial differential equation |
| ODE | Ordinary differential equation |
References
- Plastino, A. Entropic aspects of nonlinear partial differential equations: Classical and quantum mechanical perspectives. Entropy 2017, 19, 166. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Esen, A.; Bulut, H.; Baskonus, H.M. Singular solitons in the pseudo-parabolic model arising in nonlinear surface waves. Results Phys. 2019, 12, 1712–1715. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Exact bright–dark solitary wave solutions of the higher-order cubic–quintic nonlinear Schrödinger equation and its stability. Optik 2017, 138, 40–49. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Elliptic function and solitary wave solutions of the higher-order nonlinear Schrödinger dynamical equation with fourth-order dispersion and cubic-quintic nonlinearity and its stability. Eur. Phys. J. Plus 2017, 132, 371. [Google Scholar] [CrossRef]
- Yousif, M.A.; Mahmood, B.A.; Ali, K.K.; Ismael, H.F. Numerical simulation using the homotopy perturbation method for a thin liquid film over an unsteady stretching sheet. Int. J. Pure Appl. Math. 2016, 107, 289–300. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method. Open Math. 2015, 13, 547–556. [Google Scholar] [CrossRef]
- Ismael, H.F. Carreau-Casson fluids flow and heat transfer over stretching plate with internal heat source/sink and radiation. Int. J. Adv. Appl. Sci. 2017, 4, 11–15. [Google Scholar] [CrossRef]
- Ali, K.K.; Ismael, H.F.; Mahmood, B.A.; Yousif, M.A. MHD Casson fluid with heat transfer in a liquid film over unsteady stretching plate. Int. J. Adv. Appl. Sci. 2017, 4, 55–58. [Google Scholar] [CrossRef]
- Ismael, H.F.; Arifin, N.M. Flow and heat transfer in a maxwell liquid sheet over a stretching surface with thermal radiation and viscous dissipation. JP J. Heat Mass Transf. 2018, 15, 847–866. [Google Scholar] [CrossRef]
- Zeeshan, A.; Ismael, H.F.; Yousif, M.A.; Mahmood, T.; Rahman, S.U. Simultaneous Effects of Slip and Wall Stretching/Shrinking on Radiative Flow of Magneto Nanofluid Through Porous Medium. J. Magn. 2018, 23, 491–498. [Google Scholar] [CrossRef]
- Gao, W.; Partohaghighi, M.; Baskonus, H.M.; Ghavi, S. Regarding the group preserving scheme and method of line to the numerical simulations of Klein–Gordon model. Results Phys. 2019, 15, 102555. [Google Scholar] [CrossRef]
- Yokus, A.; Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. Numerical simulation and solutions of the two-component second order KdV evolutionarysystem. Numer. Methods Partial Differ. Equ. 2018, 34, 211–227. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Bulut, H.; Yokus, A.; Baskonus, H.M. On the exact and numerical solutions to the coupled Boussinesq equation arising in ocean engineering. Indian J. Phys. 2019, 93, 647–656. [Google Scholar] [CrossRef]
- Bulut, H.; Ergüt, M.; Asil, V.; Bokor, R.H. Numerical solution of a viscous incompressible flow problem through an orifice by Adomian decomposition method. Appl. Math. Comput. 2004, 153, 733–741. [Google Scholar] [CrossRef]
- Ismael, H.F.; Ali, K.K. MHD casson flow over an unsteady stretching sheet. Adv. Appl. Fluid Mech. 2017, 20, 533–541. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Sulaiman, T.A. New Complex Hyperbolic Structures to the Lonngren-Wave Equation by Using Sine-Gordon Expansion Method. Appl. Math. Nonlinear Sci. 2019, 4, 141–150. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. On the soliton solutions to the Nizhnik-Novikov- Veselov and the Drinfel’d-Sokolov systems. Opt. Quantum Electron. 2018, 50, 138. [Google Scholar] [CrossRef]
- Eskitaşçıoğlu, E.İ.; Aktaş, M.B.; Baskonus, H.M. New Complex and Hyperbolic Forms for Ablowitz–Kaup– Newell–Segur Wave Equation with Fourth Order. Appl. Math. Nonlinear Sci. 2019, 4, 105–112. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, F.H.; Bulut, H.; Baskonus, H.M. Instability modulation for the (2+1)-dimension paraxial wave equation and its new optical soliton solutions in Kerr media. Phys. Scr. 2019. [Google Scholar] [CrossRef]
- Houwe, A.; Hammouch, Z.; Bienvenue, D.; Nestor, S.; Betchewe, G. Nonlinear Schrödingers equations with cubic nonlinearity: M-derivative soliton solutions by exp(-Φ(ξ))-Expansion method. Preprints 2019. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. Solitons in an inhomogeneous Murnaghan’s rod. Eur. Phys. J. Plus 2018, 133, 228. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Yel, G.; Bulut, H. Novel wave surfaces to the fractional Zakharov-Kuznetsov-Benjamin- Bona-Mahony equation. Proc. Aip Conf. Proc. 2017, 1863, 560084. [Google Scholar]
- Baskonus, H.M.; Bulut, H. Exponential prototype structures for (2+1)-dimensional Boiti-Leon-Pempinelli systems in mathematical physics. Waves Random Complex Media 2016, 26, 189–196. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A. The Riccati-Bernoulli Sub-ODE Technique for Solving the Deterministic (Stochastic) Generalized-Zakharov System. Int. J. Math. Syst. Sci. 2018, 1. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, H.F.; Mohammed, S.A.; Baskonus, H.M.; Bulut, H. Complex and real optical soliton properties of the paraxial nonlinear Schrödinger equation in Kerr media with M-fractional. Front. Phys. 2019, 7, 197. [Google Scholar] [CrossRef]
- Hammouch, Z.; Mekkaoui, T.; Agarwal, P. Optical solitons for the Calogero-Bogoyavlenskii-Schiff equation in (2 + 1) dimensions with time-fractional conformable derivative. Eur. Phys. J. Plus 2018, 133, 248. [Google Scholar] [CrossRef]
- Manafian, J.; Aghdaei, M.F. Abundant soliton solutions for the coupled Schrödinger-Boussinesq system via an analytical method. Eur. Phys. J. Plus 2016, 131, 97. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, Y.; Xu, S.; Wu, Z.; He, J. The higher order rogue wave solutions of the Gerdjikov-Ivanov equation. Phys. Scr. 2014, 89, 035501. [Google Scholar] [CrossRef]
- Ling, L.; Feng, B.F.; Zhu, Z. General soliton solutions to a coupled Fokas–Lenells equation. Nonlinear Anal. Real World Appl. 2018, 40, 185–214. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.M.S.; Akbar, M.A.; Seadawy, A.R. New applications of the two variable G′/G,1/G)-expansion method for closed form traveling wave solutions of integro-differential equations. J. Ocean Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.M.S.; Akbar, M.A.; Wazwaz, A.M. Some applications of the (G′/G,1/G)-expansion method to find new exact solutions of NLEEs. Eur. Phys. J. Plus 2017, 132, 252. [Google Scholar] [CrossRef]
- Yokuş, A. Comparison of Caputo and conformable derivatives for time-fractional Korteweg–de Vries equation via the finite difference method. Int. J. Mod. Phys. B 2018, 32, 1850365. [Google Scholar] [CrossRef]
- Yokuş, A.; Kaya, D. Conservation laws and a new expansion method for sixth order Boussinesq equation. Proc. AIP Conf. Proc. 2015, 1676, 020062. [Google Scholar]
- Yang, X.; Yang, Y.; Cattani, C.; Zhu, C.M. A new technique for solving the 1-D Burgers equation. Therm. Sci. 2017, 21, 129–136. [Google Scholar] [CrossRef][Green Version]
- Vakhnenko, V.O.; Parkes, E.J.; Morrison, A.J. A Bäcklund transformation and the inverse scattering transform method for the generalised Vakhnenko equation. Chaos Solitons Fractals 2003, 17, 683–692. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Abu-AlShaeer, M.J.; Biswas, A.; Zhou, Q.; Moshokoa, S.; Belic, M. Optical solitons to Lakshmanan-Porsezian-Daniel model for three nonlinear forms. Optik 2018, 160, 197–202. [Google Scholar] [CrossRef]
- Biswas, A.; Triki, H.; Zhou, Q.; Moshokoa, S.P.; Ullah, M.Z.; Belic, M. Cubic–quartic optical solitons in Kerr and power law media. Optik 2017, 144, 357–362. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, Z.; Li, L. New exact solutions to the high dispersive cubic–quintic nonlinear Schrödinger equation. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2018, 382, 2506–2514. [Google Scholar] [CrossRef]
- Li, H.M.; Xu, Y.S.; Lin, J. New optical solitons in high-order dispersive cubic-quintic nonlinear Schrödinger equation. Commun. Theor. Phys. 2004, 41, 829. [Google Scholar]
- Nawaz, B.; Ali, K.; Abbas, S.O.; Rizvi, S.T.R.; Zhou, Q. Optical solitons for non-Kerr law nonlinear Schrödinger equation with third and fourth order dispersions. Chin. J. Phys. 2019, 60, 133–140. [Google Scholar] [CrossRef]
- Biswas, A.; Arshed, S. Application of semi-inverse variational principle to cubic-quartic optical solitons with kerr and power law nonlinearity. Optik 2018, 172, 847–850. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Kumar, D.; Chakrabarty, A.K. Dispersive optical soliton solutions for the hyperbolic and cubic-quintic nonlinear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur. Phys. J. Plus 2018, 133, 182. [Google Scholar] [CrossRef]
- El-Dessoky, M.M.; Islam, S. Chirped Solitons in Generalized Resonant Dispersive Nonlinear Schrödinger’s equation. Comput. Sci. 2019, 14, 737–752. [Google Scholar]
- Bansal, A.; Biswas, A.; Zhou, Q.; Babatin, M.M. Lie symmetry analysis for cubic–quartic nonlinear Schrödinger’s equation. Optik 2018, 169, 12–15. [Google Scholar] [CrossRef]
- Biswas, A.; Kara, A.H.; Ullah, M.Z.; Zhou, Q.; Triki, H.; Belic, M. Conservation laws for cubic–quartic optical solitons in Kerr and power law media. Optik 2017, 145, 650–654. [Google Scholar] [CrossRef]
- Younis, M.; Cheemaa, N.; Mahmood, S.A.; Rizvi, S.T.R. On optical solitons: The chiral nonlinear Schrödinger equation with perturbation and Bohm potential. Opt. Quantum Electron. 2016, 48, 542. [Google Scholar] [CrossRef]
- Hosseini, K.; Samadani, F.; Kumar, D.; Faridi, M. New optical solitons of cubic-quartic nonlinear Schrödinger equation. Optik 2018, 157, 1101–1105. [Google Scholar] [CrossRef]
- Conte, R.; Musette, M. Elliptic general analytic solutions. Stud. Appl. Math. 2009, 123, 63–81. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Ismael, H.F.; Husien, A.M.; Bulut, H.; Baskonus, H.M. Optical Soliton Solutions of the Cubic-Quartic Nonlinear Schrödinger and Resonant Nonlinear Schrödinger Equation with the Parabolic Law. Appl. Sci. 2020, 10, 219. https://doi.org/10.3390/app10010219
Gao W, Ismael HF, Husien AM, Bulut H, Baskonus HM. Optical Soliton Solutions of the Cubic-Quartic Nonlinear Schrödinger and Resonant Nonlinear Schrödinger Equation with the Parabolic Law. Applied Sciences. 2020; 10(1):219. https://doi.org/10.3390/app10010219
Chicago/Turabian StyleGao, Wei, Hajar Farhan Ismael, Ahmad M. Husien, Hasan Bulut, and Haci Mehmet Baskonus. 2020. "Optical Soliton Solutions of the Cubic-Quartic Nonlinear Schrödinger and Resonant Nonlinear Schrödinger Equation with the Parabolic Law" Applied Sciences 10, no. 1: 219. https://doi.org/10.3390/app10010219
APA StyleGao, W., Ismael, H. F., Husien, A. M., Bulut, H., & Baskonus, H. M. (2020). Optical Soliton Solutions of the Cubic-Quartic Nonlinear Schrödinger and Resonant Nonlinear Schrödinger Equation with the Parabolic Law. Applied Sciences, 10(1), 219. https://doi.org/10.3390/app10010219





