High-Frequency Fatigue Testing of Recycled Aggregate Concrete
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Aggregates
2.2. Cement
2.3. Mix Proportions
2.4. Mechanical Properties
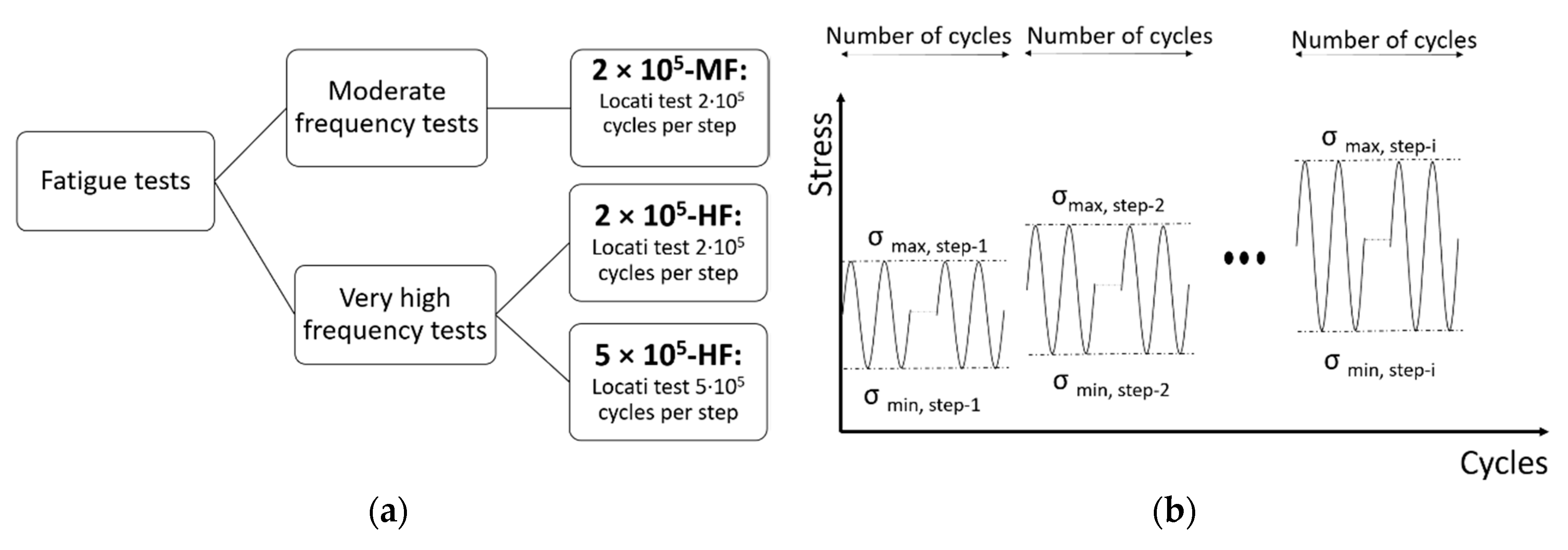
2.5. Fatigue Tests
3. Results and Discussions
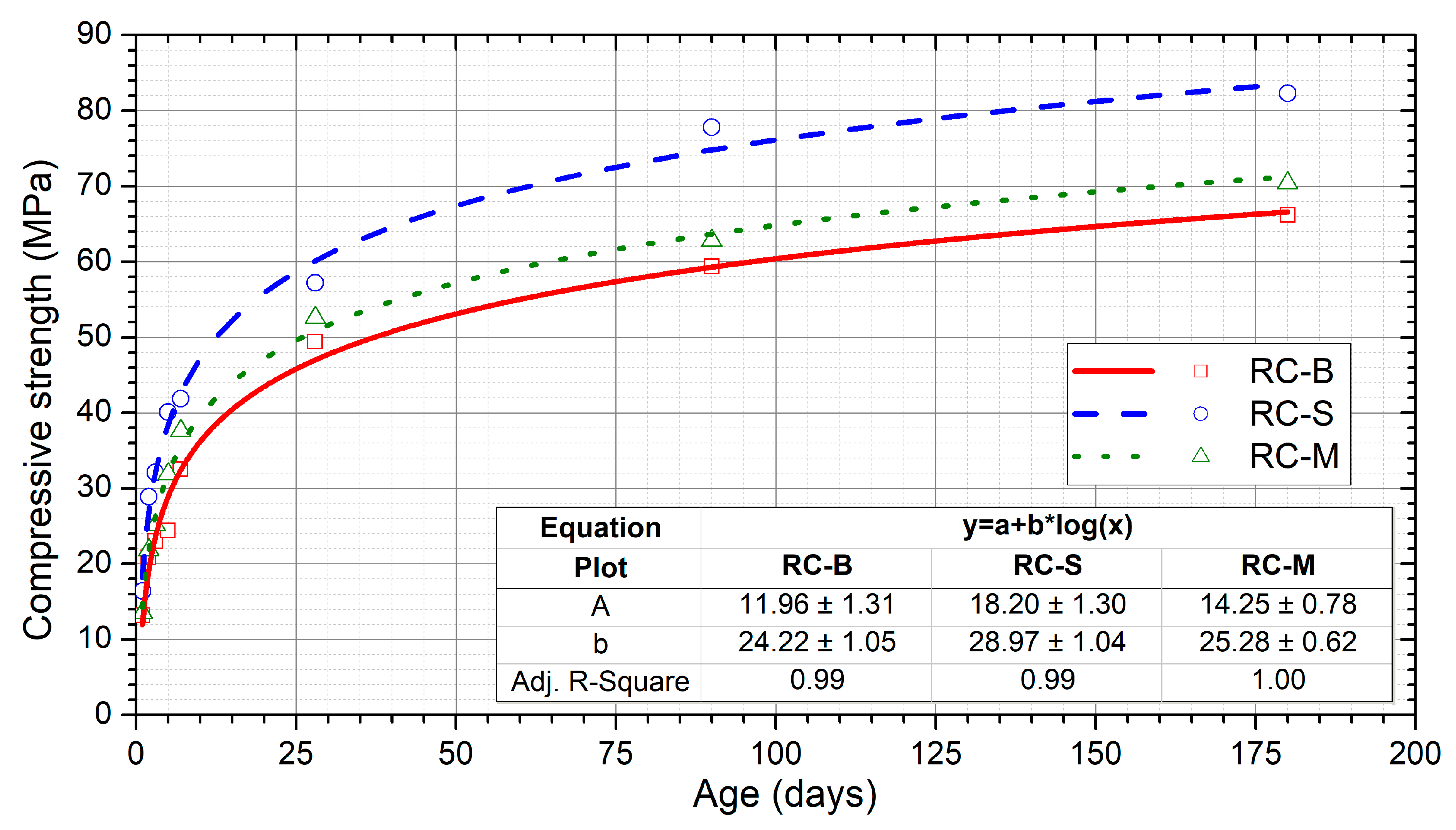
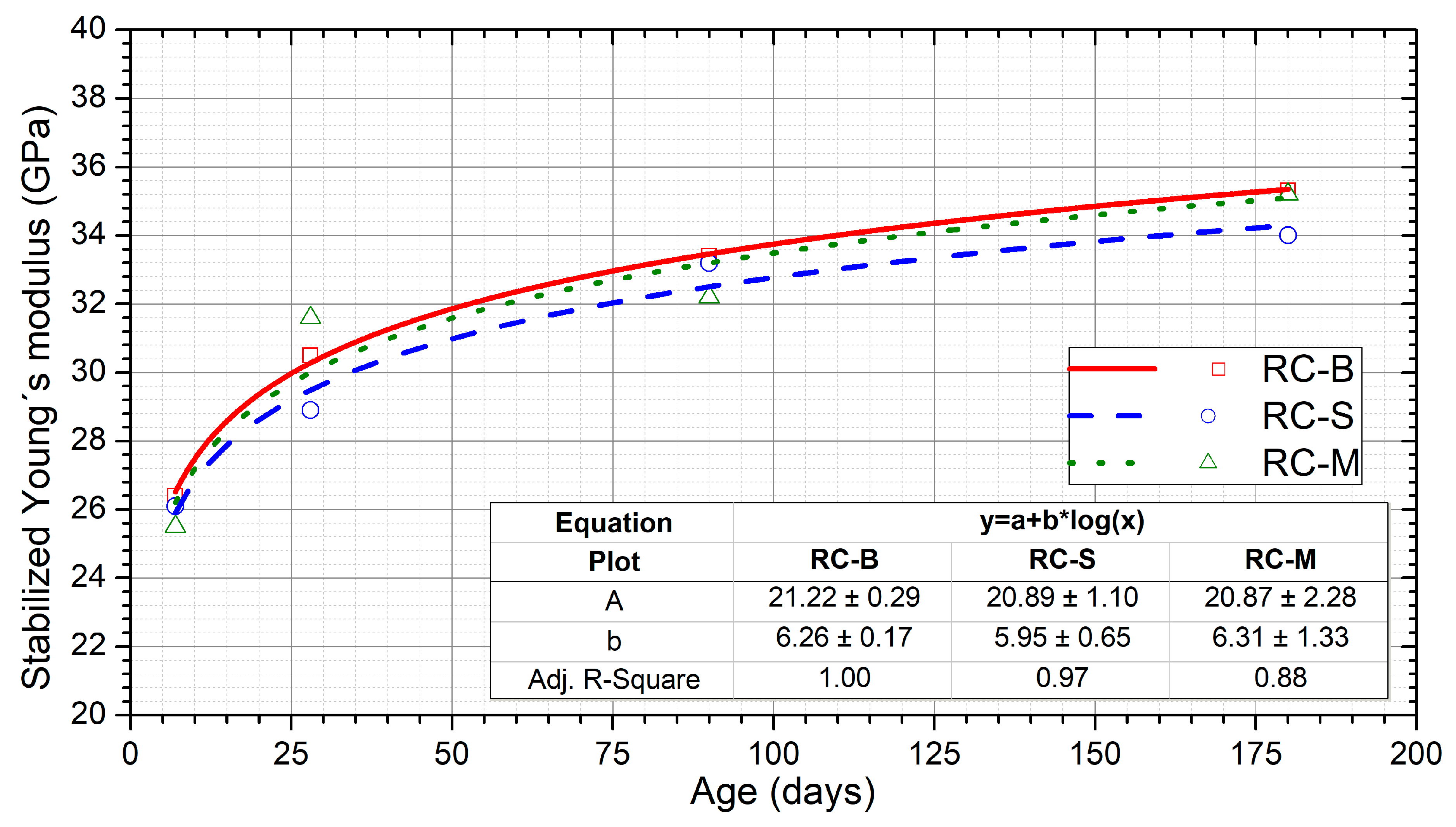
3.1. Compressive Strength and Young’s Modulus
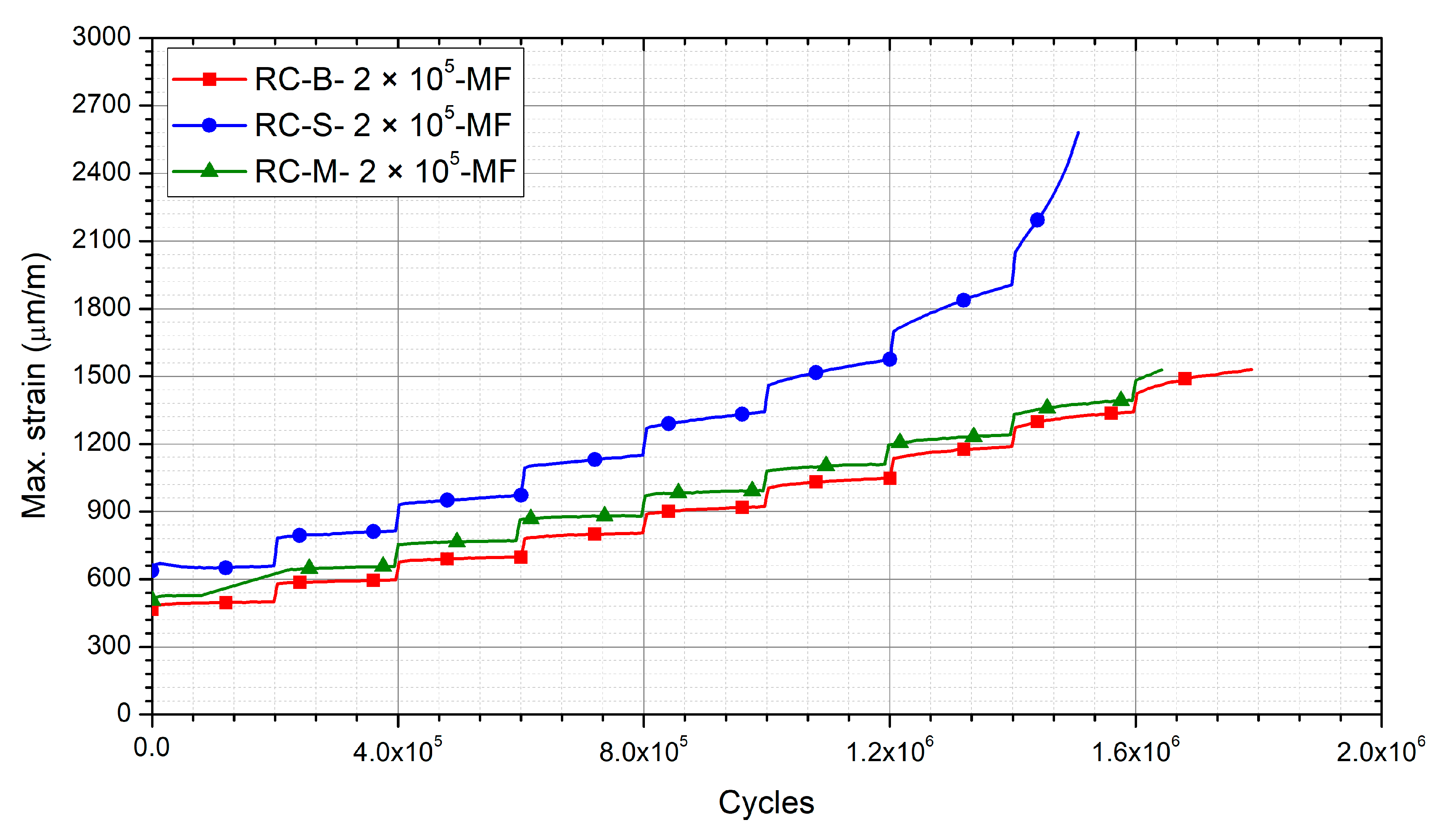
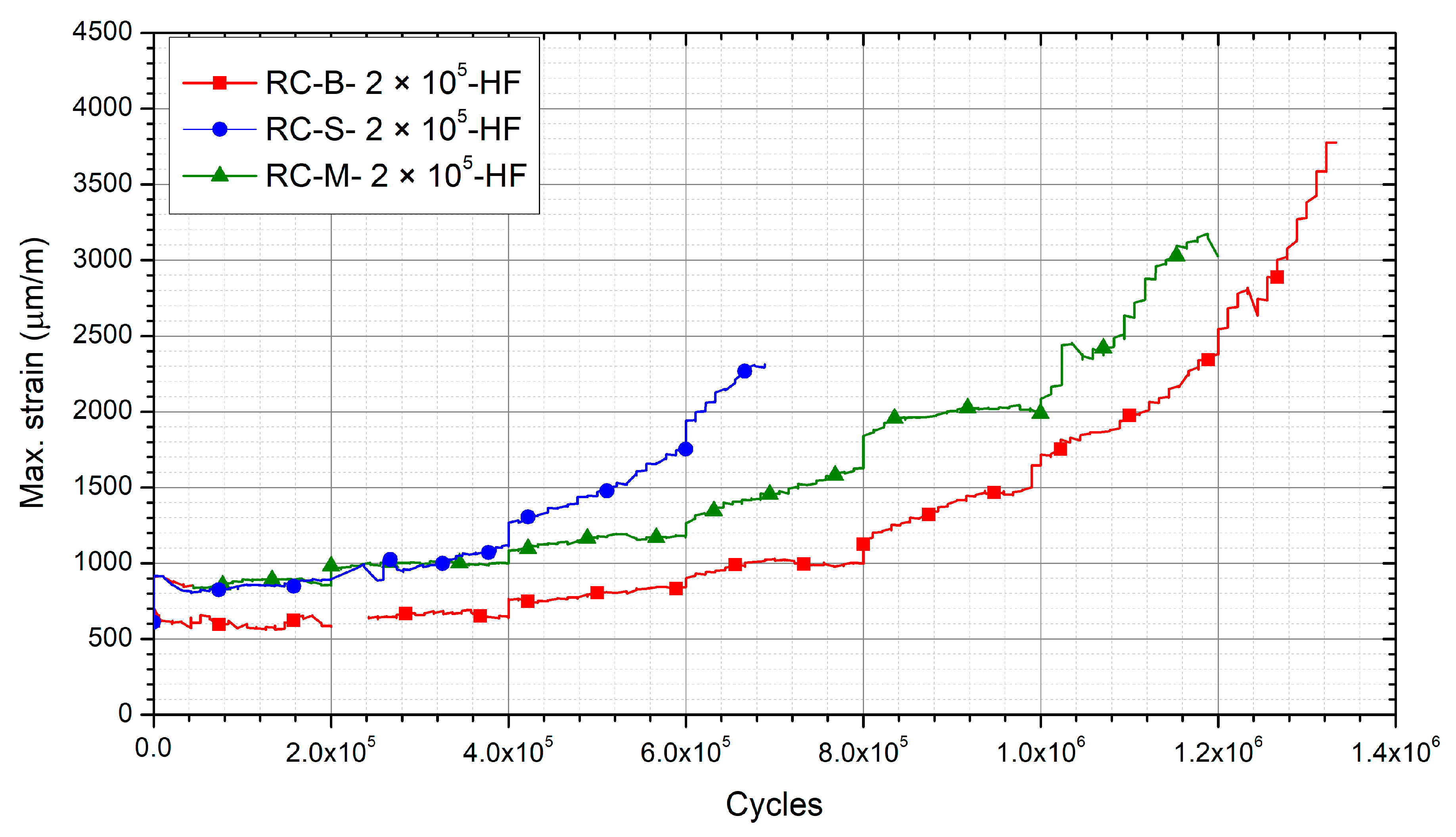
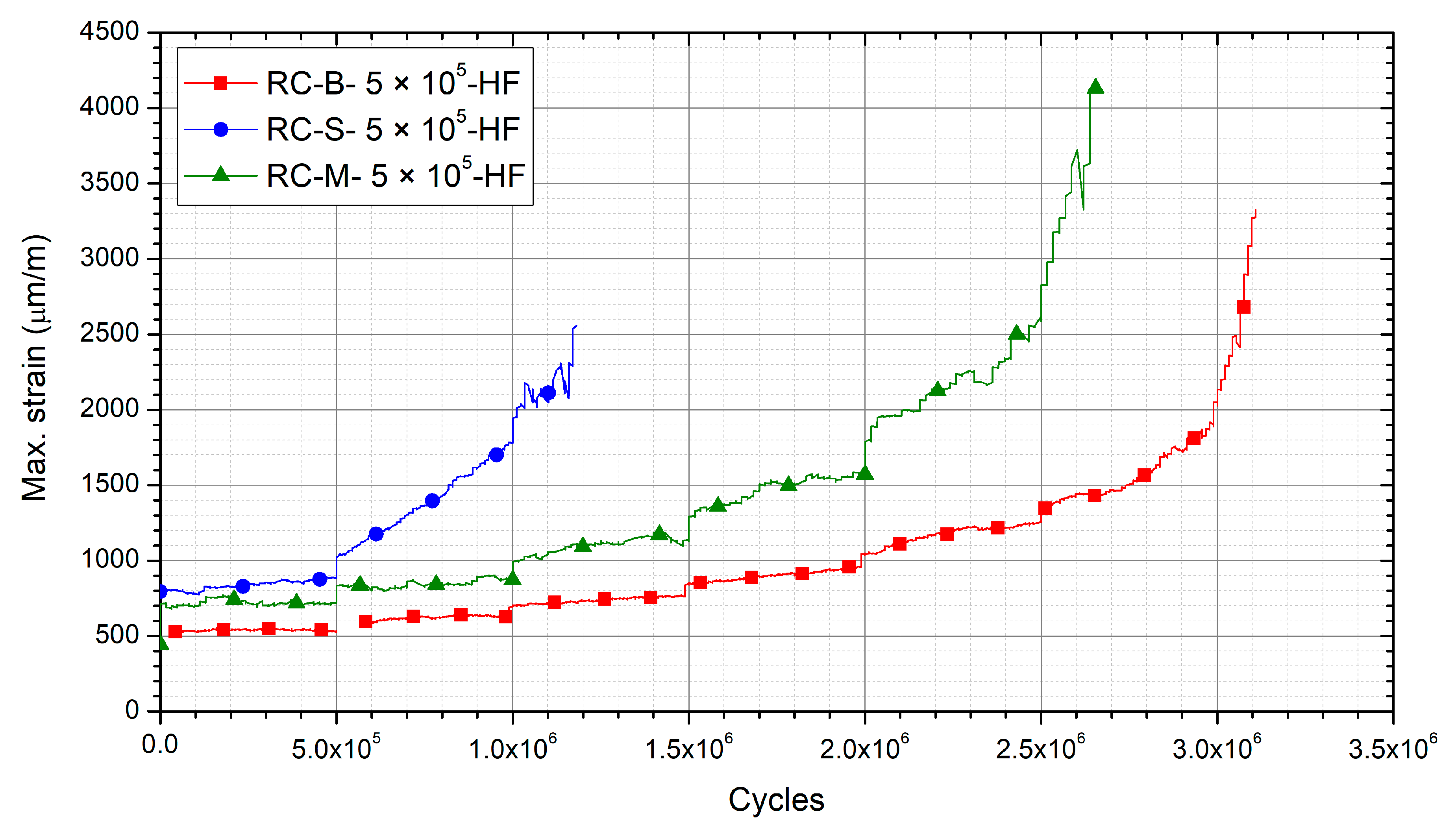
3.2. Influence of the Frequency on Fatigue
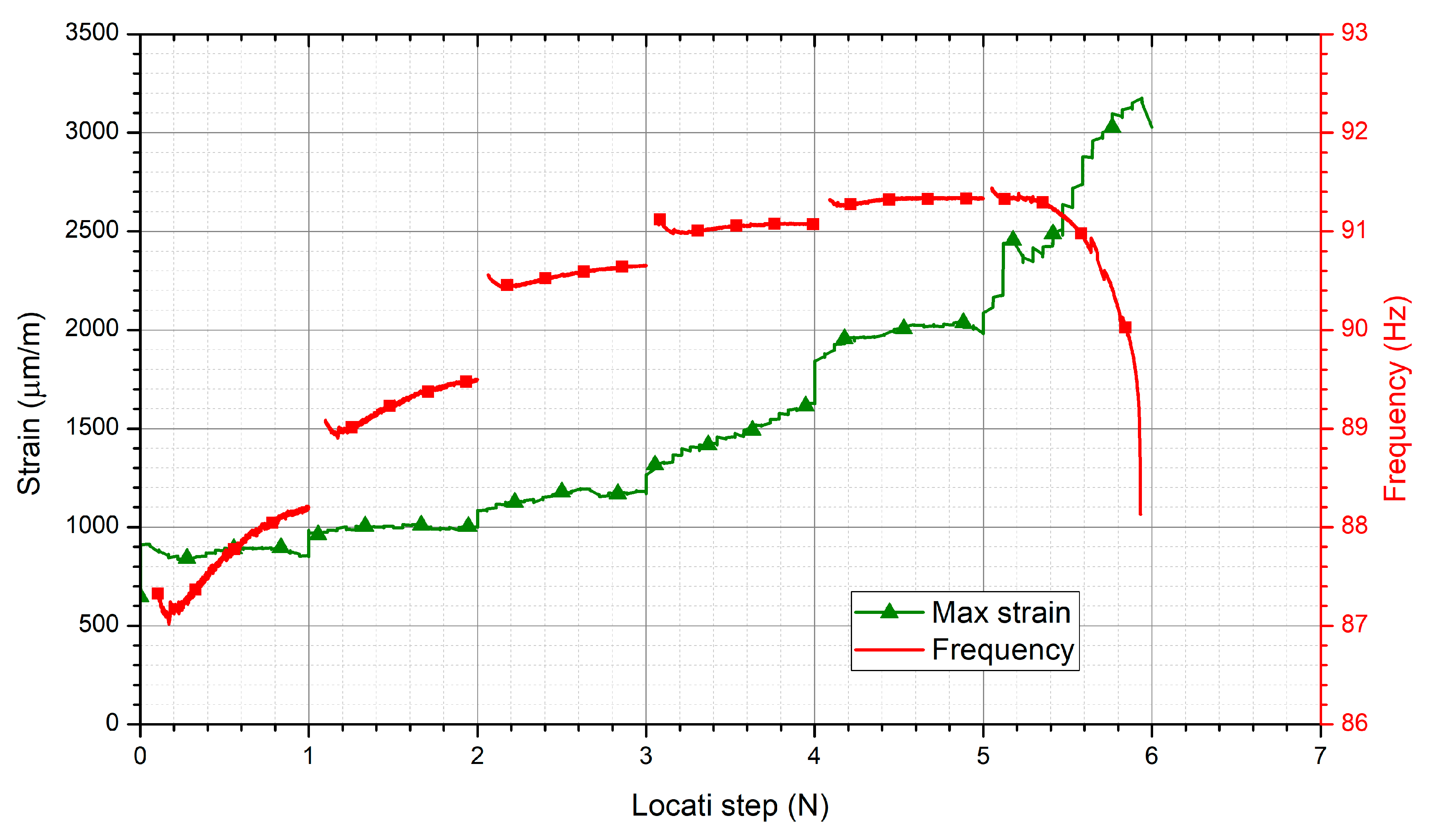
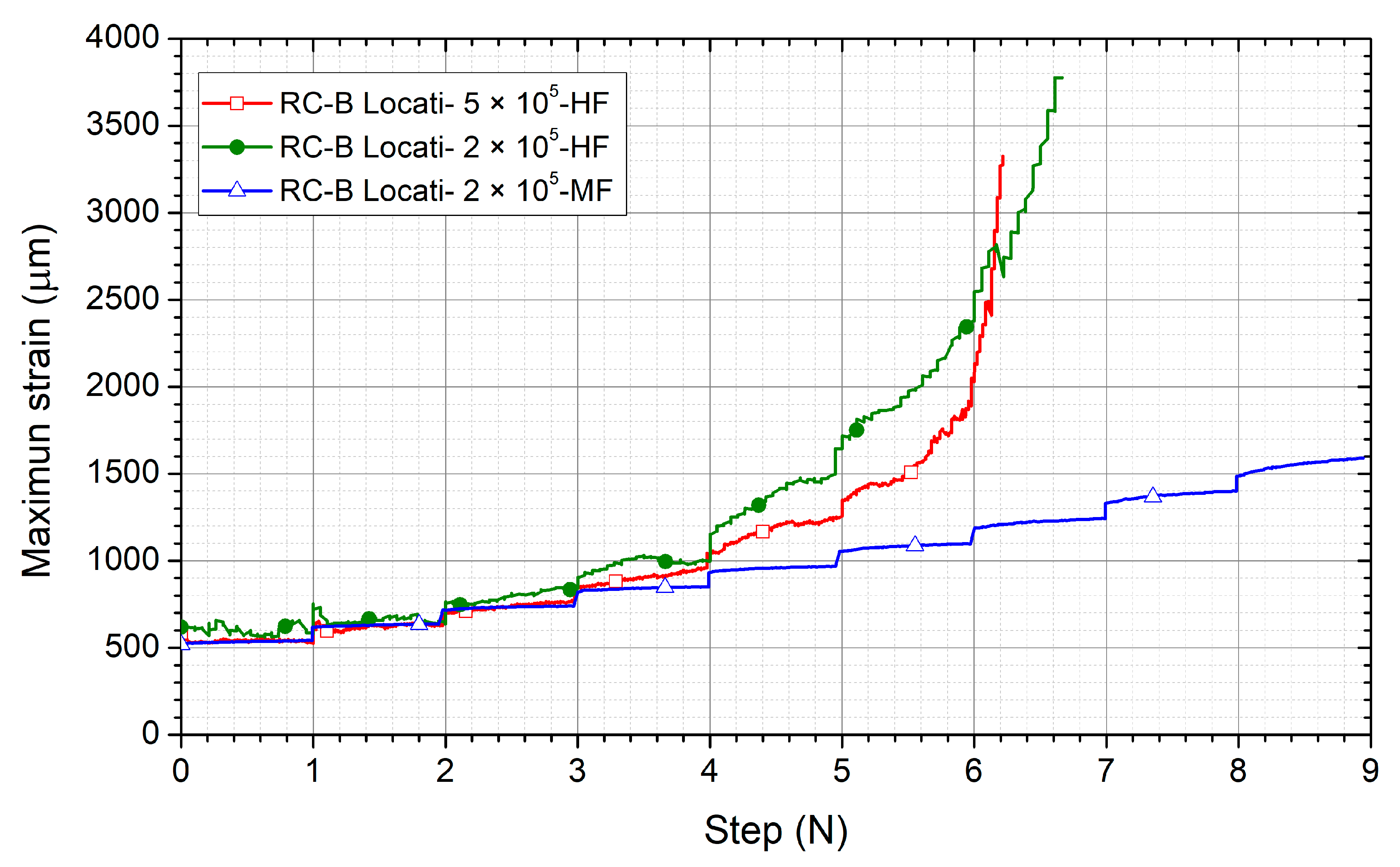
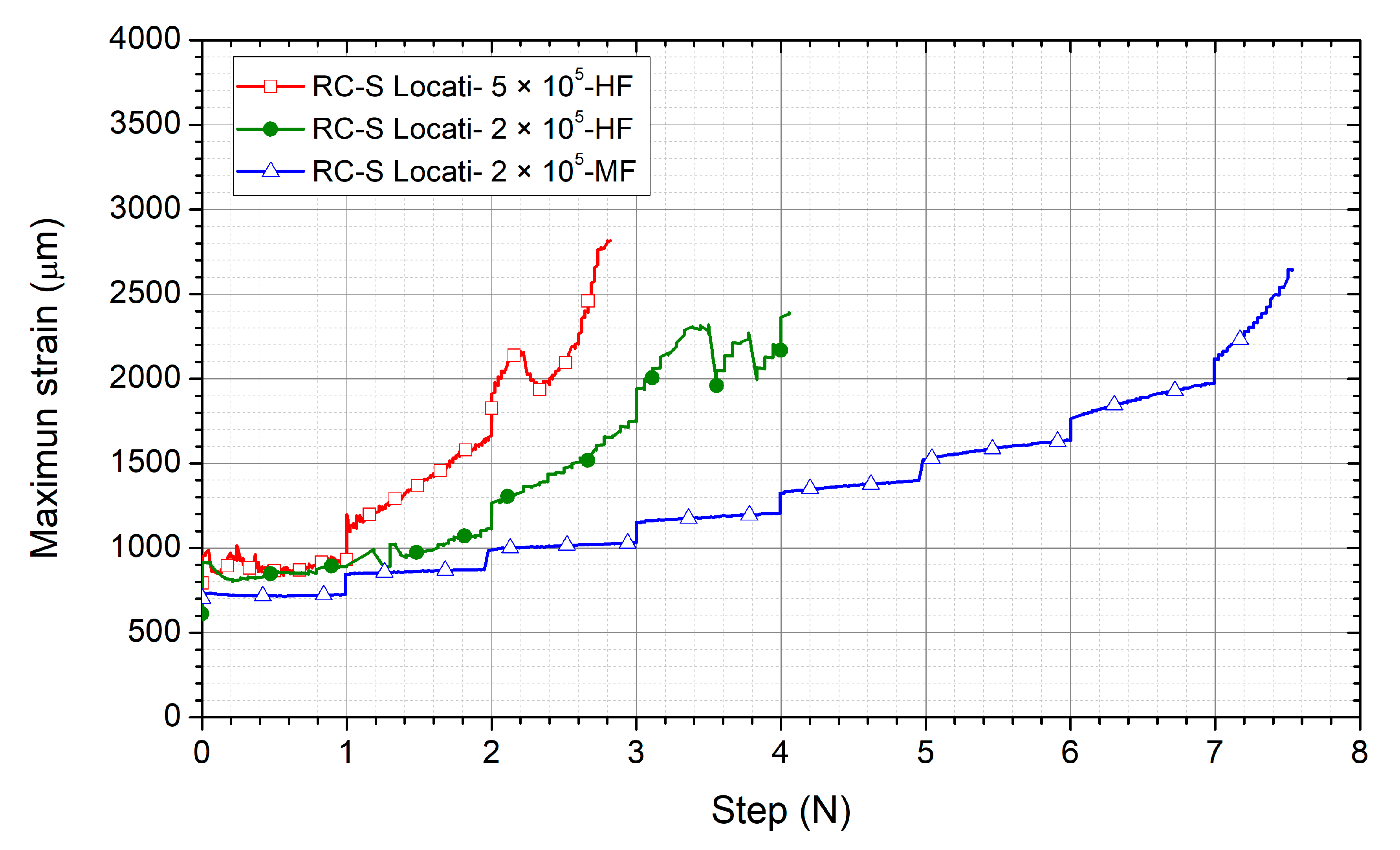
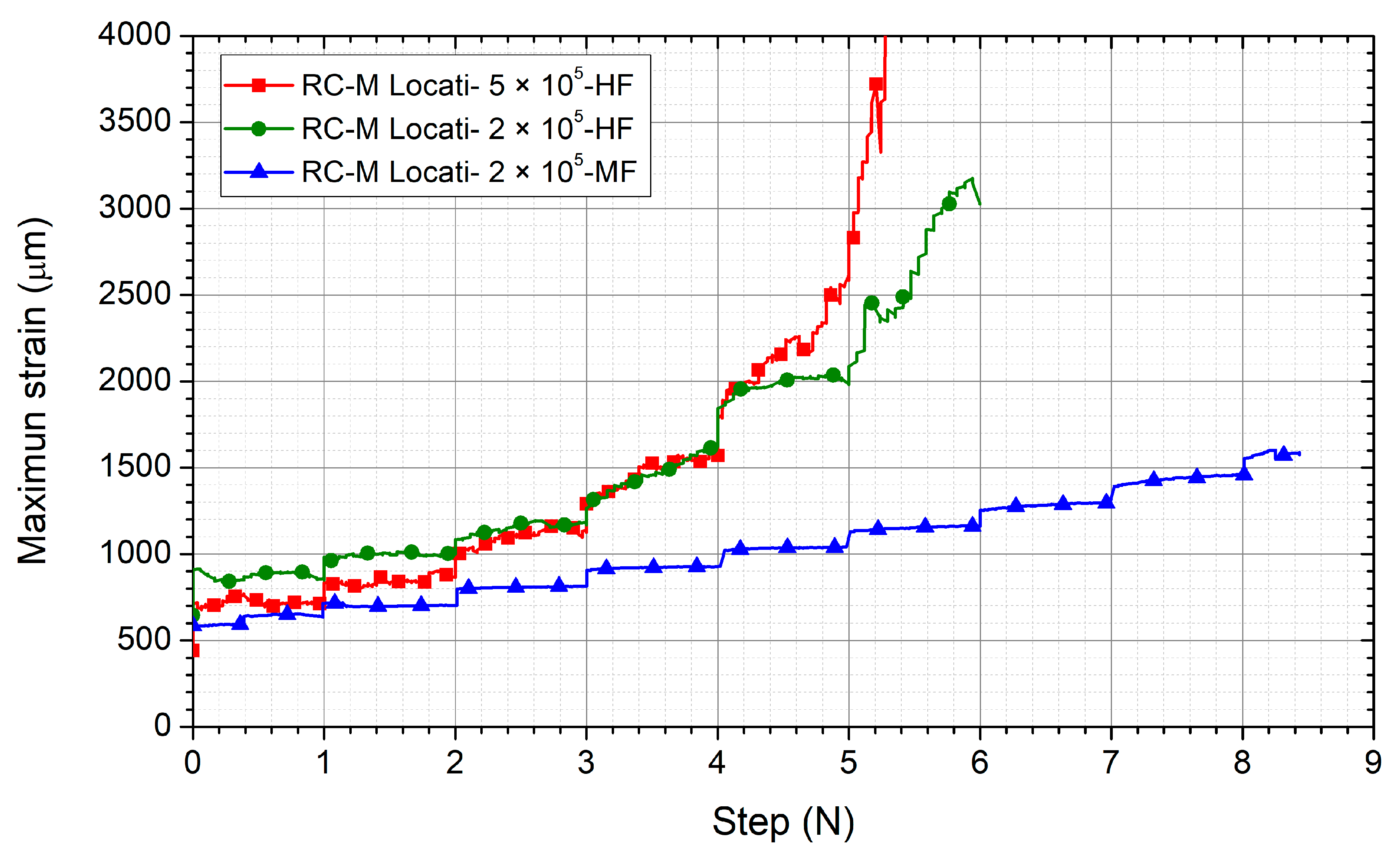
3.3. Influence of the Number of Cycles Per Step during a Locati Test
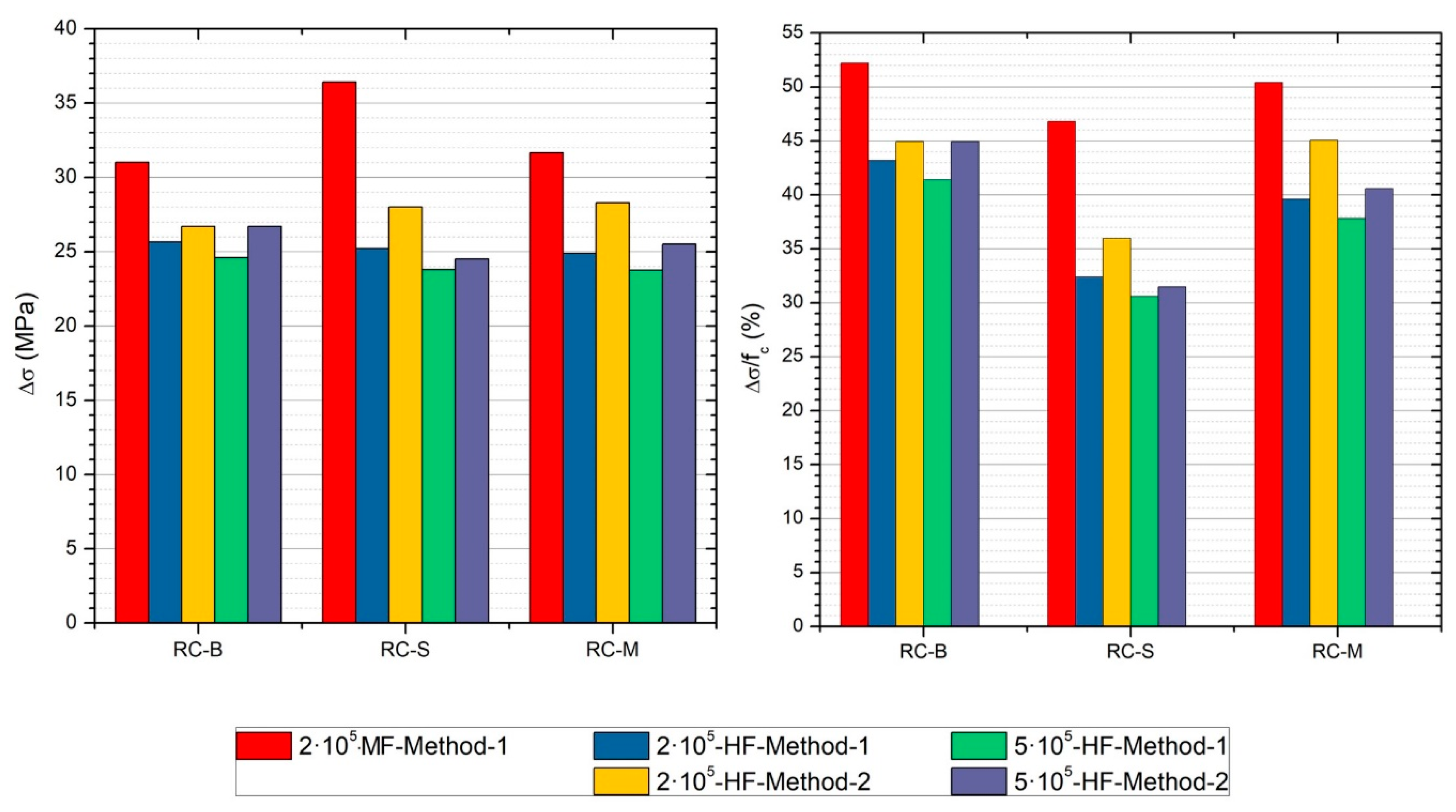
3.4. Comparison of the Different Methodologies
4. Conclusions
- In all cases, the material with the lowest fatigue limit/compression resistance ratio was RC-S, which was due to the weakness introduced by the mortar adhered to the aggregates.
- The Locati method was validated as a method to determine the fatigue limit, showing that 2 × 105 cycles per step was enough to determine the fatigue limit.
- It was found that the resonance frequency of the system was a parameter that could enable the identification of sensitive variations in the stiffness of the whole, and a symptom that the specimen was close to breaking. For this reason, the stress range of the step prior to the step in which a drop in the resonance frequency of the system occurs was defined as the criterion for determining the fatigue limit by means of the Locati tests.
- It is proposed that during very high frequency tests there is an increase in temperature that may reduce the fatigue life of the concrete. This study opens the door to the analysis of this hypothesis, which may explain why an increase in frequency reduces the fatigue life of the elements.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alnahhal, M.F.; Alengaram, U.J.; Jumaat, M.Z.; Abutaha, F.; Alqedra, M.A.; Nayaka, R.R. Assessment on engineering properties and CO2 emissions of recycled aggregate concrete incorporating waste products as supplements to Portland cement. J. Clean. Prod. 2018, 203, 822–835. [Google Scholar] [CrossRef]
- Meyer, C. The greening of the concrete industry. Cem. Concr. Compos. 2009, 31, 601–605. [Google Scholar] [CrossRef]
- Poon, C.-S.; Chan, D. The use of recycled aggregate in concrete in Hong Kong, Resour. Conserv. Recycl. 2007, 50, 293–305. [Google Scholar] [CrossRef]
- De Brito, J.; Ferreira, J.; Pacheco, J.; Soares, D.; Guerreiro, M. Structural, material, mechanical and durability properties and behaviour of recycled aggregates concrete. J. Build. Eng. 2016, 6, 1–16. [Google Scholar] [CrossRef]
- Thomas, C.; Setién, J.; Polanco, J.A.J.; Alaejos, P.; de Juan, M.S.; de Juan, M.S. Durability of recycled aggregate concrete. Constr. Build. Mater. 2013, 40, 1054–1065. [Google Scholar] [CrossRef]
- De Schutter, G.; Audenaert, K. Report 38: Durability of Self-Compacting Concrete-State-of-the-Art Report of RILEM Technical Committee 205-DSC; RILEM Publications: Paris, France, 2007. [Google Scholar]
- Kou, S.C.C.; Poon, C.S.S. Properties of self-compacting concrete prepared with coarse and fine recycled concrete aggregates. Cem. Concr. Compos. 2009, 31, 622–627. [Google Scholar] [CrossRef]
- Kareem, A.I.; Nikraz, H.; Asadi, H. Performance of hot-mix asphalt produced with double coated recycled concrete aggregates. Constr. Build. Mater. 2019, 205, 425–433. [Google Scholar] [CrossRef]
- Sainz-Aja, J.A.; Pombo, J.; Tholken, D.; Carrascal, I.; Polanco, J.; Ferreno, D.; Casado, J.; Diego, S.; Pérez, A.; Filho, J.A.; et al. Dynamic Calibration of Slab Track Models for Railway Applications using Full-Scale Testing. Comput. Struct. 2020, 228, 106180. [Google Scholar] [CrossRef]
- Alliche, A. Damage model for fatigue loading of concrete. Int. J. Fatigue 2004, 26, 915–921. [Google Scholar] [CrossRef]
- Xiao, J.; Li, H.; Yang, Z. Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Constr. Build. Mater. 2013, 38, 681–688. [Google Scholar] [CrossRef]
- Skarżyński, Ł.; Marzec, I.; Tejchman, J. Fracture evolution in concrete compressive fatigue experiments based on X-ray micro-CT images. Int. J. Fatigue 2019, 122, 256–272. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Wagner, P.; Fröhlich, D.; Weinberg, K. Dynamic fracture investigations of ultra-high performance concrete by spalling tests. Eng. Struct. 2019, 201, 109844. [Google Scholar] [CrossRef]
- Li, Q.; Huang, B.; Xu, S.; Zhou, B.; Yu, R.C. Compressive fatigue damage and failure mechanism of fiber reinforced cementitious material with high ductility. Cem. Concr. Res. 2016, 90, 174–183. [Google Scholar] [CrossRef]
- Thomas, C.; Setién, J.; Polanco, J.A.A.; Lombillo, I.; Cimentada, A. Fatigue limit of recycled aggregate concrete. Constr. Build. Mater. 2014, 52, 146–154. [Google Scholar] [CrossRef] [Green Version]
- Thomas, C.; Sosa, I.; Setién, J.; Polanco, J.A.; Cimentada, A.I. Evaluation of the fatigue behavior of recycled aggregate concrete. J. Clean. Prod. 2014, 65, 397–405. [Google Scholar] [CrossRef]
- Vicente, M.A.; Mínguez, J.; González, D.C. Computed tomography scanning of the internal microstructure, crack mechanisms, and structural behavior of fiber-reinforced concrete under static and cyclic bending tests. Int. J. Fatigue 2019, 121, 9–19. [Google Scholar] [CrossRef]
- Thomas, C.; de Brito, J.; Gil, V.; Sainz-Aja, J.A.; Cimentada, A. Multiple recycled aggregate properties analysed by X-ray microtomography. Constr. Build. Mater. 2018, 166, 171–180. [Google Scholar] [CrossRef] [Green Version]
- Thomas, C.; de Brito, J.; Cimentada, A.; Sainz-Aja, J.A. Macro-and micro-properties of multi-recycled aggregate concrete. J. Clean. Prod. 2019, 118843. [Google Scholar] [CrossRef]
- Sainz-Aja, J.A.; Carrascal, I.A.; Polanco, J.; Sosa, I.; Thomas, C. Análisis del comportamiento a fatiga de morteros con áridos reciclados provenientes de vía de ferrocarril. In Proceedings of the REHABEND 2018, Caceres, Spain, 15–18 May 2018; pp. 1313–1322. [Google Scholar]
- Sainz-Aja, J.; Carrascal, I.; Polanco, J.A.; Thomas, C. Fatigue failure micromechanisms in ed aggregate mortar by μCT analysis. J. Build. Eng. 2019, 101027. [Google Scholar] [CrossRef]
- Carloni, C.; Subramaniam, K.V. Investigation of sub-critical fatigue crack growth in FRP/concrete cohesive interface using digital image analysis. Compos. Part B Eng. 2013, 51, 35–43. [Google Scholar] [CrossRef]
- Rep, C.; Hanson, J.M.; Ballinger, C.A.; Linger, D. Considerations for Design of Concrete Structures Subjected to Fatigue Loading. J Am. Concr. Inst. 1974, 71, 97–121. [Google Scholar]
- European Concrete Committee, Ceb Committee GTG 15. Fatigue of Concrete Structures; CEB Bulletin d’information, No 188; CEB-FIP: Lausanne, Switzerland, 1988. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A. Proposal for the fatigue strength of concrete under cycles of compression. Constr. Build. Mater. 2016, 107, 138–156. [Google Scholar] [CrossRef]
- Balázs, G.L. Fatigue of bond. ACI Mater. J. 1991, 88, 620–629. [Google Scholar]
- Vicente, M.A.; Ruiz, G.; González, D.C.; Mínguez, J.; Tarifa, M.; Zhang, X. CT-Scan study of crack patterns of fiber-reinforced concrete loaded monotonically and under low-cycle fatigue. Int. J. Fatigue 2018, 114, 138–147. [Google Scholar] [CrossRef]
- Yoris, A.; Thomas, C.; Medina, C.; Polanco, J.A.; de Rojas, M.I.S.; Frias, M.; Cantero, B. Comportamiento a fatiga resonante en compresión de hormigones reciclados para uso estructural. In Proceedings of the 7th Euro-American Congress on Construction Pathology, Rehabilitation Technology and Heritage Management, REHABEND 2018, Caceres, Spain, 15–18 May 2018; pp. 1460–1467. [Google Scholar]
- Medeiros, A.; Zhang, X.; Ruiz, G.; Yu, R.C.; Velasco, M.d.L. Effect of the loading frequency on the compressive fatigue behavior of plain and fiber reinforced concrete. Int. J. Fatigue 2015, 70, 342–350. [Google Scholar] [CrossRef]
- Murdock, J.W. A Critical Review of Research on Fatigue of Plain Concrete; University of Illinois at Urbana Champaign, College of Engineering: Urbana, IL, USA, 1965. [Google Scholar]
- EN 197-1, Cement Part 1: Composition, Specifications and Conformity Criteria for Common Cements, Br. Stand. 2011. Available online: https://doi.org/10.1103/PhysRevLett.64.88 (accessed on 18 December 2019).
- Alfa, C. Ficha técnica EN 197-1 CEM IV/B (V) 32,5 N. in press.
- Test Methods of Cements. Physical Analysis. Actual Density Determination, U.N.E. 80103:2013. 2013. Available online: https://infostore.saiglobal.com/en-us/Standards/UNE-80103-2013-22841_SAIG_AENOR_AENOR_50269/ (accessed on 18 December 2019).
- Methods of Testing Cement—Part 6: Determination of Fineness, E.N. 196-6:2010. 2010. Available online: https://webstore.ansi.org/standards/din/dinen1962010 (accessed on 18 December 2019).
- Sainz-Aja, J.; Carrascal, I.; Polanco, J.A.; Thomas, C.; Sosa, I.; Casado, J.; Diego, S. Self-compacting recycled aggregate concrete using out-of-service railway superstructure wastes. J. Clean. Prod. 2019, 4, 386. [Google Scholar] [CrossRef]
- Testing Hardened Concrete—Part 3: Compressive Strength of Test Specimens, U.-E. 12390-3:2009. 2009. Available online: https://www.scirp.org/(S(vtj3fa45qm1ean45vvffcz55))/reference/ReferencesPapers.aspx?ReferenceID=1884402 (accessed on 18 December 2019).
- Testing Hardened Concrete—Part 3: Compressive Strength of Test Specimens, E.N. 12390-3:2099/AC:2011. 2011.
- Testing Hardened Concrete—Part 13: Determination of Secant Modulus of Elasticity in Compression, E.N. 12390-13:2013. 2014. Available online: http://78.100.132.106/External%20Documents/Intenational%20Specifications/British%20Standards/BS%20EN/BS%20EN%2012390-13-2013.pdf (accessed on 18 December 2019).
- Locati, L. La Fatica dei Materiali Metallici; Ulrico Hoepli: Milan, Italy, 1950. [Google Scholar]
- Locati, L. Programmed fatigue test, variable amplitude rotat. Metall. Ital. 1952, 44, 135–144. [Google Scholar]
- García, C.T. Hormigón Reciclado de Aplicación Estructural; Universidad de Cantabria: Santander, Spain, 2012. [Google Scholar]
- Thomas, C.; Carrascal, I.; Setién, J.; Polanco, J.A. Determinación del límite a fatiga en hormigones reciclados de aplicación estructural—Determining the fatigue limit recycled concrete structural application. An. Mec. Fract. 2009, 1, 283–289. (In Spanish) [Google Scholar]
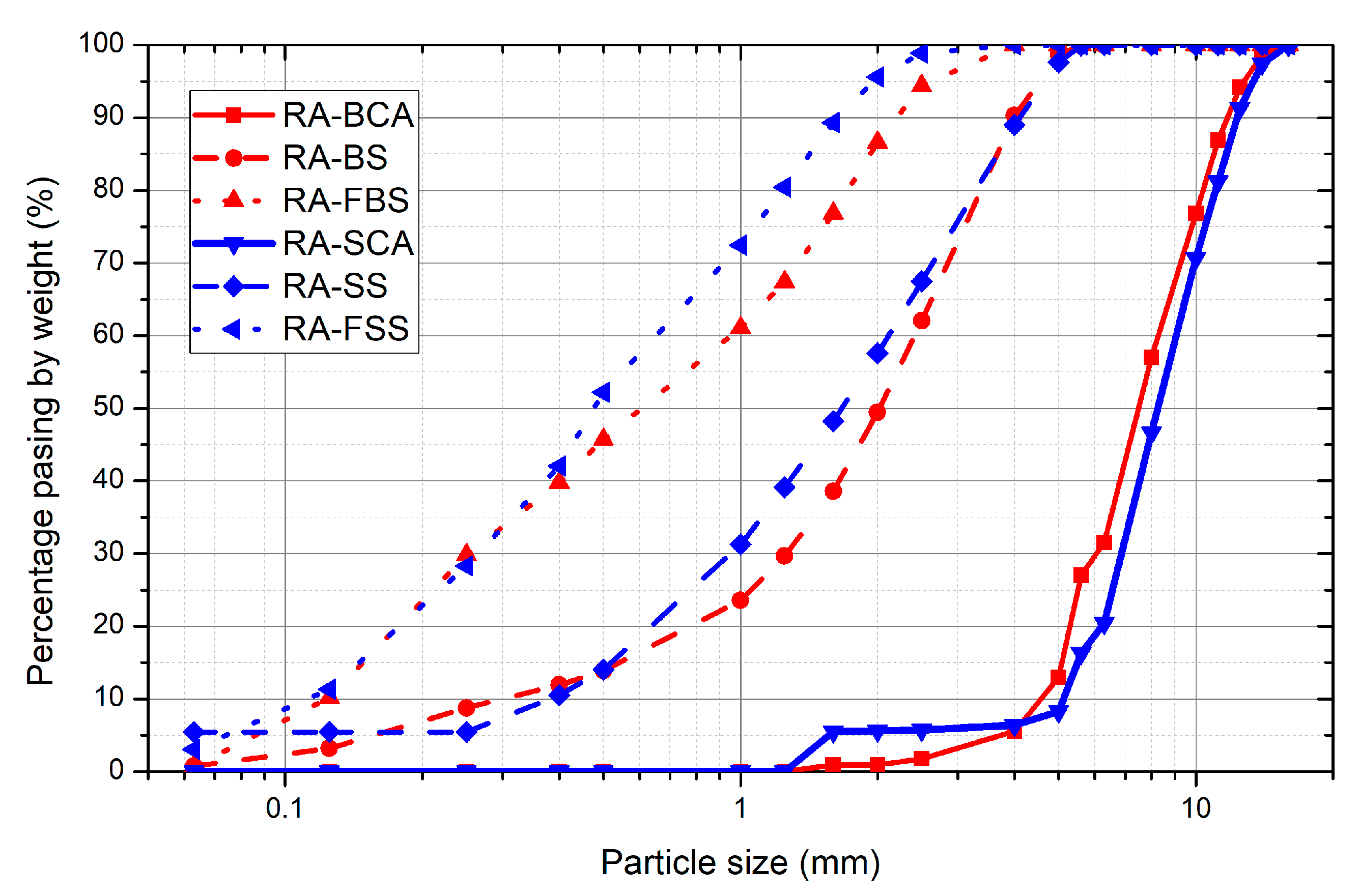

| Code | Description | Min.–Max. Size (mm) | Density (g/cm3) |
|---|---|---|---|
| RA-B-CA | Ballast coarse aggregates | 5–12 | 2.5 |
| RA-S-CA | Sleeper coarse aggregate | 5–12 | 2.3 |
| RA-B-LS | Ballast coarse sand | 2–5 | 2.7 |
| RA-S-LS | Sleeper coarse sand | 2–5 | 2.4 |
| RA-B-FS | Ballast fine sand | 0–2 | 2.8 |
| RA-S-FS | Sleeper fine sand | 0–2 | 2.5 |
| Composition (wt.%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| CaO | SiO2 | Al2O3 | Fe2O3 | MgO | K2O | SO3 | Ignition Loss | |
| CEM IV | 35.5 | 41.2 | 13.3 | 4.4 | 1.2 | 1.4 | 1.3 | 1.7 |
| Material | RC-B | RC-S | RC-M |
|---|---|---|---|
| Water | 225 | 200 | 221 |
| Cement | 500 | 500 | 500 |
| Superplasticizer additive | 10 | 10 | 10 |
| RA-FBS | 790 | - | 677 |
| RA-BS | 320 | - | 274 |
| RA-BCA | 522 | - | 447 |
| RA-FSS | - | 690 | 98 |
| RA-SS | - | 283 | 40 |
| RA-SCA | - | 587 | 83 |
| Water/cement ratio | 0.45 | 0.40 | 0.44 |
| % sand (0–2 mm) from the total sand | 70 | 70 | 70 |
| % coarse aggregate from the total aggregates | 35 | 40 | 36 |
| % superplasticizer additive/cement | 2.00 | 2.00 | 2.00 |
| N | k | RC-B | RC-S | RC-M | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σmax (MPa) | σmin (MPa) | Range (MPa) | σmax (MPa) | σmin (MPa) | Range (MPa) | σmax (MPa) | σmin (MPa) | Range (MPa) | ||
| 1 | 0.30 | 17.8 | 1.8 | 16.0 | 23.3 | 2.3 | 21.0 | 18.9 | 1.9 | 17.0 |
| 2 | 0.35 | 20.8 | 2.1 | 18.7 | 27.2 | 2.7 | 24.5 | 22.0 | 2.2 | 19.8 |
| 3 | 0.40 | 23.8 | 2.4 | 21.4 | 31.1 | 3.1 | 28.0 | 25.1 | 2.5 | 22.6 |
| 4 | 0.45 | 26.7 | 2.7 | 24.0 | 35.0 | 3.5 | 31.5 | 28.3 | 2.8 | 25.5 |
| 5 | 0.50 | 29.7 | 3.0 | 26.7 | 38.9 | 3.9 | 35.0 | 31.4 | 3.1 | 28.3 |
| 6 | 0.55 | 32.7 | 3.3 | 29.4 | 42.8 | 4.3 | 38.5 | 34.6 | 3.5 | 31.1 |
| 7 | 0.60 | 35.7 | 3.6 | 32.1 | 46.7 | 4.7 | 42.0 | 37.7 | 3.8 | 33.9 |
| 8 | 0.65 | 38.6 | 3.9 | 34.7 | 50.6 | 5.1 | 45.5 | 40.8 | 4.1 | 36.7 |
| 9 | 0.70 | 41.6 | 4.2 | 37.4 | 54.5 | 5.4 | 49.1 | 44.0 | 4.4 | 39.6 |
| Material | Δσmax | fL | IC |
|---|---|---|---|
| (MPa) | (MPa) | (%) | |
| RC-B | 38.75 | 31.0 | 52.2 |
| RC-S | 45.5 | 36.4 | 46.8 |
| RC-M | 39.6 | 31.7 | 50.4 |
| Material | Method-1 | Method-2 | |||
|---|---|---|---|---|---|
| Δσmax | fL | IC | fL | IC | |
| (MPa) | (MPa] | (%) | (MPa) | (%) | |
| RC-B | 32.09 | 25.67 | 43.19 | 26.74 | 44.93 |
| RC-S | 31.51 | 25.21 | 32.40 | 28.01 | 35.99 |
| RC-M | 31.10 | 24.88 | 39.60 | 28.27 | 45.04 |
| Material | Method-1 | Method-2 | |||
|---|---|---|---|---|---|
| Δσmax | fL | fL/fc | fL | fL/fc | |
| (MPa) | (MPa) | (%) | (MPa) | (%) | |
| RC-B | 32.09 | 24.6 | 41.39 | 26.74 | 44.93 |
| RC-S | 29.76 | 23.81 | 30.60 | 24.51 | 31.49 |
| RC-M | 29.685 | 23.75 | 37.80 | 25.45 | 40.59 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sainz-Aja, J.; Thomas, C.; Polanco, J.A.; Carrascal, I. High-Frequency Fatigue Testing of Recycled Aggregate Concrete. Appl. Sci. 2020, 10, 10. https://doi.org/10.3390/app10010010
Sainz-Aja J, Thomas C, Polanco JA, Carrascal I. High-Frequency Fatigue Testing of Recycled Aggregate Concrete. Applied Sciences. 2020; 10(1):10. https://doi.org/10.3390/app10010010
Chicago/Turabian StyleSainz-Aja, Jose, Carlos Thomas, Juan A. Polanco, and Isidro Carrascal. 2020. "High-Frequency Fatigue Testing of Recycled Aggregate Concrete" Applied Sciences 10, no. 1: 10. https://doi.org/10.3390/app10010010
APA StyleSainz-Aja, J., Thomas, C., Polanco, J. A., & Carrascal, I. (2020). High-Frequency Fatigue Testing of Recycled Aggregate Concrete. Applied Sciences, 10(1), 10. https://doi.org/10.3390/app10010010







