Effect of Track Irregularities on the Response of Two-Way Railway Tracks
Abstract
1. Introduction
2. Train-Track-Soil Interaction Model
2.1. Train Model
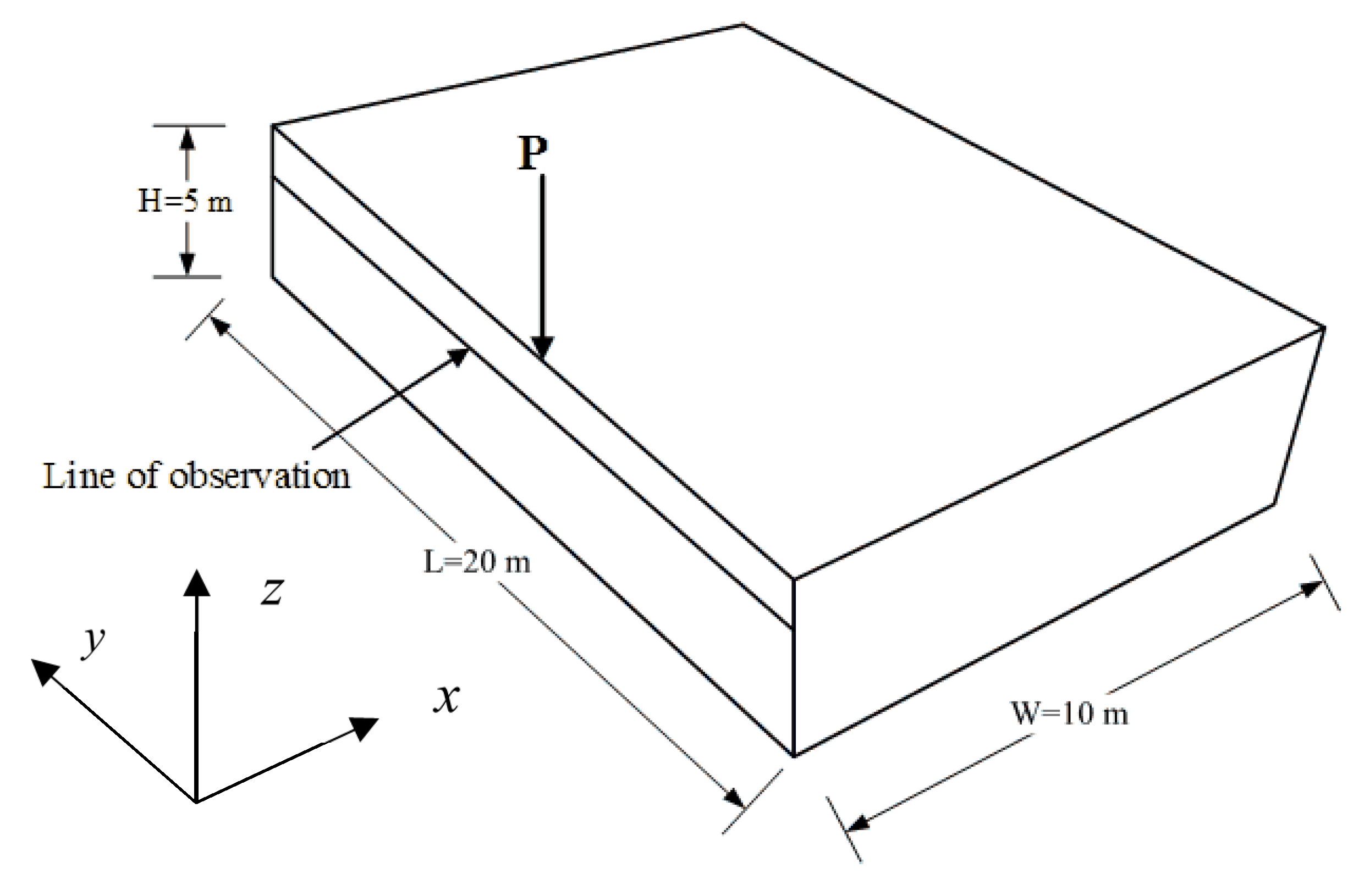
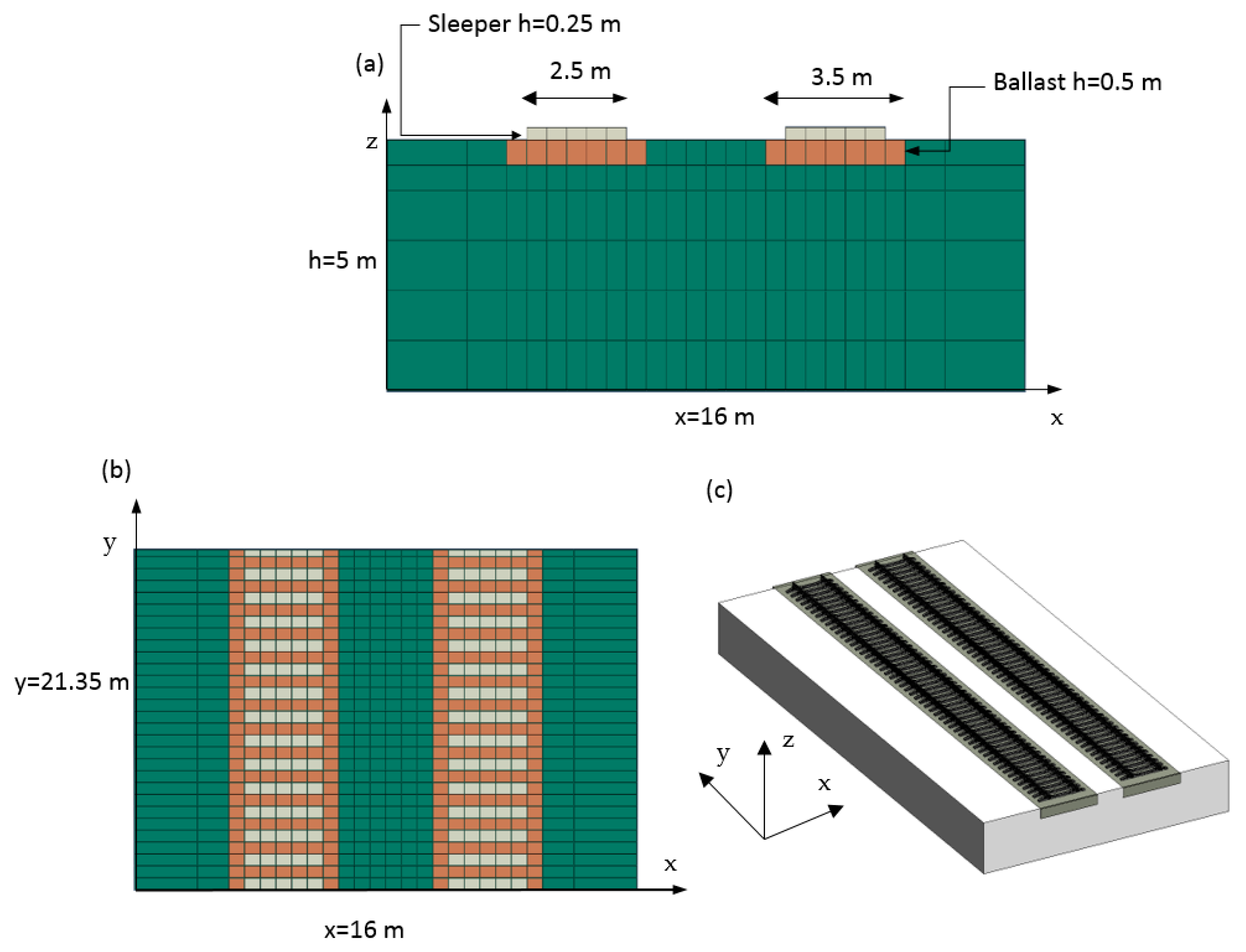
2.2. Track–Soil Model
2.3. Track Irregularities
3. Numerical Analysis Procedure
4. Numerical Results and Discussions
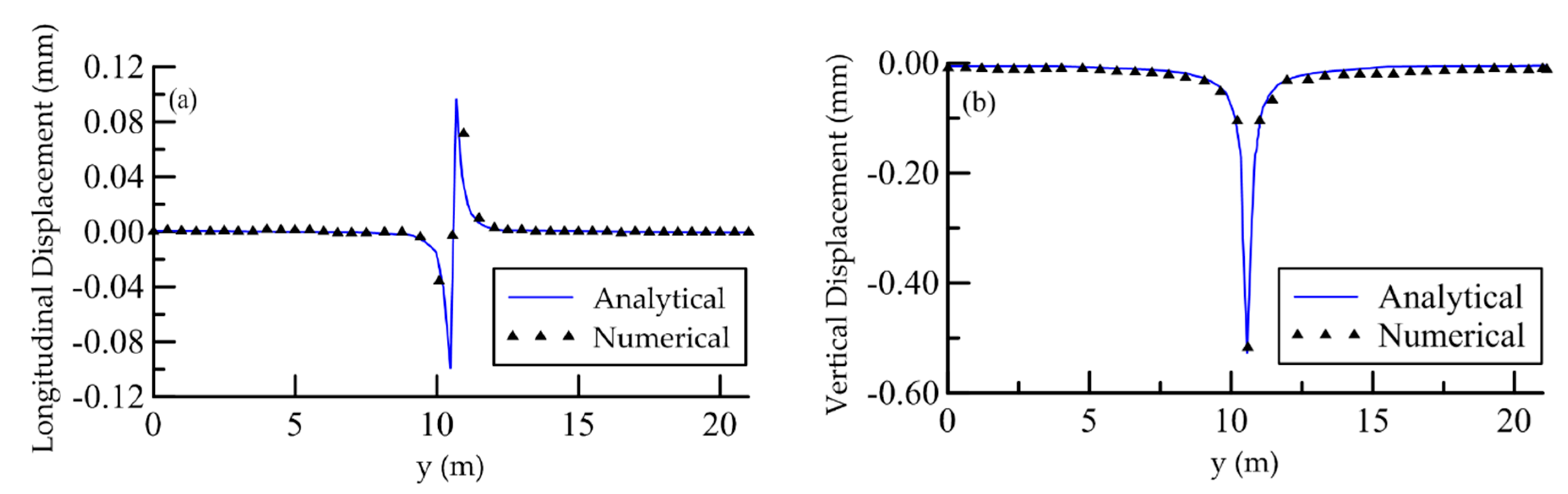
4.1. Numerical Validation
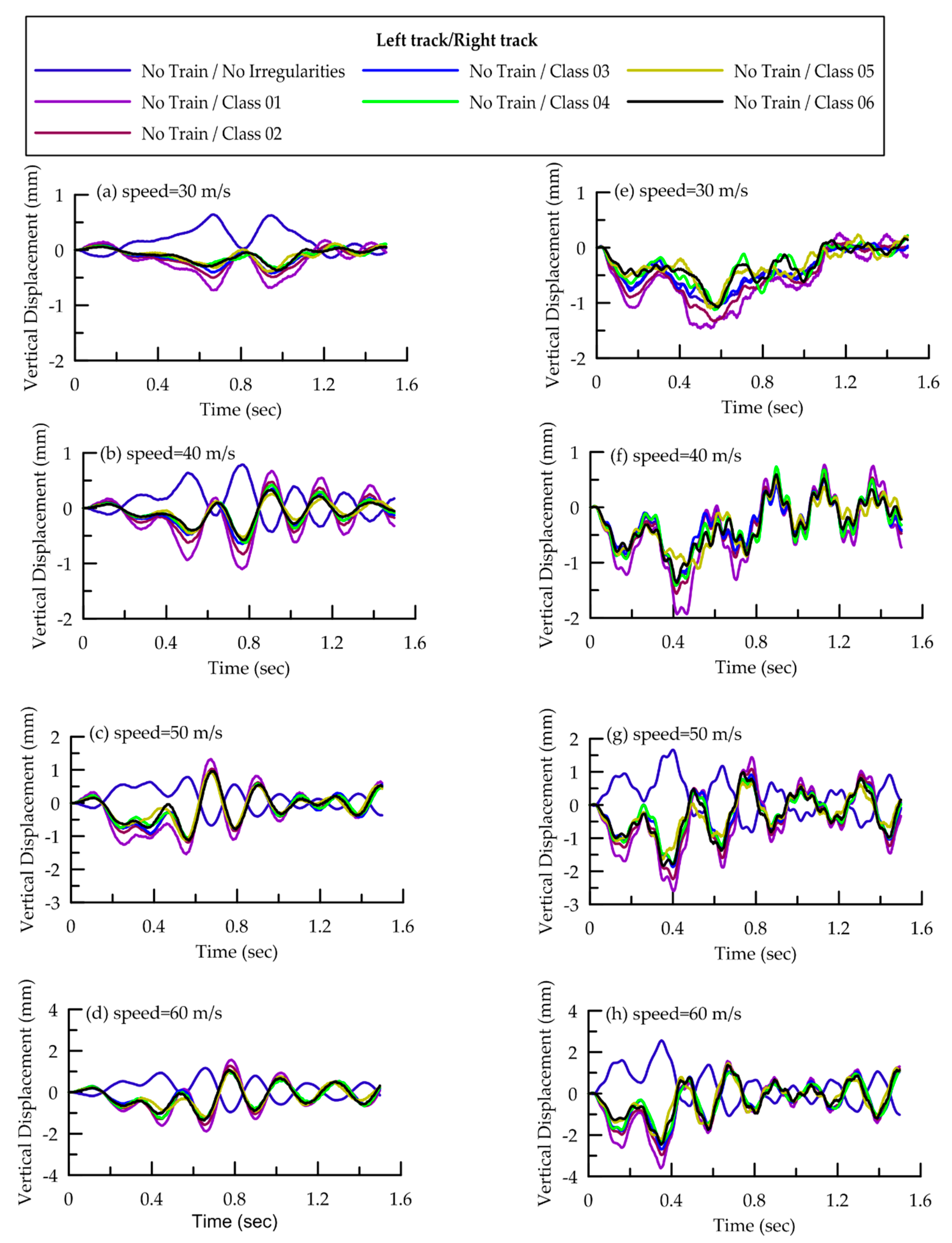
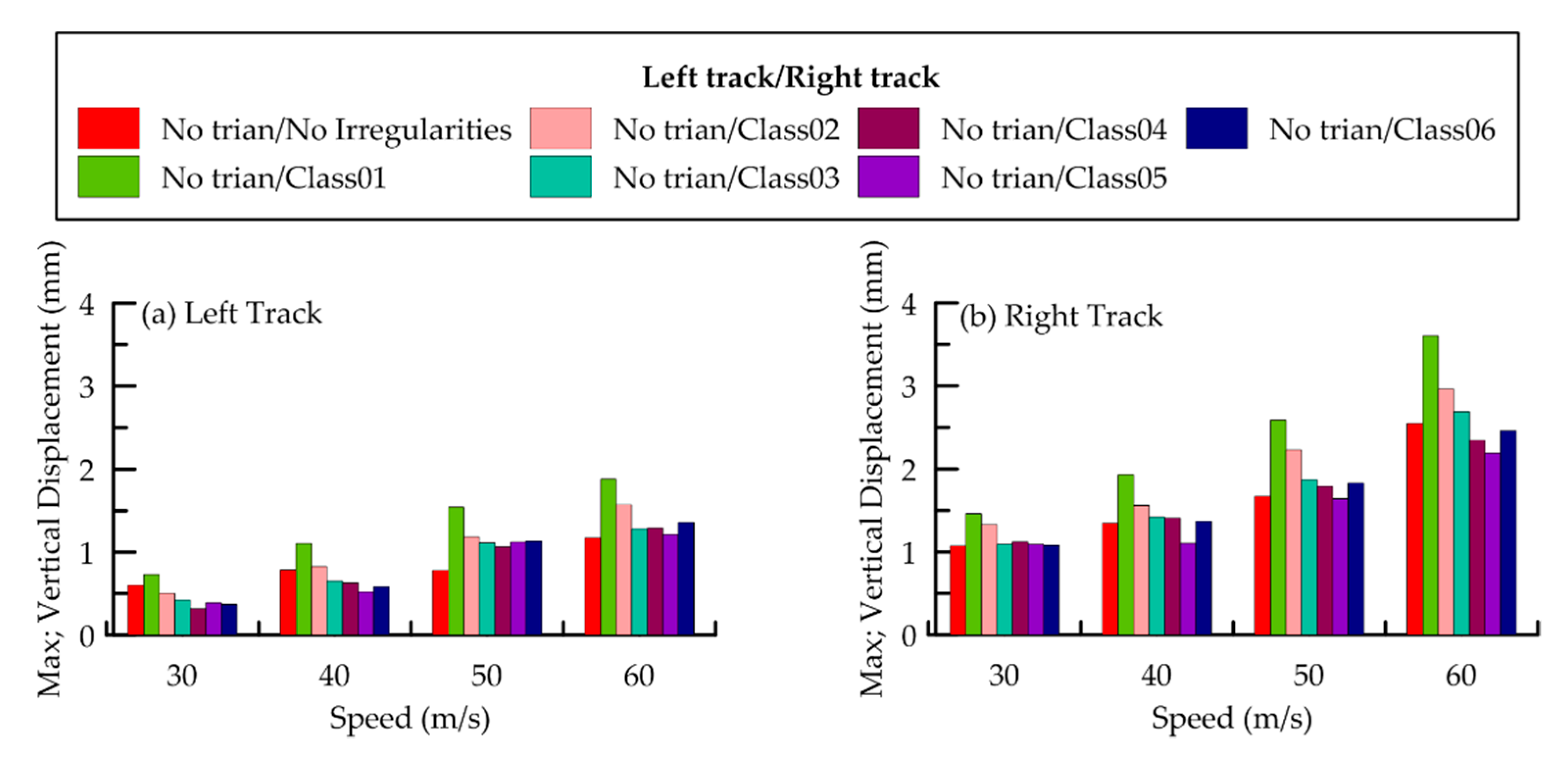
4.2. Effect of Train Speed and Track Irregularities
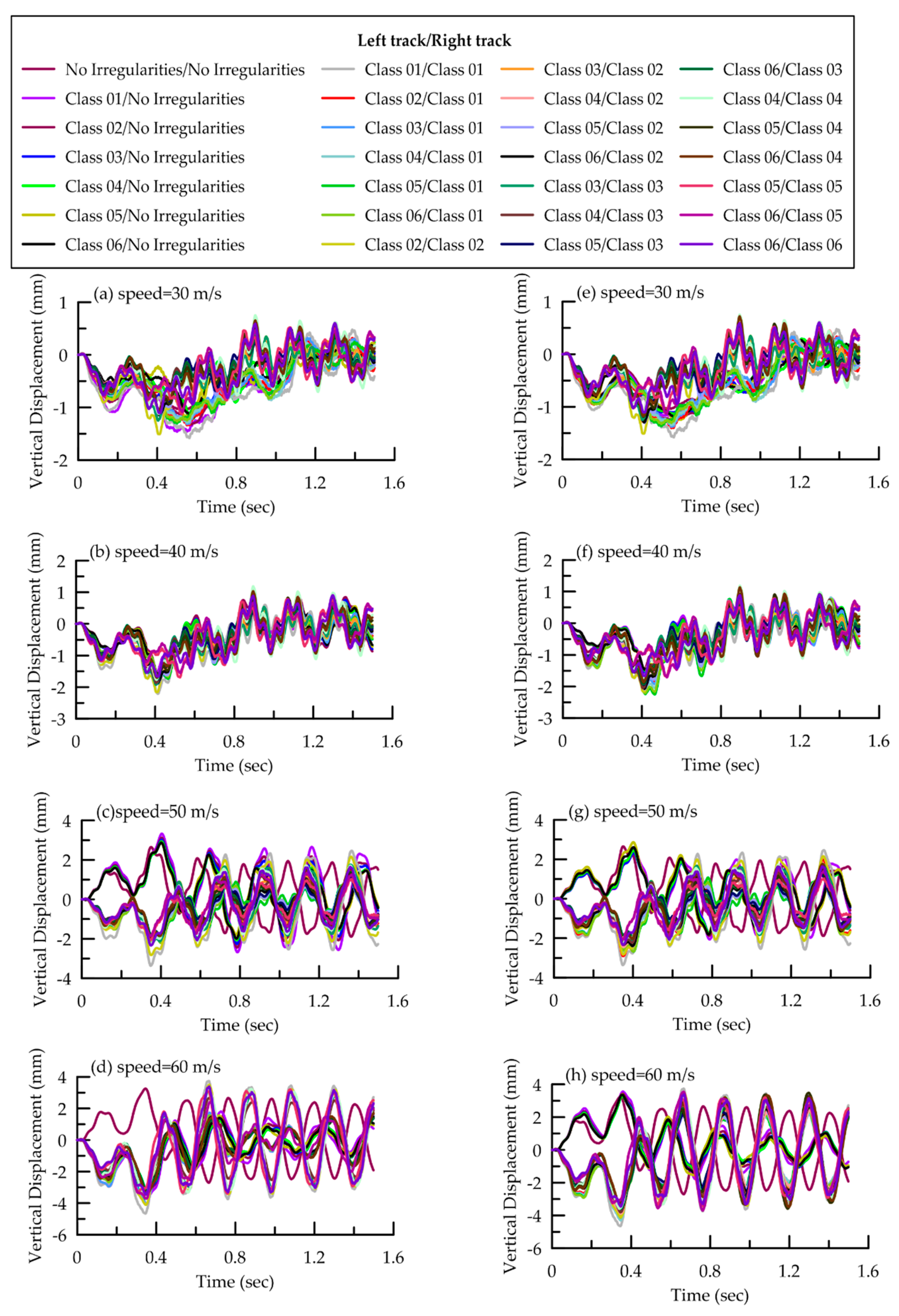
4.3. Track Dynamic Response
- Train is considered only on right track (no train on left track)
- Trains on both tracks, but moving in the opposite direction
4.3.1. Case 01
4.3.2. Case 02
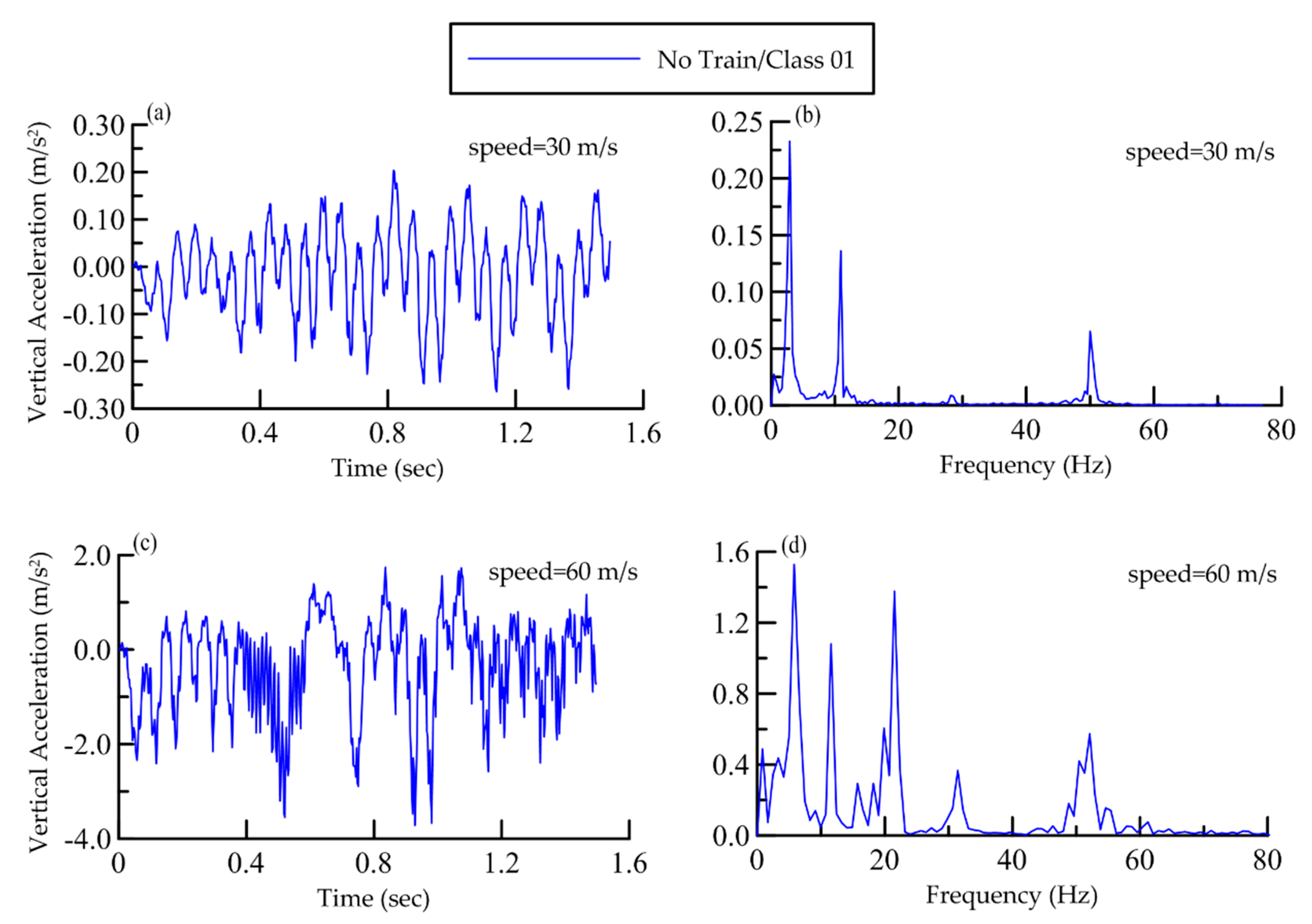
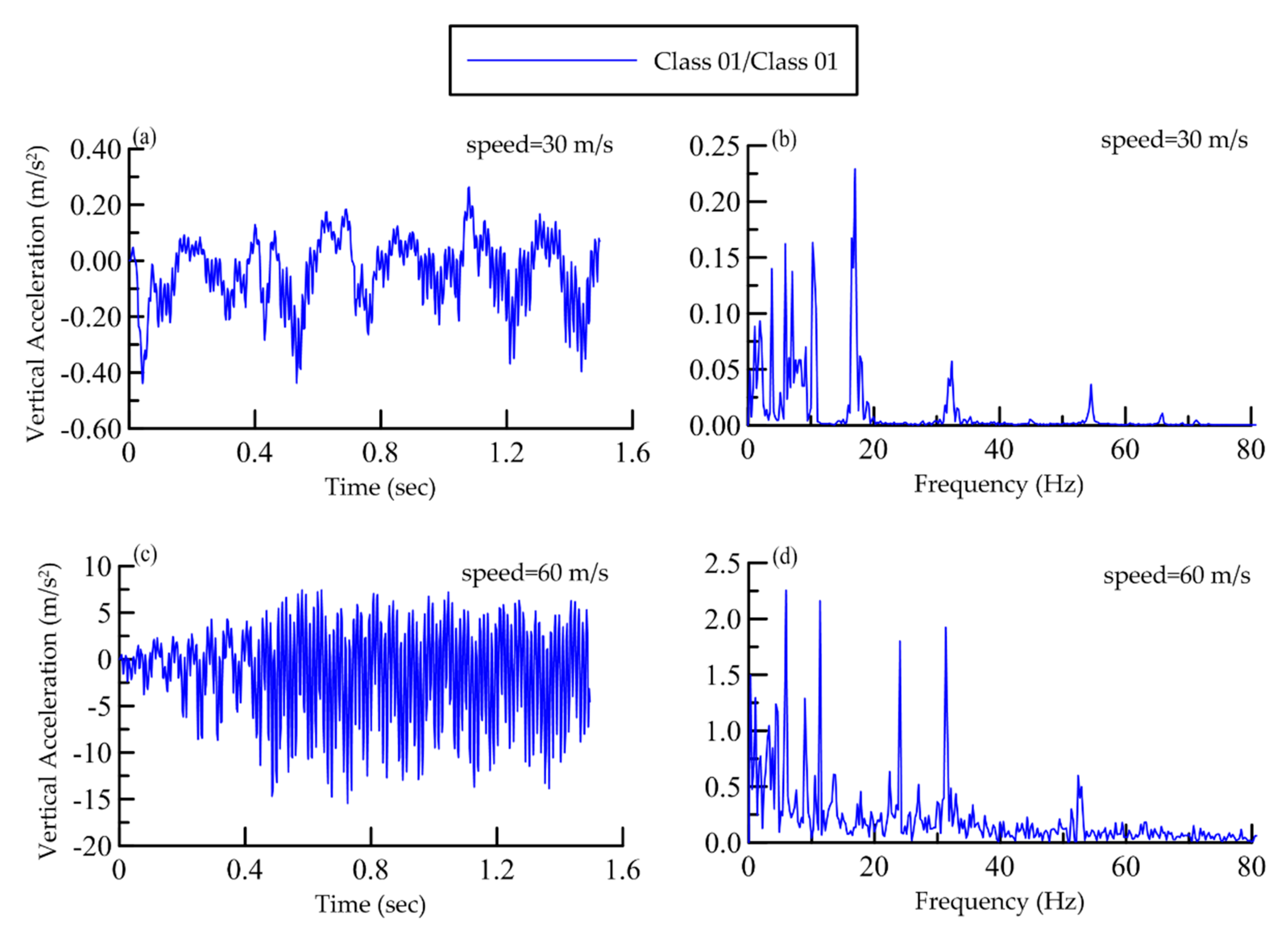
4.4. Frequency Analysis
5. Conclusions
- (1)
- When the train is moving on one track, the vibration increase as the train speed increases and the track conditions change from good to worse due to track irregularities.
- (2)
- The speed of the train has a significant effect on ground vibration. For a given track condition, an increase in speed (when train is moving on one track) causes an increase in ground response as well as shift the response spectra towards high-frequencies e.g., for train speed of 30 m/s the peak appears at 2.9 Hz, whereas it is around 5.7 Hz for 60 m/s.
- (3)
- The waves propagating due to moving trains on one track have a great influence on a nearby track. When trains are moving on two adjacent tracks the ground vibration induced by each track causes deformation in the tracks. These deformations in the tracks increase the level of track irregularities which consequently cause an increase in impact forces due to the interaction of moving train and track. Based on the results, it is concluded that the response of a track can increase up to 30% when trains are moving on both tracks.
- (4)
- The tracks have shown significantly different responses when trains are moving on two adjacent tracks. At the speed of 30 m/s a series of low-frequency peaks appear in response spectrum, whereas at speed of 60 m/s the track response spectrum not only exhibits peaks at low frequency but also at high frequency (up to 33 Hz). This significant change in track response is due to the wave propagation from one track to the other track.
- (5)
- Further studies are needed on the mitigation of track vibration so that a track does not get affected by ground vibration induced by the nearby track.
Author Contributions
Funding
Conflicts of Interest
References
- Lefeuve-Mesgouez, G.; Le Houédec, D.; Peplow, A. Ground vibration in the vicinity of a high-speed moving harmonic strip load. J. Sound Vib. 2000, 231, 1289–1309. [Google Scholar] [CrossRef]
- Krylov, V.V. Generation of ground vibrations by superfast trains. Appl. Acoust. 1995, 44, 149–164. [Google Scholar] [CrossRef]
- Krylov, V.; Ferguson, C. Calculation of low-frequency ground vibrations from railway trains. Appl. Acoust. 1994, 42, 199–213. [Google Scholar] [CrossRef]
- Takemiya, H.; Bian, X. Substructure simulation of inhomogeneous track and layered ground dynamic interaction under train passage. J. Eng. Mech. 2005, 131, 699–711. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Verlinden, O. Railway-induced ground vibrations—A review of vehicle effects. Int. J. Rail Transp. 2014, 2, 69–110. [Google Scholar] [CrossRef]
- Xia, H.; Cao, Y.; De Roeck, G. Theoretical modeling and characteristic analysis of moving-train induced ground vibrations. J. Sound Vib. 2010, 329, 819–832. [Google Scholar] [CrossRef]
- Hussein, M.F.M.; Hunt, H.E.M. A numerical model for calculating vibration due to a harmonic moving load on a floating-slab track with discontinuous slabs in an underground railway tunnel. J. Sound Vib. 2009, 321, 363–374. [Google Scholar] [CrossRef]
- Ntotsios, E.; Thompson, D.; Hussein, M. The effect of track load correlation on ground-borne vibration from railways. J. Sound Vib. 2017, 402, 142–163. [Google Scholar] [CrossRef]
- Yang, W.; Hussein, M.F.M.; Marshall, A.M. Centrifuge and numerical modelling of ground-borne vibration from an underground tunnel. Soil Dyn. Earthq. Eng. 2013, 51, 23–34. [Google Scholar] [CrossRef]
- Celebi, E.; Schmid, G. Investigation of ground vibrations induced by moving loads. Eng. Struct. 2005, 27, 1981–1998. [Google Scholar] [CrossRef]
- Andersen, L.; Nielsen, S.R.K.; Krenk, S. Numerical methods for analysis of structure and ground vibration from moving loads. Comput. Struct. 2007, 85, 43–58. [Google Scholar] [CrossRef]
- Galvín, P.; François, S.; Schevenels, M.; Bongini, E.; Degrande, G.; Lombaert, G. A 2.5D coupled FE-BE model for the prediction of railway induced vibrations. Soil Dyn. Earthq. Eng. 2010, 30, 1500–1512. [Google Scholar] [CrossRef]
- Galvín, P.; Romero, A.; Domínguez, J. Fully three-dimensional analysis of high-speed train–track–soil-structure dynamic interaction. J. Sound Vib. 2010, 329, 5147–5163. [Google Scholar] [CrossRef]
- Hamarat, M.; Kaewunruen, S.; Papaelias, M.; Silvast, M. New insights from multibody dynamic analyses of a turnout system under impact loads. Appl. Sci. 2019, 9, 4080. [Google Scholar] [CrossRef]
- El Kacimi, A.; Woodward, P.K.; Laghrouche, O.; Medero, G. Time domain 3D finite element modelling of train-induced vibration at high speed. Comput. Struct. 2013, 118, 66–73. [Google Scholar] [CrossRef]
- Gao, G.; Yao, S.; Yang, J.; Chen, J. Investigating ground vibration induced by moving train loads on unsaturated ground using 2.5D FEM. Soil Dyn. Earthq. Eng. 2019, 124, 72–85. [Google Scholar] [CrossRef]
- Gao, G.; Xu, C.; Chen, J.; Song, J. Investigation of ground vibrations induced by trains moving on saturated transversely isotropic ground. Soil Dyn. Earthq. Eng. 2018, 104, 40–44. [Google Scholar] [CrossRef]
- Connolly, D.; Giannopoulos, A.; Fan, W.; Woodward, P.K.; Forde, M.C. Optimising low acoustic impedance back-fill material wave barrier dimensions to shield structures from ground borne high speed rail vibrations. Constr. Build. Mater. 2013, 44, 557–564. [Google Scholar] [CrossRef]
- Thompson, D.J.; Kouroussis, G.; Ntotsios, E. Modelling, simulation and evaluation of ground vibration caused by rail vehicles. Veh. Syst. Dyn. 2019, 57, 936–983. [Google Scholar] [CrossRef]
- Li, T.; Su, Q.; Kaewunruen, S. Saturated ground vibration analysis based on a three-dimensional coupled train-track-soil interaction model. Appl. Sci. 2019, 9, 4991. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, X.; Fu, Q.; Xu, G.; Cai, D. Dynamic responses of asphalt concrete waterproofing layer in ballastless track. Appl. Sci. 2019, 9, 375. [Google Scholar] [CrossRef]
- Wang, H.; Silvast, M.; Markine, V.; Wiljanen, B. Analysis of the dynamic wheel loads in railway transition zones considering the moisture condition of the ballast and subballast. Appl. Sci. 2017, 7, 1208. [Google Scholar] [CrossRef]
- Ribes-Llario, F.; Marzal, S.; Zamorano, C.; Real, J. Numerical modelling of building vibrations due to railway traffic: Analysis of the mitigation capacity of a wave barrier. Shock Vib. 2017, 2017, 11. [Google Scholar] [CrossRef]
- Connolly, D.P.; Kouroussis, G.; Laghrouche, O.; Ho, C.L.; Forde, M.C. Benchmarking railway vibrations—Track, vehicle, ground and building effects. Constr. Build. Mater. 2015, 92, 64–81. [Google Scholar] [CrossRef]
- Khan, B.L.; Farooq, H.; Usman, M.; Butt, F.; Khan, A.Q.; Hanif, A. Effect of soil–structure interaction on a masonry structure under train-induced vibrations. Proc. Inst. Civil. Eng. Struct. Build. 2019, 172, 922–934. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, Y.; Yang, J. Study of the influence of train vibration loading on adjacent damaged tunnel. Shock Vib. 2019, 2019, 8. [Google Scholar] [CrossRef]
- Che, A.; Tang, Z.; Feng, S. An elastic-wave-based full-wavefield imaging method for investigating defects in a high-speed railway under-track structure. Soil Dyn. Earthq. Eng. 2015, 77, 299–308. [Google Scholar] [CrossRef]
- Feng, S.J.; Zhang, X.L.; Zheng, Q.T.; Wang, L. Simulation and mitigation analysis of ground vibrations induced by high-speed train with three dimensional FEM. Soil Dyn. Earthq. Eng. 2017, 94, 204–214. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar]
- Phillips, C.; Hashash, Y.M. Damping formulation for nonlinear 1D site response analyses. Soil Dyn. Earthq. Eng. 2009, 29, 1143–1158. [Google Scholar] [CrossRef]
- Bathe, K.-J. Finite Element Procedures; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Corbin, J. Statistical Representations of Track Geometry: Volume I, Text. 1980; FRA/ORD·Bl/22·2; Federal Railroad Administration: Washington, DC, USA, 1980. [Google Scholar]
- Kouroussis, G.; Verlinden, O.; Conti, C. A two-step time simulation of ground vibrations induced by the railway traffic. Proc. Inst. Mech. Eng. Part. C J. Mech. Eng. Sci. 2012, 226, 454–472. [Google Scholar] [CrossRef]
- Lei, X.; Noda, N.-A. Analyses of dynamic response of vehicle and track coupling system with random irregularity of track vertical profile. J. Sound Vib. 2002, 258, 147–165. [Google Scholar] [CrossRef]
- Ranjan, G.; Rao, A. Basic and Applied Soil Mechanics; New Age International: New Delhi, India, 2007. [Google Scholar]
- Kouroussis, G.; Verlinden, O.; Conti, C. Free field vibrations caused by high-speed lines: Measurement and time domain simulation. Soil Dyn. Earthq. Eng. 2011, 31, 692–707. [Google Scholar] [CrossRef]
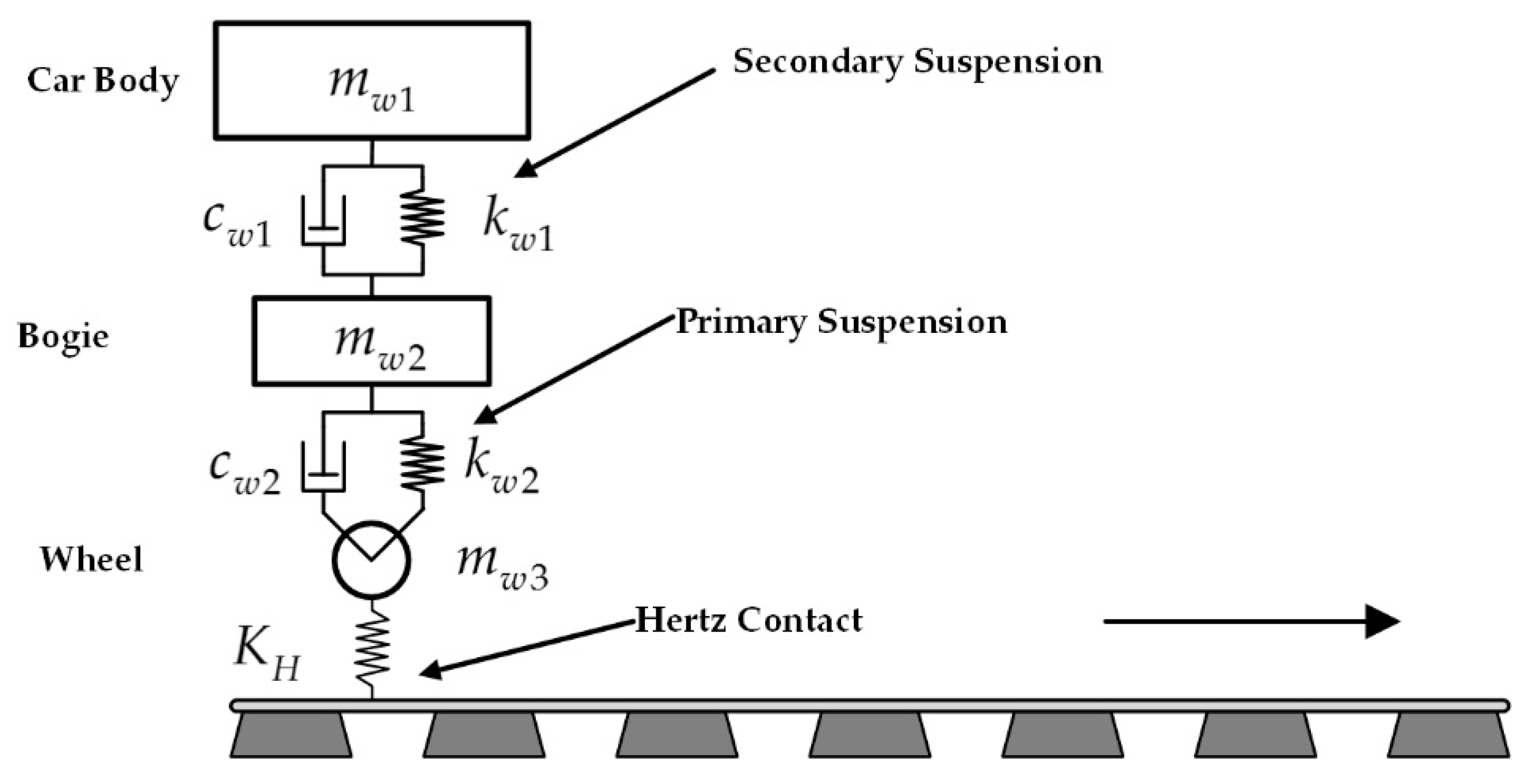


| Parameters | Value |
|---|---|
| Axle load, P (kg) | 17,679.22 |
| Car mass, (kg) | 55,963.86 |
| Bogie mass, (kg) | 3312.313 |
| Wheel mass, (kg) | 1016.047 |
| Hertz contact Stiffness, | 93.7 |
| Secondary suspension stiffness, (N/m) | 1.31 × |
| Primary suspension stiffness, (N/m) | 3.28 × |
| Secondary suspension damping, (Ns/m) | 90 |
| Primary suspension damping, (Ns/m) | 30 |
| Parameters | Value |
|---|---|
| Eastic Modulus, E (GPa) | 210 |
| Density, ρ () | 7897 |
| Bending stiffness around x, ( | 1.245 × 10–5 |
| Bending stiffness around z, ( | 4.526 × 10–6 |
| Torsional stiffness around y, ( | 6.554 × 10–3 |
| Parameters | Value |
|---|---|
| Sleeper (Concrete) | |
| Elastic Modulus, E (GPa) | 10 |
| Poisson ratio, | 0.2 |
| Density, ρ ( ) | 2400 |
| Primary wave velocity, | 2151.6 |
| Secondary wave velocity, | 1317.6 |
| Rayleigh wave velocity, | 1201.2 |
| Ballast | |
| Elastic Modulus, E (GPa) | 0.13 |
| Poisson ratio, | 0.4 |
| Density, ρ ( ) | 1600 |
| Primary wave velocity, | 417.3 |
| Secondary wave velocity, | 170.3 |
| Rayleigh wave velocity, | 160.3 |
| Soil | |
| Elastic Modulus, E (GPa) | 0.025 |
| Poisson ratio, | 0.45 |
| Density, ρ ( ) | 1800 |
| Primary wave velocity, | 229.5 |
| Secondary wave velocity, | 69.2 |
| Rayleigh wave velocity, | 65.6 |
| Parameters | Track Classes | |||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| A | 0.0954 | 0.1675 | 0.2968 | 0.5300 | 0.9540 | 1.6748 |
| 23.94 | 23.94 | 23.94 | 23.94 | 23.94 | 23.94 | |
| ) | 13.123 | 13.123 | 13.123 | 13.123 | 13.123 | 13.123 |
| Case 01 (Left Track/Right Track) Train Moving Only on Right Track | Case 02 (Left Track/Right Track) Trains Moving on Both Tracks But Opposite in Direction |
|---|---|
| no train/no irregularities | no irregularities/no irregularities |
| no train/class 01 | class 01/no irregularities |
| no train/class 02 | class 02/no irregularities |
| no train/class 03 | class 03/no irregularities |
| no train/class 04 | class 04/no irregularities |
| no train/class 05 | class 05/no irregularities |
| no train/class 06 | class 06/no irregularities |
| \ | class 01/class 01 |
| \ | class 02/class 01 |
| \ | class 03/class 01 |
| \ | class 04/class 01 |
| \ | class 05/class 01 |
| \ | class 06/class 01 |
| \ | class 02/class 02 |
| \ | class 03/class 02 |
| \ | class 04/class 02 |
| \ | class 05/class 02 |
| \ | class 06/class 02 |
| \ | class 03/class 03 |
| \ | class 04/class 03 |
| \ | class 05/class 03 |
| \ | class 06/class 03 |
| \ | class 04/class 04 |
| \ | class 05/class 04 |
| \ | class 06/class 04 |
| \ | class 05/class 05 |
| \ | class 06/class 05 |
| \ | class 06/class 06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javaid, O.; Choi, D.-H. Effect of Track Irregularities on the Response of Two-Way Railway Tracks. Appl. Sci. 2020, 10, 11. https://doi.org/10.3390/app10010011
Javaid O, Choi D-H. Effect of Track Irregularities on the Response of Two-Way Railway Tracks. Applied Sciences. 2020; 10(1):11. https://doi.org/10.3390/app10010011
Chicago/Turabian StyleJavaid, Omer, and Dong-Ho Choi. 2020. "Effect of Track Irregularities on the Response of Two-Way Railway Tracks" Applied Sciences 10, no. 1: 11. https://doi.org/10.3390/app10010011
APA StyleJavaid, O., & Choi, D.-H. (2020). Effect of Track Irregularities on the Response of Two-Way Railway Tracks. Applied Sciences, 10(1), 11. https://doi.org/10.3390/app10010011




