2.3. In Situ Modeling
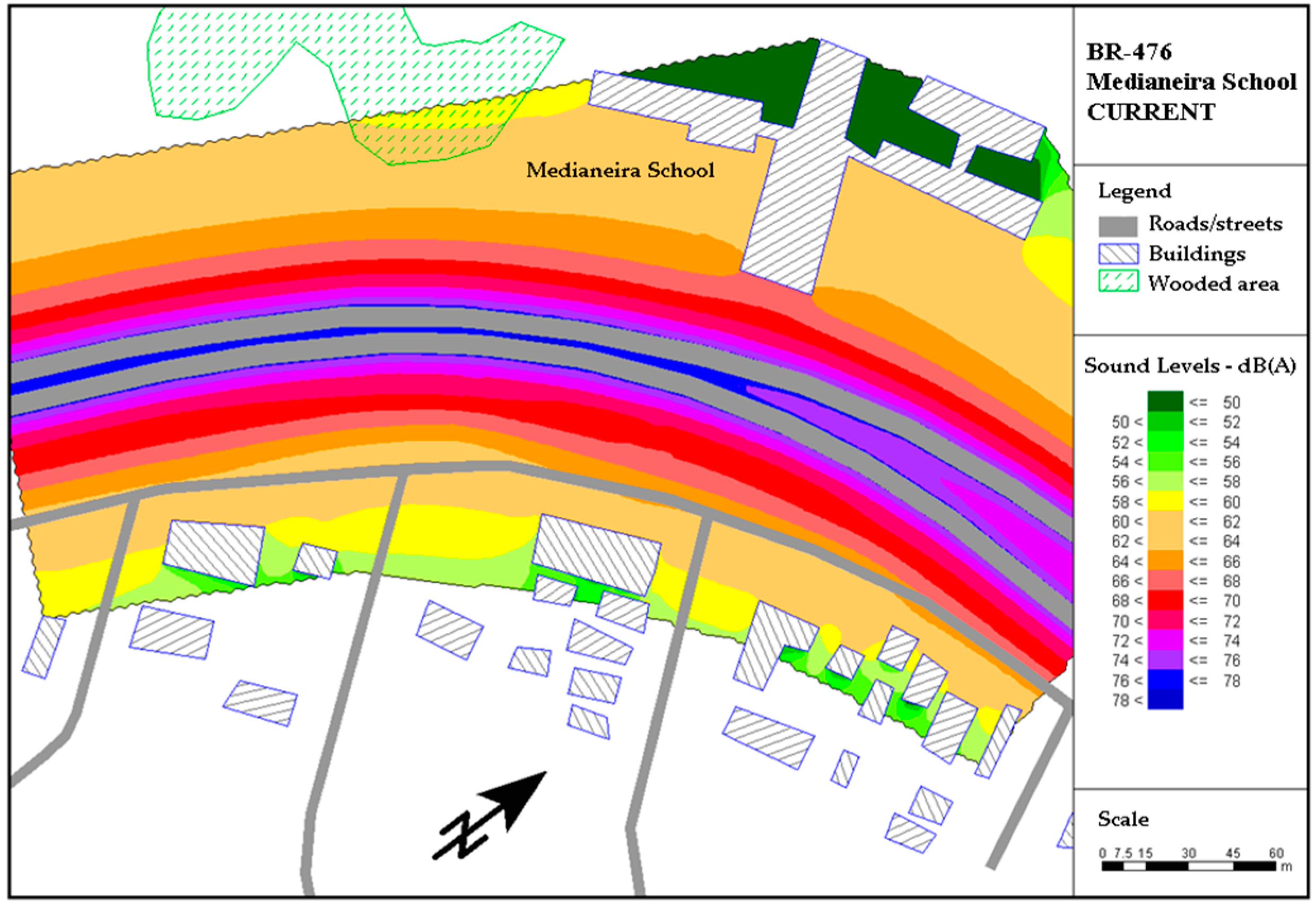
The portion of the highway selected for this study was a flat region without significant gradients. Vehicle traffic was mixed, consisting of motorcycles, light vehicles (cars and utilities), heavy vehicles (trucks and public transport buses). The surroundings of this stretch of the highway contains residential, educational and commercial establishments.
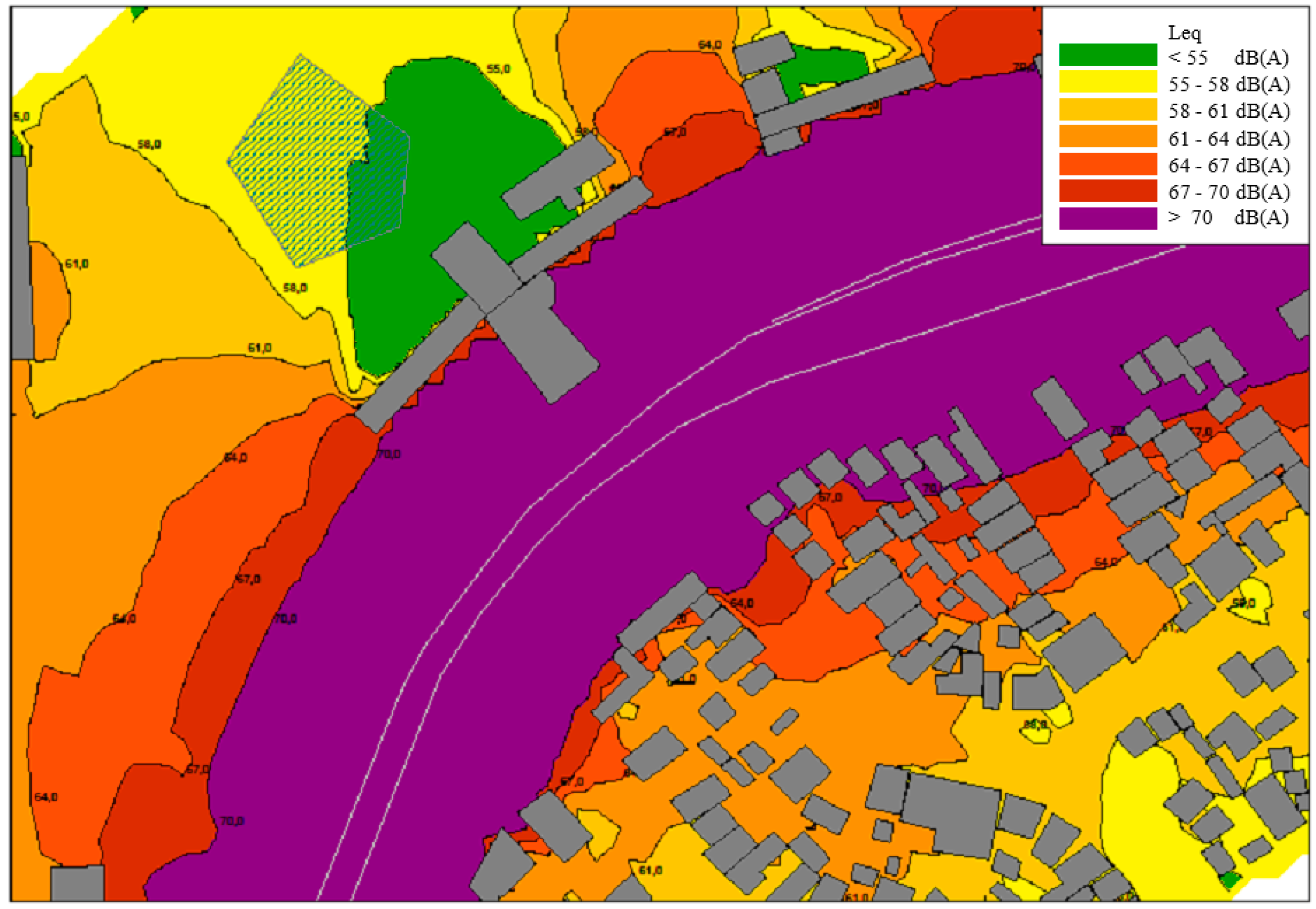
An area of evaluation was chosen within the region selected for analysis, called a “noise-sensitive area,” i.e., an area with educational buildings, where the environmental noise impact assessments were conducted. After the site was chosen, computer simulations were done of the situations of implementation and operation of the highway remodeling project, taking into account all the aforementioned characteristics of the site, using SOUNDPLAN version 6.2 software (SoundPLAN GmbH, Etzwiesenberg, Germany) dedicated exclusively to this type of graphic analysis.
To properly model the real conditions and use them for the simulations with SOUNDPLAN software, the road traffic composition was stratified into cars, heavy vehicles (metropolitan buses, trucks) and light vehicles (motorcycles). Then, after calculating the traffic composition (expressed in percentage), a visual count of vehicles was made independently by two people standing on opposite sides of the road. Road traffic speed was measured by the speedometer of a car driven by two of the authors along this stretch of road, who recorded the average vehicle flow speed, while the other two authors measured the equivalent sound pressure levels in the area.
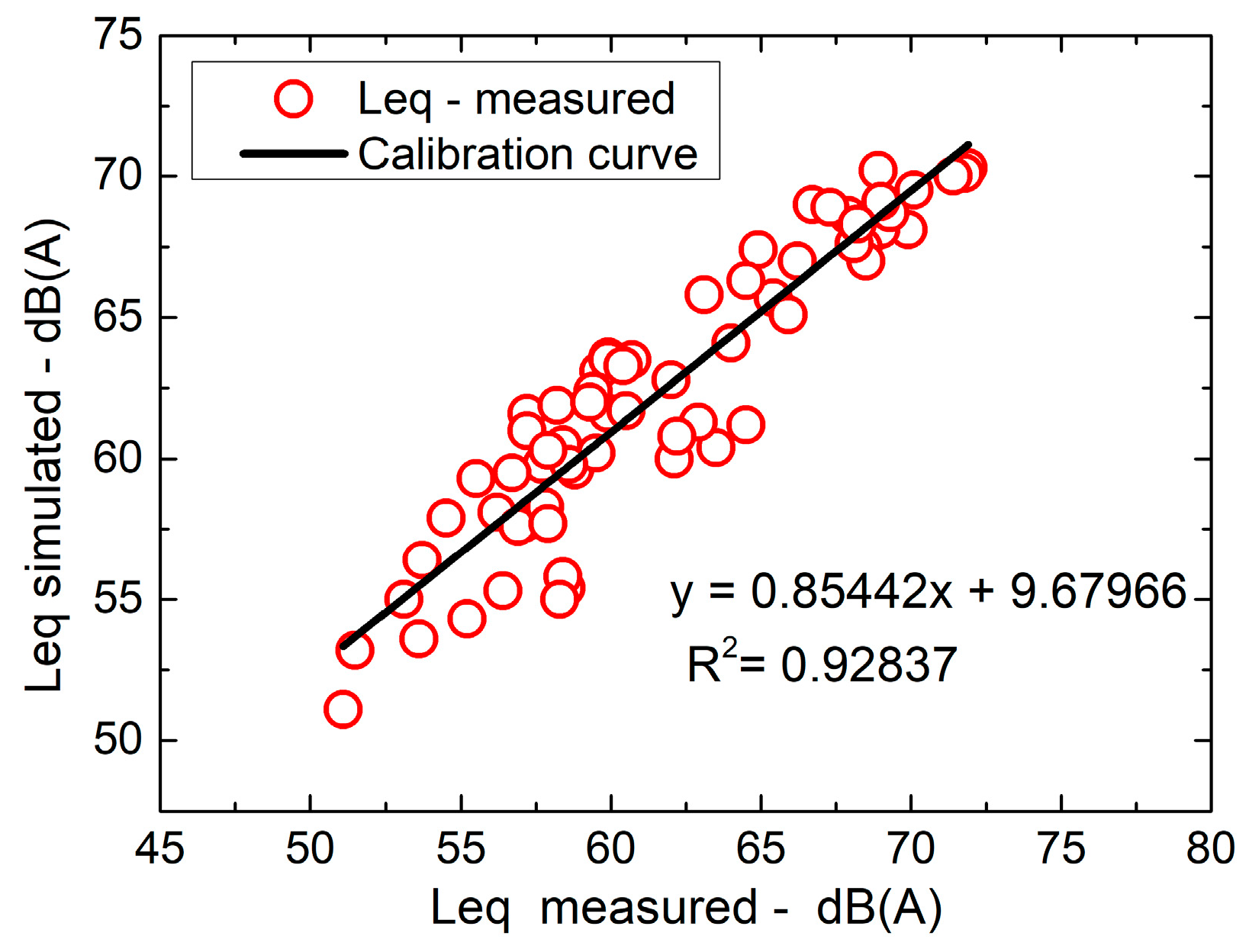
After this assessment of the study area, simulations were made and were validated by comparing the equivalent sound levels of the simulated noise map against the measured road traffic noise emissions. A calibration curve was plotted to compare these values, which were then evaluated based on Pearson’s linear correlation. The results were considered validated when the difference between the measured and simulated values did not exceed ±4.6 dB, as recommended by [
37].
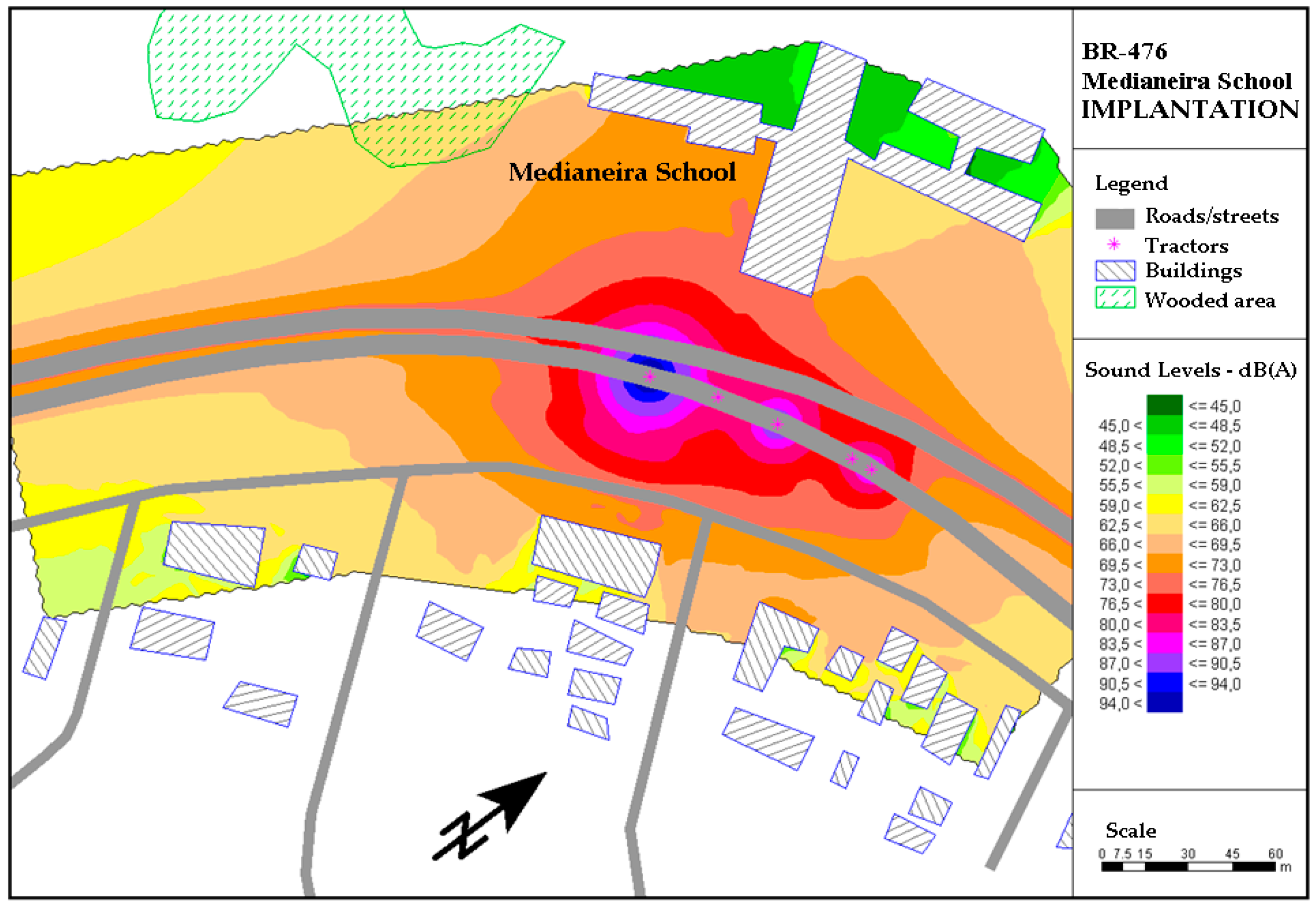
A traffic flow of 780 vehicles/h was considered, with 8.5% of the total flow corresponding to heavy vehicles, in the situations of both implementation and operation of the project. The speed considered for both heavy and light vehicles was 40 km/h during the project’s implementation phase.
To determine the environmental impact, an assessment was made of the impact attributes, i.e., classification of the qualitative characteristics of the activity based on the calculated noise maps.
Table 3 lists the attributes in question.
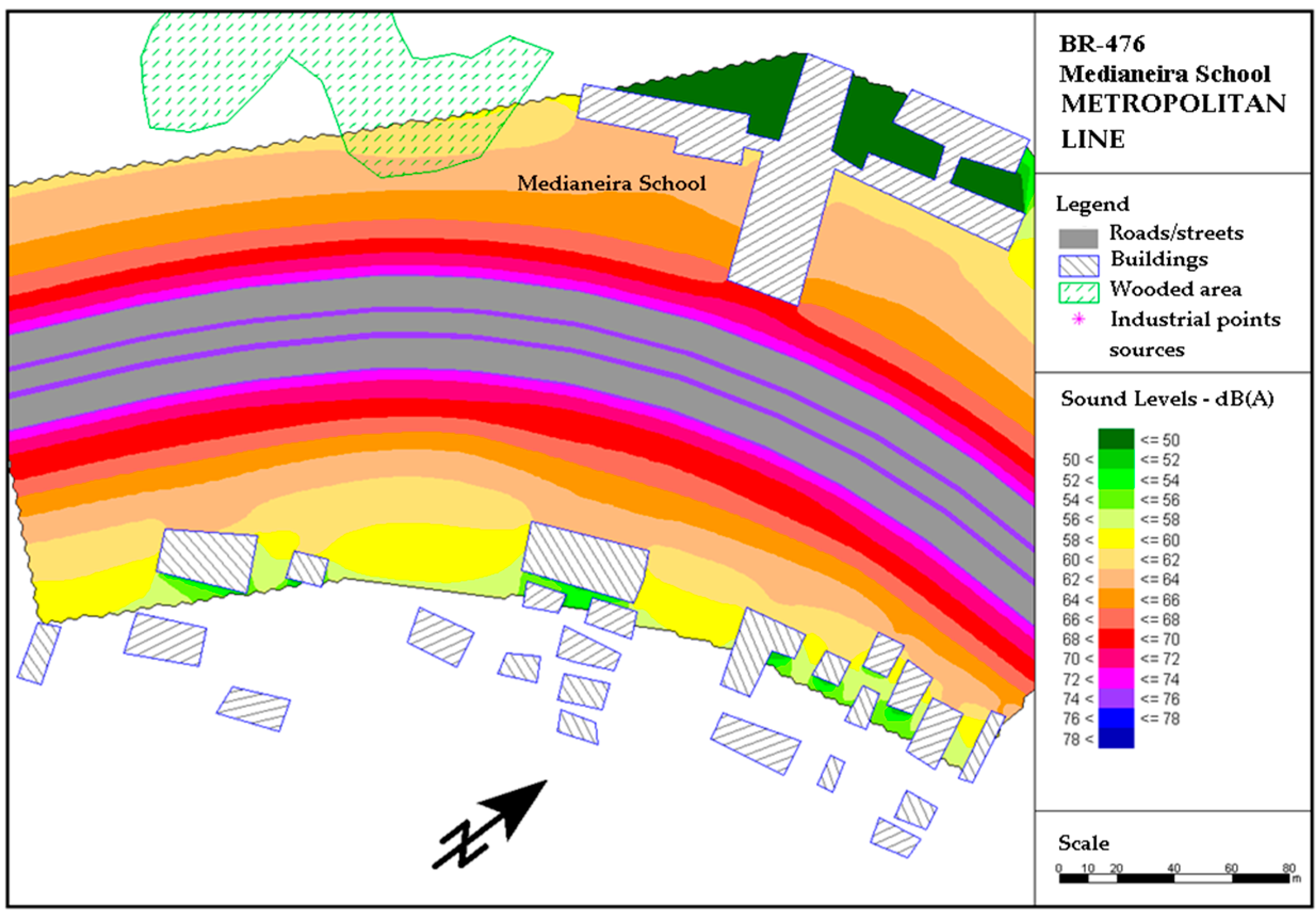
The noise maps for the situation of operationalization were prepared considering the basic project for the Metropolitan Axis of Curitiba’s Integrated Transport Network. This project includes: (1) the prioritization of public transport, with the implementation of express bus-only lanes; (2) frontage roads for the circulation of traffic between different neighborhoods of Curitiba and of metropolitan municipalities; (3) local access roads to reach neighboring activities; and (4) implementation and remodeling of bike paths and green areas. In the operation simulation, double-and triple-articulated buses were considered, passing through at 3-min intervals.
2.4. Design of Experiments
Design of Experiments (DoE) considers the linear effects of certain variables on the outputs of a given system. To this end, most of the significant factors that interfere in the simulated or measured response to a given condition of an experiment are statistically estimated [
38]. In this work, therefore, DoE was employed to evaluate the effectiveness of noise barriers designed for the acoustic protection of an educational establishment impacted by high sound pressure levels. The controllable design variables of the noise barriers were the barrier height and the sound absorption coefficient of the barrier material.
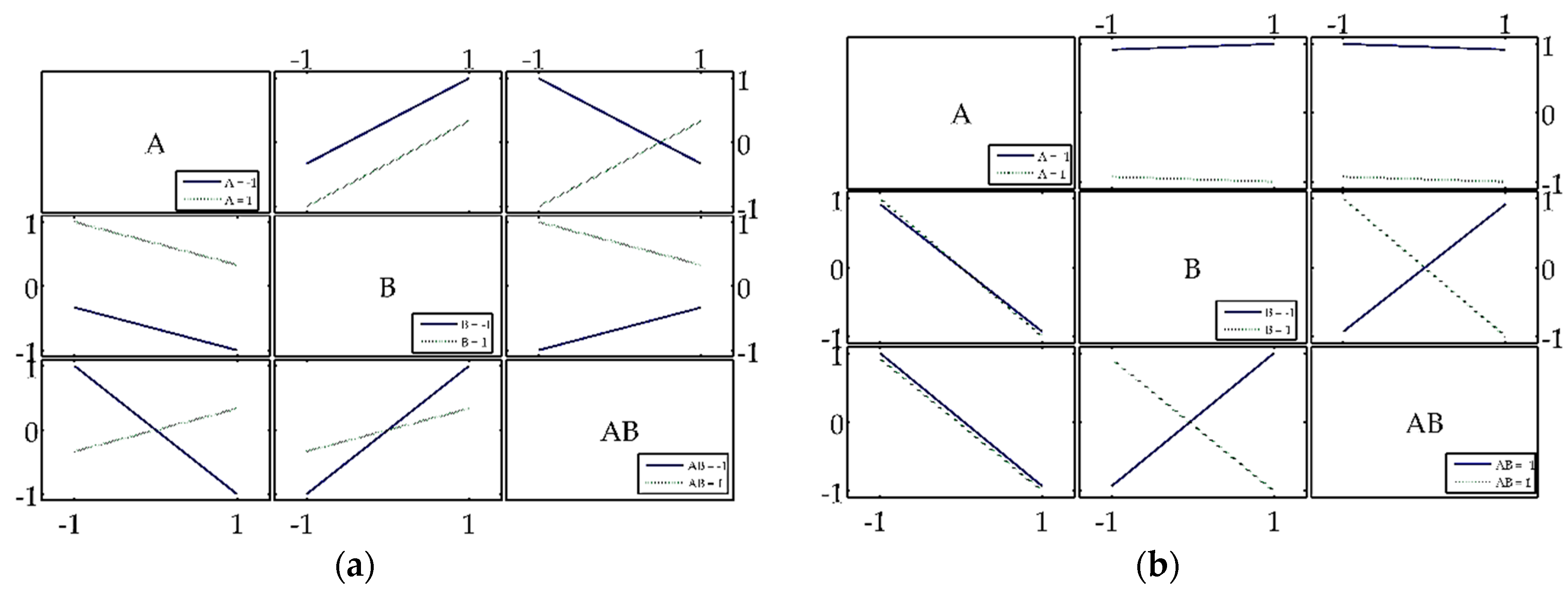
The DoE used in this study was a 2
k full factorial design, i.e., with two controllable variables and with k = 2 levels. The levels were raised from the minimum (−1) to the maximum (1). The area of acoustic shadow, with an average level of 55 dB(A), and the sound attenuation calculated from the Transmission Loss (TL) [
39] were considered responses and were defined as:
where
is the sound pressure level in dB(A) at the receiver position and
is the sound pressure level in dB(A) at the source position.
According to the ASTM C423-17 [
40], the absorption coefficient can be represented by the Noise Reduction Coefficient (NRC). The NRC is calculated as the simple average of the absorption coefficient at the frequencies of 250 Hz, 500 Hz, 1000 Hz, and 2000 Hz.
Table 4 lists the materials used here: smooth bare concrete and smooth concrete covered with 30 mm rockwool acoustic insulation slabs, with their respective sound absorption coefficients.
Based on a 2
2 factorial DoE,
Table 5 shows the relationship between natural and coded levels, indicating the factors that are controllable during the design phase. The simulated responses were therefore based on combinations of these two controllable factors.
The controllable coded factors were then arranged in tabular form, called a contrast matrix. This matrix corresponds to the arrangement of all possible combinations of the controllable coded factors between −1 and +1 with an added mean term (M). The output responses were the area of Acoustic Shadow (AS) and Transmission Loss (TL), as indicated in
Table 6.
Mathematically, the DoE estimated the effects of the controllable factors on the responses by subjecting the data listed in
Table 5 to a multiple linear regression (MLR) [
38]. The MLR was applied to each response individually. The significant effects of the input variables on the responses were calculated based on the values of the regressors, which are the
coefficients shown in Equation (2).
In Equation (2)
represents the input of the contrast matrix shown in
Table 5, and
is the estimation error. On the other hand, Equation (2) can be written in matrix form as
, thereby allowing the effects to be calculated analytically based on the Least Squares method, establishing the best set of possible regressors, which are calculated as:
, the
refers to the matrix transposition operation, the operator
stands for the inverse matrix operation, and with the
calculated through,
, using the Least Squares method generates the best possible estimations for the response variable,
when the
are coupled in Equation (2) [
38].
According to Montgomery [
38], the nominal effects are calculated as double the values of the regressors, which, in this case, are the
terms in Equation (2) However, in this work, it was considered the significance of the effects according to the values of the unweighted regressors. This was done to ensure the results would be aligned with those obtained by the neural networks methodology. The codes and computational implementations were performed using Matlab version R2016b software (MathWorks, Natick, MA, USA).
2.5. Artificial Neural Networks
As Haykin et al. [
41] proved through the Universal Approximation Theorem [
42], Artificial Neural Networks (ANNs), or simply neural networks, are considered universal approximations of functions for structured or unstructured multivariate datasets. ANNs are used in a wide range of fields, such as clustering, prediction, fitting, forecasting, and modeling [
43,
44]. ANNs learn and recognize the dynamics of a given system through the dichotomy of input-output pairing. With this, one can establish the heuristic of supervised machine learning based on error backpropagation, which is calculated as the difference between the output estimated by the network and the target value. By means of training algorithms, this error determines the direction and speed of learning. For in-depth details of neural network concepts, see Haykin et al. [
41] and Russell et al. [
45].
In this work, the ANNs were implemented based on the Multilayer Perceptron (MLP) architecture, with a topology of one input layer, two hidden layers, and one output layer. Six topologies were trained for each response variable in order to avoid biased terms, as indicated in
Table 7.
The input layer of the network contained three sensory neurons corresponding to the variables defined in the DoE, i.e., barrier height, the barrier’s NRC, and the interaction between the two, which corresponds to the coded variables A, B and AB. The size of the ANN training topologies was chosen to perform the approximation with only one neuron in the output layer. In other words, for each of the y
1 and y
2 responses listed in
Table 6, a specialized neural network was trained with only 1 neuron in the output layer.
Table 7 shows the configuration of the ANNs that were trained.
Due to the small number of samples available for ANN training, it was employed the heuristic for the training phase recommended by Hinton et al. [
46]. The samples were therefore divided as follows: 90% of the samples were used for training and 10% for validation and testing, arranged in a cross-validation scheme using Matlab defaults. These samples were allocated randomly. The input-output pairs were subjected to bipolar normalization in a range of −1 to 1, enabling us to prevent possible scaling effects from masking the real factors of significance. This mapping, which was performed in the DoE and ANNs as a preprocessing phase prior to applying the MLR, is expressed by Equation (3):
In Equation (3) represents the variable to be mapped between −1 and 1, the minimum and maximum values of are, respectively, and , and = −1 and = 1. The training stopping criteria were the normalized Mean Square Error (MSE) of 1 and −12, a maximum of 500 epochs, and a limit training time of 5 min.
The performance criteria used were the normalized Mean Square Error (MSE) and Pearson’s linear correlation (
) between the estimated output and the target output. The MSE was calculated in the context of the ANNs as:
In Equation (4) the error is:
The subscript
indicates that this is the network’s output layer. The error
was calculated as the difference between the real value of the network’s output
, and the
value estimated by the network, considering a total number of samples of
. The level of Pearson’s linear correlation
between
and
is:
and the components of Equation (6) are:
where the terms
and
are respectively the standard deviation for the output (
) and to the target (
).
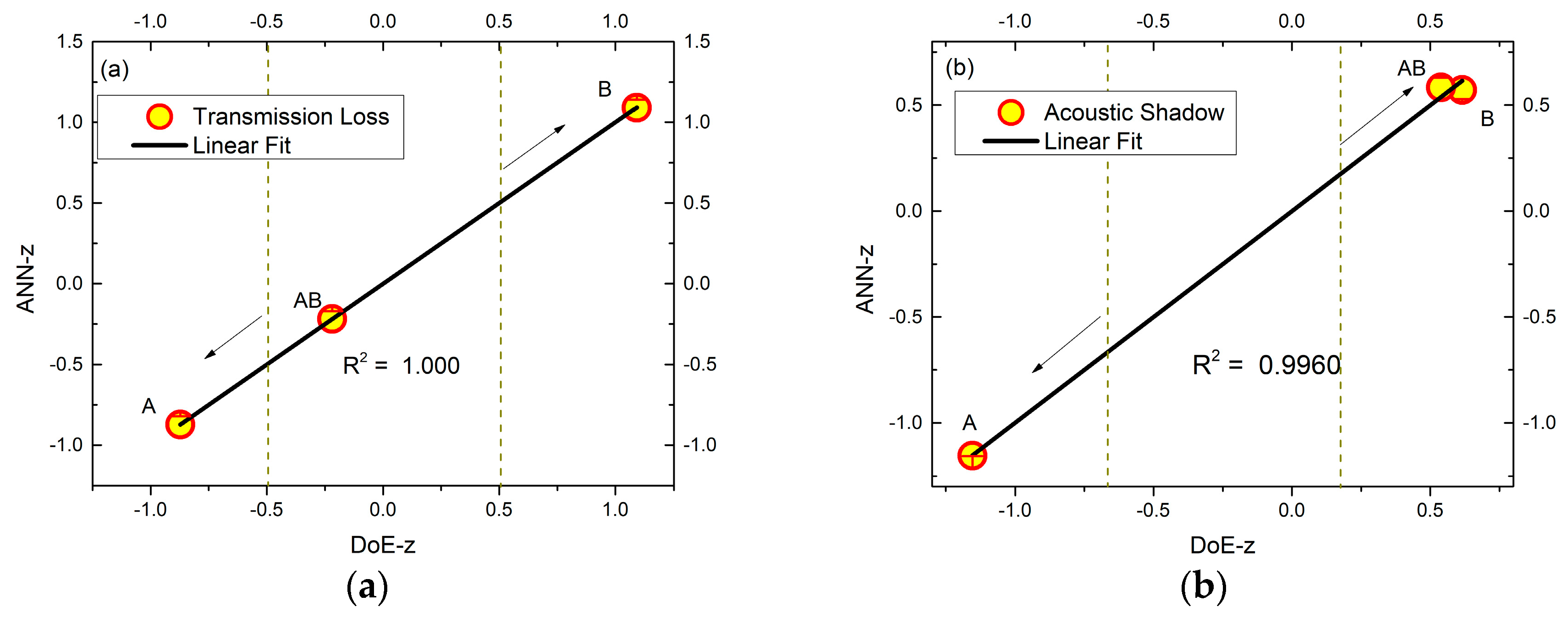
Equation (6) therefore tells us how aligned the estimated errors are in their variances. In this work, the level of correlation between the outputs was R2. This is the most important metric to be evaluated when comparing the performance of the ANNs and the DoE.
To obtain an optimized response for the various training sessions of the neural network, a mean equivalent neural network, (ANNeq)mean, was calculated for each topology. The following steps were carried out:
- (i)
50 independent training sessions were performed for each topology shown in
Table 7. The spatial weights matrix was reset to zero in each new training session. The normalized mean square error (MSE) training performance indicator of each training session was stored as MSE(i), with i = 1 up to 50.
- (ii)
The simple average of the set of 50 MSE values corresponding to the training session of the previous step was calculated for each of the 5 topologies shown in
Table 6. This average value was calculated as:
- (ii)
It was checked whether the MSE(i) of each of the 50 trained neural networks was greater than the MSEmean value. If the MSE(i) < MSEmean, then this MSE(i) network was added to the new optimized MSEopt set.
- (iv)
The simple average of this new MSEopt set was calculated, thus generating the (ANNeq)mean.
In this work, it was employed the modified version of the Profile Method (PM) [
47,
48], hereinafter referred to as the Modified Profile Method (MPM), which was successfully applied by Nascimento and Oliveira [
49] and by Nascimento et al. [
50]. According to Lek et al. [
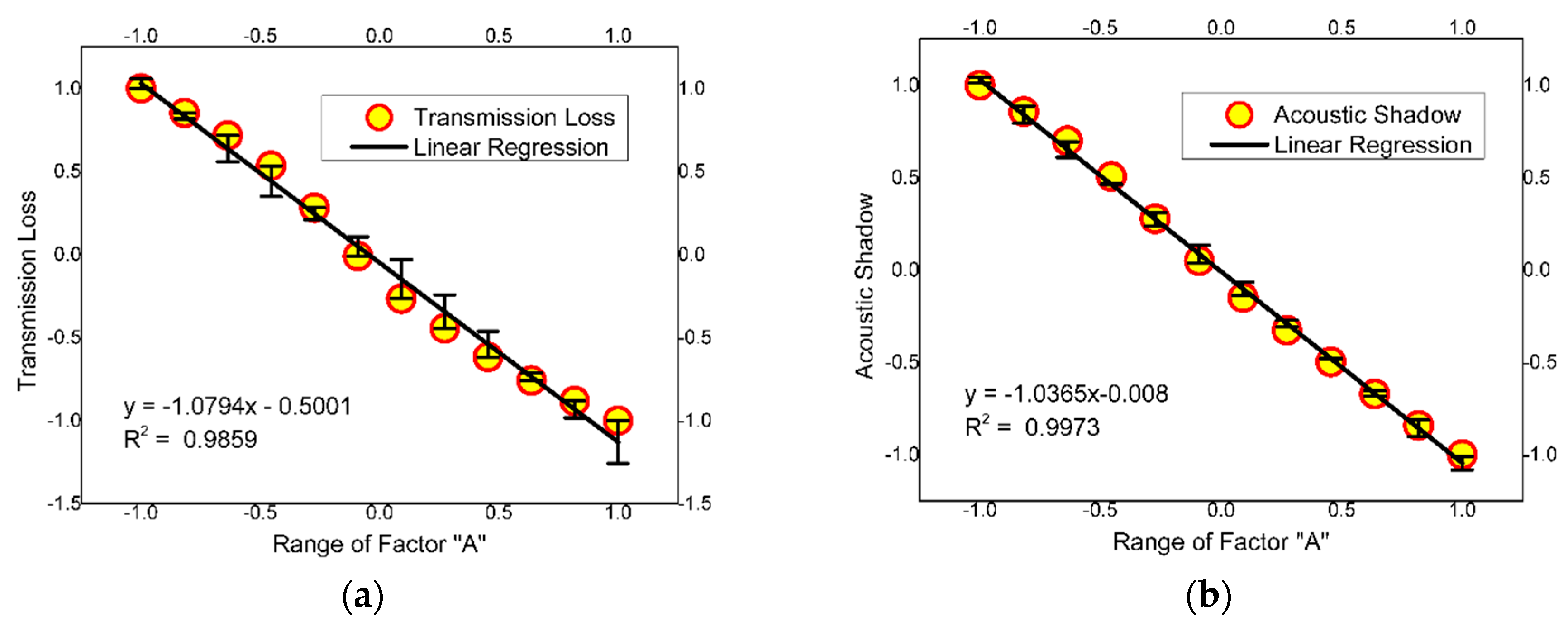
47], the original PM calculated the profile curves of each variable. A profile curve can be understood as a curve which contains the scale of the variable on the abscissa axis, i.e., the number of discrete points to which the input variable is segmented within its range, from its minimum to its maximum. Thus, the independent variable is calculated considering the average of five points applied at the output of the trained neural network. These points are the minimum value, the 1st, 2nd, and 3rd quartiles and the maximum value. As a function of the scale, the resulting curve is called the profile curve that corresponds to the input variable.
The MPM therefore calculates the significance of a given input variable of the ANN by subjecting the optimized profile curve to a linear regression. In addition, as explained earlier herein, six topologies, each trained 50 times, were considered, from which an optimized equivalent mean neural network, (ANNeq)mean, was derived. In contrast, the original PM calculates the significance based only on the maximum value of the profile curve for each input variable.
In order to make a proper graphical comparison of the performances and estimate the significance of the controllable factors, the results of the ANN and DoE regression coefficients were normalized to ANN-z and DoE-z. This normalized transformation of the data on the z-scale weighs the residual difference of the estimators based on their standard deviation, as shown in Equation (8).
The standard deviation (S) for a random population is:
where
is the number of regressors, in this case corresponding to A, B and AB, which generates
= 4 in Equation (9), while
corresponds to the samples of the controllable factors, as indicated in
Table 4.