Impact of Modified Spacer on Flow Pattern in Narrow Spacer-Filled Channels for Spiral-Wound Membrane Modules
Abstract
:1. Introduction
2. Materials and Methods
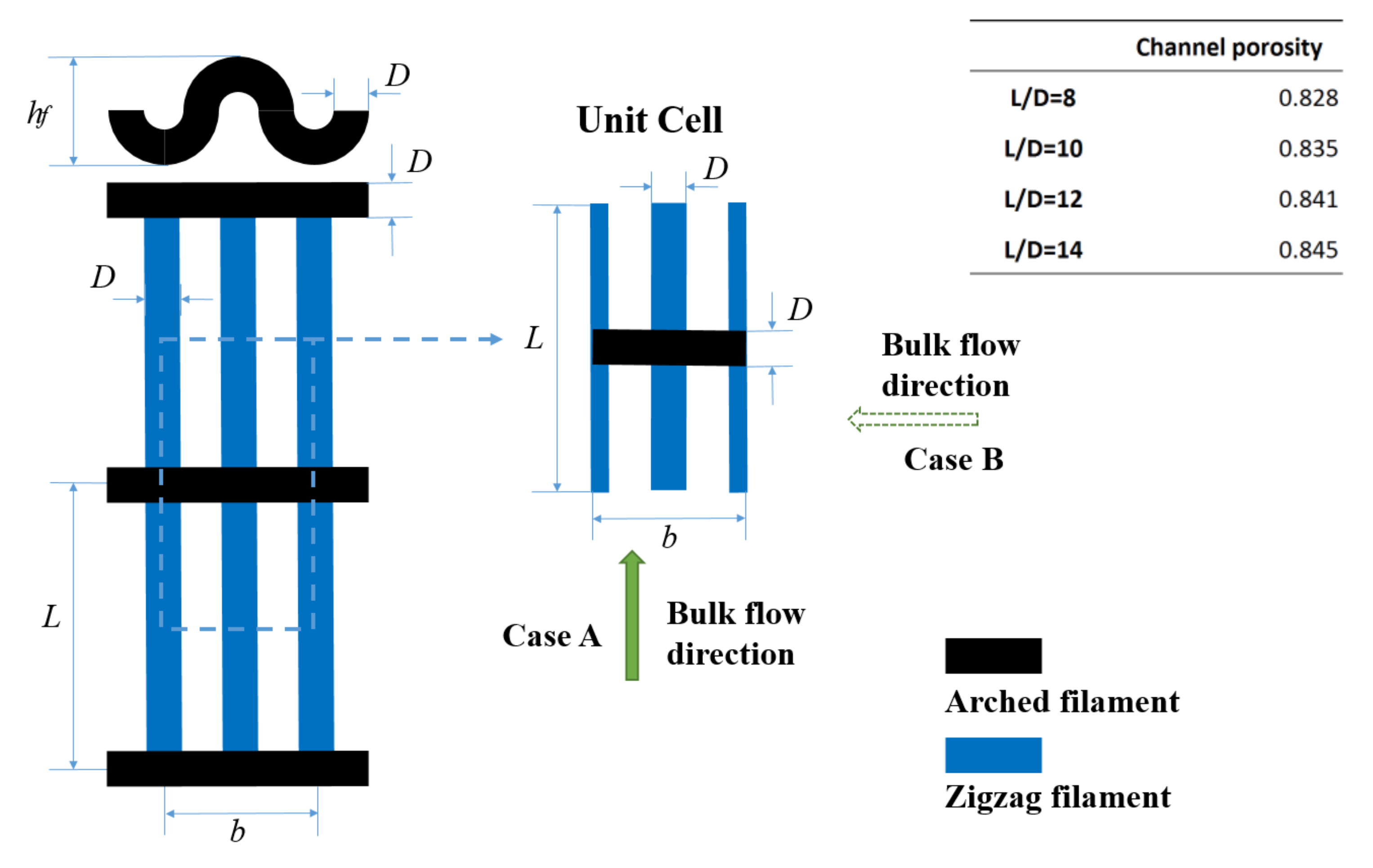
2.1. Characterization of the Modified feed Spacer
2.2. Model Description
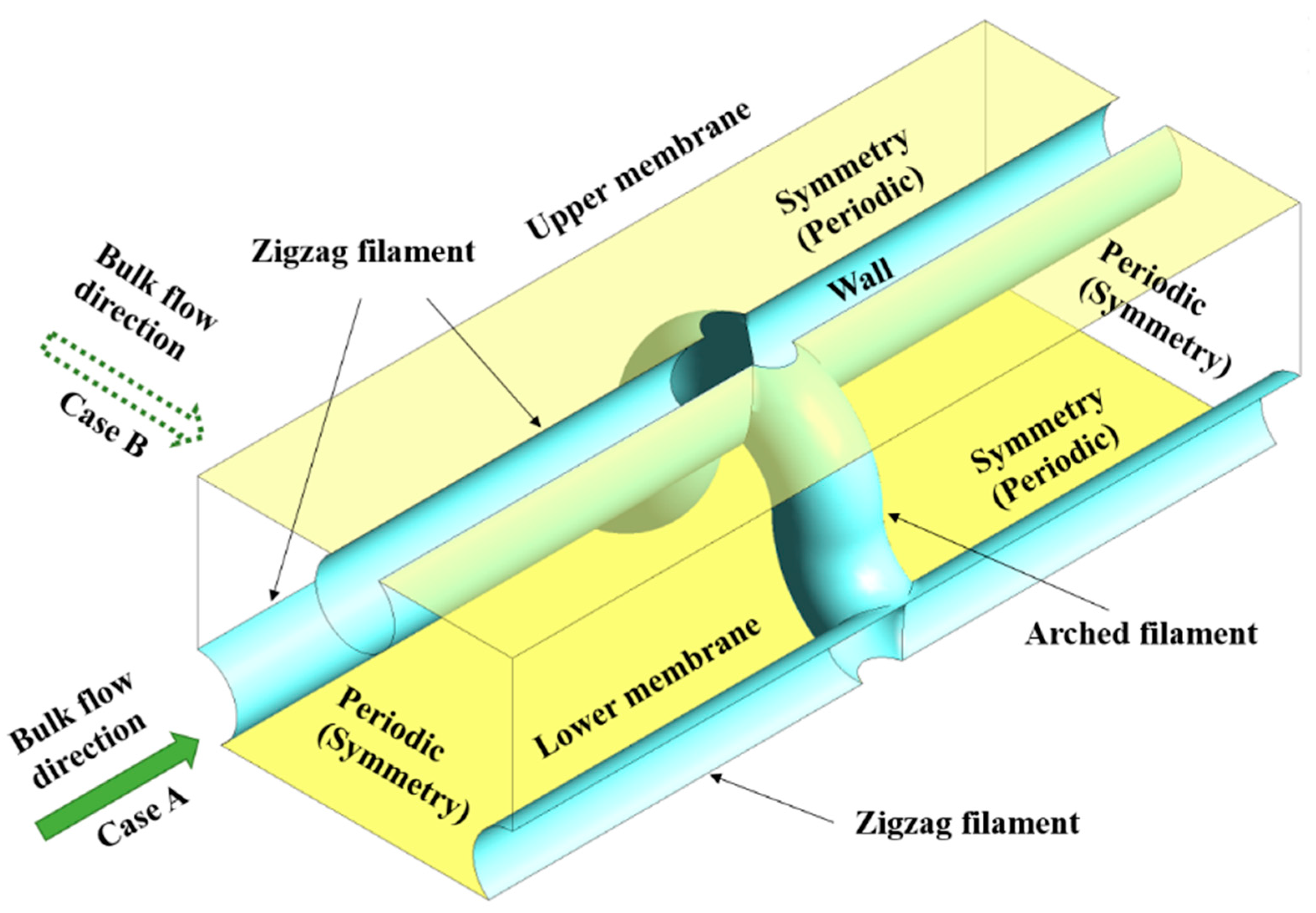
2.2.1. Computational Domain
2.2.2. Simulation of Flow Patterns
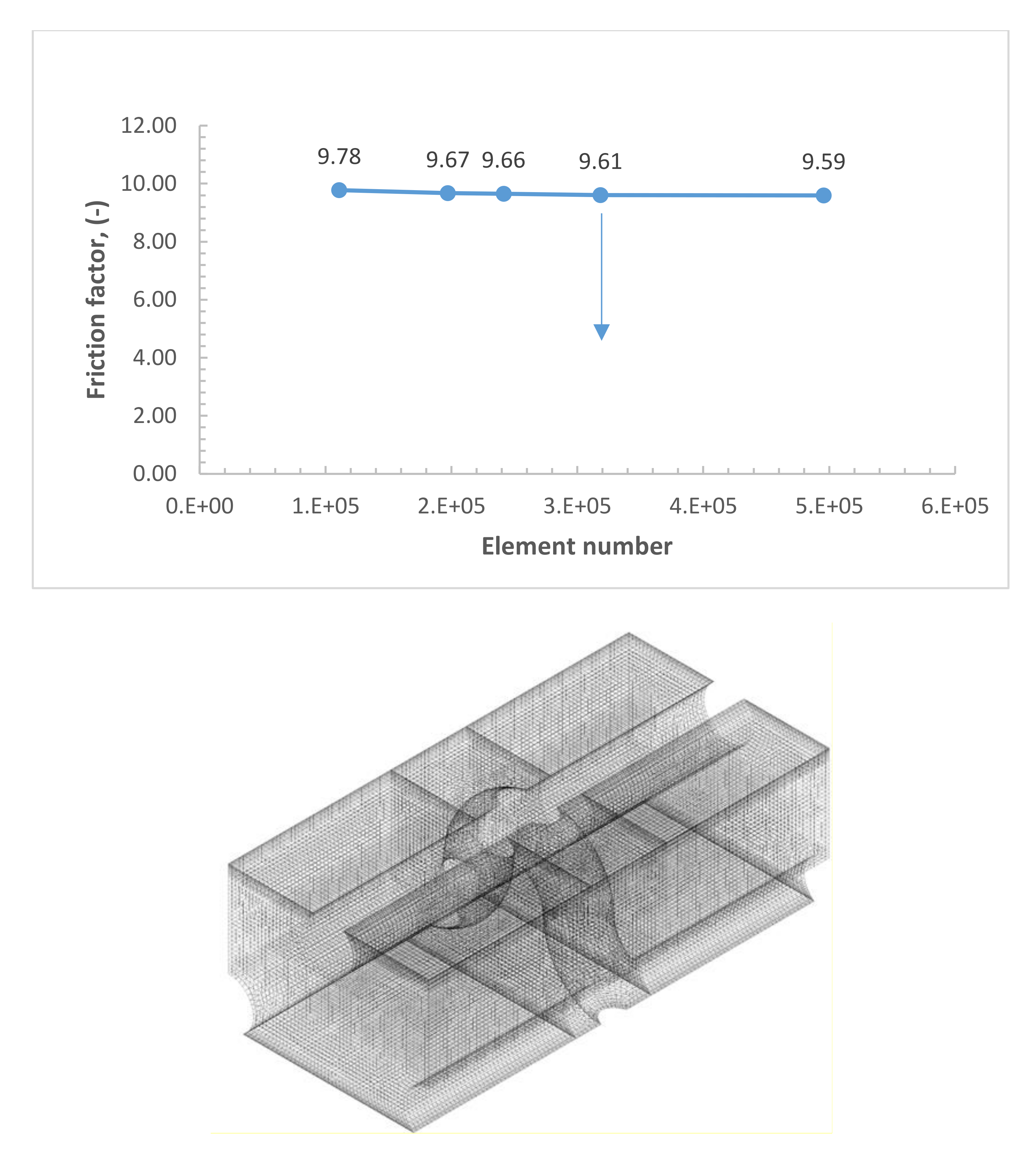
2.2.3. Model Solution
3. Results and Discussion
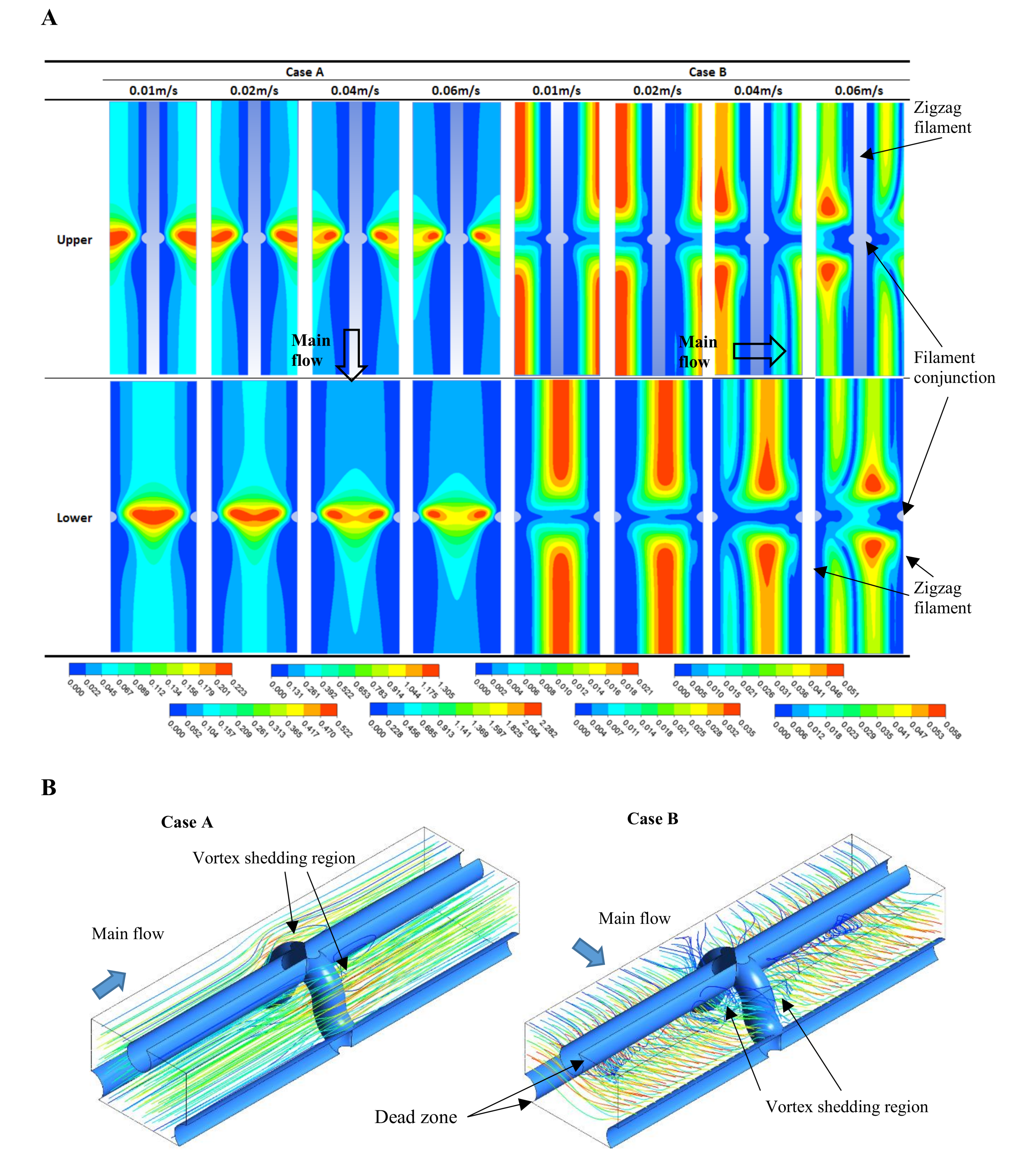
3.1. Flow Pattern and Shear Stress Distribution
3.2. Validation of Modified Spacer Simulation
3.2.1. Friction Factor
3.2.2. The Modified Friction Factor
4. Conclusions
- –
- When the main flow was normal to the arched filament, the area of the dead zone behind the zigzag filament, which was connected with the membrane, decreased with an increasing Reynolds number. In addition, the zone of vortex shedding behind the arched filament caused different flow fields, which generated a high gradient of velocity, improving the mixing of the feed solution.
- –
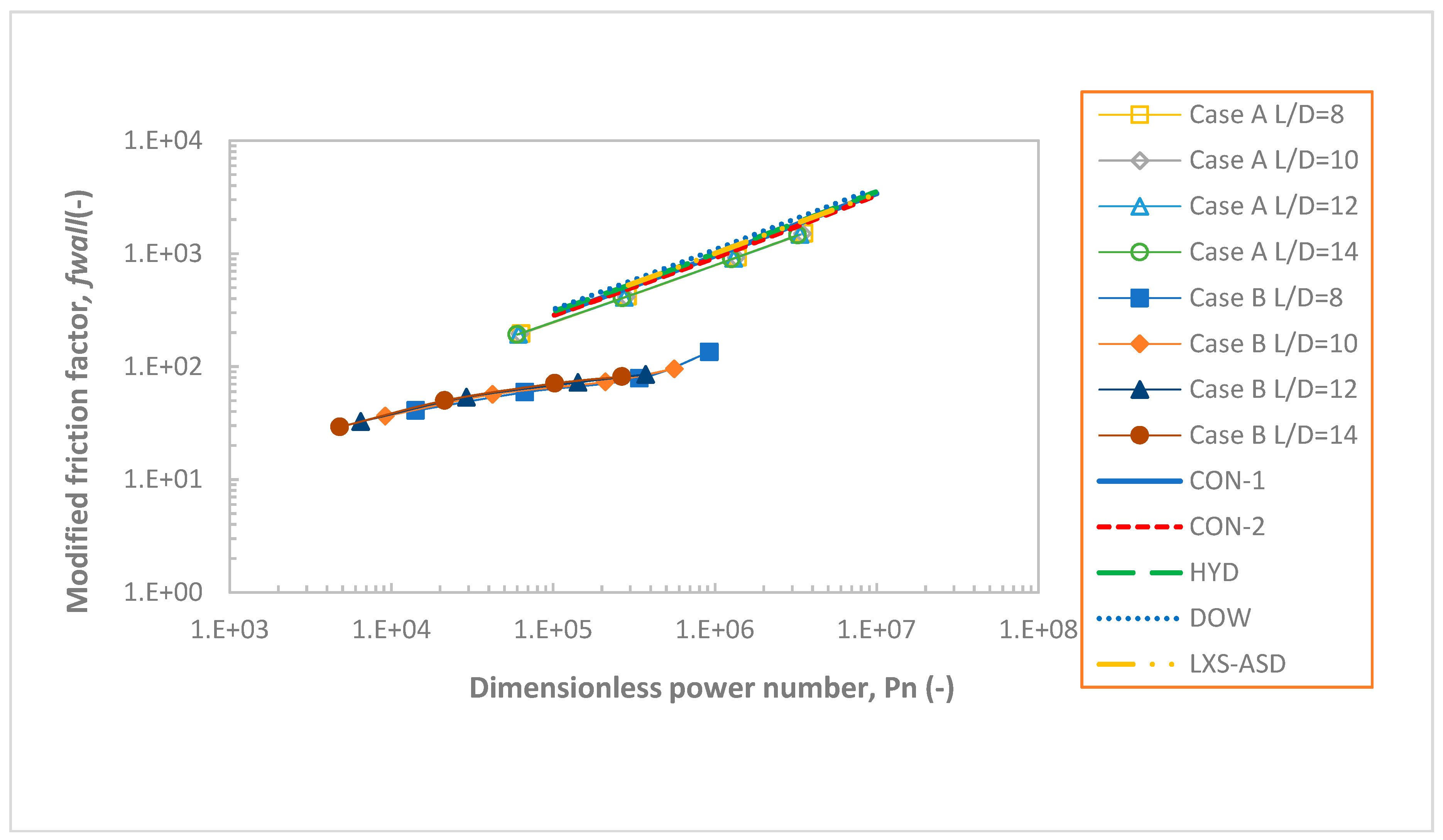
- The investigated data of power consumption (friction factor) was approximated to the conventional commercial spacer. The value was a little lower than the commercial spacer at high Reynolds numbers when the main flow was normal to the arched filament. From comparison with previous work, it can be extrapolated that the changing of flow patterns from the structure of the modified spacer did not cause too much energy consumption.
- –
- The value of the modified friction factor as a dimensionless number was similar to the results of previous work on commercial spacers when the main flow was normal to the arched filament.
- –
- The effect of porosity (element length) on the energy consumption of the modified spacer was in agreement with previous studies, but on shear stress, was smaller. This conclusion was indicated by result lines qualitatively.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| D | thickness of feed spacer filaments/cylinders (m) |
| DH | the channel hydraulic diameter (m) (defined in Equation (3)) |
| f | friction factor (-) (defined in Equation (4)) |
| fwall | the modified friction factor (-) (defined in Equation (6)) |
| hf | height of feed channel (m) |
| ΔL | the element length (m) |
| P | pressure (Pa) |
| ΔP | the pressure drop (Pa) |
| Pn | the dimensionless power number (-) (defined in Equation (5)) |
| Q | flow rate (m3 s−1) |
| Re | Reynolds number (-) (defined in Equation (2)) |
| Uave | average velocity (m s−1) |
| Usup | superficial velocity (m s−1) |
| VSpacer | feed spacer volume (m3) |
| VTotal | channel space volume (m3) |
| Greek letters | |
| ε | feed spacer porosity/voidage (defined in Equation (1)) |
| µ | fluid viscosity (Pa s) |
| v | the kinematic viscosity (-) |
| ρ | fluid density (kg m−3) |
| τwall | average shear stress (Pa) |
| Subscripts | |
| ave | average |
| sup | superficial |
References
- Jamaly, S.; Darwish, N.N.; Ahmed, I.; Hasan, S.W. A short review on reverse osmosis pretreatment technologies. Desalination 2014, 354, 30–38. [Google Scholar] [CrossRef]
- Gu, B.; Adjiman, C.S.; Xu, X.Y. The effect of feed spacer geometry on membrane performance and concentration polarisation based on 3D CFD simulations. J. Memb. Sci. 2017, 527, 78–91. [Google Scholar] [CrossRef] [Green Version]
- Sablani, S.S.; Goosen, M.F.A.; Al-Belushi, R.; Gerardos, V. Influence of spacer thickness on permeate flux in spiral-wound seawater reverse osmosis systems. Desalination 2002, 146, 225–230. [Google Scholar] [CrossRef]
- Radu, A.I.I.; Vrouwenvelder, J.S.S.; van Loosdrecht, M.C.M.C.M.; Picioreanu, C. Effect of flow velocity, substrate concentration and hydraulic cleaning on biofouling of reverse osmosis feed channels. Chem. Eng. J. 2012, 188, 30–39. [Google Scholar] [CrossRef]
- Fernández-Sempere, J.; Ruiz-Beviá, F.; García-Algado, P.; Salcedo-Díaz, R. Experimental study of concentration polarization in a crossflow reverse osmosis system using Digital Holographic Interferometry. Desalination 2010, 257, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Wiley, D.E.; Fane, A.G. CFD simulations of net-type turbulence promoters in a narrow channel. J. Memb. Sci. 2001, 185, 157–176. [Google Scholar] [CrossRef]
- Karabelas, A.J.; Kostoglou, M.; Koutsou, C.P. Modeling of spiral wound membrane desalination modules and plants—Review and research priorities. Desalination 2015, 356, 165–186. [Google Scholar] [CrossRef]
- Ranade, V.V.; Kumar, A. Fluid dynamics of spacer filled rectangular and curvilinear channels. J. Memb. Sci. 2006, 271, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Shakaib, M.; Hasani, S.M.F.; Mahmood, M. Study on the effects of spacer geometry in membrane feed channels using three-dimensional computational flow modeling. J. Memb. Sci. 2007, 297, 74–89. [Google Scholar] [CrossRef]
- Haaksman, V.A.; Siddiqui, A.; Schellenberg, C.; Kidwell, J.; Vrouwenvelder, J.S.; Picioreanu, C. Characterization of feed channel spacer performance using geometries obtained by X-ray computed tomography. J. Memb. Sci. 2017, 522, 124–139. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Fell, C.J.D.; Franken, A.C.M. Optimal channel spacer design for ultrafiltration. J. Memb. Sci. 1991, 62, 275–291. [Google Scholar] [CrossRef]
- Ma, S.; Song, L. Numerical study on permeate flux enhancement by spacers in a crossflow reverse osmosis channel. J. Memb. Sci. 2006, 284, 102–109. [Google Scholar] [CrossRef]
- Koutsou, C.P.; Yiantsios, S.G.; Karabelas, A.J. Numerical simulation of the flow in a plane-channel containing a periodic array of cylindrical turbulence promoters. J. Memb. Sci. 2004, 231, 81–90. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.A.; Wiley, D.E. Review of 3D CFD modeling of flow and mass transfer in narrow spacer-filled channels in membrane modules. Chem. Eng. Process. Process Intensif. 2010, 49, 759–781. [Google Scholar] [CrossRef]
- Hayes, R.E. Computational Flow Modelling for Chemical Reactor Engineering; Academic Press: San Diego, CA, USA, 2002; Volume 80, ISBN 0125769601. [Google Scholar]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.A.; Wiley, D.E. Numerical study of mass transfer in three-dimensional spacer-filled narrow channels with steady flow. J. Memb. Sci. 2007, 306, 228–243. [Google Scholar] [CrossRef]
- Geraldes, V.; Semião, V.; De Pinho, M.N. Flow management in nanofiltration spiral wound modules with ladder-type spacers. J. Memb. Sci. 2002, 203, 87–102. [Google Scholar] [CrossRef]
- Koutsou, C.P.; Yiantsios, S.G.; Karabelas, A.J. Direct numerical simulation of flow in spacer-filled channels: Effect of spacer geometrical characteristics. J. Memb. Sci. 2007, 291, 53–69. [Google Scholar] [CrossRef]
- Song, L.; Ma, S. Numerical studies of the impact of spacer geometry on concentration polarization in spiral wound membrane modules. Ind. Eng. Chem. Res. 2005, 44, 7638–7645. [Google Scholar] [CrossRef]
- Santos, J.L.C.; Geraldes, V.; Velizarov, S.; Crespo, J.G. Investigation of flow patterns and mass transfer in membrane module channels filled with flow-aligned spacers using computational fluid dynamics (CFD). J. Memb. Sci. 2007, 305, 103–117. [Google Scholar] [CrossRef]
- Schwinge, J.; Wiley, D.E.; Fletcher, D.F. Simulation of the flow around spacer filaments between narrow channel walls. 1. Hydrodynamics. Ind. Eng. Chem. Res. 2002, 41, 2977–2987. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. CFD analysis of the fluid flow behavior in a reverse electrodialysis stack. Desalin. Water Treat. 2012, 48, 390–403. [Google Scholar] [CrossRef] [Green Version]
- Lim, S.Y.; Liang, Y.Y.; Fimbres Weihs, G.A.; Wiley, D.E.; Fletcher, D.F. A CFD study on the effect of membrane permeance on permeate flux enhancement generated by unsteady slip velocity. J. Memb. Sci. 2018, 556, 138–145. [Google Scholar] [CrossRef]
- Kavianipour, O.; Ingram, G.D.; Vuthaluru, H.B. Investigation into the effectiveness of feed spacer configurations for reverse osmosis membrane modules using Computational Fluid Dynamics. J. Memb. Sci. 2017, 526, 156–171. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Saeed, A.; Vuthaluru, R.; Vuthaluru, H.B. Impact of Feed Spacer Filament Spacing on Mass Transport and Fouling Propensities of RO Membrane Surfaces. Chem. Eng. Commun. 2015, 202, 634–646. [Google Scholar] [CrossRef]
- Haidari, A.H.; Heijman, S.G.J.; van der Meer, W.G.J. Effect of spacer configuration on hydraulic conditions using PIV. Sep. Purif. Technol. 2018, 199, 9–19. [Google Scholar] [CrossRef]
- Schwinge, J.; Wiley, D.E.; Fletcher, D.F. Simulation of the Flow around Spacer Filaments between Channel Walls. 2. Mass-Transfer Enhancement. Ind. Eng. Chem. Res. 2002, 41, 4879–4888. [Google Scholar] [CrossRef]
- Saeed, A.; Vuthaluru, R.; Vuthaluru, H.B. Investigations into the effects of mass transport and flow dynamics of spacer filled membrane modules using CFD. Chem. Eng. Res. Des. 2015, 93, 79–99. [Google Scholar] [CrossRef]
- Lau, K.K.; Abu Bakar, M.Z.; Ahmad, A.L.; Murugesan, T. Effect of feed spacer mesh length ratio on unsteady hydrodynamics in 2D spiral wound membrane (swm) channel. Ind. Eng. Chem. Res. 2010, 49, 5834–5845. [Google Scholar] [CrossRef]
- Zimmerer, C.C.; Kottke, V. Effects of spacer geometry on pressure drop, mass transfer, mixing behavior, and residence time distribution. Desalination 1996, 104, 129–134. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Wiley, D.E. Spacer characterization and pressure drop modeling in spacer-filled channels.pdf. J. Memb. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Siddiqui, A.; Lehmann, S.; Haaksman, V.; Ogier, J.; Schellenberg, C.; van Loosdrecht, M.C.M.; Kruithof, J.C.; Vrouwenvelder, J.S. Porosity of spacer-filled channels in spiral-wound membrane systems: Quantification methods and impact on hydraulic characterization. Water Res. 2017, 119, 304–311. [Google Scholar] [CrossRef] [PubMed]
- Haidari, A.H.; Heijman, S.G.J.; van der Meer, W.G.J. Visualization of hydraulic conditions inside the feed channel of Reverse Osmosis: A practical comparison of velocity between empty and spacer-filled channel. Water Res. 2016, 106, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Meindersma, W.; De Haan, A.B.; Reith, T. Experimental validation of CFD mass transfer simulations in flat channels with non-woven net spacers. J. Memb. Sci. 2004, 232, 19–30. [Google Scholar] [CrossRef]

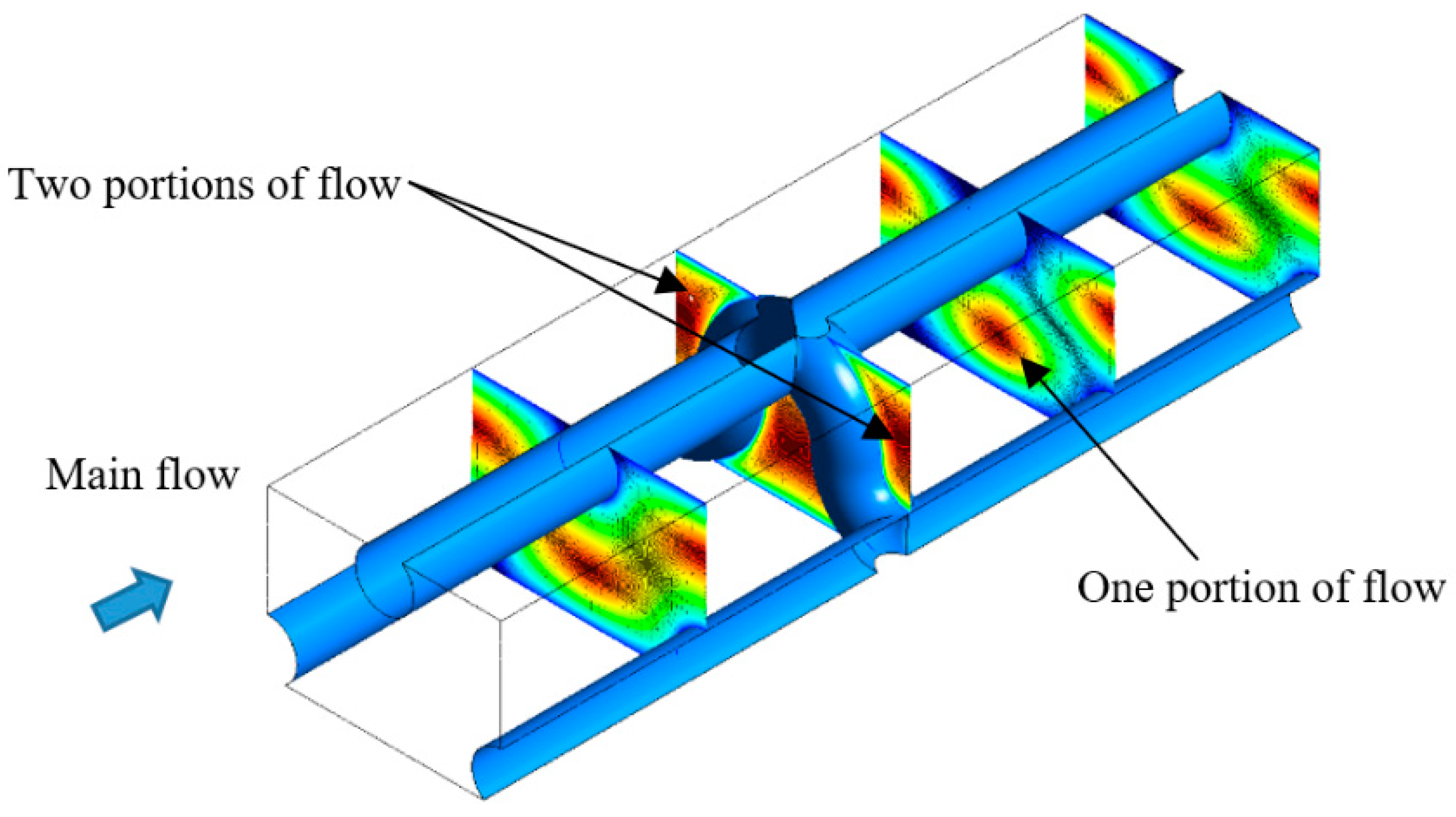
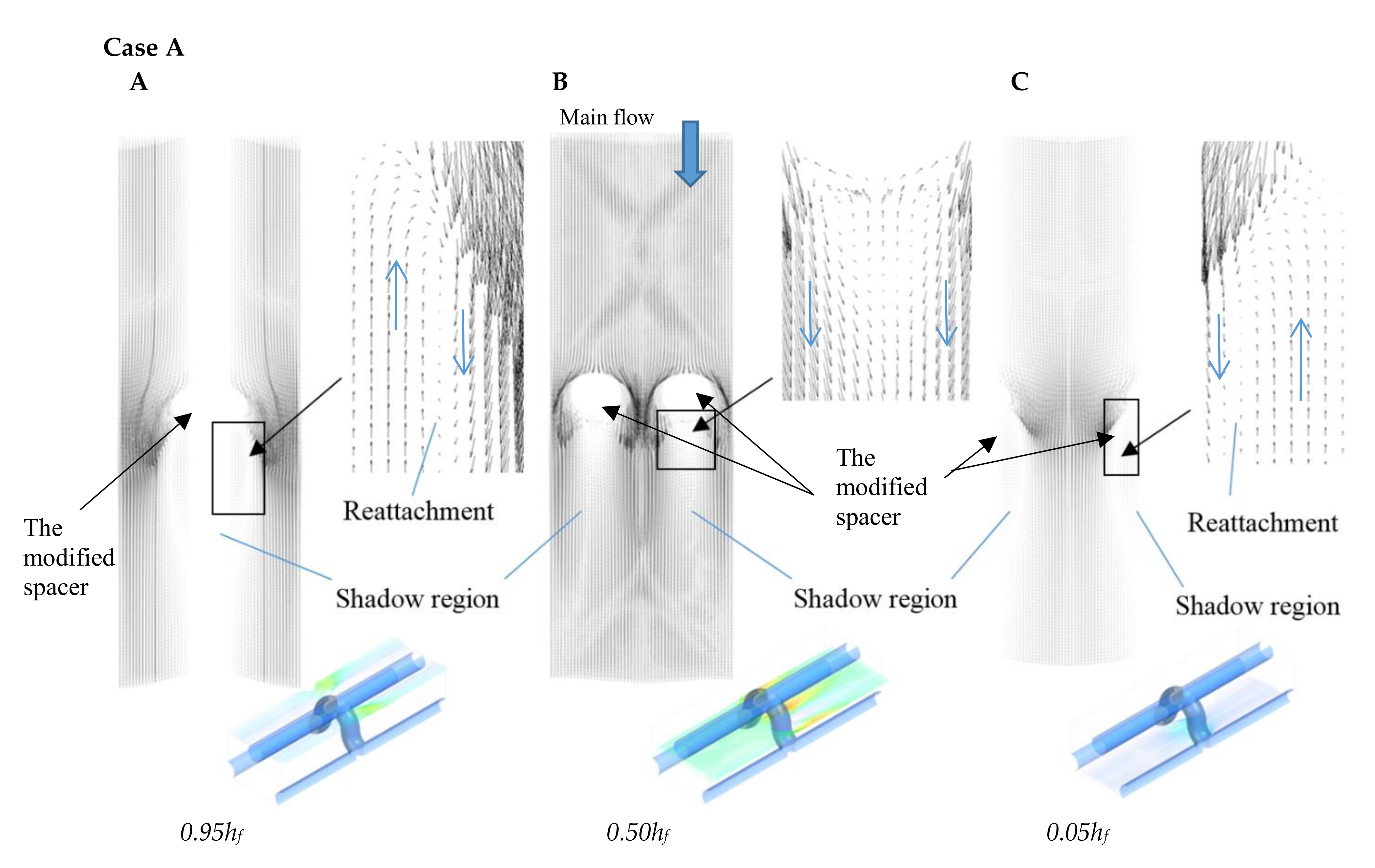
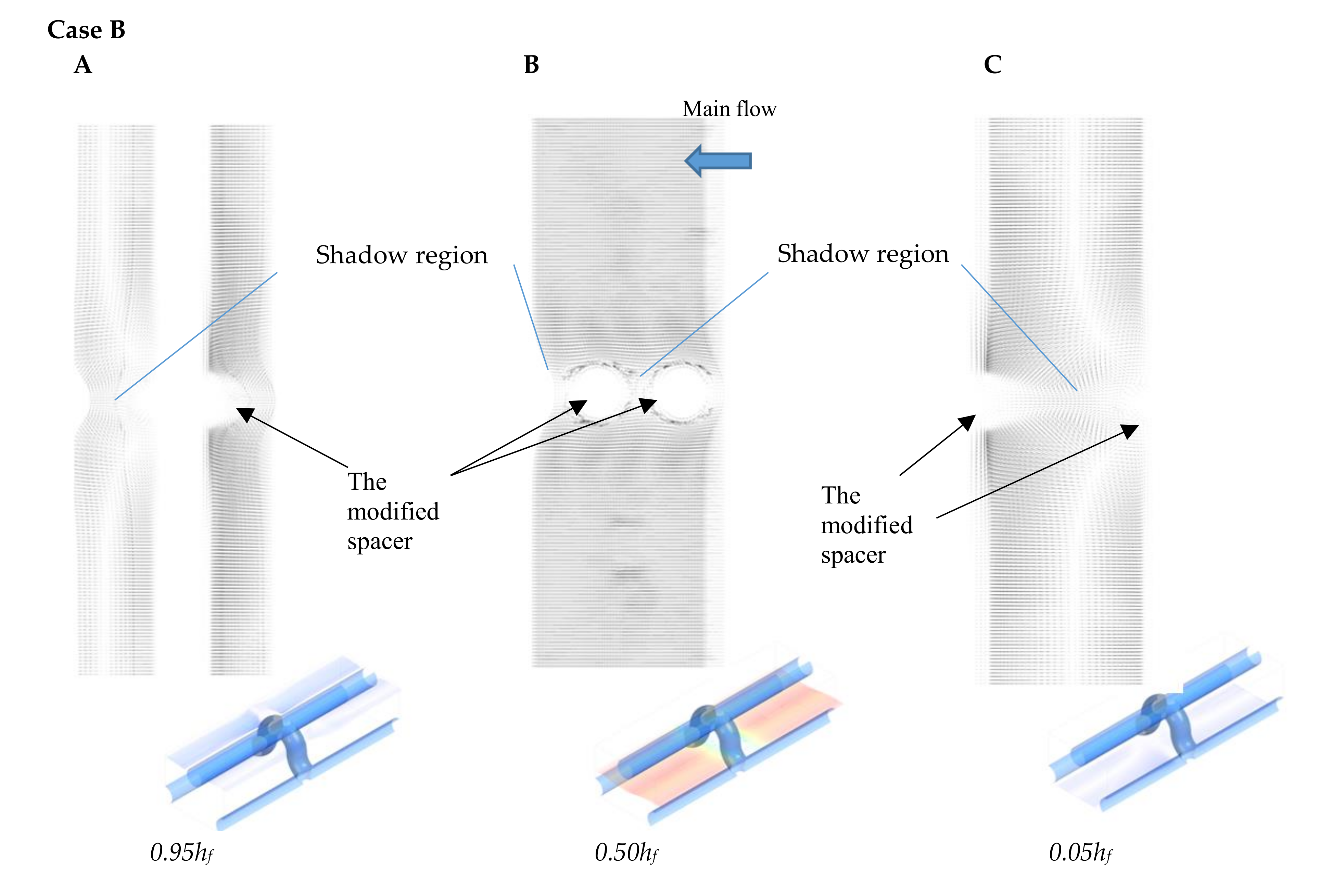

| 0.01 m/s | 0.02 m/s | 0.04 m/s | 0.06 m/s | |||
|---|---|---|---|---|---|---|
| Case A | upper | smaller | 23.916% | 29.274% | 37.002% | 42.018% |
| greater | 2.056% | 1.605% | 0.758% | 0.552% | ||
| lower | smaller | 23.855% | 29.099% | 36.751% | 41.720% | |
| greater | 2.093% | 1.753% | 0.814% | 0.572% | ||
| Case B | upper | smaller | 33.544% | 35.614% | 29.087% | 23.815% |
| greater | 13.788% | 12.603% | 4.015% | 1.937% | ||
| lower | smaller | 33.427% | 35.987% | 29.285% | 23.635% | |
| greater | 13.954% | 13.133% | 3.838% | 1.815% |
| Channel porosity | SPC(Pa/s) | ||
|---|---|---|---|
| Case A | L/D=8 | 0.828 | 10.399 |
| L/D=10 | 0.835 | 8.663 | |
| L/D=12 | 0.841 | 7.554 | |
| L/D=14 | 0.845 | 6.802 | |
| Case B | L/D=8 | 0.828 | 69.736 |
| L/D=10 | 0.835 | 92.111 | |
| L/D=12 | 0.841 | 124.068 | |
| L/D=14 | 0.845 | 151.636 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Terashima, M.; Liu, B.; Yasui, H. Impact of Modified Spacer on Flow Pattern in Narrow Spacer-Filled Channels for Spiral-Wound Membrane Modules. Environments 2018, 5, 116. https://doi.org/10.3390/environments5110116
Han Z, Terashima M, Liu B, Yasui H. Impact of Modified Spacer on Flow Pattern in Narrow Spacer-Filled Channels for Spiral-Wound Membrane Modules. Environments. 2018; 5(11):116. https://doi.org/10.3390/environments5110116
Chicago/Turabian StyleHan, Zhiming, Mitsuharu Terashima, Bing Liu, and Hidenari Yasui. 2018. "Impact of Modified Spacer on Flow Pattern in Narrow Spacer-Filled Channels for Spiral-Wound Membrane Modules" Environments 5, no. 11: 116. https://doi.org/10.3390/environments5110116
APA StyleHan, Z., Terashima, M., Liu, B., & Yasui, H. (2018). Impact of Modified Spacer on Flow Pattern in Narrow Spacer-Filled Channels for Spiral-Wound Membrane Modules. Environments, 5(11), 116. https://doi.org/10.3390/environments5110116





