Methods to Invert Temperature Data and Heat Flow Data for Thermal Conductivity in Steady-State Conductive Regimes
Abstract
1. Introduction
2. Thermal Data Background
3. Forward Modeling
3.1. Governing Equations
3.2. Finite Volume Method
3.3. Discretization
3.4. Interpolating Fields
3.5. Boundary Conditions
- Known temperatures (Dirichlet boundary condition) are enforced at the top of the model.
- The heat flow through the sides of the model is assumed to be zero (zero Neumann boundary condition).
- At the base of the model, either the temperature (Dirichlet) or the vertical heat flow rate (Neumann) can be specified, depending on the situation being modeled. For example, the heat flow rate may be measured at the surface. If it is reasonable to assume that the horizontal variation of heat flow is negligible at depth, then a constant Neumann boundary condition is appropriate to use at the base of the model. The heat flow at the bottom of the model may be set to the average heat flow at the surface, subtracting the contributions of any known heat sources or sinks within the region of interest. Alternatively, a Dirichlet boundary condition may be desirable if there is information about temperatures at depth from other geophysical methods. This modeling approach can accommodate either type of boundary condition at any surface. For the examples in this study, we use a constant Neumann boundary condition at the base of the model.
3.5.1. Dirichlet Boundary Conditions
3.5.2. Neumann Boundary Conditions
3.6. Solving for Temperature and Heat Flow
3.7. Accuracy and Convergence
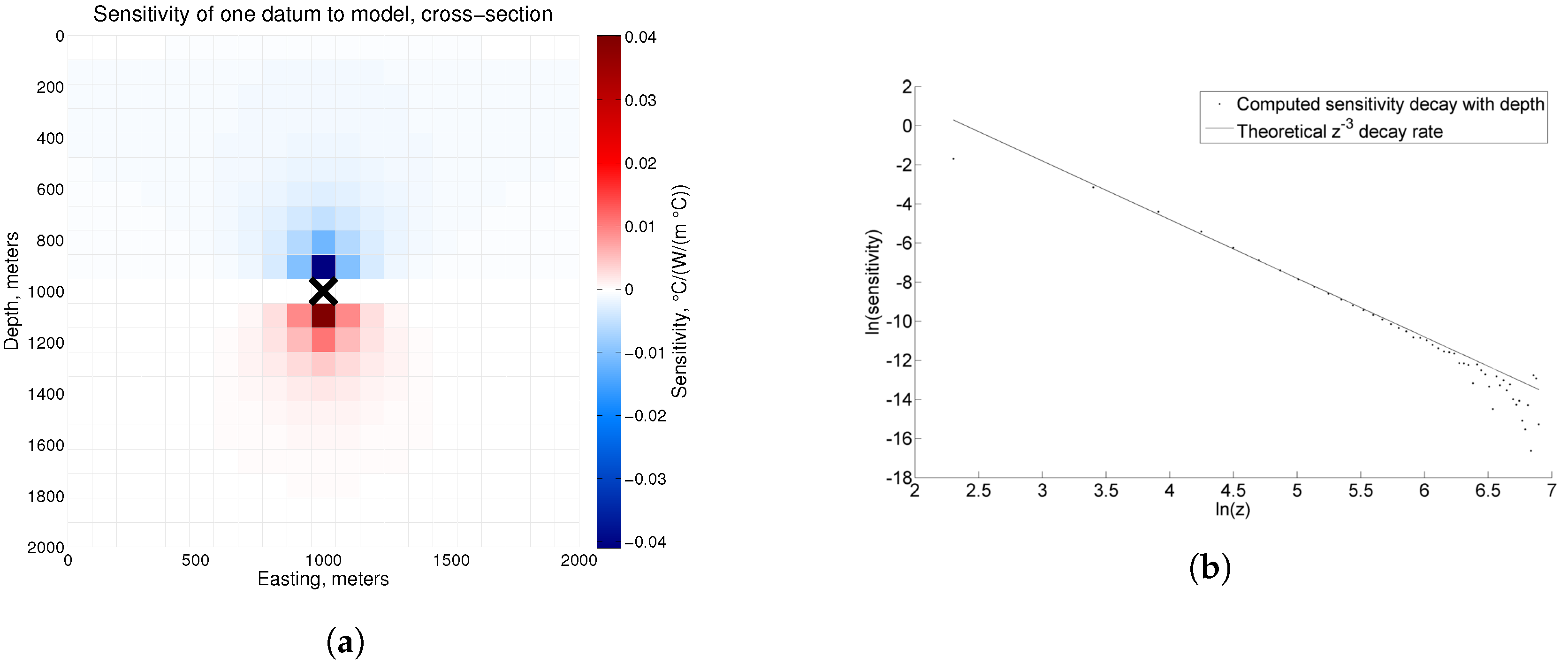
4. Sensitivity
5. Inversion Methodology
5.1. The Inverse Problem
5.2. The Gauss-Newton Method
5.3. Weighting Function
5.3.1. Sensitivity Weighting
5.3.2. Depth Weighting
5.3.3. Distance Weighting
6. Inversions of Synthetic Data
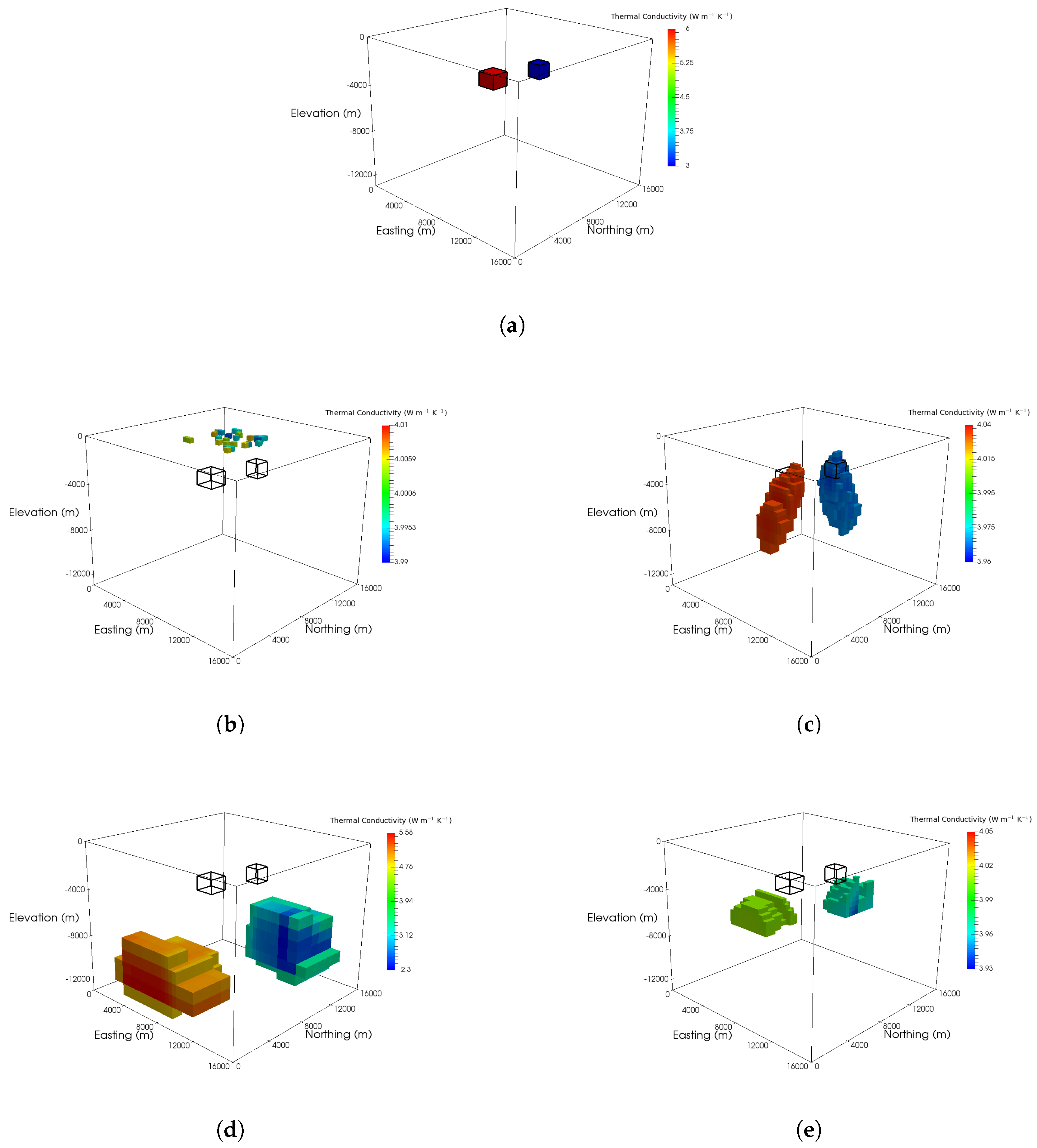
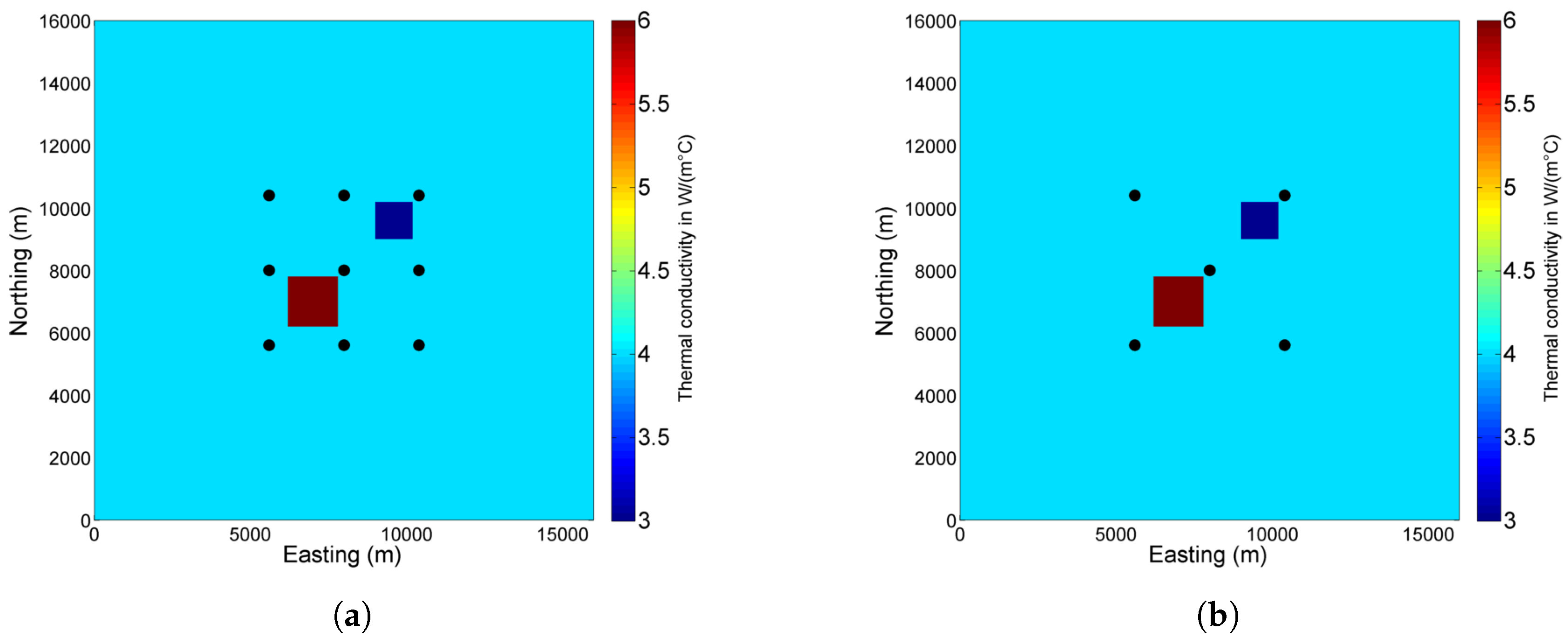
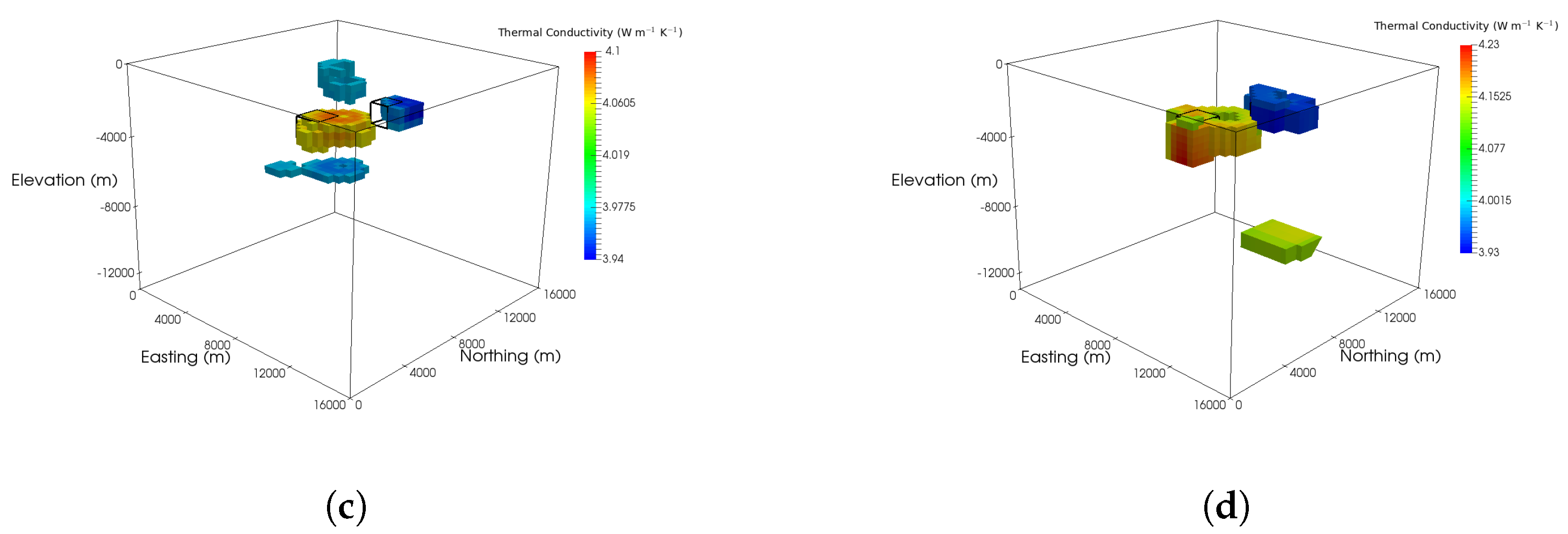
6.1. Block Model
6.1.1. Surface Heat Flow Data Inversion
6.1.2. Borehole Temperature Data Inversion
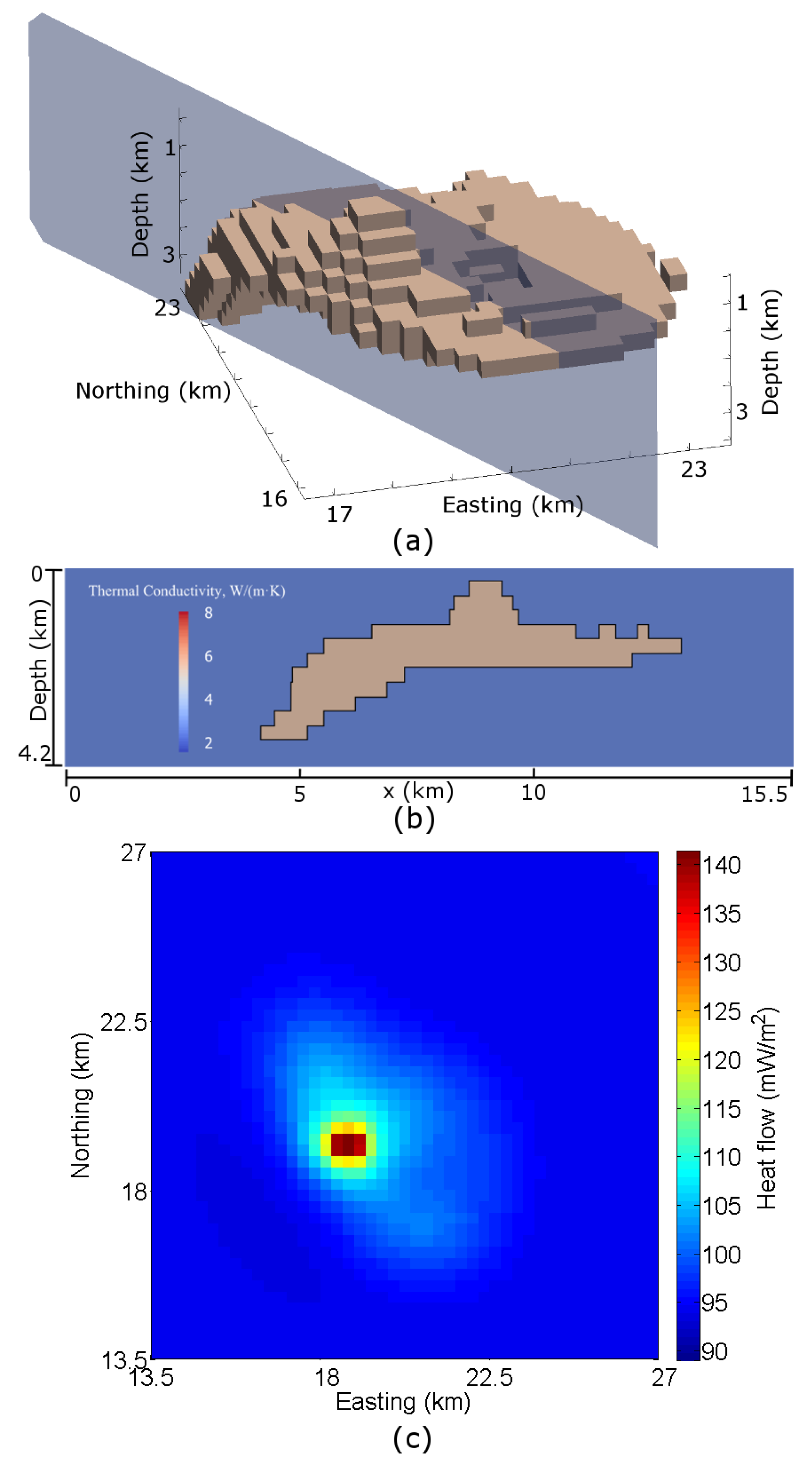
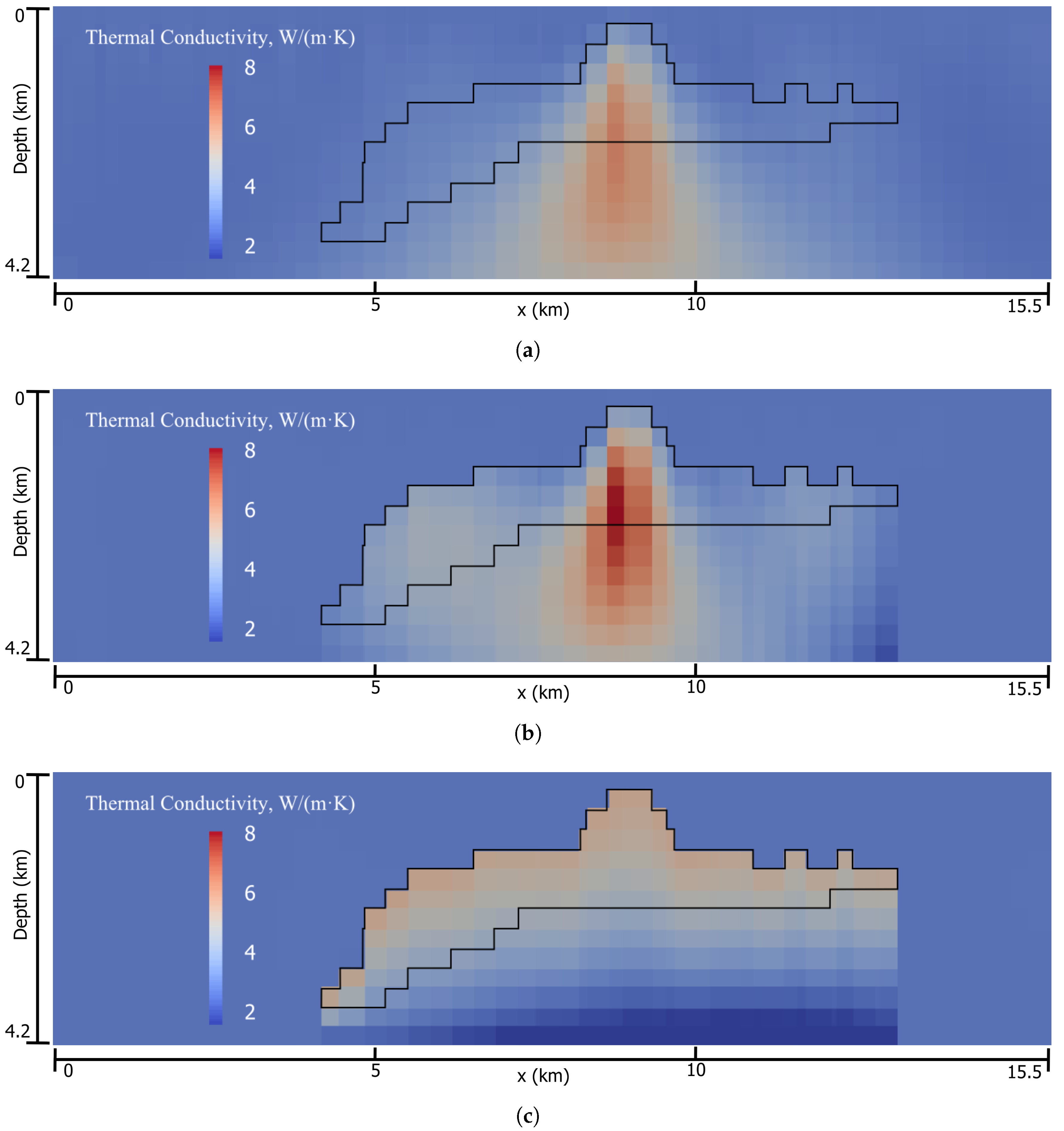
6.2. SEG/EAGE Salt Model
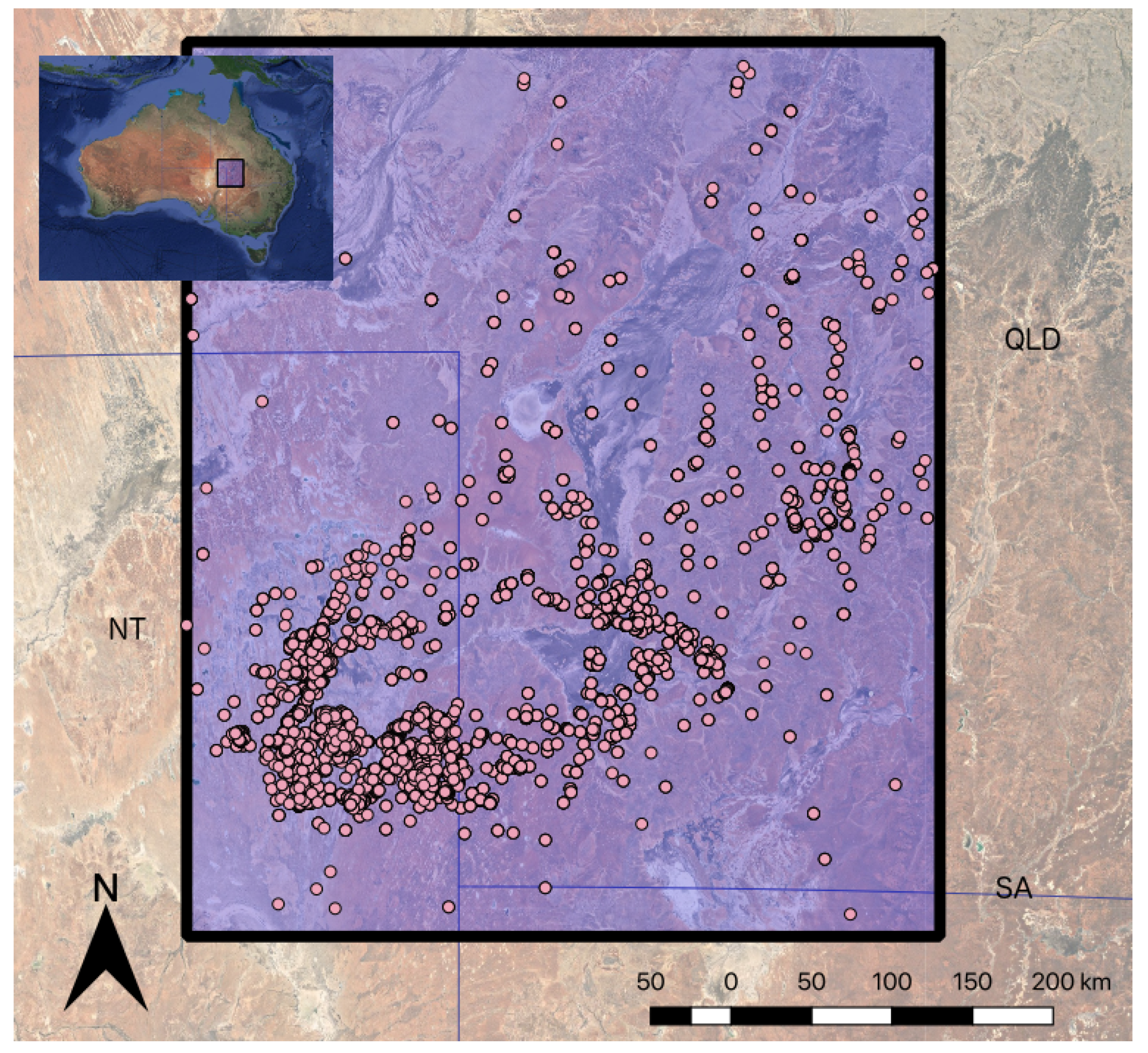
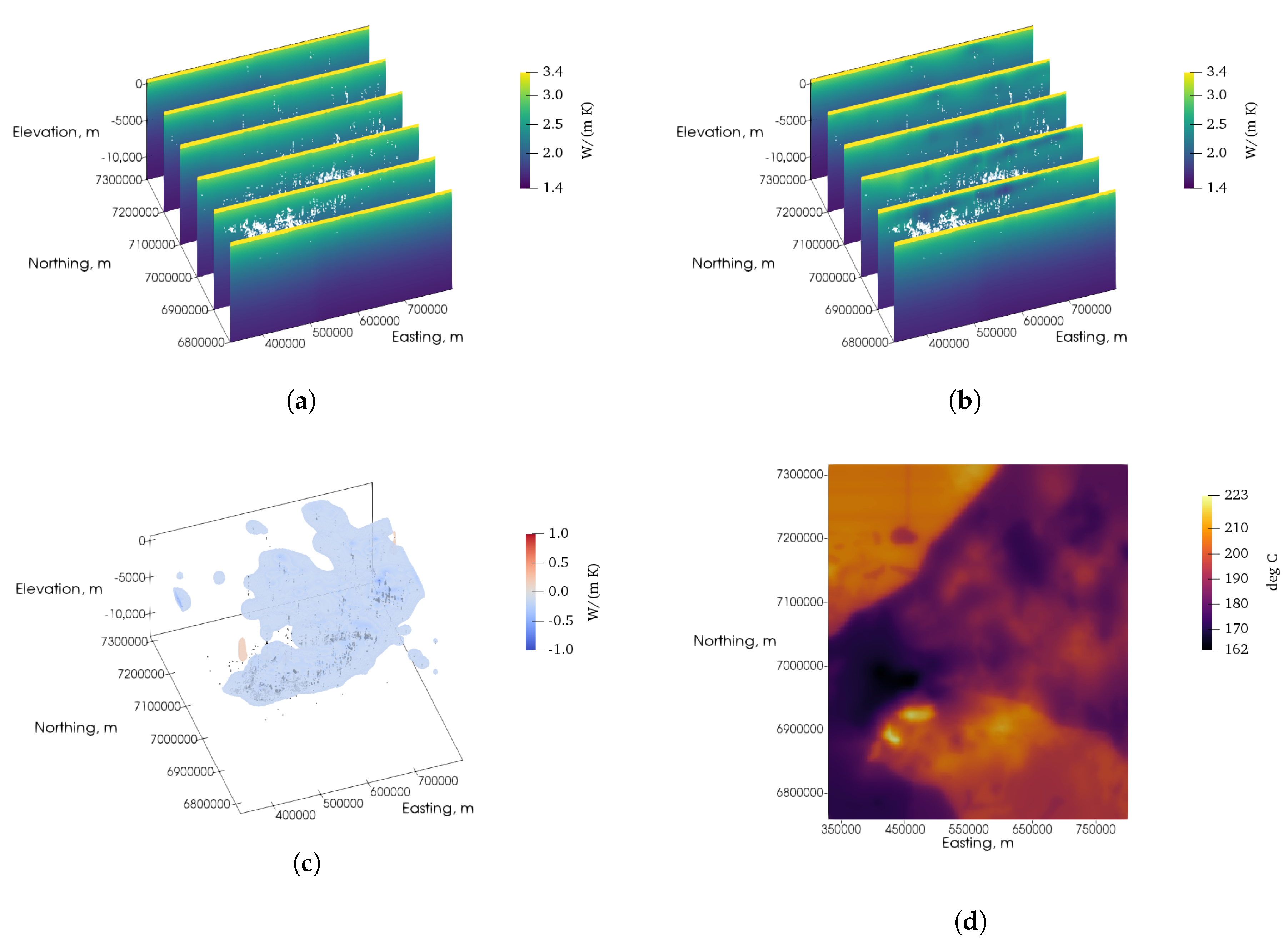
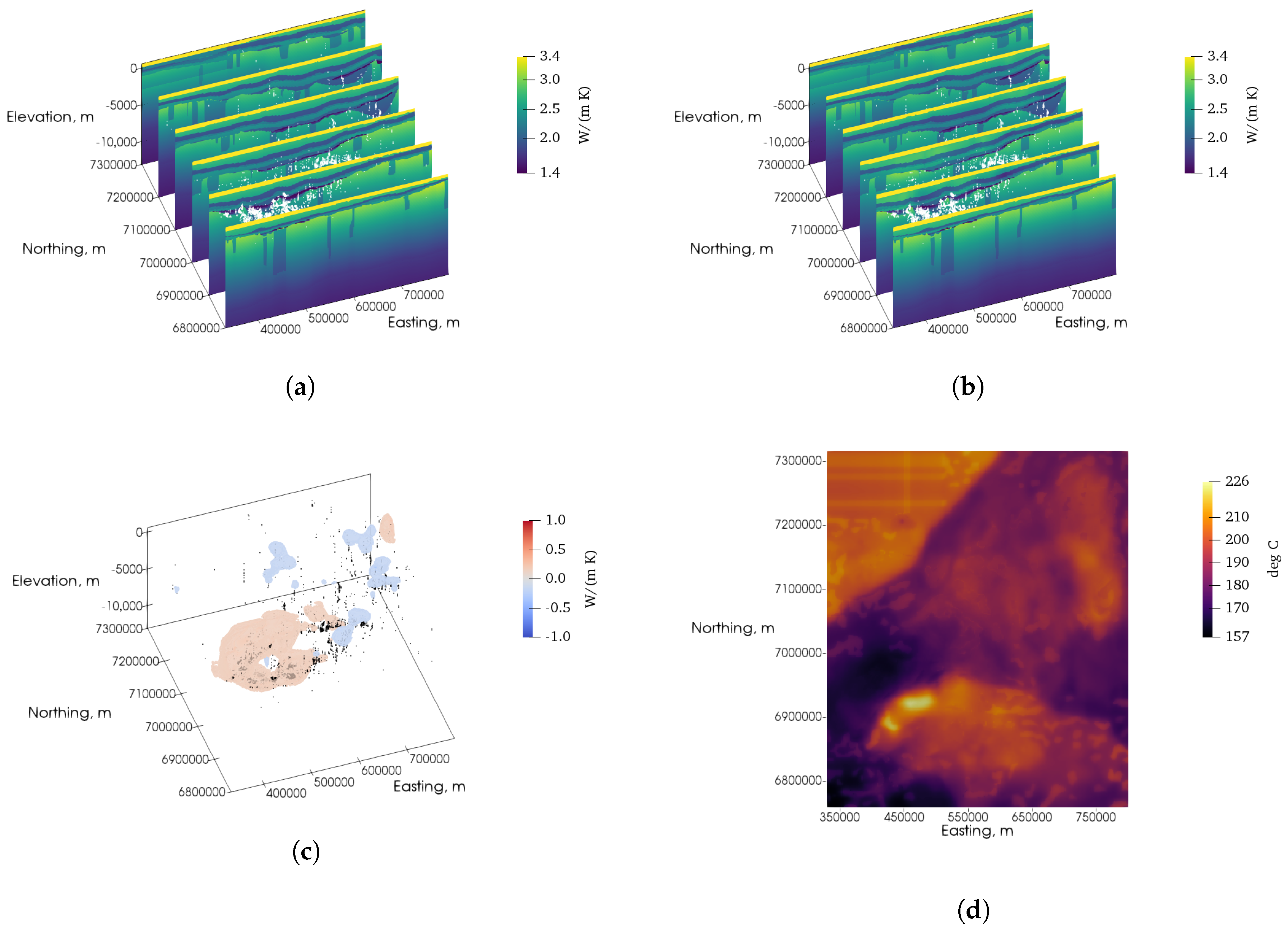
7. Inversions of Cooper Basin Data
Field Data Inversions
8. Discussion
8.1. Information Content of Temperature Data
8.2. Information Content of Heat Flow Data
8.3. Practical Considerations and Assumptions
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Matrix Definitions
Appendix A.1. The Gradient Operator
Appendix A.2. The Harmonic Interpolant
Appendix A.3. The Full Forward Operation
Appendix A.4. Interpolation
Appendix B. Sensitivity Derivation and Computation
Appendix B.1. Temperature Sensitivity
Appendix B.2. Heat Flow Sensitivity
Appendix B.3. Computing Sensitivity Vector Products
- Temperature: Compute
- Compute .
- Solve for .
- Compute .
- Temperature: Compute
- Compute .
- Solve for (equivalently, solve since is symmetric).
- Compute .
- Heat flow: Compute
- Compute .
- Solve for .
- Compute .
- Heat flow: Compute
- Compute .
- Compute .
- Solve for .
- Compute .
References
- Beardsmore, G.R.; Cull, J.P. Crustal Heat Flow: A Guide to Measurement and Modelling; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Stein, C.A.; Stein, S. A model for the global variation in oceanic depth and heat flow with lithospheric age. Nature 1992, 359, 123–129. [Google Scholar] [CrossRef]
- Mottaghy, D.; Pechnig, R.; Vogt, C. The geothermal project Den Haag: 3D numerical models for temperature prediction and reservoir simulation. Geothermics 2011, 40, 199–210. [Google Scholar] [CrossRef]
- Anderson, M.P. Heat as a ground water tracer. Groundwater 2005, 43, 951–968. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Beck, A. An inverse approach to heat flow study in hydrologically active areas. Geophys. J. Int. 1989, 98, 69–84. [Google Scholar] [CrossRef]
- Jokinen, J.; Kukkonen, I.T. Inverse simulation of the lithospheric thermal regime using the Monte Carlo method. Tectonophysics 1999, 306, 293–310. [Google Scholar] [CrossRef]
- Rath, V.; Wolf, A.; Bücker, H. Joint three-dimensional inversion of coupled groundwater flow and heat transfer based on automatic differentiation: Sensitivity calculation, verification, and synthetic examples. Geophys. J. Int. 2006, 167, 453–466. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A. Stochastic joint inversion of temperature and self-potential data. Geophys. J. Int. 2009, 179, 640–654. [Google Scholar] [CrossRef]
- Nagihara, S. Three-dimensional inverse modeling of the refractive heat-flow anomaly associated with salt diapirism. AAPG Bull. 2003, 87, 1207–1222. [Google Scholar] [CrossRef]
- Papadopoulos, D.; Herty, M.; Rath, V.; Behr, M. Identification of uncertainties in the shape of geophysical objects with level sets and the adjoint method. Comput. Geosci. 2011, 15, 737–753. [Google Scholar] [CrossRef]
- Oliver, D.S.; Reynolds, A.C.; Liu, N. Inverse Theory for Petroleum Reservoir Characterization and History Matching; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Shen, P.Y.; Beck, A. Least squares inversion of borehole temperature measurements in functional space. J. Geophys. Res. Solid Earth 1991, 96, 19965–19979. [Google Scholar] [CrossRef]
- Ollinger, D.; Baujard, C.; Kohl, T.; Moeck, I. Distribution of thermal conductivities in the Groß Schönebeck (Germany) test site based on 3D inversion of deep borehole data. Geothermics 2010, 39, 46–58. [Google Scholar] [CrossRef]
- Hermanrud, C.; Cao, S.; Lerche, I. Estimates of virgin rock temperature derived from BHT measurements: Bias and error. Geophysics 1990, 55, 924–931. [Google Scholar] [CrossRef]
- Andaverde, J.; Verma, S.P.; Santoyo, E. Uncertainty estimates of static formation temperatures in boreholes and evaluation of regression models. Geophys. J. Int. 2005, 160, 1112–1122. [Google Scholar] [CrossRef]
- Goutorbe, B.; Lucazeau, F.; Bonneville, A. Comparison of several BHT correction methods: A case study on an Australian data set. Geophys. J. Int. 2007, 170, 913–922. [Google Scholar] [CrossRef]
- Nagihara, S.; Christie, C.H.; Richards, M. Comparison of Methodologies for Correcting Bottom-Hole Temperature Measurements: An Example from the East Cameron and West Cameron Federal Lease Areas in the Gulf of Mexico. Gulf Coast Assoc. Geol. Soc. Trans. 2014, 64, 293–302. [Google Scholar]
- Stuwe, K. Energetics: Heat and Temperature. In Geodynamics of the Lithosphere: An Introduction; Springer: Berlin/Heidelberg, Germany, 2007; pp. 51–137. [Google Scholar] [CrossRef]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- Hyman, J.M.; Knapp, R.J.; Scovel, J.C. High order finite volume approximations of differential operators on nonuniform grids. Phys. D Nonlinear Phenom. 1992, 60, 112–138. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; John Hopkins University Press: Baltimore, MD, USA, 2012; Volume 3. [Google Scholar]
- Forsyth, P.; Sammon, P. Quadratic convergence for cell-centered grids. Appl. Numer. Math. 1988, 4, 377–394. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Oldenburg, D.W. Non-linear inversion using general measures of data misfit and model structure. Geophys. J. Int. 1998, 134, 213–227. [Google Scholar] [CrossRef]
- Hansen, P.C. The L-Curve and its Use in the Numerical Treatment of Inverse Problems. In Computational Inverse Problems in Electrocardiology; Johnston, P., Ed.; WIT Press: Southampton, UK, 2001. [Google Scholar]
- Vogel, C.R. Computational Methods for Inverse Problems; Society of Industrial and Applied Mathematics, Frontiers in Applied Mathematics: Philadelphia, PA, USA, 2002; Volume 23. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research; Springer: New York, NY, USA, 1999. [Google Scholar]
- Li, Y.; Oldenburg, D.W. Joint inversion of surface and three-component borehole magnetic data. Geophysics 2000, 65, 540–552. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Hyndman, R.D.; Davis, E.E.; Wright, J.A. The measurement of marine geothermal heat flow by a multipenetration probe with digital acoustic telemetry and insitu thermal conductivity. Mar. Geophys. Res. 1979, 4, 181–205. [Google Scholar] [CrossRef]
- Houseman, G.A.; Cull, J.P.; Muir, P.M.; Paterson, H.L. Geothermal signatures and uranium ore deposits on the Stuart Shelf of South Australia. Geophysics 1989, 54, 158–170. [Google Scholar] [CrossRef]
- Jones, I.F.; Davison, I. Seismic imaging in and around salt bodies. Interpretation 2014, 2, SL1–SL20. [Google Scholar] [CrossRef]
- Routh, P.S.; Jorgensen, G.J.; Kisabeth, J.L. Base of the salt imaging using gravity and tensor gravity data. In SEG Technical Program Expanded Abstracts 2001; Society of Exploration Geophysicists: Tulsa, OK, USA, 2001; pp. 1482–1484. [Google Scholar]
- Hoversten, G.M.; Constable, S.C.; Morrison, H.F. Marine magnetotellurics for base-of-salt mapping: Gulf of Mexico field test at the Gemini structure. Geophysics 2000, 65, 1476–1488. [Google Scholar] [CrossRef]
- Aminzadeh, F.; Brac, J.; Kunz, T. 3-D Salt and Overthrust Models; Society of Exploration Geophysicists: Tulsa, OK, USA, 1997. [Google Scholar]
- Holgate, F.; Gerner, E. OZTemp Well Temperature Data; Geoscience Australia: Canberra, Australia, 2010. [Google Scholar]
- Holl, H.G. What Did We Learn about EGS in the Cooper Basin? Geodynamics Limited: Milton, Australia, 2015. [Google Scholar]
- Meixner, A.; Kirkby, A.; Lescinsky, D.; Horspool, N. The Cooper Basin 3D Map Version 2: Thermal Modelling and Temperature Uncertainty; Geoscience Australia: Canberra, Australia, 2012; Volume 60. [Google Scholar]
- Haber, E. Computational Methods in Geophysical Electromagnetics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014. [Google Scholar]

| Control Volumes in Each Direction | Maximum Error in u, °C | ROC of Maximum Error in u | Maximum Error in q, °C | ROC of Maximum Error in q |
|---|---|---|---|---|
| 5 | 0.588 | 15.84 | ||
| 7 | 0.304 | 1.958 | 8.14 | 1.978 |
| 9 | 0.185 | 1.974 | 4.92 | 2.008 |
| 11 | 0.124 | 1.982 | 3.30 | 1.985 |
| 13 | 0.089 | 1.987 | 2.38 | 1.968 |
| 15 | 0.067 | 1.989 | 1.79 | 1.973 |
| 17 | 0.052 | 1.991 | 1.40 | 1.990 |
| 19 | 0.042 | 1.993 | 1.12 | 2.000 |
| 21 | 0.034 | 1.994 | 0.92 | 1.989 |
| 23 | 0.029 | 1.994 | 0.76 | 1.997 |
| 25 | 0.024 | 1.995 | 0.65 | 1.984 |
| 27 | 0.021 | 1.996 | 0.56 | 1.990 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McAliley, W.A.; Li, Y. Methods to Invert Temperature Data and Heat Flow Data for Thermal Conductivity in Steady-State Conductive Regimes. Geosciences 2019, 9, 293. https://doi.org/10.3390/geosciences9070293
McAliley WA, Li Y. Methods to Invert Temperature Data and Heat Flow Data for Thermal Conductivity in Steady-State Conductive Regimes. Geosciences. 2019; 9(7):293. https://doi.org/10.3390/geosciences9070293
Chicago/Turabian StyleMcAliley, Wallace Anderson, and Yaoguo Li. 2019. "Methods to Invert Temperature Data and Heat Flow Data for Thermal Conductivity in Steady-State Conductive Regimes" Geosciences 9, no. 7: 293. https://doi.org/10.3390/geosciences9070293
APA StyleMcAliley, W. A., & Li, Y. (2019). Methods to Invert Temperature Data and Heat Flow Data for Thermal Conductivity in Steady-State Conductive Regimes. Geosciences, 9(7), 293. https://doi.org/10.3390/geosciences9070293





