Evaluation of Different Pooling Methods to Establish a Multi-Century δ18O Chronology for Paleoclimate Reconstruction
Abstract
1. Introduction
2. Material and Methods
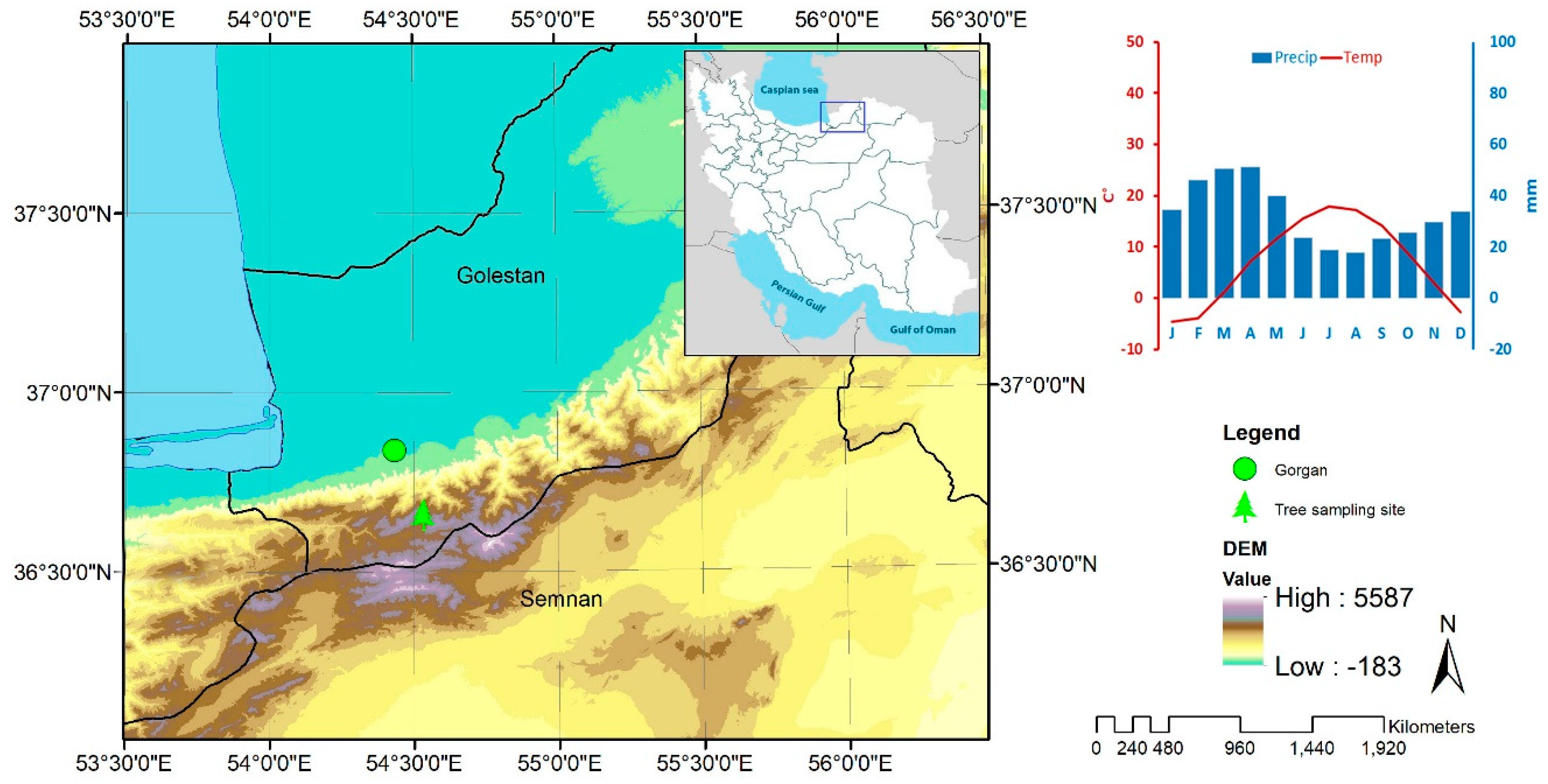
2.1. Study Site and Climate Data
2.2. Tree-Ring Material
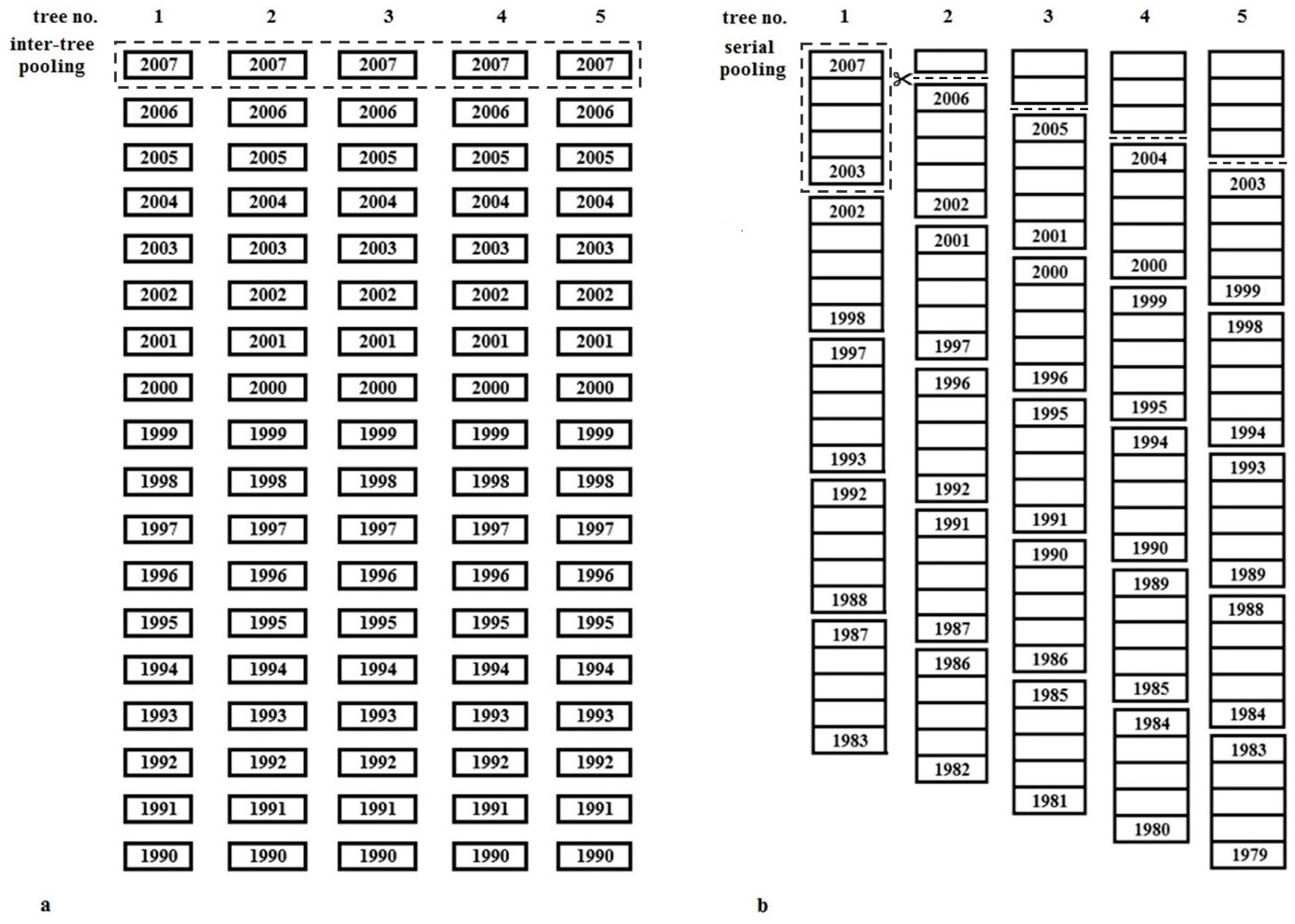
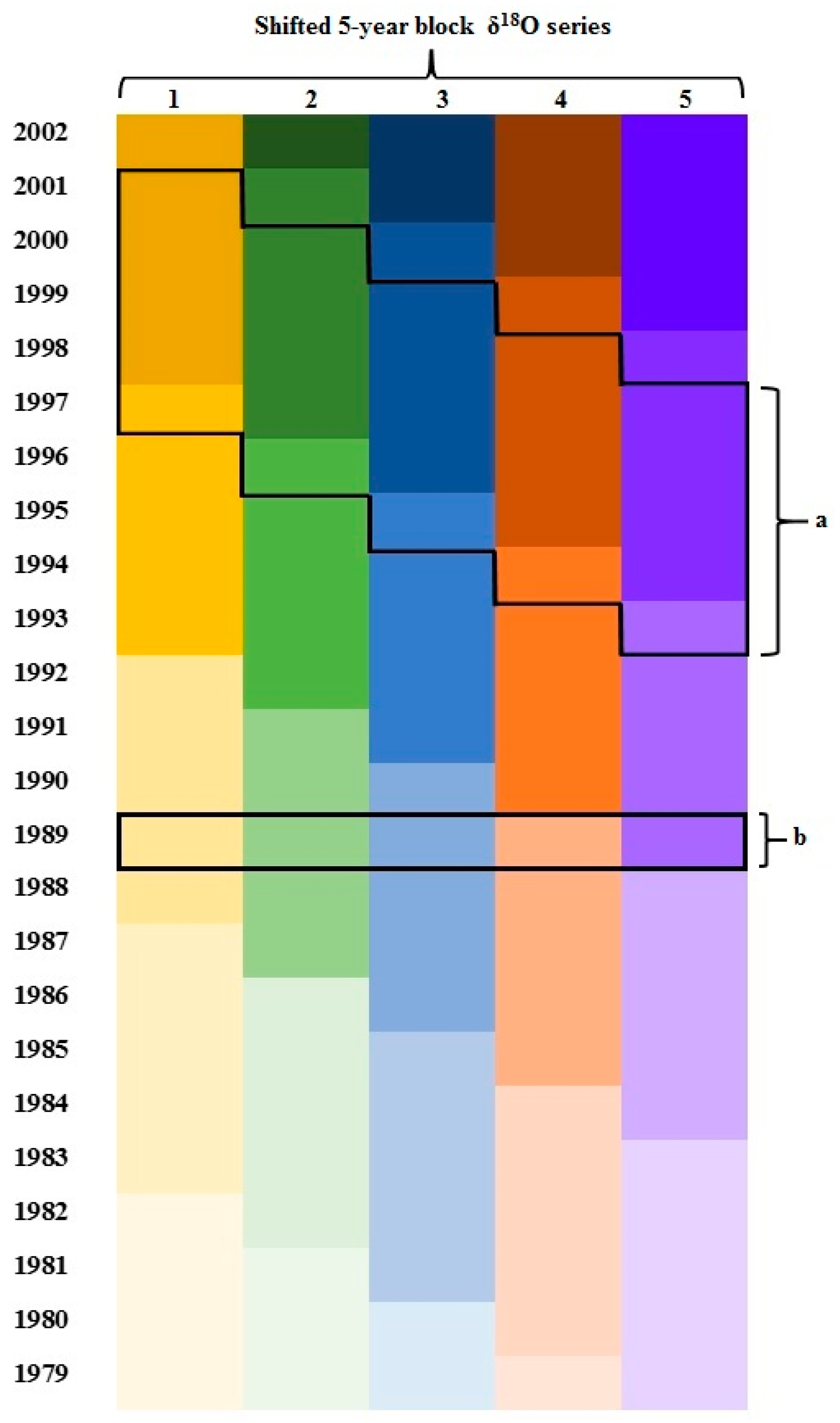
2.3. Pooling Strategies for Tree-Ring Isotope Samples
2.4. Stable Isotope Measurements
2.5. Constructing Pooling Chronologies
3. Results and Discussion
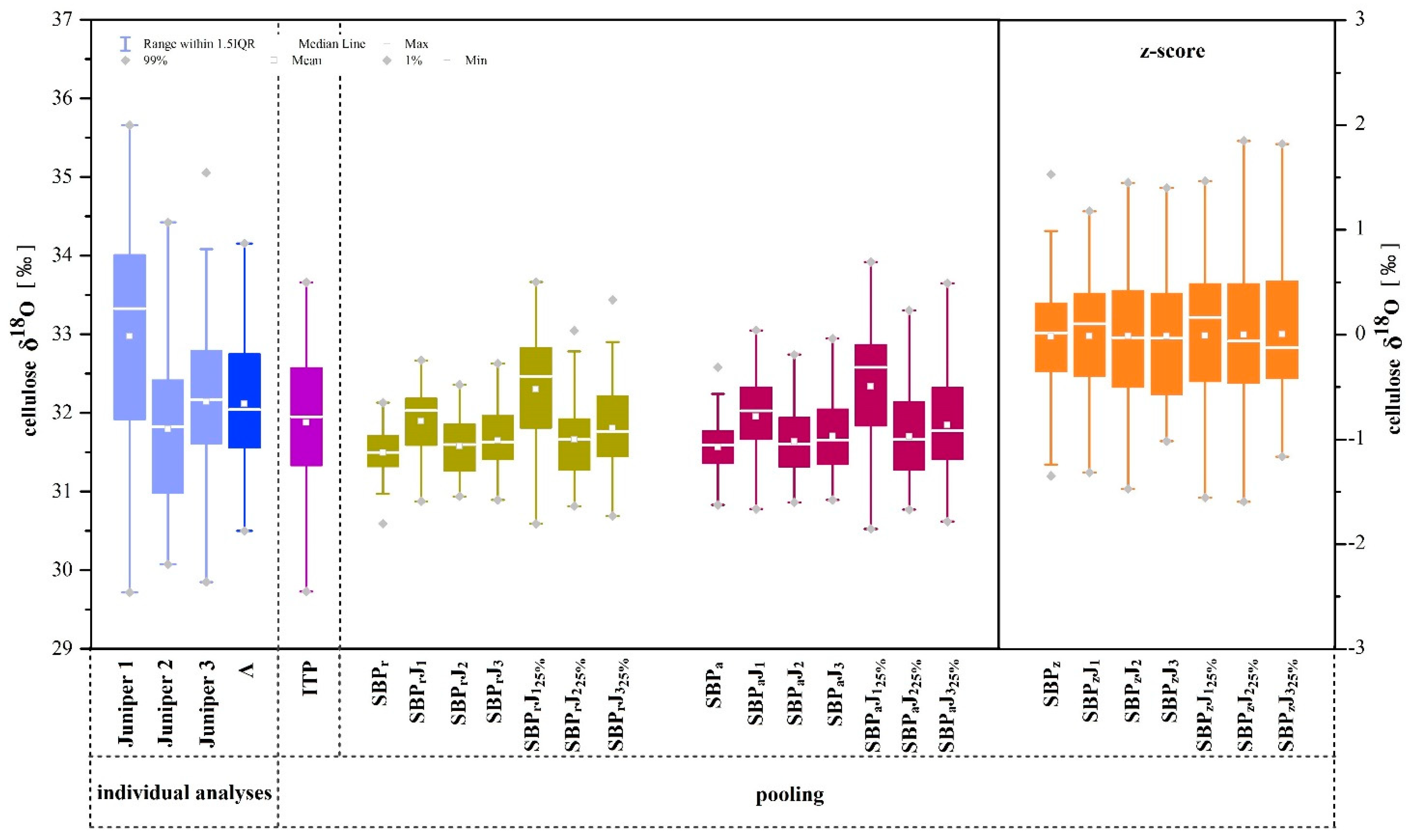
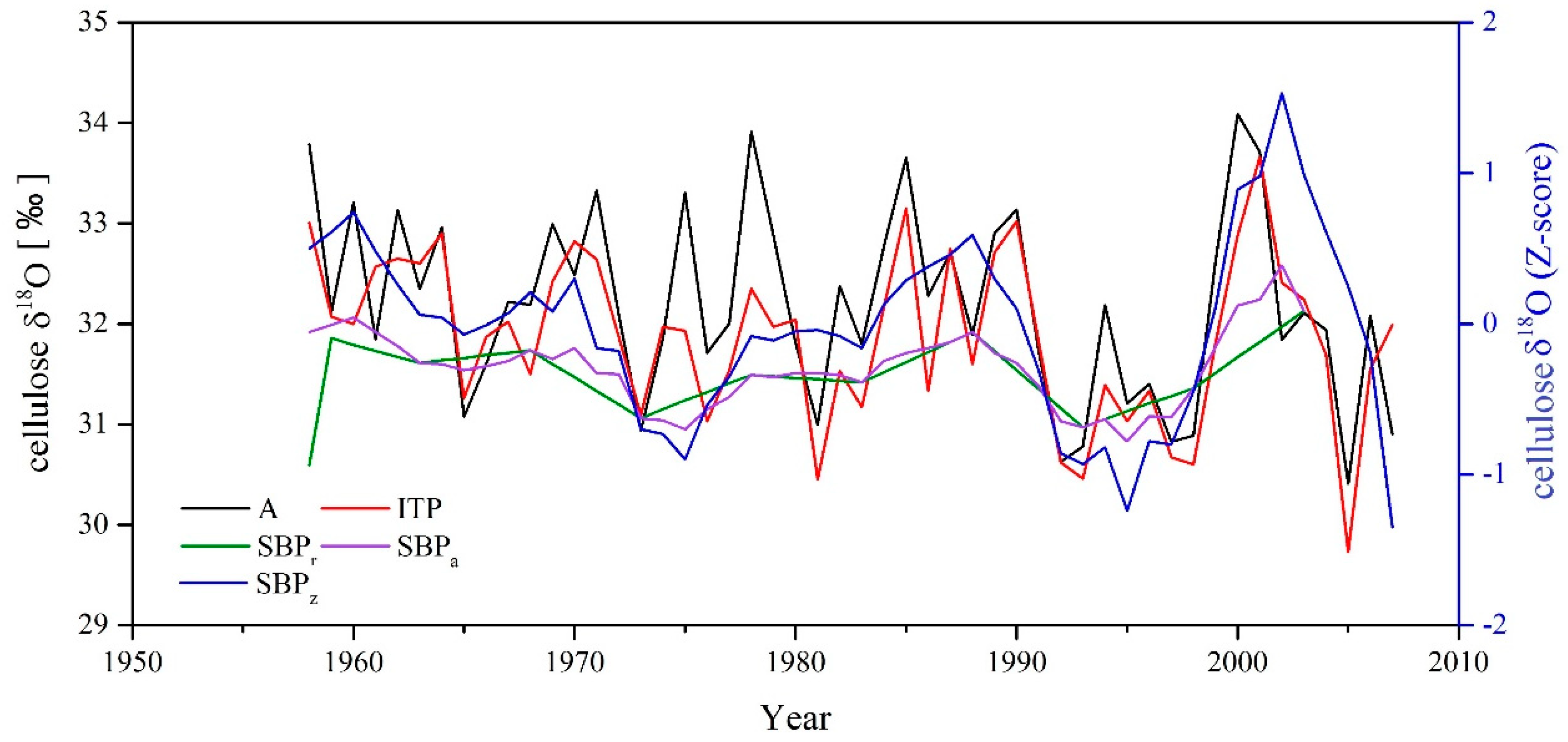
3.1. δ18O Variations among Different Individual and Pooled Chronologies
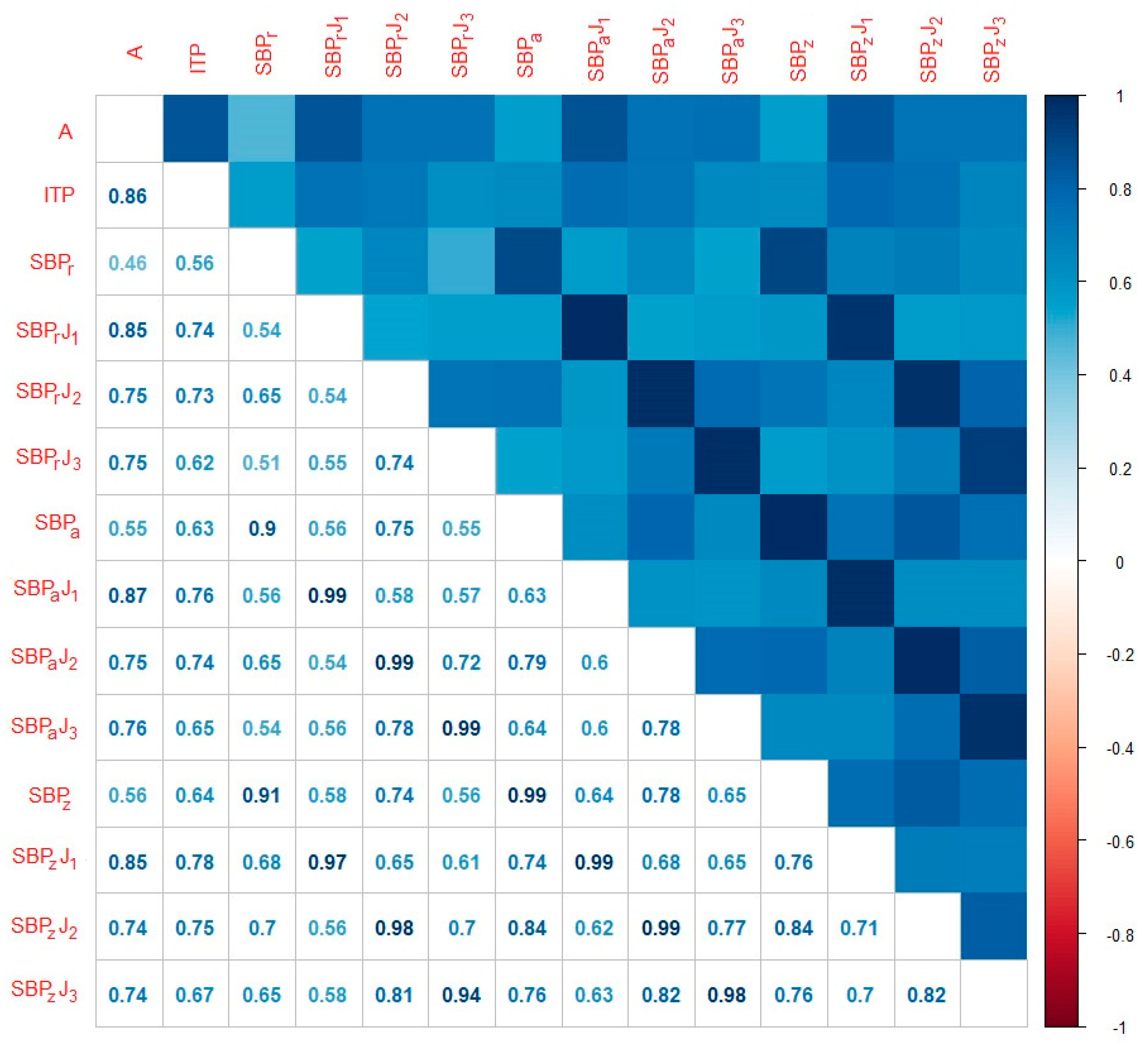
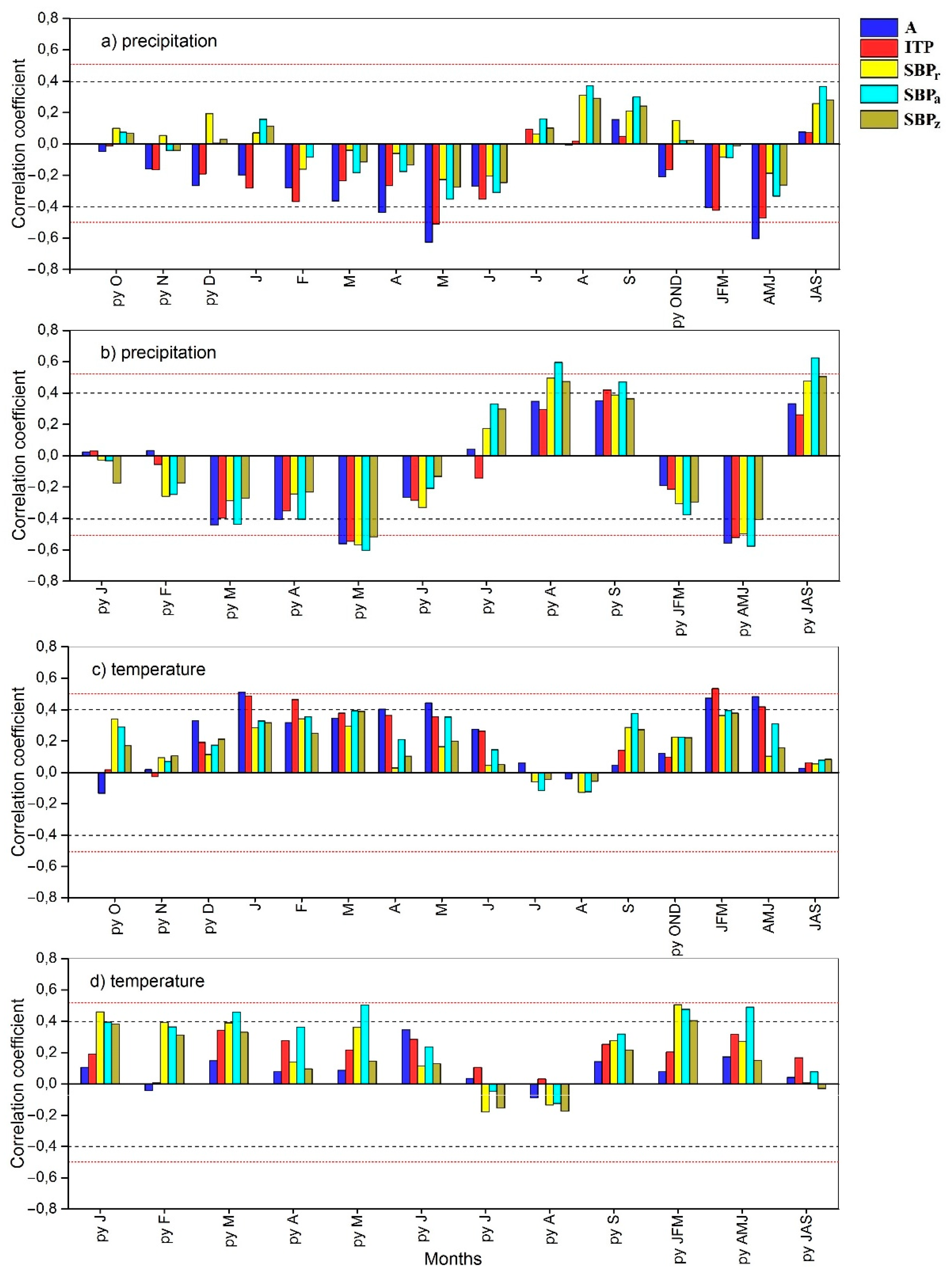
3.2. Correlations between Isotope Chronologies and Climate Parameters
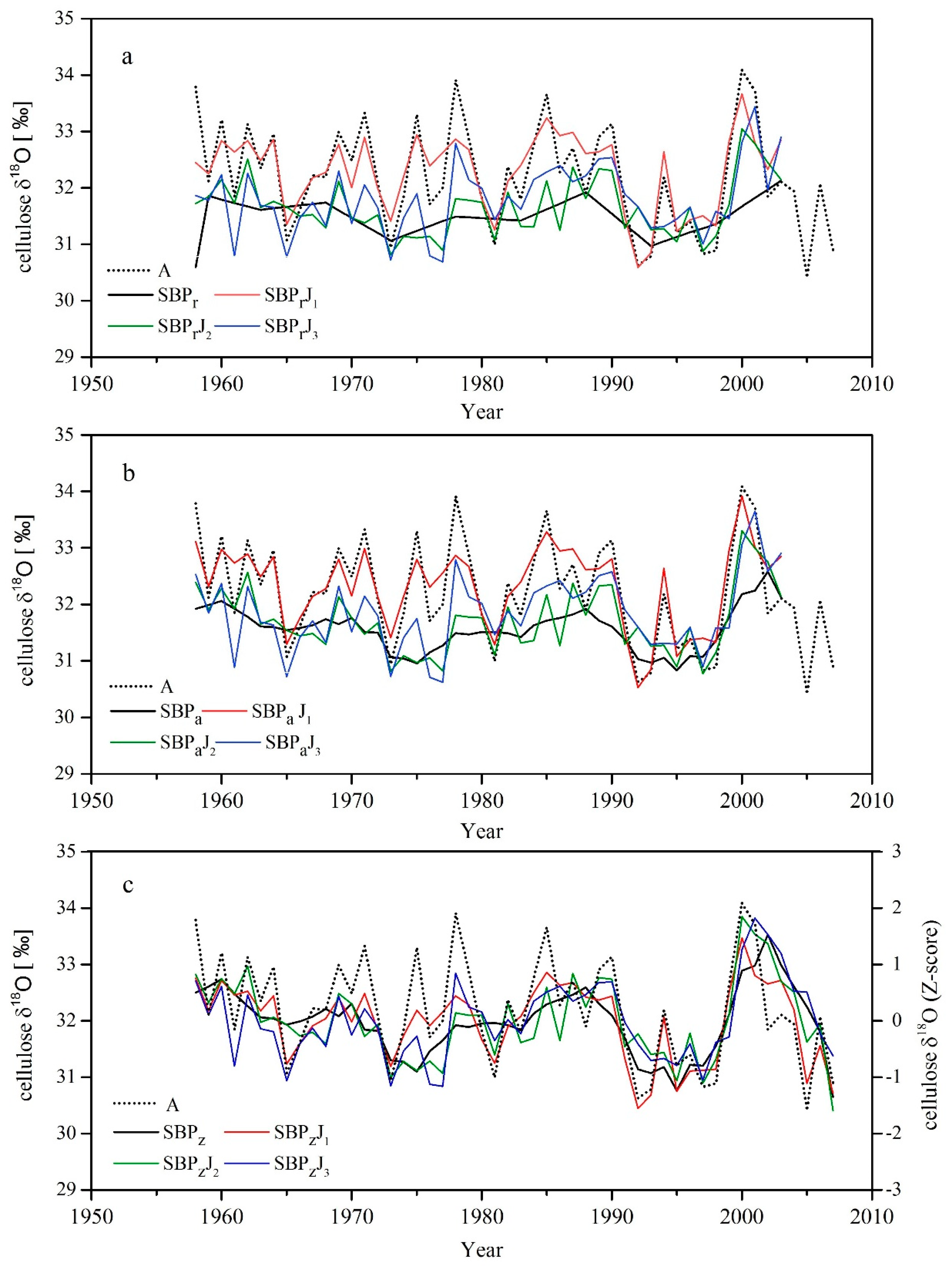
3.3. Mixed Block-Pooling and Individual Series Chronology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Esper, J.; Frank, D.C.; Battipaglia, G.; Büntgen, U.; Holert, C.; Treydte, K.; Siegwolf, R.; Saurer, M. Low-frequency noise in δ13 C and δ18 O tree ring data: A case study of Pinus uncinata in the Spanish Pyrenees. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Liu, X.; An, W.; Leavitt, S.W.; Wang, W.; Xu, G.; Zeng, X.; Qin, D. Recent strengthening of correlations between tree-ring δ13C and δ18O in mesic western China: Implications to climatic reconstruction and physiological responses. Glob. Planet. Chang. 2014, 113, 23–33. [Google Scholar] [CrossRef]
- Gagen, M.; Zorita, E.; McCarroll, D.; Young, G.H.F.; Grudd, H.; Jalkanen, R.; Loader, N.J.; Robertson, I.; Kirchhefer, A. Cloud response to summer temperatures in Fennoscandia over the last thousand years. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Szymczak, S.; Joachimski, M.M.; Bräuning, A.; Hetzer, T.; Kuhlemann, J. Are pooled tree ring δ13C and δ18O series reliable climate archives—A case study of Pinus nigra spp. laricio (Corsica/France). Chem. Geol. 2012, 308–309, 40–49. [Google Scholar] [CrossRef]
- Frank, D.C.; Poulter, B.; Saurer, M.; Esper, J.; Huntingford, C.; HELLE, G.; Treydte, K.; Zimmermann, N.E.; SCHLESER, G.H.; Ahlström, A.; et al. Water-use efficiency and transpiration across European forests during the Anthropocene. Nat. Clim. Chang. 2015, 5, 579–583. [Google Scholar] [CrossRef]
- Liu, Y.; Cobb, K.M.; Song, H.; Li, Q.; Li, C.-Y.; Nakatsuka, T.; An, Z.; Zhou, W.; Cai, Q.; Li, J.; et al. Recent enhancement of central Pacific El Niño variability relative to last eight centuries. Nat. Commun. 2017, 8, 15386. [Google Scholar] [CrossRef]
- Young, G.H.F.; Demmler, J.C.; Gunnarson, B.E.; Kirchhefer, A.J.; Loader, N.J.; McCarroll, D. Age trends in tree ring growth and isotopic archives: A case study of Pinus sylvestris L. from northwestern Norway. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef]
- Xu, H.; Hong, Y.; Hong, B. Erratum to: Decreasing Indian summer monsoon intensity after 1860 AD in the global warming epoch. Clim. Dyn. 2012, 39, 2089. [Google Scholar] [CrossRef]
- Loader, N.J.; Santillo, P.M.; Woodman-Ralph, J.P.; Rolfe, J.E.; Hall, M.A.; Gagen, M.; Robertson, I.; Wilson, R.; Froyd, C.A.; McCarroll, D.; et al. Multiple stable isotopes from oak trees in southwestern Scotland and the potential for stable isotope dendroclimatology in maritime climatic regions. Chem. Geol. 2008, 252, 62–71. [Google Scholar] [CrossRef]
- Zuidema, P.A.; Baker, P.J.; Groenendijk, P.; Schippers, P.; van der Sleen, P.; Vlam, M.; Sterck, F. Tropical forests and global change: Filling knowledge gaps. Trends Plant Sci. 2013, 18, 413–419. [Google Scholar] [CrossRef]
- Schollaen, K.; Heinrich, I.; Neuwirth, B.; Krusic, P.J.; D’Arrigo, R.D.; Karyanto, O.; Helle, G. Multiple tree-ring chronologies (ring width, δ13C and δ18O) reveal dry and rainy season signals of rainfall in Indonesia. Quat. Sci. Rev. 2013, 73, 170–181. [Google Scholar] [CrossRef]
- Baker, J.C.A.; Hunt, S.F.P.; Clerici, S.J.; Newton, R.J.; Bottrell, S.H.; Leng, M.J.; Heaton, T.H.E.; Helle, G.; Argollo, J.; Gloor, M.; et al. Oxygen isotopes in tree rings show good coherence between species and sites in Bolivia. Glob. Planet. Chang. 2015, 133, 298–308. [Google Scholar] [CrossRef]
- Leavitt, S.W. Tree-ring isotopic pooling without regard to mass: No difference from averaging δ13C values of each tree. Chem. Geol. 2008, 252, 52–55. [Google Scholar] [CrossRef]
- Boettger, T.; Friedrich, M. A new serial pooling method of shifted tree ring blocks to construct millennia long tree ring isotope chronologies with annual resolution. Isot. Environ. Health Stud. 2009, 45, 68–80. [Google Scholar] [CrossRef] [PubMed]
- Dorado Liñán, I.; Gutiérrez, E.; Helle, G.; Heinrich, I.; Andreu-Hayles, L.; Planells, O.; Leuenberger, M.; Bürger, C.; Schleser, G. Pooled versus separate measurements of tree-ring stable isotopes. Sci. Total Environ. 2011, 409, 2244–2251. [Google Scholar] [CrossRef] [PubMed]
- Woodley, E.J.; Loader, N.J.; McCarroll, D.; Young, G.H.F.; Robertson, I.; Heaton, T.H.E.; Gagen, M.H. Estimating uncertainty in pooled stable isotope time-series from tree-rings. Chem. Geol. 2012, 294–295, 243–248. [Google Scholar] [CrossRef]
- Gagen, M.; McCarroll, D.; Jalkanen, R.; Loader, N.J.; Robertson, I.; Young, G.H.F. A rapid method for the production of robust millennial length stable isotope tree ring series for climate reconstruction. Glob. Planet. Chang. 2012, 82–83, 96–103. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y. A simple and rapid preparation of pure cellulose confirmed by monosaccharide compositions, δ13C, yields and C%. Dendrochronologia 2013, 31, 273–278. [Google Scholar] [CrossRef]
- Haupt, M.; Friedrich, M.; Shishov, V.V.; Boettger, T. The construction of oxygen isotope chronologies from tree-ring series sampled at different temporal resolution and its use as climate proxies: Statistical aspects. Clim. Chang. 2014, 122, 201–215. [Google Scholar] [CrossRef]
- Kagawa, A.; Sano, M.; Nakatsuka, T.; Ikeda, T.; Kubo, S. An optimized method for stable isotope analysis of tree rings by extracting cellulose directly from cross-sectional laths. Chem. Geol. 2015, 393–394, 16–25. [Google Scholar] [CrossRef]
- Loader, N.J.; Young, G.H.F.; McCarroll, D.; Wilson, R.J.S. Quantifying uncertainty in isotope dendroclimatology. Holocene 2013, 23, 1221–1226. [Google Scholar] [CrossRef]
- Treydte, K.; Schleser, G.H.; Schweingruber, F.H.; Winiger, M. The climatic significance of δ13C in subalpine spruces (Lötschental, Swiss Alps). Tellus B 2001, 53, 593–611. [Google Scholar] [CrossRef]
- Treydte, K.; Frank, D.; Esper, J.; Andreu, L.; Bednarz, Z.; Berninger, F.; Boettger, T.; D’Alessandro, C.M.; Etien, N.; Filot, M.; et al. Signal strength and climate calibration of a European tree-ring isotope network. Geophys. Res. Lett. 2007, 34, 224. [Google Scholar] [CrossRef]
- McCarroll, D.; Loader, N.J. Stable isotopes in tree rings. Quat. Sci. Rev. 2004, 23, 771–801. [Google Scholar] [CrossRef]
- Gagen, M.; McCarroll, D.; Loader, N.J.; Robertson, I.; Jalkanen, R.; Anchukaitis, K.J. Exorcising the segment length curse: Summer temperature reconstruction since AD 1640 using non-detrended stable carbon isotope ratios from pine trees in northern Finland. Holocene 2007, 17, 435–446. [Google Scholar] [CrossRef]
- Leavitt, S.W. Tree-ring C-H-O isotope variability and sampling. Sci. Total Environ. 2010, 408, 5244–5253. [Google Scholar] [CrossRef] [PubMed]
- Esper, J.; Carnelli, A.L.; Kamenik, C.; Filot, M.; Leuenberger, M.; Treydte, K. Spruce tree-ring proxy signals during cold and warm periods. Dendrobiology 2017, 77, 3–18. [Google Scholar] [CrossRef]
- Grießinger, J.; Bräuning, A.; Helle, G.; Hochreuther, P.; Schleser, G. Late Holocene relative humidity history on the southeastern Tibetan plateau inferred from a tree-ring δ 18 O record: Recent decrease and conditions during the last 1500 years. Quat. Int. 2017, 430, 52–59. [Google Scholar] [CrossRef]
- Andreu-Hayles, L.; Ummenhofer, C.C.; Barriendos, M.; Schleser, G.H.; Helle, G.; Leuenberger, M.; Gutiérrez, E.; Cook, E.R. 400 Years of summer hydroclimate from stable isotopes in Iberian trees. Clim. Dyn. 2017, 49, 143–161. [Google Scholar] [CrossRef]
- Labuhn, I.; Daux, V.; Girardclos, O.; Stievenard, M.; Pierre, M.; Masson-Delmotte, V. French summer droughts since 1326 CE: A reconstruction based on tree ring cellulose δ18O. Clim. Past 2016, 12, 1101–1117. [Google Scholar] [CrossRef]
- Gennaretti, F.; Huard, D.; Naulier, M.; Savard, M.; Bégin, C.; Arseneault, D.; Guiot, J. Bayesian multiproxy temperature reconstruction with black spruce ring widths and stable isotopes from the northern Quebec taiga. Clim. Dyn. 2017, 49, 4107–4119. [Google Scholar] [CrossRef]
- Wernicke, J.; Grießinger, J.; Hochreuther, P.; Bräuning, A. Variability of summer humidity during the past 800 years on the eastern Tibetan Plateau inferred from δ18O of tree-ring cellulose. Clim. Past 2015, 11, 327–337. [Google Scholar] [CrossRef]
- Naulier, M.; Savard, M.M.; Bégin, C.; Gennaretti, F.; Arseneault, D.; Marion, J.; Nicault, A.; Bégin, Y. A millennial summer temperature reconstruction for northeastern Canada using oxygen isotopes in subfossil trees. Clim. Past 2015, 11, 1153–1164. [Google Scholar] [CrossRef]
- Young, G.H.F.; Loader, N.J.; McCarroll, D.; Bale, R.J.; Demmler, J.C.; Miles, D.; Nayling, N.T.; Rinne, K.T.; Robertson, I.; Watts, C.; et al. Oxygen stable isotope ratios from British oak tree-rings provide a strong and consistent record of past changes in summer rainfall. Clim. Dyn. 2015, 45, 3609–3622. [Google Scholar] [CrossRef]
- Lavergne, A.; Daux, V.; Villalba, R.; Pierre, M.; Stievenard, M.; Vimeux, F.; Srur, A.M. Are the oxygen isotopic compositions of Fitzroya cupressoides and Nothofagus pumilio cellulose promising proxies for climate reconstructions in northern Patagonia? J. Geophys. Res. Biogeosci. 2016, 121, 767–776. [Google Scholar] [CrossRef]
- Lavergne, A.; Daux, V.; Villalba, R.; Pierre, M.; Stievenard, M.; Srur, A.M. Improvement of isotope-based climate reconstructions in Patagonia through a better understanding of climate influences on isotopic fractionation in tree rings. Earth Planet. Sci. Lett. 2017, 459, 372–380. [Google Scholar] [CrossRef]
- Loader, N.J.; Young, G.H.F.; Grudd, H.; McCarroll, D. Stable carbon isotopes from Torneträsk, northern Sweden provide a millennial length reconstruction of summer sunshine and its relationship to Arctic circulation. Quat. Sci. Rev. 2013, 62, 97–113. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, R.; Leavitt, S.W.; Song, H.; Linderholm, H.W.; Li, Q.; An, Z. Individual and pooled tree-ring stable-carbon isotope series in Chinese pine from the Nan Wutai region, China: Common signal and climate relationships. Chem. Geol. 2012, 330–331, 17–26. [Google Scholar] [CrossRef]
- Grießinger, J.; Bräuning, A.; Helle, G.; Thomas, A.; Schleser, G. Late Holocene Asian summer monsoon variability reflected by δ18 O in tree-rings from Tibetan junipers. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Leavitt, S.W.; Long, A. Sampling strategy for stable carbon isotope analysis of tree rings in pine. Nature 1984, 311, 145. [Google Scholar] [CrossRef]
- Borella, S.; Leuenberger, M.; Saurer, M.; Siegwolf, R. Reducing uncertainties in δ 13 C analysis of tree rings: Pooling, milling, and cellulose extraction. J. Geophys. Res. 1998, 103, 19519–19526. [Google Scholar] [CrossRef]
- Pourtahmasi, K.; Parsapajouh, D.; Bräuning, A.; Esper, J.; Schweingruber, F.H. Climatic analysis of pointer years in tree-ring chronologies from Northern Iran and neighboring high mountain areas. Geokodynamik 2007, 28, 27–42. [Google Scholar]
- Pourtahmasi, K.; Bräuning, A.; Poursartip, L.; Burchardt, I. Growth-climate responses of oak and juniper trees in different exposures of the Alborz Mountains, northern Iran. Trace 2012, 10, 49–53. [Google Scholar]
- Pourtahmasi, K.; Poursartip, L.; Bräuning, A.; Parsapajouh, D. Comparison between the radial growth of Juniper (Juniperus polycarpos) and Oak (Quercus macranthera) in two sides of the Alborz Mountains in the Chaharbagh region of Gorgan. Iran J. For. Wood Prod. 2009, 62, 159–169. [Google Scholar]
- Bayramzadeh, V.; Zhu, H.; Lu, X.; Attarod, P.; Zhang, H.; Li, X.; Asad, F.; Liang, E. Temperature variability in northern Iran during the past 700 years. Sci. Bull. 2018, 63, 462–464. [Google Scholar] [CrossRef]
- Akhani, H.; Djamali, M.; Ghorbanalizadeh, A.; Ramezani, E. Plant biodiversity of Hyrcanian relict forests, N Iran: An overview of the flora, vegetation, palaeoecology and conservation. Pak. J. Bot. 2010, 42, 231–258. [Google Scholar]
- Sagheb-Talebi, K.; Pourhashemi, M.; Sajedi, T. Forests of Iran. A Treasure from the Past, a Hope for the Future; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 9400773714. [Google Scholar]
- Nadi, M.; Khalili, A.; Pourtahmasi, K.; Bazrafshan, J. Comparing the various interpolation techniques of climatic data for determining the most important factors affecting tree growth at the elevated areas of Chaharbagh, Gorgan. Iran J. For. Wood Prod. 2013, 66, 83–95. [Google Scholar]
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; University of Chicago Press: Chicago, IL, USA; London, UK, 1968. [Google Scholar]
- Raffalli-Delerce, G.; Masson-Delmotte, V.; Dupouey, J.L.; Stievenard, M.; Breda, N.; Moisselin, J.M. Reconstruction of summer droughts using tree-ring cellulose isotopes: A calibration study with living oaks from Brittany (western France). Tellus B 2004, 56, 160–174. [Google Scholar] [CrossRef]
- Treydte, K.S.; Schleser, G.H.; Helle, G.; Frank, D.C.; Winiger, M.; Haug, G.H.; Esper, J. The twentieth century was the wettest period in northern Pakistan over the past millennium. Nature 2006, 440, 1179–1182. [Google Scholar] [CrossRef]
- Wieloch, T.; Helle, G.; Heinrich, I.; Voigt, M.; Schyma, P. A novel device for batch-wise isolation of α-cellulose from small-amount wholewood samples. Dendrochronologia 2011, 29, 115–117. [Google Scholar] [CrossRef]
- Laumer, W.; Andreu, L.; Helle, G.; Schleser, G.H.; Wieloch, T.; Wissel, H. A novel approach for the homogenization of cellulose to use micro-amounts for stable isotope analyses. Rapid Commun. Mass Spectrom. 2009, 23, 1934–1940. [Google Scholar] [CrossRef]
- Foroozan, Z.; Pourtahmasi, K.; Bräuning, A. Stable oxygen isotopes in juniper and oak tree rings from northern Iran as indicators for site-specific and season-specific moisture variations. Dendrochronologia 2015, 36, 33–39. [Google Scholar] [CrossRef]
- Saurer, M.; Cherubini, P.; Reynolds-Henne, C.E.; Treydte, K.S.; Anderson, W.T.; Siegwolf, R.T.W. An investigation of the common signal in tree ring stable isotope chronologies at temperate sites. J. Geophys. Res. 2008, 113, 31625. [Google Scholar] [CrossRef]
- Tranquillini, W. Water Relations and Alpine Timberline. In Water and Plant Life: Problems and Modern Approaches; Lange, O.L., Kappen, L., Schulze, E.-D., Eds.; Springer: Berlin/Heidelberg, Germany, 1976; pp. 473–491. ISBN 978-3-642-66431-1. [Google Scholar]
- Valentini, R.; Anfodillo, T.; Ehleringer, J.R. Water sources and carbon isotope composition (δ 13 C) of selected tree species of the Italian Alps. Can. J. For. Res. 1994, 24, 1575–1578. [Google Scholar] [CrossRef]
- Marshall, J.D.; Monserud, R.A. Co-occurring species differ in tree-ring δ18O trends. Tree Physiol. 2006, 26, 1055–1066. [Google Scholar] [CrossRef] [PubMed]
- Loader, N.J.; McCarroll, D.; Gagen, M.; Robertson, I.; Jalkanen, R. Extracting Climatic Information from Stable Isotopes in Tree Rings. In Stable Isotopes as Indicators of Ecological Change; Dawson, T.E., Siegwolf, R.T.W., Eds.; Academic: Oxford, UK, 2007; pp. 25–48. ISBN 9780123736277. [Google Scholar]
- Danis, P.A.; Masson-Delmotte, V.; Stievenard, M.; Guillemin, M.T.; Daux, V.; Naveau, P.; Von Grafenstein, U. Reconstruction of past precipitation δ18O using tree-ring cellulose δ18O and δ13C: A calibration study near Lac d’Annecy, France. Earth Planet. Sci. Lett. 2006, 243, 439–448. [Google Scholar] [CrossRef]
- Roden, J. Cross-dating of tree ring δ18O and δ13C time series. Chem. Geol. 2008, 252, 72–79. [Google Scholar] [CrossRef]
- Kress, A.; Young, G.H.F.; Saurer, M.; Loader, N.J.; Siegwolf, R.T.W.; McCarroll, D. Stable isotope coherence in the earlywood and latewood of tree-line conifers. Chem. Geol. 2009, 268, 52–57. [Google Scholar] [CrossRef]
- Qin, C.; Yang, B.; Bräuning, A.; Grießinger, J.; Wernicke, J. Drought signals in tree-ring stable oxygen isotope series of Qilian juniper from the arid northeastern Tibetan Plateau. Glob. Planet. Chang. 2015, 125, 48–59. [Google Scholar] [CrossRef]
- Roden, J.S.; Lin, G.; Ehleringer, J.R. A mechanistic model for interpretation of hydrogen and oxygen isotope ratios in tree-ring cellulose. Geochimica et Cosmochimica Acta 2000, 64, 21–35. [Google Scholar] [CrossRef]
- Gessler, A.; Ferrio, J.P.; Hommel, R.; Treydte, K.; Werner, R.A.; Monson, R.K. Stable isotopes in tree rings: Towards a mechanistic understanding of isotope fractionation and mixing processes from the leaves to the wood. Tree Physiol. 2014, 34, 796–818. [Google Scholar] [CrossRef] [PubMed]
- Treydte, K.; Boda, S.; Graf Pannatier, E.; Fonti, P.; Frank, D.; Ullrich, B.; Saurer, M.; Siegwolf, R.; Battipaglia, G.; Werner, W.; et al. Seasonal transfer of oxygen isotopes from precipitation and soil to the tree ring: Source water versus needle water enrichment. New Phytol. 2014, 202, 772–783. [Google Scholar] [CrossRef] [PubMed]
| AC1 | AC2 | Skewness | Kurtosis | Shapiro–Wilk | ||
|---|---|---|---|---|---|---|
| Individual analyses | Juniper1 | 0.37 ** | 0.06 | −0.52 | −0.29 | 0.08 |
| Juniper2 | 0.21 | 0.29 | 0.54 | 0.15 | 0.43 | |
| Juniper3 | 0.16 | 0.13 | −0.04 | 0.37 | 0.59 | |
| A | 0.26 | 0.06 | 0.2 | −0.52 | 0.42 | |
| Pooling | ITP | 0.38 ** | 0.08 | −0.29 | −0.09 | 0.86 |
| SBPr | 0.69 ** | 0.50 ** | −0.52 | 0.75 | 0.65 | |
| SBPrJ1 | 0.45 ** | 0.11 | −0.66 | −0.16 | 0.01 | |
| SBPrJ2 | 0.40 ** | 0.37 * | 0.67 | 0.06 | 0.15 | |
| SBPrJ3 | 0.25 | 0.17 | 0.23 | 0.20 | 0.56 | |
| SBPrJ125% | 0.60 ** | 0.27 | −0.64 | −0.28 | 0.04 | |
| SBPrJ225% | 0.61 ** | 0.48 ** | 0.36 | −0.69 | 0.23 | |
| SBPrJ325% | 0.47 ** | 0.37 * | 0.33 | −0.20 | 0.66 | |
| SBPa | 0.87 ** | 0.68 ** | 0.17 | 0.01 | 0.41 | |
| SBPaJ1 | 0.49 ** | 0.15 | −0.60 | −0.10 | 0.01 | |
| SBPaJ2 | 0.49 ** | 0.41 ** | 0.60 | 0.15 | 0.22 | |
| SBPaJ3 | 0.38 * | 0.25 | 0.24 | 0.10 | 0.67 | |
| SBPaJ125% | 0.67 ** | 0.38 * | −0.46 | −0.18 | 0.23 | |
| SBPaJ225% | 0.71 ** | 0.56 ** | 0.45 | −0.04 | 0.24 | |
| SBPaJ325% | 0.64 ** | 0.45 ** | 0.34 | −0.12 | 0.49 | |
| SBPz | 0.83 ** | 0.6 ** | −0.04 | 0.10 | 0.72 | |
| SBPzJ1 | 0.58 ** | 0.29 * | −0.50 | −0.41 | 0.03 | |
| SBPzJ2 | 0.54 ** | 0.44 ** | 0.34 | 0.10 | 0.88 | |
| SBPzJ3 | 0.55 ** | 0.37 ** | 0.39 | −0.08 | 0.35 | |
| SBPzJ125% | 0.75 ** | 0.49 ** | −0.33 | −0.27 | 0.52 | |
| SBPzJ225% | 0.73 ** | 0.55 ** | 0.08 | −0.01 | 0.83 | |
| SBPzJ325% | 0.74 ** | 0.51 ** | 0.23 | −0.40 | 0.22 |
| Precipitation | Temperature | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Apr | May | Winter | Spring | Jan | Feb | Mar | Apr | May | Winter | Spring | ||
| A | –0.44 * | –0.59 ** | –0.39 * | –0.59 ** | A | 0.50 ** | 0.42 * | 0.45 * | 0.45 * | 0.50 * | ||
| ITP | –0.51 ** | –0.42 * | –0.47 * | ITP | 0.49 * | 0.46 * | 0.53 ** | 0.42 * | ||||
| SBPr | SBPr | |||||||||||
| SBPrJ1 | –0.66 ** | –0.60 ** | SBPrJ1 | 0.48 * | 0.53 * | |||||||
| SBPrJ2 | SBPrJ2 | 0.45 * | 0.52 * | 0.46 * | 0.50 * | |||||||
| SBPrJ3 | SBPrJ3 | |||||||||||
| SBPrJ125% | –0.58 ** | –0.52 * | SBPrJ125% | 0.46 * | 0.46 * | 0.43 * | ||||||
| SBPrJ225% | SBPrJ225% | 0.45 * | 0.46 * | |||||||||
| SBPrJ325% | SBPrJ325% | |||||||||||
| SBPa | SBPa | |||||||||||
| SBPaJ1 | –0.67 ** | –0.61 ** | SBPaJ1 | 0.49 * | 0.55 ** | 0.44 * | ||||||
| SBPaJ2 | –0.43 * | SBPaJ2 | 0.44 * | 0.44 * | 0.54 * | 0.47 * | 0.52 * | |||||
| SBPaJ3 | SBPaJ3 | |||||||||||
| SBPaJ125% | –0.59 ** | –0.54 * | SBPaJ125% | 0.45 * | 0.51 * | 0.46 * | ||||||
| SBPaJ225% | SBPaJ225% | 0.44 * | 0.49 * | 0.48 * | 0.46 * | |||||||
| SBPaJ325% | SBPaJ325% | 0.43 * | ||||||||||
| SBPz | SBPz | |||||||||||
| SBPzJ1 | –0.57 ** | –0.50 * | SBPzJ1 | 0.53 ** | 0.46 * | |||||||
| SBPzJ2 | SBPzJ2 | 0.43 * | 0.46 * | |||||||||
| SBPzJ3 | SBPzJ3 | 0.42 * | ||||||||||
| SBPzJ125% | –0.46 * | –0.41 * | SBPzJ125% | 0.45 * | 0.44 * | |||||||
| SBPzJ225% | SBPzJ225% | 0.43 * | 0.44 * | |||||||||
| SBPzJ325% | SBPzJ325% | 0.40 * | ||||||||||
| Precipitation | Temperature | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Py Mar | Py Apr | Py May | Py Aug | Py Sep | Py Spring | Py Summer | Py Jan | Py Feb | PMar | Py May | Py Sep | Py Winter | Py Spring | ||
| A | –0.40 * | –0.37 | –0.53 ** | –0.52 ** | A | ||||||||||
| ITP | –0.40 * | –0.55 ** | 0.42 * | –0.52 ** | ITP | ||||||||||
| SBPr | –0.57 ** | 0.50 * | –0.50 * | 0.48 * | SBPr | 0.46 * | 0.51 * | ||||||||
| SBPrJ1 | –0.53 * | –0.64 ** | 0.45 * | –0.60 ** | SBPrJ1 | ||||||||||
| SBPrJ2 | 0.49 * | 0.44 * | 0.57 ** | SBPrJ2 | 0.58 ** | 0.45 * | 0.50 * | ||||||||
| SBPrJ3 | –0.52 * | –0.50 * | 0.47 * | –0.51 * | SBPrJ3 | 0.46 * | |||||||||
| SBPrJ225% | –0.49 * | –0.66 ** | 0.50 * | –0.61 ** | 0.48 * | SBPrJ225% | |||||||||
| SBPrJ225% | –0.50 * | 0.540 * | 0.46 * | 0.59 ** | SBPrJ225% | 0.46 * | 0.57 ** | 0.55 ** | |||||||
| SBPrJ325% | –0.46 * | –0.56 ** | 0.46 * | –0.53 * | 0.46 * | SBPrJ325% | 0.46 * | 0.44 * | 0.51 * | ||||||
| SBPa | –0.44 * | –0.60 ** | 0.60 ** | 0.47 * | –0.58 ** | 0.63 ** | SBPa | 0.46 * | 0.51 * | 0.48 * | 0.49 * | ||||
| SBPaJ1 | –0.55 ** | –0.65 ** | 0.49 * | –0.62 ** | 0.48 * | SBPaJ1 | |||||||||
| SBPaJ2 | –0.43 * | 0.52 * | 0.46 * | 0.61 ** | SBPaJ2 | 0.58 ** | 0.45 * | 0.49 * | |||||||
| SBPaJ3 | –0.56 ** | –0.55 ** | 0.50 * | –0.56 ** | 0.50 * | SBPaJ3 | 0.44 * | 0.50 * | 0.49 * | 0.52 * | |||||
| SBPaJ125% | –0.54 * | –0.43 * | –0.67 ** | 0.55 ** | –0.64 ** | 0.56 ** | SBPaJ125% | ||||||||
| SBPaJ225% | –0.53 * | 0.58 ** | 0.49 * | –0.49 * | 0.65 ** | SBPaJ225% | 0.56 ** | 0.51 * | 0.46 * | ||||||
| SBPaJ325% | –0.53 * | –0.59 ** | 0.49 * | 0.51 * | –0.59 ** | 0.57 ** | SBPaJ325% | 0.46 * | 0.52 * | 0.51 * | 0.52 * | ||||
| SBPz | –0.52 ** | 0.47 * | –0.41 * | 0.51 ** | SBPz | 0.41 * | |||||||||
| SBPzJ1 | –0.41 * | –0.61 ** | 0.43 * | –0.56 ** | SBPzJ1 | ||||||||||
| SBPzJ2 | –0.43 * | 0.44 * | 0.50 * | SBPzJ2 | 0.41 * | ||||||||||
| SBPzJ3 | –0.44 * | –0.54 ** | 0.47 * | –0.46 * | 0.49 * | SBPzJ3 | 0.45 * | 0.43 * | 0.50 * | ||||||
| SBPzJ125% | –0.59 ** | 0.48 * | –0.52 ** | 0.47 * | SBPzJ125% | ||||||||||
| SBPzJ225% | –0.49 * | 0.48 * | 0.52 ** | SBPzJ225% | 0.41 * | ||||||||||
| SBPzJ325% | –0.53 ** | 0.44 * | 0.41 * | –0.44 * | 0.50 * | SBPzJ325% | 0.42 * | 0.45 * | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foroozan, Z.; Grießinger, J.; Pourtahmasi, K.; Bräuning, A. Evaluation of Different Pooling Methods to Establish a Multi-Century δ18O Chronology for Paleoclimate Reconstruction. Geosciences 2019, 9, 270. https://doi.org/10.3390/geosciences9060270
Foroozan Z, Grießinger J, Pourtahmasi K, Bräuning A. Evaluation of Different Pooling Methods to Establish a Multi-Century δ18O Chronology for Paleoclimate Reconstruction. Geosciences. 2019; 9(6):270. https://doi.org/10.3390/geosciences9060270
Chicago/Turabian StyleForoozan, Zeynab, Jussi Grießinger, Kambiz Pourtahmasi, and Achim Bräuning. 2019. "Evaluation of Different Pooling Methods to Establish a Multi-Century δ18O Chronology for Paleoclimate Reconstruction" Geosciences 9, no. 6: 270. https://doi.org/10.3390/geosciences9060270
APA StyleForoozan, Z., Grießinger, J., Pourtahmasi, K., & Bräuning, A. (2019). Evaluation of Different Pooling Methods to Establish a Multi-Century δ18O Chronology for Paleoclimate Reconstruction. Geosciences, 9(6), 270. https://doi.org/10.3390/geosciences9060270







