Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Conditions
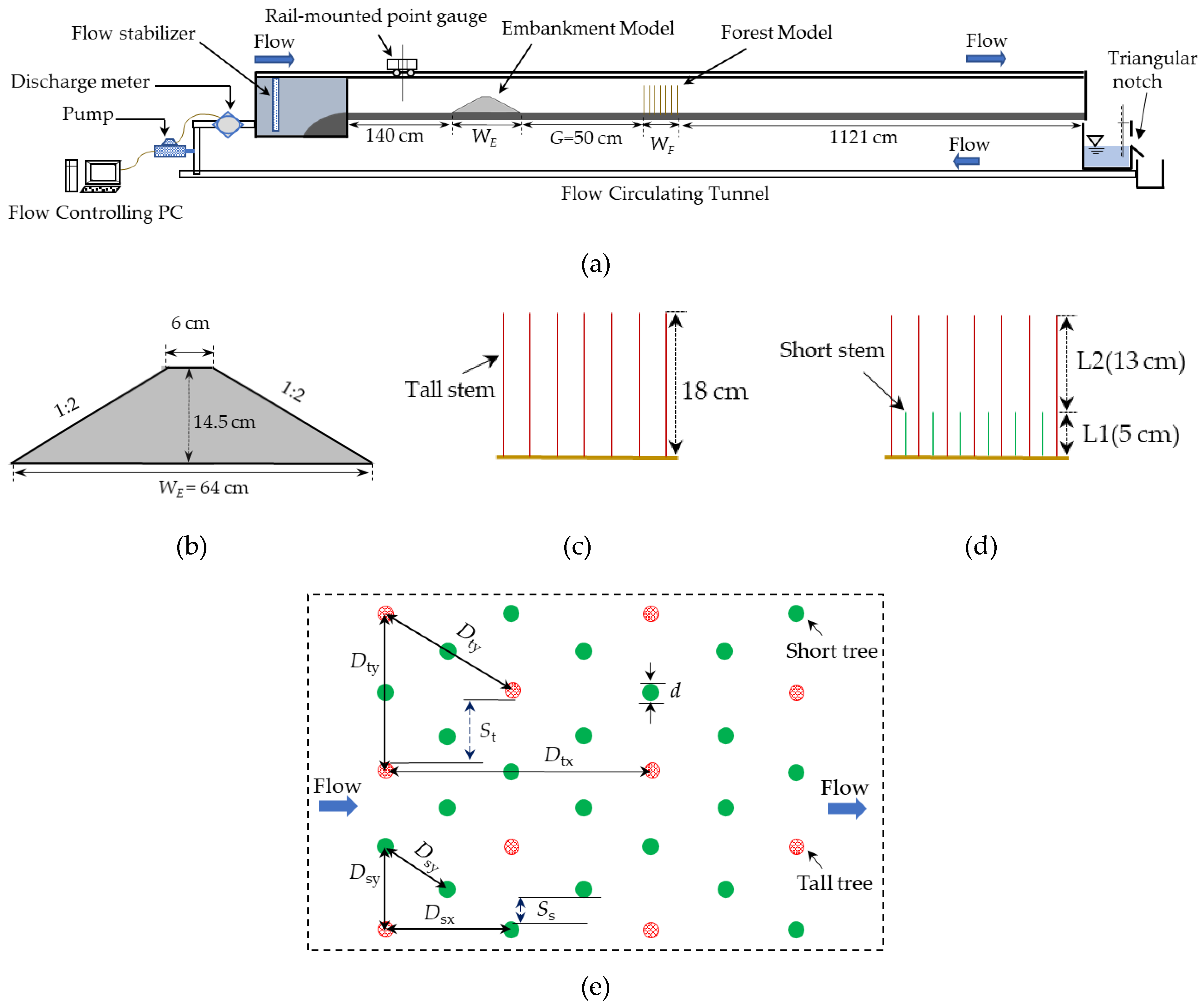
2.1.1. Flume Characteristic and Flow Condition
2.1.2. Physical Model of the Hybrid Defense System
2.2. Experimental Procedures and Data Analysis
2.2.1. Water Depth and Velocity Measurement
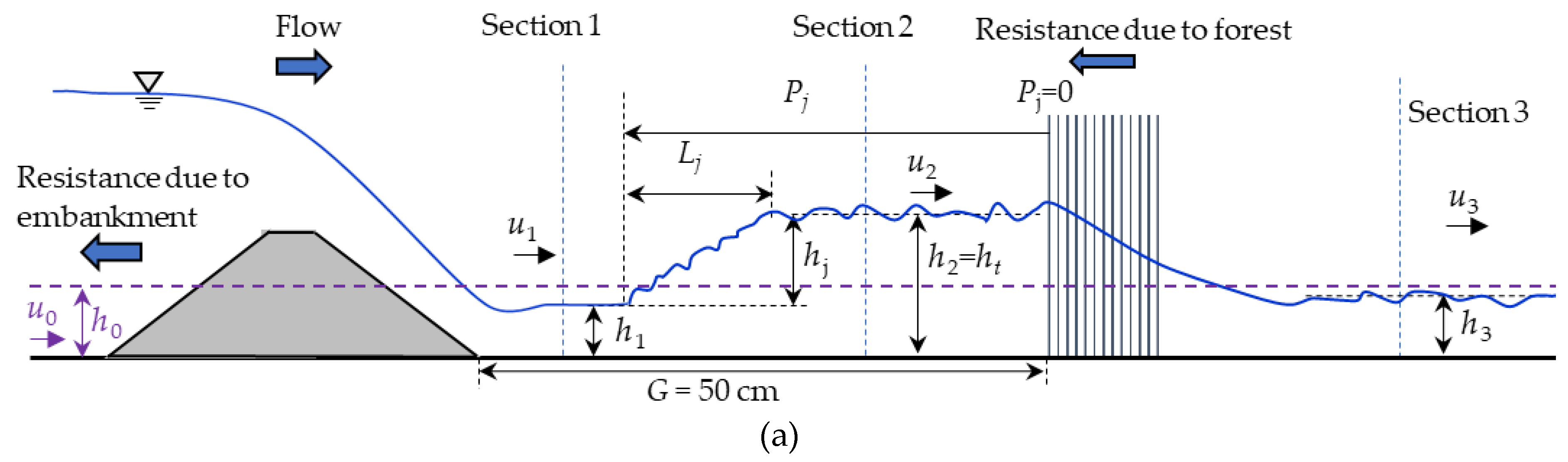
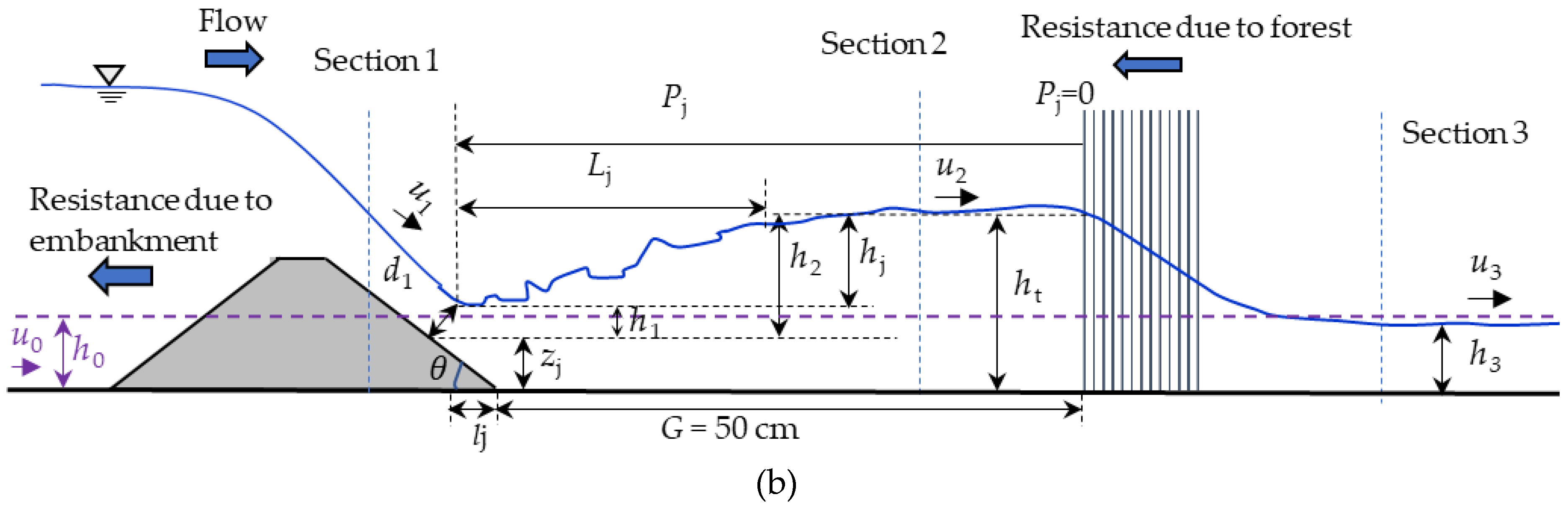
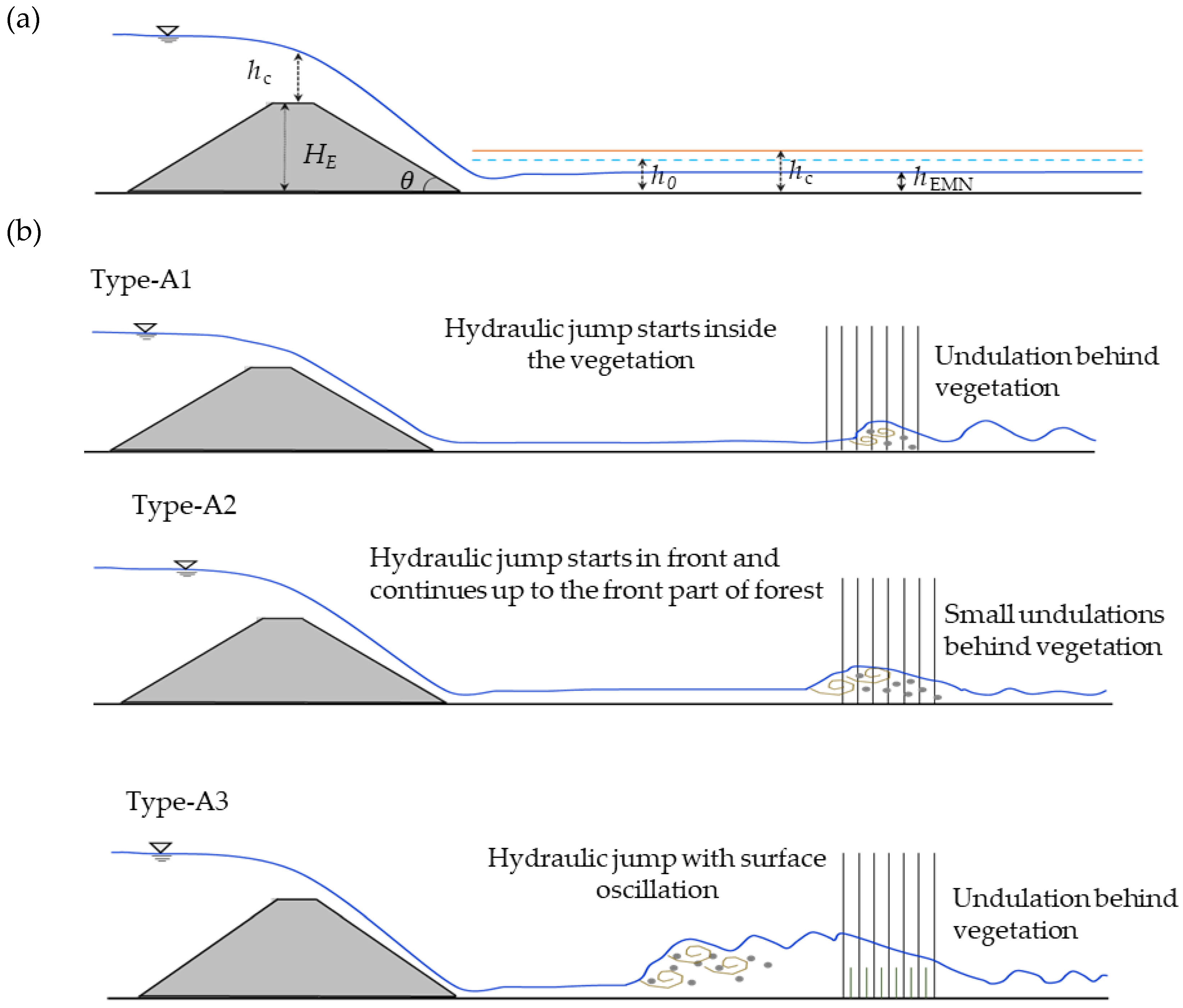
2.2.2. Definition of Hydraulic Jump
2.2.3. Nondimensional Parameters Used in this Study
2.2.4. Evaluation of Energy Reduction
3. Results
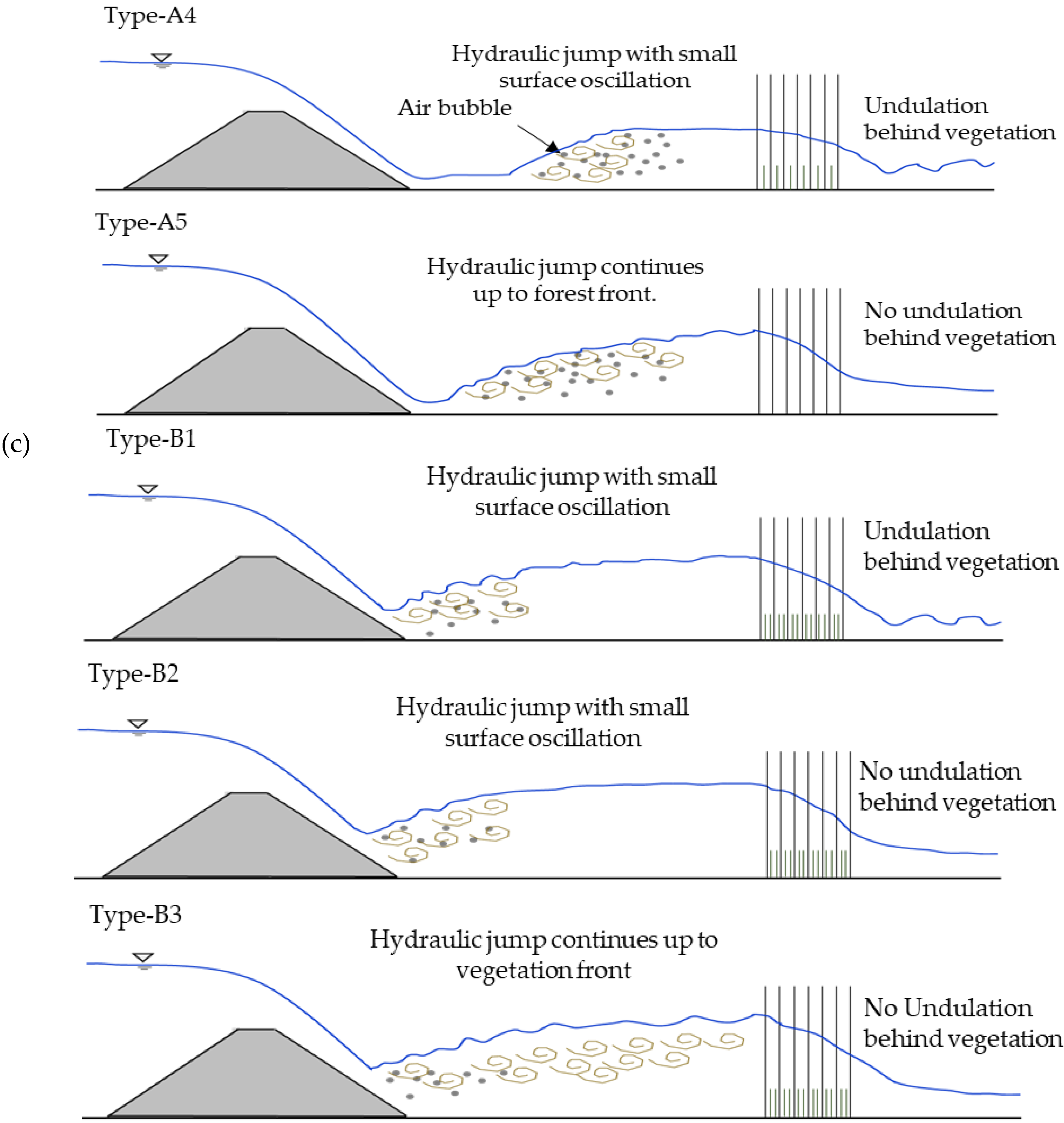
3.1. Formation of Hydraulic Jump
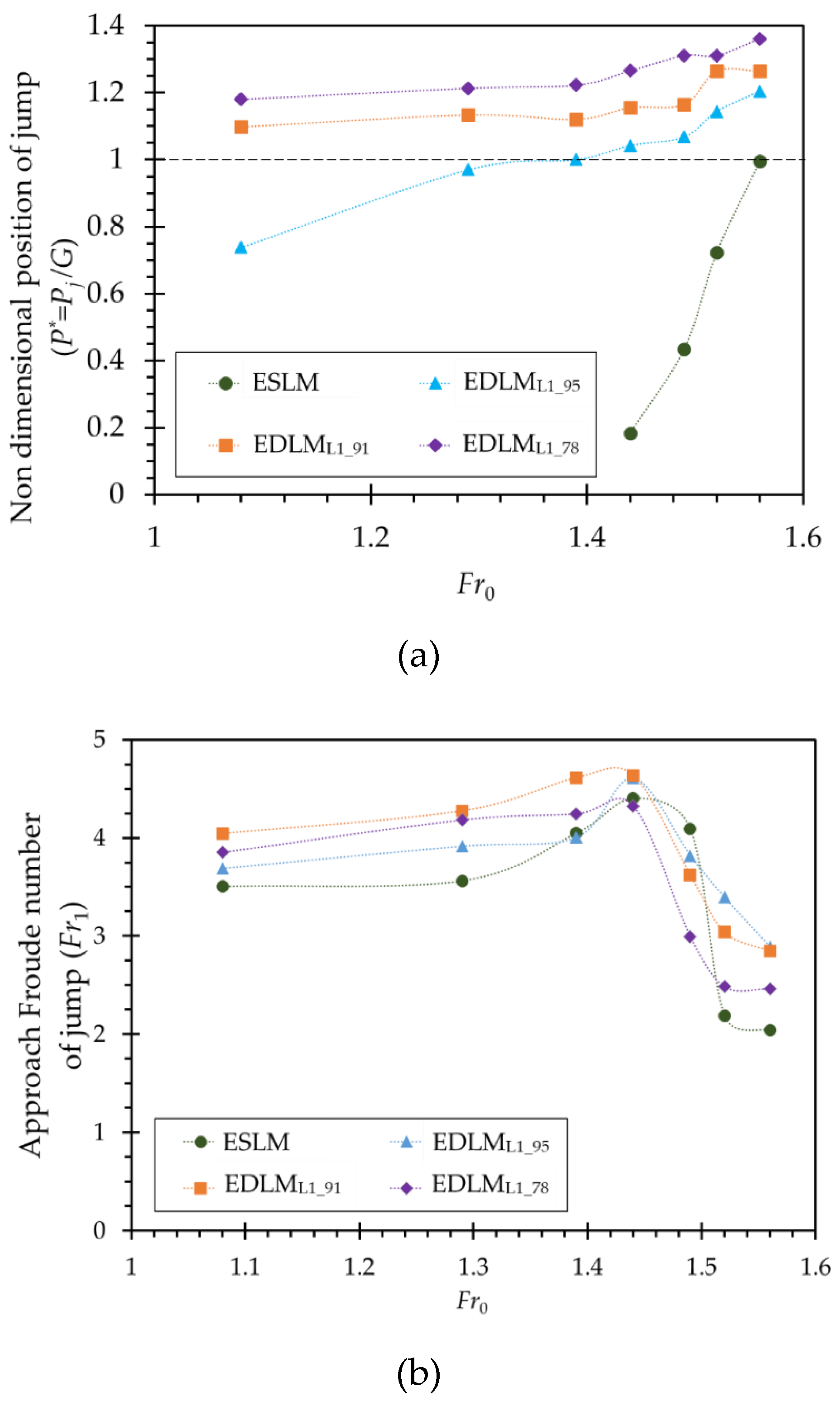
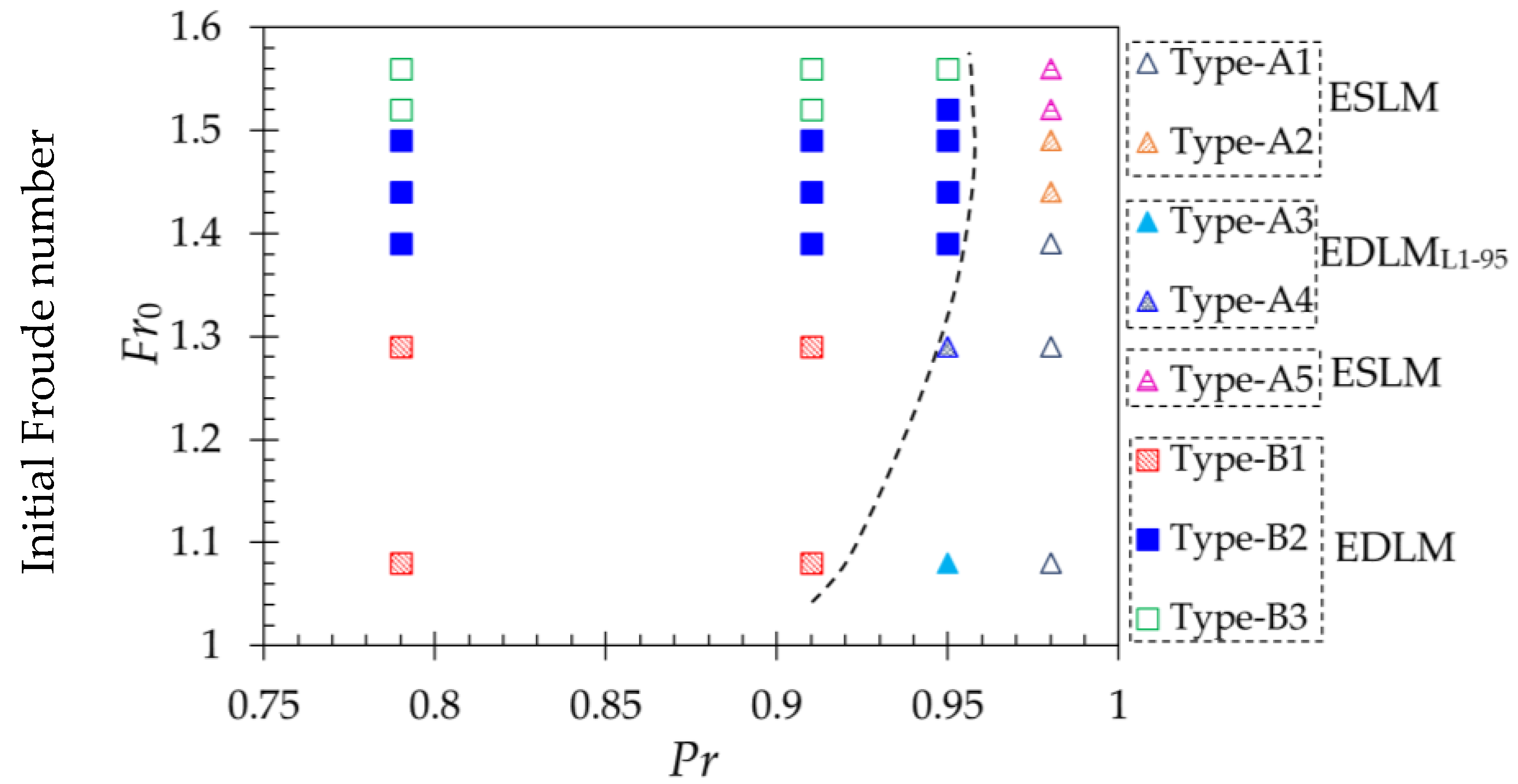
3.2. Hydraulic Jump and Its Classification in the Defense System
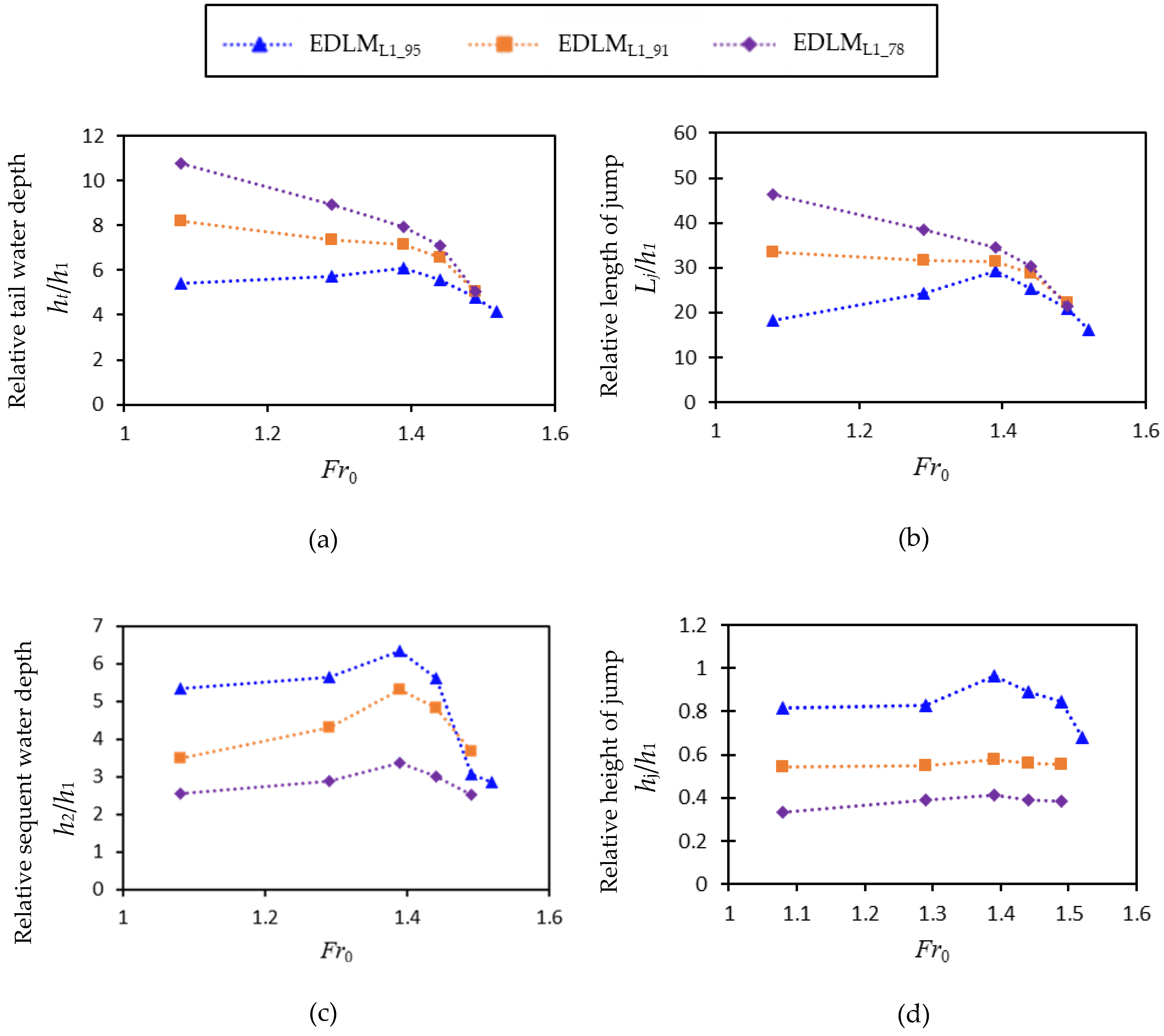
3.3. Characteristics of Hydraulic Jump
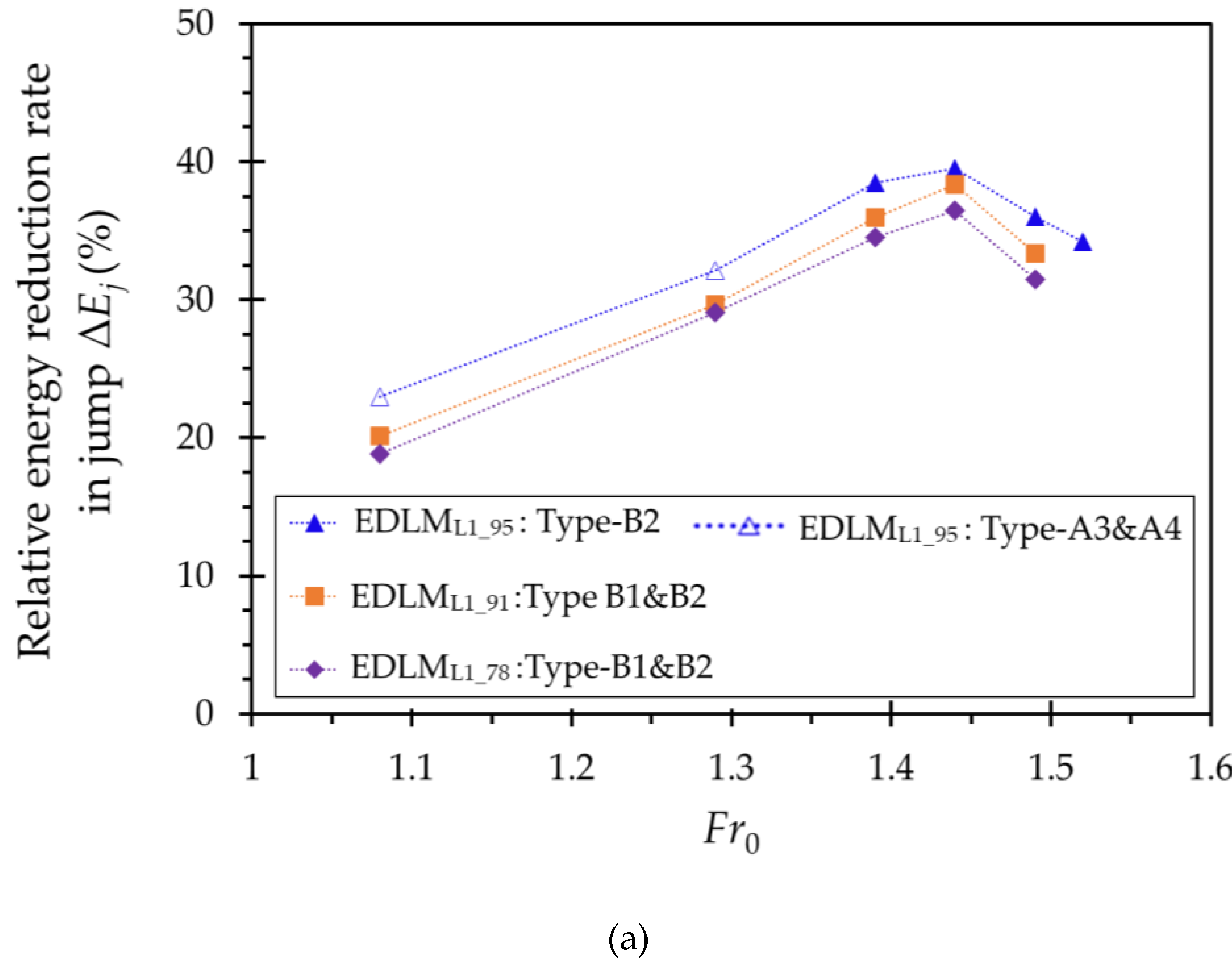
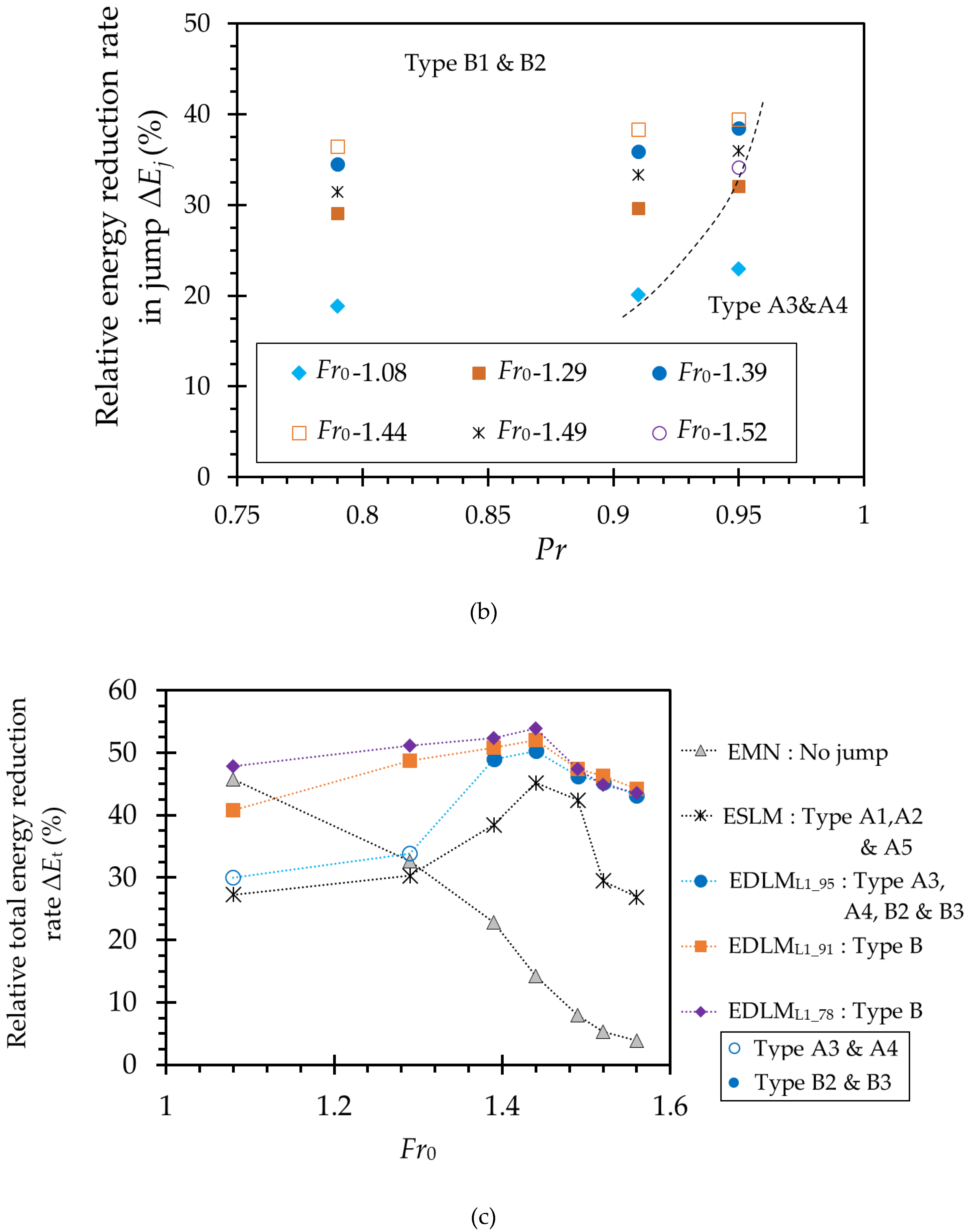
3.4. Energy Reduction through the Hybrid Defense System
4. Discussion
4.1. Changes in Flow Structure in the Hybrid Defense System
4.2. Energy Reduction
4.3. Control of Scouring to Reduce the Destruction of Defense Structures
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notations
| L1 | submerged layer, defined in Figure 1d |
| L2 | emergent layer, defined in Figure 1d |
| WE | width of the embankment model |
| HE | height of the embankment model |
| WF | width of the forest model |
| θ | angle of the embankment slope |
| G | gap between the embankment model and forest model, G = 50 cm |
| d | diameter of a cylinder |
| Ds | center-to-center distance between short cylinders |
| Dt | center-to-center distance between tall cylinders |
| Dsx | center-to-center distance between short cylinders in the stream wise direction |
| Dtx | center-to-center distance between tall cylinders in the stream wise direction |
| Dsy | center-to-center distance between short cylinders in the transverse direction of the flow |
| Dty | center-to-center distance between tall cylinders in the transverse direction of the flow |
| Ss | spacing between neighboring cylinders in L1 along the transverse direction of the flow |
| St | spacing between neighboring cylinders in L2 along the transverse direction of the flow |
| Pr | porosity of the forest model, Pr = 1 − ntπd2/4, nt: number of trees per unit area |
| dn | thickness of forest, |
| Q | discharge |
| b | width of the hydraulic flume |
| h0 | initial water depth (without placing embankment and forest model) |
| hEMN | water depth downstream of the embankment model (without forest model; Case EMN) |
| h1 | water depth upstream of a hydraulic jump, in Section 1 in Figure 2 |
| h2 | water depth downstream of a hydraulic jump, in Section 2 in Figure 2 |
| h3 | water depth downstream of the forest model, in Section 3 in Figure 2 |
| ht | tail water depth (from the end of the roller vortex of a hydraulic jump to the forest front) |
| hj | height of a hydraulic jump |
| d1 | water depth upstream of a hydraulic jump on the embankment slope |
| Pj | position of a hydraulic jump (distance of the jump toe from the front line of the forest) |
| u0 | initial velocity (without placing embankment and forest model) |
| u1 | velocity upstream of a hydraulic jump, in the Section 1 in Figure 2 |
| u2 | velocity downstream of a hydraulic jump, in the Section 2 in Figure 2 |
| u3 | velocity downstream of the forest model, in the Section 3 in Figure 2 |
| Lj | length of a hydraulic jump |
| lj | length of a hydraulic jump on the embankment slope |
| zj | elevation of the jump toe when it is on the embankment slope |
| g | acceleration due to gravity |
| E1 | energy head upstream of a jump, in Section 1 in Figure 2 |
| E2 | energy head downstream of a jump, in Section 2 in Figure 2 |
| E3 | energy head downstream of the forest model, in Section 3 in Figure 2 |
| α | energy coefficient |
| P* | nondimensional position of a jump |
| Fr0 | initial Froude number, |
| Fr1 | Froude number upstream of a hydraulic jump, |
| Fr2 | average Froude number within the model zone (with embankment and forest model), ) |
| ΔEj (%) | energy reduction rate in the hydraulic jump (defined in Equation (3)) |
| ΔEt (%) | total energy reduction rate through the hybrid defense system (downstream of the forest model; defined in Equation (3)) |
References
- Okumura, N.; Jonkman, S.N.; Esteban, M.; Hofland, B.; Shibayama, T. A method for tsunami risk assessment: A case study for Kamakura, Japan. Nat. Hazards 2017, 88, 1451–1472. [Google Scholar] [CrossRef]
- Esteban, M.; Glasbergen, T.; Takabatake, T.; Hofland, B.; Nishizaki, S.; Nishida, Y.; Stolle, J.; Nistor, I.; Bricker, J.; Takagi, H.; et al. Overtopping of coastal structures by tsunami waves. Geosciences 2017, 7, 121. [Google Scholar] [CrossRef]
- Suppasri, A.; Shuto, N.; Imamura, F.; Koshimura, S.; Mas, E.; Yalciner, A.C. Lessons learned from the 2011 Great East Japan Tsunami: Performance of tsunami countermeasures, coastal buildings, and tsunami evacuation in Japan. Pure Appl. Geophys. 2013, 170, 993–1018. [Google Scholar] [CrossRef]
- Nandasena, N.A.K.; Sasaki, Y.; Tanaka, N. Modeling field observations of the 2011 Great East Japan tsunami: Efficacy of artificial and natural structures on tsunami mitigation. Coast. Eng. 2012, 67, 1–13. [Google Scholar] [CrossRef]
- Pakoksung, K.; Suppasri, A.; Imamura, F. Systematic evaluation of different infrastructure systems for tsunami defense in Sendai City. Geosciences 2018, 8, 173. [Google Scholar] [CrossRef]
- Igarashi, Y.; Tanaka, N. Effectiveness of a compound defense system of sea embankment and coastal forest against a tsunami. Ocean Eng. 2018, 151, 246–256. [Google Scholar] [CrossRef]
- Tanaka, N.; Sasaki, Y.; Mowjood, M.I.M. Effects of sand dune and vegetation in the coastal area of sri lanka at the indian ocean tsunami. In Advances in Geosciences: Volume 6: Hydrological Science (HS); World Scientific Co.: Singapore, 2006; pp. 149–159. ISBN 9789812708915. [Google Scholar]
- Fadly, U.; Murakami, K. Study on reducing tsunami inundation energy by the modification of topography based on local wisdom. J. Jpn. Soc. Civ. Eng. Ser. B3 2013, 68, I_66–I_71. [Google Scholar] [CrossRef]
- Tsujimoto, G.; Kakinoki, T.; Mineura, R.; Uno, K.; Yamada, F. Scouring mechanism behind seawall from tsunami overflow and optimum conditions to reduce tsunami energy with an artificial trench. Coast. Eng. Proc. 2015, 1, 38. [Google Scholar] [CrossRef]
- Rahman, M.M.; Schaab, C.; Nakaza, E. Experimental and numerical modeling of tsunami mitigation by canals. J. Waterw. Port Coast. Ocean Eng. 2016, 143, 04016012. [Google Scholar] [CrossRef]
- Igarashi, Y.; Tanaka, N.; Zaha, T. Changes in flow structures and energy reduction through compound tsunami mitigation system with embankment and lined piles. Ocean Eng. 2018, 164, 722–732. [Google Scholar] [CrossRef]
- Zaha, T.; Tanaka, N.; Kimiwada, Y. Flume experiments on optimal arrangement of hybrid defense system comprising an embankment, moat, and emergent vegetation to mitigate inundating tsunami current. Ocean Eng. 2019, 173, 45–57. [Google Scholar] [CrossRef]
- Igarashi, Y.; Tanaka, N. Multiple defense for tsunami inundation by two embankment system and prevention of oscillation by trees on embankment. In Proceedings of the 20th Congress of IAHR APD Congress, Colombo, Sri Lanka, 28–31 August 2016. [Google Scholar]
- Strusińska-Correia, A. Tsunami mitigation in Japan after the 2011 Tōhoku Tsunami. Int. J. Disaster Risk Reduct. 2017, 22, 397–411. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J.; Yasuda, S. Breaking pattern and critical breaking condition of Japanese pine trees on coastal sand dunes in huge tsunami caused by Great East Japan Earthquake. Nat. Hazards 2013, 65, 423–442. [Google Scholar] [CrossRef]
- Matsuba, S.; Mikami, T.; Jayaratne, R.; Shibayama, T.; Esteban, M. Analysis of tsunami behavior and the effect of coastal forest in reducing tsunami force around the coastal dikes. Coast. Eng. Proc. 2014, 1, 37. [Google Scholar] [CrossRef]
- Shuto, N. The effectiveness and limit of tsunami control forests. Coast. Eng. Jpn. 1987, 30, 143–153. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Effectiveness of finite length inland forest in trapping tsunami-borne wood debris. J. Earthq. Tsunami 2016, 10, 1650008. [Google Scholar] [CrossRef]
- Tanaka, N.; Onai, A. Mitigation of destructive fluid force on buildings due to trapping of floating debris by coastal forest during the Great East Japan tsunami. Landsc. Ecol. Eng. 2017, 13, 131–144. [Google Scholar] [CrossRef]
- Tanaka, N.; Sasaki, Y.; Mowjood, M.I.M.; Jinadasa, K.B.S.N.; Homchuen, S. Coastal vegetation structures and their functions in tsunami protection: Experience of the recent Indian Ocean tsunami. Landsc. Ecol. Eng. 2007, 3, 33–45. [Google Scholar] [CrossRef]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular hydraulic jump formation and energy loss in a flow through emergent vegetation of varying thickness and density. Ocean Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Tanaka, N.; Jinadasa, K.B.S.N.; Mowjood, M.I.M.; Fasly, M.S.M. Coastal vegetation planting projects for tsunami disaster mitigation: Effectiveness evaluation of new establishments. Landsc. Ecol. Eng. 2011, 7, 127–135. [Google Scholar] [CrossRef]
- Tanaka, N. Vegetation bioshields for tsunami mitigation: Review of effectiveness, limitations, construction, and sustainable management. Landsc. Ecol. Eng. 2009, 5, 71–79. [Google Scholar] [CrossRef]
- Rashedunnabi, A.H.M.; Tanaka, N. Physical modelling of tsunami energy reduction through vertically two layered rigid vegetation. In Proceedings of the 12th ISE, Tokyo, Japan, 19–24 August 2018. [Google Scholar]
- Chow, V. Te Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; p. 728. [Google Scholar]
- Hager, W.H. B-jump in sloping channel. J. Hydraul. Res. 1988, 26, 539–558. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Hydraulic jump in sloping channels. J. Hydraul. Eng. 1991, 117, 905–921. [Google Scholar] [CrossRef]
- Ali, H.M.; El Gendy, M.M.; Mirdan, A.M.H.; Ali, A.A.M.; Abdelhaleem, F.S.F. Minimizing downstream scour due to submerged hydraulic jump using corrugated aprons. Ain Shams Eng. J. 2014, 5, 1059–1069. [Google Scholar] [CrossRef] [Green Version]
- Nandasena, N.A.K.; Tanaka, N.; Sasaki, Y.; Osada, M. Boulder transport by the 2011 Great East Japan tsunami: Comprehensive field observations and whither model predictions? Mar. Geol. 2013, 346, 292–309. [Google Scholar] [CrossRef]
- Foytong, P.; Ruangrassamee, A.; Shoji, G.; Hiraki, Y.; Ezura, Y. Analysis of Tsunami Flow Velocities during the March 2011 Tohoku, Japan, Tsunami. Earthq. Spectra 2013, 29, S161–S181. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Tanaka, N.; Yasuda, S.; Iimura, K.; Yagisawa, J. Combined effects of coastal forest and sea embankment on reducing the washout region of houses in the Great East Japan tsunami. J. Hydro-Environ. Res. 2014, 8, 270–280. [Google Scholar] [CrossRef]
- Yanagisawa, H.; Koshimura, S.; Goto, K.; Miyagi, T.; Imamura, F.; Ruangrassamee, A.; Tanavud, C. The reduction effects of mangrove forest on a tsunami based on field surveys at Pakarang Cape, Thailand and numerical analysis. Estuar. Coast. Shelf Sci. 2009, 81, 27–37. [Google Scholar] [CrossRef]
- Thuy, N.B.; Nandasena, N.A.K.; Hai Dang, V.; Tanaka, N.; Quoc Viet, H.; Giay, C. Simplified formulae for designing coastal forest against tsunami run-up: One-dimensional approach. Mar. Geophys. Geol. 2018, 92, 327–346. [Google Scholar] [CrossRef]
- Japan Society of Fluid Mechanics. Handbook of Fluid Mechanics, 2nd ed.; Japan Society of Fluid Mechanics, Maruzen: Tokyo, Japan, 1998; pp. 237–240. (In Japanese) [Google Scholar]
- Tanaka, N.; Yagisawa, J. Flow structures and sedimentation characteristics around clump-type vegetation. J. Hydro-Environ. Res. 2010, 4, 15–25. [Google Scholar] [CrossRef]
- Takemura, T.; Tanaka, N. Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 2007, 39, 694–710. [Google Scholar] [CrossRef]
- Tanaka, N.; Sato, M. Scoured depth and length of pools and ditches generated by overtopping flow from embankments during the 2011 Great East Japan Tsunami. Ocean Eng. 2015, 109, 72–82. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Open Channel Flow: An Introduction: Basic Principles, Sediment Motion, Hydraulic Modelling, Design of Hydraulic Structures, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2004; ISBN 9780080472973. [Google Scholar]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; Engineering Monograph Number-25; U.S. Bureau of Reclamation: Denver, CO, USA, 1963.
- Chanson, H. Air Bubble Entrainment in Hydraulic Jumps: Physical Modelling and Scale Effects; IAHR: Madrid, Spain, 2007; Volume 1, pp. 1–10. [Google Scholar]
- Ohtsu, I.; Yasuda, Y. B-jump in sloping channel. J. Hydraul. Res. 1990, 28, 105–119. [Google Scholar] [CrossRef]
- Chanson, H.; Paintal, A. Hydraulics of stepped chutes and spillways. Appl. Mech. Rev. 2003, 56, B10. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Novak, P.; Moffat, A.; Nalluri, C.; Narayanan, R. Hydraulic Structures, 4th ed.; CRC Press: Boca Raton, FL, USA, 2014; ISBN 9780415306089. [Google Scholar]
- Achenbach, E. Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 1971, 46, 321–335. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Two-phase flow characteristics of stepped spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Kawagoshi, N.; Hager, W.H. B-jump in sloping channel, II. J. Hydraul. Res. 1990, 28, 461–480. [Google Scholar] [CrossRef]
- Nistor, I.; Esteban, M.; Premaratne, B.; Mikami, T.; Matsuba, S.; Adewale, A.; Shibayama, T.; Jayaratne, M.P.R. Failure mechanisms and local scour at coastal structures induced by tsunami. Coast. Eng. J. 2016, 58, 1640017. [Google Scholar]
- Ohtsu, I.; Yasuda, Y.; Takahashi, M. Flow characteristics of skimming flows in stepped channels. J. Hydraul. Eng. 2004, 130, 860–869. [Google Scholar] [CrossRef]
- Adam, A.M.; Ruff, J.F.; AlQaser, G.; Abt, S.R. Characteristics of B-jump with different toe locations. J. Hydraul. Eng. 1993, 119, 938–948. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J.; Yasuda, S. Characteristics of damage due to tsunami propagation in river channels and overflow of their embankments in Great East Japan Earthquake. Int. J. River Basin Manag. 2012, 10, 269–279. [Google Scholar] [CrossRef]
- Gonzalez, C.A.; Chanson, H. Hydraulic design of stepped spillways and downstream energy dissipators for embankment dams. Dam Eng. 2007, 17, 223–244. [Google Scholar]

| Exp. Case | Initial Froude Number (Fr0) | Ds (cm) | Dt (cm) | Ss (cm) | St (cm) | d (cm) | WF (cm) | Porosity (Pr) of L1 % | Porosity (Pr) of L2 % |
|---|---|---|---|---|---|---|---|---|---|
| EMN | 1.08,1.29,1.39,1.44, 1.49,1.52,1.56 | - | - | - | - | - | - | - | - |
| ESLM | 1.08,1.29,1.39,1.44, 1.49,1.52,1.5 | - | 2.5 | - | 0.85 | 0.4 | 24.27 | - | 98 |
| EDLML1_95 | 1.08,1.29,1.39,1.44, 1.49,1.52,1.56 | 1.25 | 2.5 | 0.85 | 0.85 | 0.4 | 24.27 | 95 | 98 |
| EDLML1_91 | 1.08,1.29,1.39,1.44, 1.49,1.52,1.56 | 1.25 | 2.5 | 0.225 | 0.85 | 0.4 | 24.27 | 91 | 98 |
| EDLML1_78 | 1.08,1.29,1.39,1.44, 1.49,1.52,1.56 | 0.83 | 2.5 | 0.017 | 0.85 | 0.4 | 24.27 | 78 | 98 |
| Result | Exp. Cases | Fr0 | ||||||
|---|---|---|---|---|---|---|---|---|
| Fr2 | 1.08 | 1.29 | 1.39 | 1.44 | 1.49 | 1.52 | 1.56 | |
| EMN | 2.92 | 3.24 | 3.35 | 3.52 | 3.59 | 3.67 | 3.75 | |
| ESLM | 2.73 | 3.23 | 3.28 | 3.10 | 2.67 | 1.04 | 0.70 | |
| EDLML1_95 | 0.98 | 0.91 | 0.54 | 0.54 | 0.58 | 0.54 | 0.53 | |
| EDLML1_91 | 0.20 | 0.25 | 0.31 | 0.35 | 0.40 | 0.42 | 0.42 | |
| EDLML1_78 | 0.12 | 0.18 | 0.23 | 0.26 | 0.32 | 0.35 | 0.35 | |
| lj/HE | EMN | - | - | - | - | - | - | - |
| ESLM | - | - | - | - | - | - | - | |
| EDLML1_95 | - | - | - | 0.142 | 0.228 | 0.486 | 0.689 | |
| EDLML1_91 | 0.331 | 0.452 | 0.408 | 0.525 | 0.559 | 0.897 | 0.897 | |
| EDLML1_78 | 0.609 | 0.722 | 0.753 | 0.897 | 1.051 | 1.217 | 1.221 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali Hasan Muhammad, R.; Tanaka, N. Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest. Geosciences 2019, 9, 247. https://doi.org/10.3390/geosciences9060247
Ali Hasan Muhammad R, Tanaka N. Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest. Geosciences. 2019; 9(6):247. https://doi.org/10.3390/geosciences9060247
Chicago/Turabian StyleAli Hasan Muhammad, Rashedunnabi, and Norio Tanaka. 2019. "Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest" Geosciences 9, no. 6: 247. https://doi.org/10.3390/geosciences9060247
APA StyleAli Hasan Muhammad, R., & Tanaka, N. (2019). Energy Reduction of a Tsunami Current through a Hybrid Defense System Comprising a Sea Embankment Followed by a Coastal Forest. Geosciences, 9(6), 247. https://doi.org/10.3390/geosciences9060247





