Nanoindentation Studies of Plasticity and Dislocation Creep in Halite
Abstract
:1. Introduction
2. Methods
3. Results
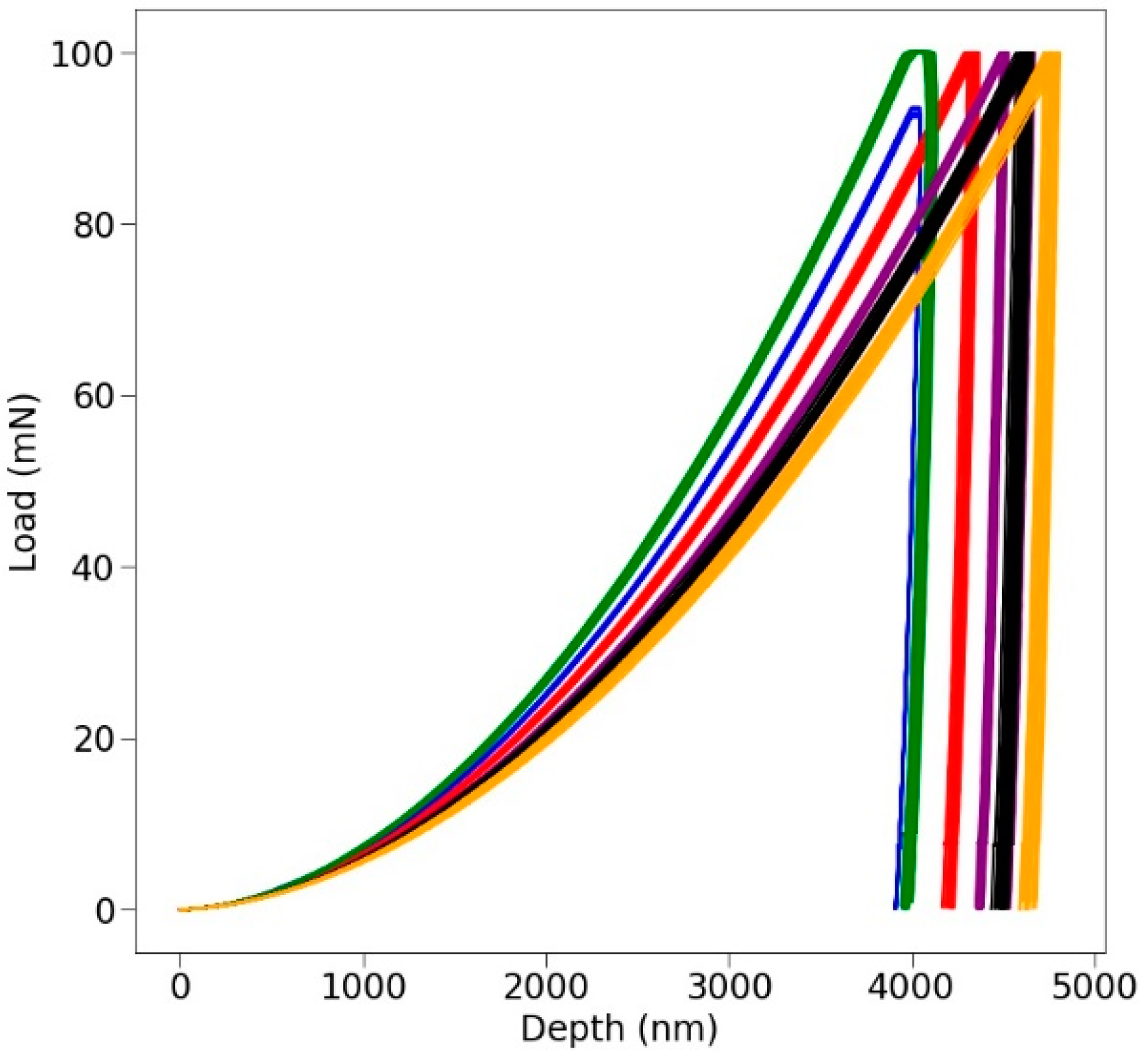
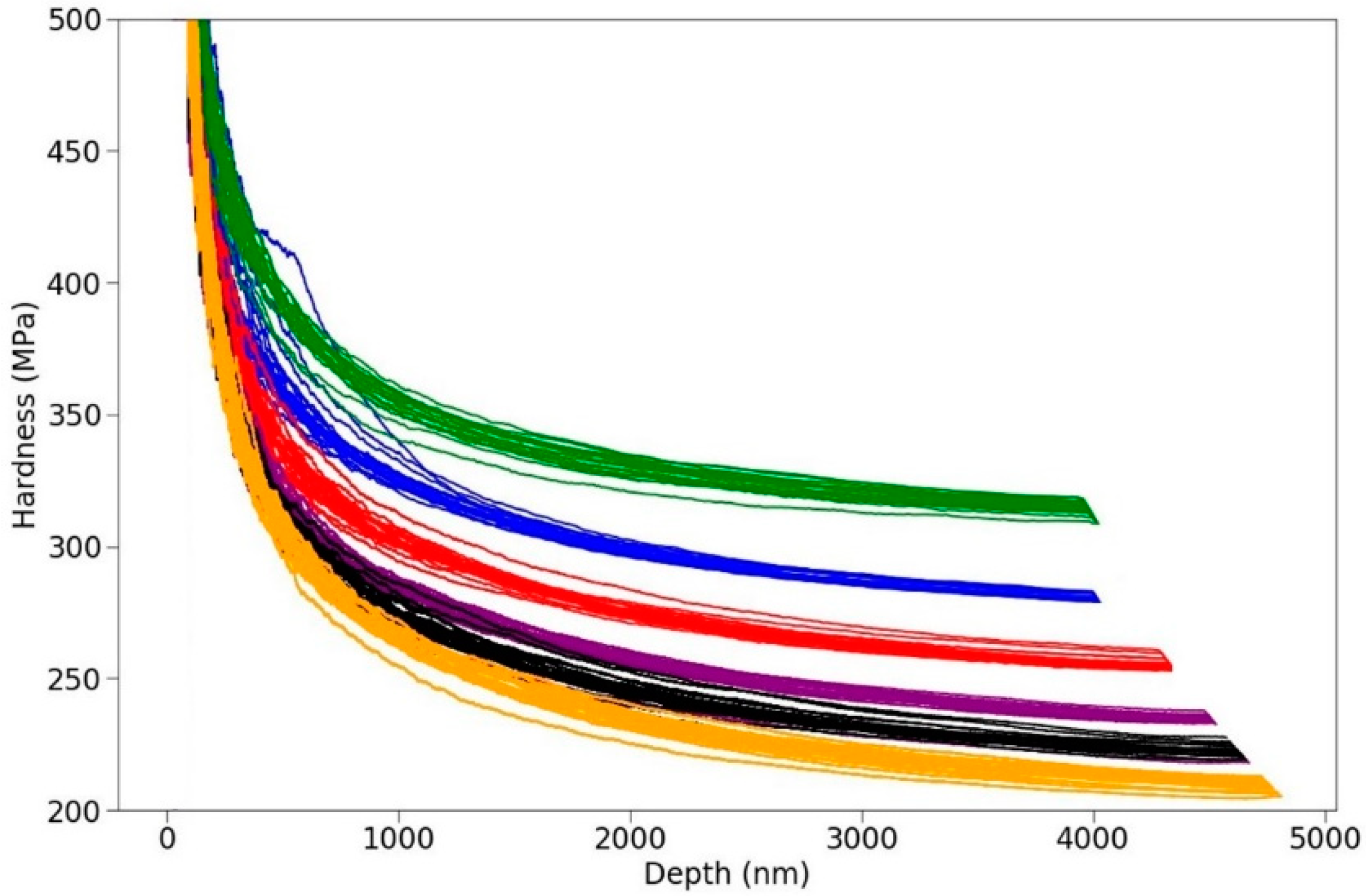
3.1. Constant Strain Rate Experiments
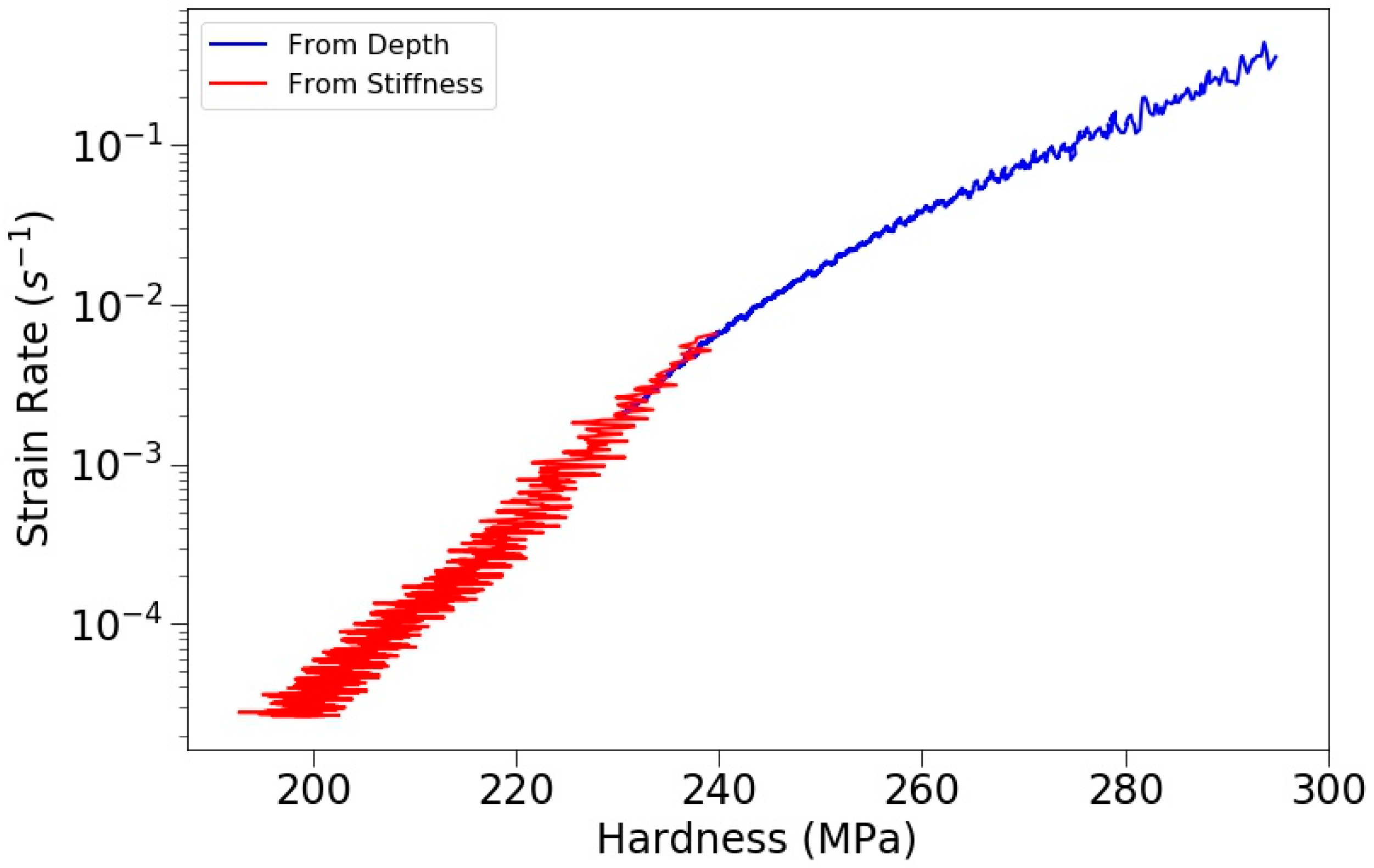
3.2. Constant Load and Hold Creep Experiments
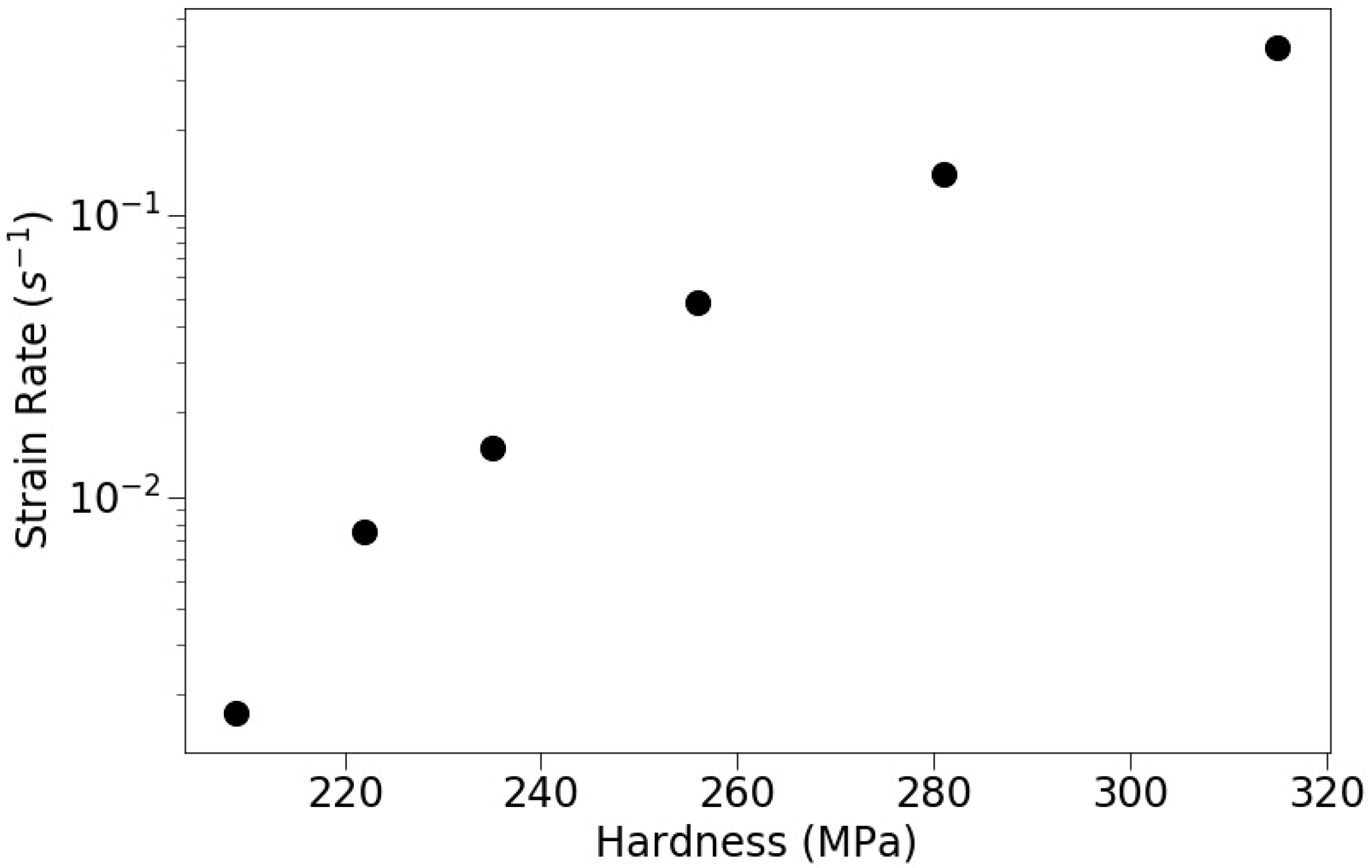
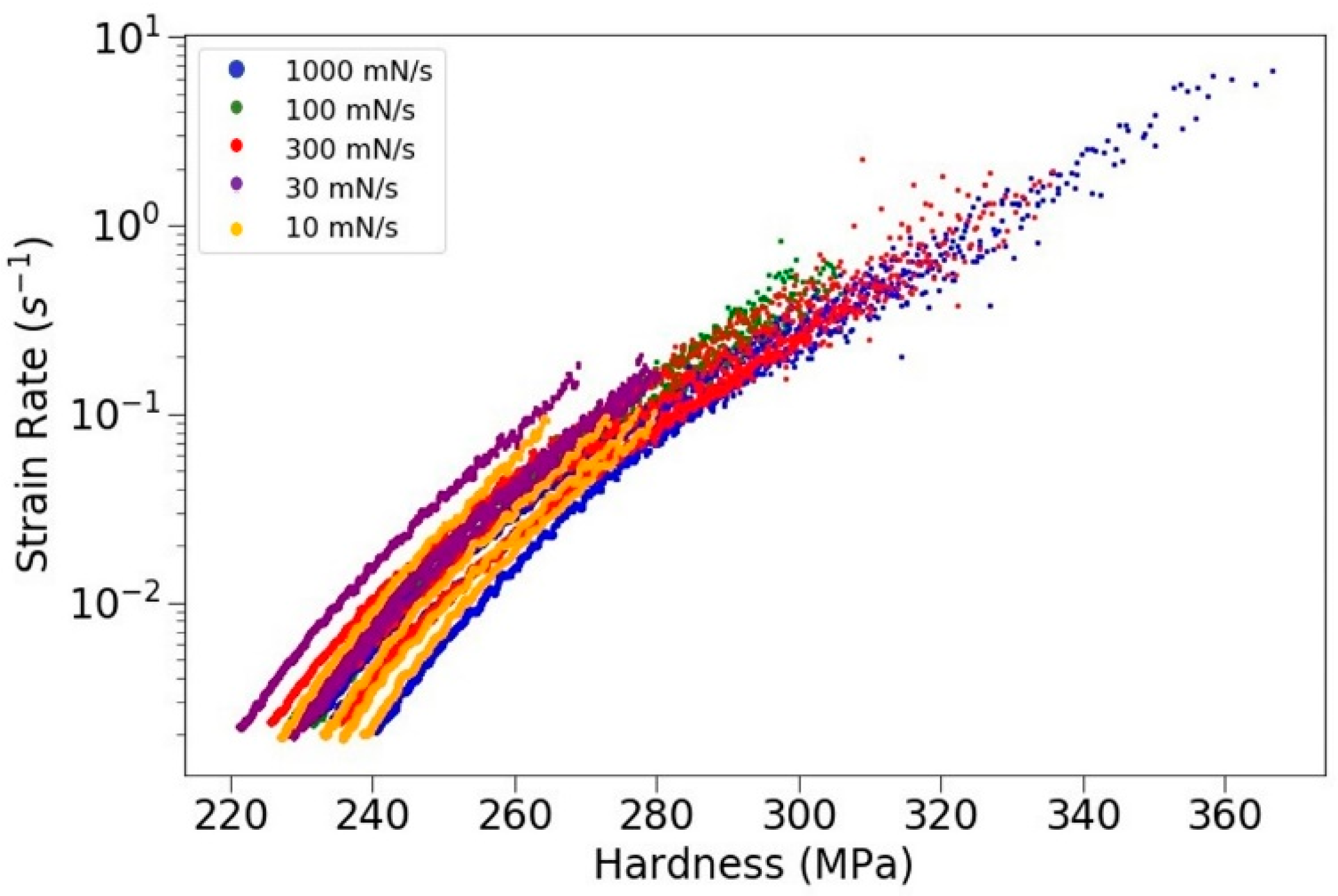
3.3. Effect of Loading Rate
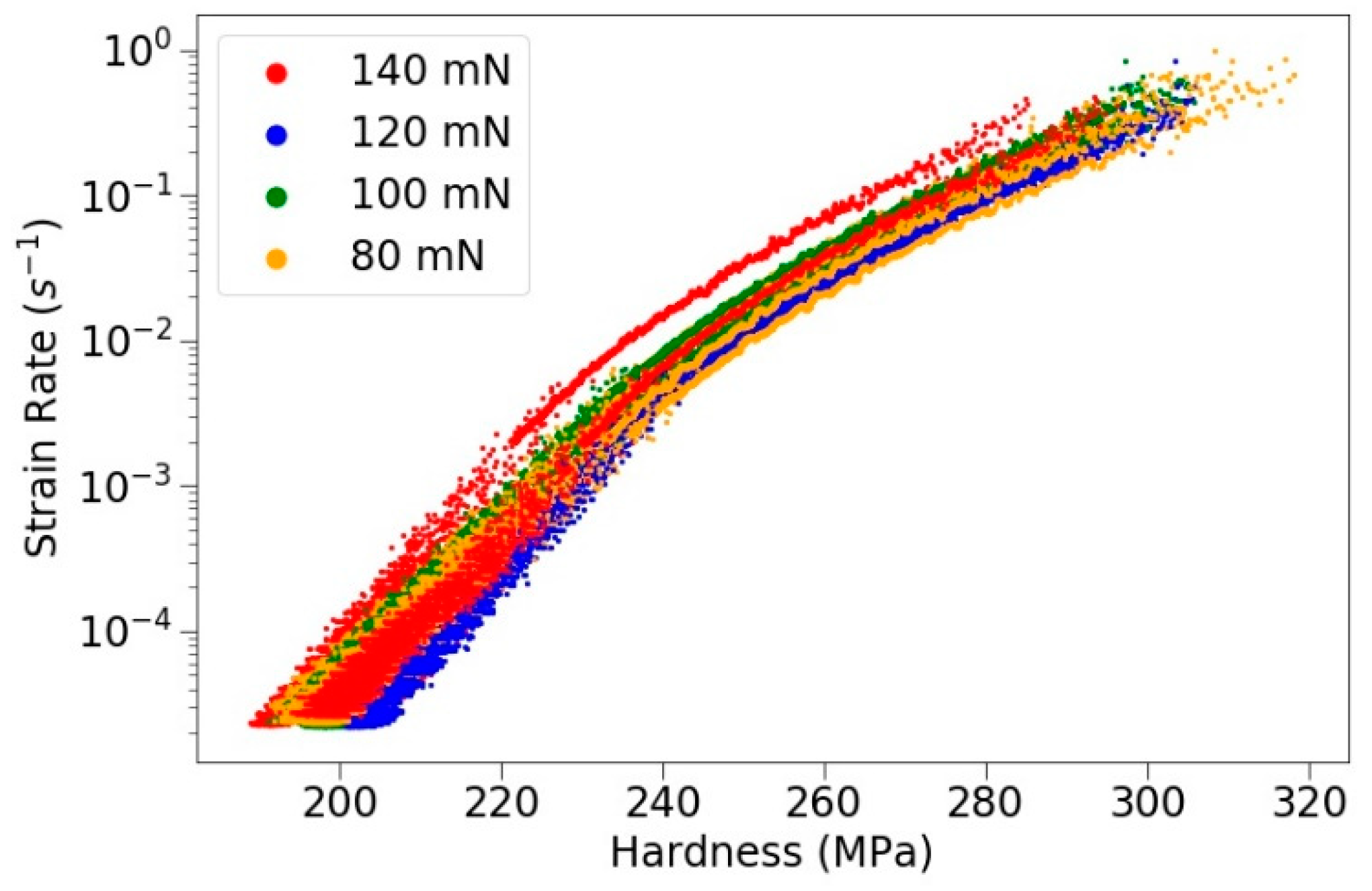
3.4. Effect of Peak Load
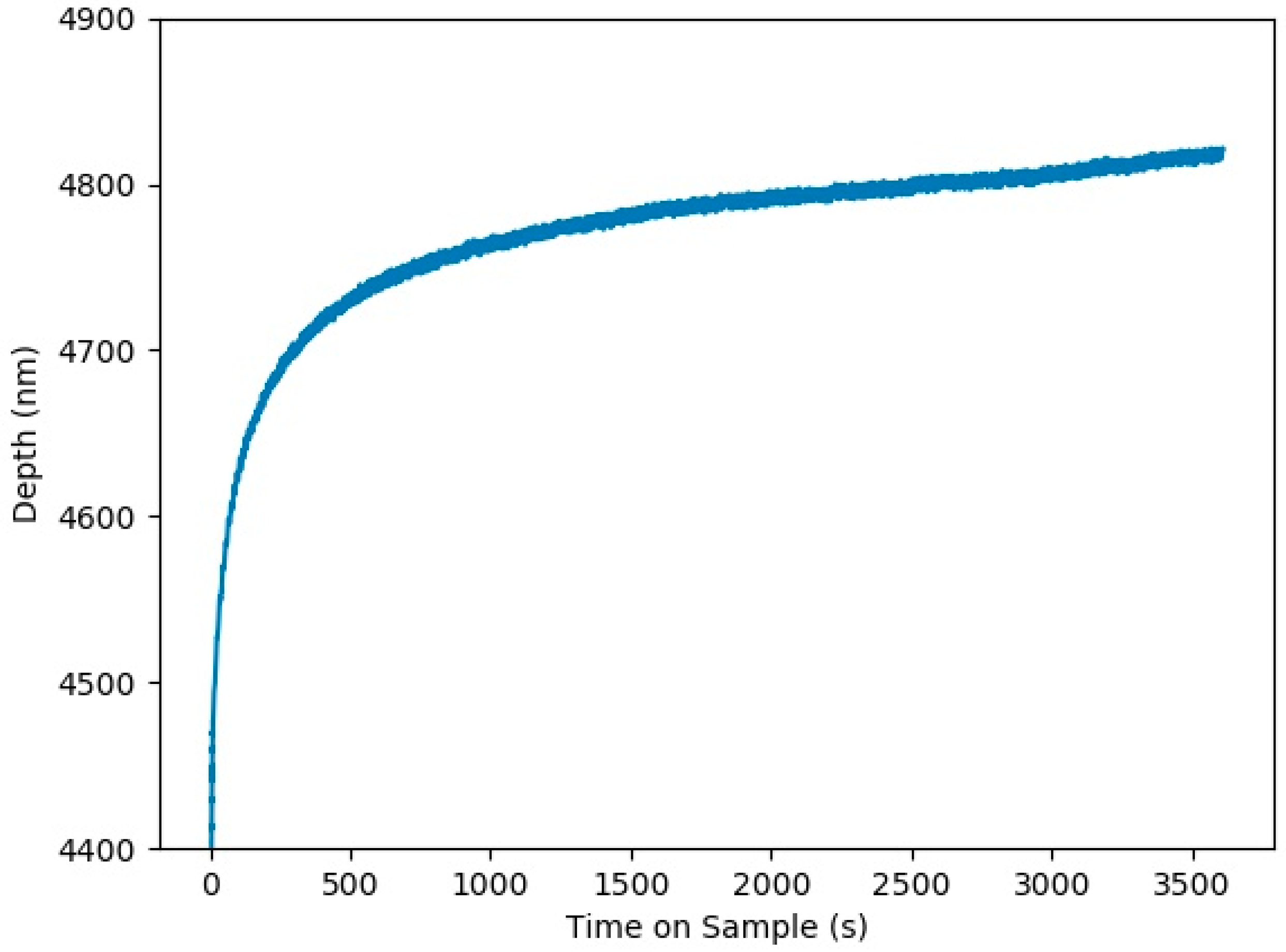
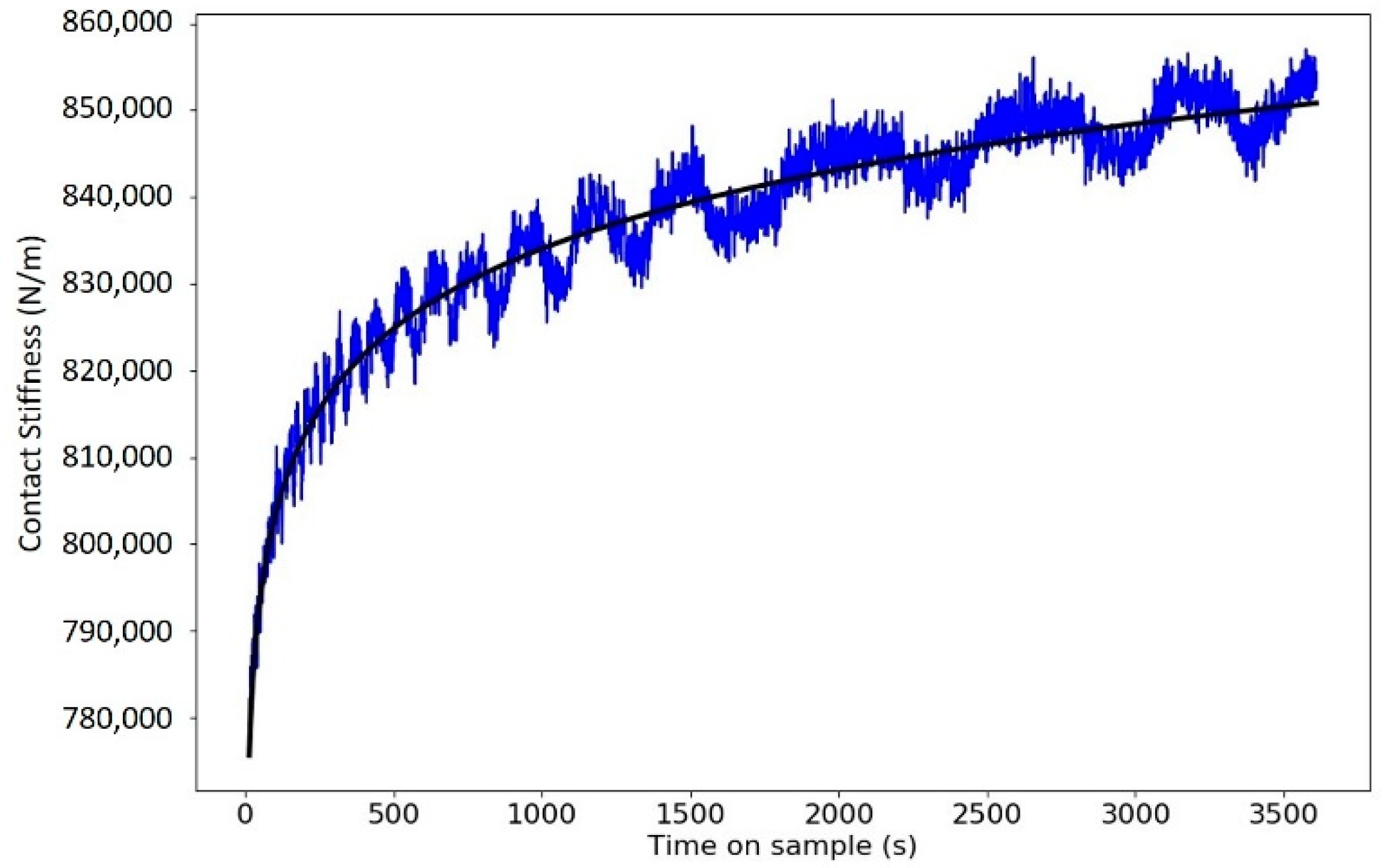
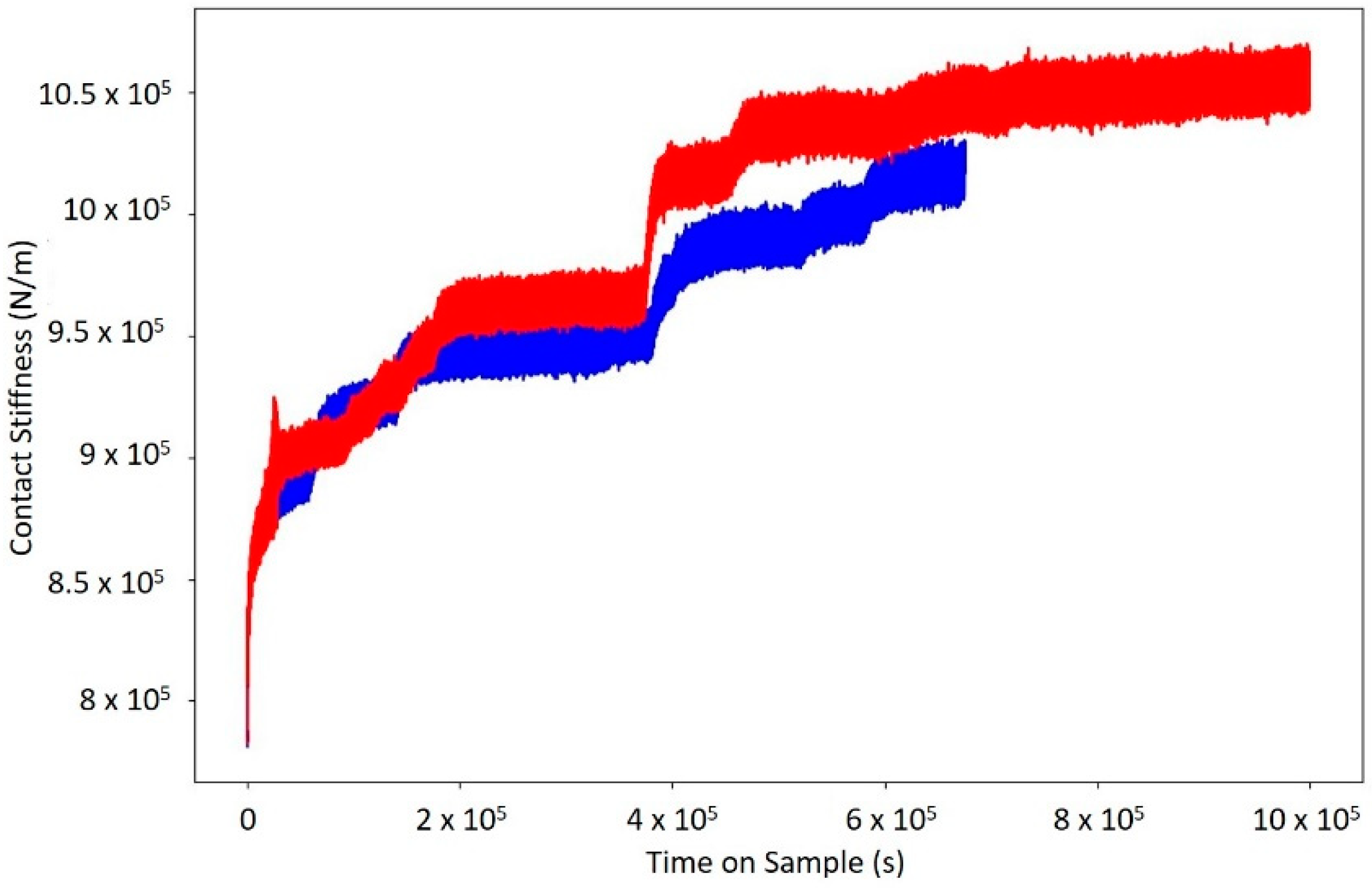
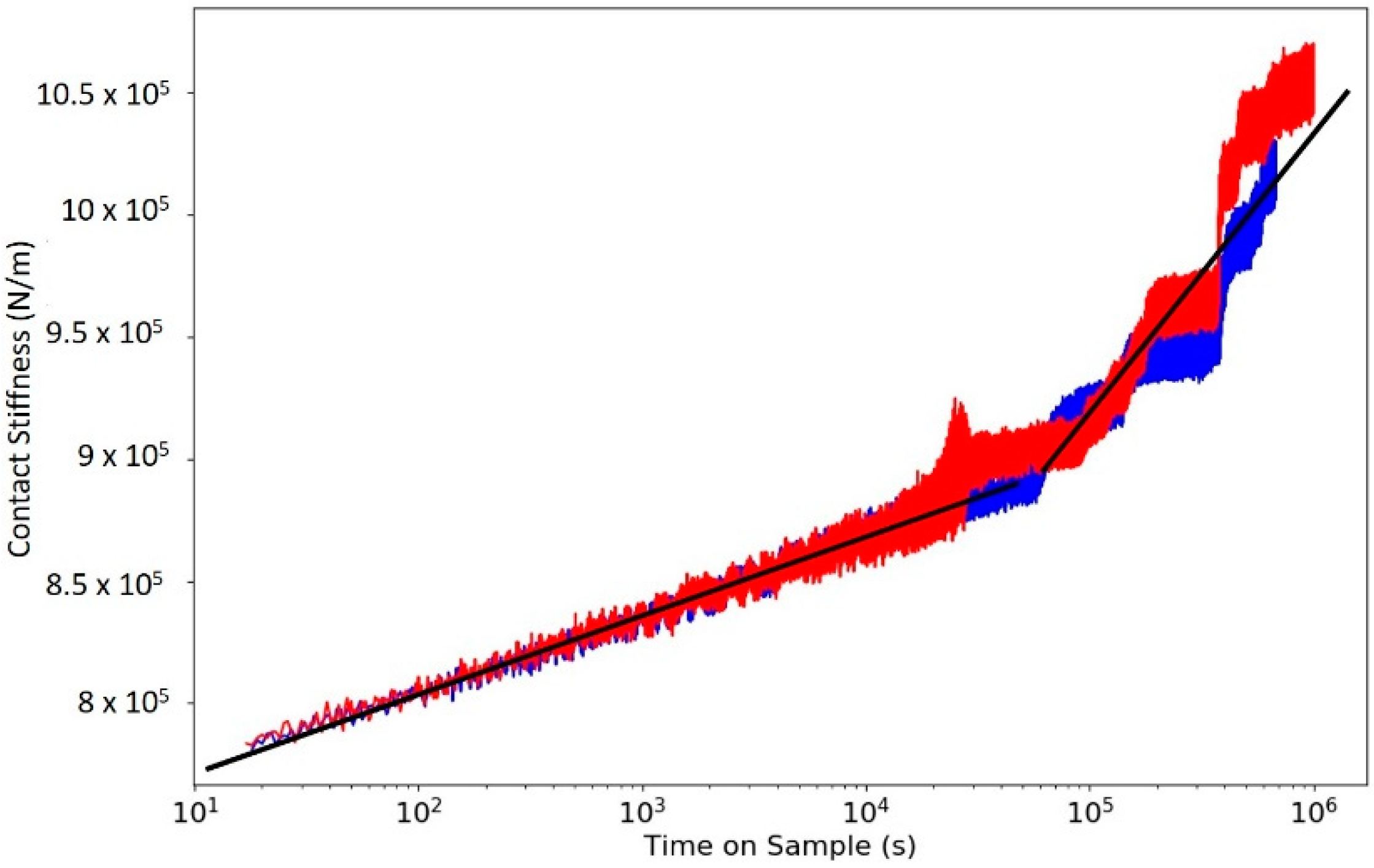
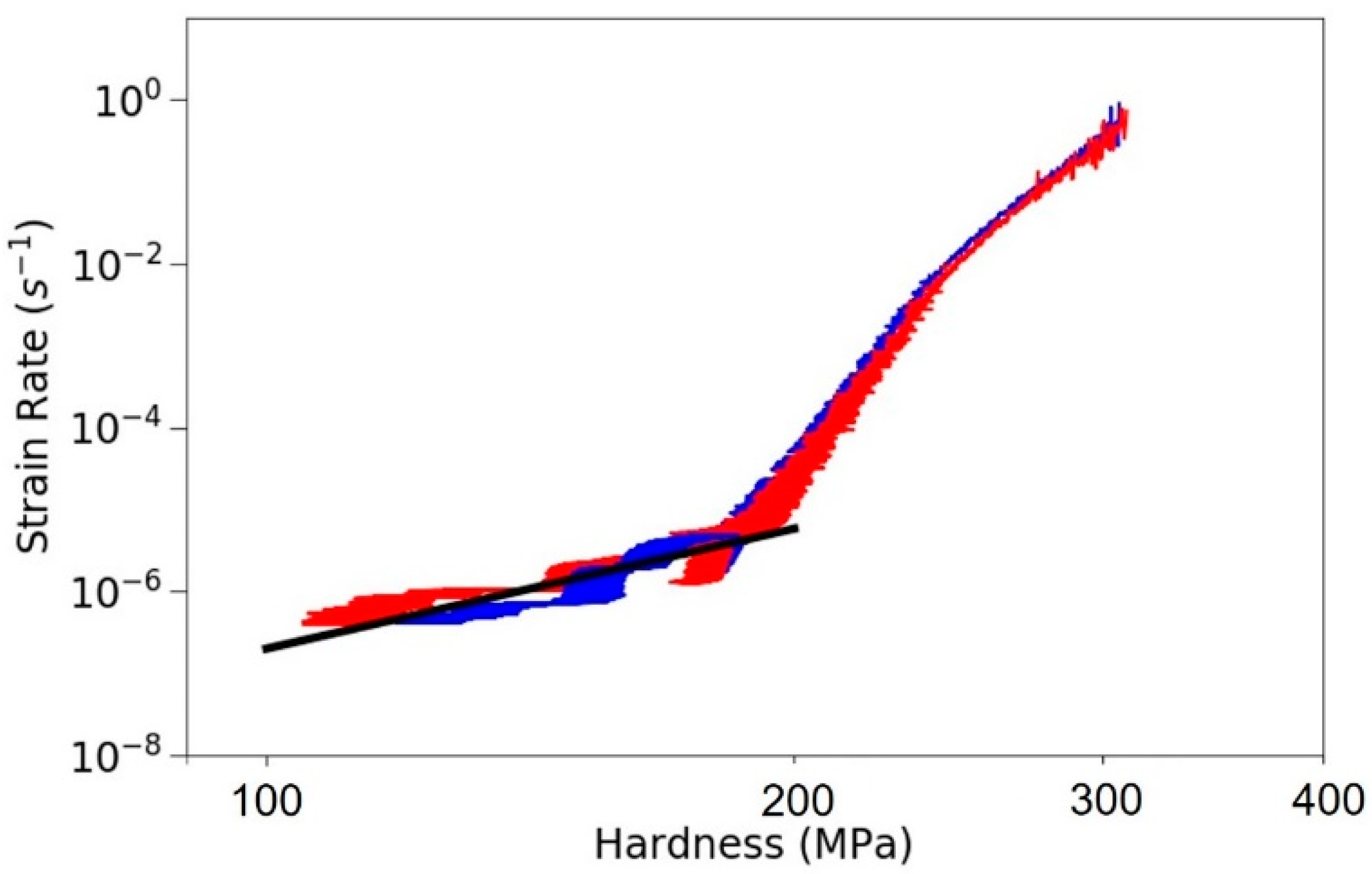
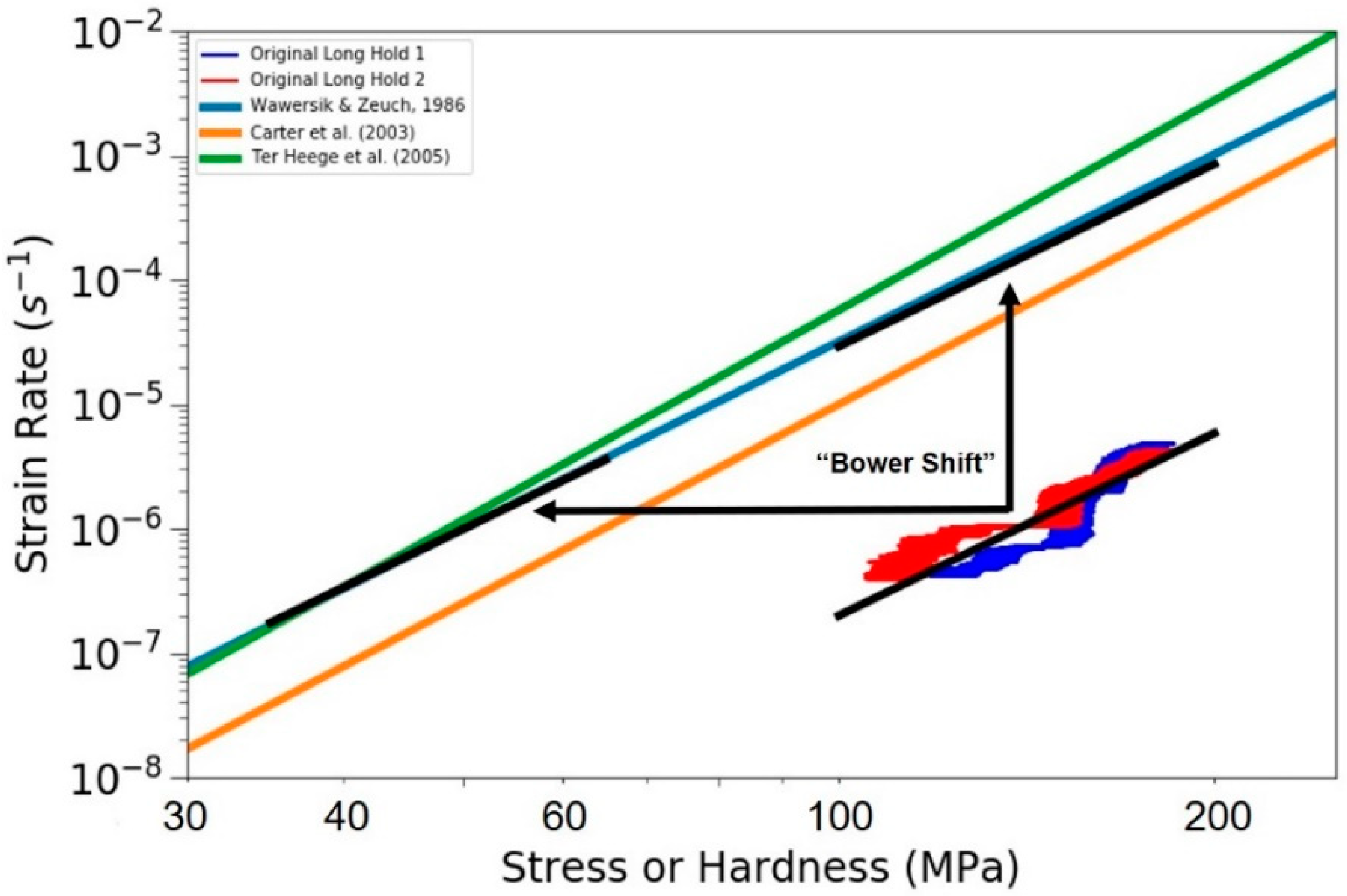
3.5. Very Long Hold Creep Tests
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Jackson, M.P.A.; Talbot, C.J. External shapes, strain rates, and dynamics of fault structures. GSA Bull. 1986, 97, 305–323. [Google Scholar] [CrossRef]
- van Keken, P.E.; Spiers, C.J.; van den Berg, A.P.; Muyzert, E.J. The effective viscosity of rocksalt: Implementation of steady-state creep laws in numerical models of salt diapirism. Tectonophysics 1993, 225, 457–476. [Google Scholar] [CrossRef]
- Li, S.; Abe, S.; Reuning, L.; Becker, S.; Urai, J.L.; Kukla, P.A. Numerical modelling of the displacement and deformation of embedded rock bodies during salt tectonics: A case study from the South Oman Salt Basin. Geol. Soc. Lond. 2012, 363, 503–520. [Google Scholar] [CrossRef]
- Heard, H.C. Steady-state flow in polycrystalline halite at pressure of 2 kilobars. Flow Fract. Rocks 1972, 16, 191–209. [Google Scholar]
- Heard, H.C.; Ryerson, F.J. Effect of cation impurities on steady-state flow of salt. Miner. Rock Def. Lab. Stud. 1986, 36, 99–115. [Google Scholar]
- Wawersik, W.R.; Zeuch, D.H. Modeling and mechanistic interpretation of creep of rock salt below 200 °C. Tectonophysics 1986, 121, 125–152. [Google Scholar] [CrossRef]
- Carter, N.L.; Horseman, S.T.; Russell, J.E.; Handin, J. Rheology of rocksalt. J. Struct. Geol. 1993, 15, 1257–1271. [Google Scholar] [CrossRef]
- Frannsen, R.C.M.W. The rheology of synthetic rocksalt in uniaxial compression. Tectonophysics 1994, 233, 1–40. [Google Scholar] [CrossRef]
- Hunsche, U.; Hampel, A. Rock salt—The mechanical properties of the host rock material for a radioactive waste repository. Eng. Geol. 1999, 52, 271–291. [Google Scholar] [CrossRef]
- Ter Heege, J.H.; De Bresser, J.H.; Spiers, C.J. Dynamic recrystallization of wet synthetic polycrystalline halite: Dependence of grain size distribution on flow stress, temperature and strain. Tectonophysics 2005, 396, 35–57. [Google Scholar] [CrossRef]
- Schoenherr, J.; Schleder, Z.; Urai, J.L.; Fokker, P.A.; Schulze, O. Deformation mechanisms and rheology of Pre-cambrian rocksalt from the South Oman Salt Basin. In Proceedings of the 6th Conference on the Mechanical Behavior of Salt: Understanding of THMC Processes in Salt Rocks, Hannover, Germany, 22–25 May 2007; pp. 167–173. [Google Scholar]
- Linckens, J.; Zulauf, G.; Hammer, J. Experimental deformation of course-grained rock salt to high strain. J. Geophys. Res. Solid Earth 2016, 121, 6150–6171. [Google Scholar] [CrossRef]
- Carter, N.L.; Hansen, F.D. Creep of rocksalt. Tectonophysics 1983, 92, 275–333. [Google Scholar] [CrossRef]
- Skrotzki, W.; Liu, Z.G. Analysis of the cross slip process in alkali halides. Phys. Stat. Sol. 1982, 73, K225–K229. [Google Scholar] [CrossRef]
- Skrotzki, W.; Haasen, P. The influence of texture on the creep of salt. In Proceedings of the 2nd Conference of Mechanical Behavior of Salt, Hannover, Germany, 24–28 September 1984; pp. 83–88. [Google Scholar]
- Senseny, P.E.; Hansen, F.D.; Russell, J.E.; Carter, N.L.; Handin, J.W. Mechanical behavior of rock salt: Phenomenology and micromechanisms. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 1992, 29, 363–378. [Google Scholar] [CrossRef]
- Berest, P.; Brouard, B. A tentative classification of salts according to their creep properties. In Proceedings of the SMRI spring meeting, New Orleans, LA, USA, 19–22 April 1998; pp. 19–22. [Google Scholar]
- Fossum, A.F.; Friedrich, J.T. Salt Mechanics Primer for Near-Salt and Sub-Salt Deepwater Gulf of Mexico Field Developments; Sandia Report 2063; Sandia National Laboratories: Albuquerque, NM, USA, 2002.
- Spiers, C.J.; Urai, J.L.; Lister, G.S.; Boland, J.N.; Zwart, H.J. The Influence of Fluid-Rock Interaction on the Rheology of Salt Rock; Bâtiment Jean Monnet: Luxembourg, 1986. [Google Scholar]
- Urai, J.L.; Spiers, C.J.; Zwart, H.J.; Lister, G.S. Weakening of rock salt by water during long-term creep. Nature 1986, 324, 554–557. [Google Scholar] [CrossRef] [PubMed]
- Spiers, C.J.; Urai, J.L.; Lister, G.S. The effect of brine (inherent or added) on rheology and deformation mechanisms in salt rock. In Proceedings of the 2nd Conference of Mechanical Behavior of Salt, Hannover, Germany, 24–28 September 1984; pp. 89–102. [Google Scholar]
- Spiers, C.J.; Schutiens, P.M.; Brzesowsky, R.H.; Peach, C.J.; Liezenberg, J.L.; Zwart, H.J. Experimental determination of constitutive parameters governing creep of rocksalt by pressure solution. Geol. Soc. Lond. Spec. Publ. 1990, 54, 215–227. [Google Scholar] [CrossRef]
- Urai, J.L.; Spiers, C.J. The effect of grain boundary water on deformation mechanisms and rheology of rocksalt during long-term deformation. In Proceedings of the 6th Conference on the Mechanical Behavior of Salt: Understanding of THMC Processes in Salt Rocks, Hannover, Germany, 22–25 May 2007; pp. 149–158. [Google Scholar]
- Shimamoto, T.; Logan, J.M. Velocity dependent behavior of simulated halite shear zones: An analog for silicates. In Earthquake Source Mechanics, 1st ed.; American Geophysical Union: Washington, DC, USA, 1986; Volume 37, pp. 49–63. [Google Scholar]
- Shimamoto, T. Transition between frictional slip and ductile flow for halite shear zones at room temperature. Science 1986, 231, 711–714. [Google Scholar] [CrossRef] [PubMed]
- Chester, F.M. The brittle-ductile transition in a deformation-mechanism map for halite. Tectonophysics 1988, 154, 125–136. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Johnson, K.L. The correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Evans, B.; Goetze, C. The temperature variation of hardness of olivine and its implication for polycrystalline yield stress. J. Geophys. Res. Solid Earth 1979, 84, 5505–5524. [Google Scholar] [CrossRef]
- Thom, C.A.; Brodsky, E.E.; Carpick, R.W.; Pharr, G.M.; Oliver, W.C.; Goldsby, D.L. Nanoscale roughness of natural fault surfaces controlled by scale-dependent yield strength. Geophys. Res. Let. 2017, 44, 9299–9307. [Google Scholar] [CrossRef]
- Kumamoto, K.M.; Thom, C.A.; Wallis, D.; Hansen, L.N.; Armstrong, D.E.; Warren, J.M.; Goldsby, D.L.; Wilkinson, A.J. Size effects resolve discrepancies in 40 years of work on low-temperature plasticity in olivine. Sci. Adv. 2017, 3, e1701338. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Bhushan, B. A review of nanoindentation continuous stiffness technique and its applications. Mater. Charact. 2002, 48, 11–36. [Google Scholar] [CrossRef]
- Pharr, G.M.; Herbert, E.G.; Gao, Y. The indentation size effect: A critical examination of experimental observations and mechanistic interpretations. Ann. Rev. Mater. Res. 2010, 40, 271–292. [Google Scholar] [CrossRef]
- Thom, C.A.; Carpick, R.W.; Goldsby, D.L. Constraints on the physical mechanism of frictional aging from nanoindentation. Geophys. Res. Let. 2018, 45, 306–311. [Google Scholar] [CrossRef]
- Lucas, B.N.; Oliver, W.C. Indentation power-law creep of high-purity indium. Metall. Mater. Trans. A 1999, 30, 601–610. [Google Scholar] [CrossRef]
- Su, C.; Herbert, E.G.; Sohn, S.; LaManna, J.A.; Oliver, W.C.; Pharr, G.M. Measurement of power-law creep parameters by instrumented indentation methods. J. Mech. Phys. Solids 2013, 61, 517–536. [Google Scholar] [CrossRef]
- Ginder, R.S.; Nix, W.D.; Pharr, G.M. A simple model for indentation creep. J. Mech. Phys. Solids 2018, 112, 552–562. [Google Scholar] [CrossRef]
- Bower, A.F.; Fleck, N.A.; Needleman, A.; Ogbonna, N. Indentation of a power law creeping solid. Proc. R. Soc. Lond. 1993, 441, 97–124. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thom, C.A.; Goldsby, D.L. Nanoindentation Studies of Plasticity and Dislocation Creep in Halite. Geosciences 2019, 9, 79. https://doi.org/10.3390/geosciences9020079
Thom CA, Goldsby DL. Nanoindentation Studies of Plasticity and Dislocation Creep in Halite. Geosciences. 2019; 9(2):79. https://doi.org/10.3390/geosciences9020079
Chicago/Turabian StyleThom, Christopher A., and David L. Goldsby. 2019. "Nanoindentation Studies of Plasticity and Dislocation Creep in Halite" Geosciences 9, no. 2: 79. https://doi.org/10.3390/geosciences9020079
APA StyleThom, C. A., & Goldsby, D. L. (2019). Nanoindentation Studies of Plasticity and Dislocation Creep in Halite. Geosciences, 9(2), 79. https://doi.org/10.3390/geosciences9020079




