Use of Geogrids and Recycled Rubber in Railroad Infrastructure for Enhanced Performance
Abstract
1. Introduction
2. A Dilatancy Model for a Synthetic Energy Absorbing Layer (SEAL) for Sub-Ballast
2.1. Laboratory Study of the Waste Matrix
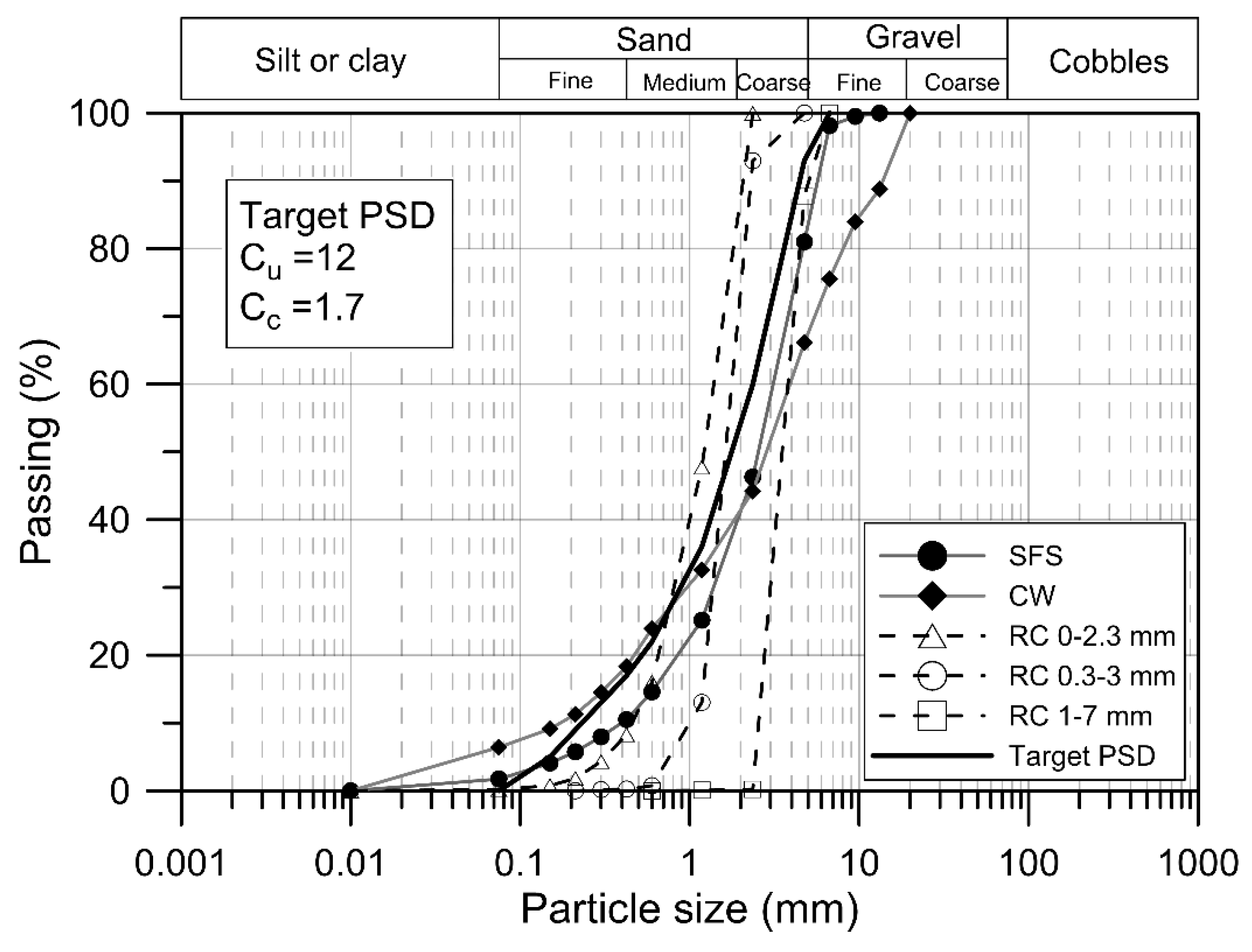
2.1.1. Materials and Test Program
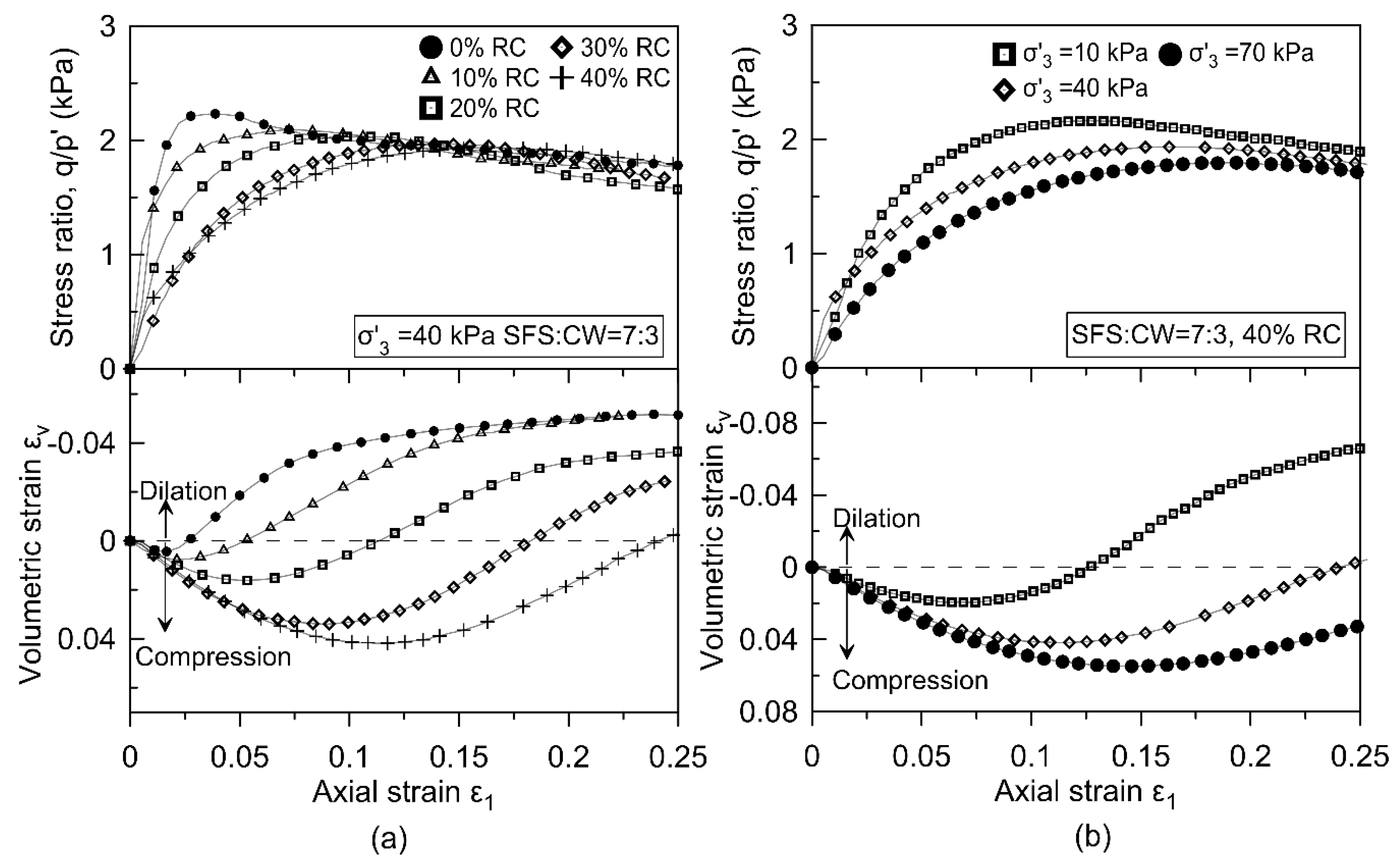
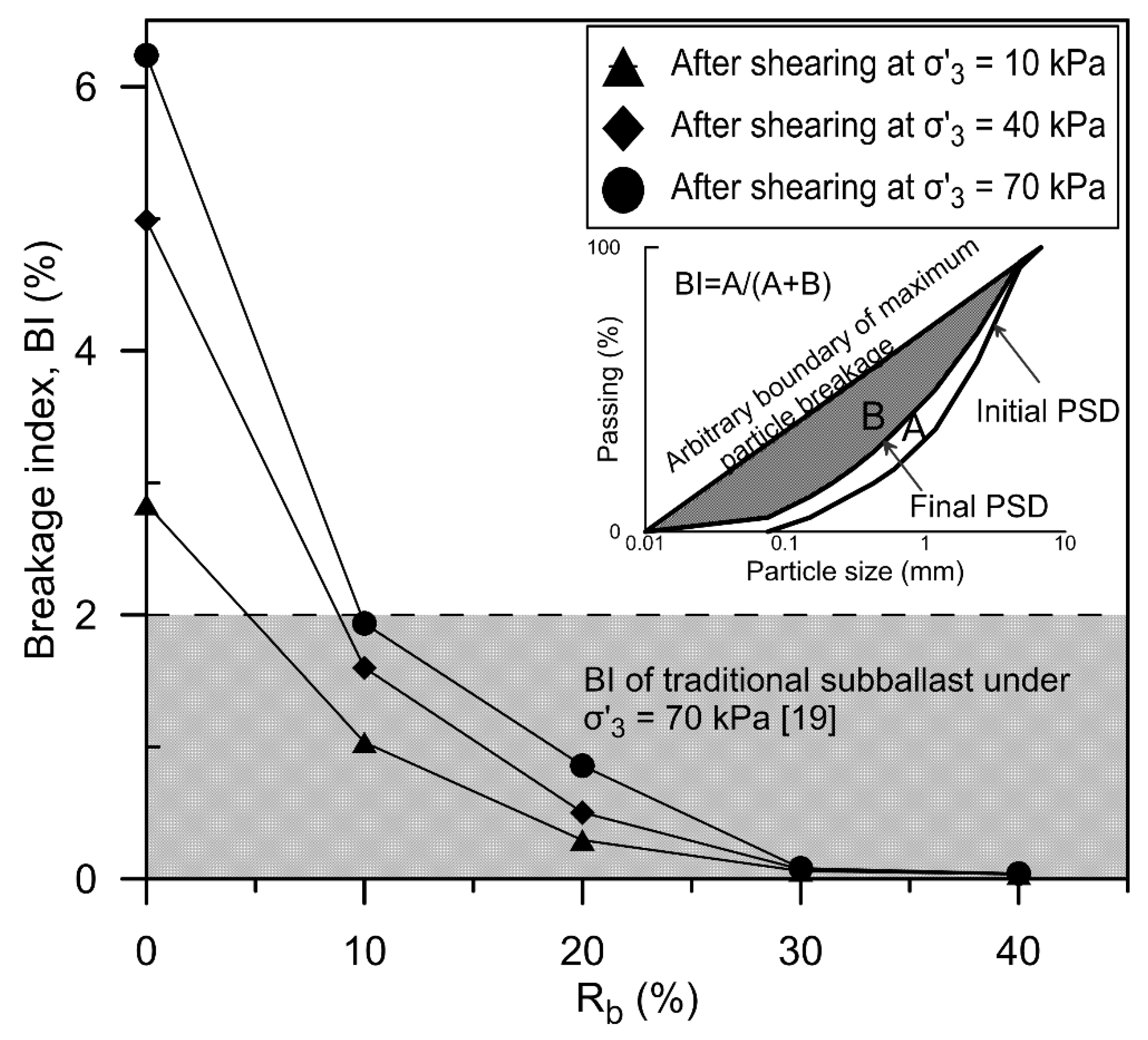
2.1.2. Test Results
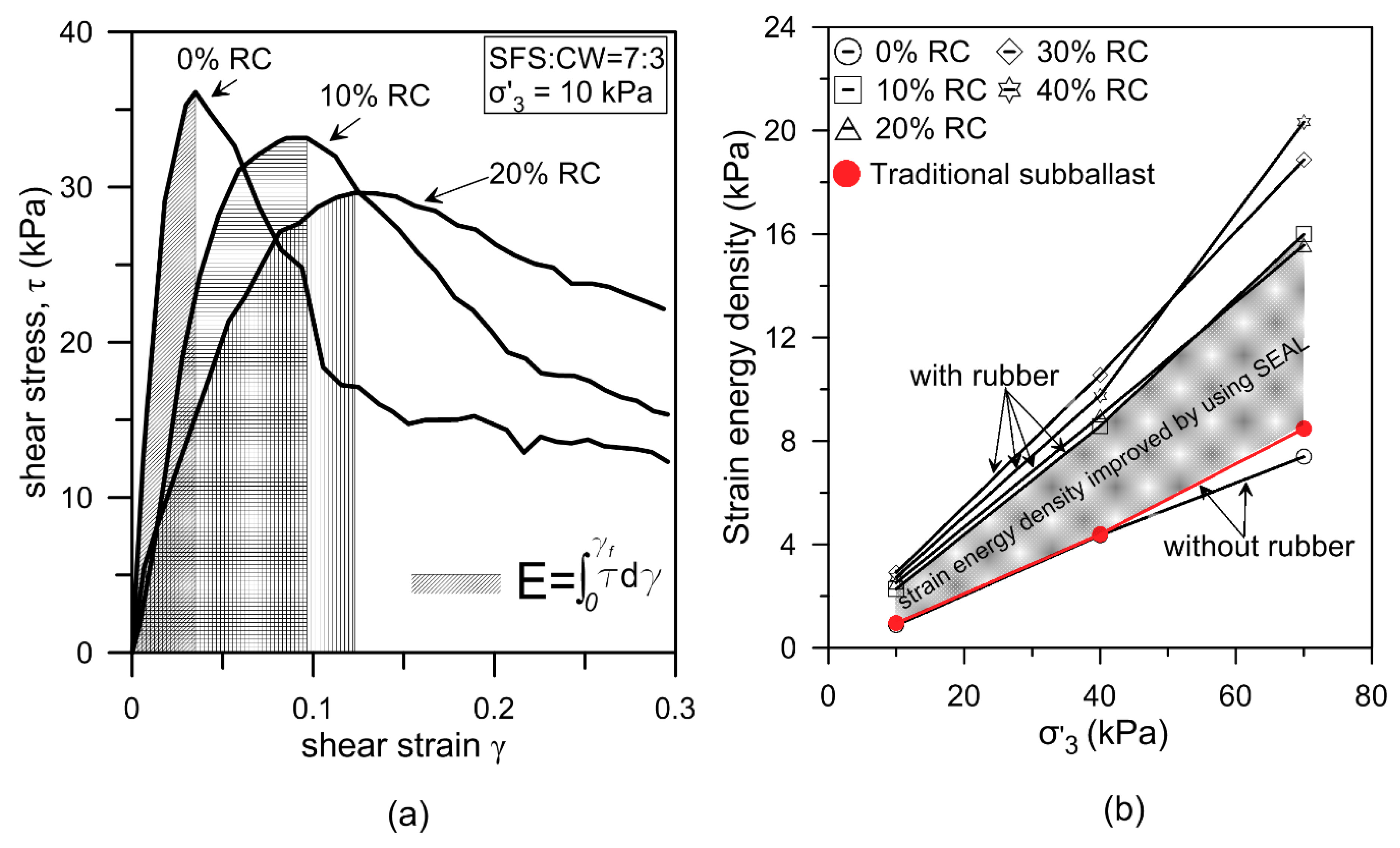
2.2. Critical State Related to Energy Absorbing Property
2.3. Dilatancy Modelling
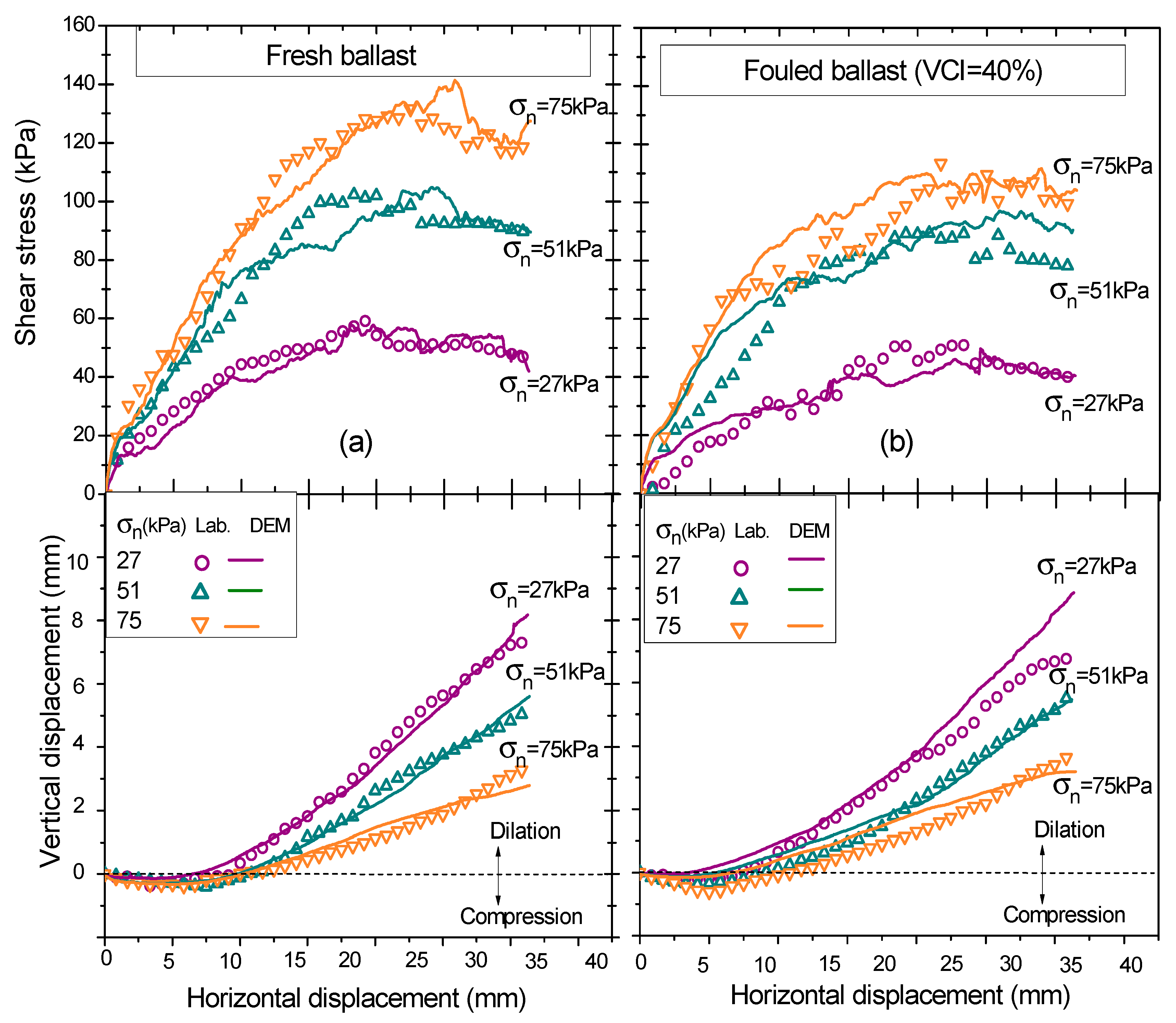
3. Laboratory Investigation for Geogrid-Reinforced Ballast
3.1. Materials and Methods
3.2. Test Results
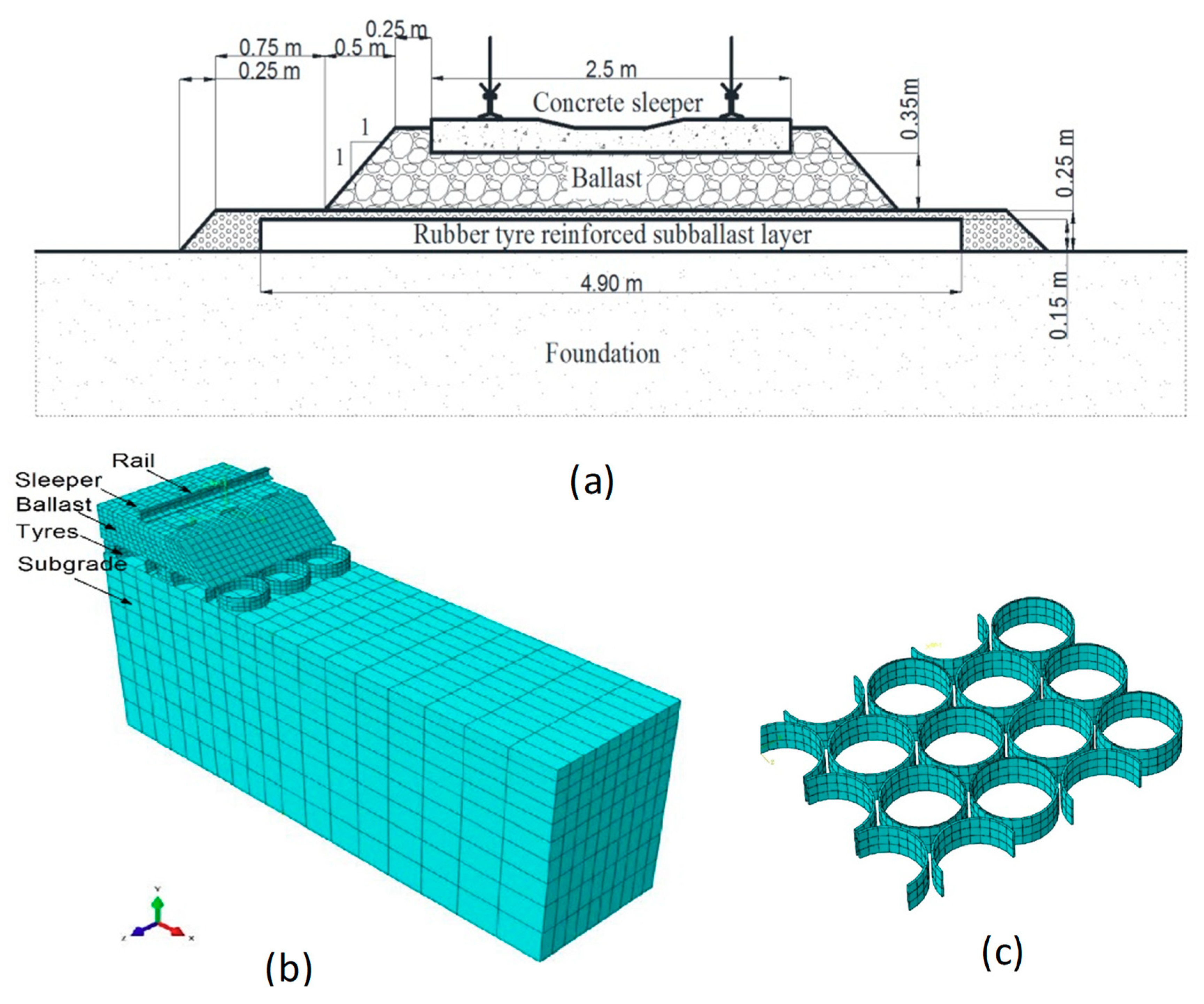
4. Finite Modelling on Tire Cell
4.1. Laboratory Investigation
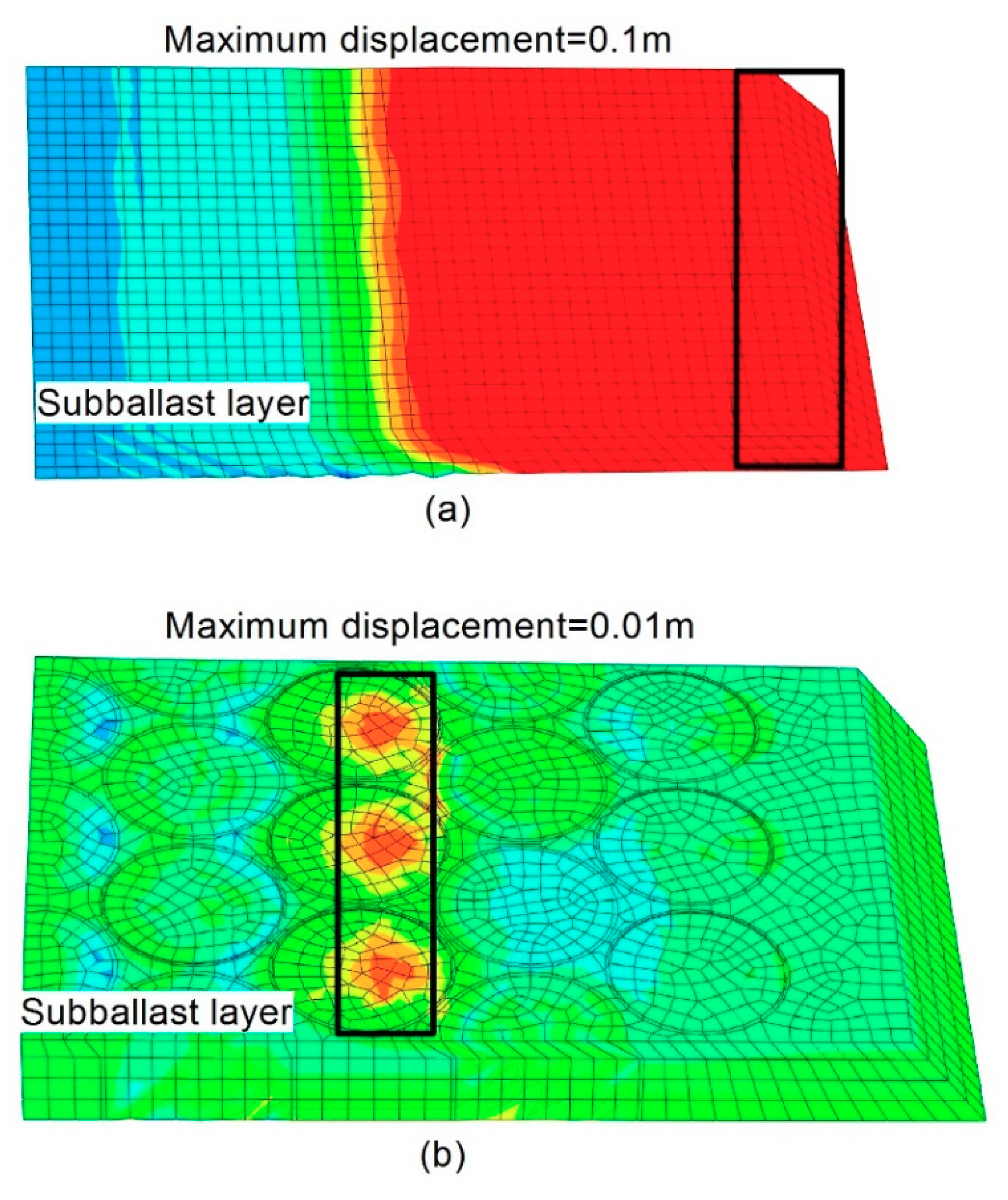
4.2. Finite Element Modelling for Recycled Tire-Reinforced Capping Layer
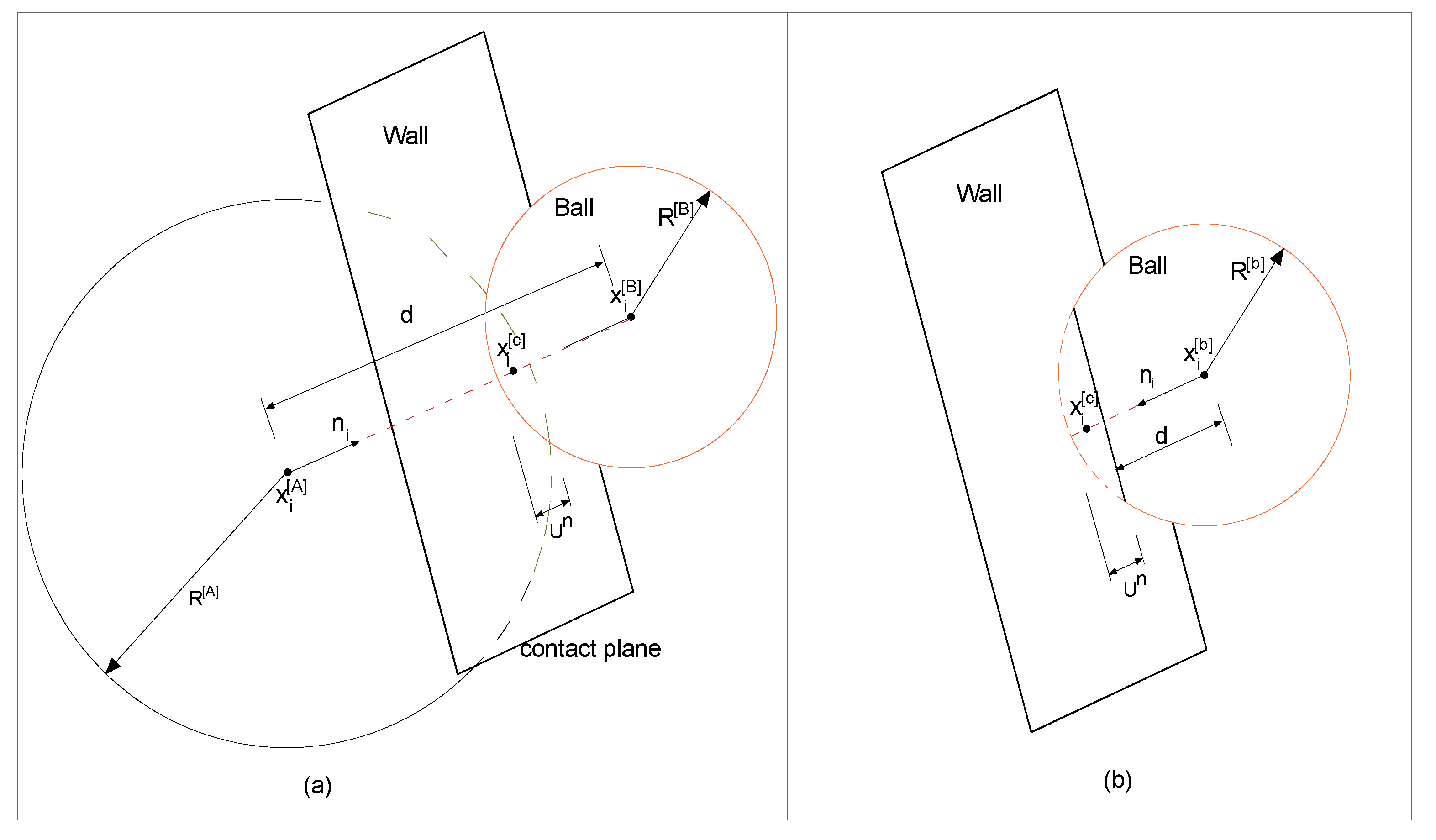
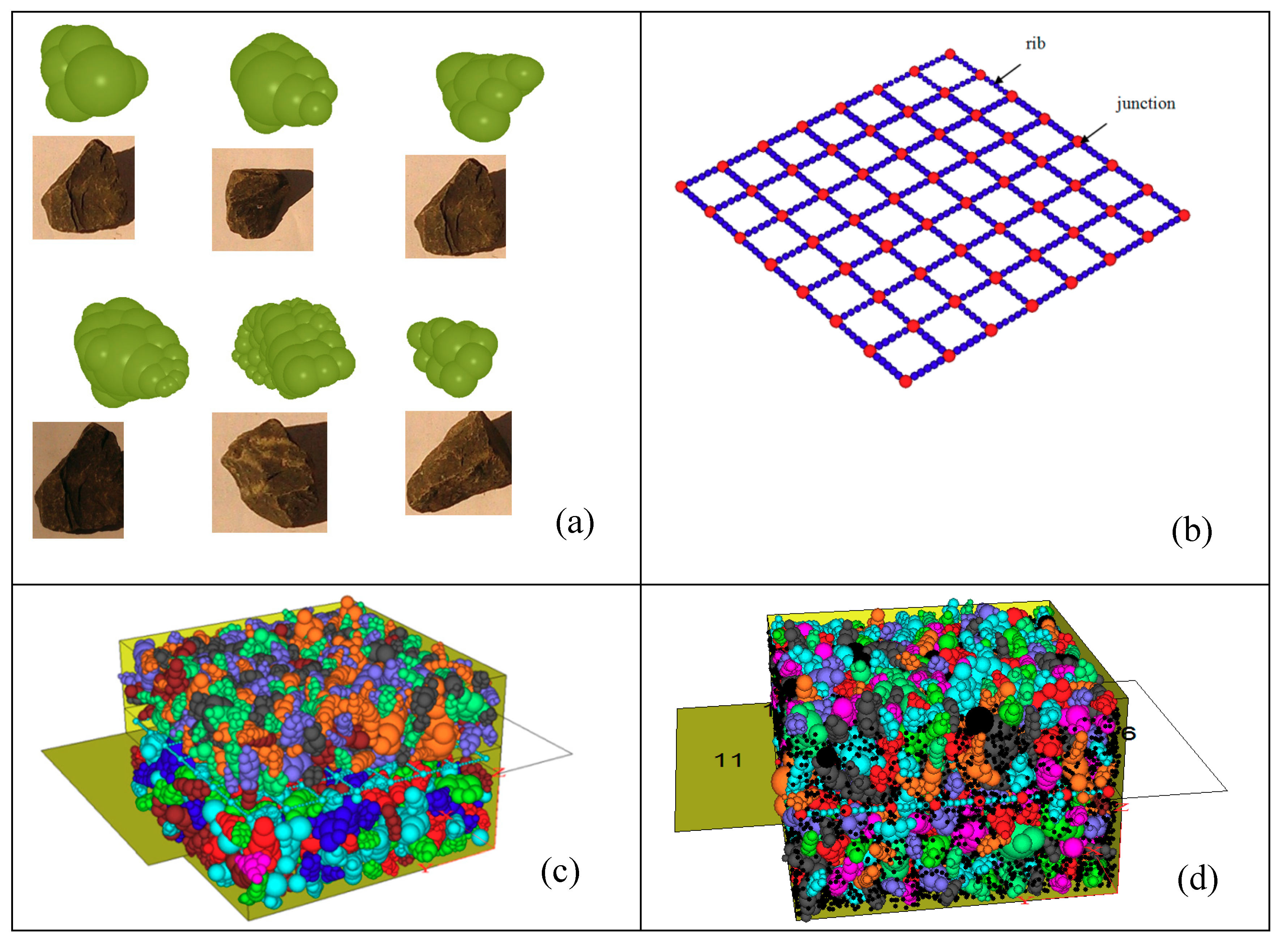
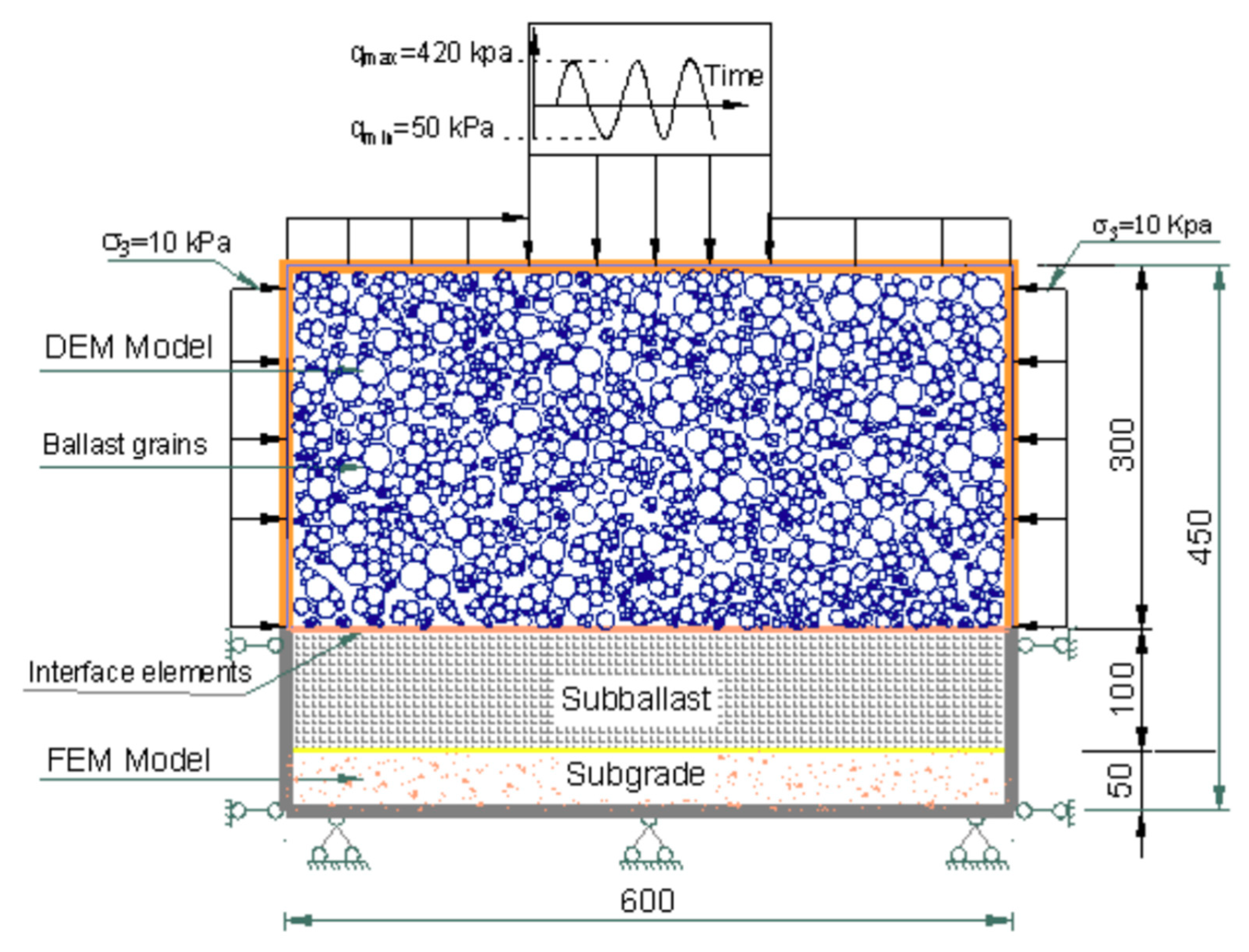
5. DEM Modelling for Geogrid-Reinforced Ballast
5.1. DEM Modelling of Geogrid-Reinforced Ballast
5.2. Coupled Discrete-Continuum Modelling
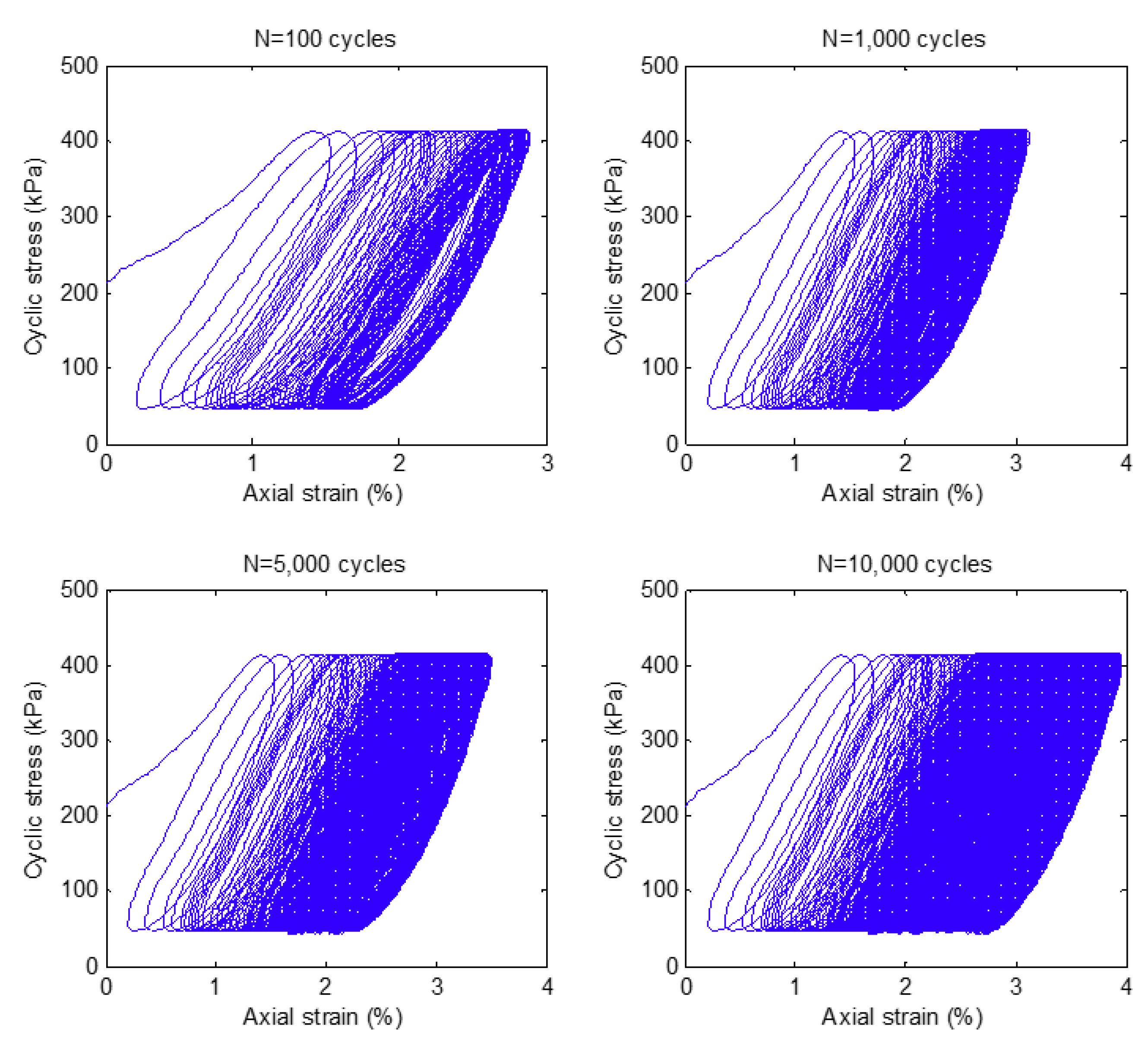
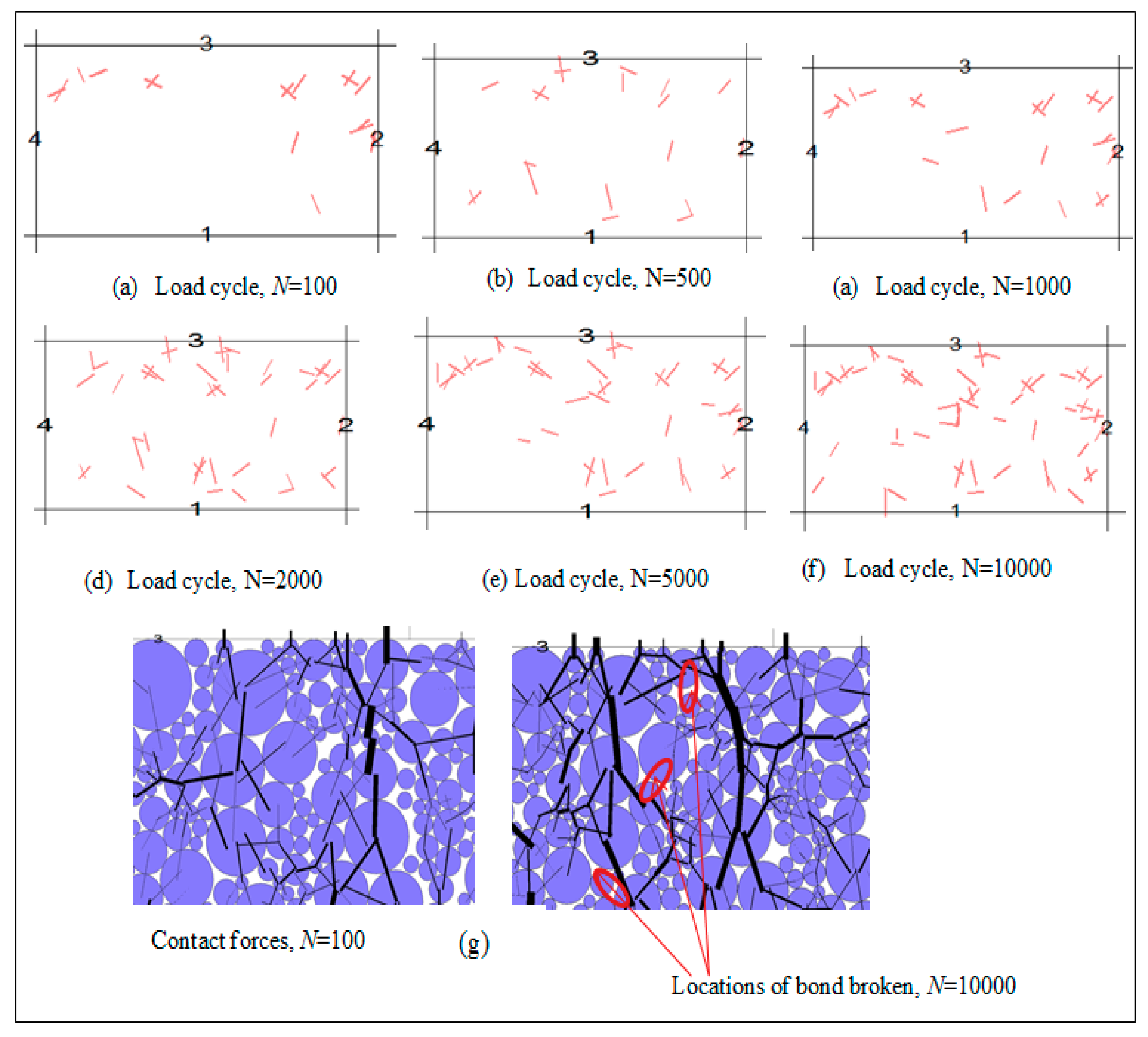
5.3. Cyclic Stress-Strain and Particle Breakage Responses
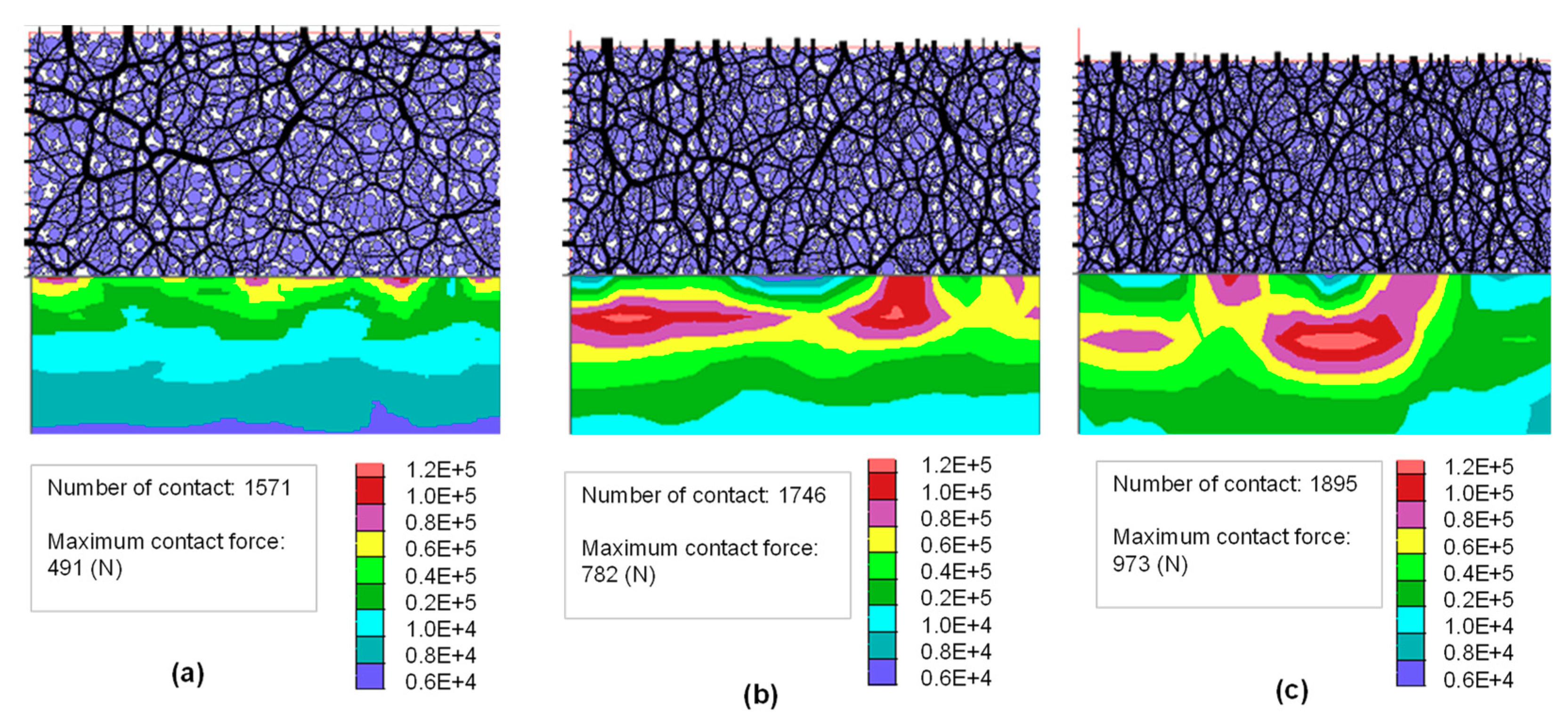
5.4. Contact Forces and Stress Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Indraratna, B.; Salim, W.; Rujikiatkamjorn, C. Advanced Rail Geotechnology—Ballasted Track; CRC Press, Taylor & Francis Group: London, UK, 2011. [Google Scholar]
- Indraratna, B.; Ngo, N.T.; Rujikiatkamjorn, C. Behavior of geogrid-reinforced ballast under various levels of fouling. Geotext. Geomembr. 2011, 29, 313–322. [Google Scholar] [CrossRef]
- Selig, E.T.; Waters, J.M. Track Geotechnology and Substructure Management; Thomas Telford: London, UK, 1994. [Google Scholar]
- Indraratna, B.; Sun, Q.; Heitor, A.; Grant, J. Performance of Rubber Tire-Confined Capping Layer under Cyclic Loading for Railroad Conditions. J. Mater. Civ. Eng. 2018, 30, 06017021. [Google Scholar] [CrossRef]
- Tutumluer, E.; Dombrow, W.; Huang, H. Laboratory characterization of coal dust fouled ballast behavior. In Proceedings of the AREMA 2008 Annual Conference & Exposition, Salt Lake City, UT, USA, 21–24 September 2008. [Google Scholar]
- Tennakoon, N.; Indraratna, B.; Rujikiatkamjorn, C.; Nimbalkar, S.; Neville, T. The role of ballast-fouling characteristics on the drainage capacity of rail substructure. Geotech. Test. J. 2012, 35, 1–11. [Google Scholar] [CrossRef]
- Sussmann, T.R.; Ruel, M.; Chrismer, S.M. Source of ballast fouling and influence considerations for condition assessment criteria. Transp. Res. Rec. J. Transp. Res. Board 2012, 2289, 87–94. [Google Scholar] [CrossRef]
- Indraratna, B.; Sun, Q.; Ngo, N.T.; Rujikiatkamjorn, C. Current research into ballasted rail tracks: Model tests and their practical implications. Aust. J. Struct. Eng. 2017, 18, 204–220. [Google Scholar] [CrossRef]
- Aursudkij, B.; McDowell, G.R.; Collop, A.C. Cyclic loading of railway ballast under triaxial conditions and in a railway test facility. Granul. Matter 2009, 11, 391–401. [Google Scholar] [CrossRef]
- Hussaini, S.K.K.; Indraratna, B.; Vinod, J. Performance of geosynthetically-reinforced rail ballast in direct shear conditions. In Proceedings of the 11th Australia–New Zealand Conference on Geomechanics: Ground Engineering in a Changing World, Melbourne, Australia, 15–18 July 2012; pp. 1268–1273. [Google Scholar]
- Indraratna, B.; Nimbalkar, S.; Christie, D.; Rujikiatkamjorn, C.; Vinod, J.S. Field assessment of the performance of a ballasted rail track with and without geosynthetics. J. Geotech. Geoenviron. Eng. 2010, 136, 907–917. [Google Scholar] [CrossRef]
- Ferreira, F.B.; Indraratna, B. Deformation and degradation response of railway ballast under impact loading—Effect of artificial inclusions. In Proceedings of the 1st International Conference on Rail Transportation—ICRT 2017: Railway Development, Operations, and Maintenance, Chengdu, China, 10–12 July 2017; pp. 1090–1101. [Google Scholar]
- Nimbalkar, S.; Indraratna, B.; Dash, S.; Christie, D. Improved performance of railway ballast under impact loads using shock mats. J. Geotech. Geoenviron. Eng. 2012, 138, 281–294. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Ferreira, F.B.; Rujikiatkamjorn, C. Improved performance of geosynthetics enhanced ballast: Laboratory and numerical studies. Proc. Inst. Civ. Eng.-Ground Improv. 2018, 171, 202–222. [Google Scholar] [CrossRef]
- Indraratna, B.; Ferreira, F.B.; Qi, Y.; Ngo, T. Application of geoinclusions for sustainable rail infrastructure under increased axle loads and higher speeds. Innov. Infrastruct. Solut. 2018, 3, 69. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. Micromechanics-based investigation of fouled ballast using large-scale triaxial tests and discrete element modeling. J. Geotech. Geoenviron. Eng. 2017, 134, 04016089. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. Stabilisation of track substructure with geo-inclusions—Experimental evidence and DEM simulation. Int. J. Rail Transp. 2017, 5, 63–86. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. A study of the geogrid–sub-ballast interface via experimental evaluation and discrete element modelling. Granul. Matter 2017, 19, 1–16. [Google Scholar] [CrossRef]
- Indraratna, B.; Qi, Y.J.; Heitor, A. Evaluating the properties of mixtures of steel furnace slag, coal wash, and rubber crumbs used as sub-ballast. J. Mater. Civ. Eng. 2018, 30, 04017251. [Google Scholar] [CrossRef]
- Navaratnarajah, S.K.; Indraratna, B. Use of rubber mats to improve the deformation and degradation behavior of rail ballast under cyclic loading. J. Geotech. Geoenviron. Eng. 2017, 143, 04017015. [Google Scholar] [CrossRef]
- Navaratnarajah, S.K.; Indraratna, B.; Ngo, N.T. Influence of under sleeper pads on ballast behavior under cyclic loading—Experimental and numerical Studies. J. Geotech. Geoenviron. Eng. 2018, 144, 04018068. [Google Scholar] [CrossRef]
- Qi, Y.; Indraratna, B.; Heitor, A.; Vinod, J.S. Effect of rubber crumbs on the cyclic behavior of steel furnace slag and coal wash mixtures. J. Geotech. Geoenviron. Eng. 2018, 144, 04017107. [Google Scholar] [CrossRef]
- Qi, Y.; Indraratna, B.; Heitor, A.; Vinod, J.S. The Influence of Rubber Crumbs on the Energy Absorbing Property of Waste Mixtures. In Proceedings of the International Symposium on Geotechnics of Transportation Infrastructure (ISGTI 2018), New Delhi, India, 7–8 April 2018; pp. 455–460. [Google Scholar]
- Qi, Y.; Indraratna, B.; Vinod, J.S. Dynamic Properties of Mixtures of Waste Materials. In Proceedings of the GeoShanghai 2018 International Conference: Advances in Soil Dynamics and Foundation Engineering. GSIC 2018; Qiu, T., Tiwari, B., Zhang, Z., Eds.; Springer: Singapore, 2018; pp. 308–317. [Google Scholar]
- Qi, Y.; Indraratna, B.; Heitor, A.; Vinod, J.S. Closure to ‘Effect of Rubber Crumbs on the Cyclic Behavior of Steel Furnace Slag and Coal Wash Mixtures’. J. Geotech. Geoenviron. Eng. 2018, 145, 07018035. [Google Scholar] [CrossRef]
- Sol-Sanchez, M.; Thom, N.H.; Moreno-Navarro, F.; Rubio-Gamez, M.C.; Airey, G.D. A study into the use of crumb rubber in railway ballast. Constr. Build. Mater. 2015, 75, 19–24. [Google Scholar] [CrossRef]
- Soltani, A.; Deng, A.; Taheri, A.; Sridharan, A. Swell–Shrink–Consolidation Behavior of Rubber–Reinforced Expansive Soils. Geotech. Test. J. 2018, 42. [Google Scholar] [CrossRef]
- Soltani, A.; Deng, A.; Taheri, A.; Mirzababaei, M. Rubber Powder–Polymer Combined Stabilization of South Australian Expansive Soils. Geosynth. Int. 2018, 25, 304–321. [Google Scholar] [CrossRef]
- Soltani, A.; Deng, A.; Taheri, A.; Sridharan, A. Consistency Limits and Compaction Characteristics of Clay Soils Containing Rubber Waste. Proc. Inst. Civ. Eng. Geotech. Eng. 2018, 1–34. [Google Scholar] [CrossRef]
- Mashiri, M.S.; Vinod, J.S.; Sheikh, M.N.; Carraro, J.A.H. Shear Modulus of Sand–Tire Chip Mixtures. Environ. Geotech. 2017. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. DEM simulation of the behavior of geogrid stabilised ballast fouled with coal. Comput. Geotech. 2014, 55, 224–231. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Raymond, G.P. Geogrid reinforcement of ballasted track. Transp. Res. Rec. 1987, 1153, 8–14. [Google Scholar]
- McDowell, G.R.; Harireche, O.; Konietzky, H.; Brown, S.F.; Thom, N.H. Discrete element modelling of geogrid-reinforced aggregates. Proce. ICE Geotech. Eng. 2006, 159, 35–48. [Google Scholar] [CrossRef]
- Indraratna, B.; Nimbalkar, S.S.; Ngo, N.T.; Neville, T. Performance improvement of rail track substructure using artificial inclusions—Experimental and numerical studies. Transp. Geotech. 2016, 8, 69–85. [Google Scholar] [CrossRef]
- Brown, S.F.; Kwan, J.; Thom, N.H. Identifying the key parameters that influencegeogrid reinforcement of railway ballast. Geotext. Geomembr. 2007, 25, 326–335. [Google Scholar] [CrossRef]
- ASTM D7181, American Society for Tests and Materials. Standard Method for Consolidated Drained Triaxial Compression Test for Soils; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Lackenby, J.; Indraratna, B.; McDowell, G.; Christie, D. Effect of confining pressure on ballast degradation and deformation under cyclic triaxial loading. Géotechnique 2007, 57, 527–536. [Google Scholar] [CrossRef]
- Kim, H.K.; Santamarina, J.C. Sand-rubber mixtures (large rubber chips). Can. Geotech. J. 2008, 45, 1457–1466. [Google Scholar] [CrossRef]
- Indraratna, B.; Lackenby, J.; Christie, D. Effect of confining pressure on the degradation of ballast under cyclic loading. Géotechnique 2005, 55, 325–328. [Google Scholar] [CrossRef]
- Mashiri, M.; Vinod, J.S.; Sheikh, M.N.; Tsang, H.H. Shear strength and dilatancy behavior of sand–tire chip mixtures. Soil Found. 2015, 55, 517–528. [Google Scholar] [CrossRef]
- Fu, R.; Coop, M.R.; Li, X.Q. The mechanics of a compressive sand mixed with tire rubber. Géotech. Lett. 2014, 4, 238–243. [Google Scholar] [CrossRef]
- Youwai, S.; Bergado, D.T. Strength and deformation characteristics of shredded rubber tire-sand mixtures. Can. Geotech. J. 2003, 40, 254–264. [Google Scholar] [CrossRef]
- Qi, Y.; Indraratna, B.; Vinod, J.S. Behavior of Steel Furnace Slag, Coal Wash, and Rubber Crumb Mixtures, with Special Relevance to Stress-dilatancy Relation. J. Mater. Civ. Eng. 2018, 30, 04018276. [Google Scholar] [CrossRef]
- Chavez, C.; Alonso, E.E. A constitutive model for crushed granular aggregates which includes suction effects. Soil Found. 2003, 43, 215–227. [Google Scholar] [CrossRef]
- Collins, I.F.; Muhunthan, B. On the relationship between stress-dilatancy, anisotropy, and plastic dissipation for granular materials. Géotechnique 2003, 53, 611–618. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M.J.; Hachey, J. The critical states of sands. Géotechnique 1991, 41, 365–381. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Dilatancy for cohesionless soils. Géotechnique 2000, 50, 449–460. [Google Scholar] [CrossRef]
- Jenkins, H.M.; Stephenson, J.E.; Clayton, G.A.; Moorland, J.W.; Lyon, D. The effect of track and vehicle parameters on wheel/rail vertical dynamic forces. Railw. Eng. J. 1974, 3, 2–16. [Google Scholar]
- Kaewunruen, S.; Remennikov, A.M. Dynamic crack propagations in prestressed concrete sleepers in railway track systems subjected to severe impact loads. J. Struct. Eng. ASCE 2010, 136, 749–754. [Google Scholar] [CrossRef]
- Frederick, C.O.; Round, D.J. Vertical Track Loading. In Track Technology; Thomas Telford: London, UK, 1985; pp. 135–149. [Google Scholar]
- Rochard, B.P.; Schmidt, F. Benefits of lower-mass trains for high speed rail operations. Proc. Inst. Civ. Eng. Transp. 2004, 157, 51–64. [Google Scholar] [CrossRef]
- Indraratna, B.; Nimbalkar, S.; Neville, T. Performance assessment of reinforced ballasted rail track. Proc. ICE Ground Improv. 2014, 167, 24–34. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Jiang, M.; Yu, H.-S.; Harris, D. Kinematic variables bridging discrete and continuum granular mechanics. Mech. Res. Commun. 2006, 33, 651–666. [Google Scholar] [CrossRef]
- Lu, M.; McDowell, G.R. Discrete element modelling of ballast abrasion. Géotechnique 2006, 56, 651–655. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, N.T.; Rujikiatkamjorn, C.; Vinod, J. Behavior of fresh and fouled railway ballast subjected to direct shear testing - a discrete element simulation. Int. J. Geomech. 2014, 14, 34–44. [Google Scholar] [CrossRef]
- Karrech, A.; Duhamel, D.; Bonnet, G.; Chevoir, F.; Roux, J.-N.; Canou, J.; Dupla, J.-C. A discrete element study of settlement in vibrated granular layers: Role of contact loss and acceleration. Granul. Matter 2008, 10, 369–375. [Google Scholar] [CrossRef]
- Lobo-Guerrero, S.; Vallejo, L.E. Discrete element method analysis of railtrack ballast degradation during cyclic loading. Granul. Matter 2006, 8, 195–204. [Google Scholar] [CrossRef]
- Itasca. Particle Flow Code in Three Dimensions (PFC3D); Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2016. [Google Scholar]
- Indraratna, B.; Ngo, T. Ballast Railroad Design: Smart-Uow Approach; CRC Press, Taylor & Francis Group: London, UK, 2018. [Google Scholar]
- Indraratna, B.; Ngo, N.T.; Rujikiatkamjorn, C. Deformation of coal fouled ballast stabilized with geogrid under cyclic load. J. Geotech. Geoenviron. Eng. 2013, 139, 1275–1289. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. Simulation Ballasted Track Behavior: Numerical Treatment and Field Application. Int. J. Geomech. 2017, 17, 04016130. [Google Scholar] [CrossRef]
- O’Sullivan, C.; Cui, L.; O’Neill, C. Discrete element analysis of the response of granular materials during cyclic loading. Soils Found. 2008, 48, 511–530. [Google Scholar] [CrossRef]
- Azéma, E.; Linero, S.; Estrada, N.; Lizcano, A. Shear strength and microstructure of polydisperse packings: The effect of size span and shape of particle size distribution. Phys. Rev. E 2017, 96, 022902. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Evans, T.J.; Shen, Y.S.; Yu, A.B.; Yang, R.Y. Discrete modelling of the compaction of non-spherical particles using a multi-sphere approach. Miner. Eng. 2018, 117, 108–116. [Google Scholar] [CrossRef]
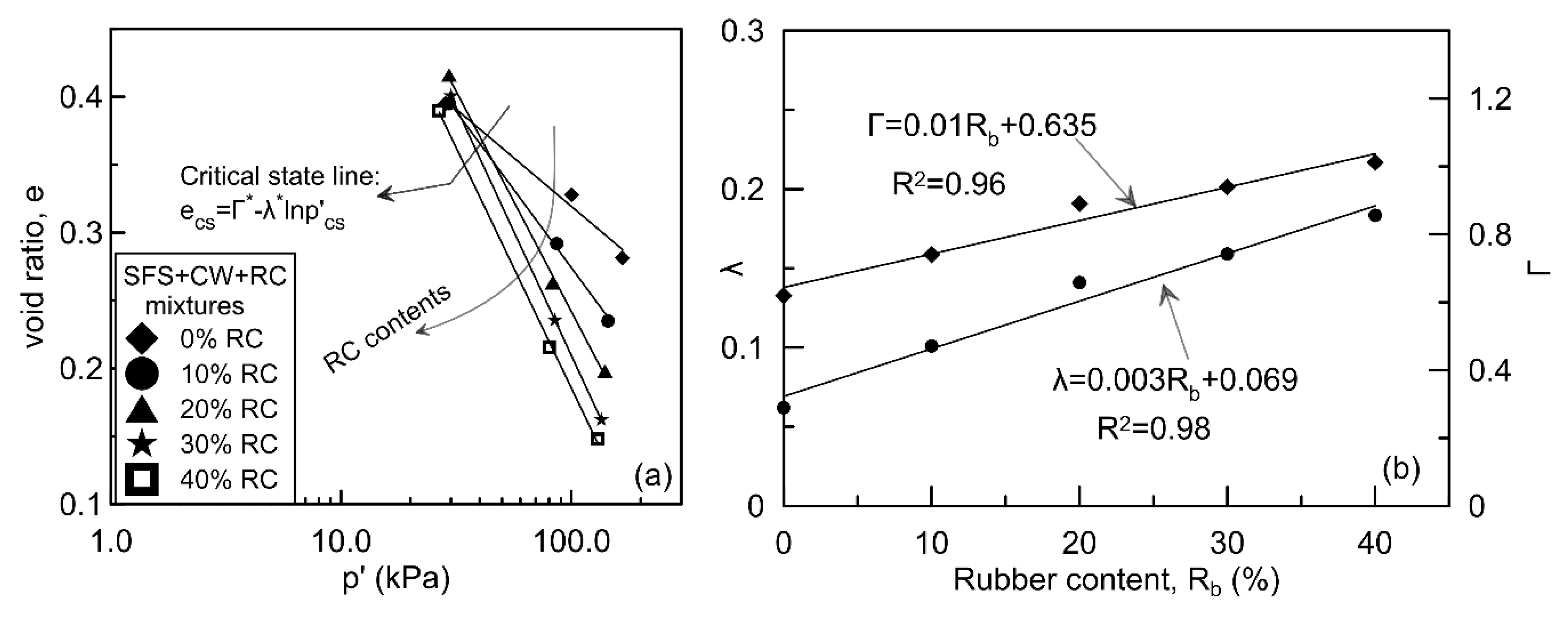
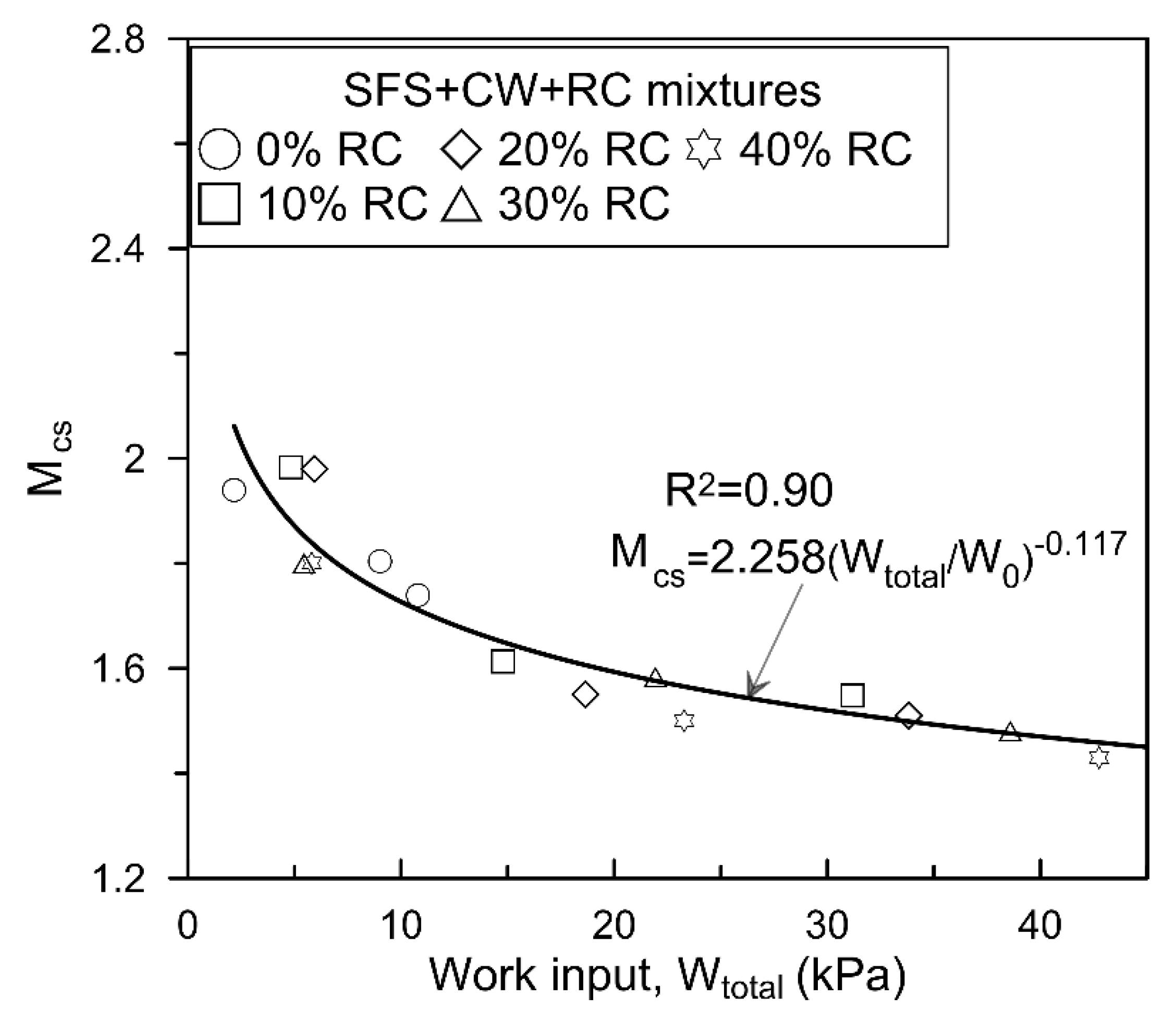
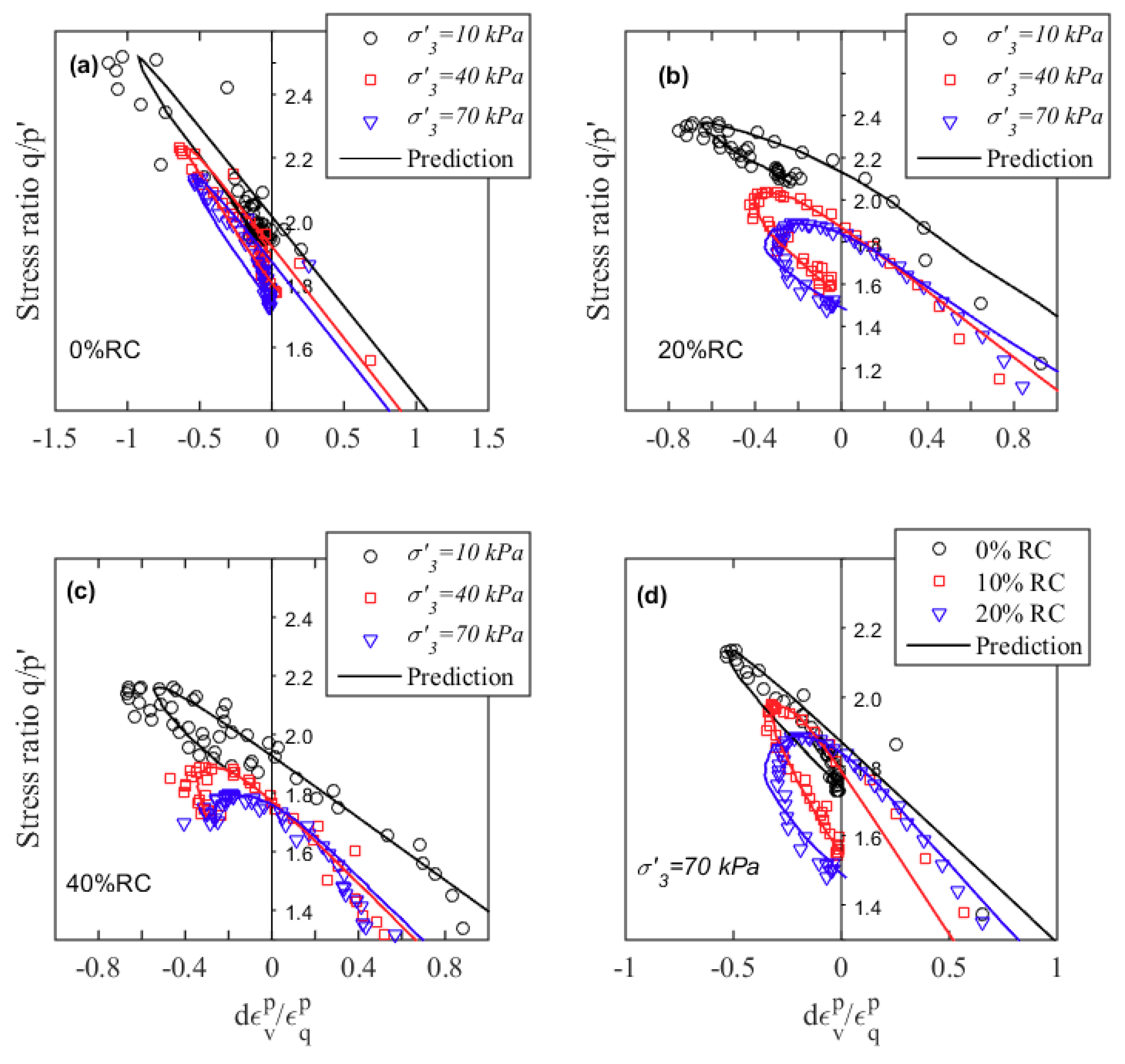
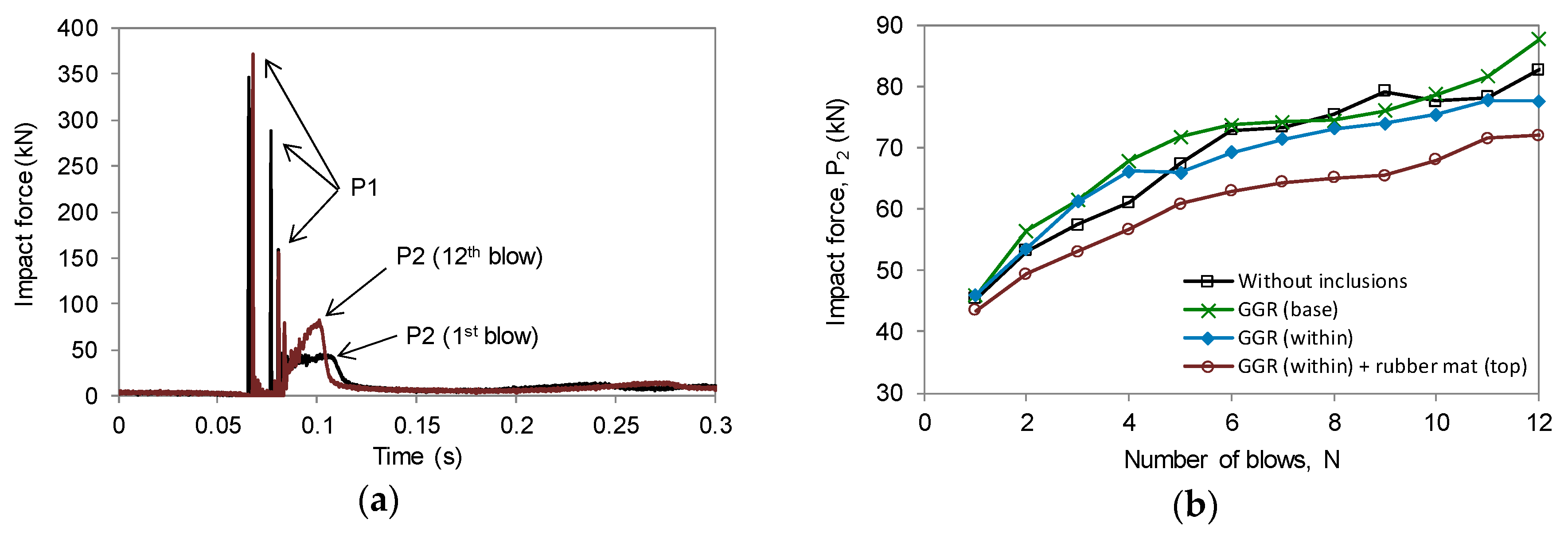

| Waste Matrix | OMC (%) | |
|---|---|---|
| SFS:CW = 7:3, 0% RC | 18.60 | 12.5 |
| SFS:CW = 7:3, 10% RC | 16.45 | 13 |
| SFS:CW = 7:3, 20% RC | 14.70 | 15 |
| SFS:CW = 7:3, 30% RC | 13.28 | 13.5 |
| SFS:CW = 7:3, 40% RC | 12.1 | 15 |
| Mixtures | m | |||||||
|---|---|---|---|---|---|---|---|---|
| SFS:CW = 7:3, 0% RC | 10 | 1.94 | 0.395 | 2.18 | −0.659 | 3.307 | 0.61 | 0.062 |
| 40 | 1.80 | 0.328 | 9.02 | −0.876 | 3.119 | |||
| 70 | 1.74 | 0.281 | 10.79 | −1.30 | 3.03 | |||
| SFS:CW = 7:3, 10% RC | 10 | 2.01 | 0.395 | 4.84 | −0.46 | 2.95 | 0.74 | 0.101 |
| 40 | 1.61 | 0.292 | 14.80 | −2.15 | 2.17 | |||
| 70 | 1.55 | 0.235 | 31.18 | −2.86 | 1.83 | |||
| SFS:CW = 7:3, 20% RC | 10 | 1.98 | 0.416 | 5.95 | −0.53 | 5.12 | 0.89 | 0.141 |
| 40 | 1.55 | 0.263 | 18.66 | −2.98 | 2.18 | |||
| 70 | 1.51 | 0.198 | 33.82 | −5.29 | 3.19 | |||
| SFS:CW = 7:3, 30% RC | 10 | 2.0 | 0.401 | 5.46 | −0.93 | 3.80 | 0.94 | 0.159 |
| 40 | 1.61 | 0.236 | 21.93 | −2.36 | 3.29 | |||
| 70 | 1.48 | 0.162 | 38.58 | −4.16 | 2.49 | |||
| SFS:CW = 7:3, 40% RC | 10 | 1.8 | 0.390 | 5.81 | −0.556 | 6.014 | 1.01 | 0.183 |
| 40 | 1.5 | 0.216 | 23.28 | −2.819 | 2.325 | |||
| 70 | 1.43 | 0.148 | 42.74 | −4.307 | 2.890 |
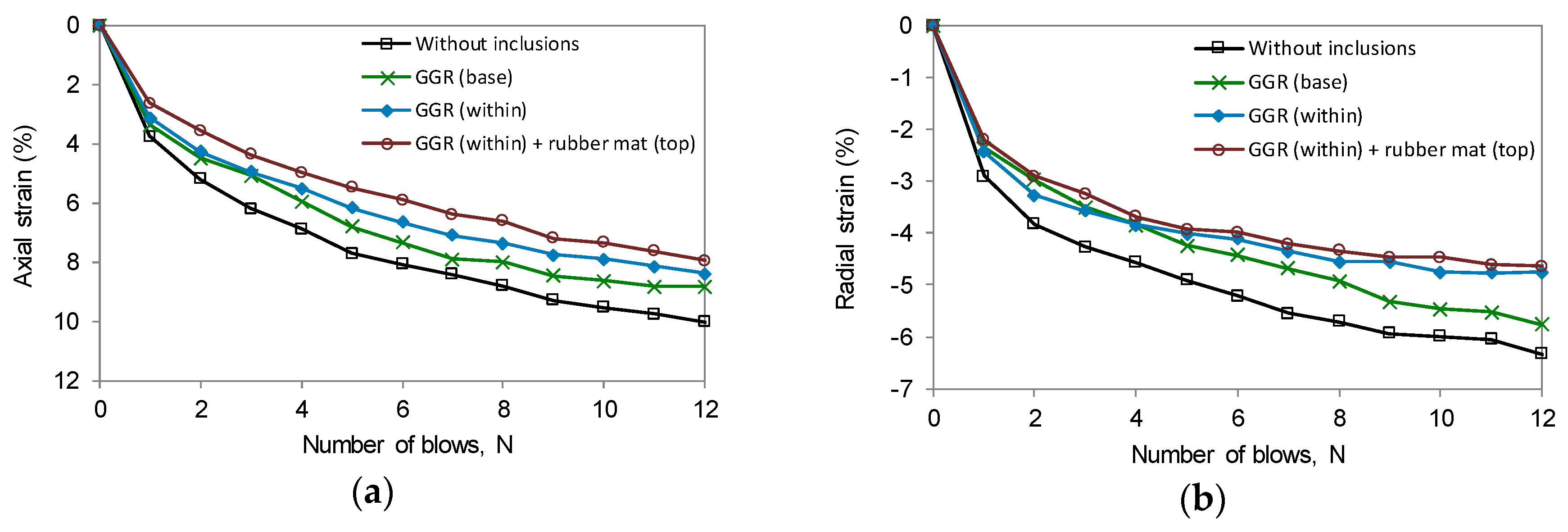
| Test | Geogrid | Rubber Mat |
|---|---|---|
| T1 | N/A | N/A |
| T2 | Base of ballast | N/A |
| T3 | Within ballast | N/A |
| T4 | Within ballast | Top of ballast |
| Test | BBI (Global) | BBI (Top) | BBI (Middle) | BBI (Bottom) |
|---|---|---|---|---|
| T1 | 0.150 | 0.187 | 0.109 | 0.155 |
| T2 | 0.141 | 0.190 | 0.122 | 0.111 |
| T3 | 0.130 | 0.155 | 0.143 | 0.091 |
| T4 | 0.093 | 0.072 | 0.107 | 0.100 |
| Track Variable | Value |
|---|---|
| Rail Properties | |
| Density (kg/m3) Young’s modulus E (MPa) Poisson’s ratio, ν | 8000 500,000 0.27 |
| Sleeper Properties | |
| Density (kg/m3) Young’s modulus E (MPa) Poisson’s ratio, ν | 2000 30,000 0.25 |
| Ballast Layer | |
| Density (kg/m3) Young’s modulus E (MPa) Poisson’s ratio, ν Internal angle of friction, ϕ (degrees) Angle of dilation, ψ (degrees) Cohesion, c (kPa) Thickness (m) | 1530 200 0.3 45 15 1 0.35 |
| Capping Layer | |
| Density (kg/m3) Young’s modulus E (MPa) Poisson’s ratio, ν Internal angle of friction, (degrees) Angle of dilation, ψ (degrees) Cohesion, c (kPa) | 2100 140 0.3 39 15 1 |
| Subgrade Layer | |
| Density (kg/m3) Young’s modulus E (MPa) Poisson’s ratio, ν | 1700 20 0.35 |
| Tire Properties | |
| Density (kg/m3) Young’s modulus E (MPa) Poisson’s ratio, ν | 1500 750 0.35 |
| Wheel Load | |
| Static wheel load (kN) Train Speed (km/h) Dynamic amplification factor (DAF) Dynamic wheel load (kN) | 122.5 100 1.54 188.2 |
| Input Parameters | Ballast | Fouling Materials | Geogrid |
|---|---|---|---|
| Particle density (kg/m3) Coefficient of friction Contact normal stiffness, kn (N/m) Contact shear stiffness, ks (N/m) Contact normal stiffness of wall-particle (N/m) Shear stiffness of wall-particle (N/m) Parallel bond radius multiplier, rp Parallel bond normal stiffness, knp (kPa/m) Parallel bond shear stiffness, ksp (kPa/m) Parallel bond normal strength, σnp (MPa) Parallel bond shear strength, σsp (MPa) | 2700 0.8 0.52 × 108 0.52 × 108 1 × 108 1 × 108 | 1250 0.2 1.27 × 104 1.27 × 104 1 × 108 1 × 108 | 800 0.5 1.77 × 107 0.88 × 107 1 × 108 1 × 108 0.5 5.68 × 108 5.68 × 108 456 456 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Indraratna, B.; Qi, Y.; Ngo, T.N.; Rujikiatkamjorn, C.; Neville, T.; Ferreira, F.B.; Shahkolahi, A. Use of Geogrids and Recycled Rubber in Railroad Infrastructure for Enhanced Performance. Geosciences 2019, 9, 30. https://doi.org/10.3390/geosciences9010030
Indraratna B, Qi Y, Ngo TN, Rujikiatkamjorn C, Neville T, Ferreira FB, Shahkolahi A. Use of Geogrids and Recycled Rubber in Railroad Infrastructure for Enhanced Performance. Geosciences. 2019; 9(1):30. https://doi.org/10.3390/geosciences9010030
Chicago/Turabian StyleIndraratna, Buddhima, Yujie Qi, Trung Ngoc Ngo, Cholachat Rujikiatkamjorn, Tim Neville, Fernanda Bessa Ferreira, and Amir Shahkolahi. 2019. "Use of Geogrids and Recycled Rubber in Railroad Infrastructure for Enhanced Performance" Geosciences 9, no. 1: 30. https://doi.org/10.3390/geosciences9010030
APA StyleIndraratna, B., Qi, Y., Ngo, T. N., Rujikiatkamjorn, C., Neville, T., Ferreira, F. B., & Shahkolahi, A. (2019). Use of Geogrids and Recycled Rubber in Railroad Infrastructure for Enhanced Performance. Geosciences, 9(1), 30. https://doi.org/10.3390/geosciences9010030





