Optimizing Rock Bolt Support for Large Underground Structures Using 3D DFN-DEM Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Discrete Fracture Network Modeling
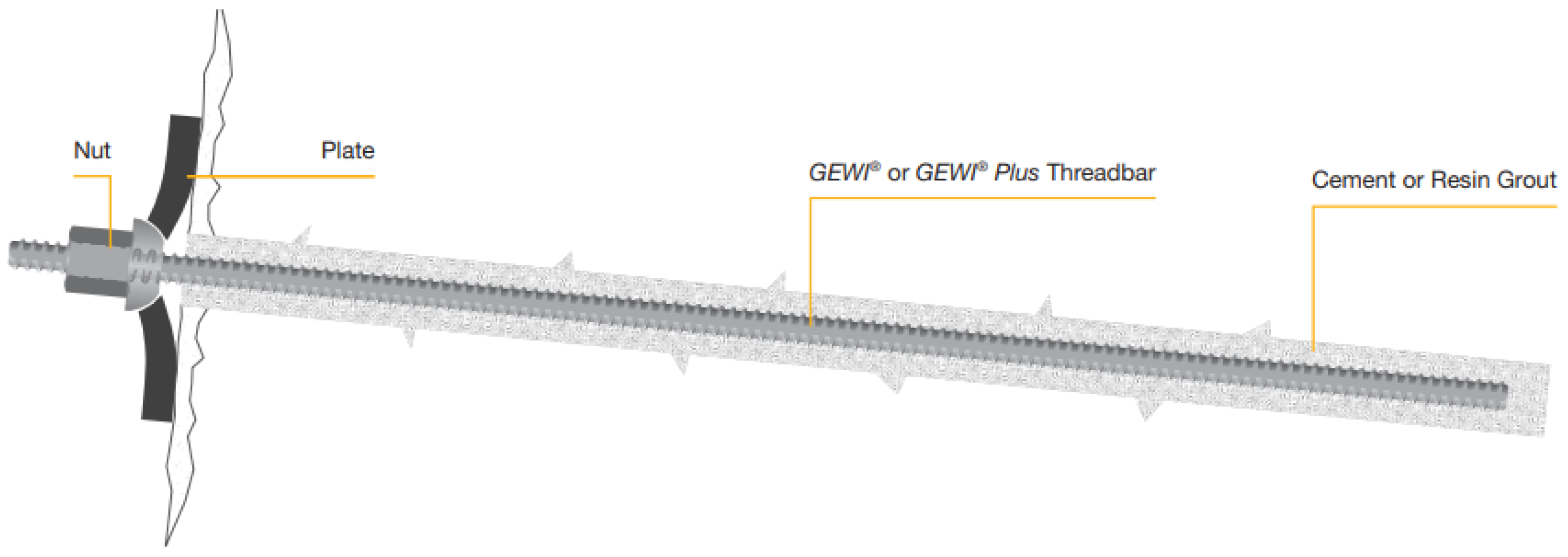
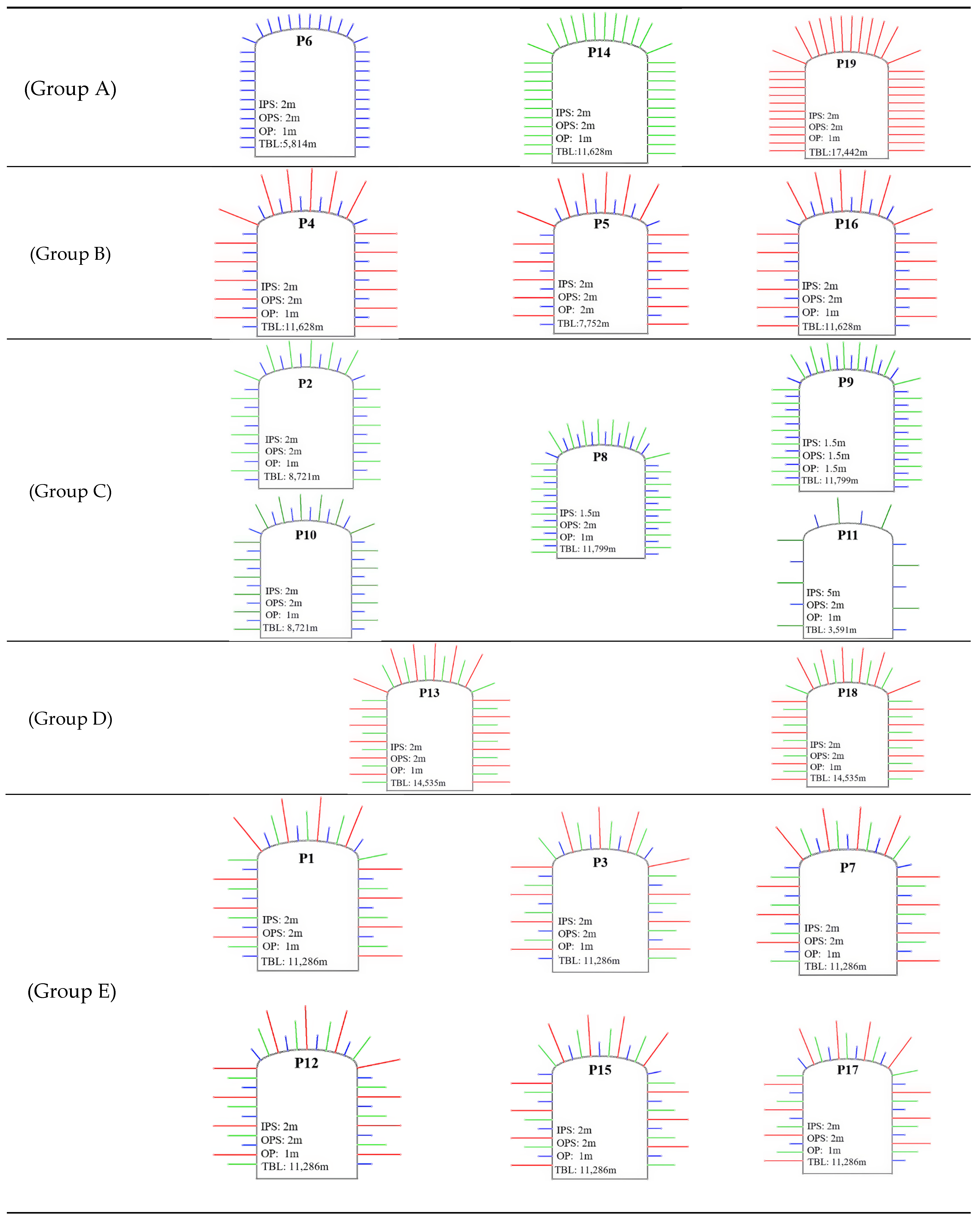
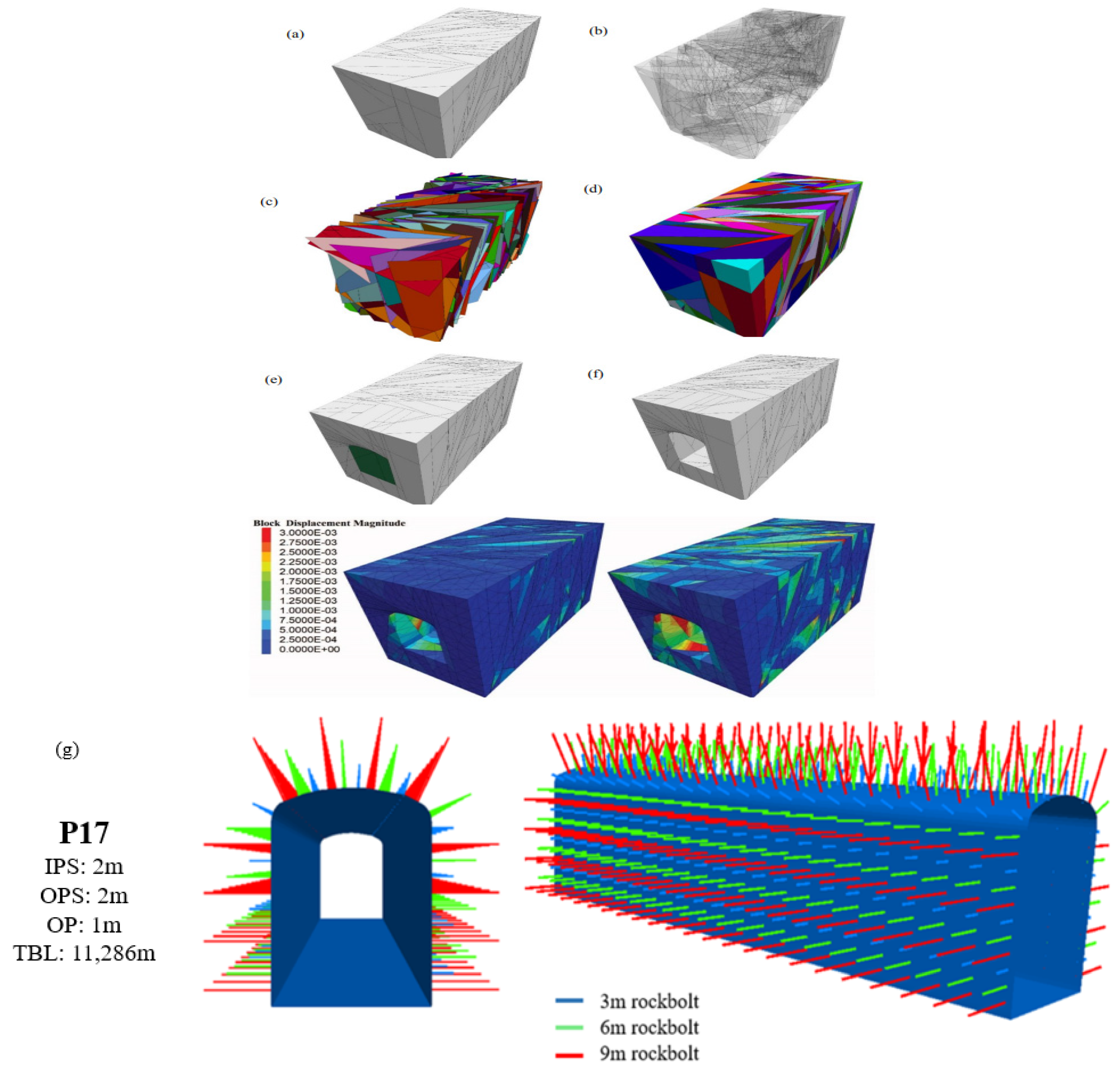
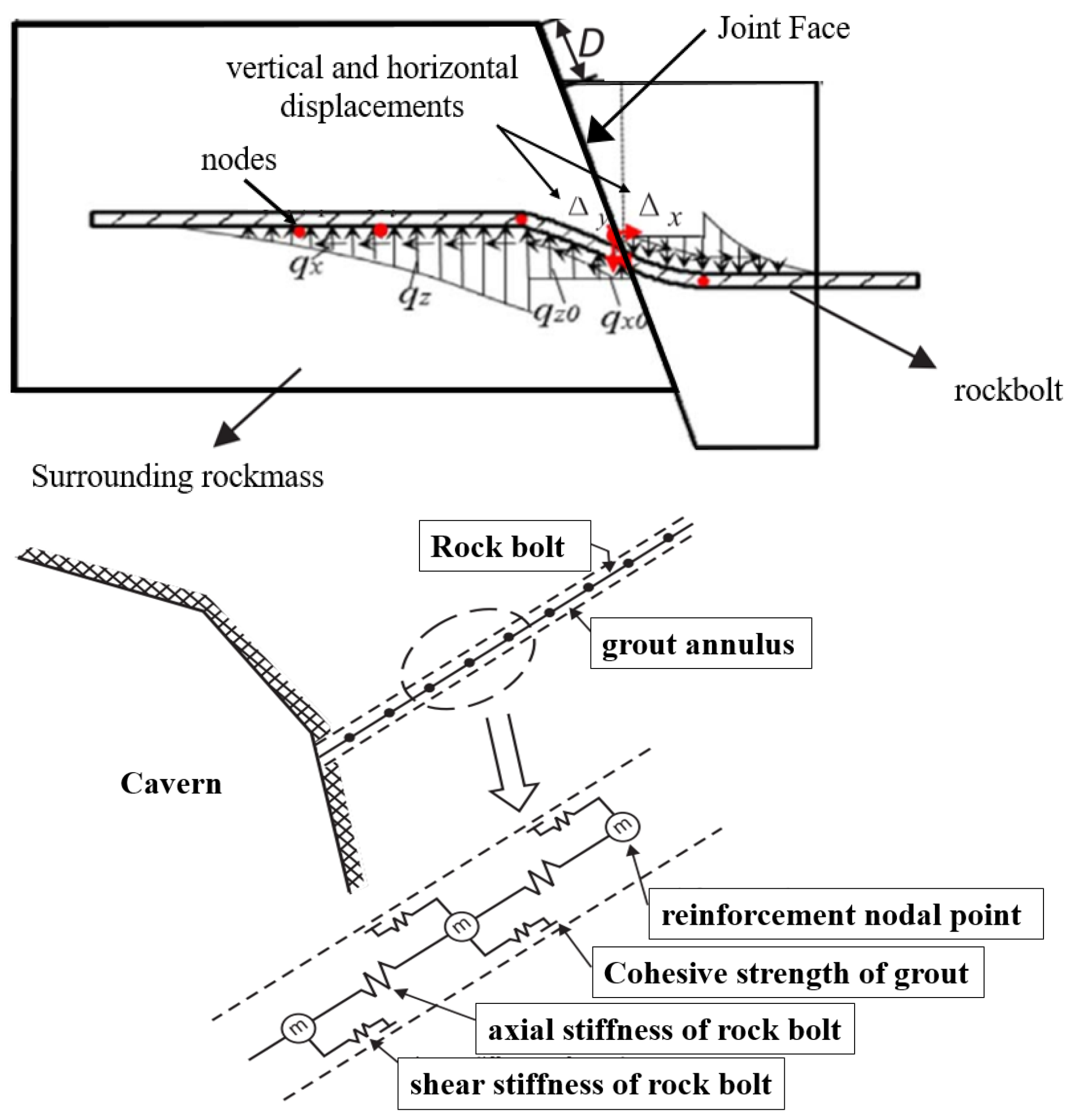
2.2. Rock Bolt Ground Support Design
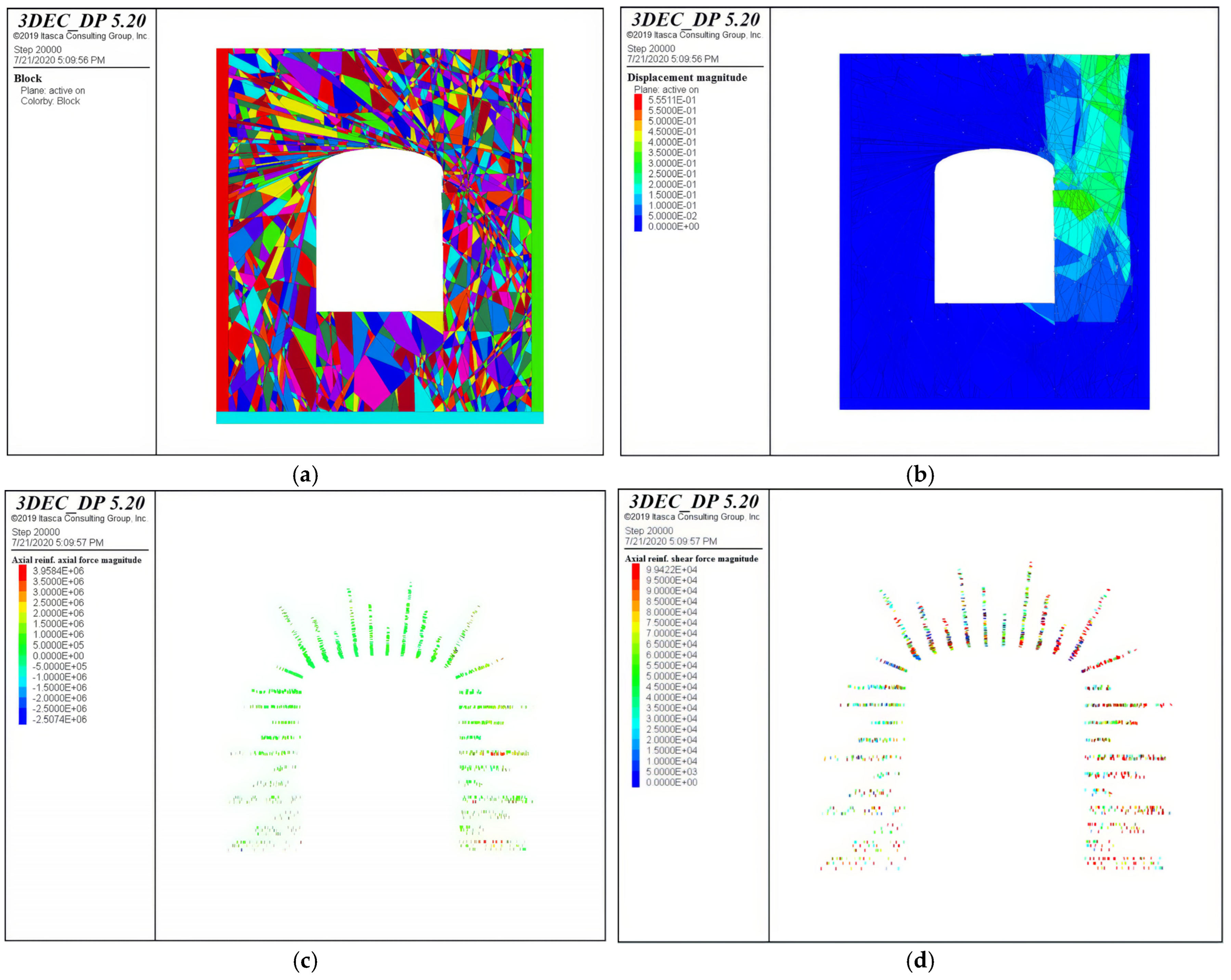
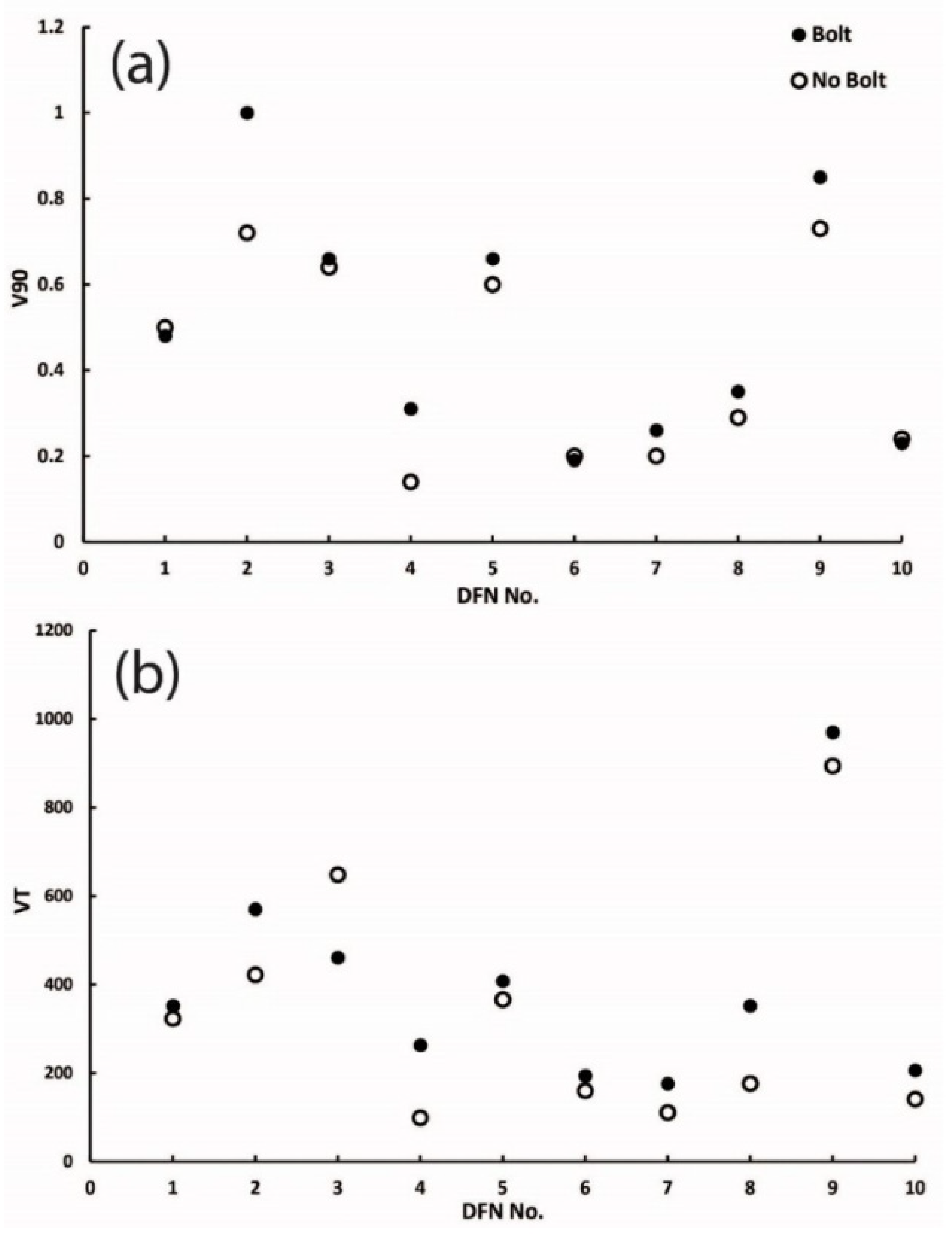
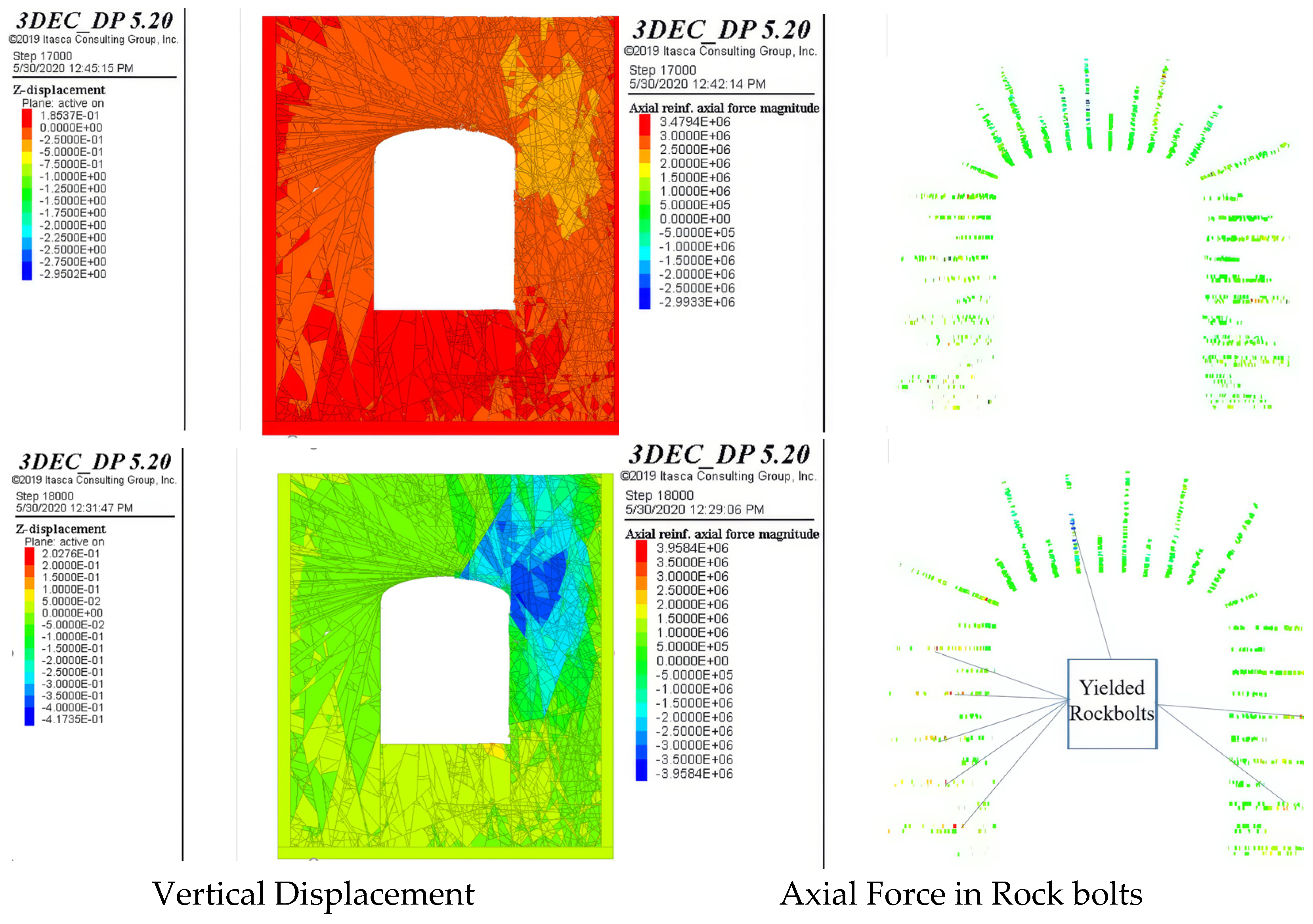
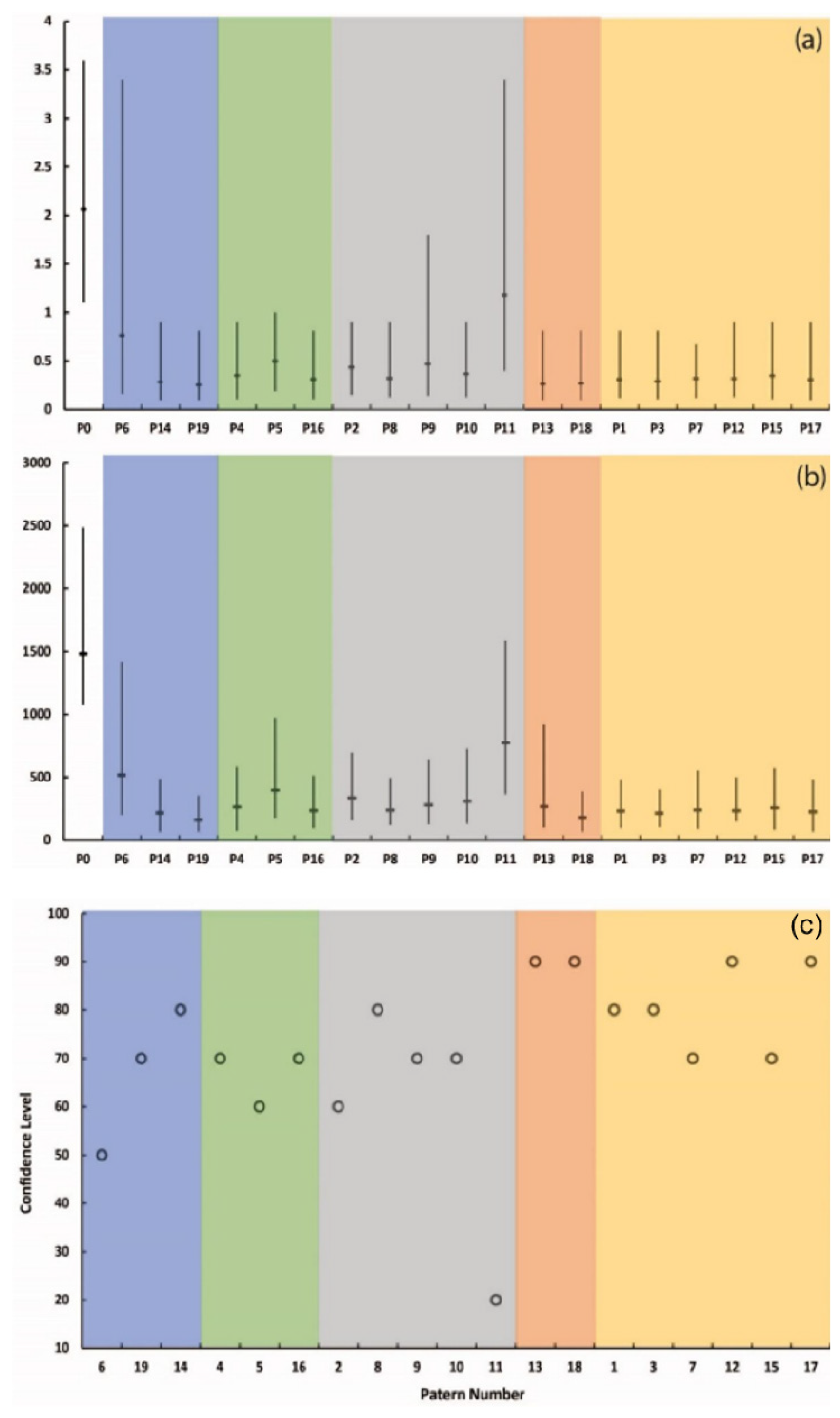
2.3. Numerical Modeling Results and Discussion
3. Summary and Conclusions
- Examining the different DFN realizations with significant stability variation has shown that generating a single DFN realization does not represent the stability condition of an excavation in a jointed rock mass. Therefore, it cannot be considered for support design;
- By comparing single-length rock bolt patterns, it is shown that increasing the rock bolt length from 3 to 6 m enhances the stability significantly. Whereas the 9 m rock bolts result in comparable stability conditions to 6 m rock bolts. It can be concluded that increasing the rock bolt length may not necessarily improve the stability of jointed rock mass exceeding a certain length;
- The results show that a similar bolt consumption in a specific DFN realization may provide drastically different stability conditions. This reveals the importance of the bolting arrangement factor in stabilizing highly jointed underground constructions;
- It is observed that the blocks located between the supported section intervals became relatively stable. This reveals the presence of interlocked blocks in the bolting section intervals;
- It was concluded that, despite the commonly used equal-length rock bolt patterns, the best stability performance was generally observed for dual- and, further, for triple-length rock bolt patterns with equal rock bolt patterns;
- The previous studies mostly consider a regular arrangement of discontinuity or, ultimately, a single stochastic fracture network. Therefore, this study provides a systematic procedure for choosing the most effective supporting patterns. It considers various fracture network arrangements. It also takes into account technical and economic criteria based on the obtained confidence level.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Das, R.; Sirdesai, N.N.; Singh, T.N. Analysis of deformational behavior of circular underground opening in soft ground using three-dimensional physical model. In Proceedings of the 51st US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Dias, D. Convergence-confinement approach for designing tunnel face reinforcement by horizontal bolting. Tunn. Undergr. Space Technol. 2011, 26, 517–523. [Google Scholar] [CrossRef]
- Barton, P.I.; Pantelides, C.C. Modeling of combined discrete/continuous processes. AIChE J. 1994, 40, 966–979. [Google Scholar] [CrossRef]
- Bhasin, R.; Grimstad, E. The use of stress-strength relationships in the assessment of tunnel stability. Tunn. Undergr. Space Technol. 1996, 11, 93–98. [Google Scholar] [CrossRef]
- Vardakos, S.S.; Gutierrez, M.S.; Barton, N.R. Back-analysis of Shimizu Tunnel No. 3 by distinct element modeling. Tunn. Undergr. Space Technol. 2007, 22, 401–413. [Google Scholar] [CrossRef]
- Hudson, J.A.; Feng, X.T. Technical auditing of rock mechanics modelling and rock engineering design. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2010, 47, 877–886. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Barton, N.; Lien, R.; Lunde, J.J.R.M. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Engineering classification of jointed rock masses. Civ. Eng. 1973, 12, 335–343. [Google Scholar]
- Barla, G.; Kovari, K.; Einstein, H.H. Manuscripts using numerical discrete element methods. Rock Mech. Rock Eng. 2013, 46, 655. [Google Scholar] [CrossRef]
- Das, R.; Singh, T.N. Effect of rock bolt support mechanism on tunnel deformation in jointed rockmass: A numerical approach. Undergr. Space 2021, 6, 409–420. [Google Scholar] [CrossRef]
- Maghous, S.; Bernaud, D.; Couto, E. Three-dimensional numerical simulation of rock deformation in bolt-supported tunnels: A homogenization approach. Tunn. Undergr. Space Technol. 2012, 31, 68–79. [Google Scholar] [CrossRef]
- Chao, T.Y. The Numerical Modelling of Rockbolts in Geomechanics by Finite Element Methods. Ph.D. Thesis, School of Information Systems, Computing and Mathematics, Brunel University, Uxbridge, UK, 1998. [Google Scholar]
- Li, A.; Li, Y.; Wu, F.; Shao, G.; Sun, Y. Simulation method and application of three-dimensional DFN for rock mass based on Monte-Carlo technique. Appl. Sci. 2022, 12, 11385. [Google Scholar] [CrossRef]
- Zhou, P.; Bazargan, M.; Lanaro, F.; Shirzadegan, S.; Nikadat, N.; Warema, S.; Yi, C.; Nordlund, E. Dynamic Modelling of Rock Bolts at Kiirunavaara Mine; BeFo: Stockholm, Sweden, 2024. [Google Scholar]
- Indraratna, B.; Kaiser, P.K. Design for grouted rock bolts based on the convergence control method. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1990, 27, 269–281. [Google Scholar] [CrossRef]
- Carranza-Torres, C. Analytical and numerical study of the mechanics of rockbolt reinforcement around tunnels in rock masses. Rock Mech. Rock Eng. 2009, 42, 175–228. [Google Scholar] [CrossRef]
- Bobet, A. Elastic solution for deep tunnels: Application to excavation damage zone and rockbolt support. Rock Mech. Rock Eng. 2009, 42, 147–174. [Google Scholar] [CrossRef]
- Sakurai, S. Modeling strategy for jointed rock masses reinforced by rock bolts in tunneling practice. Acta Geotech. 2010, 5, 121–126. [Google Scholar] [CrossRef]
- Cai, Y.; Esaki, T.; Jiang, Y. A rock bolt and rock mass interaction model. Int. J. Rock Mech. Min. Sci. 2004, 41, 1055–1067. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Wen, H.; Zhou, X. Analytical model for the load transmission law of rock bolt subjected to open and sliding joint displacements. Int. J. Rock Mech. Min. Sci. 2017, 100, 1–9. [Google Scholar] [CrossRef]
- Ma, S.; Zhao, Z.; Nie, W.; Zhu, X. An analytical model for fully grouted rockbolts with consideration of the pre-and post-yielding behavior. Rock Mech. Rock Eng. 2017, 50, 3019–3028. [Google Scholar] [CrossRef]
- Noroozi, M.; Rafiei, R.; Bajolvand, M.; Hojati Tavandashti, A. Investigate the effect of rock mass joint intensity on performance of support systems in the tunnel by using DFN-DEM numerical modeling (Case study: The access tunnel of Rudbar Lorestan Dam plant). J. Anal. Numer. Methods Min. Eng. 2018, 8, 13–27. [Google Scholar] [CrossRef]
- Yokota, Y.; Zhao, Z.; Nie, W.; Iwano, K.; Okada, Y. Experimental and numerical study on the interface behaviour between the rock bolt and bond material. Rock Mech. Rock Eng. 2019, 52, 869–879. [Google Scholar] [CrossRef]
- Boon, C.W. Study of reinforcement support mechanisms for wide-span horse-shoe-shaped openings in horizontally layered jointed rock using the distinct element method. Rock Mech. Rock Eng. 2019, 52, 1179–1191. [Google Scholar] [CrossRef]
- Fu, X.; Sheng, Q.; Zhang, Y.; Chen, J. Investigations of the sequential excavation and reinforcement of an underground cavern complex using the discontinuous deformation analysis method. Tunn. Undergr. Space Technol. 2015, 50, 79–93. [Google Scholar] [CrossRef]
- Kong, C.; Yang, T.; Xiao, M.; Yuan, Q. Numerical simulation of fully grouted rock bolts with or without faceplates based on the tri-linear bond-slip model. Constr. Build. Mater. 2023, 367, 130288. [Google Scholar] [CrossRef]
- Li, D. A new analytical model for stress distribution in the rock bolt under axial loading. Int. J. Rock Mech. Min. Sci. 2024, 176, 105690. [Google Scholar] [CrossRef]
- Li, C.C.; Høien, A.H. The experimental determination of shear stress distribution along fully grouted rock bolts with different bond lengths subjected to pull testing. Int. J. Rock Mech. Min. Sci. 2023, 170, 105557. [Google Scholar] [CrossRef]
- Boon, C.W.; Houlsby, G.T.; Utili, S. Designing tunnel support in jointed rock masses via the DEM. Rock Mech. Rock Eng. 2015, 48, 603–632. [Google Scholar] [CrossRef]
- Li, C.C. A new energy-absorbing bolt for rock support in high stress rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 396–404. [Google Scholar] [CrossRef]
- Yokota, Y.; Zhao, Z.; Shang, J.; Nie, W.; Date, K.; Iwano, K.; Okada, Y. Effect of bolt configuration on the interface behaviour between a rock bolt and bond material: A comprehensive DDA investigation. Comput. Geotech. 2019, 105, 116–128. [Google Scholar] [CrossRef]
- Li, S.; Yu, H.; Liu, Y.; Wu, F. Results from in-situ monitoring of displacement, bolt load, and disturbed zone of a powerhouse cavern during excavation process. Int. J. Rock Mech. Min. Sci. 2008, 45, 1519–1525. [Google Scholar] [CrossRef]
- Türkoğlu, M. Two-Dimensional Numerical Analysis of Tunnel Collapse Driven in Poor Ground Conditions. Master’s Thesis, Middle East Technical University, Ankara, Türkiye, 2013. [Google Scholar]
- Rao, R.V.; Naik, S.; Reddy, M.N.; Gupta, R.N. Discontinuum analysis and support design of road tunnels—A case study. In Geoecology and Computers; CRC Press: Boca Raton, FL, USA, 2000; pp. 141–150. [Google Scholar]
- Abdellah, W.R.; Ali, M.A.; Yang, H.S. Studying the effect of some parameters on the stability of shallow tunnels. J. Sustain. Min. 2018, 17, 20–33. [Google Scholar] [CrossRef]
- Zhou, F.; Sarfarazi, V.; Haeri, H.; Soleymanipargoo, M.H.; Fu, J.; Marji, M.F. A coupled experimental and numerical simulation of concrete joints’ behaviors in tunnel support using concrete specimens. Comput. Concr. 2021, 28, 189–208. [Google Scholar] [CrossRef]
- Nord, G.; Bagheri, M.; Baghbanan, A.; Stille, H. Design consideration of large caverns by using advanced drilling equipment. Felsbau 2007, 25, 131–136. [Google Scholar]
- Lanaro, F.; Fredriksson, A. Rock Mechanics Model-Summary of the Primary Data, Preliminary site description Forsmark area-version 1.2; Swedish Nuclear Fuel and Waste Management Co.: Stockholm, Sweden, 2005; SKB-R--05-83. [Google Scholar]
- Bazargan, M.; Gudmundsson, A. Dike-induced stresses and displacements in layered volcanic zones. J. Volcanol. Geotherm. Res. 2019, 384, 189–205. [Google Scholar] [CrossRef]
- Bazargan, M.; Gudmundsson, A. Stresses and displacements in layered rocks induced by inclined (cone) sheets. J. Volcanol. Geotherm. Res. 2020, 401, 106965. [Google Scholar] [CrossRef]
- Khoei, A.R.; Hirmand, M.; Vahab, M.; Bazargan, M. An Enriched FEM Technique for Modeling Hydraulically Driven Cohesive Fracture Propagation in Impermeable Media with Frictional Natural Faults: Numerical and Experimental Investigations. Int. J. Numer. Methods Eng. 2015, 104, 439–468. [Google Scholar] [CrossRef]
- Bazargan, M.; Berg, S.; Bergholm, A.; Moallemi, S.; Machado, B. Exploring the impact of shallow tunneling in fractured rock masses with pre-existing tunnels: A case study. In Tunnelling into a Sustainable Future—Methods and Technologies; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar] [CrossRef]
- Li, C.C. Principles of rockbolting design. Rock Mech. Rock Eng. 2017, 9, 396–414. [Google Scholar] [CrossRef]
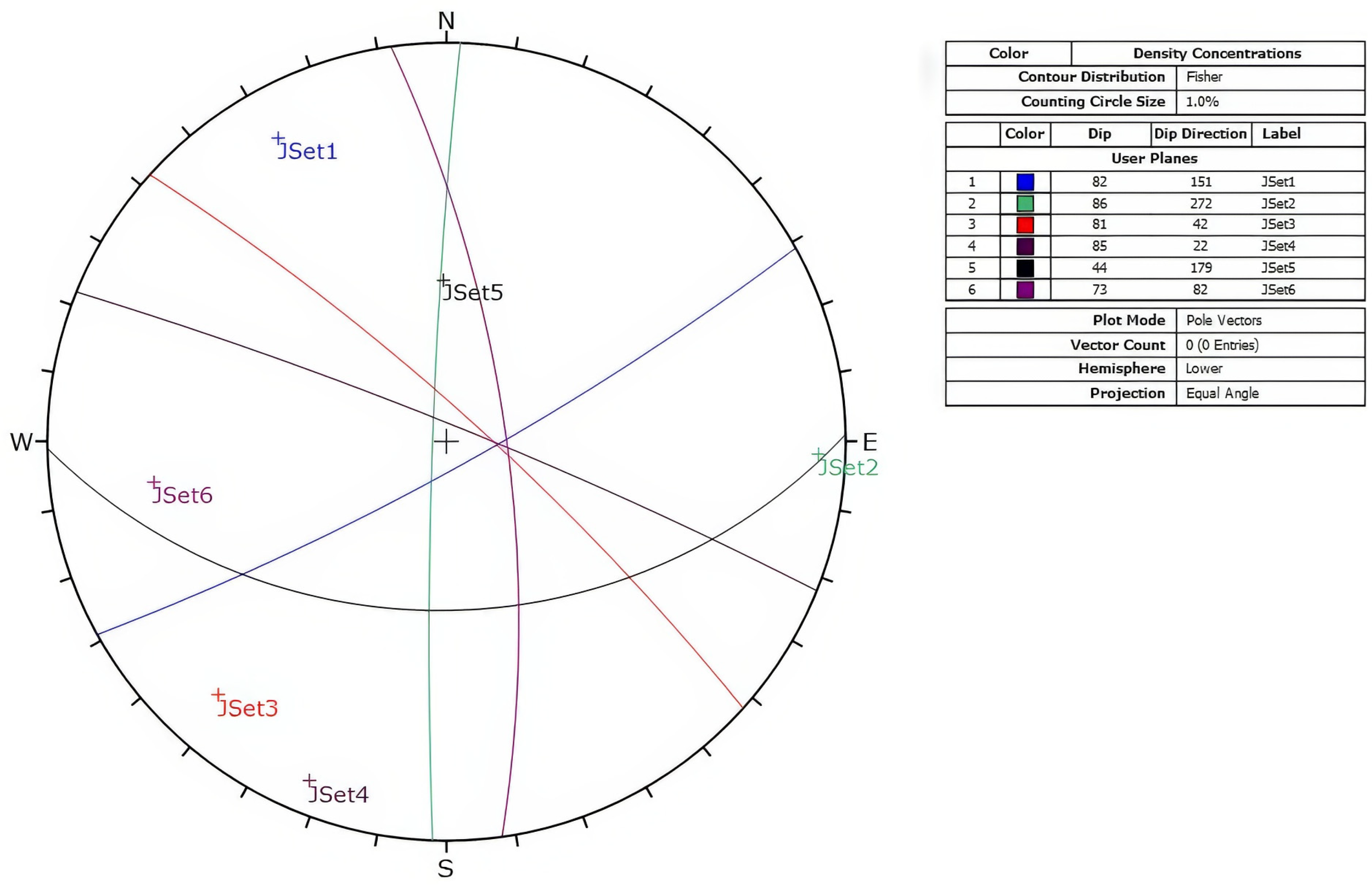
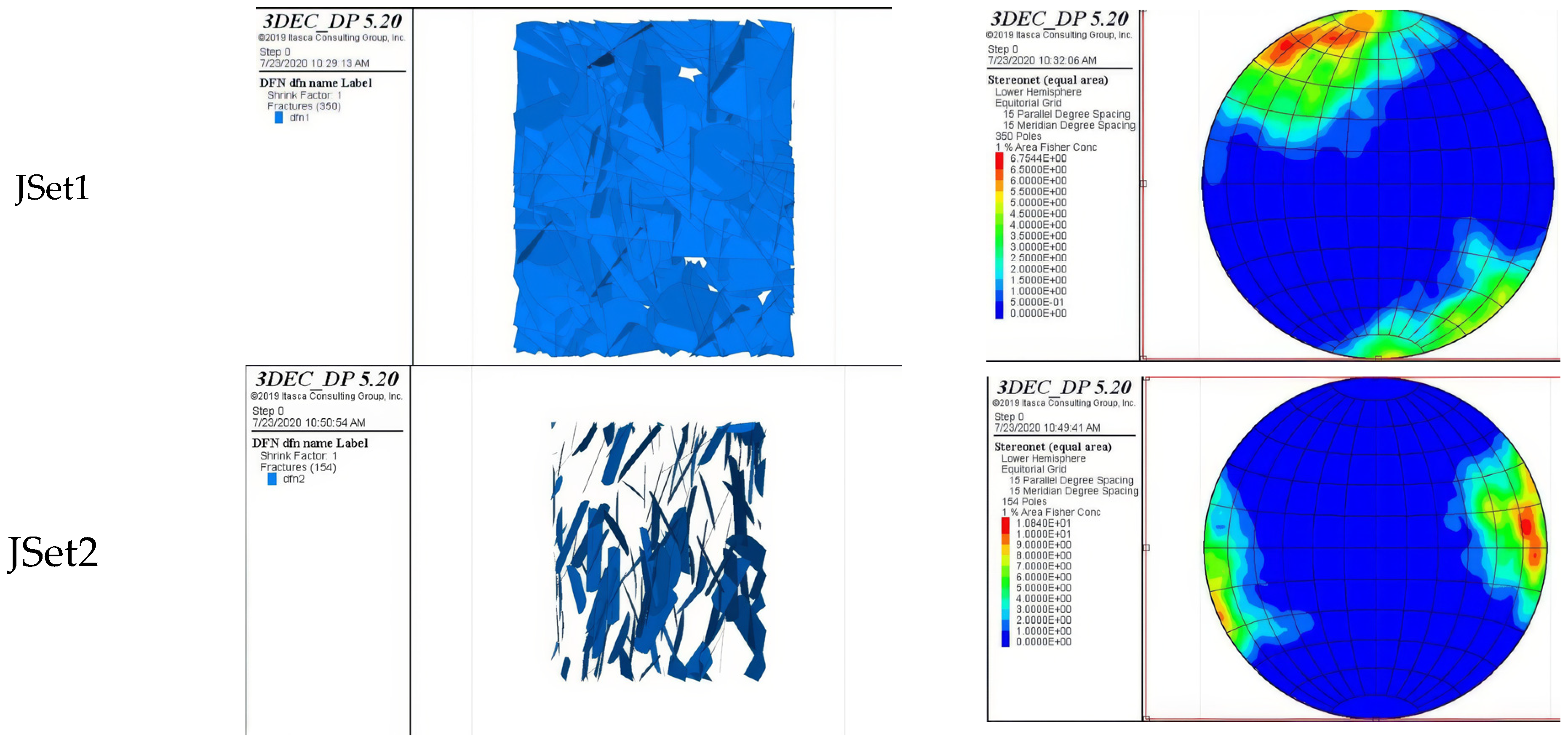
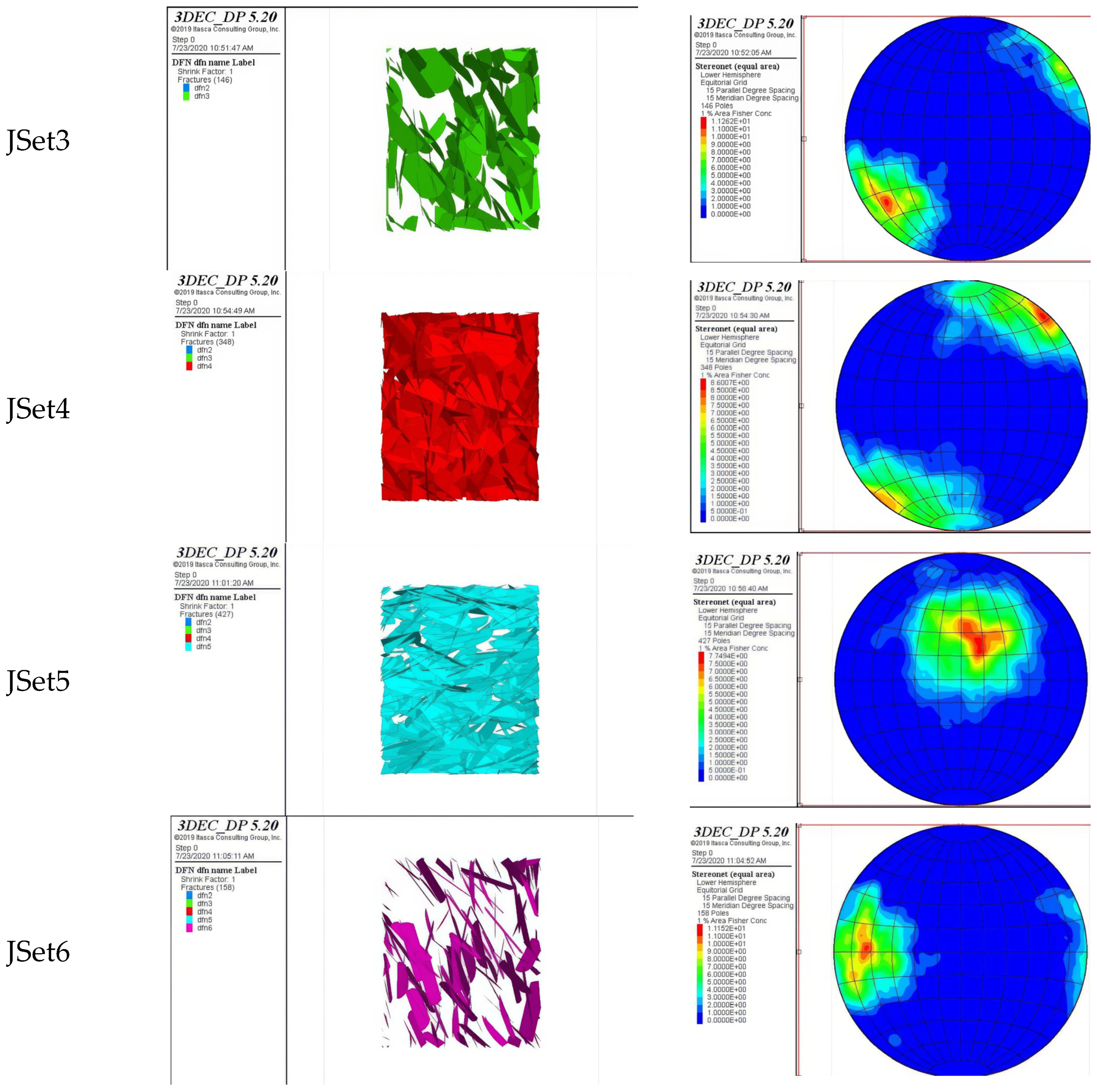


| Orientation Set (Dip/Dip Direction) | Fisher Distribution Coefficient | Fracture Percentage (%) | Intensity (P20) | Length Distribution Parameter | ||
|---|---|---|---|---|---|---|
| Distribution | Mean (m) | Std. Dev. (m) | ||||
| 80/155 | 7.63 | 22 | 0.062 | lognormal | 4.8 | 1.7 |
| 85/270 | 9.81 | 11.3 | 0.032 | lognormal | 4.5 | 1.4 |
| 80/50 | 9.81 | 11.3 | 0.032 | lognormal | 4.5 | 1.4 |
| 85/25 | 7.63 | 22 | 0.062 | lognormal | 4.8 | 1.7 |
| 85/270 | 7.63 | 22 | 0.062 | lognormal | 4.8 | 1.7 |
| 70/85 | 9.81 | 11.3 | 0.032 | lognormal | 4.5 | 1.4 |
| Intact Rock Geomechanical Properties | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Elastic Modulus (GPa), Ei | Poisson’s Ratio, ϑ | Density, Ꝭ (kg/m3) | Compressive Strength (MPa), σci | |||||||
| 77 | 0.27 | 2700 | 161 | |||||||
| Discontinuity Geomechanical Properties | ||||||||||
| JRC | JCS (MPa) | Residual Friction Angle (deg) | Basic Friction Angle (deg) | JKn (MPa/mm) | JKs (MPa/mm) | Dilation (deg) | Critical Shear Displacement (µm) | Initial Aperture Api (µm) | Residual Aperture Apr (µm) | Maximum Aperture Apmax (µm) |
| 5.8 | 83.9 | 26.3 | 30 | 128.4 | 38.8 | 5 | 770 | 70 | 10 | 100 |
| Rock Bolt Properties | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nominal Diameter [mm] | Steel Grade [N/mm2] | Ultimate Axial Strength [kN] | Ultimate Shear Strength [kN] | Cross-Sectional Area [mm2] | Second Moment of Inertia-I (m4) | Reinforcement Stiffness Eb (Pa) | Weight [kg/m] | Square Anchor Plate Dimension (mm) | |||
| 32 | 600 | 482 | 482 | 804 | 5.15 × 10−8 | 2 × 1011 | 6.31 | 150 | |||
| Grout and Steel Mesh Mechanical Properties | |||||||||||
| Grout Poisson’s Ratio—ϑ | Grout Uniaxial Compressive Strength—σc (MPa) | Grout Shear Modulus-Gg (MPa) | Grout Stiffness—Eg (Pa) | ||||||||
| 0.15 | 35 | 12,861 | 2.985 × 1010 | ||||||||
| Mesh Diameter (mm) | Mesh Tensile Strength (MPa) | Mesh Yielding Strength (MPa) | |||||||||
| 12 | 750 | 600 | |||||||||
| DFN1 | DFN2 | DFN3 | DFN4 | DFN5 | DFN6 | DFN7 | DFN8 | DFN9 | DFN10 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VT | V90 | VT | V90 | VT | V90 | VT | V90 | VT | V90 | VT | V90 | VT | V90 | VT | V90 | VT | V90 | VT | V90 | |
| P0 | 1134 | 1.9 | 1115 | 1.1 | 2486 | 2.8 | 1609 | 1.8 | 1075 | 1.4 | 1850 | 2.6 | 1120 | 1.5 | 1292 | 2 | 1457 | 1.8 | 1658 | 3.4 |
| Group A | ||||||||||||||||||||
| P6 | 361 | 0.48 | 496 | 0.72 | 448 | 0.67 | 202 | 0.16 | 446 | 0.63 | 226 | 0.19 | 224 | 0.21 | 297 | 0.32 | 1032 | 0.84 | 1411 | 3.4 |
| P14 | 165 | 0.19 | 124 | 0.12 | 485 | 0.6 | 152 | 0.13 | 102 | 0.11 | 172 | 0.17 | 68 | 0.1 | 194 | 0.29 | 207 | 0.21 | 488 | 0.9 |
| P19 | 171 | 0.25 | 104 | 0.12 | 203 | 0.35 | 135 | 0.12 | 97 | 0.11 | 142 | 0.18 | 68 | 0.1 | 172 | 0.28 | 132 | 0.18 | 354 | 0.81 |
| Group B | ||||||||||||||||||||
| P4 | 163 | 0.19 | 150 | 0.15 | 442 | 0.67 | 180 | 0.16 | 167 | 0.19 | 165 | 0.18 | 74 | 0.11 | 203 | 0.29 | 582 | 0.64 | 493 | 0.9 |
| P5 | 352 | 0.48 | 570 | 1 | 461 | 0.66 | 263 | 0.31 | 408 | 0.66 | 194 | 0.19 | 176 | 0.26 | 352 | 0.35 | 970 | 0.85 | 206 | 0.23 |
| P16 | 167 | 0.19 | 175 | 0.17 | 346 | 0.56 | 158 | 0.13 | 114 | 0.11 | 171 | 0.18 | 92 | 0.12 | 203 | 0.29 | 512 | 0.54 | 389 | 0.81 |
| Group C | ||||||||||||||||||||
| P2 | 301 | 0.45 | 161 | 0.15 | 448 | 0.67 | 183 | 0.16 | 480 | 0.68 | 190 | 0.18 | 164 | 0.2 | 228 | 0.29 | 695 | 0.65 | 501 | 0.9 |
| P8 | 142 | 0.16 | 163 | 0.16 | 392 | 0.66 | 160 | 0.13 | 141 | 0.17 | 181 | 0.18 | 121 | 0.15 | 225 | 0.29 | 331 | 0.39 | 494 | 0.9 |
| P9 | 645 | 1.8 | 159 | 0.15 | 308 | 0.49 | 217 | 0.29 | 126 | 0.14 | 168 | 0.16 | 130 | 0.14 | 240 | 0.3 | 521 | 0.53 | 268 | 0.68 |
| P10 | 228 | 0.26 | 224 | 0.2 | 507 | 0.66 | 159 | 0.13 | 151 | 0.17 | 205 | 0.19 | 132 | 0.15 | 251 | 0.31 | 726 | 0.69 | 495 | 0.9 |
| P11 | 365 | 0.48 | 930 | 1.1 | 534 | 0.7 | 663 | 1.2 | 848 | 1.4 | 482 | 0.79 | 899 | 1.5 | 439 | 0.4 | 966 | 0.82 | 1589 | 3.4 |
| Group D | ||||||||||||||||||||
| P13 | 152 | 0.19 | 111 | 0.12 | 310 | 0.5 | 155 | 0.13 | 98 | 0.11 | 160 | 0.18 | 918 | 0.1 | 181 | 0.29 | 181 | 0.18 | 389 | 0.81 |
| P18 | 148 | 0.19 | 135 | 0.15 | 320 | 0.5 | 134 | 0.12 | 146 | 0.17 | 141 | 0.17 | 69 | 0.1 | 172 | 0.28 | 142 | 0.18 | 385 | 0.81 |
| Group E | ||||||||||||||||||||
| P1 | 167 | 0.19 | 151 | 0.15 | 299 | 0.54 | 147 | 0.13 | 181 | 0.18 | 190 | 0.18 | 94 | 0.12 | 190 | 0.29 | 482 | 0.49 | 398 | 0.81 |
| P3 | 167 | 0.19 | 147 | 0.15 | 381 | 0.65 | 164 | 0.13 | 102 | 0.11 | 174 | 0.18 | 105 | 0.14 | 200 | 0.29 | 282 | 0.26 | 403 | 0.81 |
| P7 | 157 | 0.19 | 158 | 0.16 | 399 | 0.66 | 153 | 0.13 | 145 | 0.17 | 189 | 0.18 | 88 | 0.12 | 200 | 0.29 | 554 | 0.67 | 320 | 0.61 |
| P12 | 181 | 0.2 | 148 | 0.15 | 307 | 0.5 | 152 | 0.13 | 160 | 0.19 | 163 | 0.18 | 162 | 0.21 | 204 | 0.29 | 346 | 0.41 | 500 | 0.9 |
| P15 | 164 | 0.19 | 153 | 0.16 | 387 | 0.66 | 158 | 0.13 | 142 | 0.17 | 180 | 0.18 | 81 | 0.11 | 215 | 0.29 | 572 | 0.67 | 498 | 0.9 |
| P17 | 170 | 0.2 | 149 | 0.15 | 307 | 0.5 | 158 | 0.13 | 177 | 0.19 | 161 | 0.18 | 68 | 0.1 | 210 | 0.29 | 349 | 0.41 | 483 | 0.9 |
| The Most Stable Patterns | The Most Unstable Patterns | |||||||
|---|---|---|---|---|---|---|---|---|
| P12 | P13 | P17 | P18 | P19 | P2 | P5 | P6 | P11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isfahani, N.S.; Azhari, A.; Motra, H.B.; Hashemalhoseini, H.; Hosseinabadi, M.H.; Baghbanan, A.; Bazargan, M. Optimizing Rock Bolt Support for Large Underground Structures Using 3D DFN-DEM Method. Geosciences 2025, 15, 293. https://doi.org/10.3390/geosciences15080293
Isfahani NS, Azhari A, Motra HB, Hashemalhoseini H, Hosseinabadi MH, Baghbanan A, Bazargan M. Optimizing Rock Bolt Support for Large Underground Structures Using 3D DFN-DEM Method. Geosciences. 2025; 15(8):293. https://doi.org/10.3390/geosciences15080293
Chicago/Turabian StyleIsfahani, Nooshin Senemarian, Amin Azhari, Hem B. Motra, Hamid Hashemalhoseini, Mohammadreza Hajian Hosseinabadi, Alireza Baghbanan, and Mohsen Bazargan. 2025. "Optimizing Rock Bolt Support for Large Underground Structures Using 3D DFN-DEM Method" Geosciences 15, no. 8: 293. https://doi.org/10.3390/geosciences15080293
APA StyleIsfahani, N. S., Azhari, A., Motra, H. B., Hashemalhoseini, H., Hosseinabadi, M. H., Baghbanan, A., & Bazargan, M. (2025). Optimizing Rock Bolt Support for Large Underground Structures Using 3D DFN-DEM Method. Geosciences, 15(8), 293. https://doi.org/10.3390/geosciences15080293








