Two-Stage Systematic Forecasting of Earthquakes
Abstract
1. Introduction
2. Materials and Methods
2.1. Motivation
2.2. Information Model
- Representation of process properties. The processes of preparation of strong earthquakes are adequately described by grid space–time fields of the features. The values of the fields in the grid nodes correspond to the components of the feature space vectors and attributes the time slice number t and the spatial coordinates of the grid node (x, y).
- Anomalous condition. Before strong earthquakes, the anomalous behavior of seismic and/or geodynamic processes is usually observed in the focal zone. Anomalies correspond to the values of some grid fields of features that are close to maximum or minimum. The corresponding vectors of the feature space will be considered possible precursors of earthquakes. Further, to simplify the explanation, we will assume that the anomalous components of earthquake precursors take only field values close to the maximum.
- Location of earthquake precursors. The feature space vectors corresponding to the grid nodes within the cylinder preceding the target earthquake, with the base centered at the epicenter, are labeled as potential earthquake precursors. The vectors of field values at all other grid nodes cannot be labeled. As a result, there is a sample of potential precursors of target earthquakes and a set of unlabeled vectors representing the field values at all other grid nodes.
- Monotonicity condition. According to condition (3), it is natural to assume that unlabeled vectors that are component wise larger than the precursors possess the same anomalous properties as the corresponding precursors and are also earthquake precursors. However, at the time of the forecast, these unlabeled vectors have never preceded target earthquakes in the available training data. Consequently, the appearance of a precursor does not always result in an earthquake. This implies that, according to the model, the relationship between the precursors and the predicted earthquake epicenters is stochastic.
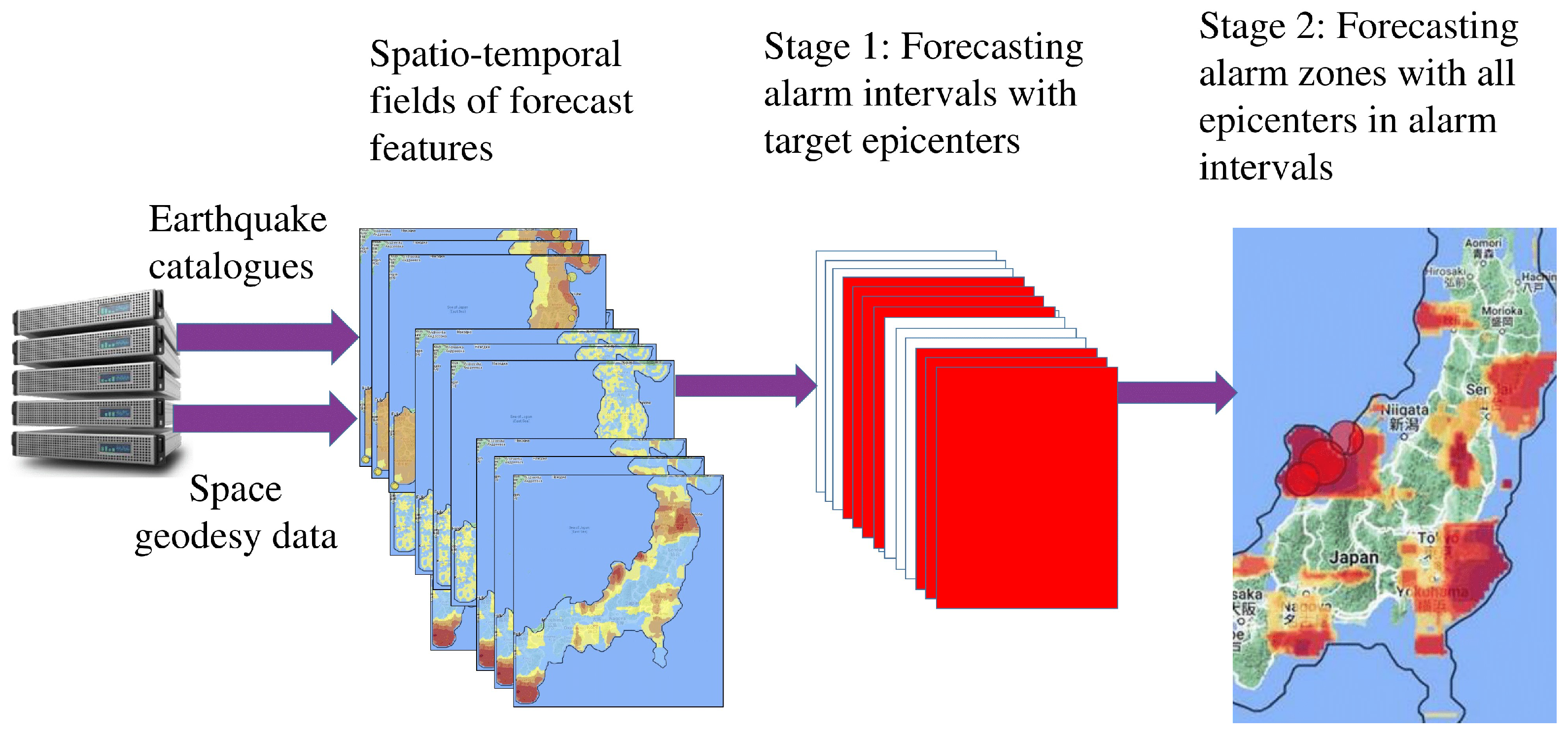
2.3. Forecast Scheme
- 1.
- Detection probability:
- 2.
- Probability of a successful forecast in the next interval:
2.4. Learning Algorithm
- The measure of information content based on the alarm volume:
- 2.
- The measure of information content based on the likelihood ratio:
3. Modeling
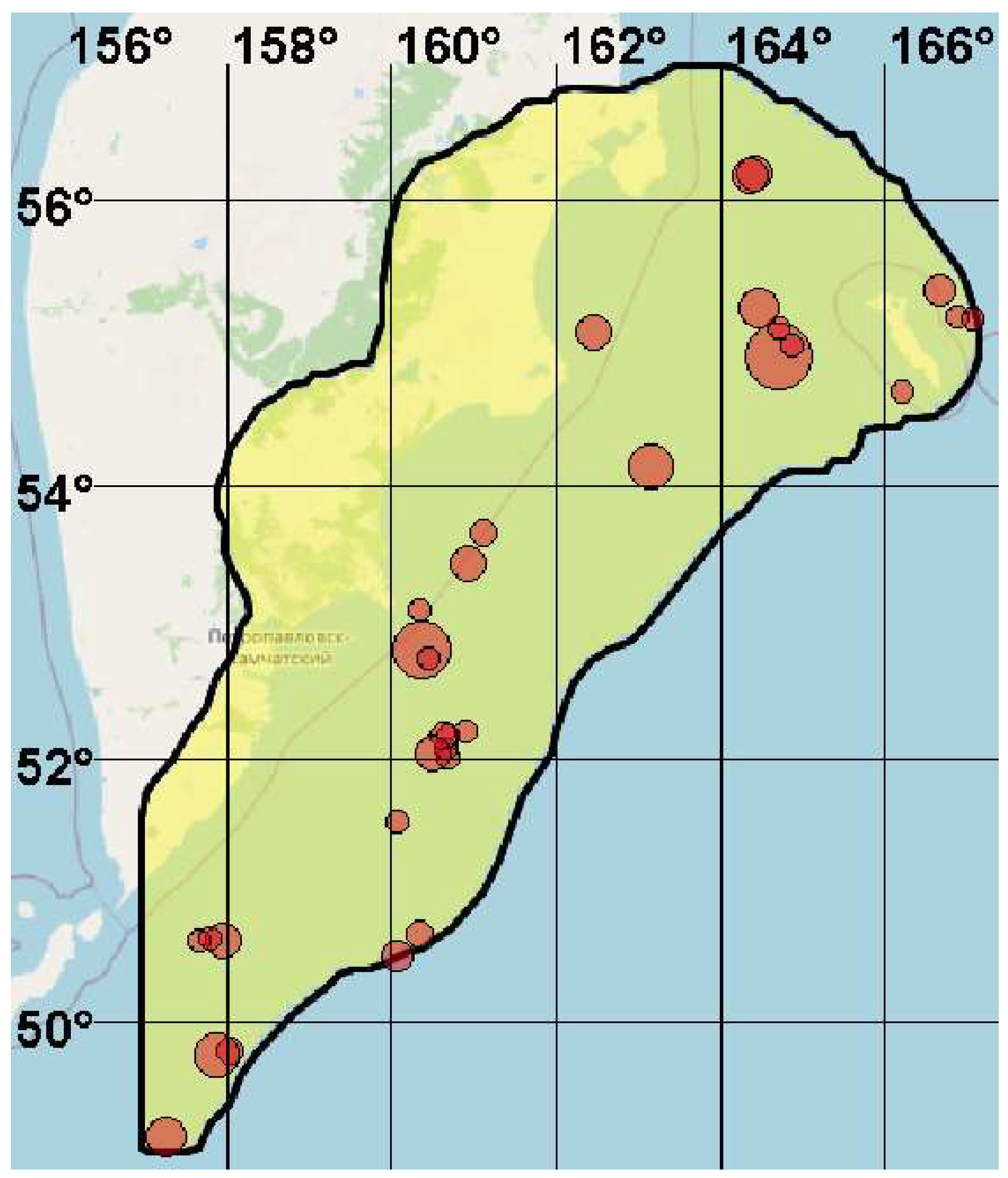
3.1. Data
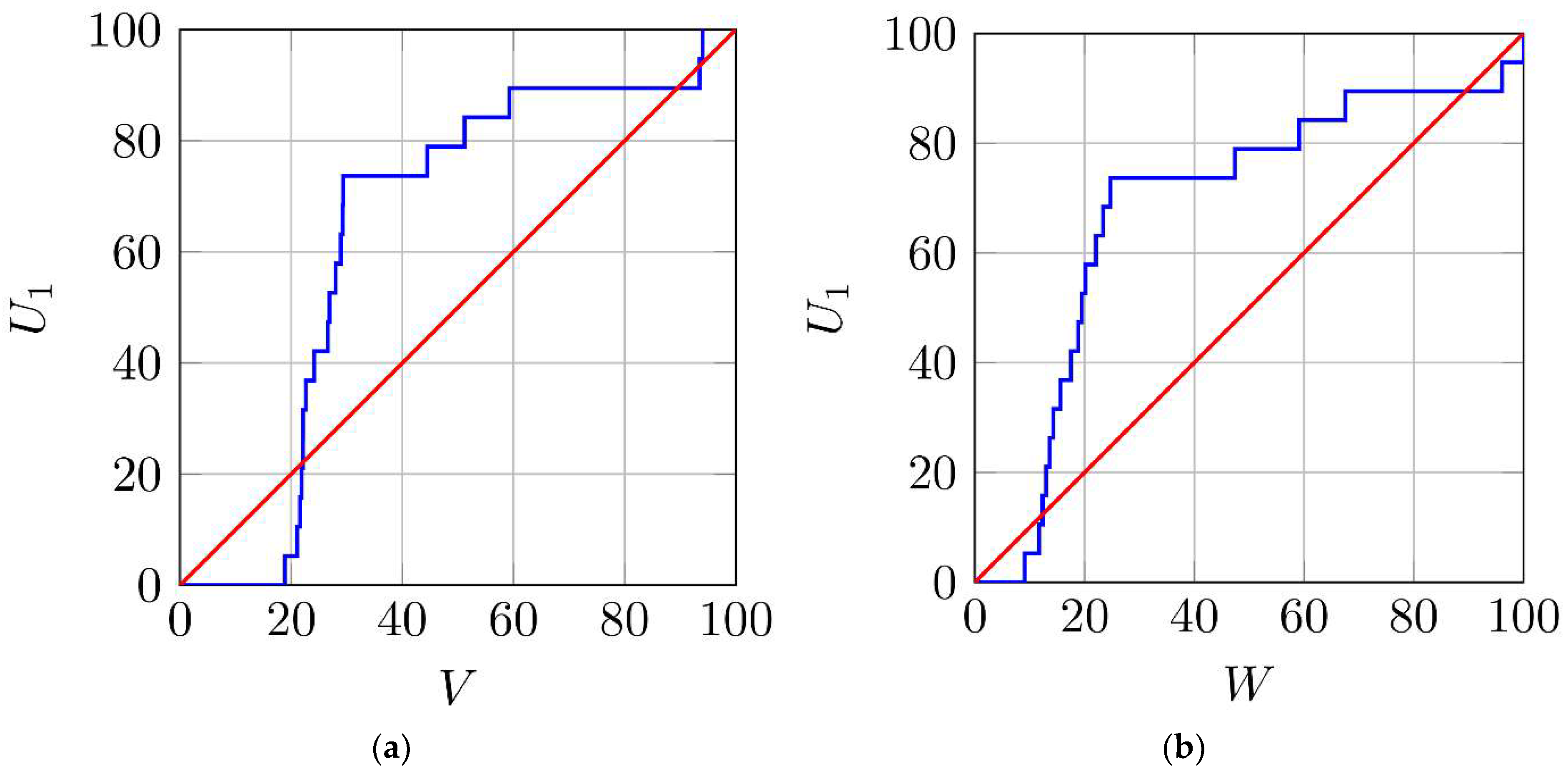
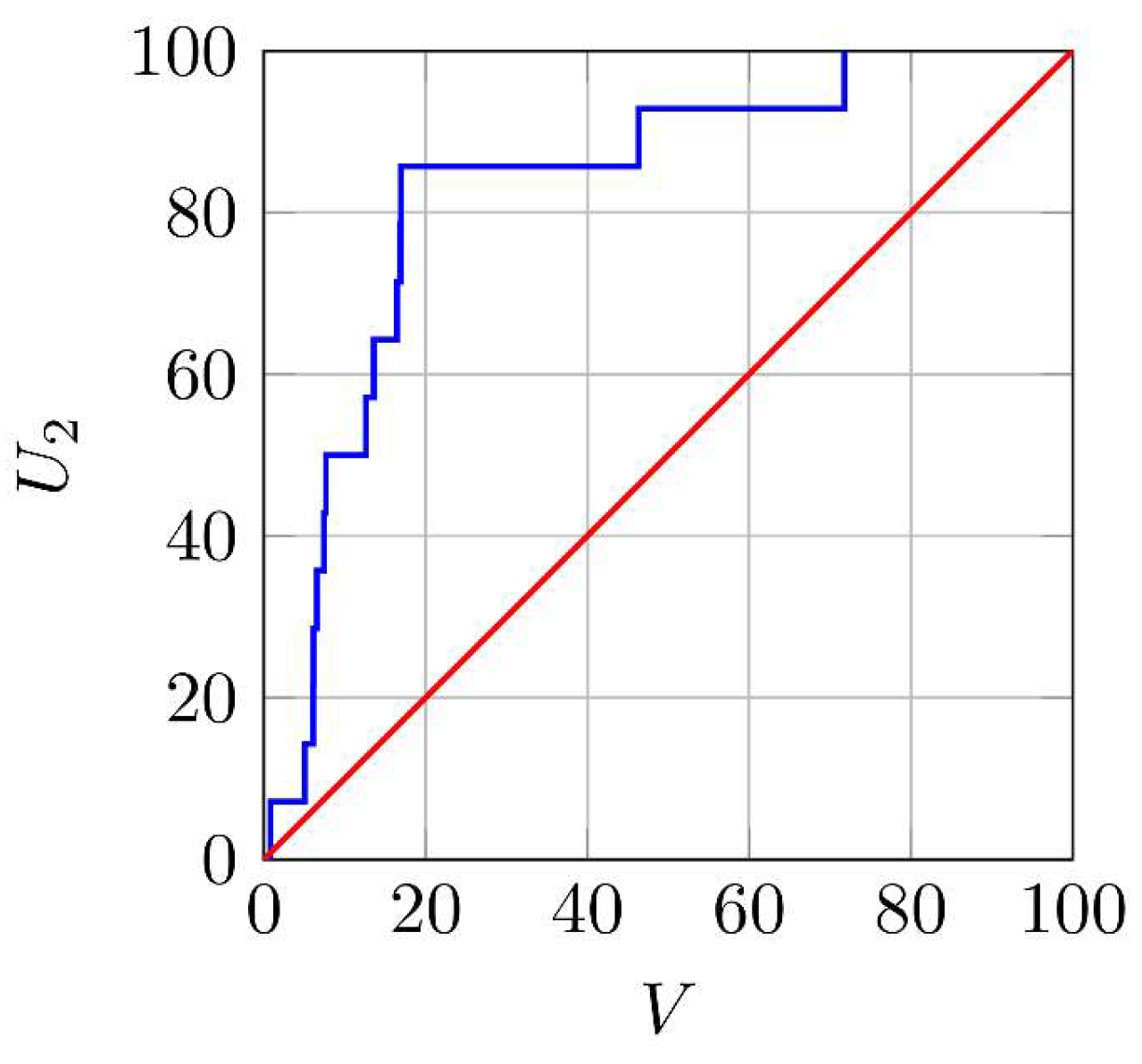
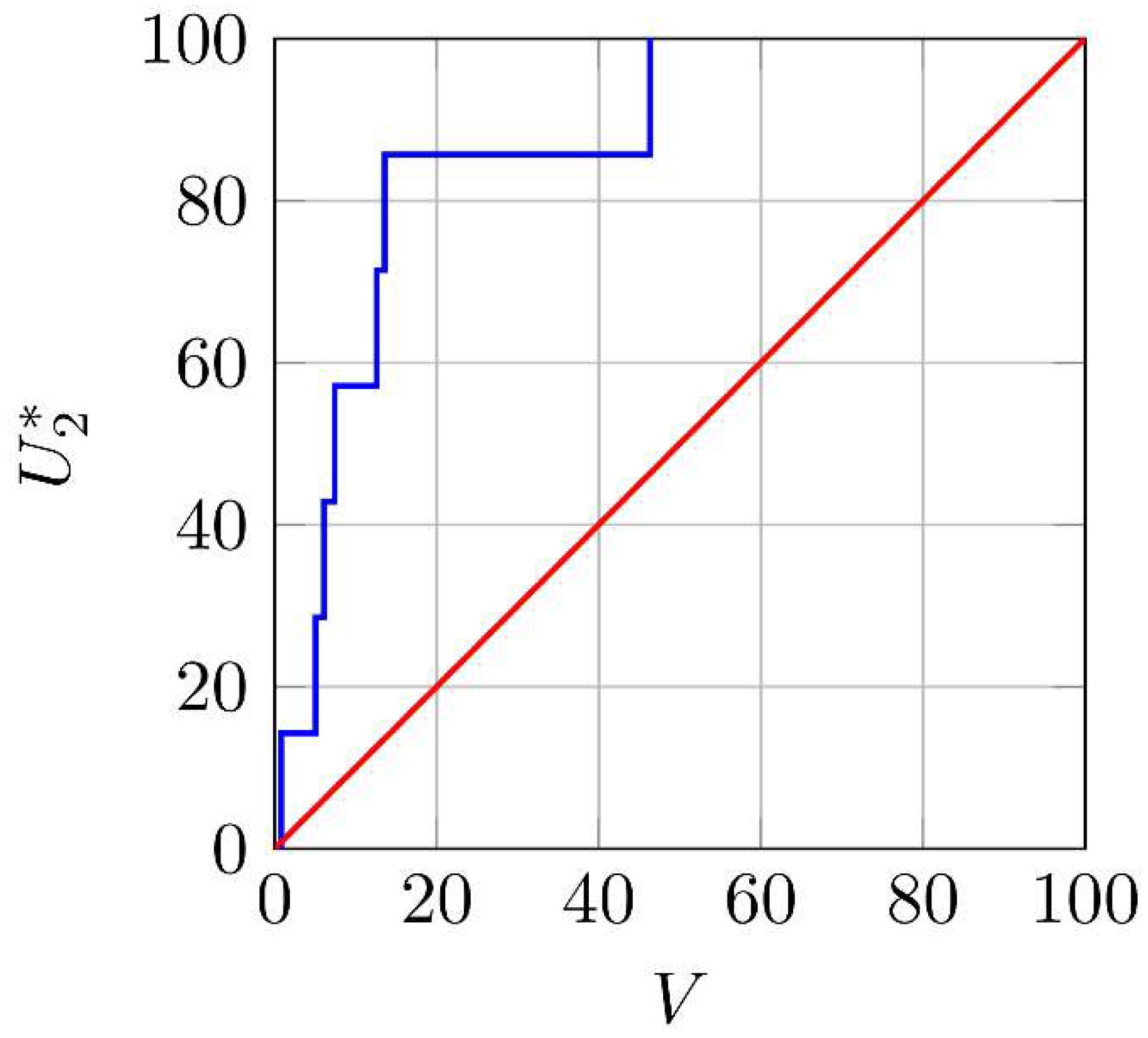
3.2. One-Stage Forecasting
3.3. Two-Stage Forecast from 19 January 2012
3.4. Two-Stage Forecast from 11 January 2018
4. Discussion
- Uncertainty in selecting earthquake precursors based on epicenters.
- Limited training data for target magnitude earthquakes.
- Incomplete and noisy data describing earthquake preparation processes.
- Ambiguity in classifying target earthquakes by magnitude thresholds.
5. Conclusions
- The absence of a training set of earthquake precursors, which is replaced by a set of earthquake epicenters.
- The anomalous nature of seismotectonic processes preceding major earthquakes.
- The existence of a monotonic dependence between the degree of anomaly in the properties of earthquake preparation processes and the identified values of precursor features.
- Methods for the automatic identification of potential earthquake precursors, assessment of their quality, and ranking by informativeness.
- Methods for optimizing new forecast quality metrics:
- ○
- Detection probability, defined as the proportion of forecast intervals during which all epicenters of target magnitude earthquakes fall within a confined alarm zone.
- ○
- Probability of detecting all epicenters of target earthquakes within the alarm zone during a forecast interval.
- A method for two-stage systematic earthquake forecasting:
- ○
- Stage A: prediction of alarm intervals during which the epicenters of target earthquakes are expected within the analysis region (first stage of forecasting).
- ○
- Stage B: prediction of alarm zones within which all epicenters of target earthquakes are expected during the alarm intervals (second stage of forecasting).
- Verbalization of the nonparametric decision rule using logical implication, enabling the interpretation of predictions in terms of the properties of the analyzed processes.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMAA | Method of the Minimum Area of Alarm |
| AWS | Adaptive Weight Smoothing |
| RTL | Region–Time–Length |
| ROC | Receiver-Operating Characteristic Curve |
| IPE | Institute of Physics of the Earth |
References
- Myachkin, V.I.; Kostrov, B.V.; Shamina, O.G.; Sobolev, G.A. Fundamentals of physics of earthquake focus and precursors. In The Physics of Earthquake Focus; Nauka: Moscow, Russia, 1975; pp. 9–41. [Google Scholar]
- Sobolev, G. Principles of Earthquake Prediction; Nauka: Moscow, Russia, 1993; p. 313. Available online: https://bigenc.ru/b/osnovy-prognoza-zemletriase-f5d385 (accessed on 6 May 2025).
- Sobolev, G.A. Avalanche Unstable Fracturing Formation Model. Izv. Phys. Solid Earth 2019, 55, 138–151. [Google Scholar] [CrossRef]
- Zavyalov, A.D. Medium-Term Earthquake Forecast: Fundamentals, Methodology, Implementation; Nauka: Moscow, Russia, 2006. [Google Scholar]
- Kagan, Y.Y. Earthquakes: Models, Statistics, Testable Forecasts; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Shebalin, P.N.; Narteau, C.; Zechar, J.D.; Holschneider, M. Combining Earthquake Forecasts Using Differential Probability Gains. Earth Planets Space 2014, 66, 37. [Google Scholar] [CrossRef]
- Zhao, Y.; Lv, S.; Liu, P. Advances in Earthquake Prevention and Reduction Based on Machine Learning: A Scoping Review. IEEE Access 2024, 12, 143908–143929. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Beroza, G.C. Machine Learning in Earthquake Seismology. Annu. Rev. Earth Planet. Sci. 2023, 51, 105–129. [Google Scholar] [CrossRef]
- Sobolev, G.; Ponomarev, A. Earthquake Physics and Precursors; Nauka: Moscow, Russia, 2003. [Google Scholar]
- Kanamori, H.; Brodsky, E.E. The Physics of Earthquakes. Rep. Prog. Phys. 2004, 67, 1429–1496. [Google Scholar] [CrossRef]
- Ommi, S.; Hashemi, M. Machine Learning Technique in the North Zagros Earthquake Prediction. Appl. Comput. Geosci. 2024, 22, 100163. [Google Scholar] [CrossRef]
- Ridzwan, N.S.M.; Yusoff, S.H.M. Machine Learning for Earthquake Prediction: A Review (2017–2021). Earth Sci. Inform. 2023, 16, 1133–1149. [Google Scholar] [CrossRef]
- Panakkat, A.; Adeli, H. Neural Network Models for Earthquake Magnitude Prediction Using Multiple Seismicity Indicators. Int. J. Neural Syst. 2007, 17, 13–33. [Google Scholar] [CrossRef]
- Rhoades, D.A. Mixture Models for Improved Earthquake Forecasting with Short-to-Medium Time Horizons. Bull. Seismol. Soc. Am. 2013, 103, 2203–2215. [Google Scholar] [CrossRef]
- Kail, R.; Burnaev, E.; Zaytsev, A. Recurrent Convolutional Neural Networks Help to Predict Location of Earthquakes. IEEE Geosci. Remote Sens. Lett. 2021, 19, 8019005. [Google Scholar] [CrossRef]
- Corbi, F.; Sandri, L.; Bedford, J.; Funiciello, F.; Brizzi, S.; Rosenau, M.; Lallemand, S. Machine Learning Can Predict the Timing and Size of Analog Earthquakes. Geophys. Res. Lett. 2019, 46, 1303–1311. [Google Scholar] [CrossRef]
- Mignan, A.; Broccardo, M. Neural Network Applications in Earthquake Prediction (1994–2019): Meta-Analytic and Statistical Insights on Their Limitations. Seismol. Res. Lett. 2020, 91, 2330–2342. [Google Scholar] [CrossRef]
- Gitis, V.; Derendyaev, A. A Technology for Seismogenic Process Monitoring and Systematic Earthquake Forecasting. Remote Sens. 2023, 15, 2171. [Google Scholar] [CrossRef]
- Gitis, V.G.; Derendyaev, A.B. Optimization of the Approach to Systematic Earthquake Forecasting. J. Commun. Technol. Electron. 2024, 69, 285–307. [Google Scholar] [CrossRef]
- Gitis, V.; Derendyaev, A.; Petrov, K. Analyzing the Performance of GPS Data for Earthquake Prediction. Remote Sens. 2021, 13, 1842. [Google Scholar] [CrossRef]
- Chebrov, D.; Tikhonov, S.; Droznin, D.; Droznina, S.; Matveenko, E.; Mityushkina, S.; Saltykov, V.; Senyukov, S.; Serafimova, Y.; Sergeev, V.; et al. Kamchatka seismic monitoring and Earthquake prediction system and its evolution. Main results of observations in 2016–2020. RJS 2021, 3, 28–49. [Google Scholar] [CrossRef]
- Sobolev, G.; Tyupkin, Y.S. Anomalies in the weak seismicity regime prior to Kamchatka strong earthquakes. Vulkanol. Seismol. 1996, 4, 64–74. [Google Scholar]
- Sobolev, G.; Tyupkin, Y.S. Effect of vibration on failure and acoustic emission in a fault zone model. Vulkanol. Seismol. 1998, 19, 829–836. [Google Scholar]
- Polzehl, J.; Spokoiny, V.G. Adaptive Weights Smoothing with Applications to Image Restoration. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2000, 62, 335–354. [Google Scholar] [CrossRef]
- Polzehl, J.; Spokoiny, V. Propagation-Separation Approach for Local Likelihood Estimation. Probab. Theory Relat. Fields 2006, 135, 335–362. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover Publications: New York, NY, USA, 1997. [Google Scholar]
- Gitis, V.G.; Derendyaev, A.B.; Pirogov, S.A.; Spokoiny, V.G.; Yurkov, E. Earthquake Prediction Using the Fields Estimated by an Adaptive Algorithm. In Proceedings of the 7th International Conference on Web Intelligence, Mining and Semantics, Amantea, Italy, 19–22 June 2017; pp. 1–8. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]



| № | Date | Longitude, Degrees | Latitude, Degrees | Depth, km | Magnitude | Alarm Volume, % |
|---|---|---|---|---|---|---|
| 1 | 15 October 2012 | 160.08 | 51.53 | 44.0 | 6.0 | 16.94 |
| 2 | 1 March 2013 | 157.94 | 50.63 | 52.0 | 6.4 | 16.44 |
| 3 | 4 March 2013 | 157.66 | 50.63 | 51.0 | 6.1 | 16.44 |
| 4 | 9 March 2013 | 157.80 | 50.65 | 49.0 | 6.1 | 6.55 |
| 5 | 24 March 2013 | 160.33 | 50.68 | 58.0 | 6.2 | 6.55 |
| 6 | 19 April 2013 | 158.04 | 49.77 | 45.0 | 6.2 | 6.13 |
| 7 | 20 April 2013 | 157.88 | 49.74 | 39.0 | 6.7 | 6.13 |
| 8 | 19 May 2013 | 160.69 | 52.01 | 50.0 | 6.1 | 8.07 |
| 9 | 19 May 2013 | 160.65 | 52.08 | 42.0 | 6.0 | 8.50 |
| 10 | 19 May 2013 | 160.67 | 52.18 | 40.0 | 6.0 | 9.63 |
| 11 | 21 May 2013 | 160.89 | 52.22 | 59.0 | 6.1 | 16.90 |
| 12 | 21 May 2013 | 160.63 | 52.18 | 43.0 | 6.2 | 9.63 |
| 13 | 21 May 2013 | 160.49 | 52.05 | 48.0 | 6.5 | 7.69 |
| 14 | 3 July 2014 | 166.86 | 55.19 | 43.0 | 6.0 | 7.67 |
| 15 | 3 July 2014 | 167.06 | 55.18 | 40.0 | 6.0 | 7.34 |
| 16 | 20 March 2016 | 163.14 | 54.14 | 42.0 | 6.7 | 17.78 |
| 17 | 14 April 2016 | 161.11 | 53.66 | 48.0 | 6.2 | 10.30 |
| 18 | 29 September 2017 | 160.33 | 53.10 | 51.0 | 6.0 | 71.77 |
| 19 | 25 January 2018 | 166.65 | 55.37 | 46.0 | 6.3 | 5.06 |
| 20 | 23 May 2018 | 162.44 | 55.08 | 56.0 | 6.4 | 7.42 |
| 21 | 10 October 2018 | 157.26 | 49.09 | 41.0 | 6.6 | 76.43 |
| 22 | 20 December 2018 | 164.71 | 54.91 | 54.0 | 7.3 | 5.49 |
| 23 | 20 December 2018 | 164.85 | 54.99 | 54.0 | 6.0 | 5.49 |
| 24 | 22 December 2018 | 164.71 | 55.12 | 55.0 | 6.0 | 5.49 |
| 25 | 24 December 2018 | 164.46 | 55.25 | 51.0 | 6.6 | 7.21 |
| 26 | 28 March 2019 | 160.07 | 50.51 | 49.0 | 6.3 | 46.34 |
| 27 | 25 June 2019 | 164.41 | 56.18 | 57.0 | 6.4 | 0.82 |
| 28 | 26 June 2019 | 164.36 | 56.16 | 53.0 | 6.5 | 0.82 |
| 29 | 9 August 2019 | 162.04 | 55.78 | 60.0 | 6.0 | 6.10 |
| 30 | 20 February 2020 | 160.92 | 53.44 | 52.0 | 6.4 | 12.60 |
| 31 | 4 April 2020 | 166.21 | 54.67 | 37.0 | 6.0 | 13.59 |
| 32 | 2024 August 17 | 160.37 | 52.81 | 46.0 | 7.1 | 6.37 |
| 33 | 21 August 2024 | 160.45 | 52.75 | 40.0 | 6.1 | 6.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gitis, V.; Derendyaev, A. Two-Stage Systematic Forecasting of Earthquakes. Geosciences 2025, 15, 170. https://doi.org/10.3390/geosciences15050170
Gitis V, Derendyaev A. Two-Stage Systematic Forecasting of Earthquakes. Geosciences. 2025; 15(5):170. https://doi.org/10.3390/geosciences15050170
Chicago/Turabian StyleGitis, Valery, and Alexander Derendyaev. 2025. "Two-Stage Systematic Forecasting of Earthquakes" Geosciences 15, no. 5: 170. https://doi.org/10.3390/geosciences15050170
APA StyleGitis, V., & Derendyaev, A. (2025). Two-Stage Systematic Forecasting of Earthquakes. Geosciences, 15(5), 170. https://doi.org/10.3390/geosciences15050170






