Abstract
Geomagnetic field data have been found to contain earthquake (EQ) precursory signals; however, analyzing this high-resolution, imbalanced data presents challenges when implementing machine learning (ML). This study explored feasibility of principal component analyses (PCA) for reducing the dimensionality of global geomagnetic field data to improve the accuracy of EQ predictive models. Multi-class ML models capable of predicting EQ intensity in terms of the Mercalli Intensity Scale were developed. Ensemble and Support Vector Machine (SVM) models, known for their robustness and capabilities in handling complex relationships, were trained, while a Synthetic Minority Oversampling Technique (SMOTE) was employed to address the imbalanced EQ data. Both models were trained on PCA-extracted features from the balanced dataset, resulting in reasonable model performance. The ensemble model outperformed the SVM model in various aspects, including accuracy (77.50% vs. 75.88%), specificity (96.79% vs. 96.55%), F1-score (77.05% vs. 76.16%), and Matthew Correlation Coefficient (73.88% vs. 73.11%). These findings suggest the potential of a PCA-based ML model for more reliable EQ prediction.
1. Introduction
The non-linear, chaotic, scale-invariant phenomena of earthquakes (EQs) have led some researchers to conclude that predicting EQs in the conventional sense is inherently impossible due to complex interactions involving plate tectonics, fault mechanics, and material properties within the Earth’s crust []. EQ precursor studies have shown that many short-term precursors are non-seismic, with the ionosphere, atmosphere, and lithosphere being perturbed prior to an EQ []. Various methods can be employed for EQ prediction, including the study of precursor phenomena such as fluctuations in electric and magnetic fields [], variations in the total electron content of the ionosphere [], observations of animal behavior [], and the use of multiple remote sensing data sources such as electron and ion density data [,]. Hattori et al. [] and Ouyang et al. [], in their studies, observed distinctive perturbations in the spectral density ratio between the horizontal and vertical components of Ultra-Low-Frequency (ULF) geomagnetic field measurements. ULF magnetic data can provide useful EQ precursory information with optimal prediction performance depending on the distance and event size [].
The dynamic nature of seismic events poses a challenge for traditional prediction methods based on historical and empirical observations. These methods often struggle to account for the complex factors that trigger EQs, leading to limitations in accuracy and reliability. However, machine learning (ML) algorithms like the Support Vector Machine (SVM), decision trees, and ensemble have demonstrated promising results in EQ forecasting [,,,]. ML classifiers have also shown potential for making accurate EQ magnitude predictions, which could significantly improve seismic risk assessment and preparedness efforts []. EQ prediction using geomagnetic data faces a significant challenge in large classification datasets. As data dimensions multiply, issues such as overfitting lead to increased computational costs and decreased model stability, which become major concerns. The dynamic nature and large coverage of the global geomagnetic field, including both spatial and temporal variations, translates into a large number of variables within the dataset []. Chen et al. [] emphasize the need for effective dimensionality reduction techniques to alleviate these challenges, recommending methods like principal component analysis (PCA) or feature selection strategies to extract relevant information while handling large dimensionality.
PCA is a widely utilized technique for dimensionality reduction in high-dimensional datasets, including the electromagnetic or geomagnetic data that are consecutively applied in EQ predictions [,]. Hattori et al. [] demonstrated the effectiveness of PCA in extracting the ULF signals associated with potential EQ precursors. Their study showcased PCA’s ability to unravel the essential patterns within geomagnetic data, particularly those linked to ULF phenomena indicative of EQs. Ensemble methods like bagging and boosting have emerged as powerful tools for EQ prediction []. A study by Mukherjee et al. [] demonstrated that ensemble models not only capture complex spatiotemporal patterns in seismic data but also exhibit a superior generalization performance compared to individual models. The ensemble approach leverages diverse learning strategies and mitigates the risk of overfitting, providing a robust framework for addressing the inherent uncertainties and dynamic nature of seismic processes.
This study applies a PCA with ensemble and SVM models to enhance EQ prediction using geomagnetic data categorized by the Mercalli Intensity Scale. Utilizing global geomagnetic data spanning from 1970 to 2021, sourced from SuperMAG (Laurel, MA, USA), alongside EQ records from the USGS and focusing on events with magnitudes M5.0 and above, this approach emphasizes dimensionality reduction via PCA to manage complex datasets for ML. Model efficacy is evaluated through accuracy, precision, recall, F1-score, and the Matthew Correlation Coefficient (MCC). By identifying key data components that correlate with seismic activity, the integration of a PCA with the ensemble and SVM algorithms aims to advance seismic risk mitigation by improving EQ prediction studies.
2. Data and Methods
This study utilized low-frequency 1 min global geomagnetic field data sourced from the SuperMAG database [], combined with EQ data from the USGS [], covering the period from 1970 to 2021. The dataset was filtered to include only EQs with a magnitude equal to or exceeding M5.0 and hypocentral locations situated within a radius of 200 km from their corresponding geomagnetic observatories, as can be observed in Figure 1 []. The study focused on earthquakes occurring within a seven-day window prior to significant seismic events, coinciding with the availability of station data []. The length of the observation period was chosen to maximize the number of constructed datasets as well as to balance between model optimization and computational cost. A total of 7525 EQs that met the criteria were selected. To refine the analysis, the Ap index was applied, using values below 27 to eliminate and exclude periods of geomagnetic quiescence, which represent geomagnetically quiet conditions. This ensures that the analysis is focused on more dynamic conditions []. Additionally, a Dst index cutoff of −30, which is commonly used to filter out instances of severe magnetic field disturbances, was applied []. The EQ magnitude scale was categorized according to the Mercalli Intensity Scale to allow for a more refined multi-class model, encompassing distinct seismic intensities ranging from Non (non-seismic days) to VI (M5.0 to M5.5), VII (M5.5 and M6.0), VIII (M6.0 to M6.5), IX (M6.5 to M7.0), X (M7.0 to M7.5), XI (M7.5 and M8.0), and XII (>M8.0). The scale, which is based on observed effects and damage, offers a complementary perspective that can potentially help mitigate these limitations, therefore providing a more comprehensive picture for prediction purposes. The Mercalli Intensity Scale allows for a more refined categorical classification (in this case, 8 classes) compared to the Richter Scale, which uses a more generalized single-integer scale and could potentially increase computational costs [].
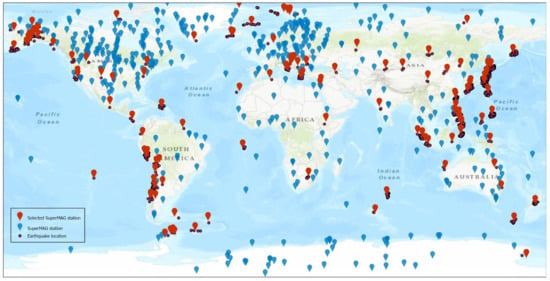
Figure 1.
SuperMAG geomagnetic observatory locations around the world (blue pins) and filtered geomagnetic observatory locations based on selected EQ events (red pins).
The resolution of SuperMAG data (1 min sampling period) into 7-day windows resulted in a complex dataset, even with only three features (X, Y, Z). These features exhibited intricate relationships and variations over time, crucial for understanding EQ precursors. Applying a PCA addressed the complexity of the task by extracting the most informative temporal patterns and reducing dimensionality, while preserving the key interactions among the features. This approach facilitated the simplification of the data for analysis, allowing the extraction of the most pertinent information for the EQ prediction models. These components revealed key insights, including projected data points that represent observations in the reduced space, the variance explained by each component, and the contributions of features as indicated by the coefficient. While the coefficient provided interpretability, the projected data points served as the primary input for subsequent ML models. By choosing a cumulative explained variance threshold that captured 87% of the data’s variance (number of components retained) based on a combination of grid and random search, the approach ensured that most of the relevant information was preserved while maintaining model flexibility. PCA proved to be a valuable tool in navigating the challenges of high-dimensional data, facilitating further analysis and model development.
To address the class imbalance caused by low-magnitude EQs, Synthetic Minority Oversampling Technique (SMOTE) was employed [] to potentially improve EQ prediction accuracy. Bao et al. [] successfully addressed the data imbalance issue in their EQ prediction model by employing SMOTE. This technique augmented the minority class within the dataset, enabling the model to learn their characteristics more effectively. This improvement did not compromise the model’s sensitivity to smaller EQs, for example, class VII to IX, ensuring their proper identification and prediction. By oversampling the minority, SMOTE created a more balanced dataset, allowing the model to learn equally from both positive and negative examples. This reduced bias towards the majority class. A new synthetic instance, , can be generated using the following formula:
where represents a minority class instance and represents its randomly selected neighbor, while 0 ≤ λ ≤ 1 controls the proportion of synthetic samples created.
Leveraging the dimensionality reduction achieved through PCA and the balanced dataset obtained via oversampling, a 10-fold k-fold cross-validation was implemented. This approach iteratively trained and tested the models on various data subsets, providing a more reliable estimate of their generalizability compared to a simple train–test split and mitigating potential biases specific to individual data distributions. Subsequently, two models—an SVM and an ensemble model—were developed on the full dataset. Each model underwent hyperparameter tuning through a grid search method, optimizing their key settings to maximize their predictive power. The details of this hyperparameter selection process are further discussed in Section 3.2. This comprehensive approach ensured the models were not only accurate on the specific training data but also generalizable to unseen examples, providing a more reliable estimate of their generalizability.
Model evaluation was conducted using the following multi-class classification metrics:
where TP = True Positive, TN = True Negative, FP = False Positive, and FN = False Negative.
Given the multi-class nature of the EQ prediction model, the evaluation employed metrics that provided a comprehensive understanding of its performance across all EQ intensity levels. Metrics like precision, recall, and F1-score were utilized to assess the model’s ability to correctly identify different EQ intensities, balancing the trade-off between true positives and false positives/negatives. Additionally, the MCC offered a balanced perspective on overall model performance by considering all true and false classifications. The detailed workflow is shown in Figure 2.
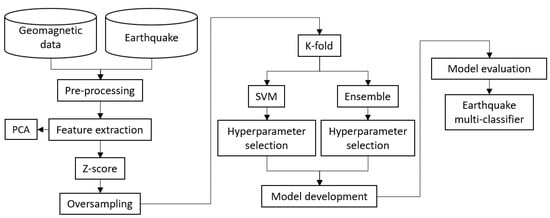
Figure 2.
Illustration of the detailed workflow of a PCA-based approach for feature extraction and dimensionality reduction, leading to the construction of a multi-class model for EQ prediction.
3. Results and Discussion
3.1. PCA Scores for Model Development
In the PCA results, each principal component was plotted with all three of its original geomagnetic components. This approach was adopted to visually ascertain the relationships and correlations of each PCA result with the geomagnetic components to determine which components are most suitable for feature extraction. The position of each point on the first principal component (PC1) in Figure 3a indicates its similarity to its geomagnetic X component. Negative values aligned strongly with PC1, with a minimum of −2017.8 nT, and positive values also showed strong alignment, reaching a maximum of 1334.9 nT. The spread of points around zero values, highlighted by the yellow dashed box, reflects the correlation between PC1 and the X component. A tight cluster, as shown in the red dashed box, suggests a linear relationship, while a wider spread indicates a weaker or non-linear connection. The interpretation of PC1 relied on its correlation with other variables. In this case, its strong correlation with the X component signified northward variations in the Earth’s magnetic field. The statistical values presented in Table 1 justified the resemblance between PC1 and the X component, indicating a minimal trade-off between the X component and PC1 when compared to the Y and Z components. The PC1 had a variance of 598.34 nT, slightly lower than the X component, with its variance of 624.26 nT. Similarly, the standard deviation for PC1 was 24.46 nT, closely matching that of the X component, which was 24.98 nT.
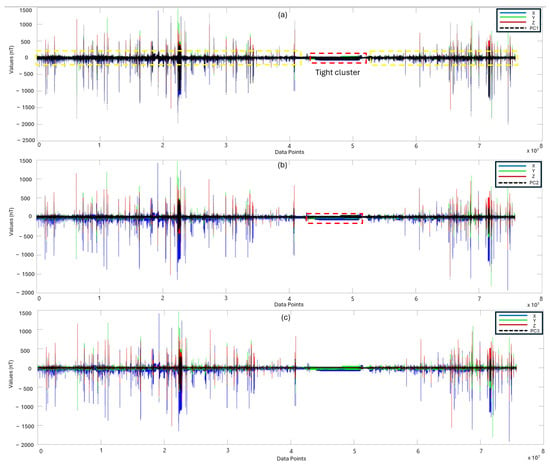
Figure 3.
Comparative plots of principal component and geomagnetic field components (X (blue), Y (green), Z (red)) over data points. The y axis represents geomagnetic field values, and the x axis enumerates data points. Subfigures: (a) PC1 against X, Y, and Z; (b) PC2 against X, Y, and Z; (c) PC3 against X, Y, and Z, with the PCs depicted by black lines. The unit values are nanoTesla (nT).

Table 1.
Statistical value of geomagnetic components (X, Y, and Z) and principal components (PC1, PC2, and PC3).
Similarly, points on the second principal component (PC2) axis in Figure 3b illustrate their alignment within the Y axis. PC2 had a broader spread compared to PC1, capturing a wider range of geomagnetic variability. The clustering of points slightly above zero for PC2 indicated a correlation with the Y component. The statistical values for PC2 revealed a similarity with the Y component. Specifically, PC2 exhibited a similar variance of 138.28 nT compared to the variance of the Y component, which was 132.58 nT. Furthermore, the standard deviation of PC2 was 11.75 nT, compared to the standard deviation of the Y component, which was 11.51 nT.
The third principal component (PC3), as shown in Figure 3c, had a spread comparable to PC2, suggesting that it captured a similar level of variability. However, its correlations with geomagnetic components were even weaker than for PC2, indicating that PC3 most likely captured subtle or complex variations influenced by multiple factors or smaller-scale fluctuations. The statistical results showed no correlation with any component. Understanding PC3 might require additional context such as location, time, or specific geomagnetic events. Therefore, PC3 was not included in the model training.
3.2. Hyperparameter Tuning and Algorithm Selection
This study evaluated Random Undersampling Boosting (RUSBoost), AdaBoostM2, bagging, and SVM algorithms for multi-class EQ prediction. Despite being compared to a baseline model, boosting methods like RUSBoost and AdaBoostM2 demonstrated poor predictive accuracy. In contrast, bagging achieved a good performance across all EQ classes. This finding underscores the importance of careful algorithm selection for multi-class problems, as distinct methodologies exhibit varying sensitivities to class imbalance and data complexity.
The optimization of SVM hyperparameters in Table 2 shows that the Gaussian kernel function was selected for its effectiveness in handling non-linear data relationships. The box constraint, set at 50, and the kernel scale, chosen as 0.5, were pivotal in balancing the trade-off between model complexity and overfitting, ensuring its robust predictive capability. The Nu parameter, fixed at 0.01, regulated the model’s margin of error in classification, fine-tuning its sensitivity to seismic activity indicators. Subsequent hyperparameter tuning further optimized the bagging model, as shown in Table 2. Two hundred base learners were identified as offering a balance between model complexity and computational efficiency. A split size of 13,000 facilitated effective data partitioning, enhancing the model’s ability to capture underlying patterns. Additionally, a minimum leaf size of 0.01 prevented overfitting while maintaining optimized model performance. The predictor selection strategy focusing on curvature had a minimal impact on performance.

Table 2.
Optimized hyperparameter selection for the SVM and ensemble models.
The accuracy of the models in Table 3, which represents the overall correctness of the predictions, showed that the ensemble model’s algorithm outperformed the SVM with 77.50% accuracy compared to 75.88%. Sensitivity, which measures the ability to correctly identify positive instances, also favored the ensemble model at 77.50%, surpassing the SVM’s performance of 75.88%. Both models exhibited high specificity, with the SVM at 96.55% and the ensemble model at 96.79%, indicating that both models correctly identified negative cases and rarely predicted an EQ when none actually occurred. High specificity might indicate inherent biases in the models due to their architecture, the potential oversampling of negative data instances, and the imbalanced nature of the EQ data itself, as negative cases greatly outnumbered positive classes. Precision, which reflects the accuracy of positive predictions, was slightly higher for the SVM, at 77.56%, compared to the ensemble model, at 76.69%. However, the F1-score, which considers both precision and sensitivity, favored the ensemble model at 77.06% against the SVM at 76.16%. The MCC values for both models were almost identical at 73.88% for the ensemble and 73.11% for the SVM, suggesting a balanced performance in capturing true and false positives and negatives. Overall, the ensemble model demonstrated superior predictive capabilities for EQ prediction in this multi-class model, showcasing its effectiveness across multiple performance metrics.

Table 3.
Performance measurements demonstrate that the ensemble model outperforms the SVM model.
3.3. Handling Imbalanced Data Using SMOTE
The implementation of SMOTE successfully mitigated the imbalance challenge by oversampling the underrepresented high-magnitude events. SMOTE’s effectiveness is reflected in the showcased model’s performance, as shown in the confusion matrix presented in Figure 4. The model achieved high precision and recall values for low-magnitude EQs, indicating its accurate identification of both positive and negative cases. Furthermore, for high-magnitude EQs exceeding scale VII, the model demonstrated near-perfect accuracy. By oversampling the scarce high-magnitude data, the model received more training examples to learn patterns specific to these critical events. However, it is important to acknowledge the potential limitations of SMOTE. While oversampling increases the representation of the minority class, it is crucial to ensure the introduced synthetic data points maintain proximity to their original distribution. Otherwise, overfitting or biased predictions could occur. In this case, the quality of the synthetic data generated was carefully monitored and its impact on model performance was evaluated through cross-validation techniques. Despite oversampling, the overall EQ data might still be limited, particularly for rare events like class XI and XII EQs. This limitation could restrict the generalizability of the study’s findings and potentially lead to the models’ overfitting to the specific dataset used. While the employed models offered good overall performance, their “black-box” nature presents another challenge. The lack of interpretability makes it difficult to fully understand their decision-making process, potentially hindering the evaluation of their prediction validity and identification of potential biases or inaccuracies.
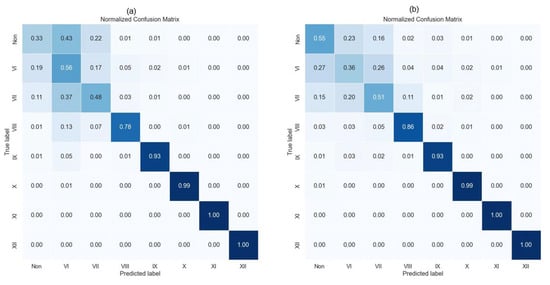
Figure 4.
SVM (a) and ensemble (b) tend to produce confusion matrices that are susceptible to non- and low-magnitude EQs.
3.4. Ensemble Model Performance Based on PCA
This study explored EQ prediction using various ML models and addressed challenges like imbalanced data through oversampling. Both the ensemble and SVM models benefited from using a reduced feature set derived from PCA. This mitigates the risk of overfitting on the limited EQ data, especially for rare events like “XII” EQs, where overfitting can lead to unreliable predictions. By focusing on the most significant features extracted through PCA, both models can generalize better and potentially improve their performance on unseen data. This improvement can be attributed to two key factors. First, the improved separability of EQ classes: reduced dimensionality helps emphasize the essential features that distinguish different EQ categories, leading to more accurate classifications. Second, enhanced computational efficiency: working with fewer features reduces training time and complexity, which is particularly beneficial for complex models like SVMs. The ensemble model’s advantage lies in its inherent diversity. Combining multiple decision tree models captures different perspectives on the data, which is particularly valuable in complex, non-linear domains like EQ prediction, where SVMs, with their single hyperplane approach, might struggle. This aligns with previous findings by Cui et al. [], where stacking ensembles outperformed individual models, including SVMs, in EQ magnitude prediction. Furthermore, ensembles exhibit greater resilience to data imbalances compared to individual models like SVMs. This advantage stems from their ability to collectively learn from scarce data points across multiple models, potentially addressing the imbalanced classes suggested by the oversampling used in these models.
4. Conclusions
As a conclusion, this study investigated the feasibility of ML models for EQ prediction based on the Mercalli Intensity Scale, while simultaneously addressing the challenge of imbalanced data. PCA proved valuable in reducing the dimensionality of geomagnetic data and as feature extraction, potentially mitigating overfitting and improving model performance. Among the evaluated models, the ensemble approach achieved the highest performance across multiple metrics (accuracy: 77.50%, sensitivity: 77.50, precision: 76.69%, F1-score: 77.05%, and MCC: 73.88%). This suggests a significant potential for accurate EQ prediction, reflecting the method’s effectiveness despite the fundamental challenges of this field. These results suggest the promising potential for integrating such techniques into existing earthquake monitoring systems to enhance their prediction capabilities and disaster risk reduction. Overall, this study has demonstrated the feasibility of utilizing ML techniques for EQ prediction based on the Mercalli Intensity Scale. This study is part of the ongoing challenges we face in understanding earthquakes, and in specifically aiming to minimize false alarms. Further research exploring new dimensionality reduction methods and interpretable models could pave the way for even more accurate and reliable predictions, ultimately contributing to enhanced EQ preparedness and risk mitigation.
Author Contributions
K.Q. and K.A.Y., methodology; K.Q. and K.A.Y., formal analysis; K.Q. and K.A.Y., resources; K.Q. and K.A.Y., software; K.Q., writing—original draft; M.A., K.A.Y. and M.H. supervision; M.A., K.A.Y. and M.H., writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Malaysia Ministry of Higher Education (MOHE); the support of this work is under the FRGS/1/2020/TK0/UKM/01/1.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from SuperMAG database and USGS, accessible at https://supermag.jhuapl.edu/ and www.earthquake.usgs.gov respectively.
Acknowledgments
This study is supported by the Fundamental Research Grant Scheme, Ministry of Higher Education, Malaysia (FRGS/1/2020/TK0/UKM/01/1) and the research was made possible through the generous contribution of geomagnetic field data by SuperMAG and its collaborators. Sincere gratitude is also extended to the United States Geological Survey (USGS) for providing critical earthquake data. We utilized AI tools for English language corrections (Quillbot and Grammarly) and code debugging (ChatGPT). No text entirely generated by AI is included in the manuscript; all content, analyses, and methodologies are original and were authored by us.
Conflicts of Interest
Masashi Hayakawa was employed by the company Hayakawa Institute of Seismo Electromagnetics Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Wang, Z. Predicting or Forecasting Earthquakes and the Resulting Ground-Motion Hazards: A Dilemma for Earth Scientists. Seismol. Res. Lett. 2015, 86, 1–5. [Google Scholar] [CrossRef]
- Ghamry, E.; Mohamed, E.K.; Abdalzaher, M.S.; Elwekeil, M.; Marchetti, D.; de Santis, A.; Hegy, M.; Yoshikawa, A.; Fathy, A. Integrating Pre-Earthquake Signatures from Different Precursor Tools. IEEE Access 2021, 9, 33268–33283. [Google Scholar] [CrossRef]
- Han, R.; Cai, M.; Chen, T.; Yang, T.; Xu, L.; Xia, Q.; Jia, X.; Han, J. Preliminary Study on the Generating Mechanism of the Atmospheric Vertical Electric Field before Earthquakes. Appl. Sci. 2022, 12, 6896. [Google Scholar] [CrossRef]
- Yue, Y.; Koivula, H.; Bilker-Koivula, M.; Chen, Y.; Chen, F.; Chen, G. TEC Anomalies Detection for Qinghai and Yunnan Earthquakes on 21 May 2021. Remote Sens. 2022, 14, 4152. [Google Scholar] [CrossRef]
- Zöller, G.; Hainzl, S.; Tilmann, F.; Woith, H.; Dahm, T. Comment on “Potential short-term earthquake forecasting by farm animal monitoring” by Wikelski, Mueller, Scocco, Catorci, Desinov, Belyaev, Keim, Pohlmeier, Fechteler, and Mai. Ethology 2021, 127, 302–306. [Google Scholar] [CrossRef]
- Moro, M.; Saroli, M.; Stramondo, S.; Bignami, C.; Albano, M.; Falcucci, E.; Gori, S.; Doglioni, C.; Polcari, M.; Tallini, M.; et al. New insights into earthquake precursors from InSAR. Sci. Rep. 2017, 7, 12035. [Google Scholar] [CrossRef] [PubMed]
- Asaly, S.; Gottlieb, L.-A.; Inbar, N.; Reuveni, Y. Using Support Vector Machine (SVM) with GPS Ionospheric TEC Estimations to Potentially Predict Earthquake Events. Remote Sens. 2022, 14, 2822. [Google Scholar] [CrossRef]
- Hattori, K.; Han, P. Statistical Analysis and Assessment of Ultralow Frequency Magnetic Signals in Japan As Potential Earthquake Precursors: 13. In Pre-Earthquake Processes; American Geophysical Union (AGU): Washington, DC, USA, 2018; pp. 229–240. ISBN 9781119156949. [Google Scholar]
- Ouyang, X.-Y.; Parrot, M.; Bortnik, J. ULF Wave Activity Observed in the Nighttime Ionosphere above and Some Hours before Strong Earthquakes. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028396. [Google Scholar] [CrossRef]
- Han, P.; Zhuang, J.; Hattori, K.; Chen, C.-H.; Febriani, F.; Chen, H.; Yoshino, C.; Yoshida, S. Assessing the Potential Earthquake Precursory Information in ULF Magnetic Data Recorded in Kanto, Japan during 2000–2010: Distance and Magnitude Dependences. Entropy 2020, 22, 859. [Google Scholar] [CrossRef]
- Asim, K.M.; Martínez-Álvarez, F.; Basit, A.; Iqbal, T. Earthquake magnitude prediction in Hindukush region using machine learning techniques. Nat. Hazards 2017, 85, 471–486. [Google Scholar] [CrossRef]
- Asim, K.M.; Idris, A.; Iqbal, T.; Martínez-Álvarez, F. Earthquake prediction model using support vector regressor and hybrid neural networks. PLoS ONE 2018, 13, e0199004. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Zou, B.; Guo, J.; Zhu, G.; Li, W.; Li, W. One sliding PCA method to detect ionospheric anomalies before strong Earthquakes: Cases study of Qinghai, Honshu, Hotan and Nepal earthquakes. Adv. Space Res. 2017, 59, 2058–2070. [Google Scholar] [CrossRef]
- Gitis, V.G.; Derendyaev, A.B. Machine Learning Methods for Seismic Hazards Forecast. Geosciences 2019, 9, 308. [Google Scholar] [CrossRef]
- Debnath, P.; Chittora, P.; Chakrabarti, T.; Chakrabarti, P.; Leonowicz, Z.; Jasinski, M.; Gono, R.; Jasińska, E. Analysis of Earthquake Forecasting in India Using Supervised Machine Learning Classifiers. Sustainability 2021, 13, 971. [Google Scholar] [CrossRef]
- Arafa-Hamed, T.; Khalil, A.; Nawawi, M.; Marzouk, H.; Arifin, M. Geomagnetic Phenomena Observed by a Temporal Station at Ulu-Slim, Malaysia during The Storm of March 27, 2017. Sains Malays. 2019, 48, 2427–2435. [Google Scholar] [CrossRef]
- Chen, B.H. Minimum standards for evaluating machine-learned models of high-dimensional data. Front. Aging 2022, 3, 901841. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yong, S.; He, C.; Wang, X.; Bao, Z.; Xie, J.; Zhang, X. An Earthquake Forecast Model Based on Multi-Station PCA Algorithm. Appl. Sci. 2022, 12, 3311. [Google Scholar] [CrossRef]
- Li, J.; Li, Q.; Yang, D.; Wang, X.; Hong, D.; He, K. Principal Component Analysis of Geomagnetic Data for the Panzhihua Earthquake (Ms 6.1) in August 2008. Data Sci. J. 2011, 10, IAGA130–IAGA138. [Google Scholar] [CrossRef]
- Hattori, K.; Serita, A.; Gotoh, K.; Yoshino, C.; Harada, M.; Isezaki, N.; Hayakawa, M. ULF geomagnetic anomaly associated with 2000 Izu Islands earthquake swarm, Japan. Phys. Chem. Earth Parts A/B/C 2004, 29, 425–435. [Google Scholar] [CrossRef]
- Fernández-Gómez, M.; Asencio-Cortés, G.; Troncoso, A.; Martínez-Álvarez, F. Large Earthquake Magnitude Prediction in Chile with Imbalanced Classifiers and Ensemble Learning. Appl. Sci. 2017, 7, 625. [Google Scholar] [CrossRef]
- Mukherjee, S.; Gupta, P.; Sagar, P.; Varshney, N.; Chhetri, M. A Novel Ensemble Earthquake Prediction Method (EEPM) by Combining Parameters and Precursors. J. Sens. 2022, 5321530. [Google Scholar] [CrossRef]
- SuperMAG Database. Available online: https://supermag.jhuapl.edu/ (accessed on 9 October 2023).
- United States Geological Survey (USGS) Database. Available online: www.earthquake.usgs.gov (accessed on 9 October 2023).
- Yusof, K.A.; Abdullah, M.; Hamid, N.S.A.; Ahadi, S.; Ghamry, E. Statistical Global Investigation of Pre-Earthquake Anomalous Geomagnetic Diurnal Variation Using Superposed Epoch Analysis. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Yusof, K.A.; Mashohor, S.; Abdullah, M.; Rahman, M.A.A.; Hamid, N.S.A.; Qaedi, K.; Matori, K.A.; Hayakawa, M. Earthquake Prediction Model Based on Geomagnetic Field Data Using Automated Machine Learning. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Ismail, N.H.; Ahmad, N.; Mohamed, N.A.; Tahar, M.R. Analysis of Geomagnetic Ap Index on Worldwide Earthquake Occurrence using the Principal Component Analysis and Hierarchical Cluster Analysis. Sains Malays. 2021, 50, 1157–1164. [Google Scholar] [CrossRef]
- Xu, G.; Han, P.; Huang, Q.; Hattori, K.; Febriani, F.; Yamaguchi, H. Anomalous behaviors of geomagnetic diurnal variations prior to the 2011 off the Pacific coast of Tohoku earthquake (Mw9.0). J. Asian Earth Sci. 2013, 77, 59–65. [Google Scholar] [CrossRef]
- Alvarez, D.A.; Hurtado, J.E.; Bedoya-Ruíz, D.A. Prediction of modified Mercalli intensity from PGA, PGV, moment magnitude, and epicentral distance using several nonlinear statistical algorithms. J. Seismol. 2012, 16, 489–511. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F. A Comprehensive Analysis of Synthetic Minority Oversampling Technique (SMOTE) for handling class imbalance. Inf. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Bao, Z.; Zhao, J.; Huang, P.; Yong, S.; Wang, X. A Deep Learning-Based Electromagnetic Signal for Earthquake Magnitude Prediction. Sensors 2021, 21, 4434. [Google Scholar] [CrossRef]
- Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2021, 101, 107038. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).