Abstract
A joint analysis of solar wind, geomagnetic field, and earthquake catalog data showed that before the catastrophic M = 7.8 and M = 7.5 Kahramanmaras earthquake sequence on 6 February 2023, a closed strong magnetic storm occurred on 7 November 2022, SYM/H = −117 nT. The storm started at 08:04 UT. At this time, the high-latitudinal part of Turkey’s longitudinal region of future epicenters was located under the polar cusp, where the solar wind plasma would directly access the Earth’s environment. The time delay between storm onset and earthquake occurrence was ~91 days. We analyzed all seven strong (M7+) earthquakes from 1967 to 2020 to verify the initial findings. A similar pattern has been revealed for all events. The time delay between magnetic storm onset and earthquake occurrence varies from days to months. To continue these investigations, a retrospective analysis of seismic and other geophysical parameters just after preceded geomagnetic storms in the epicenter areas is desirable.
1. Introduction
It has been found in some papers, for example [1,2,3,4,5] and references therein, that earthquake occurrence may be preceded by a geomagnetic storm, which is one of Earth’s most striking manifestations of solar wind activity. A lag time between a magnetic storm onset and an earthquake occurrence varies; it could be about 2–6 days [1], 12–14 days [2], 26–27 days [3], several months [4], and for very large earthquakes (M7.5+), it may reach up to multiple years [5]. Nevertheless, the idea of a relationship between earthquake occurrence and a magnetic storm has been considered controversial up to now. In this direction, the most famous and cited work is [6], where at a high statistical level, a hypothesis was analyzed to see if the solarterrestrial interaction, as measured by sunspots, solar wind velocity, and geomagnetic activity, might play a role in triggering earthquakes. The authors of [6] counted the number of earthquakes occurring globally with magnitudes exceeding chosen thresholds in calendar years, months, and days. Then, they ordered these counts by the corresponding rank of the solarterrestrial variables’ annual, monthly, and daily averages. A statistical significance of the difference between the earthquake number distributions below and above the median of the solar–terrestrial averages was estimated by χ2 and Student’s t-tests. They found no consistent and statistically significant distributional differences. When they introduced time lags (±5 days) between the solar–terrestrial variables and the number of earthquakes, again, no statistically significant distributional difference was found. Since they could not reject the null hypothesis of no solar–terrestrial triggering of earthquakes, they concluded that there was insignificant solar–terrestrial triggering of earthquakes. However, the results of [6] can be interpreted so that the Earth’s crust does not respond to solar events immediately or over the next five days. In [7], a similar result was obtained for a limited territory (Anatolian Peninsula). This work investigated the ratio of earthquakes that occurred during geomagnetically disturbed days (Dst ≤ −30 nT) to those that occurred on geomagnetically quiet days using data on 122,838 events with magnitudes from 3.0 to 7.9 that occurred from 1965 to 2005 in the Anatolian Peninsula. It was concluded: “As a result of all these data, a hypothesis cannot be put forward which suggests that geomagnetic storms trigger earthquakes in the Anatolian peninsula”. In the same work [7], the author concluded, “However, these results should not hinder the conduct of further research. A global study on this subject can potentially provide new approaches”. Indeed, a new, to some extent, approach (discussed below) gives us a hint that the solar–terrestrial interaction has an impact on earthquake occurrence, but its nature may not be a trigger. The basis for this approach is our previous results [4], which showed that sometimes earthquakes can look like targeted earthquakes. Namely, they may occur near the footprint in the Earth’s crust of those geomagnetic lines, which were populated by high-energy electrons pouring out from the outer radiation belt downwards at the time of geomagnetic storms, in other words, when conductivity in surrounding media is increased. Increasing conductivity in the ionosphere, for example, is a key parameter in the mathematical model [8], which considers the hypothesis of the electromagnetic generation of earthquakes due to the influence of solar flare energy on the ionosphere–atmosphere–lithosphere system and the intensification of telluric currents in the lithosphere, including around tectonic faults. The essence of the model [8] is that the absorption of solar flare radiation in the ionosphere creates additional ionization in it, which is accompanied by the appearance of an additional electric current and an additional electric field, which will ultimately lead to an increase in the telluric current in the Earth’s crust. It has been well known for many decades that at the dayside of the high latitudes, there is a funnel-shaped area (polar cusp) where the solar wind plasma has direct access to the atmosphere. As summarized in [9], the polar cusp is a vital connection point for the solar wind–magnetosphere–ionosphere interaction, where the plasma density irregularities have a wide range of spatial scales. The reconnection of the solar wind magnetic field with the geomagnetic field at the dayside magnetopause impacts the polar cusp through flux transfer events that enhance ionospheric flow, input to the appearance of the field-aligned currents, and auroral particle precipitation. Often, polar-orbiting spacecraft observe Alfven waves with scale sizes perpendicular to the geomagnetic field of the order of an electron skin depth [10]. In the cusp, the density of the neutral atmosphere is always increased, on average, by one and a half times, relative to the density in neighboring areas [11,12]. From a magnetic field point of view, the polar cusp is a funnel-shaped region where the high-latitude dayside (compressed) and nightside (elongated) magnetic field lines converge toward the geomagnetic poles [13]. Cusps have small sizes and small ionospheric footprints; nevertheless, they are essential in transferring solar wind energy, momentum, and plasma to the atmosphere. The investigation of the penetration through the polar cusps of the shocked solar wind is one of the primary science objectives of the Cluster mission, which is composed of four identical spacecraft flying around the Earth [14]. The Cluster data revealed [15] that most of the time, the cusp is located at magnetic latitudes ~75–80° and in a longitudinal region of 10–14 h magnetic ocal time (MLT). However, sometimes its longitudinal extension may be more comprehensive, depending, for example, on the length of the reconnection X-line at the magnetopause [16]. So, data from the Polar satellite demonstrate [17] that the polar cusp may be between 8 and 16 h MLT. Considering the above, it can be assumed that strong earthquakes can occur “targeted” in the longitudinal region, in which its high-latitude area was located under the polar cusp at the time of the arrival of the shocked solar wind (at the time of geomagnetic storm onset). Below, we test this assumption.
2. Materials and Methods
This study investigates earthquakes from the United States Geological Survey (USGS) global seismological catalog (https://earthquake.usgs.gov/earthquakes/search/ accessed on 20 February 2023), which presents the moment magnitude (Mw, hereafter referred to as M for simplicity). The data on the solar wind parameters are taken from the OMNI database (http://cdaweb.gsfc.nasa.gov, accessed on 20 February 2023), which was obtained from current and past space missions and projects. From the World Data Center for Geomagnetism, Kyoto (https://wdc.kugi.kyoto-u.ac.jp/ accessed on 20 February 2023), the onset and intensity of the geomagnetic storms were revealed using the 1 h Dst (Disturbance Storm Time Index) before 1981 and the 1 min “SYM-H” index after 1981, since the latter is absent before 1981. The “SYM-H” index, measured at the Earth’s surface, is, in fact, the high-resolution Dst index [18], allowing one to determine the onset and intensity of a magnetic storm more precisely. According to [19], depending on the Dst value, geomagnetic storms are classified into weak (Dst from −30 to −50 nT), moderate (Dst from −50 to −100 nT), strong (Dst from −100 to −200 nT), powerful (Dst from −200 to −350 nT), and extreme (Dst below −350 nT). Also, we used data on the storm sudden commencement—SSC, which were obtained by the Observatorio del Ebro, Roquetes, Spain, from the web page (ftp://ftp.ngdc.noaa.gov/STP/SOLARDATA/suddencommencements/storm2.SSC, accessed on 20 February 2023). We suggest that the occurrence of a strong earthquake may follow a particular geomagnetic storm in only a specific longitudinal region (depending on the time of geomagnetic storm onset). At this step, the method of investigation was manual (visual). Since we know the date of the earthquake and the coordinates of its epicenter, we visually determine those preceded by geomagnetic storms, during the beginning of which (in time of SSC) the longitude of the earthquake epicenter was located under the polar cusp; that is, the magnetic local time at the point of the future epicenter was within 8–16 h. The MLT is often used to describe the position in near-Earth space because the longitude, which rotates with the Earth, is not a helpful parameter for this (https://ecss.nl/item/?glossary_id=1619, accessed on 20 February 2023). The MLT has a value of 0 (midnight) in the anti-sunward direction, noon in the sunward direction, and 6 (dawn) and 18 (dusk) perpendicular to the sunward/anti-sunward line. This system is essential for understanding phenomena in geospace, such as the aurora, plasma motion, ionospheric currents, and associated magnetic field disturbances, which are highly organized by Earth’s main magnetic field. The MLT values were estimated using the online program (https://omniweb.gsfc.nasa.gov/vitmo/cgm.html, accessed on 20 February 2023). In Table 1, the data on the nine analyzed earthquakes are presented, and in Figure 1, the location of their epicenters is shown.

Table 1.
Data on strong M ≥ 7.0 earthquakes inside and around the Anatolian Plate, preceding geomagnetic storms, magnetic local time at the area of an epicenter at the time of geomagnetic storm onset, and lag time between storm onset and earthquake occurrence. Shades of gray indicate two Prime events. in this manuscript. Everything starts with these two events.
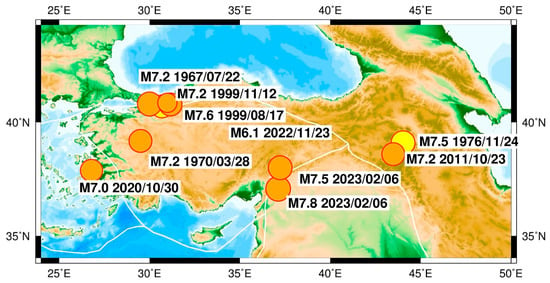
Figure 1.
A map of strong earthquakes M ≥ 7.0 that occurred inside and around the Anatolian Plate in 1967–2023. The orange indicates a depth of <30 km, and the yellow indicates earthquakes with a depth of >30 km. An added epicenter of M = 6.1 occurred on 23 November 2022 and is discussed in the text.
2.1. Case Study for M = 7.8 and M = 7.5 of 6 February 2023
Two catastrophic earthquakes in Turkey on 6 February 2023, M = 7.8 at 01:17:34 UTC with epicenter 37.226° N, 37.014° E, 10.0 km depth, and M = 7.5 at 10:24:48 UTC with epicenter 38.011° N, 37.196° E, 7.4 km depth, were preceded by a strong geomagnetic storm on 7 November 2022, with the most significant negative “SYM/H” = −117 nT (Figure 2). This storm started at 08:04 UT with positive peak “SYM/H” = +10 nT. At this time, in the area of the future M = 7.8 earthquake epicenter (37.226° N, 37.014° E), the magnetic local time was equal to MLT = ~10.96 h, and in the area of the future M = 7.5 earthquake epicenter (38.011° N, 37.196° E), it was equal to MLT = ~10.97 h. Thus, the storm on 7 November 2022, met a given criterion: at the time of its onset, the high-latitude part of the longitudinal region where, in the future, the Kahramanmaras earthquake sequence occurred was located under the polar cusp.
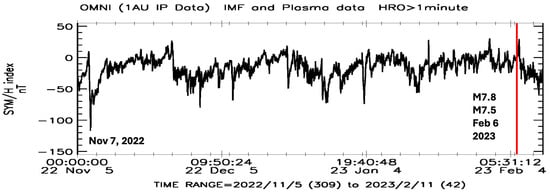
Figure 2.
The 1 min data on the geomagnetic “SYM/H” index from 1 November 2022 to 10 February 2023; on the right, a Red line marks the date of the M = 7.8 and M = 7.5 Kahramanmaras earthquake sequence on 6 February 2023; on the left, a preceding geomagnetic storm on 7 November 2022, is indicated.
To consider in more detail the solar wind (space weather) parameters that provoked this geomagnetic storm and then earthquakes (as we suppose), let us consider Figure 3, which presents not only the “SYM/H” index but also the solar wind proton density, solar wind dynamic pressure at the magnetopause, and the vertical component of the solar wind magnetic field (interplanetary magnetic field) in the GSM coordinate system (Bz_GSM), which is a critical parameter for development of a magnetic storm. In this plot, we show data from the OMNI database for only a short time interval (6–9 November 2022) for better visualization. It can be seen from Figure 3 that on 7 November 2022, at 06:25 UT, the “SYM/H” index changed its value from negative to positive and reached its positive peak at 08:04 UT. The solar wind flux density (n) and, accordingly, the dynamic pressure of the solar wind on the dayside magnetopause (P) also started to increase and reached their peaks on 7 November 2022, at 10:23 UT (n = 27.88 cm−3, P = 8.81 nPa). A change in the orientation of the vertical component of the interplanetary magnetic field Bz_GSM from positive to negative (at which an effective reconnection of the solar wind magnetic lines with geomagnetic lines occurs) began at 09:31 UT. At 10:37 UT, the “SYM/H” index changed its value from positive to negative (the main phase of the geomagnetic storm started). Thus, the initial phase of the magnetic storm on 7 November 2022 lasted from ~08:04 UT to ~10:37 UT. At 10:37 UT, the magnetic local time in the areas of the future Kahramanmaras earthquake sequence was equal to 13.51 h and 13.52 h, respectively. This means that during the initial storm phase, the high-latitudinal area of the Kahramanmaras longitudinal region was located under the polar cusp. The time delay between geomagnetic storm onset and earthquake occurrence equals ~91 days (Table 1).
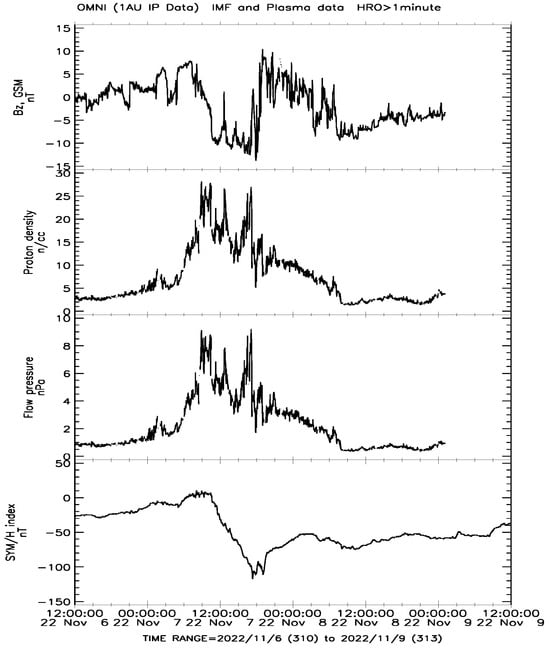
Figure 3.
rom bottom to top: The 1 min data on the geomagnetic “SYM/H” index, the pressure of the solar wind at the magnetopause, solar wind protons density, and the vertical component of the interplanetary magnetic field in the GSM coordinate system (Bz_GSM) in the Earth’s orbit for 6–9 November 2022, from the OMNI database.
2.2. Case Study of M = 7.0 of 30 October 2020
On 30 October 2020, a strong M = 7.0 earthquake occurred in the Aegean Sea at 11:51:27 UTC with coordinates of the epicenter 37.897° N, 26.784° E, at a depth of 21.0 km. This earthquake was preceded by two sequential small magnetic storms (Figure 4), which satisfied the chosen criteria: at the time of geomagnetic storm onset, the high-latitudinal area of the longitudinal region of the earthquake epicenter was located under the polar cusp.
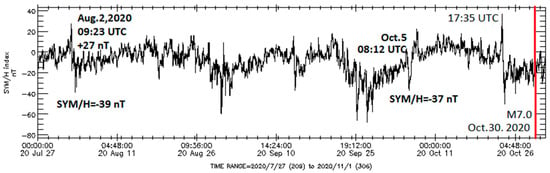
Figure 4.
The 1 min data on the geomagnetic “SYM/H” index for 27 July–30 October 2020; on the right, a red line marks the date of the M = 7.0 earthquake on 30 October 2020 (37.897° N, 26.784° E); on the left, parameters of two small geomagnetic storms, which satisfied the given criteria, are indicated.
The first such minor geomagnetic storm started on 2 August 2020, at 09:23 UT with a positive “SYM/H” = +27 nT and reached its most significant negative “SYM/H” = −39 nT on 3 August at 03:31 UT (Figure 5). In the initial phases of this storm, the magnetic local time around the future epicenter (37.897° N, 26.784° E) was equal to MLT = ~11.66 h. Thus, at the time of this storm’s onset, the high-latitude part of the longitudinal region, where the M = 7.0 earthquake later occurred, was located under the polar cusp. The delay between this magnetic storm onset and earthquake occurrence equals ~89 days (Table 1).
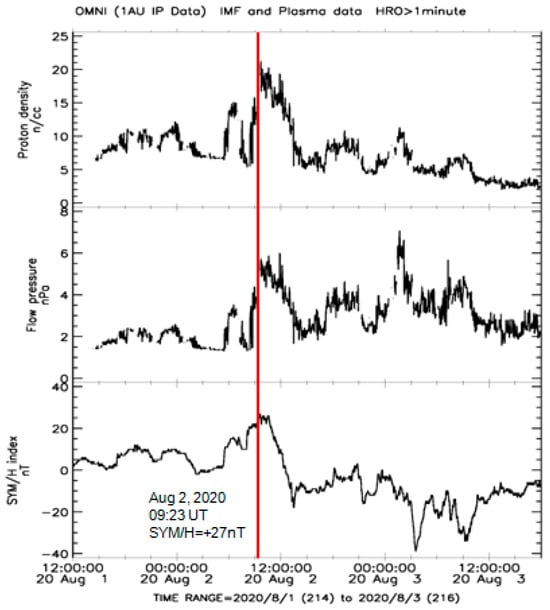
Figure 5.
From bottom to top: The 1 min data on the geomagnetic “SYM/H” index, the dynamic pressure of the solar wind at the magnetopause, and the solar wind proton density for 1–3 August 2020; a red line marks the positive peaks in the solar wind and geomagnetic field parameters on 2 August 2020, at 09:23 UT.
The second small geomagnetic storm “SYM/H” = −37 nT on 5 October 2020, at 22:38 UT, started on 5 October at 08:12 UT with a sudden jump in the “SYM/H” index from −9 nT to +1 nT (Figure 6). In the initial phases of this storm (08:12 UT), the magnetic local time in the area of the future epicenter (37.897° N, 26.784° E) was equal to MLT = 10.48 h. Thus, this storm met a given criterion: at the time of its onset, the high-latitude part of the longitudinal region, where in the future the M = 7.0 earthquake occurred, was located under the polar cusp. The delay between this magnetic storm onset and earthquake occurrence equals ~25 days (Table 1).
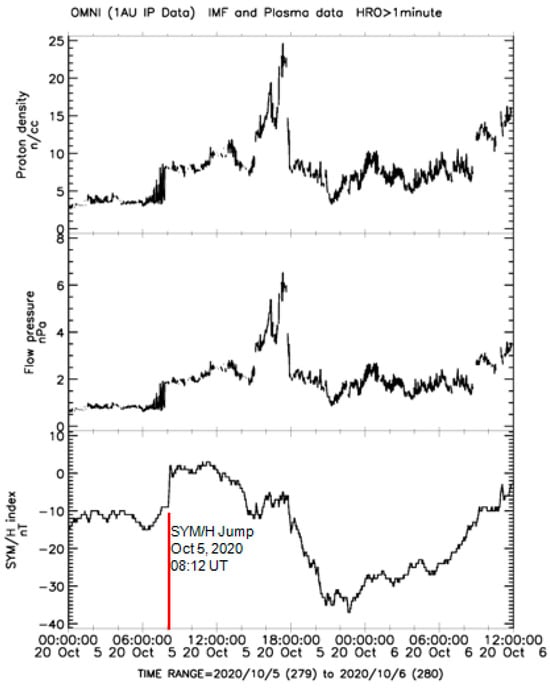
Figure 6.
rom bottom to top: The 1 min data on the geomagnetic SYM/H index, the dynamic pressure of the solar wind at the magnetopause, and the solar wind proton density for 5–6 October 2020; a red line marks a sharp positive jump in the solar wind and geomagnetic field parameters on 5 October 2020, at 08:12 UT.
2.3. Case Study of M = 7.1 of 23 October 2011
On 23 October 2011, a strong M = 7.1 earthquake occurred at 10:41:23 UTC with coordinates of the epicenter 38.721° N, 43.508° E, at a depth of 18.0 km. This event was preceded by three geomagnetic storms in September 2011 with clear, sudden onsets (Figure 7).
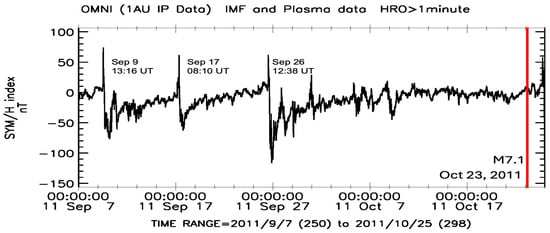
Figure 7.
The 1 min data on the geomagnetic “SYM/H” index from 7 September 2011 to 24 October 2011; on the right, a red line marks the date of the M7.1 earthquake on 23 October 2011 (38.721° N, 43.508° E); on the left, sudden onsets of the three preceding geomagnetic storms are indicated.
The first moderate storm, “SYM/H” = −77 nT, started on 9 September at 13:16 UT with positive “SYM/H” = +74 nT; the second weak storm, “SYM/H”= −43 nT, started on 17 September at 08:10 UT with positive “SYM/H” = +61 nT; and the third strong storm, “SYM/H” = −111 nT, started on 26 September at 12:38 UT with positive “SYM/H” = +62 nT. In the initial phases of these three geomagnetic storms, the MLT values in the area of the future epicenter (38.721° N, 43.508° E) were equal to ~16.63 h, 11.53 h, and 15.99 h, respectively. Thus, in the initial phase of these geomagnetic storms, the high-latitude area of the longitudinal region where the M = 7.1 earthquake occurred was located near the cusp at the time of the first and the third magnetic storms, while being strictly under the cusp at the time of the second storm. The lag times between the magnetic storm onsets and earthquake occurrence are equal to ~44, ~36, and ~27 days, respectively (Table 1).
2.4. Case Study for M = 7.2 of 12 November 1999
On 12 November 1999, a strong M = 7.2 earthquake occurred at 16:57:19 UTC with coordinates of the epicenter 40.758° N, 31.161° E, at a depth of 10.0 km. It was preceded by a strong geomagnetic storm on 22 September 1999, “SYM/H” = −166 nT, and a powerful one on 21 October 1999, “SYM/H” = −211 nT (Figure 8).
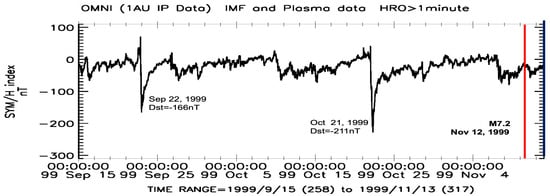
Figure 8.
The 1 min data on the geomagnetic “SYM/H” index from 15 September 1999 to November 15, 1999; on the right, a red line marks the date of the M = 7.2 earthquake on 12 November 1999 (40.758° N, 31.161° E); on the left, two preceding geomagnetic storms are indicated.
Below, we analyze these two storms in more detail. Figure 9 shows that the first storm started on 22 September 1999, at 12:34 UT, due to the arrival of a dense solar wind proton flux (upper panel), which increased dynamic pressure at the magnetopause (middle panel). At the time of storm onset, a magnetic local time around the future epicenter (40.758° N, 31.161° E) was equal to MLT = 15.27 h; that is, the high-latitude part of the M = 7.2 epicenter longitudinal region (31.161° E) was under the cusp. The delay time between the geomagnetic storm onset and earthquake occurrence equals ~51 days (Table 1).
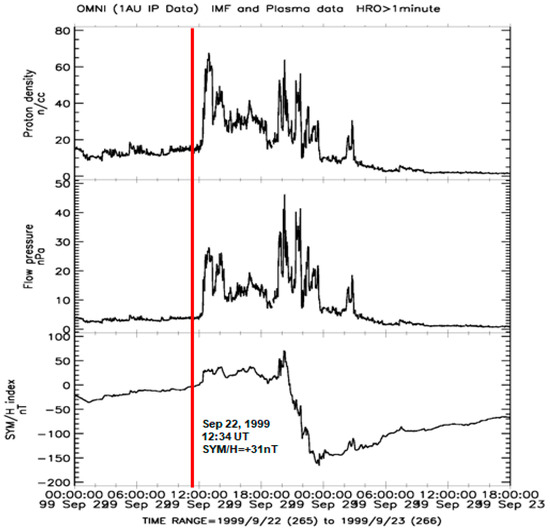
Figure 9.
From bottom to top: The 1 min data on the geomagnetic “SYM/H” index, the dynamic pressure of the solar wind at the magnetopause, and the solar wind proton density for 22–23 September of 1999; a red line marks a sharp increase in these parameters, which started on 22 September 1999, at 12:34 UT.
Besides this, Figure 9 shows that during this storm, the second arrival of a dense solar wind flux occurred, which resulted in increasing positive “SYM/H” up to +71 nT at 20:12 UT. It is not difficult to estimate that this time, the high-latitude part of an American longitudinal region was located under the polar cusp; one could expect a strong earthquake in this region. Indeed, according to the USGS seismic catalog, three strong earthquakes occurred here, namely, M = 7.5 in Mexico (16.059° N, 96.931° W) on 30 September 1999, with a time lag of ~8 days; M = 7.1 in California (34.603° N, 116.265° W) on 16 October 1999 with a time lag of ~24 days, and M = 7.0 at Alaska (57.342° N, 154.347° W) on 6 December 1999 with a time lag of ~75 days.
In Figure 10, we show the solar wind parameters for the powerful geomagnetic storm with “SYM/H” = −219 nT, which started on 21 October 1999, at 23:41 UT, with positive “SYM/H” = +42 nT. It is not difficult to calculate that at this time (23:41 UT), the high-latitude part of the longitudinal region ~125–245 E could be located under the polar cusp if it is between 8 and 16 h. Again, one could expect strong earthquakes in this region, which is indeed what happened. According to the USGS seismological catalog, on 19 November 1999, an M = 7.0 event occurred in Papua New Guinea (6.351° S, 148.763° E), a time lag of ~29 days; on 26 November 1999, an M = 7.5 event occurred in Vanuatu (16.423° S, 168.214° E), a time lag of ~36 days; and on 6 December 1999, an M = 7.0 event occurred in Alaska (57.342° N, 154.347° W = 205.653 E), a time lag of ~46 days.
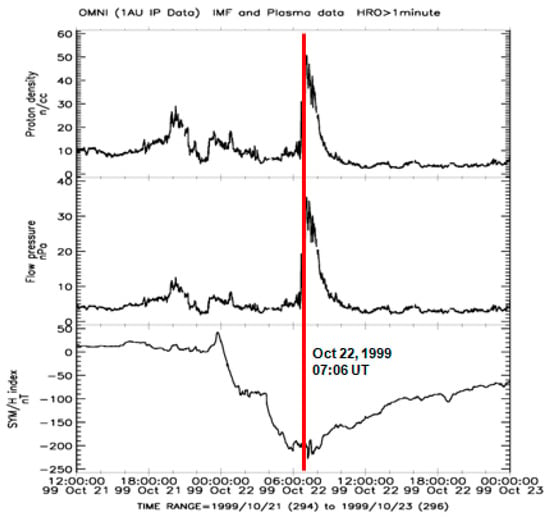
Figure 10.
From bottom to top: The 1 min data on the geomagnetic “SYM/H” index, the dynamic pressure of the solar wind at the magnetopause, and the solar wind proton density in the Earth’s orbit for 21–22 October 1999. The red line marks the arrival of a dense solar wind flux.
Besides this, Figure 10 shows that at the negative peak of the main phase of this powerful magnetic storm, the arrival of a dense solar wind flux occurred, which resulted in a sharp increase in the solar wind dynamic pressure at the magnetopause up to 35 nPa on 22 October 1999, at 07:06 UT. At this time, a magnetic local time in the area of the future epicenter (40.758° N, 31.161° E) was equal to MLT = 9.8 h; that is, the high-latitude part of the M = 7.2 epicenter longitudinal region (31.161° E) was under the polar cusp. The arrival of this dense solar wind flux could add some energy to the region of earthquake preparation. The delay between the arrival of a dense solar wind flux on 22 October 1999 at 07:06 UT and the M = 7.2 earthquake occurrence on 12 November 1999 was equal to ~21 days (Table 1).
2.5. Case Study for M = 7.6 of 17 August 1999
On 17 August 1999, a catastrophic M = 7.6 earthquake occurred at 00:01:39 UT with epicenter coordinates 40.748° N, 29.864° E, at a depth of 17 km. This earthquake was preceded by a strong magnetic storm “SYM/H” = −123 nT on 16 April 1999 (Figure 11). According to the Observatorio del Ebro, Roquetes, Spain, the sudden onset of this storm (SSC) occurred at ~11:25 UT on 16 April 1999, with a positive “SYM/H” = +10 nT, which then increased up to “SYM/H” = +63 nT at ~14:49 UT. During geomagnetic storm onset (SSC at ~11:25 UT), the magnetic local time at the territory of the future epicenter (40.748° N, 29.864° E) was equal to MLT = ~14.04 h. The high-latitude zone of the longitudinal region in which the M = 7.6 occurred was under the polar cusp.
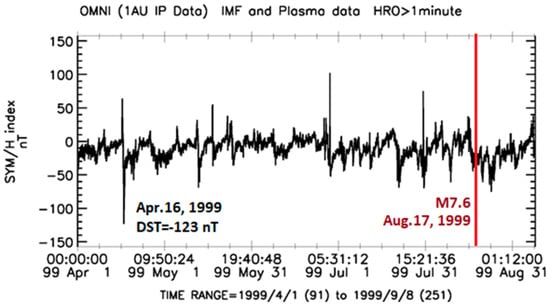
Figure 11.
The 1 min data on the geomagnetic “SYM/H” index from 1 April 1999 to 31 August 1999; on the right, a red line marks the date of the M = 7.6 earthquake on 17 August 1999 (40.748° N, 29.864° E); on the left, a preceding geomagnetic storm on 16 April 1999 is indicated.
Besides this, an analysis of the solar wind and geomagnetic field behavior before the earthquake on 17 August 1999 has revealed (Figure 12) that on the eve of the M = 7.6 event, the positive value of the “SYM/H” index sharply increased up to 36 nT on 15 August 1999, at 11:52 UT (almost the same time as for SSC on 16 April 1999). A small geomagnetic storm (“SYM/H” = −44 nT) started. At 11:52 UT, the magnetic local time at the territory of the future epicenter (40.748° N, 29.864° E) was equal to MLT = ~14.49 h; that is, the high-latitude area of the epicenter longitudinal region was under the polar cusp. Considering two geomagnetic storms that preceded the M = 7.6 earthquake, one may conclude that the delay times between storm onsets and earthquake occurrence were equal to ~123 and ~1.5 days, respectively (Table 1). Again, it seems that the arrival of the dense solar wind flux on 15 August 1999, at 11:52 UT, could add some energy to the region of earthquake preparation, which could start after a magnetic storm onset on 16 April 1999, at ~11:25 UT.
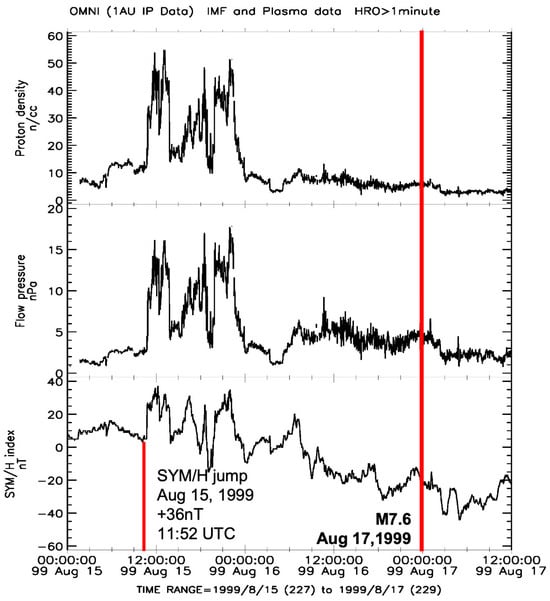
Figure 12.
From bottom to top: The 1 min data on the “SYM/H” index, the dynamic pressure of the solar wind at the magnetopause, and the solar wind proton density in the Earth’s orbit for 15–17 August 1999; on the right, a red line marks the date of the M = 7.6 earthquake on 17 August 1999 (40.748° N, 29.864° E); on the left, the date of a sharp jump in the solar wind and geomagnetic field parameters on 15 August at 11:52 UTC is indicated.
2.6. Case Study for M = 7.3 of 24 November 1976
On 24 November 1976, a strong M = 7.3 earthquake occurred at 12:22:18 UT with coordinates of the epicenter 39.121° N, 44.029° E, at a depth of 36.0 km. This event was preceded by a moderate geomagnetic storm (Dst= −57 nT) that started on 30 October 1976, at 10:30 UTC, with positive Dst = +18 nT (Figure 13). At this time, the magnetic local time in the area of the future epicenter (39.121° N, 44.029° E) was equal to MLT = 14.03 h. The high-latitude zone of the longitudinal region where the M = 7.3 earthquake occurred was located under the polar cusp. The delay between the magnetic storm onset and earthquake occurrence equals ~25 days (Table 1).
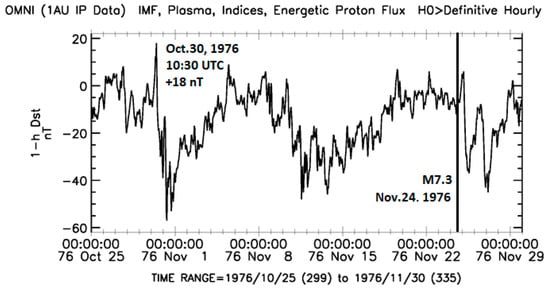
Figure 13.
The 1 h data on the Dst index in 1976 from 28 October to 29 November; on the right, a black line marks the date of the M = 7.3 earthquake on 24 November 1976 (39.121° N, 44.029° E); on the left, the start of a preceding geomagnetic storm on 30 October 1976 at 10:30 UTC is indicated.
2.7. Case Study for M = 7.2 28 March 1970
On 28 March 1970, a strong M = 7.2 earthquake occurred at 21:02:26 UT with coordinates of the epicenter 39.098° N, 29.570° E, at a depth of 25.0 km. This event was preceded by three geomagnetic storms in January–March 1970 (Figure 14).
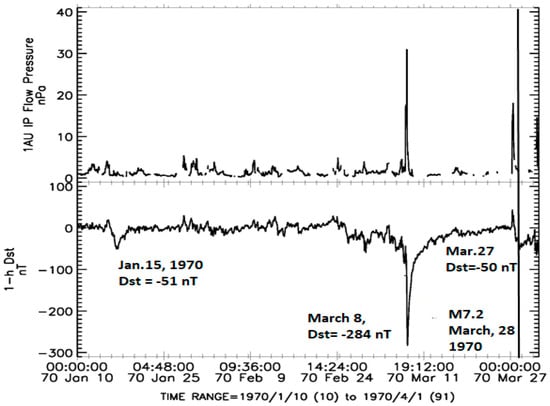
Figure 14.
From bottom to top: The 1-h data on the geomagnetic Dst index, the dynamic pressure of the solar wind at the magnetopause, and the solar wind proton density from 10 January to 1 April 1970; on the right, a black line marks the date of the M = 7.2 earthquake on 28 March 1970 (39.098° N, 29.570° E); on the left, preceding geomagnetic storms are indicated.
The first weak geomagnetic storm (Dst = −51 nT) started on 15 January at about 09:30 UT (positive Dst = +20 nT). At this time, the magnetic local time in the area of the future epicenter (39.098° N 29.570° E) was equal to MLT = ~12.2 h. Thus, this storm met a given criterion: at the time of its onset, the high-latitude part of the longitudinal region where the M = 7.2 earthquake later occurred was located under the polar cusp. The delay between this magnetic storm onset and earthquake occurrence equals ~72 days.
The second powerful storm (Dst = −284 nT) had no clear initial phase. However, at the negative peak of the main phase of this powerful magnetic storm, the arrival of a dense solar wind flux occurred, which resulted in a sharp increase in the solar wind dynamic pressure at the magnetopause up to 32 nPa on 8 March at 19:30 UT. It is not difficult to understand that at this time, the high-latitude area of the American longitudinal region was under the polar cusp. Three strong earthquakes occurred here with a time lag of 52, 84, and 145 days. The first M = 7.3 occurred in Mexico on 29 April 1970, and the other two occurred in Peru: M = 7.9 on 31 May and M = 8.0 on 31 July.
The third weak magnetic storm (Dst= −50 nT) started on 27 March at 08:30 UT (positive Dst = +44 nT). At this time, the magnetic local time in the area of a considered epicenter (39.098° N, 29.570° E) was equal to MLT = ~11.2 h. The high-latitude area of the longitudinal region in which the M = 7.2 earthquake occurred was located under the polar cusp. The delay times between two small magnetic storms’ onset (15 January and 27 March 1970) and earthquake occurrence on 28 March equal ~72 and ~1.5 days, respectively (Table 1). Again, it seems that as a small magnetic storm started on 27 March 1970, at 08:30 UT, it could add some energy to an area of M = 7.2 earthquake preparation, which could start after a small magnetic storm on 15 January 1970, at ~09:30 UT.
2.8. Case Study for M = 7.3 of 22 July 1967
On 22 July 1967, a strong M = 7.3 earthquake occurred at 16:57 UT with coordinates of the epicenter 40.751° N, 30.8° E, at a depth of 30.0 km. This seismic event was preceded by an extreme geomagnetic storm (Dst = −387 nT) starting on 25 May 1967, at 12:30 UT, from a sudden positive increase in the Dst index to +55 nT. Figure 15 presents the 1 h Dst data for 10 May–25 July 1967. At the time of the magnetic storm onset (12:30 UT), the magnetic local time in the area of the future epicenter (40.751° N, 30.8° E) was equal to MLT = ~15.29 h. Thus, this storm met a given criterion: at the time of its onset, the high-latitude part of the longitudinal region where the M = 7.3 earthquake later occurred was located under the polar cusp. The time delay between an extreme magnetic storm on 25 May 1967 and the M = 7.3 earthquake on 22 July 1967 was equal to ~58 days (Table 1).
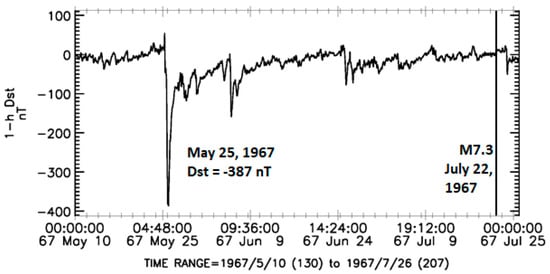
Figure 15.
The 1 h data on the geomagnetic Dst index for 10 May–25 July 1967; on the right, a black line marks the date of the M = 7.3 earthquake on 22 July 1967 (40.751° N, 30.8° E); on the left, a preceding geomagnetic storm on 25 May 1967 is indicated.
3. Discussion and Conclusions
One of the still-open questions to the Earth and space community is how the energy of the geospace environment impacts lithospheric processes. Some papers show that solar flare X-ray radiation, coronal mass ejections, and geomagnetic storms may precede the occurrence of earthquakes ([1,2,3,4,5,6,7,8,20,21,22,23] and references therein). Many years of statistical searching in this direction have led to a mathematical model [8] that considers a hypothesis of electromagnetic earthquakes being triggered by a sharp rise of telluric currents in the lithosphere, including crust faults, due to the interaction of solar flare X-ray radiation with the ionosphere–atmosphere–lithosphere system. Recently, the authors of [24] have investigated the level of the geomagnetically induced current index (GIC) in the Mediterranean region during the strongest magnetic storms of solar cycle 24 (2008–2019). The GIC index is a proxy of the geoelectric field, calculated entirely from geomagnetic field variations. Their results showed that the GIC index increased during the magnetic storm events in the 24th solar cycle, and its increase appears simultaneously with the SSC occurrence, which agrees with other GIC studies for low and middle latitudes, e.g., [25]. In the mathematical model [8], a critical point is the increase in the ionosphere’s radiation and conductivity. In the approach to explain an increase in global seismic activity in the solar minimums, again, a critical point is an increase in radiation and conductivity of the upper troposphere and lower stratosphere, produced by the galactic cosmic rays [26,27], whose intensity increases in solar minimums. It has been found recently [4] that strong earthquakes may appear addressed (targeted) because they occur near the footprints of certain geomagnetic lines belonging to a newly created radiation belt into the lower magnetosphere when the high-energy electrons in the outer radiation belt spill down due to a geomagnetic storm. Again, the critical point for this effect may be an increase in radiation and conductivity in the mesosphere and upper stratosphere due to the precipitation of energetic electrons from the radiation belt up to the stratopause, as shown in [28]. The above suggests that active space weather can provoke strong earthquakes in those longitudinal regions above which a near-space environment, including geomagnetic lines, can be sufficiently populated with charged particles (be conductive). On Earth, there are two places where geomagnetic lines may constantly be filling with charged particles. These are the polar cusps where the solar wind plasma would directly access the atmosphere [9,10,11,12,13,14,15,16,17]. The magnetic local time determines the length of the polar cusps in longitude, and its largest extension is expected to be between 8 and 16 h MLT [17]. Due to the Earth’s rotation, different longitudinal regions are located under the polar cusps during the arrival of the shocked solar wind flows. Thus, an idea was formed to check whether, after the magnetic storm, strong earthquakes will be more likely to occur in that longitudinal region, where its high-latitudinal area was located under the cusp when a shocked solar wind arrived (in time of SSC). Our analyses of nine strong (M ≥ 7.0) earthquakes inside and around the Anatolian Plate, including the M = 7.8 and M = 7.5 Kahramanmaras earthquake sequence on 6 February 2023, proved this suggestion. Moreover, for each of the other seven earthquakes, which occurred here from 1967, we could also identify preceding geomagnetic storms that met a given criterion: the magnetic local time (MLT) at an area of a future epicenter was between 8 and 16 h at the time of geomagnetic storm onset. The results showed (Table 1) that before four earthquakes (M = 7.8 and M = 7.5 on 6 February 2023, M = 7.3 on 24 November 1976, and M = 7.3 on 22 July 1967), there was only one geomagnetic storm with a given criterion (strong, moderate, and extreme, respectively). Before four earthquakes (M = 7.0 on 30 October 2020; M = 7.2 on 12 November 1999; M = 7.6 on 17 August 1999; and M = 7.2 on 28 March 1970), there were two magnetic storms with a given criterion (small + small, strong + powerful, strong + small, and small + small, respectively). Before one seismic event (M = 7.1 on 23 October 2011), there were three consecutive magnetic storms with a given criterion (moderate, small, and strong). The lag time between a magnetic storm onset and earthquake occurrence varied from ~1.5 days (two cases: M = 7.6 on 17 August 1999, and 28 March 1970, when two magnetic storms preceded earthquakes) to 123 days (one case for the M = 7.6 on 17 August 1999, preceded by two magnetic storms). On average, the delay is equal to ~50 days.
Observed long delays between geomagnetic storm onset and earthquake occurrence may tell us that space weather phenomena do not trigger earthquakes immediately. Instead, the solar wind stimulates the lithosphere processes that we see, which then, with a time delay, result in earthquakes. These processes may be related to geoelectricity, for example. So, the authors of [29] investigated seismicity and geoelectric potential changes, possibly associated with the seismic swarm activity in the Izu Island region, Japan, which took place in June–September of 2000. They showed that a swarm activity was preceded by pronounced electrical activity with innumerable signals that started two months before the swarm onset. The authors [30] also revealed a time delay for the ULF geomagnetic anomaly associated with the 2000 Izu Islands earthquake swarm. Namely, about three months before the beginning of swarm activity, the local signal level around the magnetometer associated with crustal activity (such as the vibration of the ground) was slightly enhanced. A similar result was obtained in [31] for the M = 7.8 earthquake at the Anatolian Fault on 6 February 2023. The authors of [31] performed a natural time analysis (NTA) of the seismicity preceding the Kahramanmaras earthquake doublet. They revealed a minimum fluctuation of the order parameter of seismicity that ended on 18 October 2022, pointing to the initiation of seismic electrical activity. This occurred almost three and a half months before the M = 7.8 earthquake. Table 1 shows that this earthquake occurred three months (91 days) after the start of the geomagnetic storm on 7 November 2022. There may be a connection between the initiation of seismic and electrical activity detected in [31] and the geomagnetic storm that occurred. If such a connection could be strictly established, it could provide direct evidence of the contribution of space weather to the earthquake preparation process.
Also, a time delay could appear if the shocked solar wind influences the upward lifting of fluids, which are active participants in tectonic earthquakes [32]. We cannot know what happens to fluids at a depth of the earthquake source, but we can expect that sometimes (in exceptional situations), the effects of fluids can manifest themselves at the Earth’s surface. It is possible that one of these exceptions was the sharp emanation of radon before the M = 6.9 earthquake in Kobe, Japan, on 16 January 1995 [33].
If the idea with fluids is true, then, depending on the fragmentation of the lithosphere in different places, the time duration of fluid rise could vary. It is possible that such a situation occurred after the magnetic storm on 7 November 2022. It is shown above that the Kahramanmaras earthquake doublet occurred 91 days after the magnetic storm. However, 16 days after the storm, on 23 November 2022, an earthquake M = 6.1 occurred in the north of the Anatolian Fault, with epicenter coordinates 40.836° N, 30.983° E (Figure 1). Here, in the recent past, three strong events occurred, namely, M = 7.6 on 17 August 1999, M = 7.2 on 12 November 1999, and M = 7.2 on 22 July 1967. It is possible that previous strong earthquakes caused the conditions created in this fault area, and the rise of fluids was facilitated here.
If this proves to be true, in the frame of our investigation, the next question could be: “How is it possible that the fluid uplifting happens very efficiently only in the time sector of a cusp and is not efficient in all other longitudinal sectors?” To our mind, the processes into the cusp could give us a small hint. So, the CHAMP and DMSP satellites discovered that the density of the neutral atmosphere in the cusp funnel is always increased, on average, by one and a half times relative to the density in neighboring areas [11,12]. A leading candidate driver mechanism for explaining the density anomaly in the cusp involves soft auroral precipitation driving neutral upwelling. The authors of [12] say: “Our preferred explanation is that dayside reconnection fuels Joule heating of the thermosphere causing air upwelling and at the same time heating of the electron gas that pulls up ions along affected flux tubes”. Thus, in the outer geospheres (magnetosphere, ionosphere), the rise of thermospheric gases occurs most effectively in the polar cusp funnel. In the middle geosphere (troposphere), the upward rise of air masses occurs, as we know, most effectively in the funnel of an atmospheric tornado. Suppose the processes in different geospheres are electrically interconnected. In that case, it is possible that the solar wind energy received by a beam of geomagnetic lines in the polar cusp will be delivered to the inner geospheres precisely along these geomagnetic lines (via Alfven waves, for example). Then, the upward rise of intra-terrestrial gases (fluids) can also occur along the bundle of these specific geomagnetic lines, and earthquakes will occur “targeted” at the footprint of these geomagnetic lines. The journey of intra-terrestrial fluids from the deep Earth is a fascinating process. As they move upward, they create fractures, mainly in the upward direction, as the rock overburden finishes and becomes less resistant to gas-pressure fracturing. These fractures then serve as conduits through the solid lithosphere [34]. By holding the faces apart, gas inflow into fault lines significantly reduces internal friction, thereby facilitating earthquakes. When these fluids reach near-surface pressure, they transform into invisible gases such as methane, carbon dioxide, hydrogen sulfide, hydrogen, nitrogen, helium, and various trace gases like radon [35,36].
Electrical coupling between an external and internal geosphere is expected; it is suggested in [37] that the process of earthquake preparation and realization could be related to the functioning of the global electric circuit (GEC). One of the main characteristics of the GEC is a unitary variation—a dependence of the fair-weather electric field on universal time, called the Carnegie curve, which demonstrates a steady increase of the electric field in fair-weather regions at ~19:00 UT. It was revealed in [38,39] that the global seismic activity also shows a unitary variation, which correlates relatively strongly with the Carnegie curve. It is shown in [40] that statistically significant anomalous changes appear simultaneously before major earthquakes in independent datasets of different geophysical observables. Therefore, the authors of [37,39] noted that electromagnetic monitoring of earthquake-prone areas is needed to identify and verify these precursory changes in future major earthquakes. Besides this, a retrospective analysis of the solid-earth parameters in the epicenter areas after identifying preceding geomagnetic storms is desirable.
Author Contributions
D.O. and G.K. provided the concepts for the manuscript. G.K. organized and wrote the manuscript. All authors provided critical feedback and helped shape the research, analysis, and manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The research of G.K. is partly funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP19677977).
Data Availability Statement
The original contributions presented in the study are included in the article: further inquiries can be directed to the corresponding author.
Acknowledgments
We thank the US Geological Survey and European–Mediterranean Seismological Centre for providing earthquake information services and data. We acknowledge the use of the NASA/GSFC’s Space Physics Data Facility’s CDAWeb service, OMNIdata. We are also very grateful to all anonymous reviewers for their valuable comments, which helped improve the work.
Conflicts of Interest
The authors declare that the research was conducted without any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sobolev, G.A.; Zakrzhevskaya, N.A.; Kharin, E.P. On the relation between seismicity and magnetic storms. Phys. Solid Earth 2001, 37, 917–927. [Google Scholar]
- Urata, N.; Duma, G.; Freund, F. Geomagnetic Kp Index and Earthquakes. Open J. Earthq. Res. 2018, 7, 39–52. [Google Scholar] [CrossRef]
- Chen, H.; Wang, R.; Miao, M.; Liu, X.; Ma, Y.; Hattori, K.; Han, P. A Statistical Study of the Correlation between Geomagnetic Storms and M ≥ 7.0 Global Earthquakes during 1957–2020. Entropy 2020, 22, 1270. [Google Scholar] [CrossRef]
- Ouzounov, D.; Khachikyan, G. Studying the Impact of the Geospace Environment on Solar Lithosphere Coupling and Earthquake Activity. Remote Sens. 2024, 16, 24. [Google Scholar] [CrossRef]
- Marchetti, D.; DeSantis, A.; Campuzano, S.A.; Zhu, K.; Soldani, M.; D’Arcangelo, S.; Orlando, M.; Wang, T.; Cianchini, G.; Di Mauro, D.; et al. Worldwide Statistical Correlation of Eight Years of Swarm Satellite Data with M5.5+ Earthquakes: New Hints about the Preseismic Phenomena from Space. Remote Sens. 2022, 14, 2649. [Google Scholar] [CrossRef]
- Love, J.J.; Thomas, J.N. Insignificant solar-terrestrial triggering of earthquakes. Geophys. Res. Lett. 2013, 40, 1165–1170. [Google Scholar] [CrossRef]
- Yesugey, S.C. Comparative evaluation of the influencing effects of geomagnetic solar storms on earthquakes in Anatolian peninsula. Earth Sci. Res. J. 2009, 13, 82–89. [Google Scholar]
- Sorokin, V.; Yaschenko, A.; Mushkarev, G.; Novikov, V. Telluric Currents Generated by Solar Flare Radiation: Physical Model and Numerical Estimations. Atmosphere 2023, 14, 458. [Google Scholar] [CrossRef]
- Ivarsen, M.F.; Jin, Y.; Spicher, A.; St-Maurice, J.-P.; Park, J.; Billett, D. GNSS scintillations in the cusp, and the role of precipitating particle energy fluxes. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031849. [Google Scholar] [CrossRef]
- Goertz, C.K. Kinetic Alfven waves on auroral field lines. Planet. Space Sci. 1984, 32, 1387–1392. [Google Scholar] [CrossRef]
- Lühr, H.; Rother, M.; Köhler, W.; Ritter, P.; Grunwaldt, L. Thermospheric up-welling in the cusp region: Evidence from CHAMP observations. Geophys. Res. Lett. 2004, 31, L06805. [Google Scholar] [CrossRef]
- Kervalishvili, G.N.; Lühr, H. The relationship of thermospheric density anomaly with electron temperature, small-scale FAC, and ion up-flow in the cusp region, as observed by CHAMP and DMSP satellites. Ann. Geophys. 2013, 31, 541–554. [Google Scholar] [CrossRef]
- Pitout, F.; Bogdanova, Y.V. The polar cusp seen by Cluster. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029582. [Google Scholar] [CrossRef]
- Escoubet, C.P.; Fehringer, M.; Goldstein, M. The Cluster mission. Ann. Geophys. 2001, 19, 1197–1200. [Google Scholar] [CrossRef]
- Pitout, F.; Escoubet, C.P.; Klecker, B.; Rème, H. Cluster survey of the middle altitude cusp: 1. size, location, and dynamics. Ann. Geophys. 2006, 24, 3011–3026. [Google Scholar] [CrossRef]
- Crooker, N.U. Dayside merging and cusp geometry. J. Geophys. Res. 1979, 84, 951–959. [Google Scholar] [CrossRef]
- Russell, C.T. Polar Eyes the Cusp Cluster-II Workshop: Multiscale/Multipoint Plasma Measurements. In Proceedings of the Workshop Held at Imperial College, London, UK, 22–24 September 1999; European Space Agency (ESA), ESA-SP: Paris, Italy, 2000; p. 47, ISBN 9290927968. Available online: https://articles.adsabs.harvard.edu//full/2000ESASP.449...47R/0000050.000.html (accessed on 20 February 2023).
- Wanliss, J.A.; Showalter, K.M. High-resolution global storm index: Dst versus SYM-H. J. Geophys. Res. 2006, 111, A02202. [Google Scholar] [CrossRef]
- Loewe, C.A.; Prolss, G.W. Classification and Mean Behavior of Magnetic Storms. J. Geophys. Res. 1997, 102, 14209. [Google Scholar] [CrossRef]
- Novikov, V.; Ruzhin, Y.; Sorokin, V.; Yaschenko, A. Space weather and earthquakes: Possible triggering of seismic activity by strong solar flares. Ann. Geophys. 2020, 63, PA554. [Google Scholar] [CrossRef]
- Shestopalov, I.P.; Kharin, E.P. Secular variations of solar activity and seismicity of the Earth. Geophys. J. 2006, 28, 59–70. [Google Scholar]
- Zhang, G.Q. Relationship between global seismicity and solar activities. Acta Seismol. Sin. 1998, 11, 495–500. [Google Scholar] [CrossRef]
- Huzaimy, J.M.; Yumoto, K. Possible correlation between solar activity and global seismicity. In Proceeding of the 2011 IEEE International Conference on Space Science and Communication (IconSpace), Penang, Malaysia, 12–13 July 2011; pp. 138–141. [Google Scholar]
- Boutsi, A.Z.; Balasis, G.; Dimitrakoudis, S.; Daglis, I.A.; Tsinganos, K.; Papadimitriou, C.; Giannakis, O. Investigation of the geomagnetically induced current index levels in the Mediterranean region during the strongest magnetic storms of solar cycle 24. Space Weather 2023, 21, e2022SW003122. [Google Scholar] [CrossRef]
- Zhang, J.J.; Wang, C.; Sun, T.R.; Liu, C.M.; Wang, K.R. GIC due to storm sudden commencement in low-latitude high-voltage power network in China: Observation and simulation. Space Weather 2015, 13, 643–655. [Google Scholar] [CrossRef]
- Bazilevskaya, G.A.; Usoskin, I.G.; Flückiger, E.O.; Harrison, R.G.; Desorgher, L.; Bütikofer, R.; Krainev, M.B.; Makhmutov, V.S.; Stozhkov, Y.I.; Svirzhevskaya, A.K.; et al. Cosmic ray induced ion production in the atmosphere. Space Sci. Rev. 2008, 137, 149–173. [Google Scholar] [CrossRef]
- Phillips, T.; Johnson, S.; Koske-Phillips, A.; White, M.; Yarborough, A.; Lamb, A.; Schultz, J. Space weather ballooning. Space Weather 2016, 14, 697–703. [Google Scholar] [CrossRef]
- Kavanagh, A.J.; Cobbett, N.; Kirsch, P. Radiation Belt Slot Region Filling Events: Sustained Energetic Precipitation Into the Mesosphere. J. Geophys. Res. Space Phys. 2018, 123, 7999–8020. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M.; Tanaka, H. Analysis of electrical activity and seismicity in the natural time domain for the volcanic-seismic swarm activity in 2000 in the Izu Island region, Japan. J. Geophys. Res. 2009, 114, B02310. [Google Scholar] [CrossRef]
- Hattori, K.; Serita, A.; Gotoh, K.; Yoshino, C.; Harada, M.; Isezaki, N.; Hayakawa, M. ULF geomagnetic anomaly associated with 2000 Izu Islands earthquake swarm, Japan. Phys. Chem. Earth Parts A/B/C 2004, 29, 425–435. [Google Scholar] [CrossRef]
- Nicholas, V.S.; Efthimios, S.S.; Stavros-Richard, G.C.; Panayiotis, K.V. Identifying the Occurrence Time of the Destructive Kahramanmaraş-Gazientep Earthquake of Magnitude M7.8 in Turkey on 6 February 2023. Appl. Sci. 2024, 14, 1215. [Google Scholar] [CrossRef]
- Miller, S.A. The Role of Fluids in Tectonic and Earthquake Processes. Adv. Geophys. 2013, 54, 1–38. [Google Scholar] [CrossRef]
- Yasuoka, Y.; Igarashi, G.; Ishikawa, T.; Tokonami, S.; Shinogi, M. Evidence of precursor phenomena in the Kobe earthquake obtained from atmospheric radon concentration. Appl. Geochem. 2006, 21, 1064–1072. [Google Scholar] [CrossRef]
- Pulinets, S.A. Physical mechanism of the vertical electric field generation over active tectonic faults. Adv. Space Res. 2009, 44, 767–773. [Google Scholar] [CrossRef]
- Gold, T. The Deep Hot Biosphere. In The Myth of Fossil Fuels; Springer: Heidelberg, Germany, 1998; p. 243. [Google Scholar]
- Soter, S.; Gold, T. The Deep-Earth-Gas Hypothesis. Sci. Am. Mag. 1980, 242, 154. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Liu, J.-Y.; Hattori, K.; Han, P. Multiparameter Assessment of Pre-Earthquake Atmospheric Signals. In Pre-Earthquake Processes; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; American Geophysical Union; John Wiley & Sons: Hoboken, NJ, USA, 2018; 385p. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Khachikyan, G.Y. Unitary Variation in the Seismic Regime of the Earth: Carnegie-Curve Matching. Geomagn. Aeron 2020, 60, 787–792. [Google Scholar] [CrossRef]
- Pulinets, S.; Khachikyan, G. The Global Electric Circuit and Global Seismicity. Geosciences 2021, 11, 491. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Direct interconnection of seismicity with variations of the Earth’s electric and magnetic field before major earthquakes. Europhys. Lett. 2024, 146, 22001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).