Abstract
Landslide impact is potentially hazardous to an urban environment. Landslides occur at certain slope levels over time and require practical slope analysis to assess the nature of the slope where a landslide is likely to occur. Thus, acquiring very high-resolution remote sensing data plays a significant role in determining the slope surface. For this study, 12 landslide conditioning parameters with 10 × 10 cell sizes that have never been previously collectively applied were created. These factors were created directly from the LiDAR (Light Detection and Ranging) DEM (digital elevation model)using their layer toolboxes, which include slope, aspect, elevation, curvature, and hill shade. Stream power index (SPI), topographic wetness index (TWI), and terrain roughness index (TRI) were created from spatial layers such as slope, flow direction, and flow accumulation. Shapefiles of distances to roads, lakes, trees, and build-up were digitized as land use/cover from the LiDAR image and produced using the Euclidean distance method in ArcGIS. The parameters were selected based on expert knowledge, previous landslide literature, and the study area characteristics. Moreover, multicriteria decision-making analysis, which includes the analytic hierarchy process (AHP) and fuzzy logic approaches not previously utilized with a LiDAR DEM, was used in this study to predict the possibility of a landslide. The receiver operating characteristics (ROC) were used for the validation of results. The area under the curve (AUC) values obtained from the ROC method for the AHP and fuzzy were 0.859 and 0.802, respectively. The final susceptibility results will be helpful to urban developers in Malaysia and for sustainable landslide hazard mitigation.
1. Introduction
Like many developing, equatorial and tropical countries with tectonic and humid hydroclimatic conditions, landslides in Malaysia are a common hazard that occurs almost every year, either on a small or large scale [1,2]. Landslides result in substantial damages, which may lead to the loss of lives and properties worldwide all year round [3,4]. The landslide-triggering factors are entirely interdependent and comprise severe rainfalls, earthquakes, erosion, geomorphological processes, and anthropogenic activities, such as deforestation, road construction, quarries, mines, etc. [5]. According to Raya [6], a previous report stated that 88% of the previous landslide cases in Malaysia are human-induced. Landslide susceptibility is the proneness of a geographical slope to failures [7]. Landslide susceptibility is a quantitative and qualitative assessment of the classification [8,9], extent (volume and size), and spatial distribution of existing or potential landslides in a given location [10]. Therefore, this study aimed to provide adequate information for assessing the stability of the slopes in Universiti Putra Malaysia (UPM), Serdang, Malaysia characteristic of different morphological units, such as slopes and rugged topography.
A landslide susceptibility map shows the areas with a potential landslide due to the correlation of varying conditioning factors that contribute to landslides [11,12]. Landslide mapping provides information on variations in the arrangement, form, location, and appearance of the topography [13], which can be analyzed traditionally or with the help of aerial photographs, satellite imagery, and geographic information systems (GIS) technologies [14]. These maps are an essential tool for landscapers, urban planners, developers, and government agencies [15,16]. Again, regarding previous landslide information and historical results, Guzzetti et al. [17] highlighted the usefulness and setbacks of the individual techniques and compared the traditional and advanced methods of landslide mapping. The study reveals that emerging technologies like surface morphological analysis using a very-high-resolution digital elevation model (DEM) can enhance the precision of landslide maps. Field surveys and optical remote sensing show that landslide hazard monitoring faces severe challenges due to dense vegetation cover, area accessibility, and mountain shadow [18].
Today, GIS plays a remarkable role in landslide susceptibility mapping (LSM), through which spatial datasets can be visualized, processed, and analyzed [19,20]. GIS is considered the most accurate and exciting technology [21]. DEM is one of the most widely used and available spatial data. Most of the spatially distributed models use the DEM of the location to derive the elevation, which is a critical input for model predictions. The sources of DEM are the Advanced Spaceborne Thermal Emission and Reflection (ASTER) [22], National Elevation Dataset (NED) [23], and Light Detection and Ranging (LiDAR) [24]. The accuracy of the grid cell elevation is an essential factor since a small error in the height may result in incorrect model output. The modeled area DEM with grid cell resolution and vertical accuracy are significant for most prediction processes. Several studies [25,26] noted in the literature that compares spatial indices derived from different DEM resolutions. The LiDAR-derived DEM is more readily influential.
Airborne LiDAR has now become one of the industry standard tools for collecting accurate and dense topographic data at very high speed [27]. Burns and Madin [28] provided a standard procedure for LiDAR data interpretation for landslide mapping. Haneberg et al. [29] suggested a system for landslide mapping using high-resolution airborne LiDAR data for the Paranuss Campus University of California, San Francisco, with dense vegetation. LiDAR offers a tremendous way to deal with these constraints by providing high-resolution topographic data. LiDAR, a relatively advanced technology, is advantageous over traditional techniques for terrain surface representation. The advantages refer to accuracy, resolution, and cost [30,31]. The most significant characteristic of LiDAR is its very high vertical accuracy which makes it possible to represent the Earth’s surface with high precision [32]. LiDAR is among the few technologies that collect data from all points and produce DEMs with 1–2 m horizontal resolution [33]. Since the study area is characterized by varying terrain, research was conducted utilizing different remote sensing and GIS techniques.
Several models for landslide susceptibility with an acceptable accuracy level have been developed and classified into data-driven [34] and expert opinions [35], and have their respective advantages and disadvantages. These models’ results may be accurate in some instances, but there is also a certain level of uncertainty, which may sometimes lead to inaccurate results [36]. These uncertainties can negatively affect the landslide susceptibility results accuracy when neglected [37]. Since these models are valuable means of solving a broad range of spatial irregularities. Several efforts have been put in place to improve the models’ accuracy [38]. Thus, the validity of spatial models and expert opinion approaches depends highly on the relative importance of each landslide factor [39]. In addition, the reliability, robustness, degree of fitting, and prediction skill of the validation process of the models [40]. Machine learning methods are sometimes considered more robust data-driven models and are often believed to have higher accuracy than multi-criteria methods [41]. However, this is not the case, and the multicriteria decision-making approach is applied in this study. Many studies directly utilize machine learning models without applying any heuristic or statistical methods, concluding that this is a robust approach. However, this would not be a universally accepted result because heuristic methods can sometimes outweigh statistical and machine-learning models [42].
This study will explore LiDAR-derived DEM for landslide susceptibility mapping, selected models based on multicriteria decision-making analysis which includes AHP and fuzzy logic as well as the 12 landslide conditioning factors as a result of the structure of the terrain. The LiDAR data when combined with these advanced numerical methods can increase the accuracy of LSM by improving data precision, resolution, accuracy, and completeness [43]. AHP and fuzzy logic involve producing LSM based on the expert’s assessment and are also termed “expert evaluation techniques” [44]. Applying this technique, the expert’s opinions are vital to estimating landslide potential from the data involving intrinsic variables [45]. Consequently, assigning weightage values and ratings to the variables is subjective, and the results are not reproducible [46]. On the other hand, quantitative methods are based on numerical expressions of the relationship between landslides and controlling parameters [47]. The technique requires less human knowledge and experience to produce and utilize susceptibility models [48]. This study will be very crucial in landslide study, to locate landslide-prone areas to assist university management in timely mitigation planning.
2. Study Area and Data Used
2.1. Study Area
UPM is a government tertiary institution located in Serdang, Selangor (Figure 1), Malaysia. Its landmass is approximately 1108 hectares and comprises natural and artificial features, such as farmlands, trees, and water bodies. It is located along Latitude: 2°59′34.19″ N and Longitude: 101°42′16.79″ E. The climate of this area is characterized by a warm and sunny tropical rainforest climate with abundant rainfall, especially in the northeast monsoon season, between October to March. The area has an annual maximum temperature between 31 °C and 33 °C, and a minimum temperature of 22 °C and 23.5 °C. The minimum yearly rainfall is about 2600 mm, with relative dryness between June and July. Rainfall typically exceeds 133 mm (5.2 in) monthly. Figure 1 shows the location of the study area.
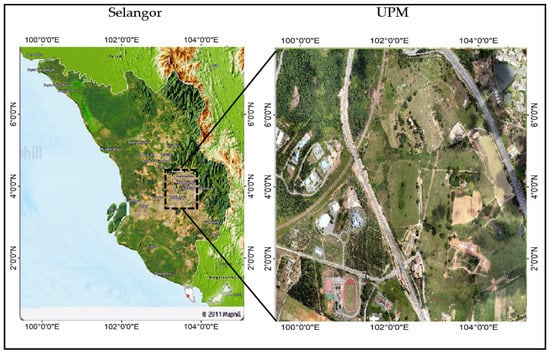
Figure 1.
Location map of Selangor (left) and location of the study area in UPM, Serdang (right).
This study is relevant in the area due to its characteristic morphological units, including slopes, valleys, and rugged topography. In the study area, the maximum elevation is 105.560 m and the minimum elevation is 34.668 m. The area is also characterized by road cuts, geosyncline folds, water bodies, weathering, and erosion. Moreover, the vegetation coverage in the study area is relatively thick and vastly distributed residual soil comprising a mixture of clay, silt, and fine sand as a result of anthropogenic activities.
According to research conducted by Santurika Hassan Aliyu (2017) in the study area, the soil data reveals a disturbed residual soil which comprises of Serdang and Malacca Series. The soil of the Serdang series is made up of sandstone and quartzite, yellowish-brown in color, while the Malacca series is made up of Sandy clay with low to moderate sub-angular structures, and friable over a few meters. The sand of the Malacca series decreases with depth while clay increases slightly with depth with low base saturation. For the past two decades, the state of Selangor has rapidly developed, with many housing schemes developed to counter high market demand [49]. The state has also been hit with the largest of landslide hazards compared to other states. Research revealed that urban soil series similar to this area are highly susceptible to landslides compared to other series. Furthermore, landslides are likely to occur in areas with similar geological, geomorphological, hydrogeological, and climatic conditions as in the past [50]. At present, traces of landslides have been detected in the study area, as shown in Figure 2.

Figure 2.
Landslide locations within the study area from google earth and field observation.
According to the field investigation and aerial inspection, the landslides in the study area are mainly distributed along the western part which harbors several anthropogenic features, such as construction and agricultural activities, which affect the terrain stability. Like tropical and developing countries worldwide, Landslides in Malaysia are a common hazard that occurs almost every year, either on a small or large scale [51].
2.2. Data
The LiDAR data used in this research were captured on the 24th of August, 2015 by Ground Data Solution Bhd using a Riegl Q780–400 kHz waveform laser scanner aboard an EC-120 Helicopter flown over UPM at an altitude of about 600 m above the terrain. A Canon EOS5D MARK III camera with a 35 mm focal length, which was mounted on the aircraft, was used to capture an RGB image of the entire terrain. The camera has a horizontal and vertical resolution of 72 Dpi, respectively, and an exposure time of 1/25 00 s. This study was carried out to cover a wide range of the study area. This area is easily accessible and represents a typical urbanized area with low and high-rise-story build-up areas, sparsely populated agricultural lands, a host of anthropogenic activities, and a randomly distributed body of water (lake). The LiDAR laser scanner, in addition to recording the 𝑥𝑦𝑧 data, also recorded the intensity of all light pulses that bounced back from the targets and stored them as a greyscale image. However, intensity images are made of pixels representative of the energy of laser pulses returning to the system [52]. The acquired point cloud has a 1-m resolution, 6 points per square meter, with 15 cm vertical accuracy on non-vegetated terrain and 25 cm horizontal accuracy. A geographic coordinate system of WGS84 datum was used to derive the different elevation zones using ESRI ArcGIS 10.5 spatial analyst software.
In addition, a landslide inventory map was produced, and possible landslide sites were identified from LiDAR ortho photo from the UPM’s Geospatial Information Science Research Centre (GISRC) and through field investigation.
2.2.1. Landslide Conditioning Factors
The DEM is a fundamental element of GIS datasets and GIS-based analyses [53]. It is a grid-based, three-dimensional representation of terrain elevation [54]. DEMs are either created from primary contours or point data using a range of techniques [55]. The use of high-density airborne laser scanning (ALS) data points gives room for producing a highly accurate, contemporary DEM [56].
In the present study, LiDAR data was optimized and converted to DEM with 1 m horizontal resolution to model some relevant landslides conditioning parameters for susceptibility analysis. Conditioning factors generally describe a range of parameters, such as data, values, and conditions, that influence the terrain as susceptibility to landslide [28]. Defining and mapping a suitable set of conditioning parameters related to landslide events involve prior knowledge of the main contributors to the landslides [57]. These conditioning factors include terrain geomorphology, climatic conditions, vegetation density, land cover/use, and anthropogenic factors. Accessibility to thematic layers changes extensively based on the type, scale, and method of data collection. Moreover, the selected parameters in this study are those used by other researchers and those with significant influence on the inconsistency potential of the terrain.
Data with sufficient detail is sometimes rarely available, and this introduces uncertainty into the model. Sources of this uncertainty may be associated with slope geometrical factors [58], soil properties [59], and a lack of understanding of the relationship between measured variables and the model parameters. Studies have assessed the effect of uncertainties related to such models [60] for field and spatially distributed landslide predictions. Such information is found to rarely support risk reduction decision-making. The uncertainties can be dealt with through standard scenario-led strategies, known as top-down approaches. With these approaches, factors of a general circulation model are downscaled to derive local rainfall intensities, frequencies, and other climatic variables [61].
The analysis involves manual data input in GIS software, such as data entry, digitization, and classification. Hence, possible intrinsic factors and extrinsic factors are derived from LiDAR bare earth models [62]. Based on expert opinion, literature, and geomorphological characteristics of the study area, a total of 12 geological, hydrological, and land use landslide conditioning factors within the study area, namely elevation, slope, aspect, curvature, hill shade, distance to trees, distance to road, distance to urban, distance to lake, stream power index (SPI), terrain roughness index (TRI), and topographic wetness index (TWI), were selected, as shown in Table 1.

Table 1.
Summary of the landslide conditioning factors.
SPI expressed as
where represents the specific catchment area, and means the local slope gradient measured in degrees. Using their layer toolboxes, the parameter maps, such as slope, aspect, elevation, curvature, and hill shade, were directly created from the LiDAR-derived DEM. Other parameter maps, such as SPI, TWI expressed mathematically as
where A represents the Catchment area (m2/m) and represents the slope in degree, and TRI s expressed mathematically as
where and represent the biggest and smallest cell values respectively, in the nine rectangular neighborhoods of altitude, were created from spatial layers, such as slope, flow direction, and flow accumulation. Furthermore, the shapefiles of distances to roads, lakes, trees, and build-up were digitized as land-use/cover from the LiDAR orthophoto and produced using the Euclidean distance method in ArcGIS with 10 × 10 m cell sizes. These parameters were prepared as a raster dataset using ArcGIS.
2.2.2. Landslide Inventory
From an archived aerial photo from the UPM’s GISRC database supported with field observation, google earth, and classified maps, a landslide inventory map with 56 landslide sites was created.
The 56 landslide points were randomly selected to create the landslide inventory used for the model validation. The landslide points were further split with a 70:30 ratio. There are no agreed splitting criteria. However, 70:30 is the most widely used in the research community [66]. These points are chosen based on the nature and size of the study area and the type of approach used. Basheer and Hajmeer [67] have recorded different splitting ratios applied for several statistical approaches. They summarized that Swingler [68] used a ratio of 80:20 for training and testing their models. Lately, Guzzetti et al. [69] applied a ratio of 70:30 to delineate landslides from high-resolution images, and Bui et al. [70] also applied a similar ratio for landslide prediction using soft computing techniques. Random sampling methods are generally used in all of the studies mentioned above. To have computationally robust models, a 70:30 ratio was chosen in this research. The compiled landslide inventory finally comprises 56 records shown in Figure 3, and 70% (39 points) were selected as the training dataset and 30% (17 points) were selected as the validation dataset, used for the landslide susceptibility model validation. Raster values of the landslide points were extracted in ArcGIS and used to build the validation datasets in SPSS.
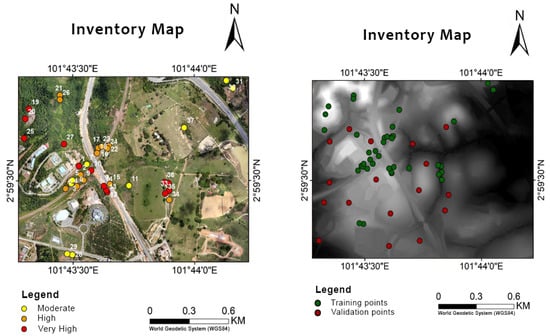
Figure 3.
Landslide location map in LiDAR orthophoto (left) and Landslide location map in DEM map (right).
3. Methodology
The point cloud acquired by Airborne LiDAR was utilized in this study to generate the high-resolution DEM. The conditioning parameters derived from DEM and shapefiles from the LiDAR orthophoto/google earth have 1-m and 10-m pixel sizes. However, all the factors were normalized to 10-m pixel sizes.
The result showed great topographic potential for terrain classification. The high-resolution LiDAR-derived DEM improved landslide investigations by implementing the AHP and fuzzy logic for susceptibility analysis following the methodology flowchart in Figure 4. Literature reveals that topographic data with a resolution relevant to the scale of morphological characteristics is vital to studying these landslide properties [71]. In this study, a general discussion of landslide mapping methods is presented. Moreover, the features of the study area have been described. The methods used to generate LSM are then discussed, followed by the production of the resulting maps. These maps are then validated to evaluate the influence of source and spatial resolution. Finally, a discussion and conclusion are presented.
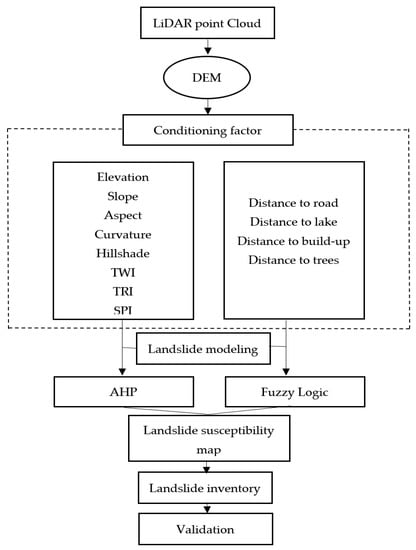
Figure 4.
Flowchart of the methodology for landslide susceptibility.
3.1. Landslide Susceptibility Mapping (LSM)
LSM is an effective strategy for identifying areas prone to landslide hazards. It plays an essential part in hazard mitigation. The LSM gives helpful information on the spatial distribution of potential slope failures [72]. In the past two decades, substantial research studies on LSM have been conducted worldwide. Over the years, different methodologies have been applied to creating LSM. LSMs are also crucial for identifying landslide-prone areas and risk management and reduction, apart from their significance to hazard mitigation [73]. The LSM can be produced by combining the necessary landslide data and independent variables [74].
3.2. Analytic Hierarchy Process (AHP)
AHP was first introduced by Saaty [75]. AHP is a multi-criteria decision analysis (MCDA) technique primarily based on model building [76] and comparative assessment of the criteria to synthesize priorities with a ratio scale [77]. It evaluates the importance of each landslide factor in a hierarchical order. For over a few decades, AHP has been widely applied in MCDA to acquire the objective weights of criteria in a GIS environment [78]. AHP incorporates the consistency ratio (CR) calculus that should be inferior to 0.1. Ensuring that the weighting of the criteria pairwise is not random. The AHP approach is generally comprised of the construction of pairwise comparison, normalization of matrix weight, derivation of priority sector, calculation of the maximum Eigenvalue, computation of the consistency index (CI) using Eigenvalue, and the analysis of random index (RI). Note that the value of CR obtained must be lower than 0.1 for the result to be acceptable [79]. The AHP entails the identification and selection of the factors influencing the outcome of the model. The pairwise comparison method involves three steps: (i) Construction of a Pairwise comparison matrix: AHP assigns weights and ranks the landslide conditioning parameters according to their level of importance through predefined scores of 1/9—1. Applying the AHP approach [80], expert evaluations are expressed in numerical values according to the assessment scale and also applied to this study. Each landslide factor was assigned a numerical value based on its relative importance in this study area. (ii) Computation of criterion weights comprises three operations, namely, find the sum of the values in each column of the matrix, and divide the element in the matrix by its column total (the resulting matrix is referred to as the normalized pairwise comparison matrix). (iii) Finally, compute the average of the elements in each row of the normalized matrix by dividing the sum of normalized scores for every row by the number of criteria. The resulting averages provide an estimate of the relative weights of the criteria being compared. The following steps are involved in the calculation of the final weights for all parameters [81]. Sum the value of the pair-wise comparison matrix in the columns using Equation (4).
where is the total column value of the pair-wise comparison matrix and is the criteria applied. Divide all components in the matrix using their total row to get a normalized pair-wise comparison matrix. Divide the sum of the matrix’s normalized row by the number of the parameter () to get the standard weight by applying Equation (5).
where = standard weight. X = the judgement matrix. To calculate the consistency vector values Equation (6) has been used:
where = consistency vector and V = consistency value
To approximate the CR, the weighted vector sum is calculated by multiplying the pairwise matrix with the weight. Each of the elements is divided by their corresponding weights. To achieve the comparison matrix, the Eigenvalue (λmax) and the total number of factors () have to be the same. The CI is mathematically expressed as Equation (7):
where CI is the consistency index, λmax represents the Eigenvalue, and n is the total number of compared factors. CR is utilized for checking the consistency of the comparison matrix expressed, as shown in Equation (8).
where CR is the consistency ratio, CI is the consistency index, and RI is the random CI of the pairwise comparison matrix. The CI rules that a CR equal to or less than 0.1 represents an acceptable matrix. In contrast, a ratio greater than 0.1 shows that the matrix is inconsistent. Table 2 shows the pairwise comparison matrix of the landslide factors for this study area.

Table 2.
The pairwise comparison matrix of the landslide parameters.
The twelve landslide factors were correlated and overlayed using the ArcGIS spatial analyst weighted overlay function to obtain the landslide susceptibility map.
3.3. Fuzzy Logic
The Fuzzy set theory, which Zadeh first introduced in 1965, is widely applied as a modeling methodology in complex systems that are difficult to define, especially in crisp numbers [82]. Generally, in fuzzy set theory, each set is assigned a varying membership value to the elements between 0 and 1, reflecting the certainty of the membership’s degree [83]. The membership values can also be user-defined or based on the normalized ratio of the percentage of occurrence to the rate of non-occurrence for a given attribute [84] which was applied in this study as in Table 3. The fuzzy membership or fuzzification transforms the input raster into a scale of 0 and 1, indicating the strength of membership in a set based on a specified fuzzification algorithm. A value of 1 indicates full membership in the fuzzy set with membership decreasing to 0, indicating that it is not a member of the fuzzy set.

Table 3.
The fuzzification conditioning factors.
All datasets have been standardized and expressed in units that can be compared based on the nature of the data and experts’ opinions. Each membership function differs in its equation and application and is based on which best captures the transformation of the data on the phenomenon being modeled. The Fuzzy Large function is used when the larger input values are more likely to be a member of the set. The Fuzzy Linear function uses a linear function between the user-specified minimum and maximum values. The Fuzzy Near function is most suitable if membership is near a specific value.
The choice of the most suitable operators to combine the conditioning factors layers is crucial. There are five different operators to choose from: “AND”, “OR”, “PRODUCT”, “SUM”, and “GAMMA”. These five fuzzy operators can be expressed mathematically as:
The fuzzy “AND” function is the minimum of the fuzzy membership from the fuzzy input raster. The “OR” function is the maximum of the fuzzy membership from the input raster. The fuzzy “PRODUCT” is a decreasing function used when multiple evidence is less critical or smaller than any input alone. The “SUM” function is an increasing function used when considerable evidence is more significant than any inputs alone. The GAMMA is the algebraic product of the fuzzy “SUM” and fuzzy “PRODUCT” both raised to the power of gamma.
A fuzzy overlay methodology was used for this analysis because it is very appropriate for the continuous datasets used and accommodates discrete datasets. The fuzzy analysis is in two stages [85]: First, each criterion in the analysis must be converted to fuzzy membership values using the fuzzy membership function (a mathematical model that creates the relationship between the observed and computed membership value. Moreover, the fuzzified data are overlaid using a fuzzy overlay tool. Assigning a fuzzy membership value to the observed data is feasible with gaussian, gamma, linear, near, large, or small relationships. When full membership is assigned to large or small observed values, a linear relationship occurs, and a consistent rate of change to non-membership. The minimum or maximum observed values in the linear function can be changed to create minimum-maximum thresholds which are useful for detecting and removal of outliers of large or small observed values. The Small function assigns membership preference to small observed values. Likewise, the large function considers large observed values. With Small or Large functions, non-linear relationships can also be created between the datasets.
Irrespective of which function is used, the rate of change can be manipulated to alter the nature of the spread of the function. For example, the midpoint (baseline for membership/non-membership) can be specified in the observed data to make the fuzzy membership value equal to 0.5. Gaussian membership transforms the data values into a normal distribution function. For a normal distribution curve, the midpoint which describes the ideal definition for the set has a value of 1; and the values of the input data decrease in membership in the positive and negative directions away from the midpoint until further where the values move far away from the ideal definition where they are no longer part of the set and are assigned 0 [86,87]. Selecting the ideal fuzzy overlay among several available operators (AND, OR, PRODUCT, SUM, GAMMA) to combine the criteria layers is critical. The fuzzy overlay analysis was carried out through the fuzzy overlay tool in the ArcGIS 10.5 software. After standardization, each one of the fuzzy types was used, while the “GAMMA” function gave the most acceptable result.
3.4. Validation
Validation is an essential scientific investigation process that reveals a model’s output [88]. LSM accuracy can be validated using different validation techniques. Receiver operating characteristics (ROC) and area under the curve (AUC) validation techniques were implemented to evaluate and compare the landslide mapping methods. The most commonly used method is the ROC curve [89]. The ROC is primarily used for model validation. It compares the value of measured and predicted variables to compute the probability correspondence in class occurrence [90]. Thus, the ROC curve was used in this study to validate and compare the landslide maps of AHP and Fuzzy. This validation approach shows the trade-off between the true positive rate (TPR) and the false positive rate (FPR) in the LSM. The classified and ground truth data sets were computed in Microsoft Excel and exported to SPSS to plot the ROC curve. The vertical axis of the curve shows the sensitivity, while the horizontal axis shows the specificity. The AUC offers the accuracy of the LSM. The AUC plot of sensitivity and specificity shows the overall accuracy from 0 to 1. The values closer to 1 has better accuracy and vice-versa. This means that when AUC = 1, the classifier can accurately differentiate between all the positive and the negative class points. However, where AUC = 0, then the classifier would be predicting all negatives as positives, and all positives as negatives. It is the measure of the ability of a classifier to differentiate between classes and is used to summarize the ROC curve. The higher the AUC, the better the model performance at differentiating the positive and negative classes.
The ROC curve was produced by plotting TPR values against the false positive rate (FPR) values using a threshold setting. From the Statistical Package for the Social Sciences (SPSS) software, the ROC curve was generated. The ROC measures the relationship between sensitivity and specificity in a binary classifier and plots against each other. Sensitivity, also known as the true positive rate (TPR) quantifies the ratio of positive classified points to all landslide classes. At the same time, specificity, also known as the false positive rate (FPR), measures the probability of falsely rejecting the null hypothesis [91].
where TP and TN represent the true positive and true negative, respectively, which are the number of landslide pixels classified correctly. FN and FP represent the false negative and false positive, respectively, which are the number of incorrectly classified landslide pixels.
A synthetic index AUC was also calculated from the ROC curves. The value of AUC ranges between 0 and 1 which represents the excellent and poor relationship between AUC and the prediction rate
4. Results
4.1. LSM by AHP
The resulting CR for all the parameters was less than 0.10. This means that the relative weights were appropriate, and the comparisons were consistent [92]. The calculation yielded an acceptable level of CR in the pairwise comparison, sufficient to recognize the weights of the parameters in the landslide susceptibility model. Moreover, the highest weight was assigned to the slope. Elevation, curvature, aspect, STP, and hill shade were also influential. Other parameters, such as TWI, TRI, distance to road, distance to the lake, distance to build up, and distance to trees, were identified as less important. The 12 different landslide factors were correlated and overlayed using the ArcGIS spatial analyst weighted overlay function to obtain the landslide susceptibility map. Using the natural break classification method, the AHP LSM was subsequently divided into; very low, low, moderate, high, and very high susceptibility classes [93,94]. From the AHP map, 20.65% of the area falls within the very-low susceptibility zone, 20.18% is for the low, 20.37% for moderate, 19.45% for the high, and 19.35% for the very-high susceptible areas.
4.2. LSM by Fuzzy Logic
The fuzzy logic applies the fuzzy membership/fuzzification functions rather than the weighted parameters approach used by the AHP method for the landslide conditioning parameter reclassification. After the initial reclassification of each parameter, it followed the reclassification to the simple interpretation of raster data by altering single input values into new output values that were further converted to the continuum of fuzzy logical values between 0 and 1; 0 represents unstable (completely false), and 1 represents stable (completely true) stable terrain. Fuzzy logic uses the reclassified conditioning parameters to create a landslide susceptibility map. Different fuzzy operators were implemented in the analysis, with the fuzzy gamma operator showing the most acceptable result. After standardization, each one of the fuzzy types was used, while the “GAMMA” function gave the most satisfactory result. Fuzzy Gamma establishes the connections between the various input criteria and simply does not return the value of a single membership set as fuzzy OR and fuzzy AND functions. Fuzzy Gamma is applied when the values are greater than the fuzzy Product but less than the fuzzy “Sum”. Where the specified gamma is 1, the result will be similar to fuzzy “Sum”; where gamma is 0, the output is similar to fuzzy Product. Values in between allow the combination of evidence between the two extremes and possibly different from fuzzy “OR” or fuzzy “AND”. Fuzzy Gamma is a compromise of the advanced effect of fuzzy “Sum” and the decreasing effect of fuzzy “Product”. The fuzzy overlay process sums up the landslide conditioning parameters in a GIS environment to produce the final susceptibility map. The output map produced by fuzzy logic was classified into five risk classes, namely: Very High, High, Moderate, Low, and Very Low, as shown in Figure 5. LSM produced by fuzzy logic offers 14.53% spatial area coverage of very low, 42.83% of low susceptibility area, 27.98% of moderate susceptible area, 12.19% of the highly susceptible area, and 2.47% of very highly susceptible areas.
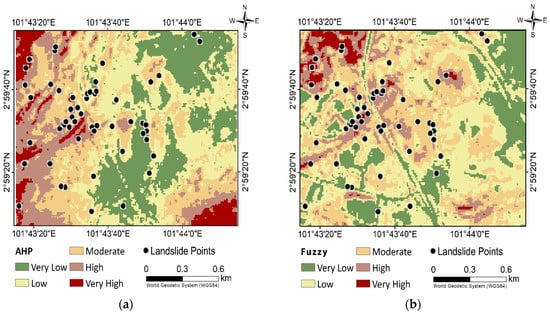
Figure 5.
Landslide susceptibility map by (a) AHP and (b) fuzzy GAMMA overlay models.
Based on a global verification of the influence of topography and environment on the terrain classification, the output maps of the landslide susceptibility models were evaluated qualitatively, which is essential in selecting the most effective method of LSM for a given study location. Table 4 explains the risk level classes and their description and implication.

Table 4.
The level of risk (Australian Geo-Mechanics Society).
4.3. LSM Validation
The LSMs validation is an integral step in every landslide modeling process. The accuracy and efficiency of the AHP and the fuzzy methods were evaluated by applying an independent ROC and the AUC threshold approach. Both methods have generally been involved in the analysis of different types of landslide susceptibility studies.
In this study, the final landslide susceptibility maps of the AHP and fuzzy were validated by comparing the locations of the existing landslides, using the prediction rate methods. The predictive rate method uses the validation dataset to evaluate the landslide susceptibility model’s predictability [95]. Moreover, the prediction rate explained the landslide susceptibility models’ prediction capability over the landslide conditioning factors. A vital point in landslide susceptibility analysis is the need to validate the results to provide significant results. For verification of the landslide susceptibility maps, the 30% validation dataset [96,97] (17 landslide locations) was used based on the random selection.
The values of the AUC show the accuracies of the landslide susceptibility methods applied. From the ROC result in Figure 6, the AUC values of the AHP and Fuzzy logic are 0.859 and 0.802 at a 95% confidence level, respectively. A higher AUC value represents a higher level of accuracy of a susceptibility map. This indicates that the AHP susceptibility map is more accurate as compared to the fuzzy. Generally, the result of the accuracy assessment shows a satisfactory outcome for the susceptibility maps.
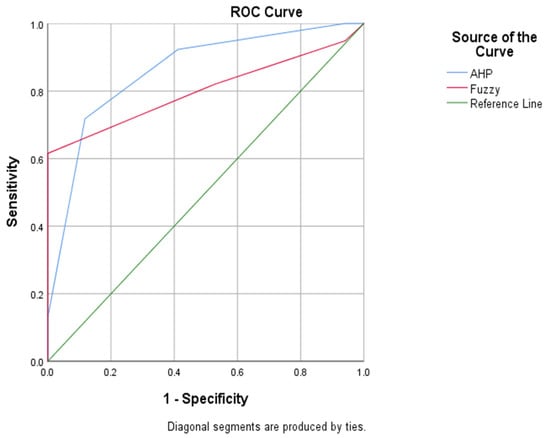
Figure 6.
ROC for validation of AHP and fuzzy models.
5. Discussion
The impact of landslide events in urbanized areas should not be underestimated because it, directly and indirectly, affects lives and properties. Some of these impacts may include loss of industrial, agricultural, forest, and tourist revenues as a result of damage to land, facilities, or transportation systems, and loss of human or animal productivity due to injury or death.
Different LSM models have previously been developed, though, there is no known better universal guideline for LSM model selection. LSM results depend on the structure of the model and data quality [98]. The landslide phenomena investigation and LSM follow a certain number of steps. Landslide conditioning parameters, landslide models, software, and DEMs are essential to successful landslide susceptibility mapping, and they are directly or indirectly connected. Advances in methodologies, software, and DEM resolutions have allowed researchers to choose the most suitable approach, software, and DEMs for the area and the research objectives. Landslide conditioning parameters are a reference to landslide studies as they can test the stability of an area. The parameter’s influence differs and can affect the accuracy of the analysis [99]. Moreover, LSM can be achieved using landslide models. Thus, many models have been developed. The most common method based on multicriteria decision-making algorithms is AHP and fuzzy.
Furthermore, the significance of DEMs in landslide susceptibility studies at either small or large scales was outlined by researchers [100]. For this reason, the importance of DEMs in landslide mapping is inevitable, though several limitations should be considered. For example, the DEMs created from topographic maps are inaccurate in steep terrains [101]. Hence, low-accuracy DEMs tend to flatten the roughness of the topography, thereby decreasing the reliability of the prediction [102]. According to Andrea et al. [103], the spatial resolution of DEMs is important for reliable landslide studies. They evaluated the effectiveness of different DEM resolutions to project ground deformation velocities measured using the PSInSAR technique in the San Fratello and Giampilieri, Italy using (i) a 20-m resolution DEM of the Italian Military Geographic Institute, (ii) a 2=m resolution DEM derived from airborne laser scanning LiDAR data for the San Fratello 2010 landslide, and (iii) a 1-m resolution DEM derived from ALS LiDAR data for the area of Giampilieri. The evaluation was performed by comparing the DEMs elevation with those of each single permanent scatterer (PS) and projecting the measured velocities along the steepest slope direction. Results showed that the 1-m DEM resolution is more suitable for landslide studies. It has been argued that the higher spatial resolution satellite images provide more details for the level of generalization relevant for decision makers at the smaller scale, rendering [104]. One of the most significant features of LiDAR is its very high vertical accuracy, which allows it to represent the Earth’s surface with high accuracy [103]. Warren et al. [105] compared slopes measured in the field with those derived from DEMs and found that higher-resolution DEMs (1 m) produced better results than lower-resolution DEMs (12 m). In this research, 1-m resolution LiDAR data were utilized for the landslide susceptibility study.
For this study, the most effective data were used, and their quality was thoroughly investigated by applying the AHP and fuzzy logic model for landslide susceptibility at Serdang, Malaysia. To achieve this, the AHP prioritized the effective criteria and variables and applied pairwise comparison to create a matrix. The AHP method is carried out in different stages; the creation of pairwise comparison, normalization of the weight of the matrix, derivation of priority sector, calculation of maximum Eigenvalue, computation of the CI with Eigenvalue, analysis of RI, and calculation of CR. The AHP weights and ranks the conditioning factors according to their influence on the location. Systematic analysis of the pair-wise comparison matrix of a list of the landslide conditioning factors was performed using expert opinion scores between 1 and 1/9 to indicate the relative importance. This is considered one of the most suitable and reliable decision-making approaches. The fuzzy membership or fuzzification transforms the input raster into a scale of 0 and 1, indicating the strength of membership in a set based on a specified fuzzification algorithm. A value of 1 indicates full membership in the fuzzy set with membership decreasing to 0, indicating that it is not a member of the fuzzy set. All the datasets have been standardized and expressed in units that can be compared based on the nature of the data and experts’ opinions.
The results of the models showed high accuracy and substantially in agreement when detecting the factor classes that have primary importance for the development of landslides in this area. High landslide susceptibility area is mainly found on cut slopes at the center and southern part of the maps. Moreover, the low susceptibility areas are mainly located in the east and northern parts of the area on the maps. Based on the terrain’s geologic materials, such as bedrock, residual soil, earth, and their mixture, slope movement may occur in five modes, including fall, topple, slide, spread, and flow [6]. The most notable landslide type in Malaysia is the shallow landslide, where the earth is usually less than 4-m deep and occurs during or immediately after intense rainfall [104]. The slopes in this area are characterized by residual soil and soil susceptible to shallow landslide.
Expert opinion is very important in solving complex landslide problems. However, opinions may differ for every individual and thus may be subjected to uncertainty and subjectivity. Therefore, it is vital to analyze the spatial relationship between the landslide conditioning parameters and landslide locations. The two test results showed the effectiveness and independence of all applied selected conditioning factors.
6. Conclusions
Landslide hazard is a complex environmental phenomenon that is gradually becoming a serious threat, especially for people living in hilly areas. This study area is highly vulnerable to landslides as it is characterized by rugged topography and earth movements. Rapid urban expansion, man-made activities, such as construction, and road cutting are aggravating landslides. Therefore, an integrated geomorphological, hydrological, meteorological, and anthropogenic approach is required to minimize risk. In this research, the production of reliable and accurate LSM of the study area to predict the possibility of landslide occurrence was carried out to evaluate and determine the areas at risk of possible future landslides by comparing the AHP and fuzzy logic methodology. Twelve landslide factor maps, i.e., elevation, slope, aspect, hill shade, curvature, SPI, TWI, TRI, distance to build up, distance to road, distance to trees, and distance to lakes, were selected based on expert opinion, literature, and geomorphological characteristics of the terrain. The LSM maps produced by AHP revealed 20.65% very low, 20.18% low, 20.37% moderate, 19.45% high, and 19.35% very high susceptible areas. At the same time, LSM produced by fuzzy revealed 14.53% very low, 42.83% low, 27.98% moderate, 12.19% high, and 2.47% very high susceptible areas. Both models were validated using a total of 56 landslide and non-landslide points. The accuracy of each landslide susceptibility result was validated using the ROC method, which reveals that both models are highly effective. The result of the AHP with an accuracy of 0.859 is slightly more acceptable than the fuzzy with an accuracy of 0.802. These analyses explain the need for the comparison of knowledge-based and data-driven models for landslide susceptibility. A precise LSM model highly depends on conditional factors. It thus assists decision-makers, landscapers, and urban planners in Malaysia in identifying hazard-prone areas for mitigation. It is highly recommended to carry out further studies in this area using different susceptibility models and to incorporate LSM into existing regional plans, especially for hilly and mountainous areas.
Author Contributions
Conceptualization, J.O.; methodology, J.O.; software, J.O.; validation, J.O.; formal analysis, J.O. and B.K.; investigation, J.O. and H.N.; resources, H.Z.M.S.; data curation, J.O.; writing—original draft preparation, J.O. and B.K.; writing—review and editing, J.O., H.N. and B.K.; visualization, B.K.; supervision, H.N., H.Z.M.S. and Z.K.; project administration, H.N.; funding acquisition, F.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is available on request due to ownership right.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pradhan, B.; Sameen, M.I.; Kalantar, B. Ensemble Disagreement Active Learning for Spatial Prediction of Shallow Landslide; Springer: Cham, Switzerland, 2017; ISBN 9783319553429. [Google Scholar]
- Ahmad, J.; Lateh, H.; Saleh, S. Landslide Hazards: Household Vulnerability, Resilience and Coping in Malaysia. J. Educ. Hum. Dev. 2014, 3, 149–155. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Lay, U.S.; Al-Najjar, H.A.H.; Halin, A.A. Conditioning Factors Determination for Landslide Susceptibility Mapping Using Support Vector Machine Learning. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9626–9629. [Google Scholar]
- Qi, T.; Zhao, Y.; Meng, X.; Chen, G.; Dijkstra, T. Ai-Based Susceptibility Analysis of Shallow Landslides Induced by Heavy Rainfall in Tianshui, China. Remote Sens. 2021, 13, 1819. [Google Scholar] [CrossRef]
- Psomiadis, E.; Papazachariou, A.; Soulis, K.X.; Alexiou, D.S.; Charalampopoulos, I. Landslide Mapping and Susceptibility Assessment Using Geospatial Analysis and Earth Observation Data. Land 2020, 9, 133. [Google Scholar] [CrossRef]
- Akter, A.; Noor, M.J.M.M.; Goto, M.; Khanam, S.; Parvez, A.; Rasheduzzaman, M. Landslide Disaster in Malaysia: An Overview. Int. J. Innov. Res. Dev. 2019, 8, 58–71. [Google Scholar] [CrossRef]
- Moradi, M.; Bazyar, M.H.; Mohammadi, Z. GIS-Based Landslide Susceptibility Mapping by AHP Method, a Case Study, Dena City, Iran. J. Basic Appl. Sci. Res. 2012, 2, 6715–6723. [Google Scholar]
- Pradhan, B.; Seeni, M.I.; Kalantar, B. Performance Evaluation and Sensitivity Analysis of Expert-Based, Statistical, Machine Learning, and Hybrid Models for Producing Landslide Susceptibility Maps; Springer: Cham, Switzerland, 2017; ISBN 9783319553429. [Google Scholar]
- Rahman, M.S.; Ahmed, B.; Di, L. Landslide Initiation and Runout Susceptibility Modeling in the Context of Hill Cutting and Rapid Urbanization: A Combined Approach of Weights of Evidence and Spatial Multi-Criteria. J. Mt. Sci. 2017, 14, 1919–1937. [Google Scholar] [CrossRef]
- Erener, A.; Düzgün, H.S.B. Landslide Susceptibility Assessment: What Are the Effects of Mapping Unit and Mapping Method? Environ. Earth Sci. 2012, 66, 859–877. [Google Scholar] [CrossRef]
- Najjar, H.A.H.A.; Pradhan, B.; Kalantar, B.; Sameen, M.I.; Santosh, M.; Alamri, A. Landslide Susceptibility Modeling: An Integrated Novel Method Based on Machine Learning Feature Transformation. Remote Sens. 2021, 13, 3281. [Google Scholar] [CrossRef]
- Roccati, A.; Paliaga, G.; Luino, F.; Faccini, F.; Turconi, L. Gis-Based Landslide Susceptibility Mapping for Land Use Planning and Risk Assessment. Land 2021, 10, 162. [Google Scholar] [CrossRef]
- Parise, M. Landslide Mapping Techniques and Their Use in the Assessment of the Landslide Hazard. Phys. Chem. Earth, Part C Solar, Terr. Planet. Sci. 2001, 26, 697–703. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.T. Landslide Inventory Maps: New Tools for an Old Problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Quesada-román, A. Landslide Risk Index Map at the Municipal Scale for Costa Rica. Int. J. Disaster Risk Reduct. 2021, 56, 102144. [Google Scholar] [CrossRef]
- Quesada-Román, A.; Fallas-López, B.; Hernández-Espinoza, K.; Stoffel, M.; Ballesteros-Cánovas, J.A. Relationships between Earthquakes, Hurricanes, and Landslides in Costa Rica. Landslides 2019, 16, 1539–1550. [Google Scholar] [CrossRef]
- Santangelo, M.; Gioia, D.; Cardinali, M.; Guzzetti, F.; Schiattarella, M. Landslide Inventory Map of the Upper Sinni River Valley, Southern Italy. J. Maps 2015, 11, 444–453. [Google Scholar] [CrossRef]
- Batar, A.K.; Watanabe, T. Landslide Susceptibility Mapping and Assessment Using Geospatial Platforms and Weights of Evidence (WoE) Method in the Indian Himalayan Region: Recent Developments, Gaps, and Future Directions. ISPRS Int. J. Geo-Inf. 2021, 10, 114. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Kalantar, B.; Pradhan, B.; Saeidi, V. Conditioning Factor Determination for Mapping and Prediction of Landslide Susceptibility Using Machine Learning Algorithms. In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications X, Strasbourg, France, 10–12 September 2019; Volume 11156, pp. 97–107. [Google Scholar] [CrossRef]
- Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A.M. Landslide Susceptibility Mapping Using Different GIS-Based Bivariate Models. Water 2019, 11, 1402. [Google Scholar] [CrossRef]
- Kareem Jebur, A. Uses and Applications of Geographic Information Systems. Saudi J. Civ. Eng. 2021, 5, 18–25. [Google Scholar] [CrossRef]
- Aher, S.; Bairagi, S.I. Applications of Advanced Spaceborne Thermal Emission and Reflection Applications of Advanced Spaceborne Thermal Emission and Reflection. Online Int. Interdiscip. Res. J. 2014, 2, 2–14. [Google Scholar]
- Gesch, B.D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The National Elevation Dataset the National Elevation Dataset. J. Am. Soc. Photogramm. Remote Sens. 2015, 68, 5–32. [Google Scholar]
- Barbarella, M.; Fiani, M.; Lugli, A. Application of Lidar-Derived DEM for Detection of Mass Movements on a Landslide. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2013, 40, 89–98. [Google Scholar] [CrossRef]
- Wolock, D.M.; McCabe, G.J. Differences in Topographic Characteristics Computed from 100- and 1000-m Resolution Digital Elevation Model Data. Hydrol. Process. 2000, 14, 987–1002. [Google Scholar] [CrossRef]
- Tarboton, D.G. Terrain Analysis Using Digital Elevation Models in Hydrology. In Proceedings of the 23rd ESRI International Users Conference, San Diego, CA, USA, 6–9 July 2003; pp. 1–14. [Google Scholar]
- Lohani, B.; Ghosh, S. Airborne LiDAR Technology: A Review of Data Collection and Processing Systems. Proc. Natl. Acad. Sci. USA India Sect. A—Phys. Sci. 2017, 87, 567–579. [Google Scholar] [CrossRef]
- Mahalingam, R.; Olsen, M.J.; O’Banion, M.S. Evaluation of Landslide Susceptibility Mapping Techniques Using Lidar-Derived Conditioning Factors (Oregon Case Study). Geomatics, Nat. Hazards Risk 2016, 7, 1884–1907. [Google Scholar] [CrossRef]
- Haneberg, W.C.; Cole, W.F.; Kasali, G. High-Resolution Lidar-Based Landslide Hazard Mapping and Modeling, UCSF Parnassus Campus, San Francisco, USA. Bull. Eng. Geol. Environ. 2009, 68, 263–276. [Google Scholar] [CrossRef]
- Telbisz, T.; Látos, T.; Deák, M.; Székely, B.; Koma, Z.; Standovár, T. The Advantage of Lidar Digital Terrain Models in Doline Morphometry Compared to Topographic Map Based Datasets—Aggtelek Karst (Hungary) as an Example. Acta Carsologica 2016, 45, 5–18. [Google Scholar] [CrossRef]
- Brubaker, K.M.; Myers, W.L.; Drohan, P.J.; Miller, D.A.; Boyer, E.W. The Use of LiDAR Terrain Data in Characterizing Surface Roughness and Microtopography. Appl. Environ. Soil Sci. 2013, 2013, 13. [Google Scholar] [CrossRef]
- Schmid, K.A.; Hadley, B.C.; Wijekoon, N. Vertical Accuracy and Use of Topographic LIDAR Data in Coastal Marshes. J. Coast. Res. 2011, 27, 116–132. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Peterson, J.; Chandra, S. Large Area DEM Generation Using Airborne LiDAR Data and Quality Control. In Proceedings of the 8th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Shanghai, China, 25–27 June 2008; pp. 79–85. [Google Scholar]
- Igwe, O.; John, U.I.; Solomon, O.; Obinna, O. GIS-Based Gully Erosion Susceptibility Modeling, Adapting Bivariate Statistical Method and AHP Approach in Gombe Town and Environs Northeast Nigeria. Geoenvironmental Disasters 2020, 7, 1–16. [Google Scholar] [CrossRef]
- Maskeliunaite, L.; Sivilevičius, H. Expert Evaluation of Criteria Describing the Quality of Travelling by International Passenger Train: Technological, Economic and Safety Perspectives. Technol. Econ. Dev. Econ. 2012, 18, 544–566. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A Review of Uncertainty Quantification in Deep Learning: Techniques, Applications and Challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. Multi-Criteria Risk Evaluation by Integrating an Analytical Network Process Approach into GIS-Based Sensitivity and Uncertainty Analyses. Geomat. Nat. Hazards Risk 2018, 9, 127–151. [Google Scholar] [CrossRef]
- Ghosh, S. Knowledge Guided Empirical Prediction of Landslide Hazard. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Norton, J. An Introduction to Sensitivity Assessment of Simulation Models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the Quality of Landslide Susceptibility Models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S.; et al. Flood Detection and Susceptibility Mapping Using Sentinel-1 Remote Sensing Data and a Machine Learning Approach: Hybrid Intelligence of Bagging Ensemble Based on K-Nearest Neighbor Classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef]
- Pham, Q.B.; Achour, Y.; Ali, S.A.; Parvin, F.; Vojtek, M.; Vojteková, J.; Al-Ansari, N.; Achu, A.L.; Costache, R.; Khedher, K.M.; et al. A Comparison among Fuzzy Multi-Criteria Decision Making, Bivariate, Multivariate and Machine Learning Models in Landslide Susceptibility Mapping. Geomatics, Nat. Hazards Risk 2021, 12, 1741–1777. [Google Scholar] [CrossRef]
- Gutierrez, R.; Gibeaut, J.C.; Smyth, R.C.; Hepner, T.L.; Andrews, J.R.; Weed, C.; Mastin, M. Precise Airborne Lidar Surveying for Coastal Research and Geohazards Applications. Int. Arch. Photogramm. Remote Sens. 2001, 34, 22–24. [Google Scholar]
- Shano, L.; Raghuvanshi, T.K.; Meten, M. Landslide Susceptibility Evaluation and Hazard Zonation Techniques—A Review. Geoenvironmental Disasters 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Nsengiyumva, J.B.; Luo, G.; Nahayo, L.; Huang, X.; Cai, P. Landslide Susceptibility Assessment Using Spatial Multi-Criteria Evaluation Model in Rwanda. Int. J. Environ. Res. Public Health 2018, 15, 243. [Google Scholar] [CrossRef]
- Toloie-Eshlaghy, A.; Homayonfar, M.; Aghaziarati, M.; Arbabiun, P. A Subjective Weighting Method Based on Group Decision Making for Ranking and Measuring Criteria Values. Aust. J. Basic Appl. Sci. 2011, 5, 2034–2040. [Google Scholar]
- Polykretis, C.; Ferentinou, M.; Chalkias, C. A Comparative Study of Landslide Susceptibility Mapping Using Landslide Susceptibility Index and Artificial Neural Networks in the Krios River and Krathis River Catchments (Northern Peloponnesus, Greece). Bull. Eng. Geol. Environ. 2014, 74, 27–45. [Google Scholar] [CrossRef]
- Saadatkhah, N.; Kassim, A.; Lee, L.M. Qualitative and Quantitative Landslide Susceptibility Assessments in Hulu Kelang Area, Malaysia. Electron. J. Geotech. Eng. 2014, 19, 545–563. [Google Scholar]
- Sulaiman, M.S.; Nazaruddin, A.; Salleh, N.M.; Abidin, R.Z.; Miniandi, N.D.; Yusoff, A.H. Landslide Occurrences in Malaysia Based on Soil Series and Lithology Factors. Int. J. Adv. Sci. Technol. 2019, 28, 1–26. [Google Scholar]
- Farooq Ahmed, M.; Rogers, J.D.; Ismail, E.H. A Regional Level Preliminary Landslide Susceptibility Study of the Upper Indus River Basin. Eur. J. Remote Sens. 2014, 47, 343–373. [Google Scholar] [CrossRef]
- Hinks, T.; Carr, H.; Gharibi, H.; Laefer, D.F. Visualisation of Urban Airborne Laser Scanning Data with Occlusion Images. ISPRS J. Photogramm. Remote Sens. 2015, 104, 77–87. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L. Using Discrete Laser Pulse Return Intensity to Model Canopy Transmittance. The Photogramm. J. Finland 2007, 20, 16–26. [Google Scholar]
- Bolstad, P.V.; Stowe, T. Evaluation of DEM Accuracy. Elevation, Slope, and Aspect. Photogramm. Eng. Remote Sens. 1994, 60, 1327–1332. [Google Scholar]
- Lakshmi, S.E.; Yarrakula, K. Review and Critical Analysis on Digital Elevation Models. Geofizika 2018, 35, 129–157. [Google Scholar] [CrossRef]
- Štular, B.; Lozić, E.; Eichert, S. Airborne LiDAR-Derived Digital Elevation Model for Archaeology. Remote Sens. 2021, 13, 1855. [Google Scholar] [CrossRef]
- Guzzetti, F.; Galli, M.; Reichenbach, P.; Ardizzone, F.; Cardinali, M. Landslide Hazard Assessment in the Collazzone Area, Umbria, Central Italy. Nat. Hazards Earth Syst. Sci. 2006, 6, 115–131. [Google Scholar] [CrossRef]
- Corominas, J.; Westen, C.J.V.; Frattini, P.; Fotopoulou, S. Recommendations for the Quantitative Analysis of Landslide Risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Beven, K.; Germann, P. Macropores and Water Flow in Soils Revisited. Water Resour. Res. 2013, 49, 3071–3092. [Google Scholar] [CrossRef]
- Arnone, E.; Dialynas, Y.G.; Noto, L.V.; Bras, R.L. Parameter Uncertainty in Shallow Rainfall-Triggered Landslide Modeling at Basin Scale: A Probabilistic Approach. Procedia Earth Planet. Sci. 2014, 9, 101–111. [Google Scholar] [CrossRef]
- Referee, A.; Carlo, M.; Comments, S.; Carlo, M. Interactive Comment on “Probabilistic Landslide Ensemble Prediction Systems: Lessons to Be Learned from Hydrology” by Ekrem Canli et Al. Nat. Hazards Earth Syst. Sci. Discuss 2018, 18, 2183–2202. [Google Scholar]
- Zawawi, A.A.; Shiba, M.; Jemali, N.J.N. Landform Classification for Site Evaluation and Forest Planning: Integration between Scientific Approach and Traditional Concept. Sains Malays. 2014, 43, 349–358. [Google Scholar]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Bui, D.T. Landslide Susceptibility Evaluation and Management Using Different Machine Learning Methods in the Gallicash River Watershed, Iran. Remote Sens. 2020, 12, 475. [Google Scholar] [CrossRef]
- Sharma, A.; Prakash, C. Evaluating the Impact of Road Construction on Landslide Susceptibility-A Case Study of Mandi District, Himachal Pradesh, India. Authorea Prepr. 2021, preprint, 1–14. [Google Scholar]
- Tanyaş, H.; Görüm, T.; Kirschbaum, D.; Lombardo, L. Could Road Constructions Be More Hazardous than an Earthquake in Terms of Mass Movement? Nat. Hazards 2022, 112, 639–663. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Oreńczak, N.; Pasternak, M. Investigating the E Ff Ect of Cross-Modeling in Landslide Susceptibility Mapping. Appl. Sci. 2020, 10, 6335. [Google Scholar] [CrossRef]
- Aslam, B.; Maqsoom, A.; Khalil, U.; Ghorbanzadeh, O.; Blaschke, T.; Farooq, D.; Tufail, R.F.; Suhail, S.A.; Ghamisi, P. Evaluation of Different Landslide Susceptibility Models for a Local Scale in the Chitral District, Northern Pakistan. Sensors 2022, 22, 3107. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial Neural Networks: Fundamentals, Computing, Design, and Application. J. Methods Microbiol. 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Peng, C.; Wen, X. Recent Applications of Artificial Neural Networks in Forest Resource Management: An Overview Applications in Forest Resource Management; AAAI: Palo Alto, CA, USA, 1999. [Google Scholar]
- Haghbin, M.; Sharafati, A.; Motta, D.; Al-ansari, N. Applications of Soft Computing Models for Predicting Sea Surface Temperature: A Comprehensive Review and Assessment. Prog. Earth Planet. Sci. 2021, 9, 1–19. [Google Scholar] [CrossRef]
- Grant, M.J.; Booth, A. A Typology of Reviews: An Analysis of 14 Review Types and Associated Methodologies. Health Info. Libr. J. 2009, 26, 91–108. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Li, L.; Tan, Y. Validation of Spatial Prediction Models for Landslide Susceptibility Mapping by Considering Structural Similarity. Int. J. Geo-Inf. 2017, 6, 103. [Google Scholar] [CrossRef]
- Westen, C.J.V.; Fonseca, F. International Society for Soil Mechanics And. In Proceedings of the SCG-XIII International Symposium on Landslides, Online, 22–26 February 2021. [Google Scholar]
- Dou, J.; Bui, D.T.; Yunus, A.P.; Jia, K.; Song, X.; Revhaug, I.; Xia, H.; Zhu, Z. Optimization of Causative Factors for Landslide Susceptibility Evaluation Using Remote Sensing and GIS Data in Parts of Niigata, Japan. PLoS ONE 2015, 10, e0133262. [Google Scholar] [CrossRef] [PubMed]
- Saaty, R.W. The Analytic Hierarchy Process-What It Is and How It Is Used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Velasquez, M.; Hester, P. An Analysis of Multi-Criteria Decision-Making Methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Nesticò, A.; Somma, P. Comparative Analysis of Multi-Criteria Methods for the Enhancement of Historical Buildings. Sustain. 2019, 11, 4526. [Google Scholar] [CrossRef]
- Zabihi, H.; Alizadeh, M.; Langat, P.K.; Karami, M.; Shahabi, H.; Ahmad, A.; Said, M.N.; Lee, S. GIS Multi-Criteria Analysis by Orderedweighted Averaging (OWA): Toward an Integrated Citrus Management Strategy. Sustainability 2019, 11, 1009. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process. McGraw, New York. Agric. Econ. Rev. 1980, 70, 333. [Google Scholar]
- Jain, K. Site Suitability Analysis for Urban Development Using GIS. J. Appl. Sci. 2017, 7, 2576–2583. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Shadman Roodposhti, M.; Jankowski, P.; Blaschke, T. A GIS-Based Extended Fuzzy Multi-Criteria Evaluation for Landslide Susceptibility Mapping. Comput. Geosci. 2014, 73, 208–221. [Google Scholar] [CrossRef] [PubMed]
- Vakhshoori, V.; Zare, M. Landslide Susceptibility Mapping by Comparing Weight of Evidence, Fuzzy Logic, and Frequency Ratio Methods. Geomatics, Nat. Hazards Risk 2016, 7, 1731–1752. [Google Scholar] [CrossRef]
- Baidya, P.; Chutia, D.; Sudhakar, S.; Goswami, C.; Goswami, J.; Saikhom, V.; Singh, P.S.; Sarma, K.K. Effectiveness of Fuzzy Overlay Function for Multi-Criteria Spatial Modeling—A Case Study on Preparation of Land Resources Map for Mawsynram Block of East Khasi Hills District of Meghalaya, India. J. Geogr. Inf. Syst. 2014, 06, 605–612. [Google Scholar] [CrossRef]
- Bamberger, S. Determining the Suitability of Yak-Based Agriculture in Illinois: A Site Suitability Analysis Using Fuzzy Overlay. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2017. [Google Scholar]
- Aziz, R.S.; Khodakarami, L. Application of GIS Models in Site Selection of Waste Disposal in an Urban Area. WIT Trans. State Art Sci. Eng. 2013, 77, 27–35. [Google Scholar]
- ESRI. ESRI How Fuzzy Overlay Works; Environmental Systems Research Institute: Redlands, CA, USA, 1995. [Google Scholar]
- Pourghasemi, H.R.; Kariminejad, N.; Gayen, A.; Komac, M. Statistical Functions Used for Spatial Modelling Due to Assessment of Landslide Distribution and Landscape-Interaction Factors in Iran. Geosci. Front. 2020, 11, 1257–1269. [Google Scholar] [CrossRef]
- Mǎrgǎrint, M.C.; Grozavu, A.; Patriche, C.V. Assessing the Spatial Variability of Coefficients of Landslide Predictors in Different Regions of Romania Using Logistic Regression. Nat. Hazards Earth Syst. Sci. 2013, 13, 3339–3355. [Google Scholar] [CrossRef]
- He, H.; Hu, D.; Sun, Q.; Zhu, L.; Liu, Y. A Landslide Susceptibility Assessment Method Based on GIS Technology and an AHP-Weighted Information Content Method: A Case Study of Southern Anhui, China. ISPRS Int. J. Geo-Inf. 2019, 8, 266. [Google Scholar] [CrossRef]
- El Jazouli, A.; Barakat, A.; Khellouk, R. GIS-Multicriteria Evaluation Using AHP for Landslide Susceptibility Mapping in Oum Er Rbia High Basin (Morocco). Geoenvironmental Disasters 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Ahmed, B. Landslide Susceptibility Mapping Using Multi-Criteria Evaluation Techniques in Chittagong Metropolitan Area, Bangladesh. Landslides 2015, 12, 1077–1095. [Google Scholar] [CrossRef]
- Fariza, A.; Abhimata, N.P.; Nur Hasim, J.A. Earthquake Disaster Risk Map in East Java, Indonesia, Using Analytical Hierarchy Process—Natural Break Classification. 2016 Int. Conf. Knowl. Creat. Intell. Comput. KCIC 2016 2017, 141–147. [Google Scholar] [CrossRef]
- Febrianto, H.; Fariza, A.; Hasim, J.A.N. Urban Flood Risk Mapping Using Analytic Hierarchy Process and Natural Break Classification (Case Study: Surabaya, East Java, Indonesia). In Proceedings of the 2016 International Conference on Knowledge Creation and Intelligent Computing (KCIC), Manado, Indonesia, 15–17 November 2016; pp. 148–154. [Google Scholar] [CrossRef]
- Gigović, L.; Drobnjak, S.; Pamučar, D. The Application of the Hybrid GIS Spatial Multi-Criteria Decision Analysis Best–Worst Methodology for Landslide Susceptibility Mapping. ISPRS Int. J. Geo-Inf. 2019, 8, 79. [Google Scholar] [CrossRef]
- Panchal, S.; Shrivastava, A.K. Landslide Hazard Assessment Using Analytic Hierarchy Process (AHP): A Case Study of National Highway 5 in India. Ain Shams Eng. J. 2022, 13, 101626. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of Fuzzy Logic and Analytical Hierarchy Process (AHP) to Landslide Susceptibility Mapping at Haraz Watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Pham, B.T.; Khosravi, K.; Prakash, I. Application and Comparison of Decision Tree-Based Machine Learning Methods in Landside Susceptibility Assessment at Pauri Garhwal Area, Uttarakhand, India. Environ. Process. 2017, 4, 711–730. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, Z.; Xu, Q.; Li, W. Risk Factor Detection and Landslide Susceptibility Mapping Using Geo-Detector and Random Forest Models: The 2018 Hokkaido Eastern Iburi Earthquake. Remote Sens. 2021, 13, 1157. [Google Scholar] [CrossRef]
- Zhong, T.; Cang, X.; Li, R.; Tang, G. Landform Classification Based on Hillslope Units from DEMs. In Proceedings of the 30th Asian Conference on Remote Sensing (ACRS), Beijing, China, 18–23 October 2009; Volume 3, pp. 1686–1691. [Google Scholar]
- Kakavas, M.P.; Nikolakopoulos, K.G. Digital Elevation Models of Rockfalls and Landslides: A Review and Meta-Analysis. Geosciences 2021, 11, 256. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Francioni, A.; Cockburn, J.M.H. LiDAR DEM Smoothing and the Preservation of Drainage Features. Remote Sens. 2019, 11, 1926. [Google Scholar] [CrossRef]
- Ciampalini, A.; Raspini, F.; Frodella, W.; Bardi, F.; Bianchini, S.; Moretti, S. The Effectiveness of High-Resolution LiDAR Data Combined with PSInSAR Data in Landslide Study. Landslides 2016, 13, 399–410. [Google Scholar] [CrossRef]
- Mahavir high (spatial) resolution vs. Low resolution Images. Int. Arch. Photogramm. Remote Sens. 2000, 33, 127–132.
- Vaze, J.; Teng, J. High Resolution LiDAR DEM—How Good Is It? In Proceedings of the MODSIM07—Land, Water and Environmental Management: Integrated Systems for Sustainability, Christchurch, New Zealand, 10–13 December 2007; pp. 692–698. [Google Scholar]
- Singh, H.; Huat, B.B.K.; Jamaludin, S. Slope Assessment Systems: A Review and Evaluation of Current Techniques Used for Cut Slopes in the Mountainous Terrain of West Malaysia. Electron. J. Geotech. Eng. 2008, 13, 1–24. [Google Scholar]
- Warren, S.D.; Hohmann, M.G.; Auerswald, K.; Mitasova, H. An Evaluation of Methods to Determine Slope Using Digital Elevation Data. Catena 2004, 58, 215–233. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).