Abstract
The use of 3D point clouds to improve the understanding of natural phenomena is currently applied in natural hazard investigations, including the quantification of rockfall activity. However, 3D point cloud treatment is typically accomplished using nondedicated (and not optimal) software. To fill this gap, we present an open-source, specific rockfall package in an object-oriented toolbox developed in the MATLAB® environment. The proposed package offers a complete and semiautomatic 3D solution that spans from extraction to identification and volume estimations of rockfall sources using state-of-the-art methods and newly implemented algorithms. To illustrate the capabilities of this package, we acquired a series of high-quality point clouds in a pilot study area referred to as the La Cornalle cliff (West Switzerland), obtained robust volume estimations at different volumetric scales, and derived rockfall magnitude–frequency distributions, which assisted in the assessment of rockfall activity and long-term erosion rates. An outcome of the case study shows the influence of the volume computation on the magnitude–frequency distribution and ensuing erosion process interpretation.
1. Introduction
3D point clouds are commonly used in different scientific domains and in geosciences. In geosciences, the use of point clouds mainly focuses on capturing outcrop geometry [1], mapping geological layers [2], or investigating surface morphological changes [3,4]. In the topic of natural hazards, point clouds are frequently used for mapping landslides and monitoring topographic changes resulting from rockfall activity or mass movement [5].
In natural hazards, point clouds originate from active sensors, such as laser scanners, also known as LiDAR technologies [6,7], or from passive sensors and workflows, such as classic photogrammetry or structure-from-motion (SFM) [8,9,10,11]. During the last decade, the popularization of point clouds acquired from ground-based LiDAR has allowed the rapid mass collection of slope surface measurements [12,13]. These high-accuracy and high-spatial-resolution data have opened new ways of investigating natural hazards [14,15,16,17]. Working with multitemporal high-density point clouds (typically over 100 million points per scan) or large datasets requires a widely applicable and powerful programming language. This has led to the development of open-source software dedicated to processing point clouds, most of which were originally dedicated to civil engineering or robotics, such as CloudCompare [18] or Point Cloud Library [19]. However, several challenges still exist in the management and extraction of this large amount of data collected for natural hazard studies, in particular for detecting and estimating the volume of rockfalls in their source areas. In addition, a key issue is how to gather all tools into a single structure, as has been done for aerial laser scanning in the domains of forestry and land use [20].
Extracting rockfall magnitudes, frequencies, and locations from high-resolution, multitemporal 3D point clouds has been an active research topic in recent decades. Examples include investigations of fragmental rockfalls in mountainous areas [16], investigations of coastal cliffs shaped by sea erosion [14,21,22,23], clustering of rockfall events [24,25,26,27], and investigations of rockfalls along transportation corridors [28,29]. From a methodological point of view, most of the abovementioned studies use grid DEMs (in 2.5D) that have been interpolated from a point cloud parallel to the rock wall, which allows the extraction of rockfall volumes by subtracting multitemporal or oblique DEMs [30,31]. However, this procedure does not facilitate computing complex shapes with “concave” faces. Some recent studies as in [32] investigated this problem. In this paper, we illustrate one possible method to semiautomatically compute the retrospective detection of rockfall sources and related complex geometries (i.e., concave hull volume) using a straightforward methodology.
To detect retrospective rockfall sources, the compared point clouds need prealignment or co-registration. The detection is performed using a point-to-surface comparison combined with a spatial filter. Then, to identify the true rockfall sources, a spatial clustering algorithm is used to segment points belonging to each rockfall source. Finally, we applied a shape reconstruction algorithm, used in the domain of computer graphics, to compute complex rockfall source shapes and volumes, including concavities. This procedure is implemented in MATLAB with the landslide specific RockfallQuantification package, which is part of the free code toolbox 3DPointCloudToolBox, based on free code components and well-established algorithms for point cloud data treatment.
We attempted to demonstrate the efficiency of this method on the study area of the rock wall of the La Cornalle cliff. The obtained results allowed us to carry out a sensitivity analysis of the rockfall source volume computation on the erosion rate, and rockfall assessment interpretation, using a magnitude–frequency plot and power-law regression as described in [22,31,33,34,35,36,37].
2. Toolbox for 3D Point Cloud Processing
We create a point cloud toolbox, referred to as the 3DPointCloudToolBox, with emphasis on specific tools used for landslide and rockfall investigations (see Appendix A). This library uses object-oriented programming under the MATLAB® environment, which enables the management of large datasets and complex functions with increased speed [38]. This selection provides a suitable environment for any user to enhance the library of the toolbox owing to the work of the MathWorks® community. Some properties, such as position, color, or intensity, are obtained as direct information extracted from LiDAR devices or photogrammetric models, whereas other properties, such as normal vectors, curvature, etc., are computed in postprocessing when needed. Other included properties are related to the spatial distribution of the points, such as Delaunay triangulation or voxel structure, Kd-tree [39]. The presented toolbox can be downloaded under link at Supplementary materials.
3. Toolbox-Specific Landslide Package: Retrospective Rockfall Source Detection and Volume Estimation Processing
3.1. Step 1: Rockfall Source Location Extract by Thresholding
The first step consists of locating retrospective rockfall sources via classification into two different classes:
- Points belonging to topographic changes assumed to result from rockfalls.
- Points belonging to unchanged topography assumed to be stable surfaces.
The changes between two point cloud acquisitions are identified by a classical method described in [40]. The detection of rockfall sources uses the difference in distance between two point clouds of different epochs. The computation of the difference is performed using a point-to-surface comparison to obtain the shortest distance (Euclidean distance) from each point to the surface as di = Δ(Pi, S), where (Pi) is, for example, a (i) point in the pre-rockfall event (pre) point cloud (P) of size (n), (S) is the surface built from the post-rockfall event (post) point cloud using the triangulation mesh, and (di) is the computed signed distance along the local normal of (S). If no acquisition bias exists in the point cloud, the distribution of distance differences without surface change follows a normal distribution centered on zero. In the locations at which a change in topography occurs, the distance comparison (di) must be larger than the standard deviation (σ). According to [5], the standard deviation of the measurements between two epochs can be high and depends on multiple factors, such as the quality of the point cloud datasets, the density of the points, the presence of vegetation, the roughness of the relief, and the quality of the alignment between the point clouds and/or the acquisition locations between the two epochs (LiDAR position or picture positions). According to [41], point cloud points are assumed to be indicative of topographic changes (i.e., here, a rockfall source) without ambiguity when the point-to-surface comparison distances are larger than two times the standard deviation (2σ). As proposed by [41], this threshold can be improved by applying a spatial filter using the mean point-to-surface comparison distance of a point and its 25 nearest neighbors. Thus, the thresholding conditions are defined as follows:
The points representing the conditions in Equations (1) and (2) are merged for each neighborhood as one set of points belonging to a rockfall source. The result is spatially distributed points that form clusters corresponding to rockfall sources and isolated points associated with noise (Figure 1).
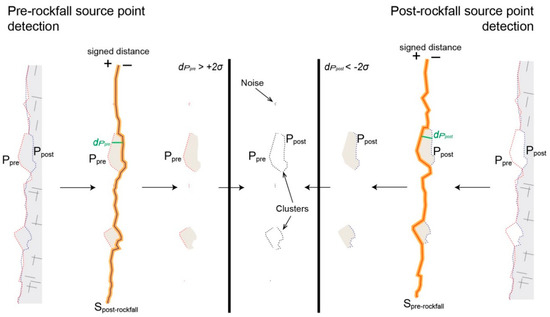
Figure 1.
Sketch of the process of localizing rockfall sources. Where P are the points, S is the reconstructed surface from point cloud at different epochs, and dP is the difference in distance from the point-to-surface comparison. The subscripts pre and post denote pre- and post-rockfall event acquisition, respectively.
3.2. Step 2: Clustering Rockfall Sources
The second step consists of the identification of each cluster representing a single source and the removal of outliers. Currently, the segmentation of point clouds into clusters uses the density-based clustering algorithm DBSCAN [42], as applied in [24]. The principle behind DBSCAN [42] consists of scanning a point cloud with a selected neighboring radius (ε) assuming the availability of the minimum number of points (k) required to create a cluster. The choice of the minimum number of points (k) and the neighboring radius (ε) depends on the point cloud point density and the volume to be detected. This point is not intuitive and is a limitation of DBSCAN as it is necessary to first identify a reasonable measure of similarity for the dataset, before selecting the optimal (ε) It can be determined by a trial-and-error procedure.
A solution to these shortcomings is to use the OPTICS algorithm (ordering points to identify the clustering structure) [43] as a variant of DBSCAN. When using the OPTICS algorithm, only the minimum number of points (k) considered as a cluster is needed. Then, the value of (ε) can be calculated from the chosen (k). Based on the reachability plot structure, an optimal neighborhood radius (ε) containing a predefined (k) points is given by [43]
where (n) is the number of points in the dataset, (m) is the dimensionality of the experimental space, (Γ) is the gamma function, and (V) is the volume of the space formed by m points. The OPTICS algorithm sorts the data within a point cloud according to their distance and core distance and categorizes the points into one of three categories: core points, border points, or outliers (Figure 2). A point (i) of a point cloud is defined as follows:
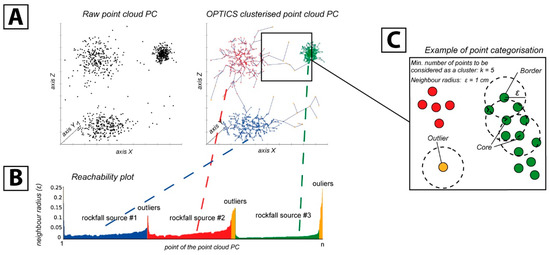
Figure 2.
(A) Example of the raw dataset required to individualize the different clusters representing the different rockfall sources. (B) The OPTICS (ordering points to identify the clustering structure) density-based clustering algorithm allows classification according to the reachability distance or neighbor radius. (C) The classification allows attributing each point as a border or core point. Moreover, the OPTICS algorithm allows the identification of outlier points to remove.
- A core point, if the neighborhood of radius (ε), has at least k-points (reachable points);
- A border point possesses at least one core point within a radius (ε);
- An outlier is a point with no point or no core point within its radius (ε).
Now, if a point (i) is a core point, then it forms a cluster together with all points (core or border) that are reachable from it. They are mutually densely connected. Each cluster contains at least one core point.
According to [43], the OPTICS algorithm is a well-suited clustering method for datasets with a large number of points. In addition, OPTICS was successfully used in chemometrics to reveal clusters of arbitrary shapes with differing densities [44].
After processing, the point cloud is divided into a series of point cloud sets corresponding to its clusters and outliers. Then, at the end of step 2, a cluster is considered a rockfall source when it is a compound of points from different epochs, pre- and post-rockfall sources. The single epoch clusters and outliers are removed.
3.3. Step 3: Rockfall Source Volume Estimation
The last step consists of calculating the volumes of the different sets of clustered points identified as rockfall sources. The volume computation utilizes the full 3D point cloud using the α-shape hull algorithm [45,46] to take into account the natural geometric complexities encountered for rockfall source shapes. This algorithm, originally developed in the domain of computer graphics to recreate complex surfaces, is applied to geometrical studies in biosciences, [47], and its uses include visualization and volume estimations. The α shape is a mathematical expression used for the representation of complex shapes (convex or concave) by the linear approximation of the original shape from a set of points [48]. According to [45], the α shape is the generalized form of the concave hull in which it is a complex of Delaunay triangulation (DT) in 2D or 3D. For a given value of α, the α-complex includes all the simplexes in the DT that have an empty circumscribing sphere with a squared radius equal to or smaller than α (Figure 3).
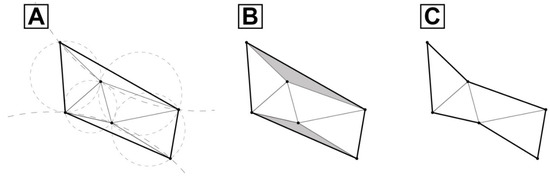
Figure 3.
Example of 2D projection of the α-shape hull construction concept. (A) Outer surface Delaunay triangulation (DT, convex shape) with all simplex triangles and circumscribing circles. (B) Gray triangles are defined by circumscribing circles with a radius larger than the defined research radius α. (C) New outer surface from the α shape with concavities formed by the points. The shape is an α-complex compound of multiple simplexes (triangles) from DT.
To define the closeness to a real shape or the envelope (Sα) formed by a set of points, the value used is an α value corresponding to a research radius in the point cloud ranging from 0 to ∞ and follows the subsequent conditions:
- If α = ∞, Sα is the convex hull of the point cloud;
- If α = 0, Sα is each point of the point cloud itself;
- If 0 < α < ∞, Sα will be the largest polyhedron or shape connecting m points of the point cloud.
In addition, we look for an efficient determination of the volume of this specific shape (Sα). As Sα is a complex of DT, we use the DT to decompose volumes defined by the envelope of Sα into tetrahedrons. The volume of a i tetrahedron with a triangular base of a given area, A, and a height, h, are given as follows:
The volume of the source of a rockfall is equal to the sum of all n tetrahedron volumes, Vi, inside an α-shaped Sα defined as follows:
This process is applied to all rockfall sources. The precision of the volume calculation depends on the α value. It is possible to have an intuitive perception of the real volume by plotting the volume versus the α value, and the best α value is then located at the first asymptotic behavior instance (Figure 4).
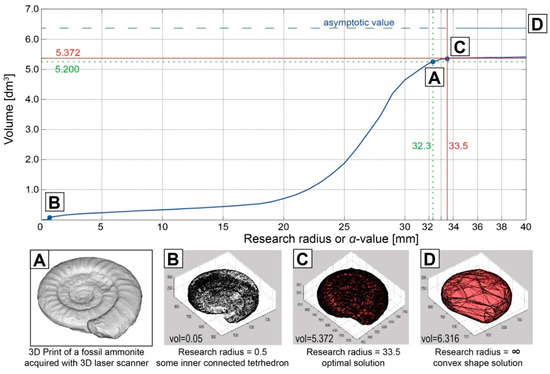
Figure 4.
Example illustrating the way to find the optimal research radius that defines the α shape to compute the closer concave hull volume. The results are plotted on a research radius/volume chart. (A) Shows the print of a fossil ammonite. (B) Point cloud with a small research radius with inner connected tetrahedrons. (C) Shows the optimal research radius defined by the flexure of the curve. (D) Results with infinite radius leading to the convex hull.
4. Case Study
To illustrate the application of the abovementioned methodology and its implementation in MATLAB, we carried out a series of point cloud acquisitions with a terrestrial LiDAR device at a study site located a few kilometers eastward of Lausanne (Vaud, Switzerland) in the Lavaux region (Figure 5A) within the Molasse Swiss Plateau [49]. The region is affected by several critical slow-moving landslides and numerous rockfall activities [50].

Figure 5.
(A)Map of the geological setting of western Switzerland. Red dots indicate the location of the study area in the Molasse Swiss Plateau near Lausanne. (B) La Cornalle cliff is the lateral scarp (green circle) of the slow-moving landslide indicated in yellow. (C) Overview of La Cornalle cliff on top of a slow-moving landslide. (D) A closer view of the cliff shows the lithology of the area composed of alternating metric layers of sandstone and marls. Source map from Swisstopo and orthophoto from Google Earth.
The pilot study area, referred to as the La Cornalle cliff, is part of the lateral scarp of a slow-moving landslide (Figure 5B) that has been well documented since the 18th century and has been active for 10,000 years, resulting in several hazardous events [50]. The cliff, which is over 35 m high and 110 m long (Figure 5C), is an interesting actual-scale laboratory used to study rockfall processes, including the triggering conditions needed for the erosion of molassic rock, which leads to estimation of the erosion rate induced by rockfall activity. The cliff is hardly accessible for direct measurement.
The La Cornalle cliff is composed of subhorizontal alternations of decimetric to metric beds (0.1–3 m) of sandstone and marls (Figure 5D) of Chattian age from the Lower Freshwater Molasse [51]. Molassic rocks are generally weak rocks that are highly affected by erosional processes. The bedding is monocline and dips in the opposite direction of the slope. Four sets of discontinuities are present: stratification S0 125/14°, joint system J1 234/86° subparallel to the cliff face, and joint systems J2 150/75° and J3 325/80° nearly perpendicular to the slope. Discontinuities are clearly present on sandstone beds. The spacing varies from 0.2 to 1.0 m for J1 and from 0.15 to 2 m for J2 and J3, respectively.
The significant rockfall sources located in the sandstone beds are caused by the differentiated erosion rate between marls and sandstone. This phenomenon induces the overhanging and toppling failure mechanisms of sandstone beds. Numerous rockfalls accumulate material on the top of the slow-moving landslide [52], which promotes movement. Based on structural analysis, the expected block volumes could vary from 0.003 m3 (0.1 × 0.2 × 0.15 m) for the minimal volume to 6.0 m3 (3.0 × 1.0 × 2.0 m) for the maximal volume.
We acquired a first point cloud of the cliff from a ground-based LiDAR survey in June 2010. A second acquisition was completed in September 2012; afterward, the cliff was monitored by LiDAR four times per year (seasonally) up to May 2015. The data were collected with an Optech/Teledyne ILIRS 3DER with theoretical accuracy of 7 mm at 100 m and a standard deviation of 10 mm [53]. The footprint at the cliff range (~300 m) was approximately 50 mm. The effective point surface density was of 860 pts/m2.
5. Results
The results are illustrated to show some output from typical datasets from 3D point clouds. Table 1 reports the input parameters used in the illustrated results, which were obtained automatically by the algorithm and manually by the user. When available, the automatic parameters proposed by the software were applied. The user-defined parameters were as follows:

Table 1.
Example of input parameters used for the La Cornalle cliff case study.
With a minimum of 34 points, it is expected to detect volumes larger than 0.5 L according to the described point surface density. The α value was determined for each point rockfall source based on the procedure described in Section 3.3.
As an example, Figure 6A shows the observed and identified major rockfall events from sandstone beds between September 2012 and March 2013 during which the northern part of the cliff experienced important rockfall activity. Thirty-one rockfall events were identified via photographic comparison, mostly the important volumes. Figure 6B shows the identified rockfall sources after computation using the developed toolbox and applying the presented methods on the LiDAR data collected between September 2012 and March 2013. Each rockfall source belongs to a different-colored point cloud. In total, 49 individualized rockfall sources extracted with the presented procedure were identified. When comparing the two results, we noted that the difference in the identified number of rockfall events comes from the small undetected rockfall sources in the picture analysis.

Figure 6.
(A) An example of the location of identified rockfalls (green) based on field observations and picture analysis between two epochs (Fall 2012–Spring 2013). (B) Identified points belonging to different rockfall sources after using the rockfall source extraction function on the acquired point cloud between Fall 2012 and Spring 2013 with a terrestrial laser scanner in the same area. The segmentation of different individualized rockfall sources plotted with a different color.
To illustrate the output results of the presented procedure, and particularly the computed rockfall volumes, we used the classic rockfall magnitude–frequency representation [22,31,33,34,35,36,37]. According to [37], volumes from rockfall source areas are assumed to follow a power-law regression:
where V is the rockfall volume, n is the number of rockfalls larger than V occurring in a rock wall during an investigation period, and the constant, a, represents the number of rockfalls whose volume is greater than 1 m3. It depends on the size of the cliff, the length of the investigation period, and the geological and geomorphological context. The exponent, b, depends on the geological and geomorphological context only. Thereby, recent studies showed that a and b are correlated to the GSI (Geological Strength Index) of the rock cliff [37]. In addition, the value of b indicates the proportion of small events as compared to larger events. Therefore, this is important in the context of a power-law distribution, where small events in sum could contribute significantly to overall volume loss. The power-law regression has some limits as described in [22], as we have potential temporal and/or spatial resolution bias.
We analyzed the sensitivity of the computed volume for a restrained series of identified rockfall source varying the α values for the whole series. We increased the α values by increment up to infinity, hence increasing the trend toward a convex shape. Figure 7 shows the magnitude–frequency relationship of the series of computed volumes from the identified rockfall sources with different complex shapes, between Fall 2012 and Spring 2013, illustrated in Figure 6B. Figure 7 outlines the influence of the α value on each series of computed volumes from rockfall sources using power-law regression on each magnitude–frequency distribution. The magnitude–frequency representation is used here to show the trend. The regressions are made from volumes ≥0.01 m3, which is the expected smallest volume identified without ambiguity from the point cloud. We observed an increase in the number of volumes greater than 1 m3, or an increasing parameter a for an increase of the α value. In contrast, we observed a decrease in the b exponent. For values α < 0.1, which are a too low research radius, we observed that most of the reconstructed volumes are not filled or contained inner holes, as in Figure 4B. For a value 0.1 ≤ α ≤ 1.25, we can reconstruct volumes conserving a close-to-reality geometry depending on block shape complexity. For a value α > 1.25, we start connecting farther points, increasing shape convexity for all rockfall volumes, and moving away from real geometry up to an infinite α value, which indicates the maximal convex shape and the maximal rockfall volume (i.e., Figure 4D).
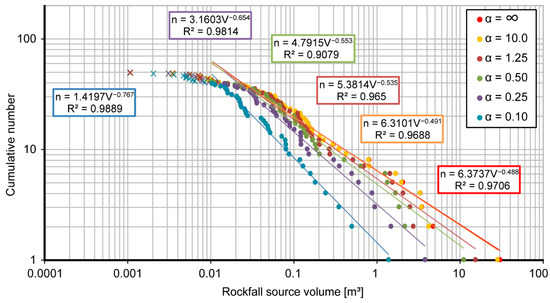
Figure 7.
Magnitude–frequency plot shows the influence of the α value on the computed volumes from identified rockfall sources with different complex shapes between Fall 2012 and Spring 2013 as shown in Figure 6B. Power laws fitted on rockfall sources with volumes >0.01 m3 show different trends according to different α value (from 0.1 to ∞ as a convex shape).
We applied the presented methodology to the overall monitoring period from 2010 to 2015 data. Thus, we identified 394 rockfall sources. Based on observation made on Figure 7, we applied on each of these rockfall sources a detailed assessment of the volume in order to compute close-to-reality volume, applying the method illustrated in Section 3.3 and Figure 4. As final result, we obtained a total volume of 105.2 m3, ranging from 0.0015 to 7.63 m3 with a mean volume of 0.2 m3 (see Figure 8). Less than 1% of the rockfall sources were smaller than 0.003 m3 (0.1 × 0.2 × 0.15 m), which is the smallest volume expected from structural analysis. Less than 25% of the rockfall sources are smaller than 0.01 m3 (0.2 × 0.2 × 0.2 m), which is the expected smallest volume identified without ambiguity from the point cloud. In Figure 8, the regression shown in red represents the rockfall sources with volumes higher than 0.01 m3, and the other regression shown in blue represents all volumes, including the smallest volumes. Green triangles were not included in the regression analysis because they represent multiple rockfall sources and were too scarce during the period of monitoring; thus, they were not considered to be representative [22,54]. We observed that the choice of the volume interval considered in the regression affects the a and b parameters. With distribution containing all rockfall sources, a increases and b decreases compare to distribution with only rockfall sources >0.01 m3.
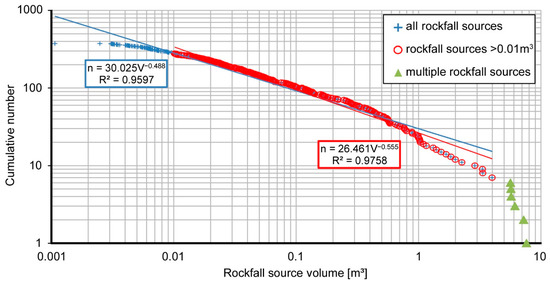
Figure 8.
Magnitude–frequency plot of the rockfall sources from the full survey period (2010–2015) using the optimal α value according to method described in Section 3.3 for each rockfall source. One power law is fitted on overall rockfall sources and a second on the rockfall sources with volume >0.01 m3. The green triangles were clearly identified as multiple rockfall sources and are not considered for the regression fit.
6. Discussion
From a processing and methodological standpoint, we note that applying the presented package for the detection and volume calculation of rockfall sources based on point clouds provides the benefit of being less time intensive compared to procedures that use manual methods and multiple software programs. This advantage is even more relevant when monitoring is performed on large outcrops based on several time series. The presented approach provides automatic thresholding, making it a robust method. Based on our experience, the presented results illustrate that segmentation permits efficient extraction of rockfall sources. However, some limitations appear in the point-to-surface method in terms of precision. Improvements could be made using finer point-to-surface comparisons in the first step by, for example, using the M3C2 algorithm comparison developed by [55] and investigated in [56]. The DBSCAN algorithm used in clustering datasets requires a homogenously spaced point cloud since the minimum number of points and ε cannot then be chosen appropriately to detect all clusters at once. If the data and scale are not well analyzed before applying this method, the results can be biased. This limitation is eclipsed by the benefits of the OPTICS algorithm, as it offers an alternative to requiring an optimal ε, even if the user does not know the ε value. The advantages of using the OPTICS algorithm are as follows: (a) This algorithm does not require prior knowledge of the number of clusters in the data; (b) this variation of the DBSCAN algorithm enables the identification arbitrarily shaped clusters and clusters completely surrounded by other clusters; and (c) using OPTICS classification, we are able to remove outliers. However, the proposed algorithm also has some disadvantages, the OPTICS algorithm was not entirely deterministic; depending on the order in which the data are processed, border points were reachable from more than one cluster. This situation could occur if two or more rockfall sources were very close.
For the volume computation, it is possible to say that using the α shape takes full advantage of the 3D surface (with overhanging, etc.) and does not reduce it to 2.5D [30]. We see that for shapes that were more complex, our estimates approach the real volume and avoid overestimation (see Figure 4D). The α shape can compute a very complex shape, as often observed in natural rockfall geometry related to a discontinuous layout. The main problem with α shapes is the determination of the best α values for surface reconstruction when the point cloud does not present a uniform density of points [32]. Some studies have shown improvement of the surface and volume computation when using the α shape as was done in [57]. Furthermore, some issues with holes from shadowing during acquisition were encountered, as was also observed by [25] with the potential to negatively impact the accuracy of the results. This indicates that acquiring the point cloud from multiple positions can help overcome these errors.
Concerning the results from the case study, a good correlation can be seen between the rockfall sources identified during fieldwork (green in Figure 6A) and sources detected with our package (shown in Figure 6B). The segmentation of rockfall sources worked sufficiently for the efficient identification of volumes at different scales, e.g., from 0.0025 to 10 m3 with a point spacing at cliff range of 3.4 cm.
When looking at the volume–frequency plot in Figure 7, we observed a decrease in b exponents, when increasing α value, which is in agreement with previous studies pointing out that the decrease in the value of b indicates a rise in the portion of larger events as compared to smaller events [33]. This is logically correlated to increasing α value, which generates a more convex and hence larger volume. Therefore, we observed variations in the volume ranging from 5% to 90% when computing concave or convex shapes depending on the selected α value and the complex geometry of the rockfall sources. The variation is particularly significant for large volumes with an increase trend for larger volumes. The structural analysis of the cliff showed four main joint sets that produced a parallelepiped unitary rockfall geometry. Thus, we can expect that larger rockfall events are a combination of several unitary parallelepipeds inducing a more complex geometry and thereby producing some concave geometries. In contrast, we also observed that volume computation influences a as computing less-complex geometries increases the overall volume size, which leads to an overestimation of volume size during the monitoring period.
This highlights the importance of measuring the complexity of the geometry of large rock falls and the use of an α shape to obtain a volume and a magnitude–frequency analysis that are closer to reality.
When looking at the volume–frequency plot in Figure 8 an underestimation of the number of rockfalls with small volumes (<0.05 m3) is suspected. The same observation is made on Figure 7. This may have been caused by the limited spatial resolution (one point every 3.4 cm), as described in [35], and the minimal number of points used for cluster detection (see Section 3.2). Some large rockfalls were related to multiple events located in the same area (i.e., triangle symbol in Figure 8) but computed as a single event due to insufficient temporal resolution [35] or too close sources. This presence of multiple unresolved events can be resolved with a higher-frequency data acquisition, such as monthly or permanent acquisition [22], instead of seasonal acquisition. Thus, errors linked to coalescence and superposition of events can be reduced with enough temporal sampling [33].
The volume estimations provided the statistics of all volumes that provided information about the erosional processes or cliff retreat [58]. Based on the volume–frequency plot, the estimated exponent value (b) was between 0.48 and 0.78, and the factors were similar to those found in the literature by [34] for seaside sandstone cliffs. This can be correlated locally high fracturation in some sandstone layers or the poor GSI of the rock cliff but suggests that the volume computation and the regression line boundaries also influenced the erosional process interpretation [37,59]. The power law shows some limits in this study site as we have temporal resolution bias and effect related to variation of thickness in sandstone layers in a too small area leading to a too large effect on sampling. Nevertheless, using the power law, it is possible to extrapolate to large volumes that were not reached during the period of monitoring [58,60,61]. The interpretation made on the rockfall activity from the presented results allowed us to state that, even though the failures were clearly episodic, the mean cliff retreat rate by rockfall was estimated to be approximately 10 mm/year for a surface of 2240 m2 in the zone of interest, assuming a mean detachment of material of ~25 m3 per year between October 2011 and October 2013 and of ~21 m3 per year over the full monitoring period from 2010 to 2015 on sandstone beds. In addition to these results, the erosional volume of marls was not considered in this study.
7. Conclusions
The proposed toolbox tries to fill an existing gap in the open-source tools available for the treatment of point clouds oriented toward the quantification of rockfall activity. This package is a compound of multiple state-of-the-art algorithms (DBSCAN, OPTICS, α shape) that are able to identify rockfall sources and their volumes by considering its complex shapes. Perspectives for the RockfallQuantification packages include an additional tool for describing the shape of each rockfall event in terms of the principal axis, which could bring interesting inputs to rockfall propagation software that takes into account the shape of the blocks, such as RocFall [62] or Rockyfor3D [63].
The application of the RockfallQuantification package to the La Cornalle cliff demonstrated a decrease in processing time and provided a robust procedure to quantify rockfall activity and determine erosion rate. We were able to compute volume with concavities observed in the field and to finally calculate the erosion rate and subsequent magnitude–frequency distribution of the local Molassic cliff. In addition, the results highlighted the importance of correctly estimating the volume of rockfall events when magnitude–frequency plots are used.
The RockfallQuantification package as well as the 3DPointCloudToolBox can also be applied to other high-resolution surface data techniques, such as aerial laser scanning or photogrammetric techniques, including Structure-from-Motion. In addition, the RockfallQuantification package can be used for other applications in geosciences to extract volume information from other natural events (e.g., lava flow, sediment transport, etc.). Finally, as a free-code package, it allows users to constantly improve the package for use in their specific needs.
Supplementary Materials
The algorithms are available on request to corresponding author or online at https://wp.unil.ch/risk/software/PointCloudToolBox under the open access policy.
Author Contributions
Conceptualization, D.C., A.A., M.-H.D., and M.J.; methodology, D.C., A.A., and M.-H.D.; software, D.C. and N.G.; validation, A.A., M.-H.D., and M.J.; formal analysis, D.C. and A.A.; investigation, D.C. and A.A.; resources, M.-H.D. and M.J.; data curation, D.C.; writing—original draft preparation, D.C., N.G., and M.J.; writing—review and editing, D.C., A.A., M.-H.D., and M.J.; visualization, D.C.; supervision, A.A., M.-H.D., and M.J.; project administration, D.C., A.A., and M.J.; funding acquisition, A.A. and M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Swiss National Science Foundation under project FNS-1440404 titled “Characterizing and analyzing 3D temporal slope evolution”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors acknowledge AJE for proper English editing of the manuscript, Gaillard et fils SA for allowing us to access the cliff and surroundings and Caroline Lefeuvre for her feedback on the RockfallQuantification package. Finally, the authors would like to acknowledge the two anonymous reviewers for their comments to improve the present manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
3DPointCloudToolBox contains general packages (Figure A1) with state-of-the-art algorithms and dedicated functions for point cloud preprocessing, including the alignment of point clouds PointCloudAlignment and PointCloudComparison for point cloud comparison (point-to-point and point-to-surface). The 3DPointCloudToolBox contains specific postprocessing packages oriented toward rockfall analysis (RockfallQuantification) presented in detail in subsequent sections. The elementary brick is the object class PointCloud created with a series of properties useful for data treatment, which includes the point’s position (X; Y; Z), intensities (I), colors (R; G; B), normal vectors (Nx; Ny; Nz), etc.
The RockfallQuantification package contains a series of functions encapsulated in the main script (Figure A2). This inner structure allows either extracting intermediary results at each step or running the full package to obtain the volume for each rockfall event as output.
Figure A2 describe all functions used in the RockfallQuantification package that enable the extraction, individualization, and computation of rockfall volumes. As input data, the package needs two point clouds acquired at different epochs. Other necessary input parameters include the minimum number of points (k) to be considered to create a cluster in step two (see Section 3.2) and the research radius (r) needed to compute the shape of the rockfall point cloud at step three (see Section 3.3). It is possible to define all automatic research parameters (such as σ and ε) to decrease processing time or affine the results. It defines the threshold to determine σ at step one (see Section 3.1) or the neighborhood radius (ε) for step two (see Section 3.2). This solution is easier if the user has an idea of the research radius parameter, but this will increase the computation time. To compute the point-to-plane comparison, RockfallDetect needs the PointCloudComparison package. The provided final output is a database with labeled rockfall event volumes and associated point cloud objects defined at the second stage.
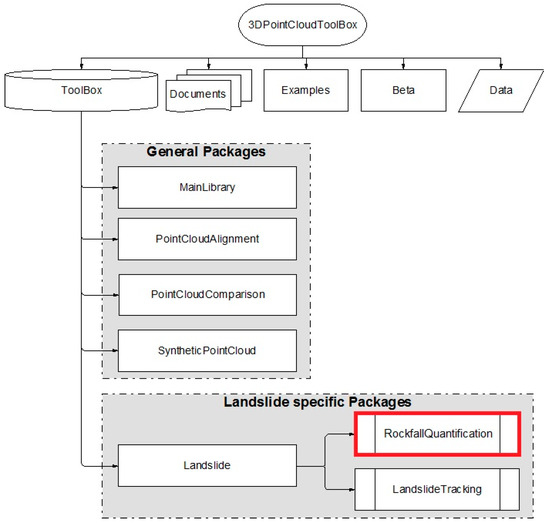
Figure A1.
The structure of the 3DPointCloudToolBox contains folders labeled as Documents for tutorials, Examples of scripts to start up, Beta for functions in development, and Data to store raw data that can be used in the 3DPointCloudToolBox. The main folder Toolbox contains subfolders for point cloud data treatments (MainLibrary, PointCloudAlignment, PointCloudComparison, SyntheticPointCloud) and a specific subfolder landslide for landslide monitoring, with one for rockfall monitoring and another for landslide surface displacement monitoring (RockfallQuantification, LandslideTracking).
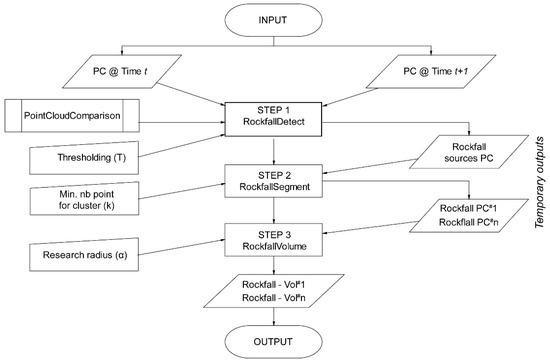
Figure A2.
Workflow for the RockfallQuantification package.

Table A1.
Functions available on the RockfallQuantification package.
Table A1.
Functions available on the RockfallQuantification package.
| RockfallQuantification Functions | |
|---|---|
| Step 1: RockfallExtract | Extract point belonging to surface change from two PointCloud objects |
| Step 2: RockfallSegment | Individualize single rockfall event by clustering index on PointCloud |
| dbscan_optics | Density-Based Spatial Clustering of Applications with Noise [42] and OPTICS improvement [43] |
| dist | Compute Euclidean distance between points in the cloud |
| epsilon | Compute optimal epsilon radius according to gamma function approximation (Daszykowski et al., 2002) |
| Step 3: RockfallVolume | Compute volume and center of mass of PointCloud |
| trueboundary | Find boundary points to define shape of PointCloud |
| volumes_tetra | Compute volume of single tetrahedron |
| alphavol | Compute α-concave hull from PointCloud [45] |

Table A2.
Key terms of the MATLAB®-oriented programming as defined in MathWorks®.
Table A2.
Key terms of the MATLAB®-oriented programming as defined in MathWorks®.
| MATLAB Classes—Key Terms | |
|---|---|
| Class definition | Description of what is common to every instance of a class |
| Classes | A class describes a set of objects with common characteristics |
| Super classes | Classes that are used as a basis for the creation of more specifically defined classes (i.e., subclasses) |
| Subclasses | Classes that are derived from other classes and that inherit the methods, properties, and events from those classes (subclasses facilitate the reuse of code defined in the superclass from which they are derived) |
| Objects | Specific instances of a class, which contain actual data values stored in the object’s properties |
| Properties | Data storage for class instances |
| Methods | Special functions that implement operations that are usually performed only on instances of the class |
| Packages | Folders that define a scope for a class and function naming |

Table A3.
PointCloud methods or functions implemented to operate on PointCloud objects only.
Table A3.
PointCloud methods or functions implemented to operate on PointCloud objects only.
| PointCloud Methods | |
|---|---|
| Add | Add the content of a given point cloud to this one |
| addNoise | Add simulated noise to the true point positions with following possibility: Gaussian position smearing Outliers to simulate completely wrong position Drop out some points by replacing points position by NaNs |
| ComputeBoundaries | Compute the Boundary points |
| ComputeCurvature | Compute the curvatures at each point using: Estimation of the curvature based on [64] Variation of the surface from correlation of point clouds based on [65] |
| ComputeDelaunayTriangulation | Compute a 3D Delaunay triangulation using built-in MATLAB® function |
| ComputeKDTree | Compute a Kd search tree using built-in MATLAB® function |
| ComputeNormals | Compute the least squares normal vector estimation of the points based on [64] |
| ComputeOptimalNormals | Compute the adaptive normals based on neighbor size, point density, and research radius based on [66] in order to reduce normals dispersion |
| ComputeTrueDistance | Compute the mean and root mean squared distances between a PointCloud positions and a given PointCloud true positions |
| CopyTrue2MeasPos | Copy the “true” positions to the “measured” ones |
| GetMissingPropFromPC | Complete properties of an object PointCloud by getting the missing ones from other PointCloud object |
| HasTrueP | Return true if the object PointCloud has true positions |
| ImportDataFromASCII | Import data from an ASCII file |
| IsEmpty | Is the object PointCloud object empty? |
| MeshPointCloud | Create a MeshPointCloud from this PointCloud |
| MoveToCM | Move to the center of mass of another given object PointCloud |
| NormalsOutTopo | For each point, compute the sign of the normal vector to be oriented toward its indexed sensor using TLSAttribute to have normals orientation to be out of the topography |
| Plot3 | Plot the 3D coordinates of each point of the object PointCloud Positions |
| PlotCurvature | Plot the computed curvatures |
| PlotNormals | Plot the computed normals |
| PlotPCLViewer | Plot for large point cloud positions with colors or intensities using Point Cloud Library Viewer [19] |
| PlotPositionsWithColors | Plot the point cloud with the colors |
| PlotPositionsWithIntensities | Plot the point cloud with the intensities |
| RemoveNans | Remove any NaNs values in P and TrueP |
| SaveInASCII | Save object PointCloud in ASCII format |
| SaveInPCD | Save object PointCloud in PCD format for open Point Cloud Library [19] |
| Size | What is the dimension of the object PointCloud? |
| Transform | Transform the object PointCloud |
| WhatColor | Query: what is the RGB color of the closest point? |
| WhatIntensity | Query: what is the intensity of the closest point? |

Table A4.
Functions available in the MainLibrary package.
Table A4.
Functions available in the MainLibrary package.
| MainLibrary | |
|---|---|
| PointCloud | Constructor of the object PointCloud and related methods |
| AffinTransform | Apply an affine transformation to object PointCloud |
| AlphaBoundary | Determine the convex hull of the object PointCloud using [45] |
| EuclDist | Compute the Euclidean distance between two vectors of 3D points. |
| HalfWayPoints | Loop on all the possible pairs in the input points and compute the halfway point |
| ImportPointCloudFromASCII | Create a PointCloud object from a given input data (in ASCII format), allowing the user selection of the specific point cloud properties |
| MeshPointCloud | Class to hold mesh grids as created by functions like GridFit |
| PlaneMesh | Create a synthetic planar grid of points |
| Plot3DPointClouds | Display one object PointCloud with defined property |
| PlotMultiPointClouds | Display several objects PointCloud with defined property |
| Quat2Rot | Convert (unit) quaternion representations to (orthogonal) rotation matrices R |
| RemoveDuplicate3DPoints | Remove the duplicates in a set of 3D points |
| Rot2Quat | Converts (orthogonal) rotation matrices R to (unit) quaternion representations |
| RotationMatrix | Compute the rotation matrix given the Eulerian rotation angles |
| SubSampling | Create a sub sample of a given object PointCloud |
| TransformMatrix | Given the rotation angles and a translation vector, provides a transformation matrix |
| TriangularMesh | Decompose a given triangle form mesh into smaller triangles |
| Vector | A class to efficiently store any other property or type of data |

Table A5.
Functions available in the PointCloudComparison package.
Table A5.
Functions available in the PointCloudComparison package.
| PointCloudComparison | |
|---|---|
| ComparePoint2Point | Compute comparison using the shortest point to point distance. Calculation is made using Euclidean distance between a given point in PointCloud A to the closest point in PointCloud B with output as absolute differences. |
| ComparePoint2Surface | Compute comparison using the shortest point to surface distance. Calculation is made between a given point in PointCloud A and the distance parallel to the normal to the closest point in PointCloud B with output as signed differences. |
References
- Buckley, S.J.; Enge, H.D.; Carlsson, C.; Howell, J.A. Terrestrial laser scanning for use in virtual outcrop geology. Photogramm. Rec. 2010, 25, 225–239. [Google Scholar] [CrossRef]
- Matasci, B.; Carrea, D.; Abellan, A.; Derron, M.-H.; Humair, F.; Jaboyedoff, M.; Metzger, R. Geological mapping and fold modeling using Terrestrial Laser Scanning point clouds: Application to the Dents-du-Midi limestone massif (Switzerland). Eur. J. Remote Sens. 2015, 48, 569–591. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river. Earth Surf. Process. Landf. 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Micheletti, N.; Tonini, M.; Lane, S.N. Geomorphological activity at a rock glacier front detected with a 3D density-based clustering algorithm. Geomorphology 2017, 278, 287–297. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.-H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef]
- Slob, S.; Hack, R. 3D Terrestrial Laser Scanning as a New Field Measurement and Monitoring Technique. In Engineering Geology for Infrastructure Planning in Europe; Lecture Notes in Earth Sciences; Hack, R., Azzam, R., Charlier, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 104, pp. 179–189. [Google Scholar]
- Sturzenegger, M.; Stead, D. Quantifying discontinuity orientation and persistence on high mountain rock slopes and large landslides using terrestrial remote sensing techniques. Nat. Hazards Earth Syst. Sci. 2009, 9, 267–287. [Google Scholar] [CrossRef]
- Lucieer, A.; Jong, S.M.d.; Turner, D. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAV photography. Prog. Phys. Geogr. 2014, 38, 97–116. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.-P.; Allemand, P.; Pierrot-Deseilligny, M.; Skupinski, G. Ground-based multi-view photogrammetry for the monitoring of landslide deformation and erosion. Geomorphology 2014, 231, 130–145. [Google Scholar] [CrossRef]
- Roncella, R.; Forlani, G. A Fixed Terrestrial Photogrammetric System for Landslide Monitoring. In Modern Technologies for Landslide Monitoring and Prediction; Springer Natural Hazards; Scaioni, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 43–67. [Google Scholar]
- Voumard, J.; Derron, M.-H.; Jaboyedoff, M.; Bornemann, P.; Malet, J.-P. Pros and Cons of Structure for Motion Embarked on a Vehicle to Survey Slopes along Transportation Lines Using 3D Georeferenced and Coloured Point Clouds. Remote Sens. 2018, 10, 1732. [Google Scholar] [CrossRef]
- Rosser, N.; Petley, D. Monitoring and modeling of slope movement on rock cliffs prior to failure. In Landslides and Engineered Slopes. From the Past to the Future; Chen, Z., Zhang, J., Ho, K., Wu, F., Eds.; Taylor and Francis Group: London, UK, 2008; pp. 1265–1271. [Google Scholar]
- Derron, M.-H.; Jaboyedoff, M. Preface “LIDAR and DEM techniques for landslides monitoring and characterization”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1877–1879. [Google Scholar] [CrossRef]
- Rosser, N.J.; Petley, D.N.; Lim, M.; Dunning, S.A.; Allison, R.J. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol. 2005, 38, 363–375. [Google Scholar] [CrossRef]
- Teza, G.; Galgaro, A.; Zaltron, N.; Genevois, R. Terrestrial laser scanner to detect landslide displacement fields: A new approach. Int. J. Remote Sens. 2007, 28, 3425–3446. [Google Scholar] [CrossRef]
- Abellán, A.; Calvet, J.; Vilaplana, J.M.; Blanchard, J. Detection and spatial prediction of rockfalls by means of terrestrial laser scanner monitoring. Geomorphology 2010, 119, 162–171. [Google Scholar] [CrossRef]
- Oppikofer, T.; Jaboyedoff, M.; Keusen, H.-R. Collapse at the eastern Eiger flank in the Swiss Alps. Nat. Geosci. 2008, 1, 531–535. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. CloudCompare v.2.11.3. 2020. Available online: http://www.danielgm.net/cc (accessed on 8 December 2020).
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- True Reality Geospatial Solutions. LIFOREST (LiDAR Software for Forestry Applications); True Reality Geospatial Solutions: Merced, CA, USA, 2014. [Google Scholar]
- Michoud, C.; Carrea, D.; Costa, S.; Derron, M.-H.; Jaboyedoff, M.; Delacourt, C.; Maquaire, O.; Letortu, P.; Davidson, R. Landslide detection and monitoring capability of boat-based mobile laser scanning along Dieppe coastal cliffs, Normandy. Landslides 2015, 12, 403–418. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude–frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, Á.; Gonçalves, G.R. Surveying coastal cliffs using two UAV platforms (multirotor and fixed-wing) and three different approaches for the estimation of volumetric changes. Int. J. Remote Sens. 2020, 41, 8143–8175. [Google Scholar] [CrossRef]
- Tonini, M.; Abellan, A. Rockfall detection from terrestrial LiDAR point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014, 8, 95–110. [Google Scholar] [CrossRef]
- Olsen, M.; Wartman, J.; McAlister, M.; Mahmoudabadi, H.; O’Banion, M.; Dunham, L.; Cunningham, K. To Fill or Not to Fill: Sensitivity Analysis of the Influence of Resolution and Hole Filling on Point Cloud Surface Modeling and Individual Rockfall Event Detection. Remote Sens. 2015, 7, 12103–12134. [Google Scholar] [CrossRef]
- Rüeger, J.M. Electronic Distance Measurement; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Schovanec, H.E.; Walton, G. Volume Filtering and Its Implications for Analyzing Rockfall Databases. In Proceedings of the 54th U.S. Rock Mechanics/Geomechanic Symposium, Golden, CO, USA, 28 June–1 July 2020. [Google Scholar]
- Lato, M.J.; Hutchinson, J.; Diederichs, M.; Ball, D.; Harrap, R. Engineering monitoring of rockfall hazards along transportation corridors: Using mobile terrestrial LiDAR. Nat. Hazards Earth Syst. Sci. 2009, 9, 935–946. [Google Scholar] [CrossRef]
- Kromer, R.A.; Hutchinson, D.J.; Lato, M.J.; Gauthier, D.; Edwards, T. Identifying rock slope failure precursors using LiDAR for transportation corridor hazard management. Eng. Geol. 2015, 195, 93–103. [Google Scholar] [CrossRef]
- Rabatel, A.; Deline, P.; Jaillet, S.; Ravanel, L. Rock falls in high-alpine rock walls quantified by terrestrial lidar measurements: A case study in the Mont Blanc area. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Santana, D.; Corominas, J.; Mavrouli, O.; Garcia-Sellés, D. Magnitude–frequency relation for rockfall scars using a Terrestrial Laser Scanner. Eng. Geol. 2012, 145, 50–64. [Google Scholar] [CrossRef]
- Bonneau, D.; DiFrancesco, P.-M.; Hutchinson, D.J. Surface Reconstruction for Three-Dimensional Rockfall Volumetric Analysis. Isprs Int. J. Geo Inf. 2019, 8, 548. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J. The Importance of Monitoring Interval for Rockfall Magnitude-Frequency Estimation. J. Geophys. Res. Earth Surf. 2019, 124, 2841–2853. [Google Scholar] [CrossRef]
- Marques, F.M.S.F. Magnitude-frequency of sea cliff instabilities. Nat. Hazards Earth Syst. Sci. 2008, 8, 1161–1171. [Google Scholar] [CrossRef]
- Guerin, A.; Hantz, D.; Rossetti, J.-P.; Jaboyedoff, M. Brief communication “Estimating rockfall frequency in a mountain limestone cliff using terrestrial laser scanner”. Nat. Hazards Earth Syst. Sci. Discuss. 2014, 2, 123–135. [Google Scholar]
- Mavrouli, O.; Corominas, J.; Jaboyedoff, M. Size Distribution for Potentially Unstable Rock Masses and In Situ Rock Blocks Using LIDAR-Generated Digital Elevation Models. Rock Mech. Rock Eng. 2015, 48, 1589–1604. [Google Scholar] [CrossRef]
- Hantz, D.; Colas, B.; Dewez, T.; Lévy, C.; Rossetti, J.-P.; Guerin, A.; Jaboyedoff, M. Caractérisation quantitative des aléas rocheux de départ diffus. Rev. Fr. Geotech. 2020, 163, 2. [Google Scholar] [CrossRef]
- MathWorks. Object-Oriented Programming 2015; MathWorks: Highton, VI, Australia, 2015. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. Acm 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Vosselman, G.; Gorte, B.G.H.; Sithol, G. Change Detection for Updating Medium Scale Maps Using Laser Altimetry. In Proceedings of the XXth ISPRS Congress, Istanbul, Turkey, 12–23 July 2004. [Google Scholar]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J.M. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. OPTICS. In SIGMOD ’99: Proceedings of the 1999 ACM SIGMOD International Conference on Management of Data, Proceedings of the SIGMOD/PODS99: International Conference on Management of Data and Symposium on Principles of Database Systems, Philadelphia, PA, USA, 1–3 June 1999; ACM Press: New York, NY, USA, 1999; pp. 49–60. [Google Scholar]
- Daszykowski, M.; Walczak, B.; Massart, D.L. Looking for Natural Patterns in Analytical Data. 2. Tracing Local Density with OPTICS. J. Chem. Inf. Comput. Sci. 2002, 42, 500–507. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mücke, E.P. Three-dimensional alpha shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Teichmann, M.; Capps, M. Surface Reconstruction with Anisotropic Density-Scaled Alpha Shapes. In Proceedings of the Visualization ’98 (Cat. No.98CB36276), Research Triangle Park, NC, USA, 18–23 October 1998; pp. 67–72. [Google Scholar]
- Hamoud Al-Tamimi, M.S.; Sulong, G.; Shuaib, I.L. Alpha shape theory for 3D visualization and volumetric measurement of brain tumor progression using magnetic resonance images. Magn. Reson. Imaging 2015, 33, 787–803. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Menon, J.; Willette, B. Surface Reconstruction Using Alpha Shapes. Comput. Graph. Forum 1997, 16, 177–190. [Google Scholar] [CrossRef]
- Weidmann, M. Feuille Lausanne de l’Atlas géologique de la Suisse; Office Fédéral de Topographie: Wabern, Switzerland, 1988. [Google Scholar]
- Bersier, A.; Blanc, P.; Weidmann, M. Le glissement de terrain de La Cornalle-Les luges (Epesses, Vaud, Suisse). Bull. Société Vaud. Sci. Nat. 1975, 72, 165–191. [Google Scholar]
- Trümpy, R. Geology of Switzerland a Guide-Book. Part A: An Outline of the Geology of Switzerland; Wepf & Co: Basel, Switzeland, 1980. [Google Scholar]
- Parriaux, A. Glissement de la Cornalle. Bull. Geol. Appl. 1998, 3, 49–56. [Google Scholar]
- Teledyne Optech. Static 3D Survey—ILRIS. Available online: https://pdf.directindustry.com/pdf/optech/ilris-3d-intelligent-laser-ranging-imaging-system-front-page/25132-7672.html (accessed on 2 February 2021).
- Benjamin, J.; Rosser, N.; Brain, M. Rockfall detection and volumetric characterisation using LiDAR. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2016; pp. 389–395. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- DiFrancesco, P.-M.; Bonneau, D.; Hutchinson, D.J. The Implications of M3C2 Projection Diameter on 3D Semi-Automated Rockfall Extraction from Sequential Terrestrial Laser Scanning Point Clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- Xu, X.; Harada, K. Automatic surface reconstruction with alpha-shape method. Vis. Comput. 2003, 19, 431–443. [Google Scholar] [CrossRef]
- Dussauge-Peisser, C.; Helmstetter, A.; Grasso, J.-R.; Hantz, D.; Desvarreux, P.; Jeannin, M.; Giraud, A. Probabilistic approach to rock fall hazard assessment: Potential of historical data analysis. Nat. Hazards Earth Syst. Sci. 2002, 2, 15–26. [Google Scholar] [CrossRef]
- Dussauge, C.; Grasso, J.-R.; Helmstetter, A. Statistical analysis of rockfall volume distributions: Implications for rockfall dynamics. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Matasci, B.; Jaboyedoff, M.; Loye, A.; Pedrazzini, A.; Derron, M.-H.; Pedrozzi, G. Impacts of fracturing patterns on the rockfall susceptibility and erosion rate of stratified limestone. Geomorphology 2015, 241, 83–97. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O.; Ruiz-Carulla, R. Rockfall Occurrence and Fragmentation. In Advancing Culture of Living with Landslides; Sassa, K., Mikoš, M., Yin, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 75–97. [Google Scholar]
- Rocscience Inc. RocFall Version 4.0—Statistical Analysis of Rockfalls; Rocscience Inc.: Toronto, ON, Canada, 2011; Available online: https://www.rocscience.com/software/rocfall (accessed on 2 December 2020).
- Dorren, L.K.A. Rockyfor3D (v5.2) revealed—Transparent description of the complete 3D rockfall model. ecorisQ Pap. 2015, 32. [Google Scholar]
- Gumhold, S.; Wang, X.; Macleod, R. Feature Extraction from Point Clouds. In Proceeding of the 10th International Meshing Roundtable, Newport Beach, CA, USA, 7–10 October 2001; pp. 293–305. [Google Scholar]
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient Simplification of Point-sampled Surfaces. In Proceedings of the Conference on Visualization ’02 (VIS02), Boston, MA, USA, 27 October–1 November 2002; IEEE Computer Society: Washington, DC, USA, 2002; pp. 163–170. [Google Scholar]
- Lalonde, J.-F.; Unnikrishnan, R.; Vandapel, N.; Hebert, M. Scale Selection for Classification of Point-Sampled 3-D Surfaces. In Proceedings of the Fifth International Conference on 3-D Digital Imaging and Modeling (3DIM’05), Ottawa, ON, Canada, 13–16 June 2005; pp. 285–292. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).