Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment
Abstract
1. Introduction
2. Part I: Directionality in the Seismic Action
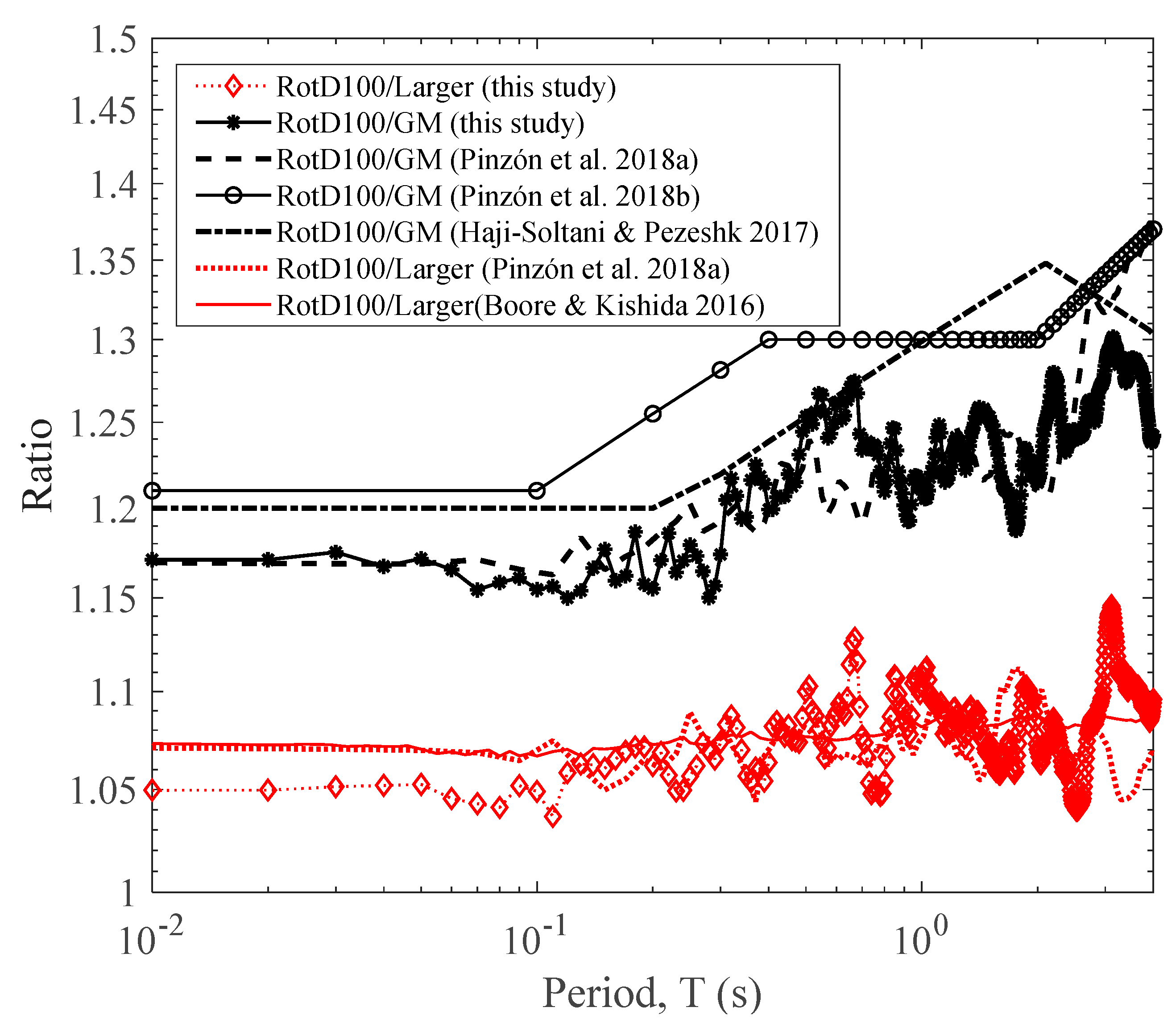
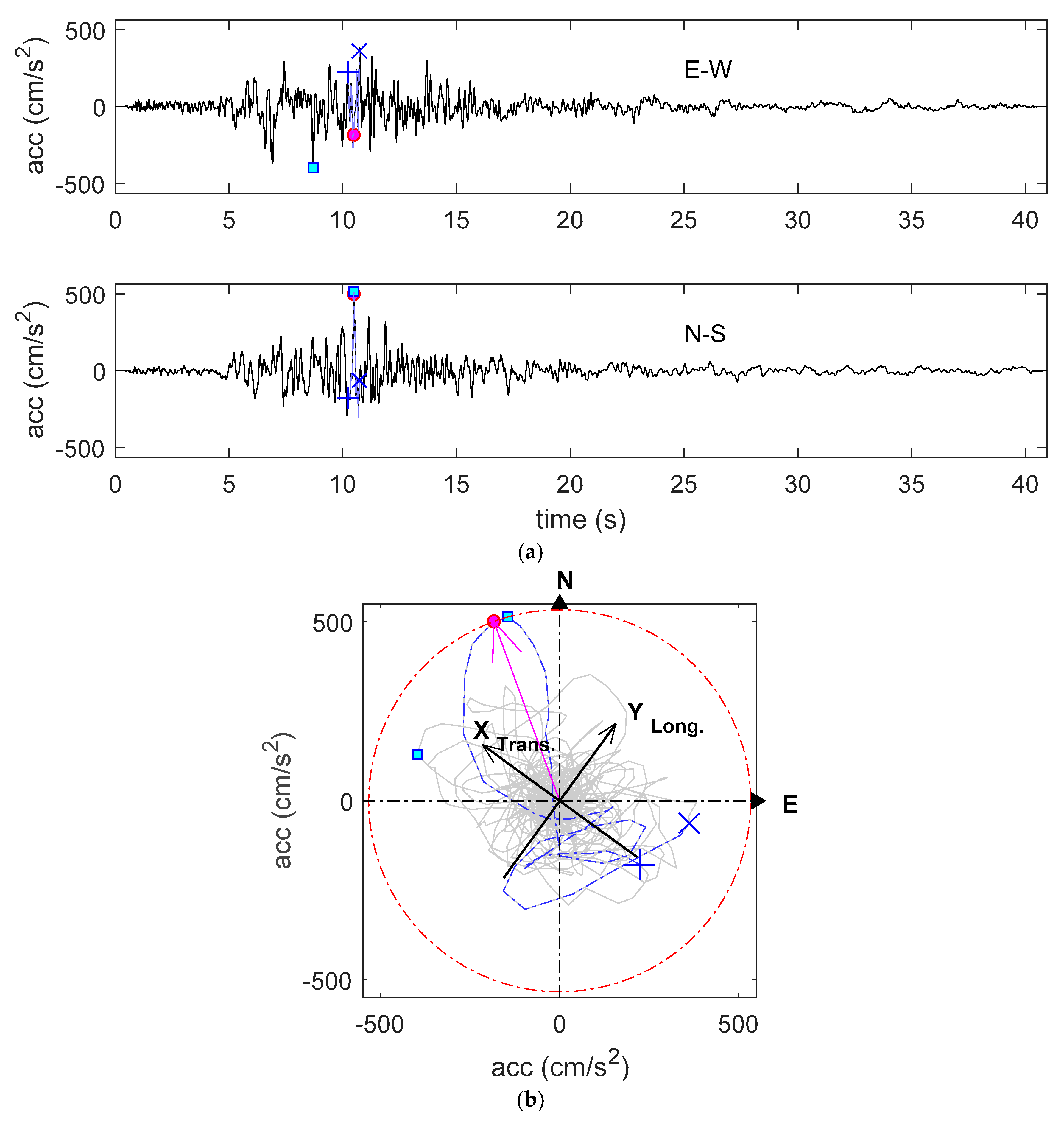
2.1. Materials and Methods
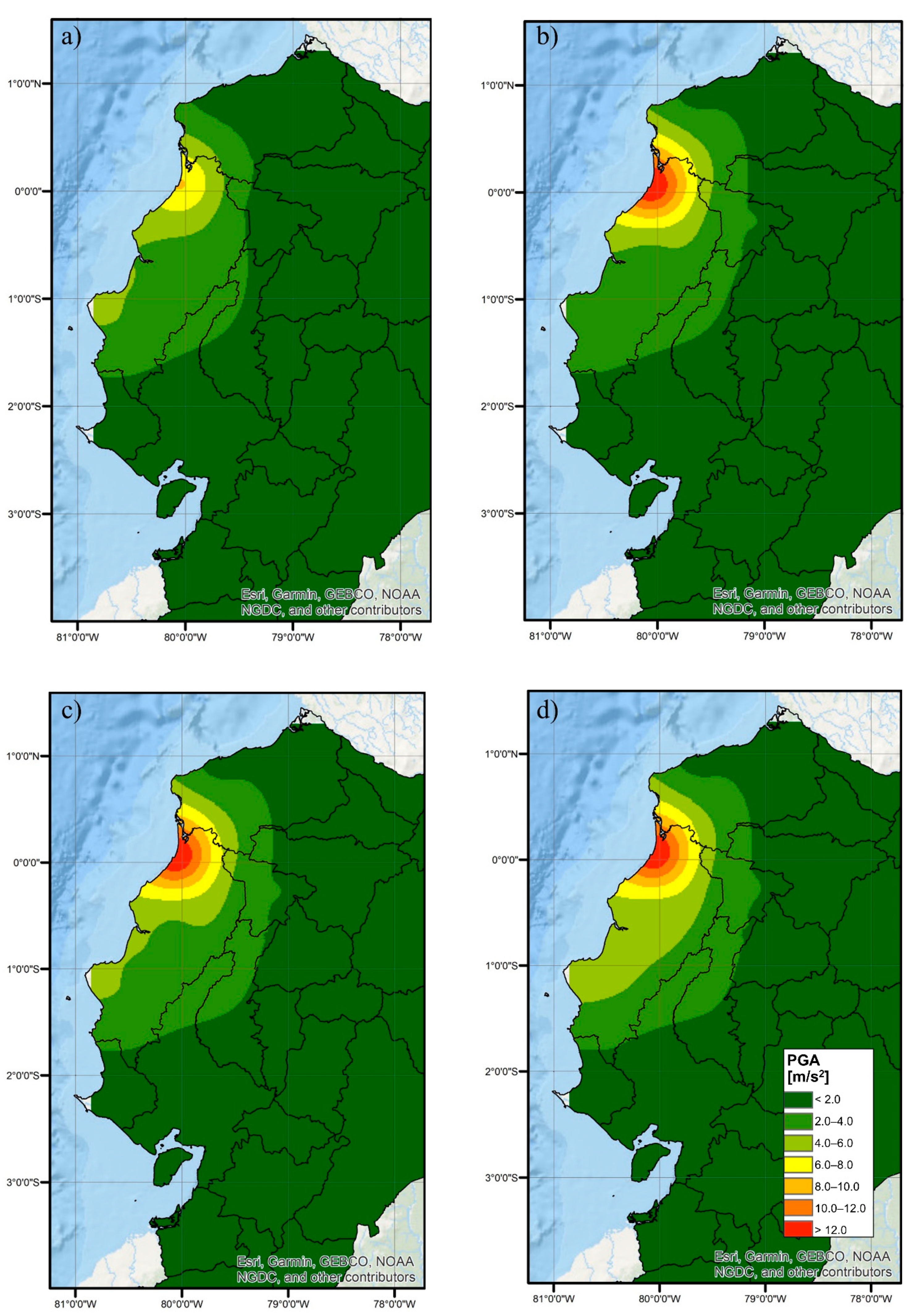
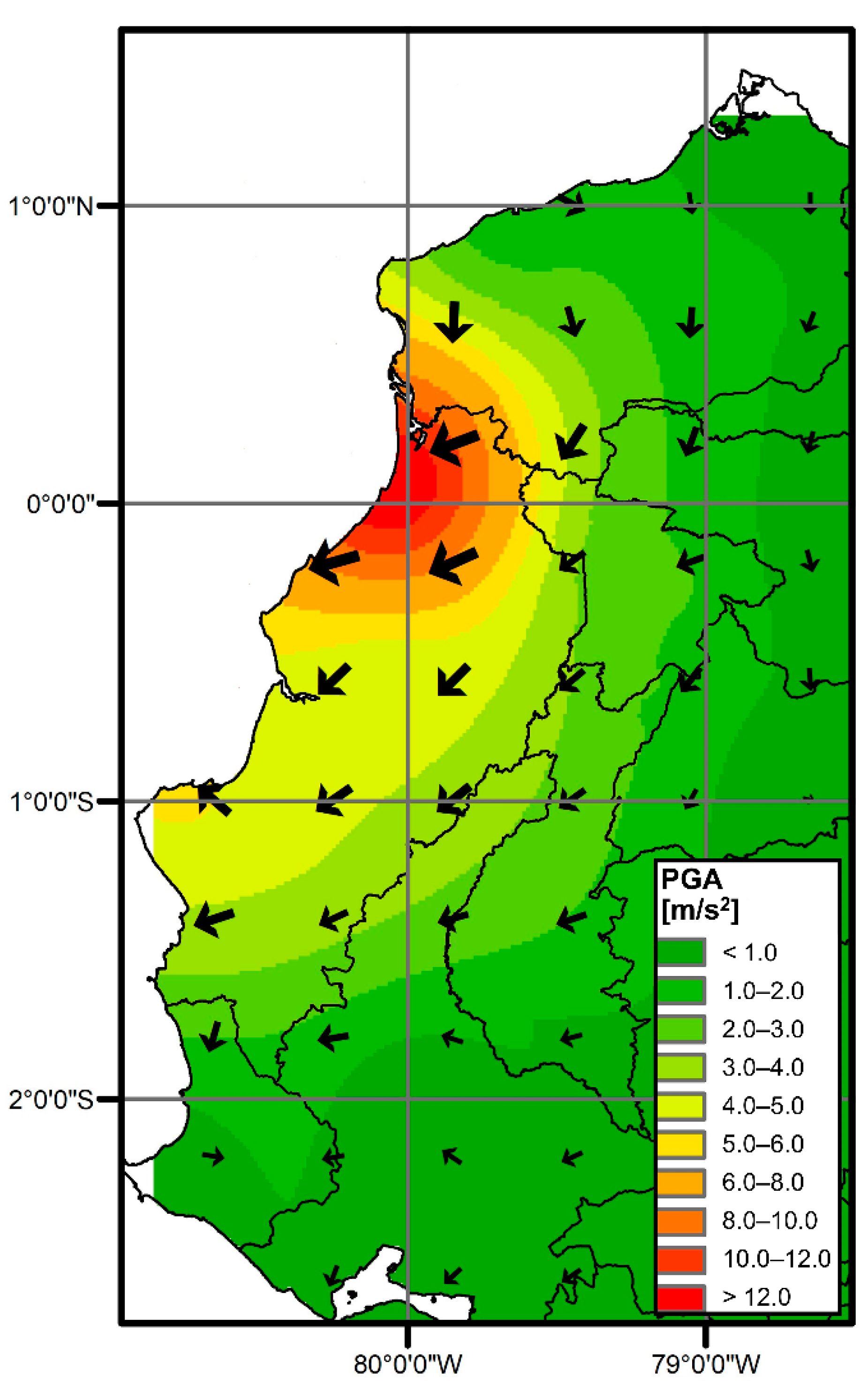
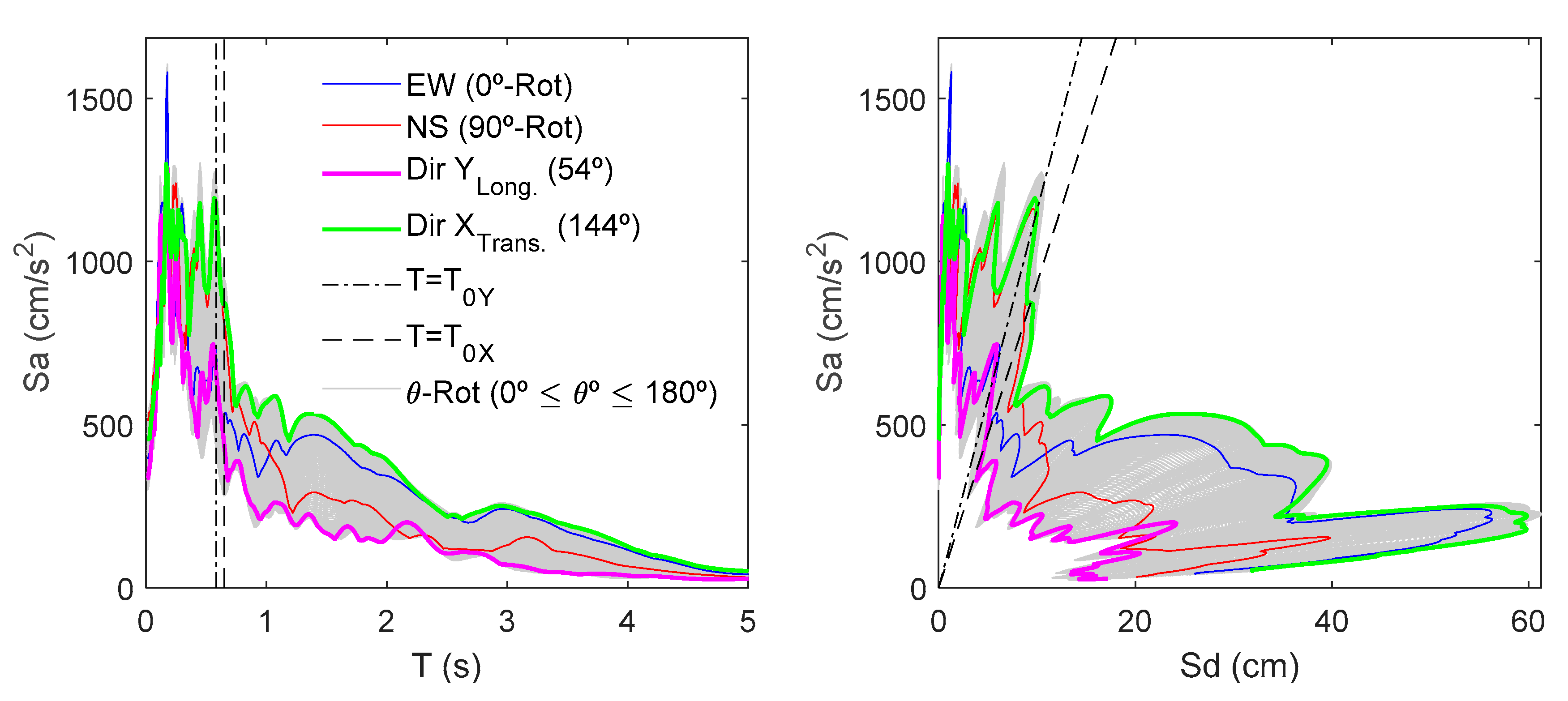
2.2. Results
3. Part II: Case Study: Damage Assessment of a Heavily Damaged Building
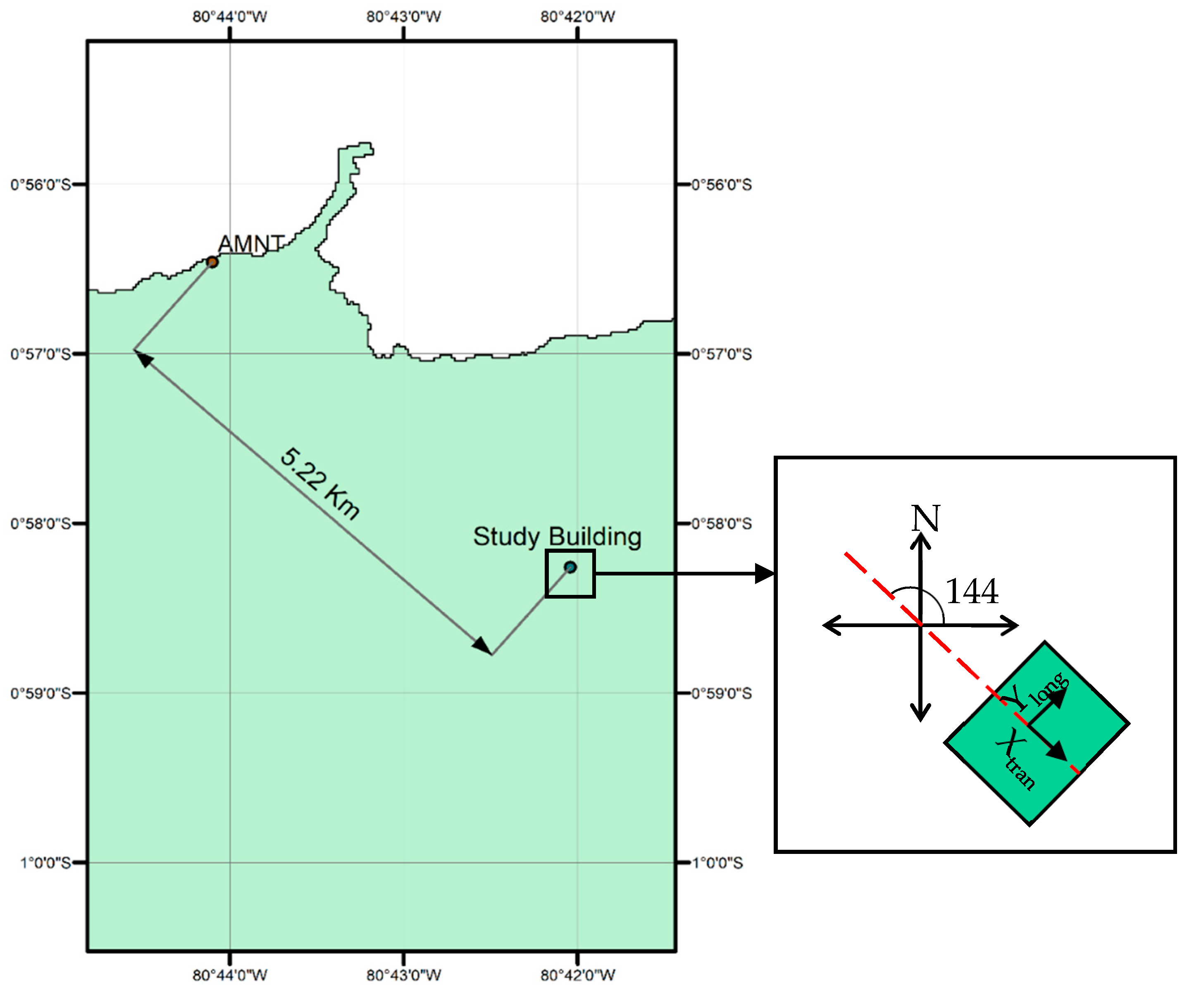
3.1. Materials and Methods
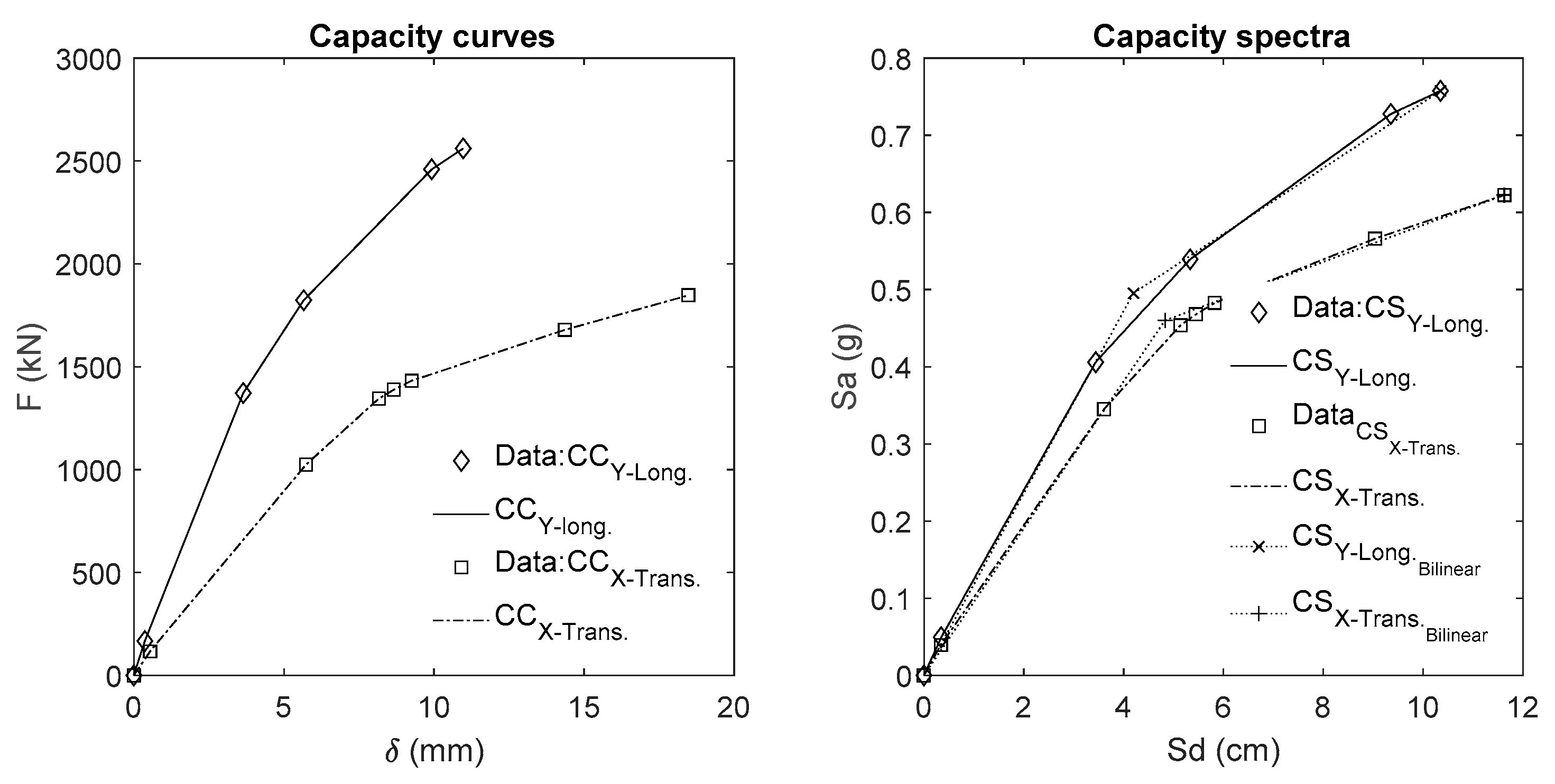
3.1.1. Structural Model
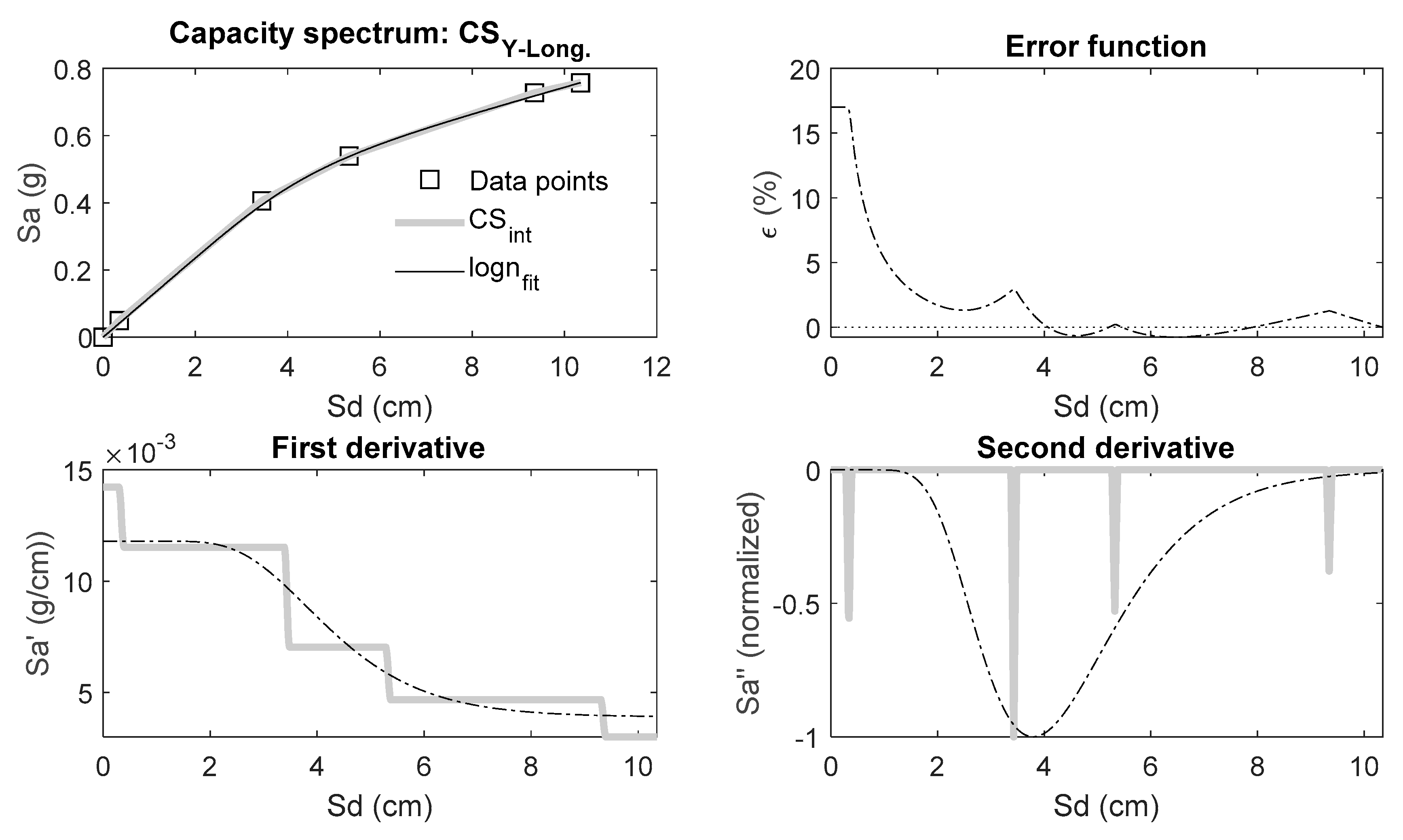
3.1.2. Parametric Model
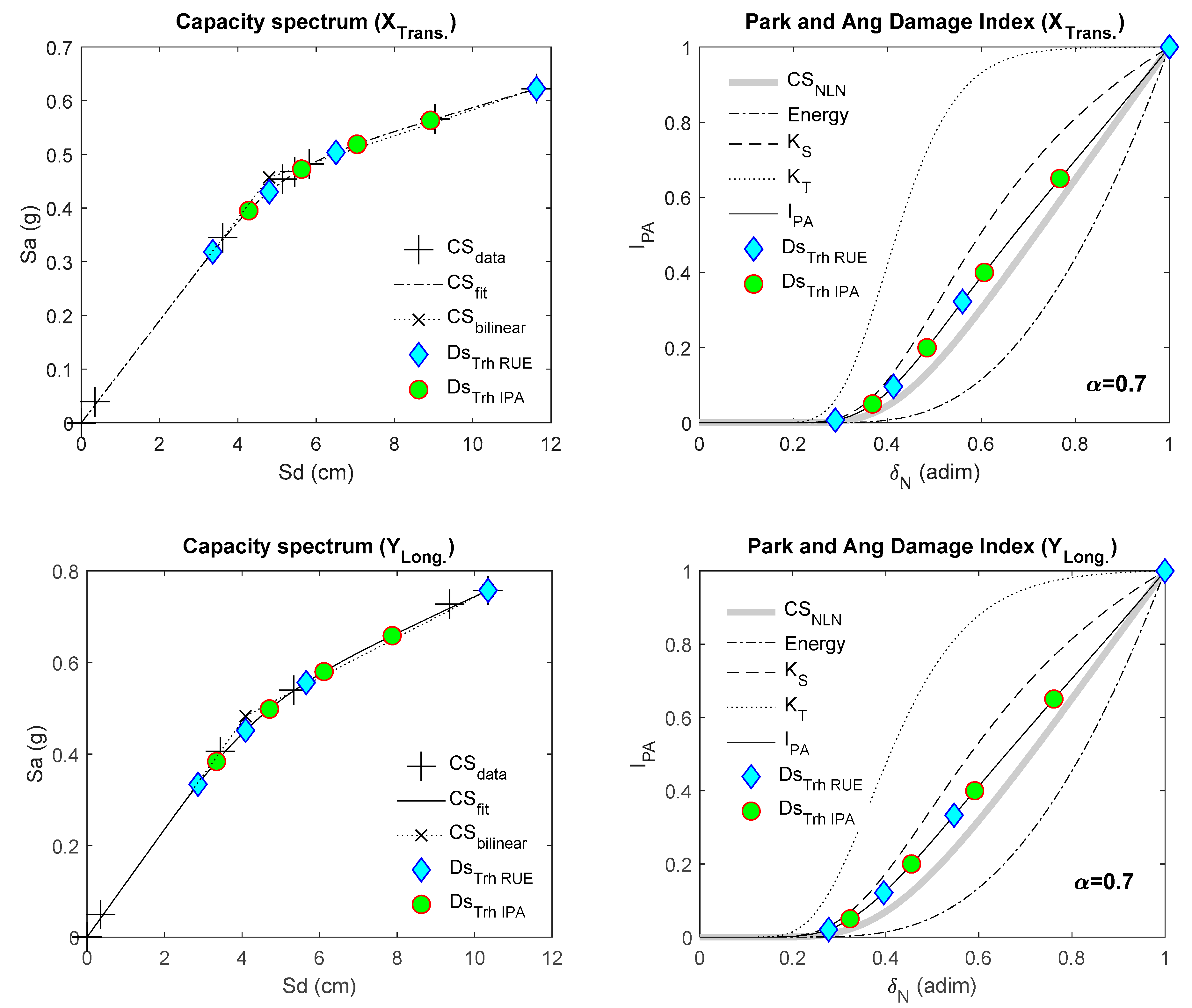
3.1.3. Park and Ang-Based Damage Index
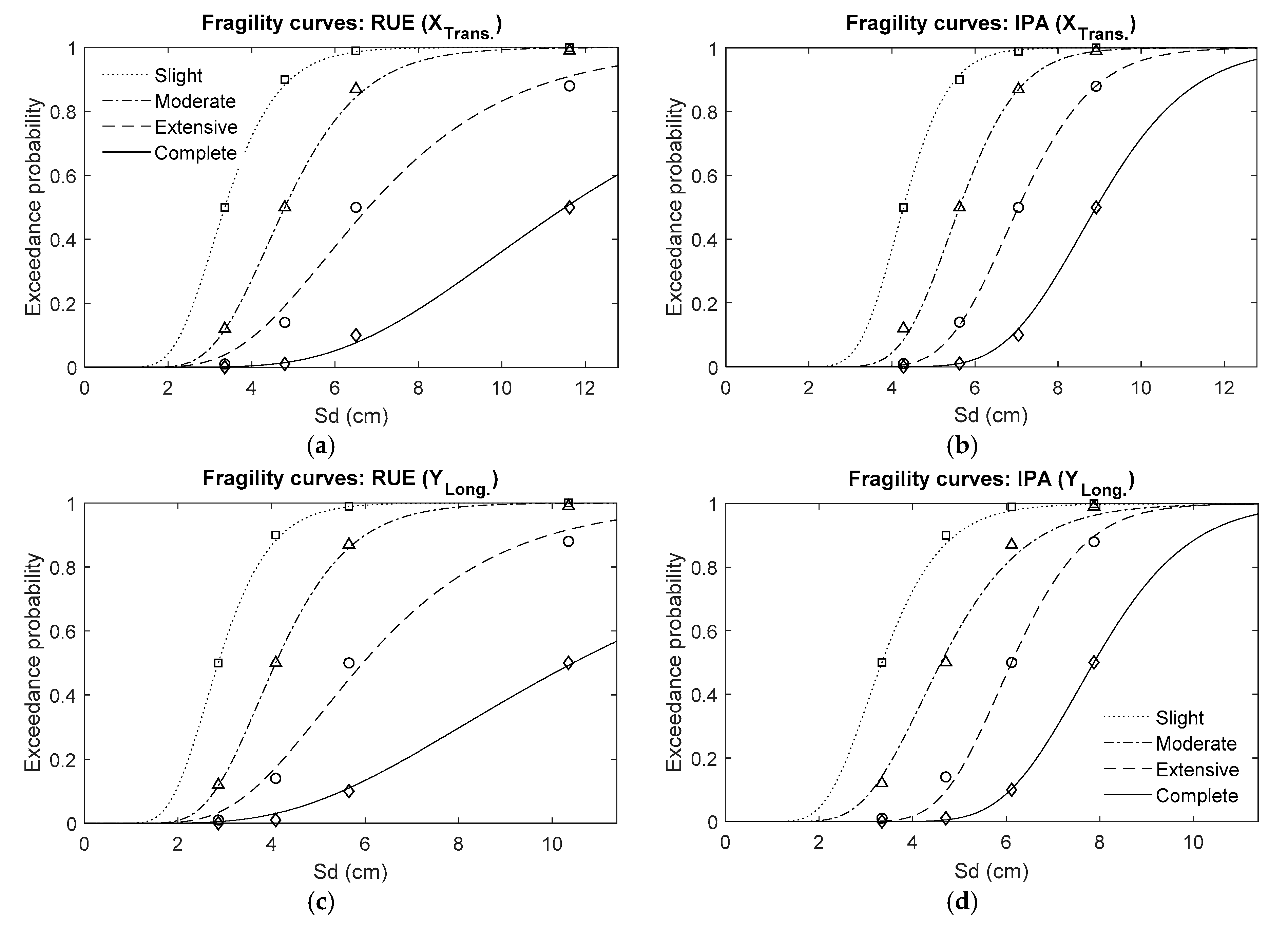
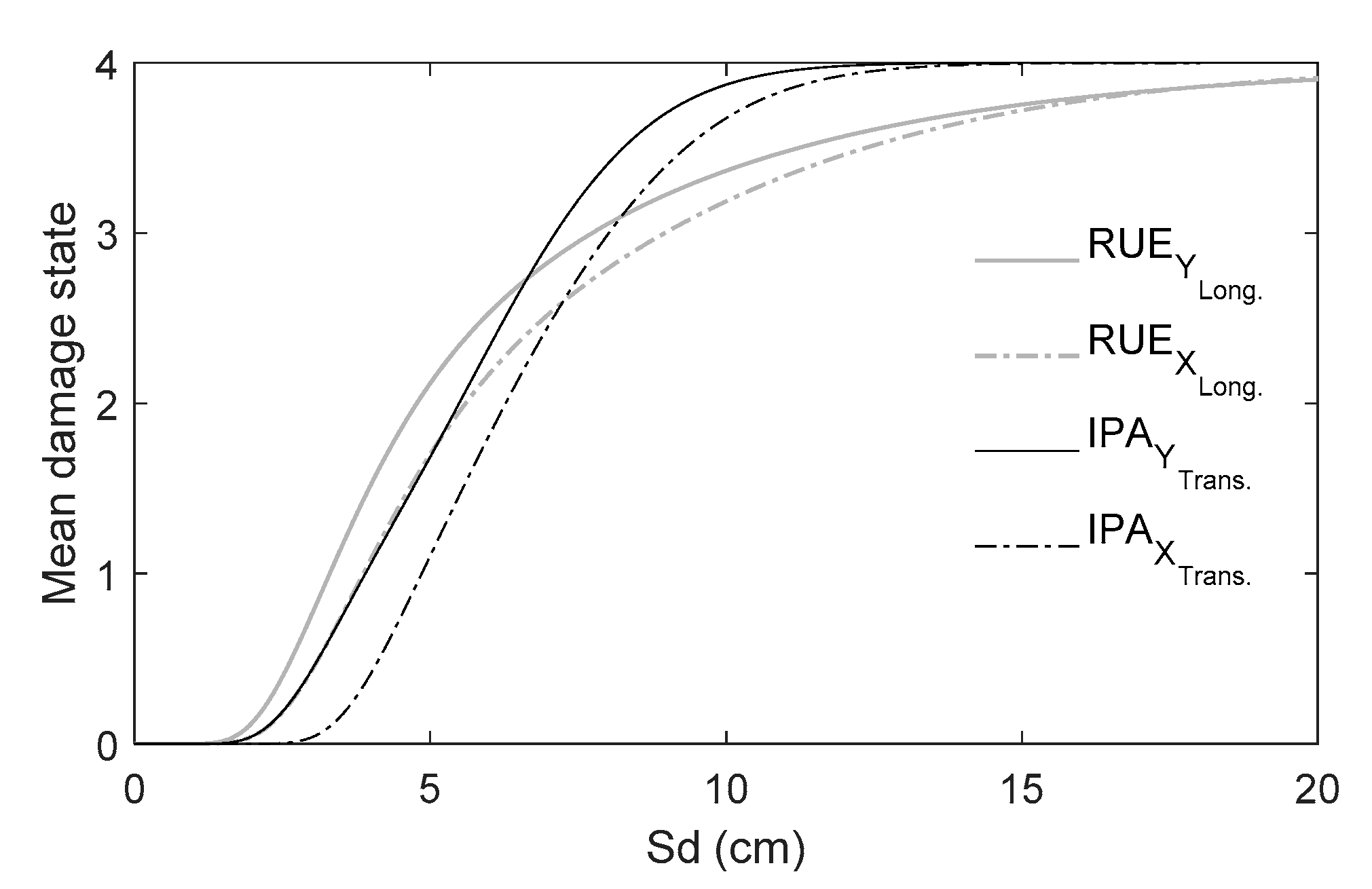
3.1.4. Fragility Curves and Mean Damage State
3.2. Results
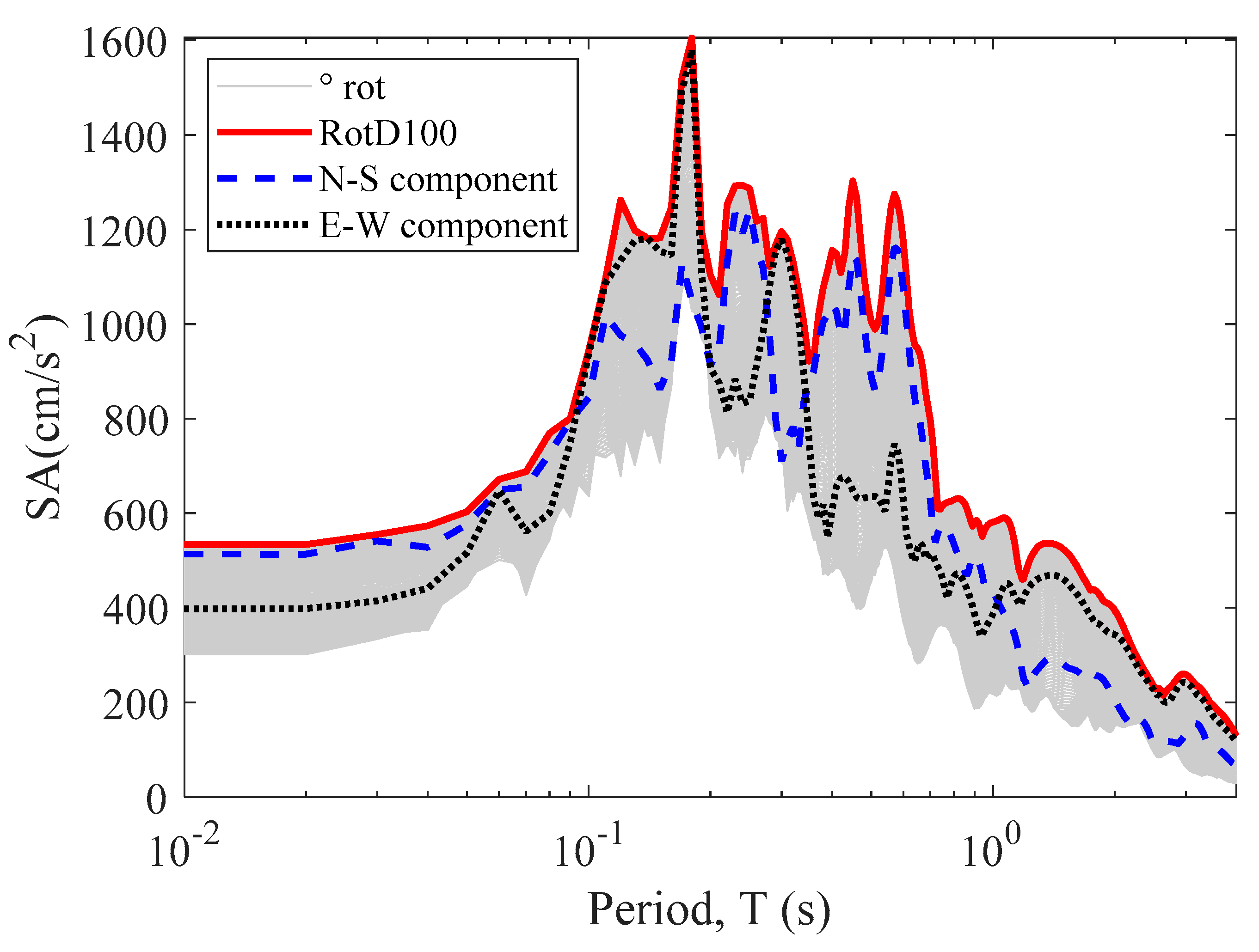
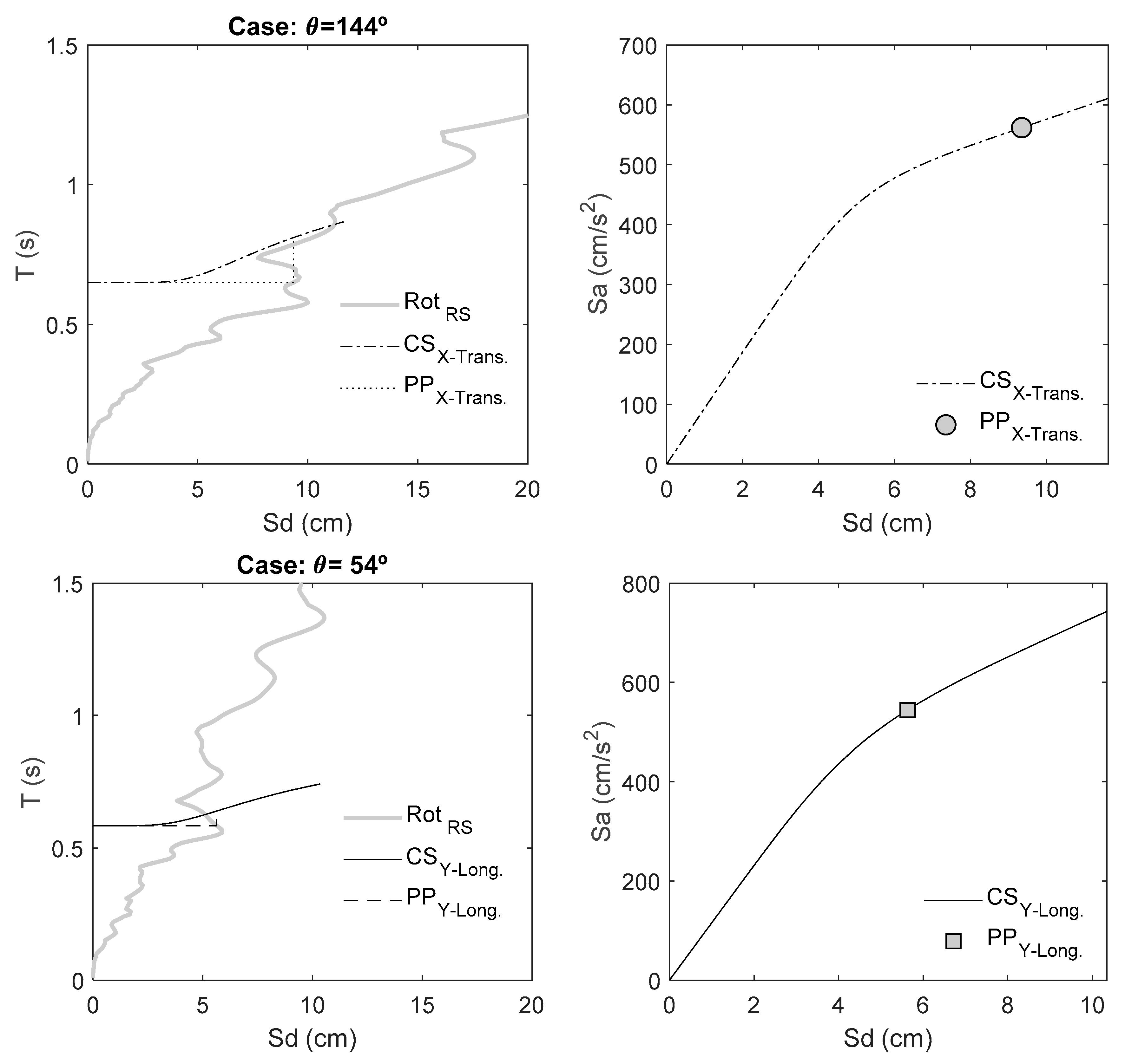
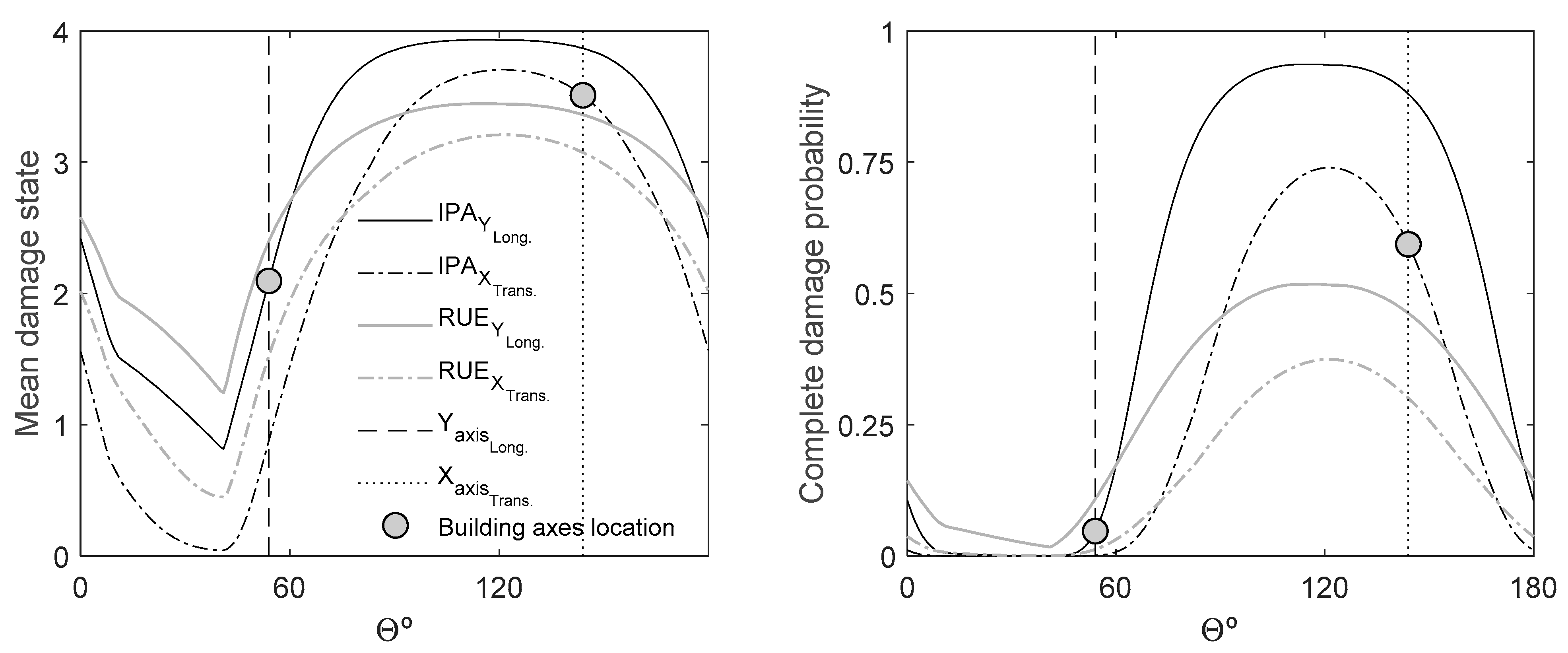
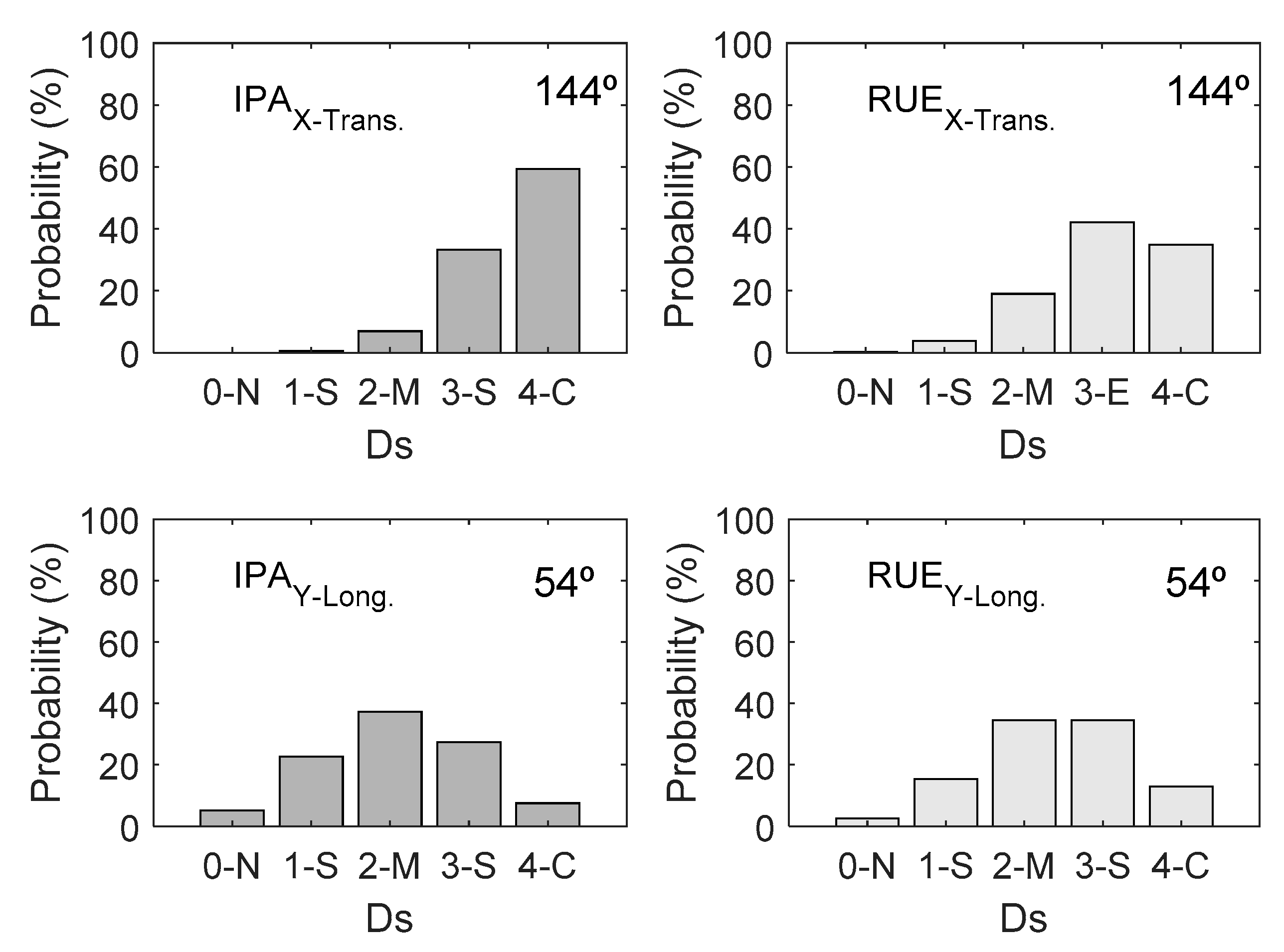
Building–Seismic Action Interaction
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singaucho, J.C.; Aurore, L.; Viracucha, C.; Ruiz, M. Observaciones del sismo del 16 de abril de 2016 de magnitud Mw 7.8. Intensidades y aceleraciones. Inf. Ref. Datos RENAC 2016, 1–20. [Google Scholar]
- Bilek, S.L. Invited review paper: Seismicity along the South American subduction zone: Review of large earthquakes, tsunamis, and subduction zone complexity. Tectonophysics 2010, 495, 2–14. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Pujades, L.G.; Macau, A.; Figueras, S. Increased seismic hazard in Barcelona (Spain) due to soil-building resonance effects. Soil Dyn. Earthq. Eng. 2019, 117, 245–250. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Pujades, L.G.; Diaz, S.A.; Alva, R.E. Do Directionality Effects Influence Expected Damage? A Case Study of the 2017 Central Mexico Earthquake. Bull. Seismol. Soc. Am. 2018, 108, 2543–2555. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Mánica, M.A.; Pujades, L.G.; Alva, R.E. Dynamic soil-structure interaction analyses considering directionality effects. Soil Dyn. Earthq. Eng. 2020, 130, 106009. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Pujades, L.G.; Hidalgo-Leiva, D.A.; Diaz, S.A. Directionality models from ground motions of Italy. Ing. Sismica 2018, 35, 43–63. [Google Scholar]
- Pinzón, L.A.; Diaz, S.A.; Pujades, L.G.; Vargas, Y.F. An efficient method for considering the directionality effect of earthquakes on structures. J. Earthq. Eng. 2019, 1–30. [Google Scholar] [CrossRef]
- Boore, D.M. Orientation-Independent, Nongeometric-Mean Measures of Seismic Intensity from Two Horizontal Components of Motion. Bull. Seismol. Soc. Am. 2010, 100, 1830–1835. [Google Scholar] [CrossRef]
- Moya-Fernández, A.; Pinzón, L.A.; Schmidt-Díaz, V.; Hidalgo-Leiva, D.A.; Pujades, L.G. A Strong-Motion Database of Costa Rica: 20 Yr of Digital Records. Seismol. Res. Lett. 2020, 91, 3407–3416. [Google Scholar] [CrossRef]
- Computers and Structures, Inc. ETABS—Integrated Analysis, Design and Drafting of Building; Systems Computers and Structures, Inc.: Walnut Creek, CA, USA, 2019. [Google Scholar]
- Pujades, L.G.; Vargas-Alzate, Y.F.; Barbat, A.H.; González-Drigo, J.R. Parametric model for capacity curves. Bull. Earthq. Eng. 2015, 13, 1347–1376. [Google Scholar] [CrossRef]
- Ye, L.; Kanamori, H.; Avouac, J.P.; Li, L.; Cheung, K.F.; Lay, T. The 16 April 2016, MW 7.8 (MS 7.5) Ecuador earthquake: A quasi-repeat of the 1942 MS 7.5 earthquake and partial re-rupture of the 1906 MS 8.6 Colombia–Ecuador earthquake. Earth Planet. Sci. Lett. 2016, 454, 248–258. [Google Scholar] [CrossRef]
- Shrivastava, M.N.; González, G.; Moreno, M.; Reddy, C.; Salazar, P.; Yáñez, G.; González, J.; de la Llera, J.C.; Báez, J.C. Coseismic and Afterslip of the Mw 8.3 Illapel Earthquake 2015 from Continuous GPS data. Geophys. Res. Lett. 2016, 43, 10710–10719. [Google Scholar] [CrossRef]
- Vigny, C.; Socquet, A.; Peyrat, S.; Ruegg, J.-C.; Métois, M.; Madariaga, R.; Morvan, S.; Lancieri, M.; Lacassin, R.; Campos, J.; et al. The 2010 Mw 8.8 Maule Megathrust Earthquake of Central Chile, Monitored by GPS. Science 2011, 330, 1417–1422. [Google Scholar] [CrossRef]
- Shahi, S.K.; Baker, J.W. NGA-West2 models for ground motion directionality. Earthq. Spectra 2014, 30, 1285–1300. [Google Scholar] [CrossRef]
- Haji-Soltani, A.; Pezeshk, S. Relationships among Various Definitions of Horizontal Spectral Accelerations in Central and Eastern North America. Bull. Seismol. Soc. Am. 2017, 108, 409–417. [Google Scholar] [CrossRef]
- Boore, D.M.; Kishida, T. Relations Between Some Horizontal-Component Ground-Motion Intensity Measures Used in Practice 1. Bull. Seismol. Soc. Am. 2016, 107, 334–343. [Google Scholar] [CrossRef]
- FEMA. Prestandard and commentary for the seismic rehabilitation of buildings, FEMA 365. Fed. Emerg. Manag. Agency 2000, 518. [Google Scholar]
- Park, Y.; Ang, A.H.S.; Wen, Y.K. Seismic damage analysis of reinforced goncrete buildings. J. Struct. Eng. 1985, I11, 740–757. [Google Scholar] [CrossRef]
- Park, Y.; Ang, A.H.-S. Mechanistic Seismic Damage Model for Reinforced Concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Hidalgo-Leiva, D.A.; Pujades, L.G.; Barbat, A.H.; Diaz, S.A.; Vargas-, Y.; Pinzón, L.A. Damage index for structures with elements of high flexural stiffness and/or brittle behavior. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018; pp. 1–12. [Google Scholar]
- Braga, F.; Dolce, M.; Liberatore, D. A Statistical Study on Damaged Buildings and an Ensuing Review of the MSK-76 Scale. In Proceedings of the Seventh European Conference on Earthquake Engineering, Athens, Greece, 20–25 September 1982; pp. 431–450. [Google Scholar]
- Braga, F.; Dolce, M.; Liberatore, D. Assessment of the relationships between Macroseismic Intensity, Type of Building and Damage, based on the recent Italy Earthquake Data. In Proceedings of the 8th European Conference on Earthquake Engineering, Lisbon, Portugal, 7–12 September 1986; pp. 39–46. [Google Scholar]
- Milutinovic, Z.V.; Trendafiloski, G.S. WP4: Vulnerability of Current Buildings; Institute of Earthquake Engineering and Engineering Seismology (IZIIS): Skopje, North Macedonia, 2003; Volume 111. [Google Scholar]
- Cosenza, E.; Manfredi, G. Damage indices and damage measures. Prog. Struct. Eng. Mater. 2000, 2, 50–59. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Pujades, L.G.; Barbat, A.H.; Hurtado, J.E.; Diaz, S.A.; Hidalgo-Leiva, D.A. Probabilistic seismic damage assessment of reinforced concrete buildings considering direccionality effects. Struct. Infrastruct. Eng. 2018, 14, 817–829. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F. KaIROS Project. Keeping and Increasing Resilience Opportunities and Sustainability of Communities against Earthquakes. European Commission: Brussels, Belgium. Available online: https://cordis.europa.eu/project/rcn/215743/factsheet/en2018 (accessed on 8 February 2021).
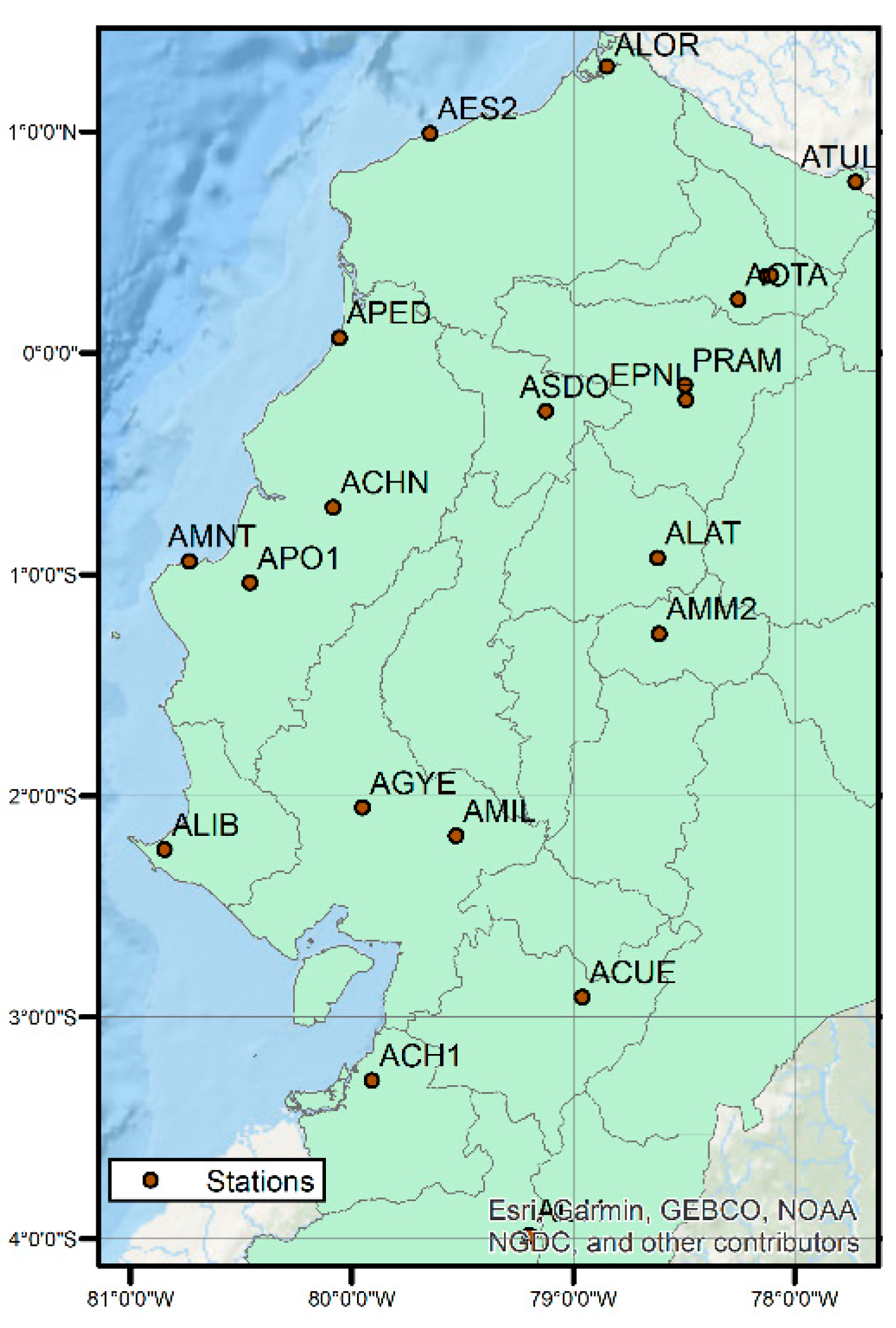



| Station | Repi (km) | PGAEW (m/s2) | PGANS (m/s2) | PGAmax (m/s2) | θPGA(max) Azimuth North | |
|---|---|---|---|---|---|---|
| AMM2 | 235 | 0.25 | 0.35 | 0.35 | 1.00 | 354° |
| ACH1 | 407 | 0.25 | 0.24 | 0.30 | 1.20 | 43° |
| ACHN | 120 | 3.20 | 3.64 | 4.12 | 1.13 | 210° |
| ACUE | 381 | 0.35 | 0.29 | 0.35 | 1.00 | 271° |
| AES2 | 76 | 1.51 | 1.08 | 1.52 | 1.00 | 96° |
| AGYE | 270 | 0.18 | 0.23 | 0.24 | 1.04 | 340° |
| AIB1 | 202 | 0.48 | 0.57 | 0.58 | 1.02 | 166° |
| AIB2 | 204 | 0.21 | 0.32 | 0.32 | 1.00 | 357° |
| ALAT | 206 | 0.31 | 0.27 | 0.31 | 1.00 | 85° |
| ALIB | 308 | 0.41 | 0.39 | 0.46 | 1.12 | 56° |
| ALJ1 | 492 | 0.15 | 0.16 | 0.17 | 1.06 | 209° |
| ALOR | 159 | 0.26 | 0.26 | 0.26 | 1.00 | 175° |
| AMIL | 288 | 0.51 | 0.45 | 0.53 | 1.04 | 244° |
| AMNT | 171 | 3.97 | 5.14 | 5.34 | 1.04 | 340° |
| AOTA | 188 | 0.42 | 0.34 | 0.48 | 1.14 | 240° |
| APED | 36 | 13.80 | 8.13 | 13.97 | 1.01 | 279° |
| APO1 | 167 | 3.11 | 3.74 | 4.16 | 1.11 | 226° |
| ASDO | 115 | 2.02 | 1.09 | 2.06 | 1.02 | 260° |
| ATUL | 251 | 0.16 | 0.21 | 0.21 | 1.00 | 0° |
| EPNL | 174 | 0.26 | 0.20 | 0.27 | 1.04 | 260° |
| PRAM | 171 | 0.24 | 0.23 | 0.25 | 1.04 | 44° |
| Section Code | fc (kg/cm2) | Dimensions (mm) | Steel Rebar | Rebar |
|---|---|---|---|---|
| C-1 and C-2 | 180 | 400 × 400 | 8 #5 | A615 Grade 40 |
| C-3 | 180 | 450 × 450 | 4 #5 + 4 #6 | A615 Grade 40 |
| C-4 and C-5 | 180 | 350 × 350 | 8 #5 | A615 Grade 40 |
| C-6 | 180 | 400 × 400 | 4 #5 + 4 #6 | A615 Grade 40 |
| C-7 and C-8 | 180 | 300 × 300 | 8 #4 | A615 Grade 40 |
| C-9 | 180 | 350 × 350 | 4 #4 + 4 #5 | A615 Grade 40 |
| Beam-1 | 170 | 200 × 500 | 2 #3 + 2 #4 | A615 Grade 40 |
| Beam-2 | 170 | 200 × 300 | 2 #3 + 2 #4 | A615 Grade 40 |
| Beam-3 | 170 | 200 × 600 | 2 #3 + 2 #4 | A615 Grade 40 |
| CS | m (g/cm) | Sdu (cm) | Sau (g) | µ (adim) | σ (adim) | εL (adim) |
|---|---|---|---|---|---|---|
| X | 0.095 | 11.62 | 0.622 | 0.420 | 0.241 | 7.35 × 10−3 |
| Y | 0.118 | 10.35 | 0.757 | 0.410 | 0.331 | 1.28 × 10−2 |
| Axis | Angle | Sapp (cm/s2) | Sdpp (cm) |
|---|---|---|---|
| X-Trans. | 144° | 561.8 | 9.3 |
| Y-Long. | 54° | 544.2 | 5.6 |
| Axis | Angle | Mean Damage State | Complete Damage Probability (%) | ||
|---|---|---|---|---|---|
| IPA | RUE | IPA | RUE | ||
| X-Trans. | 144° | 3.50 | 3.07 | 59.24 | 34.85 |
| Y-Long. | 54° | 2.09 | 2.40 | 7.52 | 12.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinzón, L.A.; Pujades, L.G.; Medranda, I.; Alva, R.E. Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment. Geosciences 2021, 11, 74. https://doi.org/10.3390/geosciences11020074
Pinzón LA, Pujades LG, Medranda I, Alva RE. Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment. Geosciences. 2021; 11(2):74. https://doi.org/10.3390/geosciences11020074
Chicago/Turabian StylePinzón, Luis A., Luis G. Pujades, Irving Medranda, and Rodrigo E. Alva. 2021. "Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment" Geosciences 11, no. 2: 74. https://doi.org/10.3390/geosciences11020074
APA StylePinzón, L. A., Pujades, L. G., Medranda, I., & Alva, R. E. (2021). Case Study of a Heavily Damaged Building during the 2016 MW 7.8 Ecuador Earthquake: Directionality Effects in Seismic Actions and Damage Assessment. Geosciences, 11(2), 74. https://doi.org/10.3390/geosciences11020074






