Application of Nonhydraulic Delineation Method of Flood Hazard Areas Using LiDAR-Based Data
Abstract
1. Introduction
2. Materials and Methods
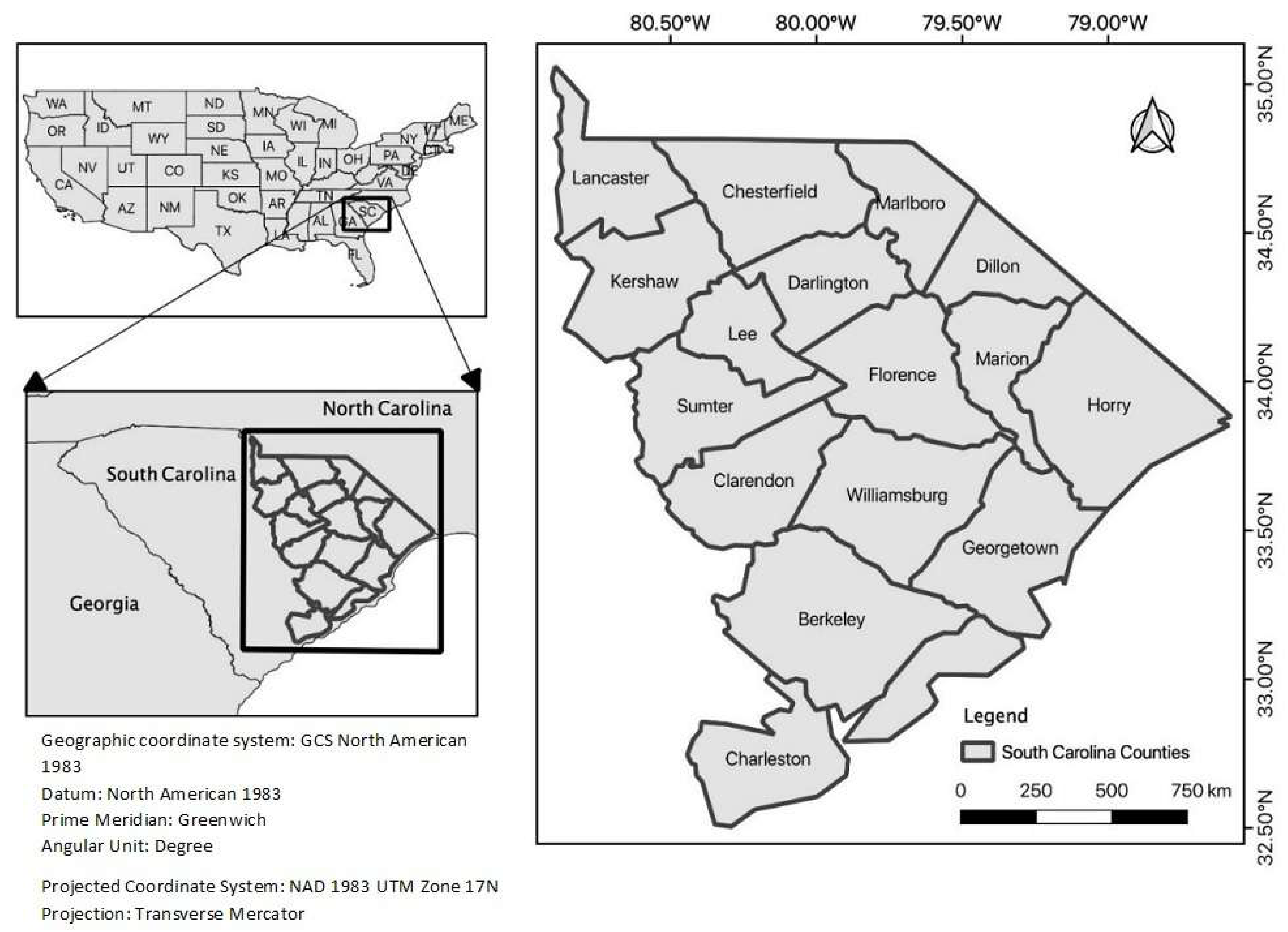
2.1. Study Area
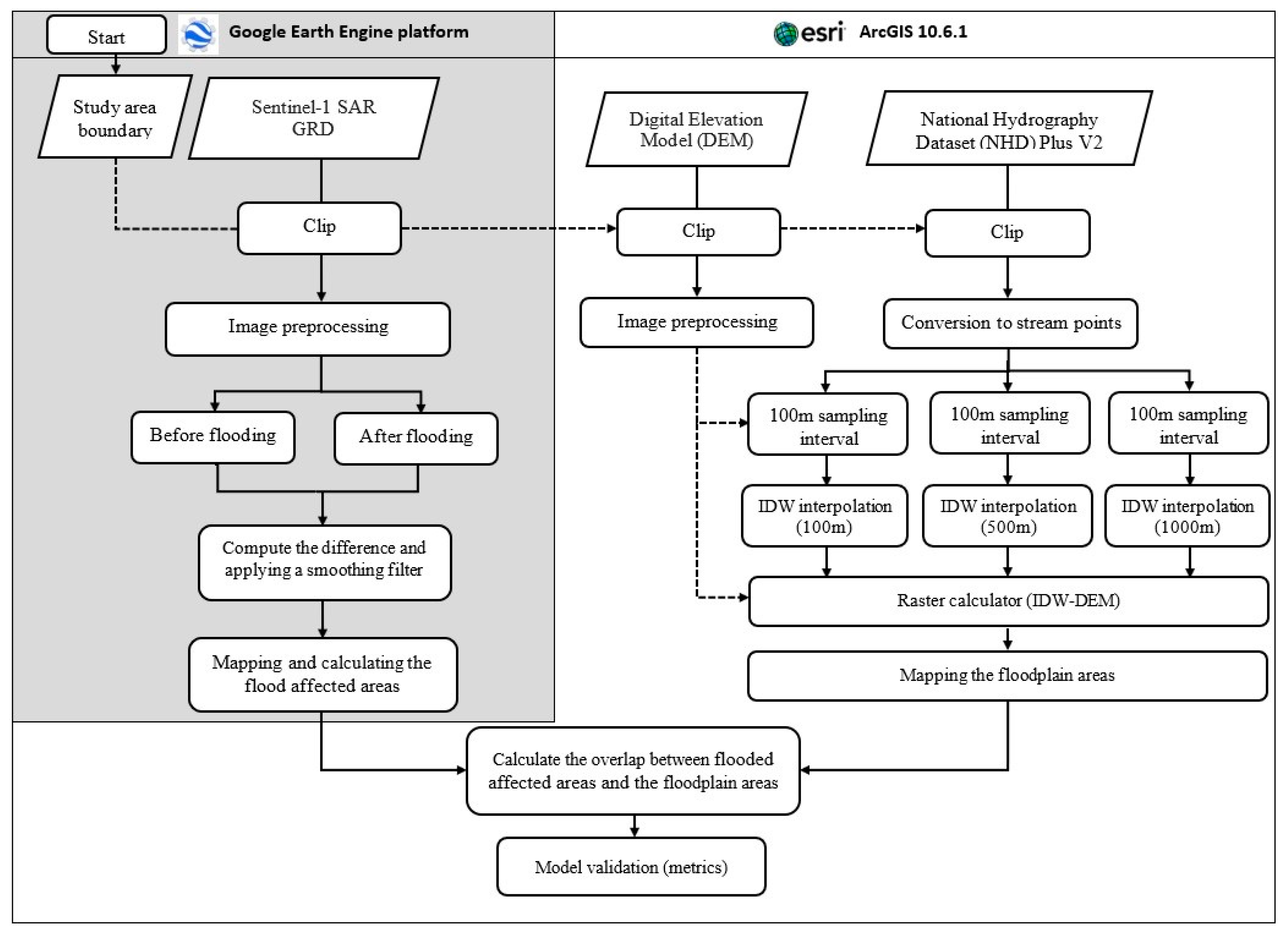
2.2. Flooding Analysis Using Google Earth Engine
2.3. Flood Hazard Area Derivation from DEM and Hydrolines
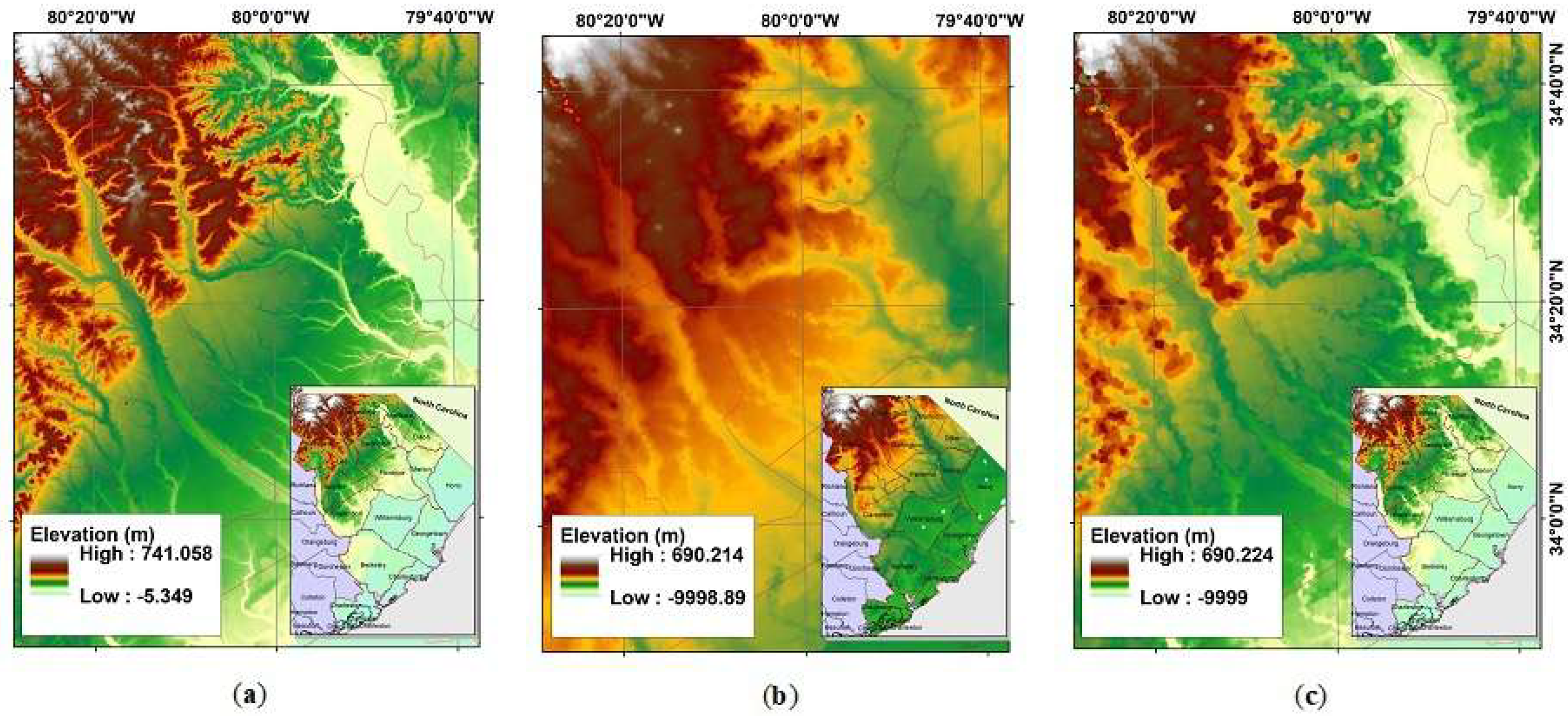
2.3.1. Data and Preprocessing
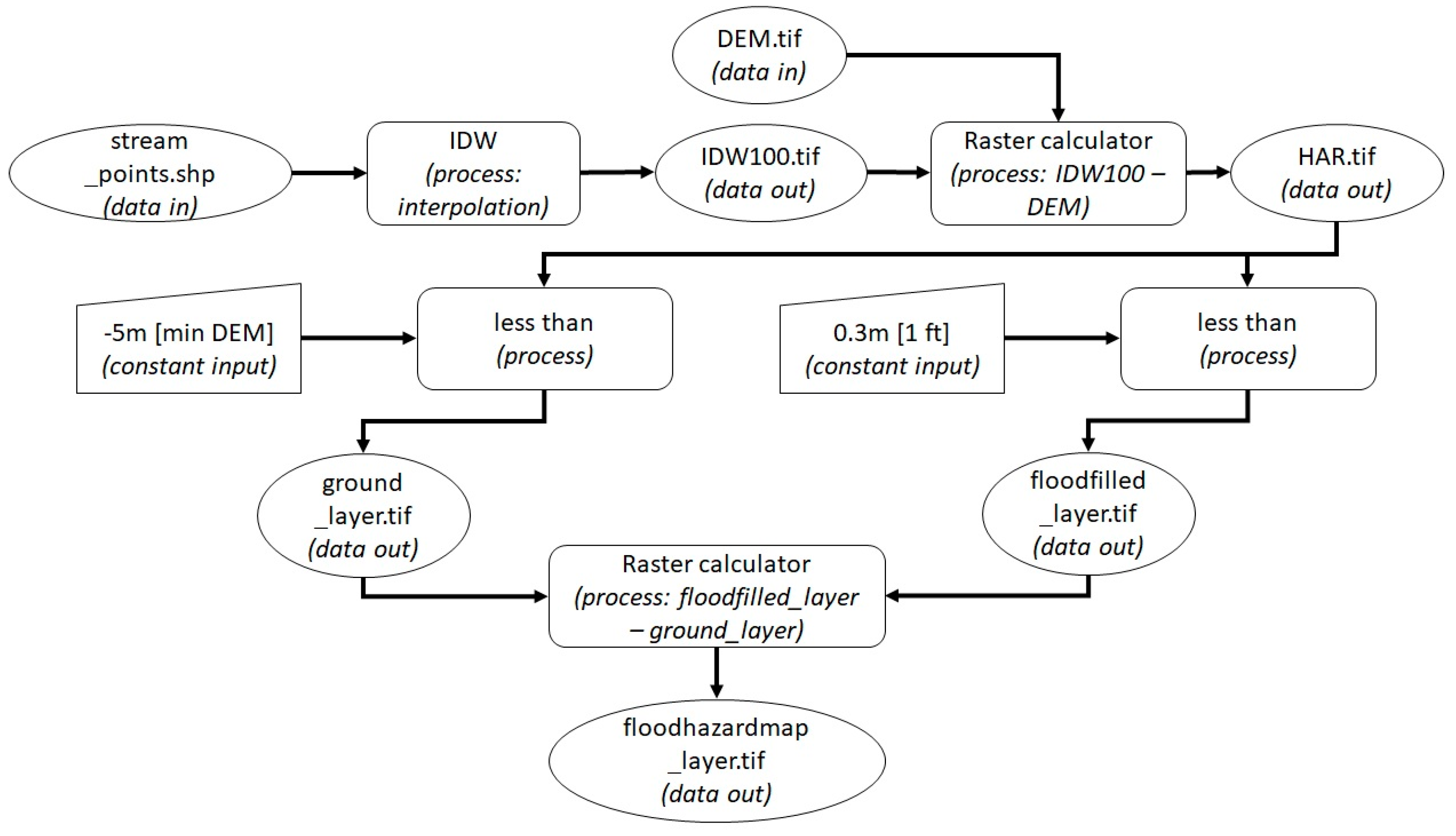
2.3.2. Generating the Flood Hazard Areas Layer
2.4. Model Validation
2.4.1. Validating Metrics
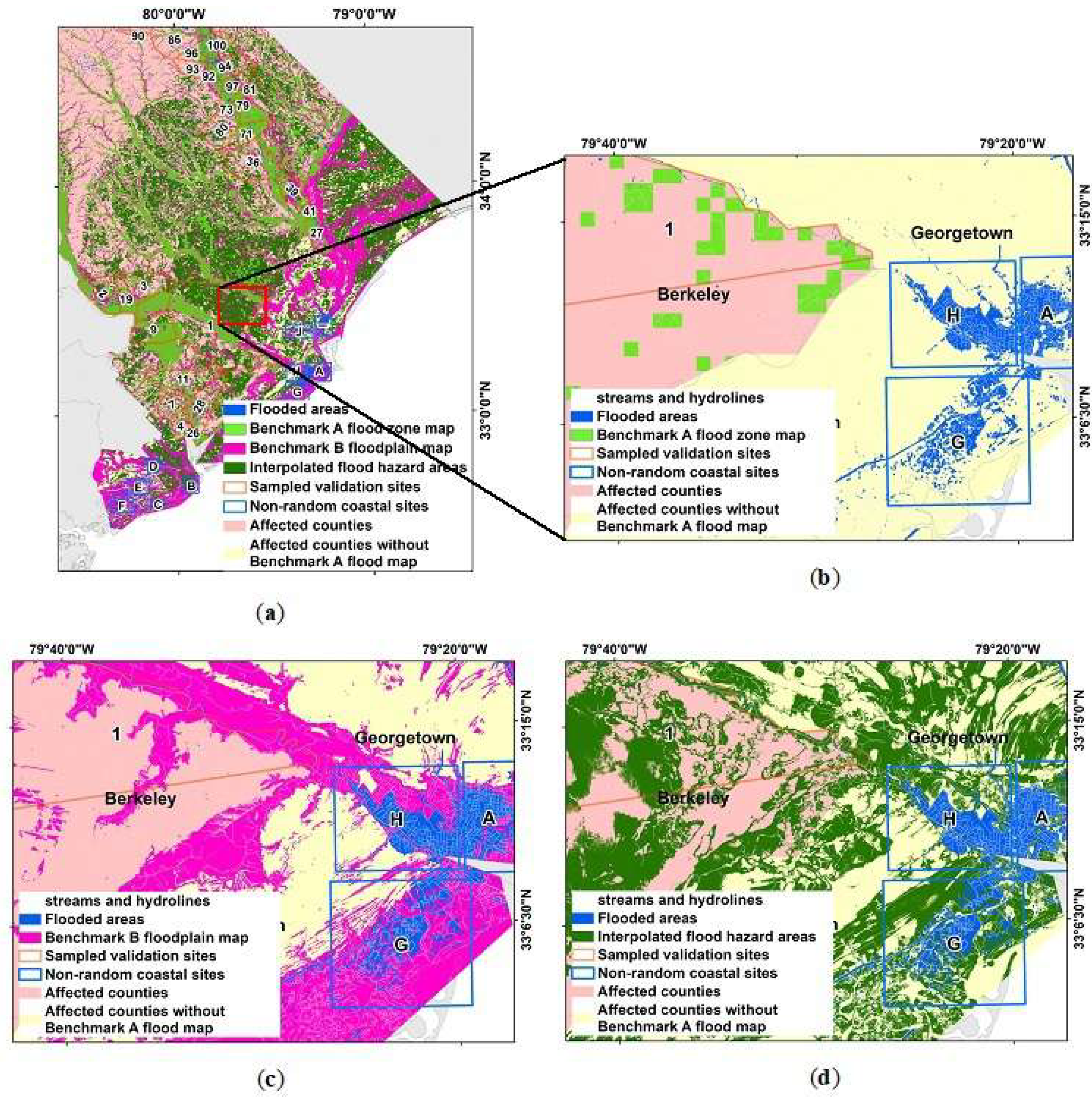
2.4.2. Selection of Sampled Sites for Validation
3. Results
3.1. Flooding Distribution using Google Earth Engine
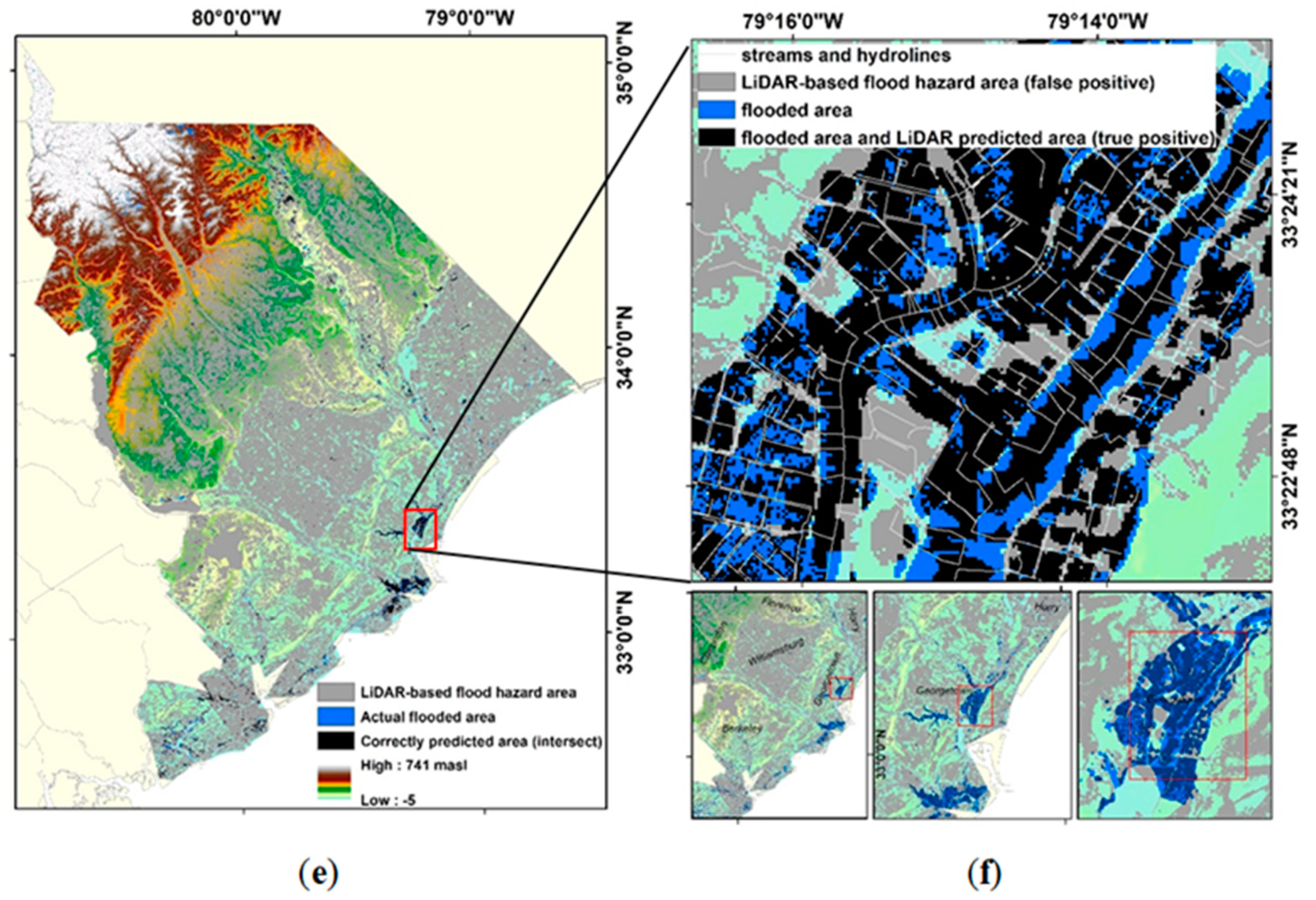
3.2. Spatial Distribution of Predicted Flood Hazard Areas
3.3. Validating the Delineated Floodplain Maps
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lubinski, K. Floodplain river ecology and the concept of river ecological health. Available online: https://umesc.usgs.gov/documents/reports/1999/status_and_trends/99t001_ch02lr.pdf (accessed on 21 August 2020).
- Schindler, S.; O’Neill, F.H.; Biró, M.; Damm, C.; Gasso, V.; Kanka, R.; van der Sluis, T.; Krug, A.; Lauwaars, S.G.; Sebesvari, Z.; et al. Multifunctional Floodplain Management and Biodiversity Effects: A Knowledge Synthesis for Six European countries. Biodivers. Conserv. 2016, 25, 1349–1382. [Google Scholar] [CrossRef]
- Department of Regional Development and Environment Executive Secretariat for Economic and Social Affairs Organization of American States. Primer on Natural Hazard Management in Integrated Regional Development Planning. Available online: https://www.oas.org/usde/publications/Unit/oea66e/begin.htm#Contents (accessed on 25 June 2019).
- Belanger, P.; Bourdeau-Brien, M. The Impact of Flood Risk on the Price of Residential Properties: The Case of England. Hous. Stud. 2018, 33, 876–901. [Google Scholar] [CrossRef]
- Beltrán, A.; Maddison, D.; Elliott, R. The Impact of Flooding on Property Prices: A Repeat-Sales Approach. J. Environ. Econ. Manage. 2019, 95, 62–86. [Google Scholar] [CrossRef]
- McKenzie, R.; Levendis, J. Flood Hazards and Urban Housing Markets: The Effects of Katrina on New Orleans. J. Real Estate Financ. Econ. 2010, 40, 62–76. [Google Scholar] [CrossRef]
- Rajapaksa, D.; Wilson, C.; Managi, S.; Hoang, V.; Lee, B. Flood Risk Information, Actual Floods and Property Values: A Quasi-Experimental Analysis. Econ. Rec. 2016, 92, 52–67. [Google Scholar] [CrossRef]
- Association of State Floodplain Managers (ASFPM). Flood Mapping for the Nation: A Cost Analysis for the Nation’s Flood Map Inventory; Association of State Floodplain Managers (ASFPM): Madison, WI, USA, 2013. [Google Scholar]
- Flavelle, C.; Lu, D.; Denise, P.V.; Popovich, N.; Schwartz, J. New Data Reveals Hidden Flood Risk Across America - The New York Times. New York Times. Available online: https://www.nytimes.com/interactive/2020/06/29/climate/hidden-flood-risk-maps.html?mc=aud_dev&ad-keywords=auddevgate&subid1=TAFI&ad_name=INTER_20_XXXX_XXX_1P_CD_XX_XX_SITEVISITXREM_X_XXXX_COUSA_P_X_X_EN_FBIG_OA_XXXX_00_EN_JP_NFLINKS&adset_name=https://www (accessed on 24 July 2020).
- Federal Emergency Management Agency (FEMA). Floodplain Management Requirements: A Study Guide and Desk Reference for Local Officials; National Flood Insurance Program, FEMA: Washington, DC, USA, 2005. [Google Scholar]
- Jung, Y.; Merwade, V. Estimation of Uncertainty Propagation in Flood Inundation Mapping Using a 1-D Hydraulic Model. Hydrol. Process. 2015, 29, 624–640. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Merwade, V. A DEM-based approach for large-scale floodplain mapping in ungauged watersheds. J Hydrol. 2017, 550, 650–662. [Google Scholar] [CrossRef]
- Gallant, J.C.; Wilson, J.P. Digital terrain analysis in terrain analysis. In Terrain Analysis: Principles and Applications; John Wiley \& Sons Inc: New York, NY, USA, 2000. [Google Scholar]
- Wilson, J.P.; Fotheringham, A.S. The Handbook of Geographic Information Science; John Wiley & Sons Oxford: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Sofia, G.; Eltner, A.; Nikolopoulos, E.; Crosby, C. Leading Progress in Digital Terrain Analysis and Modeling. ISPRS Int. J. Geo-Inf. 2019, 8, 372. [Google Scholar] [CrossRef]
- Nardi, F.; Vivoni, E.R.; Grimaldi, S. Investigating a floodplain scaling relation using a hydrogeomorphic delineation method. Water Resour Res. 2006, 42. [Google Scholar] [CrossRef]
- Nobre, A.D.; Cuartas, L.A.; Hodnett, M.; Rennó, C.D.; Rodrigues, G.; Silveira, A.; Saleska, S. Height Above the Nearest Drainage - a hydrologically relevant new terrain model. J Hydrol. 2011, 404, 13–29. [Google Scholar] [CrossRef]
- da Costa, R.T.; Manfreda, S.; Luzzi, V.; Samela, C.; Mazzoli, P.; Castellarin, A.; Bagli, S. A web application for hydrogeomorphic flood hazard mapping. Environ Model Softw. 2019, 118, 172–186. [Google Scholar] [CrossRef]
- Samela, C.; Troy, T.J.; Manfreda, S. Geomorphic classifiers for flood-prone areas delineation for data-scarce environments. Adv Water Resour. 2017, 102, 13–28. [Google Scholar] [CrossRef]
- Manfreda, S.; Samela, C. A digital elevation model based method for a rapid estimation of flood inundation depth. J Flood Risk Manag. 2019, 12, e12541. [Google Scholar] [CrossRef]
- Woznicki, S.A.; Baynes, J.; Panlasigui, S.; Mehaffey, M.; Neale, A. Development of a Spatially Complete Floodplain Map of the Conterminous United States Using Random Forest. Sci. Total Environ. 2019, 647, 942–953. [Google Scholar] [CrossRef] [PubMed]
- Caletka, M.; Šulc Michalková, M.; Koli, M.; Trizna, M. Quality of Flood Extents Delineated by a Non-Hydrodynamic GIS Tool. Catena 2019, 175, 367–387. [Google Scholar] [CrossRef]
- Williams, W.A.; Jensen, M.E.; Winne, J.C.; Redmond, R.L. An automated technique for delineating and characterizing valley-bottom settings. In Environmental Monitoring and Assessment; Springer: Dordrecht, The Netherlands, 2000; Volume 64, pp. 105–114. [Google Scholar]
- Zhang, Q.; Wang, C.; Huang, P. Method of Constructing Distributed Hydrological Model Based on GIS and RS. In Proceedings of the Geoinformatics 2006: GNSS and Integrated Geospatial Applications, Wuhan, China, 28 October 2006; Volume 6420, p. 64201T. [Google Scholar] [CrossRef]
- Mcinnes, K.L.; Church, J.; Monselesan, D.; Hunter, J.R.; O’grady, J.G.; Haigh, I.D.; Zhang, X. Information for Australian Impact and Adaptation Planning in Response to Sea-Level Rise. Aust. Meteorol. Oceanogr. J. 2015, 65, 127–149. [Google Scholar] [CrossRef]
- Seenath, A.; Wilson, M.; Miller, K. Hydrodynamic versus GIS Modelling for Coastal Flood Vulnerability Assessment: Which Is Better for Guiding Coastal Management? Ocean Coast. Manag. 2016, 120, 99–109. [Google Scholar] [CrossRef]
- Degiorgis, M.; Gnecco, G.; Gorni, S.; Roth, G.; Sanguineti, M.; Taramasso, A.C. Classifiers for the detection of flood-prone areas using remote sensed elevation data. J Hydrol. 2012, 470, 302–315. [Google Scholar] [CrossRef]
- Samela, C.; Manfreda, S.; Paola, F.D.; Giugni, M.; Sole, A.; Fiorentino, M. DEM-Based Approaches for the Delineation of Flood-Prone Areas in an Ungauged Basin in Africa. J. Hydrol. Eng. 2016, 21, 06015010. [Google Scholar] [CrossRef]
- Zurqani, H.A.; Post, C.J.; Mikhailova, E.A.; Schlautman, M.A.; Sharp, J.L. Geospatial Analysis of Land Use Change in the Savannah River Basin Using Google Earth Engine. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 175–185. [Google Scholar] [CrossRef]
- Zurqani, H.A.; Post, C.J.; Mikhailova, E.A.; Ozalas, K.; Allen, J.S. Geospatial Analysis of Flooding from Hurricane Florence in the Coastal South Carolina Using Google Earth Engine. Clemson, SC. 2019. Available online: https://tigerprints.clemson.edu/grads_symposium/230/ (accessed on 21 August 2020).
- Zurqani, H.A.; Post, C.J.; Mikhailova, E.A.; Cope, M.P.; Allen, J.S.; Lytle, B. Evaluating the Integrity of Forested Riparian Buffers over a Large Area Using LiDAR Data and Google Earth Engine. Clemson, SC. 2019. Available online: https://tigerprints.clemson.edu/grads_symposium/225/ (accessed on 8 August 2020).
- Smith, T. Hurricane Florence, Another 1,000-Year Event, Caused at Least $1.2 Billion in Damage in SC. The Greenville News. Available online: https://www.greenvilleonline.com/story/news/local/south-carolina/2018/09/20/south-carolina-damage-florence-estimated-1-2-billion/1368815002/ (accessed on 8 August 2020).
- South Carolina Dept of Natural Resources. SCDNR - LiDAR Data Status by County. Available online: http://www.dnr.sc.gov/GIS/lidarstatus.html (accessed on 25 June 2019).
- USGS. National Hydrography Dataset. Available online: https://www.usgs.gov/core-science-systems/ngp/national-hydrography/national-hydrography-dataset?qt-science_support_page_related_con=0#qt-science_support_page_related_con (accessed on 25 June 2019).
- USGS. The National Map. Available online: https://www.usgs.gov/core-science-systems/national-geospatial-program/national-map (accessed on 25 June 2020).
- Wijeratne, V.; Manawadu, L. VALIDATION OF SPATIAL INTERPOLATION TECHNIQUES IN GIS. Semant. Sch. 2016. Available online: https://www.semanticscholar.org/paper/VALIDATION-OF-SPATIAL-INTERPOLATION-TECHNIQUES-IN-Wijeratne-Manawadu/46aef90578d275b9254ffa98150f950abcec10f1 (accessed on 21 June 2020).
- Environmental Systems Research Institute, Inc. How IDW works—Help | ArcGIS for Desktop. Available online: http://desktop.arcgis.com/en/arcmap/10.3/tools/3d-analyst-toolbox/how-idw-works.htm (accessed on 13 June 2019).
- Dilts, T.E.; Yang, J.; Weisberg, P.J. Mapping Riparian Vegetation with Lidar Data: Predicting Plant Community Distribution Using Height above River and Flood Height. Available online: https://www.semanticscholar.org/paper/Mapping-Riparian-Vegetation-with-Lidar-Data-plant-Dilts-Yang/999c815efbc4b337f46b43f3061952b6411d5325 (accessed on 21 June 2020).
- Federal Emergency Management Agency (FEMA). Definitions of FEMA Flood Zone Designations. Available online: http://msc.fema.gov/webapp/wcs/stores/servlet/info?storeId=10001&catalogId=10001&langId=- (accessed on 13 June 2019).
- Bates, P.D.; De Roo, A.P.J. A Simple Raster-Based Model for Flood Inundation Simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Horritt, M.S. A Methodology for the Validation of Uncertain Flood Inundation Models. J. Hydrol. 2006, 326, 153–165. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). National Flood Hazard Layer (NFHL). Available online: https://www.fema.gov/national-flood-hazard-layer-nfhl (accessed on 29 June 2019).


| Configuration Name | Configuration Specifics | ||
|---|---|---|---|
| Stream Sampling Points Interval | DEM Source | IDW Configuration | |
| IDW100 | 100 m | LiDAR-based | Default (pval = 2) |
| IDW100opt | 100 m | LiDAR-based | Optimal (pval = 39) |
| IDW100_NED | 100 m | National Elevation Dataset | Default (pval = 2) |
| IDW100opt_NED | 100 m | National Elevation Dataset | Optimal (pval = 39) |
| IDW500 | 500 m | LiDAR-based | Default (pval = 2) |
| IDW500opt | 500 m | LiDAR-based | Optimal (pval = 39) |
| IDW500_NED | 500 m | National Elevation Dataset | Default (pval = 2) |
| IDW500opt_NED | 500 m | National Elevation Dataset | Optimal (pval = 39) |
| IDW1000 | 1000 m | LiDAR-based | Default (pval = 2) |
| IDW1000opt | 1000 m | LiDAR-based | Optimal (pval = 39) |
| IDW1000_NED | 1000 m | National Elevation Dataset | Default (pval = 2) |
| IDW1000opt_NED | 1000 m | National Elevation Dataset | Optimal (pval = 39) |
| Benchmark A | FEMA flood zone map from NFHL | ||
| Benchmark B | US EPA floodplain map by random forest (Woznicki et al. 2019) | ||
| Model Configuration | 30 Sampled Areas Validated | 10 Coastal Sites Applied | ||
|---|---|---|---|---|
| Mean (%) | SD | Mean (%) | SD | |
| Benchmark A | 62 | 27 | – | – |
| Benchmark B | 66 | 26 | 97 | 3 |
| IDW100 | 50 | 15 | 69 | 16 |
| IDW100opt | 55 | 14 | 73 | 11 |
| IDW500 | 40 | 16 | 63 | 18 |
| IDW500opt | 51 | 14 | 69 | 13 |
| IDW1000 | 36 | 17 | 61 | 19 |
| IDW1000opt | 46 | 16 | 65 | 15 |
| IDW100_NED | 56 | 14 | 57 | 16 |
| IDW100opt_NED | 69 | 11 | 73 | 14 |
| IDW500_NED | 51 | 15 | 52 | 12 |
| IDW500opt_NED | 70 | 13 | 70 | 11 |
| IDW1000_NED | 50 | 14 | 49 | 13 |
| IDW1000opt_NED | 70 | 11 | 68 | 12 |
| Model Configuration | 30 Sampled Areas Validated | 10 Coastal Sites Applied | |||
|---|---|---|---|---|---|
| Mean (SD) | Test vs. Bmark A | Test vs. Bmark B | Mean (SD) | Test vs. Bmark B | |
| Benchmark A | −0.82 (0.11) | ||||
| Benchmark B | −0.84 (0.09) | 0.024 | −0.27 (0.25) | ||
| IDW100 | −0.85 (0.12) | 0.007 | 0.091 | −0.28 (0.26) | 0.403 |
| IDW100opt | −0.86 (0.12) | 0.001 | 0.032 | −0.31 (0.23) | 0.214 |
| IDW500 | −0.84 (0.13) | 0.123 | 0.490 | −0.25 (0.28) | 0.330 |
| IDW500opt | −0.85 (0.13) | 0.025 | 0.210 | −0.28 (0.24) | 0.432 |
| IDW1000 | −0.82 (0.14) | 0.432 | 0.178 | −0.23 (0.28) | 0.201 |
| IDW1000opt | −0.84 (0.14) | 0.143 | 0.483 | −0.25 (0.26) | 0.361 |
| IDW100_NED | −0.91 (0.08) | 0.000 | 0.000 | −0.37 (0.22) | 0.048 |
| IDW100opt_NED | −0.91 (0.07) | 0.000 | 0.000 | −0.39 (0.20) | 0.018 |
| IDW500_NED | −0.91 (0.08) | 0.000 | 0.000 | −0.38 (0.23) | 0.035 |
| IDW500opt_NED | −0.91 (0.07) | 0.000 | 0.000 | −0.39 (0.21) | 0.017 |
| IDW1000_NED | −0.91 (0.08) | 0.000 | 0.000 | −0.39 (0.23) | 0.047 |
| IDW1000opt_NED | −0.91 (0.07) | 0.000 | 0.000 | −0.38 (0.21) | 0.024 |
| Model Configuration | 30 Sampled Areas Validated | 10 Coastal Sites Applied | |
|---|---|---|---|
| vs. Bmark A | vs. Bmark B | vs. Bmark B | |
| Benchmark A | 1.00 | 0.85 | |
| Benchmark B | 1.15 | 1.00 | 1.00 |
| IDW100 | 1.20 | 1.13 | 0.72 |
| IDW100opt | 1.31 | 1.24 | 0.76 |
| IDW500 | 0.97 | 0.92 | 0.65 |
| IDW500opt | 1.23 | 1.16 | 0.71 |
| IDW1000 | 0.86 | 0.82 | 0.63 |
| IDW1000opt | 1.12 | 1.05 | 0.67 |
| IDW100_NED | 1.29 | 1.20 | 0.60 |
| IDW100opt_NED | 1.61 | 1.51 | 0.76 |
| IDW500_NED | 1.21 | 1.12 | 0.53 |
| IDW500opt_NED | 1.62 | 1.51 | 0.73 |
| IDW1000_NED | 1.21 | 1.14 | 0.51 |
| IDW1000opt_NED | 1.64 | 1.53 | 0.71 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ureta, J.C.; Zurqani, H.A.; Post, C.J.; Ureta, J.; Motallebi, M. Application of Nonhydraulic Delineation Method of Flood Hazard Areas Using LiDAR-Based Data. Geosciences 2020, 10, 338. https://doi.org/10.3390/geosciences10090338
Ureta JC, Zurqani HA, Post CJ, Ureta J, Motallebi M. Application of Nonhydraulic Delineation Method of Flood Hazard Areas Using LiDAR-Based Data. Geosciences. 2020; 10(9):338. https://doi.org/10.3390/geosciences10090338
Chicago/Turabian StyleUreta, J. Carl, Hamdi A. Zurqani, Christopher J. Post, Joan Ureta, and Marzieh Motallebi. 2020. "Application of Nonhydraulic Delineation Method of Flood Hazard Areas Using LiDAR-Based Data" Geosciences 10, no. 9: 338. https://doi.org/10.3390/geosciences10090338
APA StyleUreta, J. C., Zurqani, H. A., Post, C. J., Ureta, J., & Motallebi, M. (2020). Application of Nonhydraulic Delineation Method of Flood Hazard Areas Using LiDAR-Based Data. Geosciences, 10(9), 338. https://doi.org/10.3390/geosciences10090338







