Abstract
Seismic wave-propagation simulations are limited in their frequency content by two main factors: (1) the resolution of the seismic wave-speed structure of the region in which the seismic waves are propagated through; and (2) the extent of our understanding of the rupture process, mainly on the short length scales. For this reason, high-frequency content in the ground motion must be simulated through other means. Toward this end, we adopt a variant of the classical empirical Green’s function (EGF) approach of summing, with suitable time shift, recorded seismograms from small earthquakes in the past to generate high-frequency seismograms (0.5–5.0 Hz) for engineering applications. We superimpose these seismograms on low-frequency seismograms, computed from kinematic source models using the spectral element method, to produce broadband seismograms. The non-uniform time- shift scheme used in this work alleviates the over-estimation of high-frequency content of the ground motions observed. We validate the methodology by simulating broadband motions from the 1999 Hector Mine and the 2006 Parkfield earthquakes and comparing them against recorded seismograms.
Keywords:
empirical Green’s function; ground motion simulation; seismic wave-propagation; kinematic source models; rise-time; source sampling function; hybrid simulation; rupture directivity; spectral-element method; seismic slip; displacement amplitude spectrum; San Andreas fault; Hector Mine earthquake; Parkfield earthquake 1. Introduction
The broader purpose of this work is to produce site-specific broadband ground motions (<5 Hz) in southern California from a suite of large earthquakes on the San Andreas fault [1]. A major challenge in seismology is predicting the expected ground motions from large earthquakes for future events. These predictions are essential for engineering design, hazard estimation, and risk analysis. Theoretically, to produce site-specific ground motions deterministically, one needs a detailed description of: (1) the earthquake rupture process and (2) the three-dimensional regional wave-speed structure of the earth. The frequency content of the ground motions generated using finite element, spectral-element or finite- difference approaches is limited by our knowledge and resolution of these aspects. Although the lack of data related to the state of stress in the earth and the laws of friction governing fault rupture nucleation and propagation has hampered our understanding of the dynamics of the rupture process, methods to develop kinematic representation of earthquake sources have matured significantly. Kinematic source models from past earthquakes at one location hold the greatest promise for predicting ground motions from future events at other locations where fault geometry and focal mechanisms are similar. The resolution of the seismic wave-speed structure is another governing factor in determining the limits of the frequency content of the propagating waves (the higher the resolution of the wave-speed structure the higher the frequency content that can be reliably propagated). This resolution is limited by the spatial density of seismic observations. Even in well-studied regions such as southern California the wave-speed models (e.g., the SCEC Community Velocity Model-Harvard (CVM-H) and the SCEC CVM-S) are capable of propagating waves reliably with frequencies of only up to about 0.5–1.0 Hz (e.g., [2,3,4,5,6,7]), well below that required for many engineering applications. We are still computationally limited in generating 5 Hz synthetics at distances of, say, 300 km. Over time, computation will not remain a limitation, however. On the other hand, inadequacy of data coverage will continue to limit the development of models to an accuracy of 0.5 Hz or so for some time to come. To overcome this limitation, several hybrid approaches that combine low-frequency waveforms from deterministic simulations and high-frequency waveforms synthesized using stochastic or empirical (e.g., EGF) approaches have been proposed and used to recreate ground motions from recent earthquakes (e.g., [8,9,10,11,12,13,14,15]). Here, we are presenting a deterministic hybrid approach for generating ground motions from large earthquakes. The low-frequency content (limited to a frequency of 0.5 Hz) of the ground motion is generated from a kinematic source model using the open-source seismic wave-propagation package SPECFEM3D (V2.0 SESAME, [4,16,17]) that implements the spectral-element method, incorporating the regional 3-D wave-speed structure of the earth. Low-frequency synthetic SPECFEM3D seismograms are combined with high-frequency seismograms generated using a variant of the classical EGF approach, which will be the main focus of this article.
Hartzell [18] was the first to outline the framework for the empirical Green’s function (EGF) method. Using aftershock records of an event as the Green’s functions (EGFs) he proposed to capture the travel paths of the seismic waves. Since then, several variants of the method have been advanced (e.g., [19,20,21,22,23,24,25]). In these methods, the rupture plane of the target event is subdivided into a grid of subfaults (uniform or non-uniform) and the seismic waves radiated from each subfault is time shifted and summed carefully to yield the shaking at any given site under the target event However, there is an inherent problem with the EGF method. Brune [26] showed that for a given source dimension, the displacement spectrum at low frequencies is controlled by the effective seismic moment, whereas at high frequencies it is controlled by the effective stress. This means, on the one hand, if we add the events such that the moment of the target event equals the total moment of all added events (in the simplest case of using one EGF this can be viewed as scaling based on the seismic moment of the EGF to that of the target event), the low-frequency content (below the corner frequency of the large event) would be correctly reproduced, but the high-frequency content (above the corner frequency of the target event) would be overestimated. On the other hand, if we fill the rupture area with non-overlapping EGF events (scaling based on area or equivalently scaling based on moment ratio to the power of 2/3) the high-frequency content (above the corner frequency of the small event) would be accurately represented, but the low-frequency content (below the corner frequency of the small event) would be underestimated. Joyner and Boore [23], who were one of the earliest to recognize this problem, suggested that if events are randomly added in time over the total rise-time of the event and the final result is multiplied by (N being the ratio of the seismic moment of the main event to the seismic moment of the EGF), then the resulting spectrum would be consistent with Brune’s spectrum. Heaton and Hartzell [20] also presented a quantitative discussion on the source of inconsistency in the use of EGFs. Somerville et al. [24] illustrated that a low bias between the simulated and observed ground motions can also be obtained by stochastically perturbing the time shifts at which the EGFs are supposed to be added. Moreover, a desirable scaling of the displacement spectrum in the high- and low-frequency bands that matches the Brune’s spectrum can be achieved by scaling, filtering, or convolving the EGFs with appropriate functions. For example, Frankel [19] suggested populating the rupture area with non-overlapping events and then applying appropriate filter (or a frequency domain operator designed based on relative magnitudes of the slip velocity of the target event and that of the EGF event) to increase the low-frequency content without modulating the high-frequency content. However, all these methods have been shown to work well only when the magnitudes of the target event and the EGF event do not differ by more than 2.
Here, we use EGF events with three or four magnitudes smaller than the target event to produce only the high-frequency (0.5–5 Hz) part of the ground motions to be combined with the low-frequency part from wave-propagation simulations. We start with kinematic source models from past earthquakes, resampled to a finer resolution (typically down to 0.5 km). The choice of this resolution is dictated by the highest frequency wave that can be reliably propagated through the spectral element mesh using the wave-speed model at hand. We then select EGFs from previously recorded events on the target fault in the 2.5–4.5 magnitude range, located within in the rupture extent of the target event or as close to it as possible. The main assumption here is that the source mechanism of the small event is the same as that of the target event. Similar to previous studies (e.g., [20,21,24]), the formulation consists of two summations, one over all the subfaults and one within each subfault. In both summations proper time shifts are applied to account for rupture front propagation. Additionally, in the second summation, the EGFs are further shifted in time to ensure that the impulse source–time functions of the EGFs collectively span the duration of slip of the target subfault. An additional correction is applied to the records to account for geometric spreading. The key advances in this work are: (i) expanding and exploring the limits of applicability of the EGF method by using the large quantity of seismic data available in the low magnitude range of 2.5–4.5 and (ii) achieving good agreement in the synthetics with [26] spectrum without artificial filtering or convolution in the frequency band of interest by introducing a new method of selecting time shifts. This method is based on the assumption that seismic moment in each subfault is released in equal-moment steps by EGFs assigned to that subfault. We validate our approach by simulating the 2004 Parkfield ( 6.0) and the 1999 Hector Mine ( 7.1) earthquakes at various stations across southern California.
1.1. Source Model Selection
Source models for earthquake simulations are selected from kinematic finite-source inversions of past earthquakes on faults that are geometrically similar to that of the target event, with a rupture mechanism similar to that of the target event. For example, the source model for a target event on the San Andreas fault will be a kinematic finite source inversion of an earthquake that has occurred on a right-lateral strike-slip fault with a dip angle of approximately () and a depth of 20 km (±5 km). Source spectrum is closely related to fault geometry and rupture mechanism; conforming the scenario earthquake source characteristics to the physically observed characteristics on the target fault may help produce realistic energy release on the fault. The selected source model, if coarsely sampled, is resampled to a finer resolution of about 0.5 km, to be able to generate waves of periods 2 s and longer [consistent with the highest frequency of about 0.5 Hz that can be propagated reliably through the wave-speed model used in this study (CVM-H 11.9.0)].
1.2. Low-Frequency Ground Motion Waveforms
The simulation of low-frequency ground motion using SPECFEM3D has been described in great detail in other works (e.g., [4,16,17]). Here, we give only a brief overview.
The low-frequency ground motion waveforms are generated using numerical methods incorporating the 3-D seismic wave-speed structure of the earth. Seismologists have created 3-D earth models ([17,27,28,29,30,31,32,33,34,35]) of seismic wave speeds and density, and now can study 3-D global and regional seismic wave propagation using approaches-based, for instance, on the finite element and the finite difference methods (for e.g., [4,6,36,37,38,39,40,41,42], etc.).
Here, to numerically propagate seismic waves, we use the open-source package SPECFEM3D (V2.0 SESAME) that is based on the spectral-element method ([16,43]). SPECFEM3D accounts for 3-D variations of seismic wave speeds and density, topography and bathymetry, and attenuation as dictated by SCEC Community Velocity Model (CVM-H 11.9). This model is based on current research, and incorporates tens of thousands of direct velocity measurements that describe the Los Angeles basin and other structures in southern California ([31,33,34]). The model includes background crustal tomography ([44,45]) enhanced using 3-D adjoint waveform methods ([35]), the Moho surface [31], and a teleseismic upper mantle wave-speed description ([32]). Earlier versions of this wave-speed model have been used to reliably model the basin response accurately down to a shortest period of approximately 2 s ([4,6]), based on the goodness of fit thresholds considered adequate at the time. Casarotti et al. [46] have created a spectral-element mesh of the Southern California region, compatible with the wave-speed model using an advanced unstructured mesher, CUBIT, developed by the Sandia National Laboratory, USA [47], and adapted as GeoCUBIT for large-scale geological applications. Additionally, to generate the shortest wave in this range, a burst of at least five impulses must occur within the temporal extent of one wave-period (or the spatial extent of one wavelength). Based on rupture propagation speeds and the regional wave-speed model of the earth in southern California, the kinematic source models need to be resampled to a maximum subfault dimension of about 0.5 km to be capable of generating waves in this frequency band. Each earthquake simulation was conducted using 144 processors on a parallel computer, each with a clock speed of 2.33 GHz and a memory size of 8 GB, for this simulation, interconnected through a QLogic Infiniband switch. For parallel computing purposes, the model block is divided into slices of elements on the X-Y plane that are distributed among the processors. The number of spectral elements along one side of the block (the NEX parameter) was set at 288 to accurately capture a shortest period of roughly 2 s [4]. The processing time for a typical magnitude 7.8 earthquake simulation was approximately 1 h.
1.3. High-Frequency Ground Motion Waveforms
The algorithm for producing the high-frequency ground motion waveforms consists of two major steps: (i) EGF event selection and quality check and (ii) EGF summation. Additionally, to eliminate low-frequency motion, the synthetic seismograms generated, using Green’s functions, are filtered using a second order high-pass Butterworth filter with a corner frequency of 0.5 Hz.
1.3.1. EGF Event Selection
The elastodynamic Green’s function is the displacement field resulting from a unidirectional unit impulse. If Green’s functions of all subfaults of a rupture event are known, the seismic representation theorem [48] can be used to synthesize the displacement field in both space and time due to a realistic earthquake source model describing that event. In the EGF approach, seismograms from small earthquakes are used as surrogates for Green’s functions emanating from a unit impulse. Spatial coverage and resolution of the displacement field is directly dependent upon seismic station distribution and density. It is unlikely that the location of the seismic station, at which the recording from a small earthquake is available, will exactly match the location of the target site where ground motions are to be computed. Furthermore, it is quite likely that no small earthquakes, centered exactly at the centroid of each subfault of our rupture event, have occurred or been recorded. Thus, the task of EGF event selection for a target subfault - target site pair consists of finding a record of a small earthquake whose source-to-station path closely tracks the path between the target subfault and target site. Here, “closeness” (E in Equation (1)) is measured by the weighted average of two distances: (i) distance between the hypocenter of the actual event and the target subfault of the target event and (ii) distance between the seismic station where ground motion from the actual event is recorded and the target site where ground motion is to be synthesized. For each target subfault–target site pair, we search the existing catalog of historical earthquakes () on the fault under consideration to determine the record that is “closest” by this measure (without any consideration to the magnitude). The selected record is assigned as the EGF for that target subfault-site pair if its signal-to-noise ratio and overall quality are at acceptable levels. If these aspects are not satisfactory, the next best candidate is evaluated. For far-field stations, the distance is given greater weightage because local site effects are likely to dominate over source effects (see Equation (1) and Figure 1). Both distances ( and ) are given equal weightage for near-field stations.
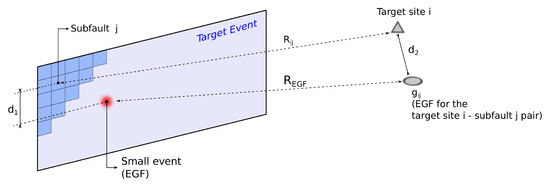
Figure 1.
Schematic representation of EGF event selection. Of all the historical records available in the vicinity of target site i from earthquakes on the target fault located in the vicinity of subfault j, the record best represents the path between target site i and subfault j [21].
- E: Closeness measure
- : Distance between the target site i and the centroid of the subfault j
- L: Length of the fault in the strike direction
- : Distance between the EGF hypocenter and the centroid of the subfault j (in 3-D space)
- : Distance between the seismic station and the target site i (in 3-D space)
1.3.2. EGF Summation
Ground motion synthesis at analysis site i involves a double summation of the selected EGFs of all the subfaults. The first sum corresponds to the number of times a given subfault EGF must be superposed to release seismic moment equivalent to the seismic moment release of the subfault as prescribed by the kinematic source model. This number, , is estimated by the ratio of the seismic moments rounded down to the nearest integer. A correction involving moments, , is needed to account for this round-off. Here, is the seismic moment of the subfault prescribed by the kinematic source model and is the seismic moment released by EGF. There is one other complication. The rise-time of the EGF will typically be much smaller than the rise-time assigned to the subfault in the kinematic sure model because of differences in the moment/energy release. To ensure that the energy release by the EGF summed times occurs over the same duration as the rise-time of the subfault prescribed by the kinematic source model, the EGF must be shifted slightly in time at each instance it is added. In previous studies (e.g., [21,22]), this time shift, termed the source sampling function , has been determined by dividing the subfault rise-time by equally spaced times (Figure 2). To remove any artificial periodicity and to reduce the high-frequency content [24] added stochastic perturbation to each of the time shifts illustrated in Figure 2. Here, we compute the time shifts by assuming that subfault seismic moment is released in equal-moment steps (red lines in Figure 3a). In other words, given , the seismic moment release in subfault j as a function of time, we compute the times corresponding to , , , …, and so on. The source–time function is then sampled by an uneven distribution of Dirac delta functions centered at each of these times (Figure 3b,c). The time spacing between delta functions decreases as up to half the rise-time and then increases symmetrically with respect to up to (see Figure 3c). This results in a lower density of delta functions at the start and the end of the subfault rupture and a higher density in the middle; it translates into higher contribution to high-frequency motions from the start and the end of the rupture process with a smoother rupture in the middle or less intense high-frequency radiation during the mid-portion of subfault rupture. The time shifts are given by:
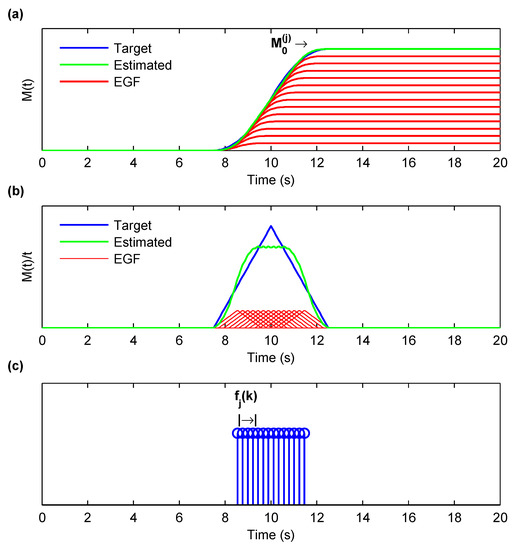
Figure 2.
Time shifts used in previous studies. (a) moment (or slip) vs. time and approximation using multiple EGFs. (b) Moment-rate (or slip rate) vs. time and approximation using multiple EGFs. (c) Subfault j time shifts used in the EGF summation.
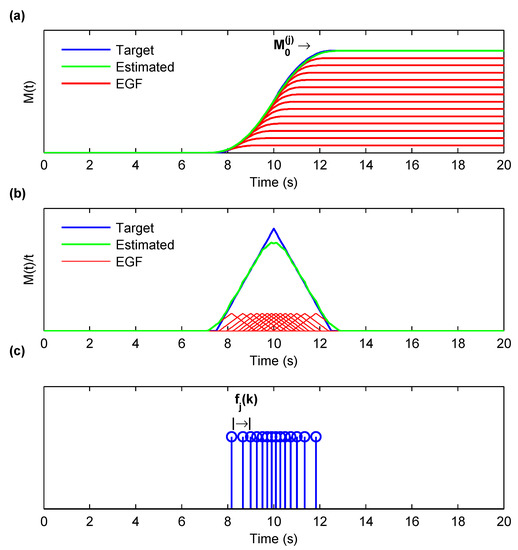
Figure 3.
Time shifts used in this study. (a) moment (or slip) vs. time and approximation using multiple EGFs. (b) Moment-rate (or slip rate) vs. time and approximation using multiple EGFs. (c) Subfault j time shifts used in the EGF summation.
The ground displacement at target site i is given by:
where is the time shift that accounts for rupture front propagation. It is inferred from the prescribed subfault rupture velocities of the kinematic source model.
Finally, the high-frequency synthetic seismograms from the EGF approach are superposed on the corresponding low-frequency spectral element synthetic waveforms to produce broadband ground motion histories. The timing of the EGF rupture event in each subfault is set to match that of the rupture time of the subfault from the kinematic source model to ensure that the arrival times of the high-frequency and low-frequency waveforms are synchronous.
2. Validation of Methodology
We simulate broadband ground motion for two earthquakes to validate our approach: (a) the 2004 6.0 Parkfield earthquake and (b) the 1999 7.1 Hector Mine earthquake. For the high-frequency component of the ground motion we use records from – earthquakes, obtained from the Southern California Earthquake Data Center’s (SCEDC—www.data.scec.org) Seismogram Transfer Program (STP), as EGFs. We limit our EGFs to high-gain broadband stations (BH) with sampling rates of s or s. For each earthquake we calculate: (i) the velocity time series at various broadband stations located within a 250 km radius of the earthquake hypocenter, (ii) velocity spectra, (iii) peak ground velocities (PGV), and (iv) the -damped acceleration response spectra. We compare the synthetic time histories, their spectra, and peak values against that of recorded ground motions in the low, the high and the broadband frequency regimes. Additionally, the velocity spectra, peak ground velocities (PGV), and the -damped response spectra of the synthetic seismograms are compared statistically against that of recorded ground motion at all stations. Mean residuals, standard deviation and model bias are computed. Although the complete synthetics dataset and figures are available in the electronic supplement to this article, we present results for only a small subset of stations here.
2.1. Validation 1: 1999 7.1 Hector Mine Earthquake
Source Model
The magnitude Hector Mine earthquake of 16th October 1999 occurred on several faults in the eastern California shear zone. The hypocenter of this earthquake was located at N– W, approximately, at a depth of 15 km. The kinematic source model, from an inversion of geodetic and seismic data by [49,50], contains three fault segments with a total seismic moment of dyne-cm. Strike and dip angles for the three segments are:
- (i)
- and , respectively, for the northern segment,
- (ii)
- and , respectively, for the central segment, and
- (iii)
- and , respectively, for the southern segment.
The maximum depth of the source model in all three segments is approximately 16 km. The average rupture velocity is about km/s, the average rise-time is approximately s, and the average rake angle is around . The original subfault dimensions for this source model are 3 km along strike and km along dip. Subfault source–time functions are assumed triangular with variable rise-times. A complete description of the source model is available in the finite-source rupture model database at www.seismo.ethz.ch. Source parameters are given in Table 1 and the source model, resampled to a km grid, is shown in Figure 4a–c. Figure 5a illustrates the location of all stations where synthetics are computed and validated. Detailed station information is provided in Appendix B.

Table 1.
Source parameters for the [49,50], the 1999 7.1 Hector Mine.
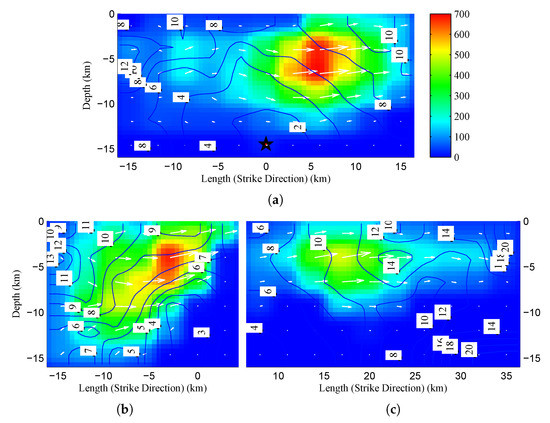
Figure 4.
Fault segments of [49,50] source model for the 1999 7.1 Hector Mine earthquake, resampled to a subfault dimension of km. Color map: Slip distributions in centimeters. Arrows: Slip direction. Counters: Rupture times in seconds. Star: Hypocenter of the event. (a) Fault Segment 1, (b) Fault Segment 2, and (c) Fault Segment 3.
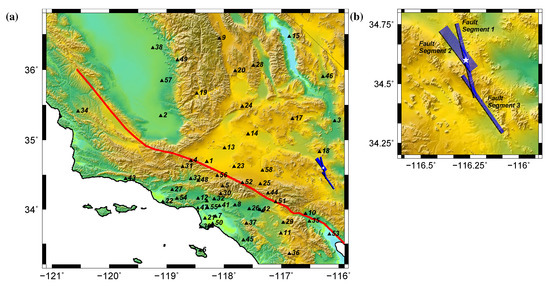
Figure 5.
(a) Location of all stations used in the 1999 Hector Mine earthquake validation. Red line: Southern section of the San Andreas fault extending from Parkfield in central California to Bombay Beach in southern California. Blue line: Surface projection of the [49,50] source model. Star: Epicenter. Black triangles: Stations (b) Fault segments in the model. Blue line: Surface projections. Black line: Surface trace. Star: Epicenter.
Figure 6a,c,e illustrate the north-south, east-west and vertical components of ground velocities at Station 9 [see Figure 5a for station location]. The first column (on the left) of each of the figures corresponds to low-frequency (<0.5 Hz) velocity waveforms generated using the spectral-element approach, the second column (middle) corresponds to high-frequency (0.5–5 Hz) velocity waveforms from the EGF approach, and the third column illustrates the broadband ground motion waveforms (<5 Hz), synthesized by superimposing the two. Figure 6b,d,f compare the corresponding velocity spectra of these components of simulated and recorded ground motion. Figure 7a–f and Figure 8a–f show similar comparisons for stations 15 and 30, respectively.
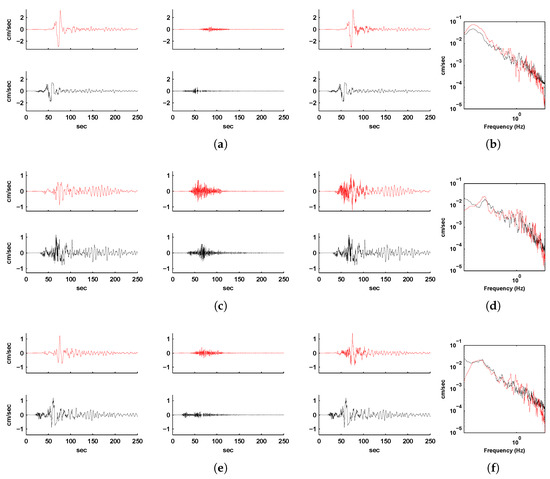
Figure 6.
(a) North-south component, (c) east-west component, and (e) vertical component of ground velocity histories at Station 9. Shown in red are the long-period spectral-element-simulated (column 1), high-frequency EGF-synthesized (column 2), and combined broadband histories (column 3) for the 1999 Hector Mine earthquake. Shown in black are the corresponding filtered observed ground velocity records for comparison. (b,d,f) show the comparison of the corresponding spectra of the broadband velocity histories (red: synthesized, black: observed).
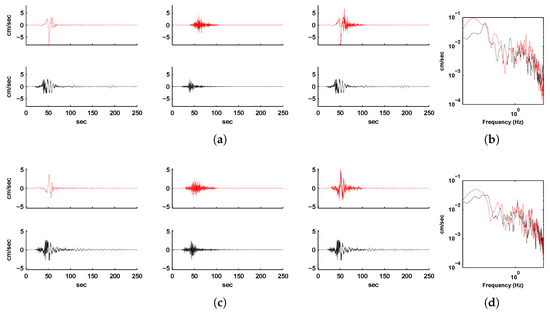
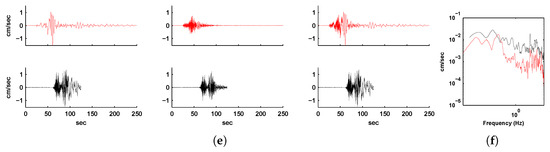
Figure 7.
(a) North-south component, (c) east-west component, and (e) vertical component of ground velocity histories at Station 15. Shown in red are the long-period spectral-element-simulated (column 1), high-frequency EGF-synthesized (column 2), and combined broadband histories (column 3) for the 1999 Hector Mine earthquake. Shown in black are the corresponding filtered observed ground velocity records for comparison. (b,d,f) show the comparison of the corresponding spectra of the broadband velocity histories (red: synthesized, black: observed).
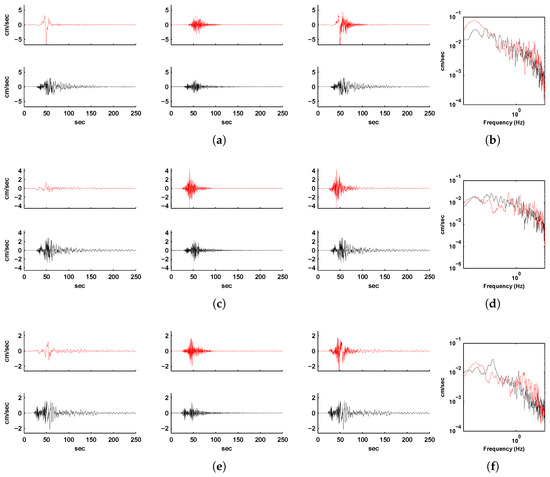
Figure 8.
(a) North-south component, (c) east-west component, and (e) vertical component of ground velocity histories at Station 30. Shown in red are the long-period spectral-element-simulated (column 1), high-frequency EGF-synthesized (column 2), and combined broadband histories (column 3) for the 1999 Hector Mine earthquake. Shown in black are the corresponding filtered observed ground velocity records for comparison. (b,d,f) show the comparison of the corresponding spectra of the broadband velocity histories (red: synthesized, black: observed).
On Figure 9a and Figure 10a we compare horizontal broadband and high-frequency peak ground velocities obtained from our simulations against that recorded at the 32 stations of interest as a function of distance to the hypocenter location. Figure 9b and Figure 10b illustrate the ratio of observed to simulated PGVs plotted on a natural log scale as a function of station distance to the hypocenter location. The PGVs in the long-period regime of the synthesized broadband ground motion histories are systematically higher than that of recorded motions [Figure 10b]. Possible sources for this mismatch can be attributed to either the source model or the differences between the wave-speed models used for the source inversion and forward wave propagation (CVM-H 11.9.0). On the other hand, there is no systematic bias in the PGV estimates in the high-frequency band of Hz to Hz. Additionally, Figure 11a–c illustrate the bias in the synthetics associated with -damped acceleration response spectra for the north component, the east component and the geometric mean of the horizontal ground motion, respectively, at the 32 stations. The procedure for computing this bias is outlined in Appendix A. The model bias is relatively low and very close to zero for the individual and the average horizontal components across all frequencies considering the distances at which the stations are located at.
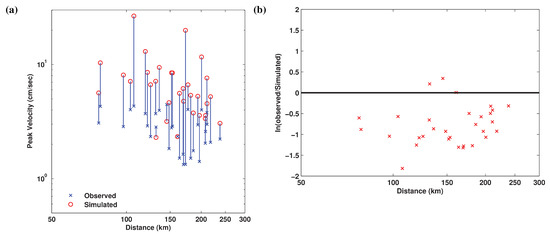
Figure 9.
(a) Comparisons of peak ground velocity (PGV) of the simulated and the recorded broadband ground motions as a function of station distance to the hypocenter of the 1999 Hector Mine earthquake. (b) Natural log of the residual of simulated and recorded values.
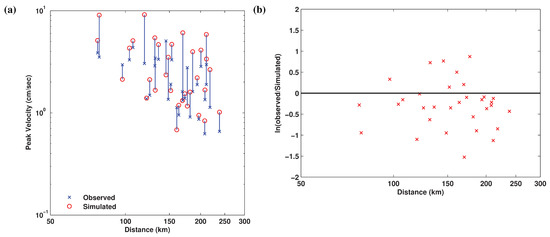
Figure 10.
(a) Comparisons of peak ground velocity (PGV) of the high-frequency content of the simulated and the recorded ground motions as a function of station distance to the hypocenter of the 1999 Hector Mine earthquake. (b) Natural log of the residual of simulated and recorded values.
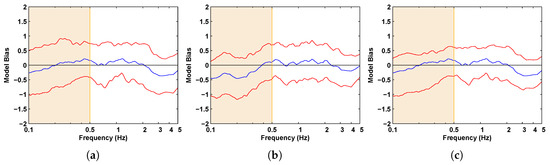
Figure 11.
Bias in the synthetic associated with -damped acceleration response spectra at 32 stations relative to the corresponding spectra of recorded ground motion during the 1999 Hector Mine earthquake. Blue line: Bias. Red line: Standard error. (a) North component, (b) East component, and (c) Geometric mean horizontal component.
3. Validation 2: 2004 6.0 Parkfield Earthquake
The Parkfield earthquake of 24th of September 2004, occurred on the San Andreas fault with its epicenter at approximately 11 km south-southeast of the city of Parkfield, California. The hypocenter was located at N, W, and a depth of km. The kinematic source model from a finite fault inversion of strong-motion data by [51] shows a total seismic moment of dyne-cm being released on a single fault segment with a rupture extent of 40 km along strike and 15 km along dip with a strike angle from the geographic north and an dip angle from the surface of the earth. Rupture starts at the southern section of the rupture plane and propagates north (south-to-north directivity) for 10 s approximately. The peak slip on the fault is about 50 cm and is located close to the hypocenter of the fault. The subfault dimensions in the model are 1.9 km along strike and 1.67 km along dip and are resampled to km in either direction (Figure 12). Source–time functions for individual subfaults are assumed triangular with variable rise-times (see finite-source rupture model database at www.seismo.ethz.ch for details). Figure 13 illustrates the location of all the stations used in this validation. Detailed station information is provided in Appendix B.
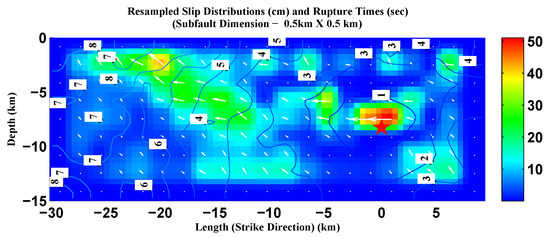
Figure 12.
Resampled kinematic source model for the 2004 6.0 Parkfield earthquake by [51]. Subfault dimension km × km. Color map: Slip distribution in centimeters. Arrows: Slip direction. Counters: Rupture times in seconds. Star: Hypocenter of the event.
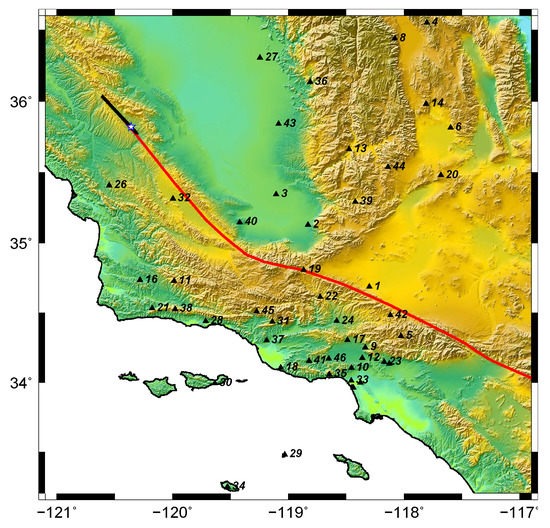
Figure 13.
Location of all stations used in the 2004 Parkfield earthquake validation. Red line: Southern section of the San Andreas fault extending from Parkfield in central California to Bombay Beach in southern California. Black line: Trace/surface projection of the [51] earthquake source model. Star: Epicenter. Black triangles: Stations.
Figure 14a,c,e illustrate the north-south, east-west and vertical components of the synthesized and the recorded ground velocities at Station 1 (see Figure 12 for Station location). The first column (on the left) of each of the figures corresponds to low-frequency (<0.5 Hz) velocity waveforms generated using the spectral-element approach, the second column (middle) corresponds to high-frequency (0.5–5 Hz) velocity waveform the EGF approach, and the third column illustrates the broadband ground motion waveforms (<5 Hz), synthesized by superimposing the two. Figure 14b,d,f compare the corresponding velocity spectra of these components of simulated and recorded ground motion. Figure 15a–f and Figure 16a–f show similar comparisons for stations 10 and 40, respectively.
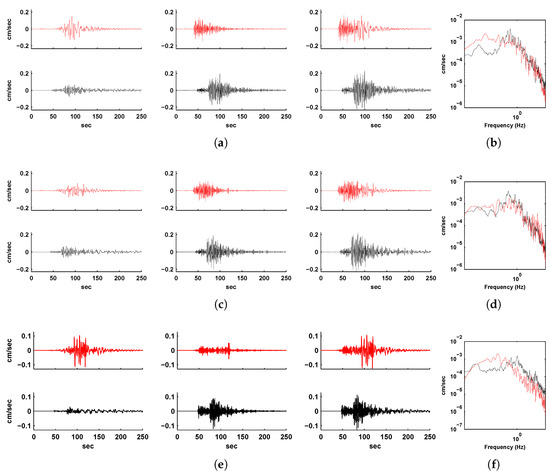
Figure 14.
(a) North-south component, (c) east-west component, and (e) vertical component of ground velocity histories at Station 1. Shown in red are the long-period spectral-element-simulated (column 1), high-frequency EGF-synthesized (column 2), and combined broadband histories (column 3) for the 2004 Parkfield earthquake. Shown in black are the corresponding filtered observed ground velocity records for comparison. (b,d,f) show the comparison of the corresponding spectra of the broadband velocity histories (red: synthesized, black: observed).
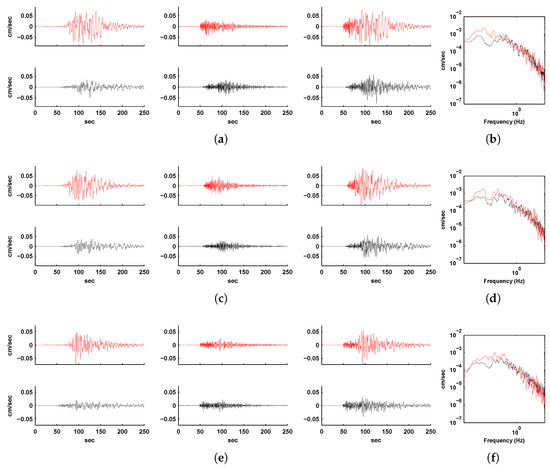
Figure 15.
(a) North-south component, (c) east-west component, and (e) vertical component of ground velocity histories at Station 10. Shown in red are the long-period spectral-element-simulated (column 1), high-frequency EGF-synthesized (column 2), and combined broadband histories (column 3) for the 2004 Parkfield earthquake. Shown in black are the corresponding filtered observed ground velocity records for comparison. (b,d,f) show the comparison of the corresponding spectra of the broadband velocity histories (red: synthesized, black: observed).
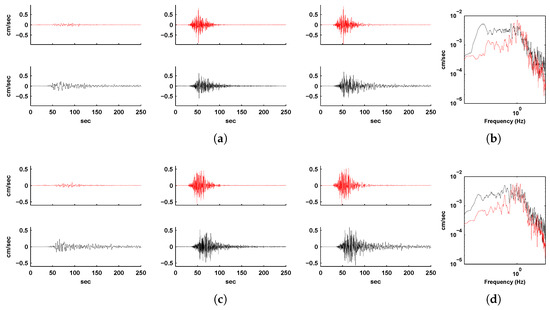
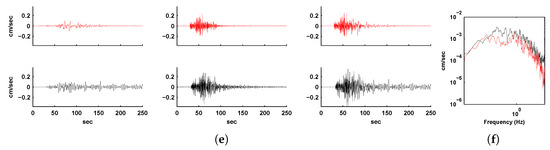
Figure 16.
(a) North-south component, (c) east-west component, and (e) vertical component of ground velocity histories at Station 40. Shown in red are the long-period spectral-element-simulated (column 1), high-frequency EGF-synthesized (column 2), and combined broadband histories (column 3) for the 2004 Parkfield earthquake. Shown in black are the corresponding filtered observed ground velocity records for comparison. (b,d,f) show the comparison of the corresponding spectra of the broadband velocity histories (red: synthesized, black: observed).
Figure 17a and Figure 18a compare the peak horizontal ground velocities for broadband and high-frequency ground motions as a function of station distance to the hypocenter location. Figure 17b and Figure 18b illustrate the residuals of observed and simulated peak ground velocities as a function of station distance [the residuals (y axis) are plotted on natural log scale]. The PGVs from the synthesized broadband ground motions appear to be slightly higher than that from the recorded ground motion (Figure 17b) at distances of 250 km or higher. This may possibly be attributed to the quality of the available wave-speed model. However, yet again, there is no particular bias in the simulation results in the high-frequency band and the attenuation of PGVs with distance is quite similar to the observations. Additionally, Figure 19a–c illustrate the bias in the synthetics associated with -damped acceleration response spectra for the north component, the east component, and the geometric mean of the horizontal ground motion, respectively, at the 46 stations (Appendix A). The model bias is relatively low and very close to zero for the individual and the average horizontal components specifically at high frequencies.
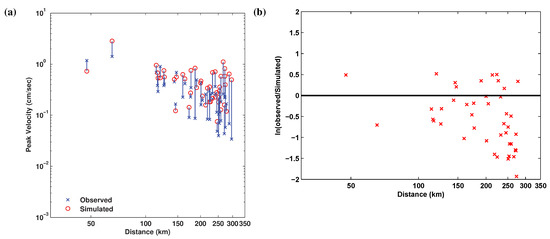
Figure 17.
(a) Comparisons of peak ground velocity (PGV) of the simulated and the recorded broadband ground motions as a function of station distance to the hypocenter of the 2004 Parkfield earthquake. (b) Natural log of the residual of simulated and recorded values.
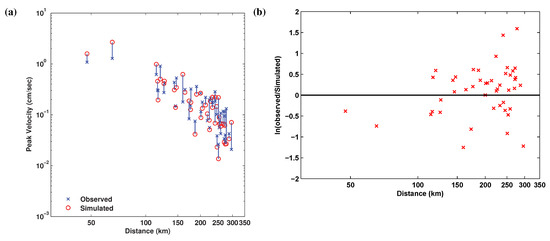
Figure 18.
(a) Comparisons of peak ground velocity (PGV) of the high-frequency content of the simulated and the observed ground motions during the 2004 Parkfield earthquake as a function of station distance. (b) Natural log of the residual of simulated and recorded values.
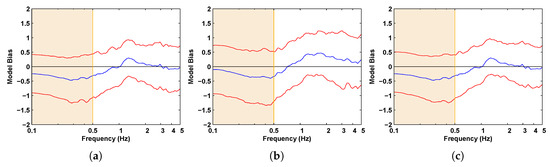
Figure 19.
Bias in the synthetic -damped acceleration response spectra at 46 stations relative to the corresponding spectra of recorded ground motion during the 2004 Parkfield earthquake. Blue line: Bias. Red line: Standard error. (a) North component, (b) East component, and (c) Geometric mean horizontal component.
4. Discussion
As we stated previously, the choice of alleviates the over-estimation of the high-frequency content typically encountered in EGF-based ground motion simulation methods. We illustrate this point by expanding the double summation for the synthetic ground displacement at target site i (Equation (3)) and comparing it to theory. Additionally, we illustrate the improvements and reductions in bias in -damped acceleration response spectra. Without loss of generality, a single EGF can be used for all subfaults by substituting in Equation (3):
The Green’s function evaluated at time can be replaced with a convolution of evaluated at time t and a Dirac delta function located at leading to:
Rearranging Equation (5):
All terms, except on the right-hand side of Equation (6) can be consolidated into a single time function . This represents a mapping (or transfer function) of on to :
and in frequency domain:
where is:
If EGF records are available for each subfault–target site combination, and would be equal. Additionally, if the number of EGFs needed to match the seismic moment of the target subfault is an integer amount, would be unity. With these two assumptions, Equation (10) reduces to:
Expanding the right-hand side of Equation (11):
s are inferred from the rupture times in the prescribed kinematic source model. The distribution of s controls the duration of the rupture, and all terms within the square brackets [terms with ], govern the time distribution of the EGFs within a subfault and this distribution greatly effects the high frequencies content of the ground motion.
The theoretical displacement amplitude spectrum with a average high-frequency fall-off rate [26] can be expressed as:
where is the seismic moment of the earthquake and is the corner frequency of the event. Using Brune’s spectrum, the theoretical form of the transfer function (Equation (9)) can be written as:
We should note that this equation is equivalent to Equation (5) in [19]. However, Frankel [19] used this equation as a frequency domain operator to increase the low frequency without changing the high-frequency content of the ground motion.
Now, the theoretical transfer function of Equation (14) can be compared to the empirical transfer function of Equation (12). The empirical transfer function is evaluated for two different choices of : (1) assuming a non-uniform distribution (equal moments) of events within the subfault’s rise-time as in this study (Equation (2)) (2) assuming a uniform distribution of events within the subfault’s rise-time (Figure 2), with an added randomness. This is implemented using a gaussian distribution for each with a mean at and standard deviation equal to / ( confidence interval).
These two empirical transfer functions can be compared against the theoretical transfer function of Equation (14) following [26]. Figure 20 and Figure 21 illustrate this comparison for the Parkfield and the Hector Mine earthquakes, respectively. Single magnitude 2.5 and 3.0 earthquakes are used as the EGFs for the ground motion synthesis of the two earthquakes, respectively. The black line is the amplitude of the theoretical transfer function, the red line is that of the traditional evenly distributed EGFs and the blue is that of the unevenly distributed EGFs adopted in this study. In the 2–10 Hz band, the traditional approach clearly overestimates the ground motion intensities whereas our approach agrees better with the theoretical spectrum. This is the case for both earthquakes.
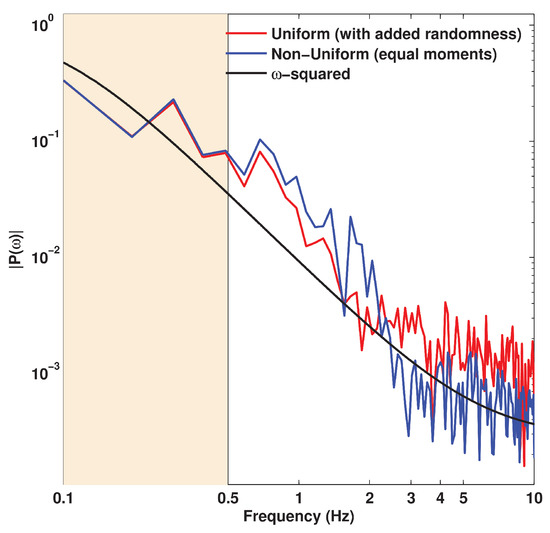
Figure 20.
Comparison of the amplitude spectra of the transfer functions [p(t)] for the 2004 Parkfield earthquake. EGF magnitude: 2.5. Black line: Theoretical value. Red line: Uniform distribution. Blue line: Non-uniform distribution used in this study.
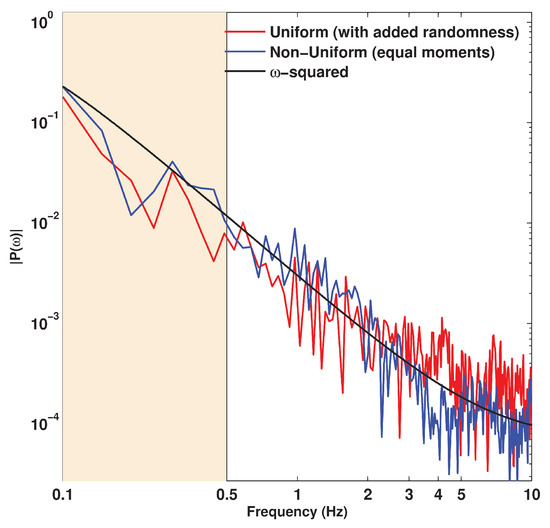
Figure 21.
Comparison of the amplitude spectra of the transfer functions [p(t)] for the 1999 Hector Mine earthquake. EGF magnitude: 3.0. Black line: Theoretical value. Red line: Uniform distribution. Blue line: Non-uniform distribution used in this study.
Additionally, we compare the bias in the -damped acceleration response spectra of the synthetics produced by the uniformly spaced EGFs (Figure 22a and Figure 23a) and that produced using our approach of non-uniformly spaced EGFs (Figure 22b and Figure 23b). The improvement in high-frequency ground motion prediction is clear.
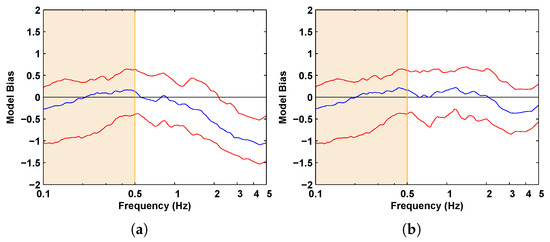
Figure 22.
Model bias in the -damped acceleration spectra of the 1999 Hector Mine earthquake synthetics produced using (a) the traditional approach of uniformly spaced EGFs and (b) using the present approach of unevenly spaced EGFs. Red line: Standard error.
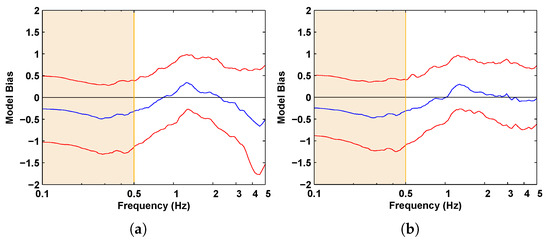
Figure 23.
Model bias in the -damped acceleration spectra of the 2004 Parkfield earthquake synthetics produced using (a) the traditional approach of uniformly spaced EGFs and (b) using the present approach of unevenly spaced EGFs. Red line: Standard error.
5. Conclusions
We have successfully presented a simple, intuitive, and effective method for generating broadband ground motions for engineering applications by superimposing long-period (>2 s) waveforms from spectral-element simulations with high-frequency waveforms from an empirical Green’s function approach. The key advancement here, pertaining to the EGF approach, is a modified summing strategy that alleviates the over-estimation of high-frequency ground motions in current EGF-based ground motion simulation methods. We have successfully used relatively lower magnitude EGFs recorded at larger distances for generating high-frequency ground motions compared to previous methods. However, we should point out that results remain sensitive to many contributing factors, including rupture velocities in kinematic source models from inversions, the resolution of these source models, as well as the number and nature of the selected EGFs. EGF features affecting the synthetics include absolute magnitude, magnitude relative to the target event, local site characteristics, signal quality, etc. Further studies are needed to quantify the effects of these factors and establish the limits and applicability of the EGF approach to ground motion prediction.
Author Contributions
Data curation, formal analysis, investigation, methodology, software, and writing—original draft preparation, R.M.; Supervision, project administration, funding acquisition, writing—review and editing, S.K. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by US National Science Foundation grant number (NSF Award No.0926962).
Acknowledgments
We are grateful to Robert Graves (USGS Pasadena) for reading the draft and providing insightful comments that have significantly enhanced the paper. We thank Chen Ji (UCSB) and Martin Mai (ETHZ, KAUST) for the source models used in this study; Dimitri Komatitsch (University of Pau, France), Jean-Paul Ampuero (Caltech-GPS) and Carl Tape (UAF) for their insights into SPECFEM3D; Thomas Heaton (Caltech) for his insights into Empirical Green’s Function methods. We appreciate the comments by two anonymous peer-reviewers whose comments have enhanced the article. The data used in this work were obtained from the Internet database of finite-source rupture models (www.seismo.ethz.ch), the California Institute of Technology’s Tectonic Observatory center (www.tectonics.caltech.edu) and the Southern California Earthquake Data Center (SCEDC—www.data.scec.org). Figure 5a,b, and Figure 13 are produced using Generic Mapping Tool (GMT—http://gmt.soest.hawaii.edu/).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EGF | Empirical Green’s Function |
| SCEC | Southern California Earthquake Center |
| CVM | Community Velocity Model |
| SCEDC | Southern California Earthquake Data Center |
| STP | Seismogram Transfer Program |
| PGV | Peak ground velocity |
Appendix A
Appendix A.1. Bias in Synthetics Associated with Sa
The error in the station i -damped response spectral acceleration at a period T is computed as [9]:
Bias in the synthetics at a given T is the average of the prediction errors at N stations for that time period:
Standard deviation of the bias is:
Appendix B
Appendix B.1. List of Stations

Table A1.
List of stations, latitude, longitude, location, and station ID whose data is used for the 1999 Hector Mine earthquake simulation. All stations belong to the Southern California Seismic Network (FDSN code: CI).
Table A1.
List of stations, latitude, longitude, location, and station ID whose data is used for the 1999 Hector Mine earthquake simulation. All stations belong to the Southern California Seismic Network (FDSN code: CI).
| Station Number | Latitude | Longitude | Location | Station |
|---|---|---|---|---|
| 1 | 34.68708 | −118.29946 | Antelope | ALP |
| 2 | 35.26930 | −116.07030 | Baker | BKR |
| 3 | 34.68224 | −118.57398 | Burnt Peak | BTP |
| 4 | 34.33341 | −118.02585 | Chilao Flat Rngr. Sta. | CHF |
| 5 | 33.40190 | −118.41502 | Catalina Island Airport | CIA |
| 6 | 34.06020 | −117.80900 | Cal Poly Pomona | CPP |
| 7 | 33.93597 | −116.57794 | Devers | DEV |
| 8 | 33.65001 | −117.00947 | Domenigoni Reservoir | DGR |
| 9 | 34.10618 | −118.45505 | Donna Jones Jenkins | DJJ |
| 10 | 34.88303 | −117.99106 | Edwards Air Force Base | EDW |
| 11 | 35.08200 | −117.58267 | Federal Prison Camp | FPC |
| 12 | 34.11816 | −118.30024 | Griffith Observatory | GR2 |
| 13 | 35.98230 | −117.80760 | Joshua Ridge | JRC |
| 14 | 34.36560 | −117.36683 | Lugo | LUG |
| 15 | 34.00460 | −117.56162 | Mira Loma Substation | MLS |
| 16 | 36.05799 | −117.48901 | Manuel Prospect Mine | MPM |
| 17 | 34.22362 | −118.05832 | Mount Wilson Obsv. | MWC |
| 18 | 34.14844 | −118.17117 | Pasadena | PAS |
| 19 | 33.35361 | −116.86265 | Palomar | PLM |
| 20 | 33.79530 | −117.60906 | Pleasants Peak | PLS |
| 21 | 33.74346 | −118.40412 | Rancho Palos Verdes | RPV |
| 22 | 33.97327 | −117.32674 | Riverside Surface | RSS |
| 23 | 34.05073 | −118.08085 | Rush | RUS |
| 24 | 33.99351 | −117.37545 | Riverside | RVR |
| 25 | 34.23240 | −117.23484 | Strawberry Peak | BPX |
| 26 | 33.55259 | −117.66171 | Saddleback | SDD |
| 27 | 35.89953 | −116.27530 | Shoshone | SHO |
| 28 | 34.01438 | −118.45617 | Santa Monica Fire Station | SMS |
| 29 | 34.41600 | −118.44900 | Solamint | SOT |
| 30 | 34.38203 | −117.67822 | Table Mountain | TA2 |
| 31 | 33.63495 | −116.16402 | Thermal Airport | THX |
| 32 | 34.48364 | −118.11783 | Vincent Substation | VCS |

Table A2.
List of stations, latitude, longitude, location, and station ID whose data is used for the 2004 Parkfield earthquake simulation. All stations belong to the Southern California Seismic Network (FDSN code: CI).
Table A2.
List of stations, latitude, longitude, location, and station ID whose data is used for the 2004 Parkfield earthquake simulation. All stations belong to the Southern California Seismic Network (FDSN code: CI).
| Station Number | Latitude | Longitude | Location | Station |
|---|---|---|---|---|
| 1 | 34.687080 | −118.29946 | Antelope | ALP |
| 2 | 35.126900 | −118.83009 | Arvin | ARV |
| 3 | 35.344440 | −119.10445 | Calstate Bakersfield | BAK |
| 4 | 36.550400 | −117.80295 | Cerro Gordo | CGO |
| 5 | 34.333410 | −118.02585 | Chilao Flat Rangr. Station | CHF |
| 6 | 35.815740 | −117.59751 | China Lake | CLC |
| 7 | 34.136240 | −118.12705 | Caltech Robinson Pit | CRP |
| 8 | 36.439880 | −118.08016 | Cottonwood Creek | CWC |
| 9 | 34.253530 | −118.33383 | Green Verdugo Microwave Site | DEC |
| 10 | 34.106180 | −118.45505 | Donna Jones Jenkins | DJJ |
| 11 | 34.728320 | −119.98803 | Figueroa Mountain | FIG |
| 12 | 34.176430 | −118.35967 | North Hollywood | HLL |
| 13 | 35.662780 | −118.47403 | Isabella | ISA |
| 14 | 35.982490 | −117.80885 | Joshua Ridge: China Lake | JRC2 |
| 15 | 34.000330 | −118.37794 | La Cienega | LCG |
| 16 | 34.735510 | −120.27996 | Los Alamos County Park | LCP |
| 17 | 34.305290 | −118.48805 | Los Angeles Filtration Plant | LFP |
| 18 | 34.108190 | −119.06587 | Laguna Peak | LGU |
| 19 | 34.807620 | −118.86775 | Lone Juniper Ranch | LJR |
| 20 | 35.479540 | −117.68212 | Laurel Mtn Radio Fac | LRL |
| 21 | 34.534120 | −120.17737 | Nojoqui County Park | NJQ |
| 22 | 34.614500 | −118.72350 | Osito Audit: Castaic Lake Dam | OSI |
| 23 | 34.148440 | −118.17117 | Pasadena | PAS |
| 24 | 34.441990 | −118.58215 | Pardee | PDE |
| 25 | 33.962730 | −118.43702 | Playa Del Rey | PDR |
| 26 | 35.407730 | −120.54556 | Park Hill | PHL |
| 27 | 36.305230 | −119.24384 | Rector | RCT |
| 28 | 34.440760 | −119.71492 | Santa Barbara | SBC |
| 29 | 33.480460 | −119.02986 | Santa Barbara Island | SBI |
| 30 | 33.995430 | −119.63510 | Santa Cruz Island 2 | SCZ2 |
| 31 | 34.436920 | −119.13750 | Summit Elementary School | SES |
| 32 | 35.314200 | −119.99581 | Simmler | SMM |
| 33 | 34.014380 | −118.45617 | Santa Monica Fire St | SMS |
| 34 | 33.247870 | −119.52437 | San Nicolas Island | SNCC |
| 35 | 34.059330 | −118.64614 | Saddle Peak Fire Camp 8 | SPF |
| 36 | 36.135500 | −118.81099 | Springville | SPG |
| 37 | 34.303020 | −119.18676 | Santa Clara | STC |
| 38 | 34.527750 | −119.97834 | Santa Ynez Peak | SYP |
| 39 | 35.291300 | −118.42079 | Cattani Ranch | TEH |
| 40 | 35.145920 | −119.41946 | Taft Base | TFT |
| 41 | 34.156070 | −118.82039 | Thousand Oaks Ventura | TOV |
| 42 | 34.483640 | −118.11783 | Vincent Substation | VCS |
| 43 | 35.840890 | −119.08469 | Vestal | VES |
| 44 | 35.536640 | −118.14035 | Bird Spring | WBS |
| 45 | 34.510850 | −119.27407 | Wheeler Gorge Ranger Station | WGR |
| 46 | 34.171700 | −118.64971 | West Side Station | WSS |
References
- Mourhatch, R.; Krishnan, S. Probabilistic Estimates of Ground Motion in the Los Angeles Basin from Scenario Earthquakes on the San Andreas Fault. Geosciences 2018, 8, 126. [Google Scholar] [CrossRef]
- Graves, R.W.; Jordan, T.H.; Callaghan, S.; Deelman, E.; Field, E.; Juve, G.; Kesselman, C.; Maechling, P.; Mehta, G.; Milner, K.; et al. CyberShake: A Physics-Based Seismic Hazard Model for Southern California. Pure Appl. Geophys. 2011, 168, 367–381. [Google Scholar] [CrossRef]
- Jordan, T.H.; Callaghan, S.; Graves, R.W.; Wang, F.; Milner, K.R.; Goulet, C.A.; Maechling, P.J.; Olsen, K.B.; Cui, Y.; Juve, G.; et al. CyberShake models of seismic hazards in southern and central California. In Proceedings of the 2018 Eleventh National Conference on Earthquake Engineering, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
- Komatitsch, D.; Liu, Q.; Tromp, J.; Süss, P.; Stidham, C.; Shaw, J.H. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method. Bull. Seismol. Soc. Am. 2004, 94, 187–206. [Google Scholar] [CrossRef]
- Lee, E.-J.; Chen, P.; Jordan, T.H. Testing waveform predictions of 3D velocity models against two recent Los Angeles earthquakes. Seismol. Res. Lett. 2014, 85, 1275–1284. [Google Scholar] [CrossRef]
- Liu, Q.; Polet, J.; Komatitsch, D.; Tromp, J. Spectral-element moment tensor inversions for earthquakes in southern California. Bull. Seismol. Soc. Am. 2004, 94, 1748–1761. [Google Scholar] [CrossRef]
- Taborda, R.; Azizzadeh-Roodpish, S.; Cheng, N.K.a.K. Evaluation of the southern California seismic velocity models through simulation of recorded events. Geophys. J. Int. 2016, 25, 1342–1364. [Google Scholar] [CrossRef]
- Frankel, A. A constant stress-drop model for producing broadband synthetic seismograms: Comparison with the next generation attenuation relations. Bull. Seismol. Soc. Am. 2009, 99, 664–680. [Google Scholar] [CrossRef]
- Graves, R.; Pitarka, A. Broadband ground-motion simulation using a hybrid approach. Bull. Seismol. Soc. Am. 2010, 100, 2095. [Google Scholar] [CrossRef]
- Hartzell, S.; Harmsen, S.; Frankel, A.; Larsen, S. Calculation of broadband time histories of ground motion: Comparison of methods and validation using strong-ground motion from the 1994 Northridge earthquake. Bull. Seismol. Soc. Am. 1999, 89, 1484–1504. [Google Scholar]
- Lee, R.L.; Bradley, B.A.; Stafford, P.J. Hybrid broadband ground motion simulation validation of small magnitude earthquakes in Canterbury, New Zealand. Earthq. Spectra 2020, 36, 673–699. [Google Scholar] [CrossRef]
- Mai, P.M.; Imperatori, W.; Olsen, K.B. Hybrid broadband ground-motion simulations: Combining long-period deterministic synthetics with high-frequency multiple S-to-S backscattering. Bull. Seismol. Soc. Am. 2010, 100, 2124–2142. [Google Scholar] [CrossRef]
- Mena, B.; Durukal, E.; Erdik, M. Effectiveness of Hybrid Green’s Function Method in the Simulation of Near-Field Strong Motion: An Application to the 2004 Parkfield Earthquake. Bull. Seismol. Soc. Am. 2006, 96, S183–S205. [Google Scholar] [CrossRef]
- Olsen, K.B.; Takedatsu, R. The SDSU Broadband Ground Motion Generation Module BBtoolbox Version 1.5. Seismol. Res. Lett. 2014, 86, 81–88. [Google Scholar] [CrossRef]
- Pitarka, A.; Somerville, P.; Fukushima, Y.; Uetake, T.; Irikura, K. Simulation of Near-Fault Strong-Ground Motion Using Hybrid Green’s Functions. Bull. Seismol. Soc. Am. 2006, 90, 566–586. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Seismic tomography of the southern California crust based on spectral element and adjoint methods. Geophys. J. Int. 2010, 180, 433–462. [Google Scholar] [CrossRef]
- Hartzell, S.H. Earthquake aftershocks as Green’s functions. Geophys. Res. Lett. 1978, 5, 1–4. [Google Scholar] [CrossRef]
- Frankel, A. Simulating strong motions of large earthquakes using recordings of small earthquakes: The Loma Prieta mainshock as a test case. Bull. Seismol. Soc. Am. 1995, 85, 1144–1160. [Google Scholar]
- Heaton, T.H.; Hartzell, S.H. Estimation of strong ground motions from hypothetical earthquakes on the Cascadia subduction zone, Pacific northwest. Pure Appl. Geophys. 1989, 129, 131–201. [Google Scholar] [CrossRef][Green Version]
- Irikura, K. Semi-empirical estimation of strong ground motions during large earthquakes. Bull. Disaster Prev. Res. Inst. 1983, 33, 63–104. [Google Scholar]
- Irikura, K. Prediction of strong acceleration motions using empirical Green’s functions. In Proceedings of the Seventh Japan Earthquake Engineering Symposium, Tokyo, Japan, 1986; pp. 151–156. [Google Scholar]
- Joyner, W.; Boore, D. On simulating large earthquakes by Green’s-function addition of smaller earthquakes. Earthq. Source Mech. 1986, 37, 269–274. [Google Scholar]
- Somerville, P.; Sen, M.; Cohee, B. Simulation of strong ground motions recorded during the 1985 Michoacan, Mexico and Valparaiso, Chile earthquakes. Bull. Seismol. Soc. Am. 1991, 81, 1–27. [Google Scholar]
- Tumarkin, A.G.; Archuleta, R.J. Empirical ground motion prediction. Annali Di Geofisica 1994, XXXVII, 1691–1720. [Google Scholar]
- Brune, J.N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
- Ely, G.; Jordan, T.H.; Small, P.; Maechling, P.J. A derived near-surface seismic velocity model. In Proceedings of the American Geophysical Union Fall Meeting, San Francisco, CA, USA, 13–17 December 2010. [Google Scholar]
- Kohler, M.D.; Magistrale, H.; Clayton, R.W. Mantle heterogeneities and the SCEC reference three-dimensional seismic velocity model version 3. Bull. Seismol. Soc. Am. 2003, 93, 757–774. [Google Scholar] [CrossRef]
- Magistrale, H.; Day, S.; Clayton, R.W.; Graves, R. The SCEC southern California reference three-dimensional seismic velocity model version 2. Bull. Seismol. Soc. Am. 2000, 90, S65–S76. [Google Scholar] [CrossRef]
- Magistrale, H.; McLaughlin, K.; Day, S. A geology-based 3D velocity model of the Los Angeles basin sediments. Bull. Seismol. Soc. Am. 1996, 86, 1161–1166. [Google Scholar]
- Plesch, A.; Tape, C.; Graves, R.; Shaw, J.H.; Small, P.; Ely, G. Updates for the CVM-H including new representations of the offshore Santa Maria and San Bernardino basins and a new Moho surface. In Proceedings of the SCEC 2011 Annual Meeting, Palm Spring, CA, USA, 11–14 September 2011; Southern California Earthquake Center: Los Angeles, CA, USA, 2011. Poster B–128. [Google Scholar]
- Prindle, K.; Tanimoto, T. Teleseismic surface wave study for S-wave velocity structure under an array: Southern California. Geophys. J. Int. 2006, 166, 601–621. [Google Scholar] [CrossRef]
- Shaw, J.H.; Plesch, A.; Tape, C.; Süss, M.P.; Jordan, T.H.; Ely, G.; Hauksson, E.; Tromp, J.; Tanimoto, T.; Graves, R.; et al. Unified Structural Representation of the southern California crust and upper mantle. Earth Planet. Sci. Lett. 2015, 415, 1–15. [Google Scholar] [CrossRef]
- Süss, M.P.; Shaw, J.H. P wave seismic velocity structure derived from sonic logs and industry reflection data in the Los Angeles basin, California. J. Geophys. Res. 2003, 108, 1–18. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Maggi, A.; Tromp, J. Adjoint tomography of the southern California crust. Science 2009, 325, 988. [Google Scholar] [CrossRef] [PubMed]
- Akcelik, V.; Bielak, J.; Biros, G.; Epanomeritakis, I.; Fernandez, A.; Ghattas, O.; Kim, E.J.; Lopez, J.; O’Hallaron, D.; Tu, T.; et al. High resolution forward and inverse earthquake modeling on terascale computers. In Proceedings of the 2003 ACM/IEEE Conference on Supercomputing, Phoenix, AZ, USA, 15–21 November 2003; p. 52. [Google Scholar]
- Bao, H.; Bielak, J.; Ghattas, O.; Kallivokas, L.F.; O’Hallaron, D.R.; Shewchuk, J.R.; Xu, J. Large-scale simulation of elastic wave propagation in heterogeneous media on parallel computers. Comput. Methods Appl. Mech. Eng. 1998, 152, 85–102. [Google Scholar] [CrossRef]
- Graves, R.W. Three-dimensional finite-difference modeling of the San Andreas fault: Source parameterization and ground-motion levels. Bull. Seismol. Soc. Am. 1998, 88, 881–897. [Google Scholar]
- Heaton, T.; Hall, J.; Wall, D.; Halling, M. Response of high-rise and base-isolated buildings to a hypothetical Mw 7.0 blind thrust earthquake. Science 1995, 267, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Komatitsch, D. Fluid-solid coupling on a cluster of GPU graphics cards for seismic wave propagation. C. R. Mec. 2011, 339, 125–135. [Google Scholar] [CrossRef]
- Komatitsch, D.; Erlebacher, G.; Göddeke, D.; Michéa, D. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster. J. Comput. Phys. 2010, 229, 7692–7714. [Google Scholar] [CrossRef]
- Olsen, K.; Archuleta, R.; Matarese, J. Three dimensional simulation of a magnitude 7.75 earthquake on the San Andreas fault. Science 1995, 270, 1628–1632. [Google Scholar] [CrossRef]
- Tromp, J.; Komattisch, D.; Liu, Q. Spectral-element and adjoint methods in seismology. Commun. Comput. Phys. 2008, 3, 1–32. [Google Scholar]
- Hauksson, E. Crustal structure and seismicity distribution adjacent to the Pacific and the north America plate boundary in southern California. J. Geophys. Res. 2000, 105, 13875–13903. [Google Scholar] [CrossRef]
- Lin, G.; Shearer, P.M.; Hauksson, E.; Thurber, C.H. A three-dimensional crustal seismic velocity model for southern California from a composite event method. J. Geophys. Res. Solid Earth 2007, 112, B11306. [Google Scholar] [CrossRef]
- Casarotti, E.; Stupazzini, M.; Lee, S.J.; Komatitsch, D.; Piersanti, A.; Tromp, J. CUBIT and seismic wave propagation based upon the spectral-element method: An advanced unstructured mesher for complex 3D geological media. In Proceedings of the 16th International Meshing Roundtable, Seattle, WA, USA, 14–17 October 2007; pp. 579–597. [Google Scholar]
- Sandia National Laboratory. CUBIT: Geometry and Mesh Generation Toolkit. 2011. Available online: http://cubit.sandia.gov (accessed on 1 May 2015).
- Burridge, R.; Knopoff, L. Body force equivalents for seismic dislocations. Bull. Seismol. Soc. Am. 1964, 54, 1875–1888. [Google Scholar] [CrossRef]
- Ji, C.; Wald, D.J.; Helmberger, D.V. Source description of the 1999 Hector Mine, California, earthquake, Part I: Wavelet domain inversion theory and resolution analysis. Bull. Seismol. Soc. Am. 2002, 92, 1192–1202. [Google Scholar] [CrossRef]
- Ji, C.; Wald, D.J.; Helmberger, D.V. Source description of the 1999 Hector Mine, California, earthquake, Part II: Complexity of slip history. Bull. Seismol. Soc. Am. 2002, 92, 1208–1226. [Google Scholar] [CrossRef]
- Custódio, S.; Liu, P.; Archuleta, R.J. The 2004 Mw 6.0 Parkfield, California, earthquake: Inversion of near-source ground motion using multiple data sets. Geophys. Res. Lett. 2005, 32, L23312. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).