A New Methodology for Measuring Tsunami Resilience Using Theory of Springs
Abstract
1. Introduction
2. Methods
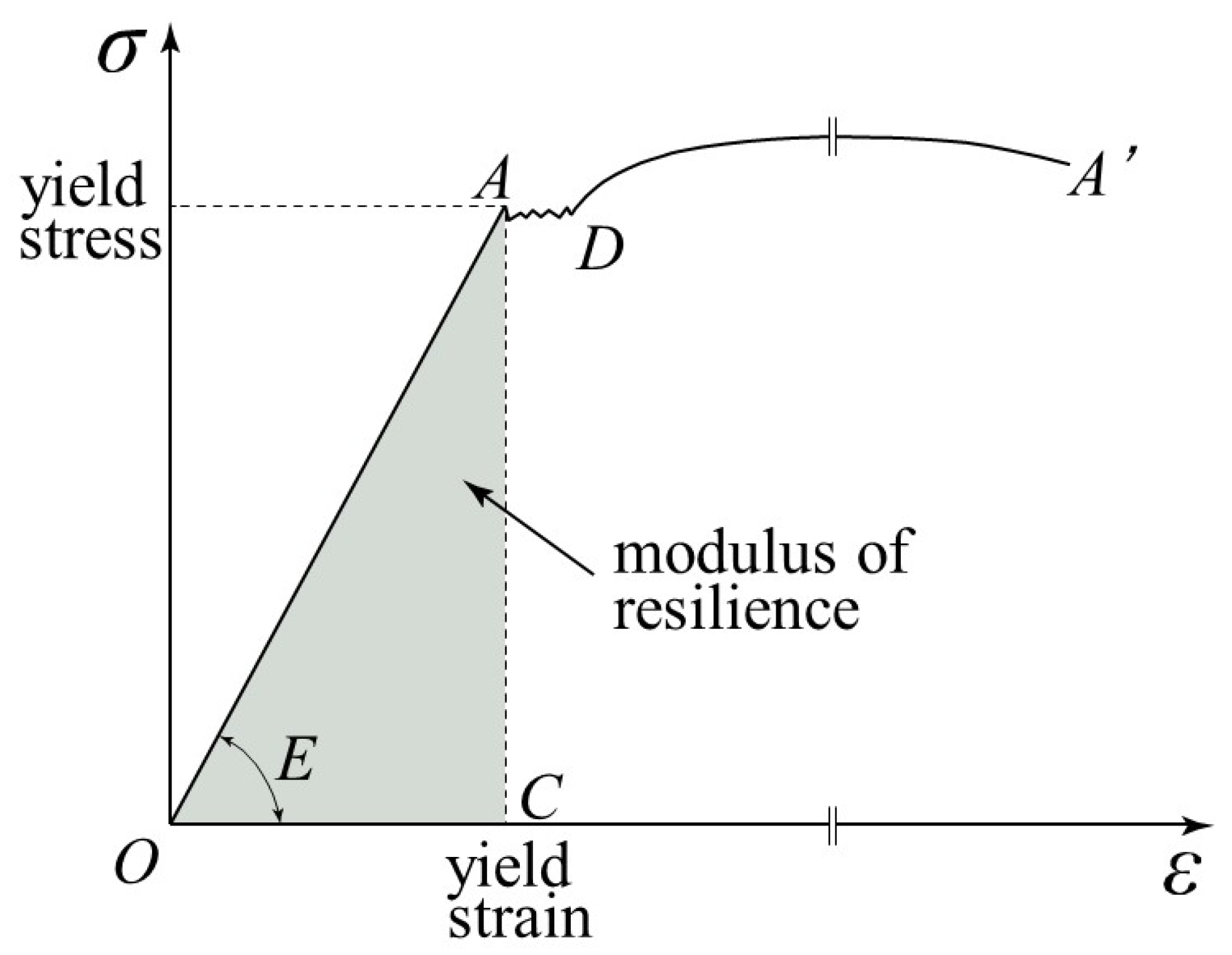
2.1. Etymology of Word “Resilience” and Theory of Elasticity
- F = force producing extension of bar;
- = length of bar;
- A = cross-sectional area of bar;
- δ = total elongation of bar;
- σ = stress of bar;
- ε = strain of bar;
- E = elastic constant of the material, called the modulus of elasticity.
2.2. Hooke’s Law, Young’s Modulus and Springs
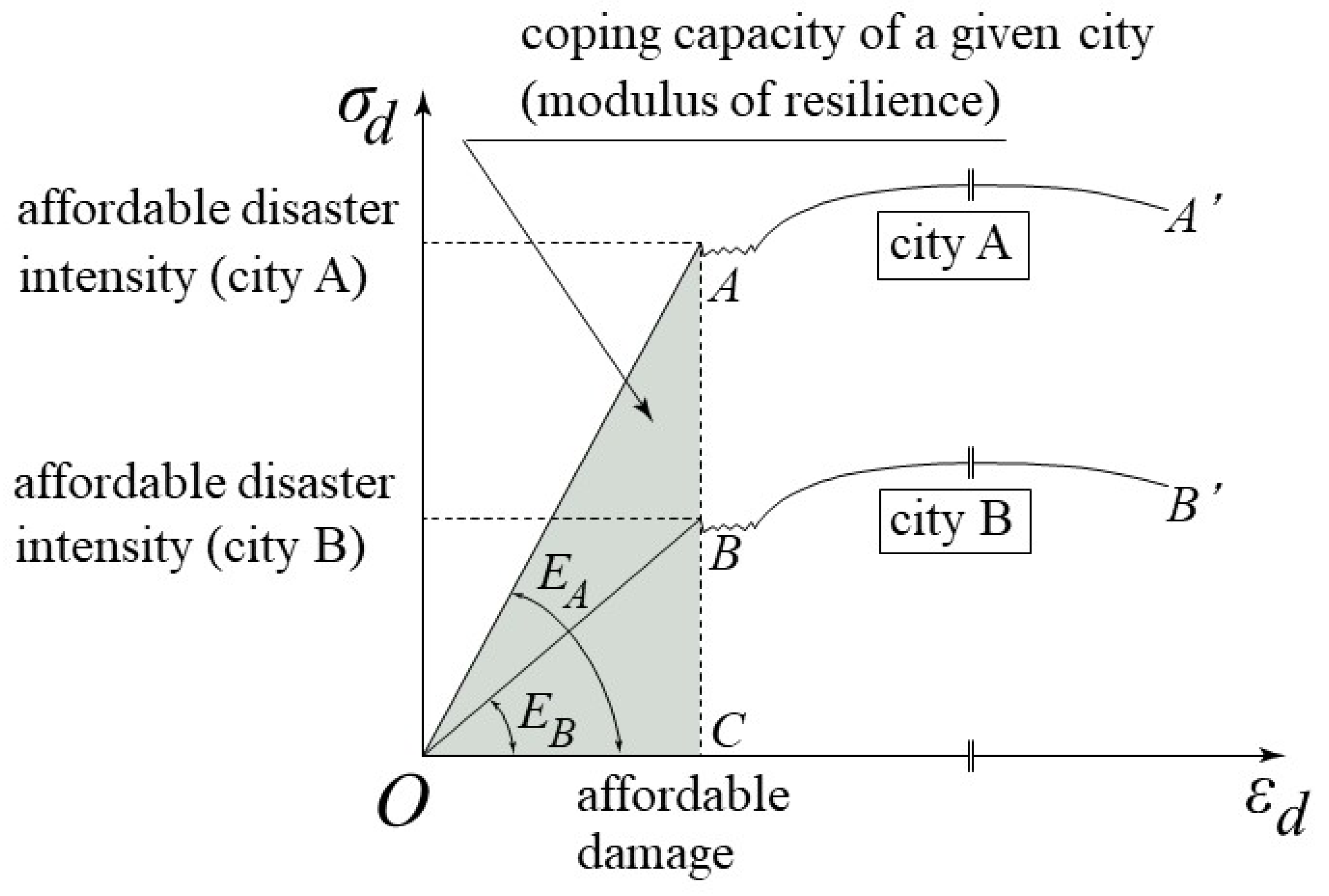
2.3. Modulus of Resilience and Coping Capacity
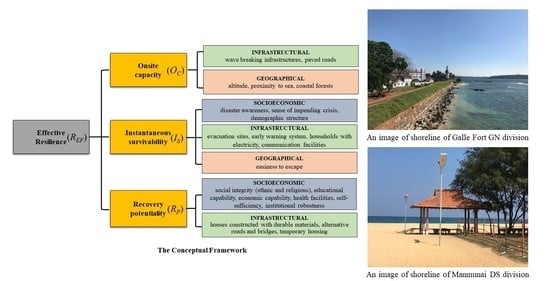
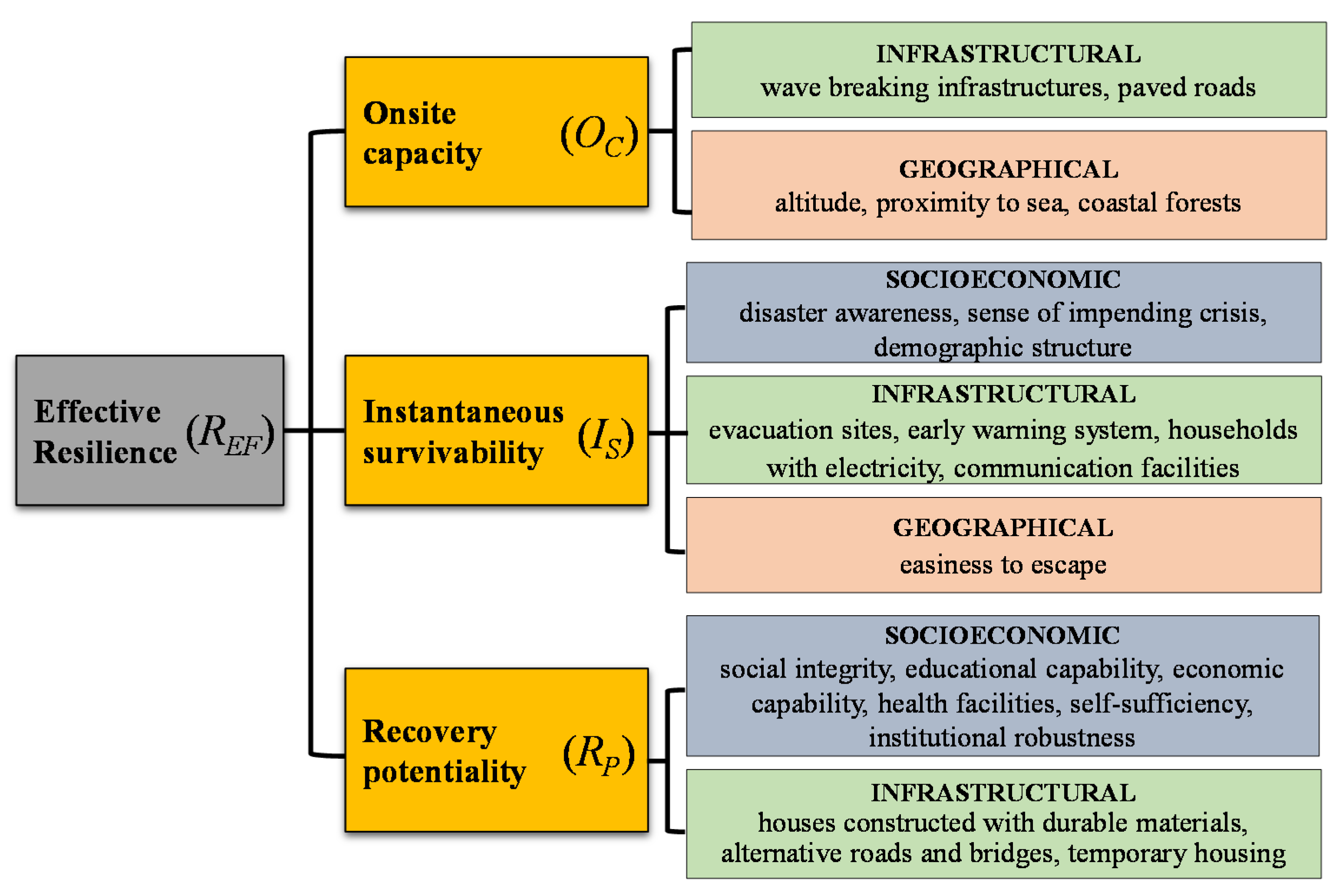
2.4. A Conceptual Framework for Evaluating Tsunami Resilience
3. Results and Discussion
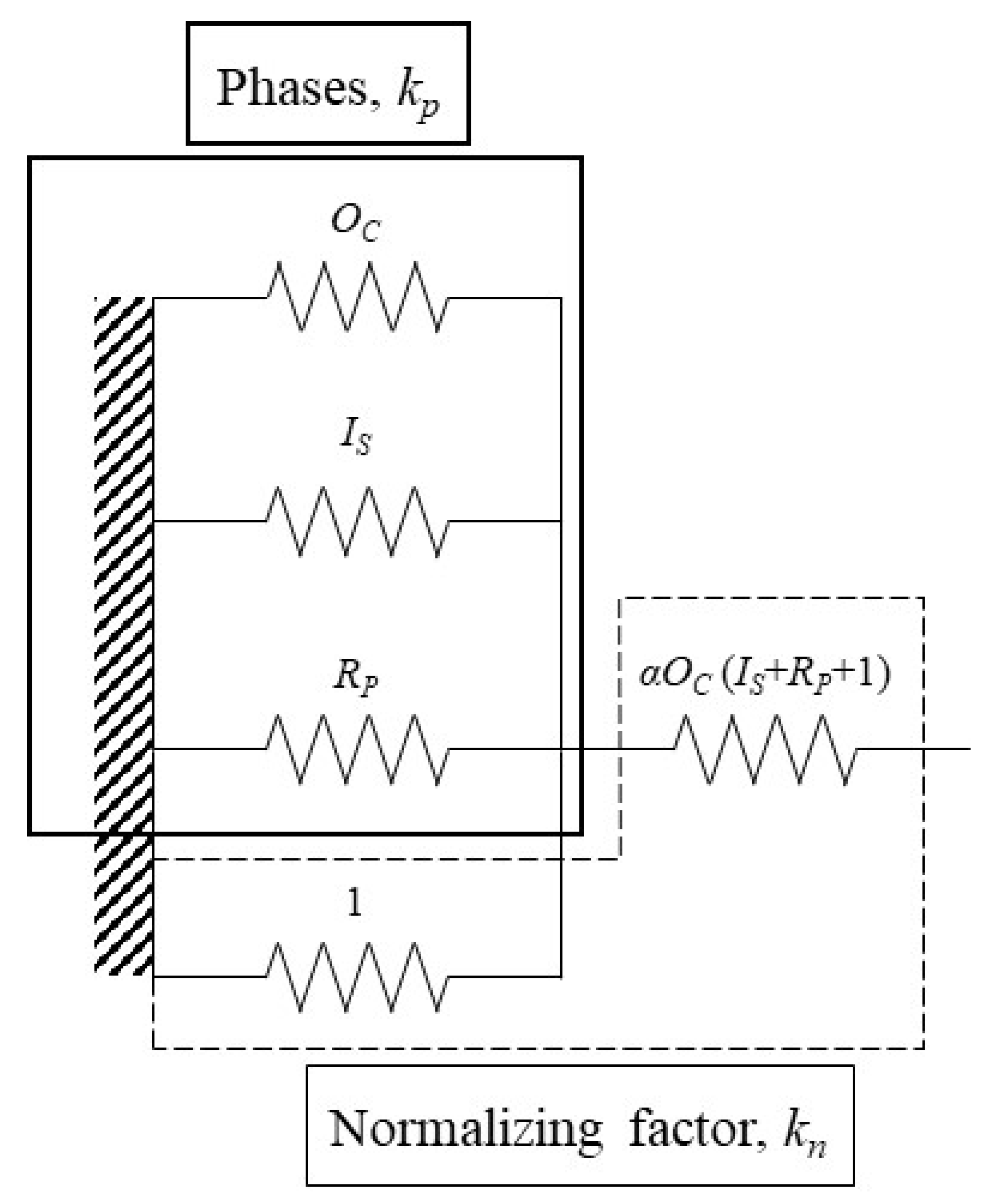
3.1. Applying Theory of Springs to Tsunami Resilience
3.2. Properties of the Mathematical Model
- The maximum effective resilience is 1.
- The minimum effective resilience is 0.
- The effective resilience is 0.36, when a place has an ideal onsite capacity (OC) but no human beings.
- The effective resilience is 0, when the onsite capacity (OC) equals 0, disregarding the value of instantaneous survivability (IS) and recovery potentiality (RP).
3.3. Limitations of the Mathematical Model
3.4. An Example of Using the Mathematical Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, J.; Wan, J.; Jia, H. Resilience to natural hazards: A geographic perspective. Nat. Hazards 2010, 53, 21–41. [Google Scholar] [CrossRef]
- UNISDR. Terminology on DRR. Available online: https://www.unisdr.org/we/inform/terminology#letter-r (accessed on 18 August 2020).
- Manyena, S.B. The concept of resilience revisited. Disasters 2006, 30, 433–450. [Google Scholar] [CrossRef] [PubMed]
- Thywissen, K. Core terminology of disaster reduction: A comparative glossary. In Measuring Vulnerability to Natural Hazards: Towards Disaster Resilient Societies; Birkmann, J., Ed.; United Nations University: Tokyo, Japan, 2006; pp. 448–496. [Google Scholar]
- Birkmann, J. Conclusion and recommendations. In Measuring Vulnerability to Natural Hazards: Towards Disaster Resilient Societies; Birkmann, J., Ed.; United Nations University: Tokyo, Japan, 2006; pp. 432–447. [Google Scholar]
- Bruneau, M.; Chang, S.; Eguchi, R.; Lee, G.; O’Rourke, T.; Reinhorn, A.; Shinozuka, M.; Tierney, K.; Wallace, W.; Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Orencio, P.M.; Fujii, M. A localized disaster-resilience index to assess coastal communities based on an analytic hierarchy process (AHP). Int. J. Disaster Risk Reduct. 2013, 3, 62–75. [Google Scholar] [CrossRef]
- Kusumastuti, R.D.; Viverita; Husodo, Z.A.; Suardi, L.; Danarsari, D.N. Developing a resilience index towards natural disasters in Indonesia. Int. J. Disaster Risk Reduct. 2014, 10, 327–340. [Google Scholar] [CrossRef]
- Pushpalal, D. A conceptual framework for evaluating tsunami resilience. IOP Conf. Ser. Earth Environ. Sci. 2017, 56. [Google Scholar] [CrossRef]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 1, 2707–2716. [Google Scholar] [CrossRef]
- Todhunter, I.; Pearson, K. A History of the Theory of Elasticity and of the Strength of Materials: From Galilei to the Present Time 1; Cambridge University Press: Cambridge, UK, 1886; p. 875. [Google Scholar]
- Young, T. A Course of Lectures on Natural Philosophy and the Mechanical Arts 2; Johnson, J., Ed.; Johnson: London, UK, 1807; p. 50. [Google Scholar]
- Timoshenko, S. History of Strength of Materials; McGraw-Hill: New York, NY, USA, 1953; pp. 18–20. [Google Scholar]
- Timoshenko, S. Strength of Materials: Part 1 Elementary Theory and Problems; Van Nostrand, D., Ed.; Van Nostrand: New York, NY, USA, 1930; p. 2. [Google Scholar]
- Den Hartog, J.P. Strength of Materials; McGraw-Hill: New York, NY, USA, 1949; p. 161. [Google Scholar]
- Morley, A. Strength of Materials; Longmans, Green, and Co.: London, UK, 1908; p. 64. [Google Scholar]
- Cutter, S.L.; Barnes, L.; Berry, M.; Burton, C.S.; Evans, E.; Tate, E.; Webb, J. A place-based model for understanding community resilience to natural disasters. Glob. Environ. Chang. 2008, 18, 598–606. [Google Scholar] [CrossRef]
- Dao, H.; Peduzzi, P. Global Risk and Vulnerability Index Trends per Year (GRAVITY) Phase IV: Technical Annex and Multi Risk Integration. 2003, pp. 1–31. Available online: https://pdfs.semanticscholar.org/27d3/ea4a8896968f17f5a3ee39cf4f238bd31cde.pdf (accessed on 18 August 2020).
- Cutter, S.L.; Boruff, B.J.; Shirley, W.L. Social vulnerability to environmental hazards. Soc. Sci. Q. 2003, 84, 242–261. [Google Scholar] [CrossRef]
- Løvholt, F.; Setiadi, N.J.; Birkmann, J.; Harbitz, C.B.; Bach, C.; Fernando, N.; Kaiser, G.; Nadim, F. Tsunami risk reduction–Are we better prepared today than in 2004? Int. J. Disaster Risk Reduct. 2014, 10, 127–142. [Google Scholar] [CrossRef]
- Wood, N.J.; Jones, J.; Spielman, S.; Schmidtlein, M.C. Community clusters of tsunami vulnerability in the US Pacific Northwest. Proc. Natl. Acad. Sci. USA 2015, 112, 5354–5359. [Google Scholar] [CrossRef] [PubMed]
- Rufat, S.; Tate, E.; Burton, C.G.; Maroof, A.S. Social vulnerability to floods: Review of case studies and implications for measurement. Int. J. Disaster Risk Reduct. 2015, 14, 470–486. [Google Scholar] [CrossRef]
- Carrão, H.; Naumann, G.; Barbosa, P. Mapping global patterns of drought risk: An empirical framework based on sub-national estimates of hazard, exposure and vulnerability. Glob. Environ. Chang. 2016, 39, 108–124. [Google Scholar] [CrossRef]
- Suppasri, A.; Muhari, A.; Syamsidik; Yunus, R.; Pakoksung, K.; Imamura, F.; Koshimura, S.; Paulik, R. Vulnerability characteristics of tsunamis in Indonesia: Analysis of the Global Centre for Disaster Statistics Database. J. Disaster Res. 2018, 13, 1039–1048. [Google Scholar] [CrossRef]
- Rajindra, R.; Wekke, I.S.; Sabara, Z.; Pushpalal, D.; Samad, M.A.; Yani, A.; Umam, R. Diversity, Resilience, and Tragedy: Three Disasters in Palu of Indonesia. Int. J. Innov. Creat. Chang. 2019. Available online: https://www.ijicc.net/images/Vol5iss2_/91_Rajindra_P1592_2019R.pdf (accessed on 18 August 2020).
- Sri Lanka Survey Department. Grama Niladari Boundary Map of Sri Lanka. Available online: http://www.it.survey.gov.lk/gn_updating/ (accessed on 18 August 2020).
- Sri Lanka Department of Census and Statistics. Housing and Non-housing Building Units Damaged by the Tsunami 2004 Batticaloa District. Available online: http://www.statistics.gov.lk/Tsunami/final/Batticaloa/p2%207.1.pdf (accessed on 18 August 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pushpalal, D.; Suzuki, A. A New Methodology for Measuring Tsunami Resilience Using Theory of Springs. Geosciences 2020, 10, 469. https://doi.org/10.3390/geosciences10110469
Pushpalal D, Suzuki A. A New Methodology for Measuring Tsunami Resilience Using Theory of Springs. Geosciences. 2020; 10(11):469. https://doi.org/10.3390/geosciences10110469
Chicago/Turabian StylePushpalal, Dinil, and Atsushi Suzuki. 2020. "A New Methodology for Measuring Tsunami Resilience Using Theory of Springs" Geosciences 10, no. 11: 469. https://doi.org/10.3390/geosciences10110469
APA StylePushpalal, D., & Suzuki, A. (2020). A New Methodology for Measuring Tsunami Resilience Using Theory of Springs. Geosciences, 10(11), 469. https://doi.org/10.3390/geosciences10110469