Abstract
Observations of the deposits, flow marks, and damages of three mixed-snow avalanches of widely different size were analyzed with regard to flow regimes, velocities, pressures, densities, flow depths, erosion modes, and mass balance. Three deposit types of different density and granulometry could be clearly discerned in these avalanches. They are attributed to dense, fluidized, and suspension flow regimes, respectively. Combining observations, we estimated the density in the fluidized layer as 35–100 kg m, in good agreement with inferences from pressure measurements. Upper bounds for the suspension layer density, arising from the run-up height, velocity, and damage pattern, are about 5 kg m at the valley bottom. An approximate momentum balance of the dense layer suggests that the snow cover was eroded to considerable depth, but only partly entrained into the flow proper. The suspension layer had largely lost its erosive power at the point where it separated from the denser parts of the avalanche. Our estimates shed doubt on collisions between snow particles and aerodynamic forces at the head of the avalanche as sole mechanisms for creating and upholding the fluidized layer. We conjecture that the drag from air escaping from the snow cover as it is being compressed by the overriding avalanche could supply the missing lift force.
1. Introduction
According to traditional lore, two flow regimes occur in dry-snow avalanches, namely dense flow and suspension flow. The term “powder-snow avalanche” (PSA) is variably used for only the suspension layer or for mixed avalanches. Several avalanche experiments from the 1970s and 1980s [1,2,3,4] indicated that there may be an additional, intermediate-density flow regime. Norem [5] termed it “saltation” in analogy with the three regimes recognized in drifting snow (reptation, saltation, and suspension), but we will call it “fluidized” as this seems to better capture the physical processes at work. Surprisingly, these important findings have not found their way into the general view of avalanche dynamics for a long time (see, e.g., [6,7]) and into avalanche flow models in practical use. We were still “avalanche greenhorns” and not aware of the mentioned work when we had the opportunity to investigate three avalanche events—ranging from medium to very large size—in the Swiss Alps in early 1995. All three avalanches exhibited deposits with three clearly distinguishable textures and thus forced us to consider that there are three distinct flow regimes in mixed snow avalanches [8]. In the years since, full-scale experiments at the test sites Vallée de la Sionne [9,10,11,12,13,14] and Ryggfonn [15,16] have confirmed and refined the measurements from the 1970s and 1980s as well as our observations and inferences.
On the theoretical side, these insights have only slowly caught on: Salm and Gubler [17] and Gubler [18] sketched a block model with flow-regime transitions based on the kinetic theory of granular materials. In the NIS model [19], the collisional normal stress may exceed the overburden at sufficiently high speed, implying a flow-regime transition, but this new flow regime is not modeled. Issler and Gauer [20] extended the NIS model as a block model with flow-regime transitions and showed that it leads to significantly different estimates of the run-out distance and the pressure distribution in the run-out zone. Issler [21] constructed a coupled two-layer model for the saltation and suspension layer, assuming that the head of the avalanche fluidizes quickly and largely decouples from the dense main body; the dynamics of the bottom layer is modeled after the processes known from drifting snow. The two-layer model SAMOS [22] allows the density to vary only in the suspension layer and condenses the intermediate-density layer into an interface condition between the dense and suspended flow. Keshari et al. [23] prescribed vertical profiles of density and velocity in their depth-averaged one-layer model. More recently, Bartelt et al. [24,25] attempted to model the transition between dense and fluidized flow by employing a balance equation for velocity fluctuations (or granular temperature) that govern a heuristic modification of the Voellmy friction law, whereas Issler et al. [26] pointed out that the relaxation times of the flow depth and density are short so that their evolution can be captured by algebraic rather than differential equations. However, present-day computational tools for practical applications still do not explicitly incorporate this intermediate flow regime despite its important consequences for avalanche hazard mapping and mitigation.
More than two decades after their occurrence, the three avalanches in 1995 still stand out as the most instructive events with regard to flow regimes that we have encountered. A reanalysis of our observations showed that especially the mass balance estimates in [8] need revision and that further interesting inferences on densities, velocities, pressures and erosion rates can be made despite the lack of quantitative information, particularly if our observations from 1995 are combined with observations from avalanches at the test site Vallée de la Sionne in 1999 and on a number of smaller events in the area of Davos, Switzerland, during the winters of 2004–2006. This shows that detailed observations of mixed snow avalanches may provide valuable information that complements the relatively few measurements at instrumented test sites. It thus appeared justified to present our observations of, and inferences from, the avalanches of 1995 and to point out the potential of novel ways of analyzing and interpreting qualitative and semi-quantitative information.
In the present paper, we focus on the interpretation of the observations and relegate the descriptive part to the Supplementary Materials, except for a brief summary in Section 2. The Supplementary Materials also present additional observations from the years 2004–2006 that will be used here and that are described in event-specific reports. Section 3 examines how the deposit properties reflect the flow regime and where the snow clods found in the deposits originate from. Useful information on the dynamical properties of the different flow regimes is extracted by combining various observations in Section 4. An important question is what mechanisms are responsible for creating and maintaining the intermediate (“fluidized”) flow regime; we discuss several possibilities in Section 5. Finally, field observations can also yield useful constraints on erosion and entrainment when suitably analyzed, as we show in Section 6.
2. Summary of Observations
The three avalanches that are described in more detail in the Supplementary Materials, Sections S2–S4, occurred in January 1995 in the Swiss Alps and were a medium-size release from Vilan (2376 m a.s.l., Seewis, Grisons), a very large event from Albristhorn (2763 m a.s.l., Adelboden, Bernese Oberland), and an extremely large one from Scex Rouge (2971 m a.s.l., Les Diablerets, Vaud). They fall into size classes 3–4, 5, and 5+, respectively, in the Canadian Snow Avalanche Size Classification System. The snow pack was cold and dry along the entire path of the Vilan avalanche, but humid in the lower track and run-out area of the Albristhorn and Scex Rouge avalanches. In all three cases, a dense granular or blocky, sharply bounded, and relatively deep deposit (called Type 1 deposit here) was clearly distinguishable from the shallower Type 2 deposit that consisted of snow clods (ranging from less than 1 cm to about 30 cm) and a matrix of fine-grained snow (see Figure 1). We found the latter type to transition gradually to a third type of deposit (Type 3) in the distal direction (and possibly also at the lateral margins) as the embedded snow clods become smaller and eventually are absent. The density of the Type 2 deposits varied from (estimated) 400 kg m (Vilan) to nearly 600 kg m (Scex Rouge); Type 3 deposits were somewhat less dense, but still above 400 kg m at both Albristhorn and Scex Rouge.

Figure 1.
Vilan avalanche, snow pit in the Type 2 deposit. The avalanche eroded approximately 1 m of cold dry snow before depositing 40–50 cm of fine-grained, compressed snow with embedded spruce twigs and snow clods. The largest clods are sintered to the surface (at their original location behind the pit).
The avalanche parts that produced Type 2 deposits were significantly more mobile than those giving rise to Type 1 deposits: The Type 2 flow of the Vilan avalanche climbed over the steep embankment at a turn of the main gully (Figure S5), while the Albristhorn and Scex Rouge avalanches ran up the opposite slope some 50 m and more than 100 m in elevation, respectively (Figure 2, Figures S9 and S17). Similar observations have been made not only on the large avalanches at the test site Vallée de la Sionne [27], but even on very small avalanches ([28], Figure 2b and Figure 3). The mobility of the suspension layer (or powder-snow cloud), which undoubtedly is associated with the Type 3 deposits, is yet much higher—in the case of the Scex Rouge avalanche, the suspension layer propagated some 3 km beyond the Type 2 deposits (Figure S17).

Figure 2.
Aerial view of the run-out zone of the Albristhorn avalanche. The boundary of the Type 2 deposit (yellow line) is much less certain than that of the Type 1 deposit (red line), particularly in the southern parts (top of photo). The damaged ski lift shed is hidden behind trees in the top center part.

Figure 3.
Cross-section and detail of a large snow clod in the run-out zone of the 10 February 2005 Salezertobel avalanche, Davos, Switzerland. The texture of the snow is made visible by spraying a mixture of ink and alcohol onto the smoothened surface, warming it carefully with a camping cooker and waiting for the ink to diffuse into the snow by capillary suction. Note the layered core (oblique stripes (left) and the small snow clods sintered onto it (right).
For all three events, rough mass balances could be established for the three types of deposit (Tables S1–S3). The ratio of total eroded and entrained mass to released mass is around 1 for the Vilan avalanche and between 2 and 3 for the Albristhorn and Scex Rouge avalanches. All three events eroded most of the available new snow in substantial parts of the overflowed area; the two large avalanches also entrained large amounts of old snow while flowing downhill. On the counter-slope, the erosive power diminished rapidly in the Albristhorn avalanche, but remained substantial in the Scex Rouge avalanche. Beyond the Type 2 deposits, the erosive power of the suspension flow appears to have been small or zero in both events. The Type 2 and 3 deposits accounted for 20–25% of the total deposited mass of the Vilan avalanche; for about 10% and 5%, respectively, in the Albristhorn avalanche; and for 10–25% and 5–10%, respectively, in the case of the Scex Rouge event.
We found no traces of damage from the Type 1 flows because their paths were already devoid of structures, boulders or trees. The suspension flows at Albristhorn and Scex Rouge broke single trees in mature forest stands outside the Type 2 deposits. Just beyond the Type 1 deposit, the Albristhorn avalanche obliterated a dense, mature spruce stand (Figure 2). The vacation homes near the distal end of the Type 2 deposit were not damaged, but the door of a ski lift shed, located more than 100 m from the edge of the Type 1 deposit, was pushed in and damaged. The Type 2 and suspension flow of the Scex Rouge avalanche damaged a low-voltage power line severely and some cabins lightly after climbing about 100 m in elevation.
3. Inferences on Flow Regimes from Deposit Properties
3.1. Correspondence between Flow Regimes and Deposit Types
In our interpretation of the observed avalanche deposits, we make the crucial assumption that different textures correspond to different flow regimes. This is quite common in the interpretation of the geologic record, e.g., when analyzing sediment cores or seismic profiles across submarine landslide deposits. Care is required when doing so, however: For example, large differences in the granulometry of sediment cores from different points along a turbidite may be the result of progressively smaller particles settling out in the run-out area, without any flow-regime transition taking place.
The three avalanche events analyzed in this paper stand out because the boundaries between the three deposit types were unusually sharp. Different flow regimes appear to be the only plausible physical explanation for such rapid spatial changes. In the Vilan path, the sharp gully bends act as a filter for avalanche parts with different velocity—the (fluidized) front of the 1995 event was fast enough to climb over the outer bank while the dense part followed the gully. In the Albristhorn and Scex Rouge events, the snow temperature in conjunction with the steep counter-slopes may have acted as discriminant: The relatively thin layer of dry new snow being eroded by the avalanche head, the avalanche body entrained humid snow, was slowed down by higher friction, and thus stopped on the valley floor.
The emplacement, dimensions, and texture of the Type 1 deposits clearly show them to result from a dense and slow to moderately fast, granular flow. Using insight from the kinetic theory of granular flows, we associate the Type 1 deposits with what is usually termed a dense-flow avalanche and interpret them as manifesting a combination of the frictional and collisional flow regimes of granular flows. This implies that the shear stresses inside the flow are due to the friction between snow particles sliding past each other as well as short, but frequent collisions. The relative importance of the two stress contributions varies with the shear rate and the coefficient of restitution.
Association of the Type 3 deposits with suspension flow (the powder-snow cloud) is similarly unequivocal due to the absence of snow particles larger than snow grains and the very high mobility of the flow. Maintaining particles in suspension over extended periods requires fully developed turbulence and imposes upper bounds on the volumetric particle concentration and the particle size. This flow type cannot be associated with a purely granular flow regime because the interstitial air plays a fundamental role.
The enhanced mobility of the flow parts leading to Type 2 deposits can be explained by the kinetic theory of granular materials if their density is substantially smaller than that of the dense-flow part. At the same time, it cannot be as low as in the suspension flow because a substantial fraction of the flow mass consists of large snow clods (and in some cases boulders) that are rafted along. Flows with such intermediate densities should be mainly in the grain inertia regime, in which momentum is transferred dominantly by particles with a mean free path of a few particle diameters. We henceforth refer to this flow regime as fluidized. Section 4 discusses what can be inferred about its dynamical properties from our observations.
3.2. Granulometry and Deposit Density
Particle size in the Type 1 deposits appears to depend mainly on the snow conditions at the time of the event. Our observations suggest that humid snow with sufficient residual strength in the released slab leads to the formation of large snow blocks with shear band failures, as exemplified by the Albristhorn and Scex Rouge avalanches (see the Supplementary Materials, Sections S3 and S4, respectively). If the snow cover is completely wet, it tends to crumble quickly during release and rounded snow clods form by aggregation during the descent [29,30]. In dry-snow avalanches, it appears that the snow clods are (or contain) intact but compacted pieces of the original layered snow cover [31].
The three avalanches described in the Supplementary Materials do not exhibit any pronounced correlation between avalanche size and mean particle size in the Type 2 deposits—the largest snow clods in the Vilan avalanche were of similar size as in the other two, much larger avalanches. In some later observations, we found horizontal grading in the distal direction of Type 2 deposits, in particular at Albristhorn where the surficial snow clods became smaller and less frequent with distance and also the size of embedded particles diminished. In three medium-size avalanches [30,31,32], we found isolated rounded or oblong snow blocks up to 0.5 m in size near the edge of the Type 2 deposit. The 10 February 1999 avalanche at Vallée de la Sionne deposited even larger, very hard snow blocks on the counter-slope above the observation bunker. Our cumulated observations suggest that small avalanches with only a weakly developed Type 2 deposit tend to transport smaller snow clods.
The density of the Type 2 deposits was much higher than the density of the released or eroded snow-cover layers in all three cases and increased with avalanche size. Experience from the 1999 avalanches at the avalanche test site Vallée de la Sionne and a fair number of observations on small avalanches in Davos during the winters of 2003–2006 support this view. The snow properties (and in particular the temperature if the measurements are made long after the event) may influence the deposit density to some degree, but apparently not as much as for the Type 1 deposits at both Albristhorn and Scex Rouge; the Type 2 deposits were relatively dry compared to the Type 1 deposits. A possible explanation of this observation is that the fluidized layer did not entrain the humid, cohesive snow below the relatively thin new-snow layer on the surface.
The most plausible mechanisms affecting the density of Type 2 deposits, , are: (i) self-compaction of the deposit under its own weight; (ii) filling of voids by small snow grains; (iii) compaction of the particles during the flow; and (iv) compaction of the matrix by particle impacts during deposition. We think that Mechanism (i) does not explain the observed size-dependence of the deposit density: The overburden in the observed Type 2 avalanche deposits was less than 3 kPa in all cases and is hardly sufficient to produce densities in excess of 500 kg m within two days, given that snow strength increases roughly exponentially with density [33].
To discuss the relative importance of Mechanisms (ii)–(iv) for the size dependence of , we write in terms of the matrix density, , the density of snow clods, , and the volume fractions of snow clods, , and of voids larger than snow grains, :
High deposit density implies small . We have never observed voids much larger than snow grains in Type 2 deposits, thus independent of avalanche size, whence Mechanism (ii) cannot explain the observed size dependence of . According to our experience, the deposited snow clods are significantly harder than the embedding matrix. We lack quantitative density measurements of snow clods, but they always felt denser than the embedding fine-grained matrix; we estimate . Within the range , one finds . Compaction of particles during avalanche flow must be due to collisions. The number of collisions per particle increases with the path length, the volume concentration in the flow and the shear rate, all three of which grow with avalanche size, hence we expect Mechanism (iii) to contribute to the avalanche-size dependence of . Our observations are not detailed enough to assess whether also grows with avalanche size. Taking the granulation experiments of Steinkogler et al. [34] as guidance, one may suspect to have been smallest in the Vilan avalanche, which released under unusually cold conditions.
The matrix density has a direct influence on and seems to increase markedly with avalanche size. This points to Mechanism (iv) as a major cause for the avalanche-size dependence of . The degree of compaction depends on the peak pressure and deposited energy of the impacts. We expect , where is the relative velocity of colliding snow clods during avalanche movement and the impact velocity at final deposition; c is the plastic shock velocity (water hammer effect). The high-frequency impact pressure measurements in the fluidized layer of the 1999 avalanches at Vallée de la Sionne revealed pressure peaks of up to about 1 MPa [9]. The dissipated energy per impact (on the ground) and unit area is of the order of for a particle of diameter . During deposition, and will be smaller—the latter perhaps in the range 30–300 kPa—than the impact pressure on a fixed obstacle during flow, but this is still one to two orders of magnitude larger than the overburden and of the correct order for compacting the matrix to the observed densities. We expect not to depend on the avalanche size, but rather on some threshold for maintaining fluidization, while c will increase with . The total energy available for compaction grows with avalanche size, but so does the mass that has to be compacted. This would leave and the number of impacts per unit area as the two determining factors. As discussed above, probably grows with the avalanche path length whereas the number of impacts correlates with the deposit depth and . did not differ as strongly between the Vilan and Albristhorn avalanches as did. In another avalanche [35], we found both the depth and the density of the Type 2 deposit to decrease in the distal direction, in agreement with our hypotheses. However, a much deeper understanding of the mechanics of fluidized flow and impact compaction is needed before firm conclusions can be drawn.
3.3. Where Do the Snow Clods Originate?
The number and size of snow clods being a distinguishing property of the three deposit types, the question of their genesis is important as it might give further clues on the flow mechanism in the fluidized regime. A priori, the following possibilities (and combinations thereof) should be considered: (1) The snow clods come from an external source (e.g., snow on trees) and are largely irrelevant in the dynamics. (2) The snow clods form during the flow by accretion in totally inelastic collisions [34]. (3) The snow clods are remnants of the released slab that were not broken up further during the avalanche descent. (4) The snow clods are pieces of the snow cover that were ripped out by the passing flow.
For all three avalanche events (and many more we have come across since), there were not sufficiently many trees (or outcrops) to provide the quantity of snow clods we observed on the debris. Hypothesis 1 can therefore be safely dismissed. We have not found direct evidence for Hypothesis 2 in that small snow clods did not show internal structure. Hypotheses 3 and 4 get support from cross-sections of a few large snow clods we studied later in two medium-size events, see Figure 3 as well as Appendix C in the Supplementary Materials and references therein. The core of the snow clods consisted of homogeneous snow with the grain characteristics of the new snow, with some hints of layering still visible. However, in both cases, the density was substantially higher than that of new snow, and smaller snow clods had sintered onto the original blocks, making them close to spherical. This observation does not discriminate between Hypotheses 3 and 4, however. The large snow block that was filmed, tracked by Doppler radar, and left visible impact marks on the deposits in an experiment in Ryggfonn, Norway in 2007 most likely was a part of the released cornice. This supports Hypothesis 3 without ruling out Hypothesis 4. In both cases, an open question is how the flow can compact pieces of a snow slab about half a meter in length to about twice their original density without breaking them. This would seem to require substantial and sufficiently isotropic pressure.
One of the avalanches mentioned above ran out in humid snow, hence it is not so surprising that small snow clods could sinter onto larger clods when the avalanche speed had become low. The other avalanche, however, was a dry-snow avalanche throughout. We conjecture that favorable conditions for accretion of particles onto a snow clod are the following: (i) Presence of sufficiently many numerous and hard small snow clods. This increases the chance that a particle can hit the large snow clod without disintegrating and then gets pressed onto it by other particle impacts. (ii) Intermediate mean collision velocities. In this way, the particles are not destroyed upon impact, but deform plastically to some degree so that they are heated somewhat and sinter more rapidly onto the large snow clod. (iii) Entrainment of deep and relatively warm snow layers. In their experiments with a concrete tumbler, Steinkogler et al. [34] found that aggregation occurred only if the snow temperature was close to 0 C. In avalanches, the temperature range favoring aggregation may be slightly lower due to more intense frictional heating [36]. Quantitative examination of these processes might lead to useful constraints on the density and shear rate or fluctuation velocity in the fluidized as well as the dense layer, where snow clod formation is equally important.
Two similar observations of large snow clods provide some insight into the transport mechanism in the last stage before the stop (Figure 4). In one case, the snow block, resembling an ellipsoid of about 0.8 × 0.4 × 0.4 m, carved an approximately 0.2 m deep furrow for about 4 m before coming to rest and abruptly turning at the very end. Low levee-like features formed on both sides of the furrow. The flow must have come to a stop just before or immediately afterwards because the furrow was not filled in, but only covered with a veil of fine-grained snow. The furrow fades gradually in the upstream direction, suggesting the following alternatives: (1) The block originally moved at the same speed as its surroundings and only slid a few meters relative to it when the flow stopped abruptly. (2) Alternatively, the block plowed through the flow at higher speed, but the surface was agitated enough to smoothen the furrow quickly, except in the very last phase when it underwent solidification. It might be possible to determine the correct answer in an avalanche of moderate size by “seeding” it with objects of diverse size and density before artificially releasing it.

Figure 4.
Large snow clod near the right edge of the avalanche artificially released from Gotschnawang, Klosters, Switzerland on 12 March 2006. Note that the approximately 10 cm deep furrow carved by the block abruptly swerves to the right at the end.
4. Dynamical Properties of the Fluidized Flow Regime
In this section, we combine observations (and sometimes also non-observations) of deposit depths, run-up heights, superelevation in bends, and damage on forest and buildings to constrain the flow depths, velocities, pressures, and densities of the three avalanche events.
4.1. Flow Depth and Density of Fluidized Flow
Indirect indications of the dense-flow depth can be gained from the depth of the Type 1 deposits if one supposes that the deposit is not much denser than the flow—an assumption supported by experiments on dense granular flows. With this assumption, we estimate dense-flow depths of 0.5–1.5 m for the Vilan avalanche, approximately 2 m for the Albristhorn avalanche on the alluvial fan (probably significantly more in the narrow gully above), and 3–5 m for the Scex Rouge avalanche (the maximum deposit depth of more than 10 m is most likely due to compression ridges, see the Supplementary Materials, Figure S19).
The only direct observation of flow depth consists of photos of the Scex Rouge avalanche (Supplementary Materials, Figure S20), showing that the suspension layer was at least 200 m high when it began its ascent on the counter-slope. One may argue that the fluidized flow was relatively shallow after climbing the torrent bank at Albristhorn and the counter-slope to Grand Moilles at Scex Rouge:
- We surmise that fluidized flow requires a minimum velocity, or else it reverts to dense flow or stops. This threshold velocity will depend on the slope angle, particle size and presumably the properties of the snow pack as well; we conjecture it to be in the range –20 m s.
- For densities in the range –100 kg m, the (time-averaged) impact pressure on a wide obstacle is –40 kPa.
- If the pressure had exceeded 10–20 kPa near the snow surface or 5–10 kPa more than 2 m above ground, the ski lift shed at Albristhorn or the cabins at Grand Moilles (Scex Rouge) would likely have been structurally damaged to some degree. At those locations, we can infer m, kg m and m s.
- Let , , and be the length, height, and density, respectively, of the Type 2 deposit, and denote the corresponding quantities of the fluidized flow shortly before deposition by , and . Then, the masses per unit width, and , should be approximately equal.
- At Albristhorn, we use the following values characterizing the deposit along its centerline: kg m, m, m, giving kg m. The corresponding values for the Scex Rouge avalanche are kg m, –500 m, –0.4 m, thus kg m.
- We assume in the range 200–400 m at Albristhorn and 400–800 m at Scex Rouge, using the profiling radar measurements at Vallée de la Sionne [9] and pressure measurements at Ryggfonn [15,37] as reference points. Mass conservation demands , and with –50 kg m we obtain the ranges –5 m at Albristhorn and –12.5 m at Scex Rouge.
When these constraints are combined, it appears likely that the fluidized flows were rather long (300–400 m at Albristhorn and more than 500 m at Scex Rouge), had a density near 50 kg m, flowed at 15–20 m s, and had a flow depth around 2 m in their run-out zones. These numbers appear consistent with the pressure measurements in a fast fluidized flow recorded at Vallée de la Sionne in February 1999 near the transition from track to run-out zone, which revealed a significant number of isolated particle impacts at least to 3–5 m above the snow surface [9].
4.2. Velocities of the Dense and Fluidized Flows
In channelized, tortuous gullies, superelevation may be used to roughly estimate flow speed [38]. Snow surface texture in gully bends indicates that the Type 1 deposits show little superelevation while there is pronounced superelevation on the scoured, usually depositless sidewalls of the gully. Moreover, it is implausible that the masses forming the Type 1 deposit in a gully slid down from the sidewalls—we found scour marks always to be more or less parallel to the gully centerline. Moreover, in the run-out zone, Type 2 deposits form along the prolongation of the scoured sidewalls while the Type 1 deposits typically are concentrated near the axis of the run-out zone. In [28,39], such observations were used to estimate the speed of the respective avalanche components in three cases, yielding ratios near 2.
In the Vilan avalanche, the pronounced bend of the Däras gully at 1630 m a.s.l. led to the dense and the fluidized flows taking different paths. We have not recorded superelevation of the Type 1 deposit in that case, but there were no signs that the dense flow ran up significantly on the outer bank. The fluidized flow broke out and still was fast enough after the climb to erode the entire new-snow layer. A rough estimate gives likely ranges of 10–15 m s for the dense flow and 25–35 m s for the fluidized flow.
In this estimate, we used the simple energy balance
where and are the avalanche velocities before and after the ascent on the counter-slope, H is the run-up height, L is the corresponding horizontal distance, and is the average effective friction coefficient of the flow. As a first approximation, we set , with the run-out angle measured from the fracture crown to the end of the deposit of the respective flow component. This simple formula cannot be used to estimate the speed of the suspension flow because it neglects the buoyancy effects that are important for the suspension layer. It gives, however, a velocity for the fluidized flow in good agreement with the measured front velocity for the avalanches approaching the bunker at Vallée de la Sionne in February 1999.
The dense flow of the Albristhorn avalanche stopped right before the southeastern bank of Allebach (°) while the fluidized flow ran up a height –40 m over a horizontal distance –250 m (°). With , we estimate the speed of the fluidized flow at the stopping point of the dense flow to –55 m s. A corresponding estimate for the Scex Rouge avalanche with –600 m, –140 m and ° yields –90 m s at the lowest point of the path, where the humid dense flow hardly was faster than 30 m s. This value of may seem very high, but this avalanche exceeded all avalanches measured in experiments anywhere with regard to drop height, release depth and run-up height. One can argue for a lower effective friction coefficient of the fully fluidized flow (a small dry-snow avalanche observed at Tyinstølen in Norway in 2008 had a run-out angle of only 14.5°, corresponding to ), but even with and –20 m s, –80 m s is necessary to explain the observed run-up.
Despite the large uncertainties, these estimates are consistent with other observations [40,41] and experimental findings from later experiments: Velocity measurements with range-gating Doppler radar [42,43] clearly show the head of dry-snow avalanches to be faster than the body, the speed diminishing approximately linearly with distance from the front. This leads to a marked increase in the length of the flow with distance. Profiling radar systems overflowed by the avalanche and oriented perpendicular to the ground [44] installed at the Vallée de la Sionne test site clearly confirm that there often is a marked density difference between the head and the body [40,45,46]. One may combine the lag time of the dense part relative to the front with front-velocity estimates from Doppler radar or time-lapse photographs to find that the fluidized front of large avalanches attains a length of 300–500 m at the end of the track. At the somewhat smaller test site Ryggfonn in Norway, typical head lengths (inferred from abrupt changes in the impact pressure on obstacles in the flow path) are in the range 50–100 m [15].
The ratio of the front velocities of the fluidized front and the dense core depends strongly on the position along the path. The available information points to typical values in the range 1.5–2 in the track and increasingly larger ratios as the dense part approaches its stopping point.
4.3. Relative Mobility of the Three Flow Regimes
For practical purposes such as hazard mapping, the difference between the run-out angles of the dense and fluidized flows, , and their relation to the so-called angle is of interest. is the angle between the horizontal and the line from the top of the fracture crown to the point along the path where the slope angle falls below 10°, see Figure 5. The topographical–statistical – model [47] postulates a linear regression between and . On the basis of about 200 recorded events—mostly medium to large avalanches from western Norway that are assumed to represent the extreme run-out in the respective path—the following relation and standard deviation is obtained for Norway:
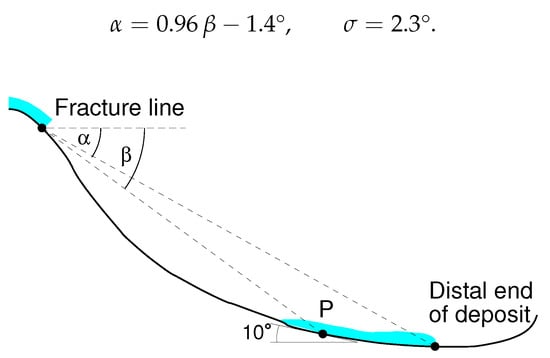
Figure 5.
Definition sketch of the topographic quantities referred to in the topographical–statistical – model.
Similar values were found using data from the Austrian Alps, the Pyrenees, Canada, and Iceland.
Table 1 shows the values for the Albristhorn and Scex Rouge avalanches. Despite becoming quite humid at low altitudes, the dense parts were at least as mobile as predicted by the model. This is all the more remarkable as, presumably, most of the run-out angles in the Norwegian database pertain to the fluidized flow, without this being explicitly recognized. of the fluidized part was, respectively, 2.5° and 4.6° less than . This difference, while probably less in smaller and only partially fluidized avalanches, is a rather significant difference and amounts to one and two standard deviations, respectively, in the correlation in Equation (3).

Table 1.
Approximate run-out angles , of the dense (d) and fluidized (f) parts of the Albristhorn and Scex Rouge avalanches and twelve selected events from the experimental site Ryggfonn (western Norway). These values are compared to the predictions of the Norwegian topographical–statistical – model (, ).
From the field survey data at NGI’s test site Ryggfonn—in particular, the deposit depth profiles along the approximate centerline of the avalanche—the extent of the Type 1 and 2 deposits could be deduced with reasonable confidence in a number of cases [48]. We used these data to see how much the relative mobility of the dense and fluidized parts varies between events in the same avalanche path. Table 1 shows to range from 0° to 4°. However, the 16 m high dam (with variable freeboard due to deposits from earlier avalanches) influences the run-out of both flow regimes considerably. In particular, it stopped the dense flow of about half of the events. It nevertheless emerges that there is strong variability, and we conjecture that may increase significantly with the run-out distance and the return period of the event.
A corresponding comparison for the run-out angle of the suspension part would be interesting, but is hampered by the fact that we could not fully survey the run-out areas of the suspension flow in any of the three cases. Moreover, the very notion of run-out distance is fuzzy for powder-snow avalanches. A recent statistical analysis of observations of powder-snow avalanches with long return periods from Austria, Switzerland, and Norway is presented in [49].
4.4. Density Estimates for the Suspension Layer
As mentioned above, the simple Equation (2) relating speed and run-up height does not apply to the suspension flow because the air in the mixture is neutrally buoyant and its kinetic energy also contributes to transporting the snow grains up the counterslope. Thus, the lower is the density of the cloud for a given velocity, the higher the cloud can climb. An approximate energy balance for the suspension flow, derived in Appendix A, leads to the inequality
which constrains the average particle concentration at the valley bottom. and are the densities of air and ice, respectively. corrects the run-up height H for effects of particle settling at speed m s, with the mean front speed during the ascent and the mean inclination of the counter-slope. The coefficients A, B, and C represent the ratio of kinetic energy of vortical motion of the head relative to translational kinetic energy, the fraction of particles lost during the ascent and the relative increase of air volume, respectively.
For the Albristhorn avalanche, we estimate –50 m s, –10 m s, m, , –0.7, and –10. The most plausible input values yield . Considering that the flow velocity and density a few meters above ground near the bottom of the suspension flow can easily be a factor 2 higher than the depth-averaged values, we deduce stagnation pressures in the range 6–50 kPa near the torrent bank. However, only values at the lower end of this range appear consistent with the observed damage pattern (see Section 4.5 and the Supplementary Materials, Section S3), i.e., m s and .
When applying the formula to the Scex Rouge avalanche, we tentatively set , , m, and m s, similar to the estimated speed of the fluidized flow at the valley bottom. For the denominator in Equation (A5) to remain positive and reasonably large, the speed at Grand Moilles should then have been at least m s. This limits C, the ratio of air volumes after and before the ascent, to about 1.3. At this speed, the stagnation pressure at Grand Moilles would exceed 10 kPa and more extensive damage should have occurred. The most plausible explanation is that was significantly less than the speed of the fluidized flow due to violent ingestion of ambient air and sideways spreading of the suspension layer at the valley bottom, which is narrow and strongly curved relative to the 200 m deep suspension flow. Laboratory experiments indicate that the height, width, and length of density currents [50] and particle suspensions [51] grow linearly with distance. A large cloud volume before the ascent would then explain why the volume ratio C is relatively small in this case. By trial and error, m s, m s, emerge as a parameter set giving consistent values kg m and kg m for the average suspension density at the valley bottom and at Grand Moilles, respectively. From the depth-averaged velocity and density, one obtains kPa, but the stagnation pressure near the ground would be in the range 5–10 kPa, which is compatible with the observed damage.
4.5. Impact Pressures and Densities
Some information from the observed damage patterns is used in Section 4.1 and Section 4.4 to constrain the density and flow depth of the fluidized flow. Here, we exploit the damage observations more systematically to obtain bounds on densities and velocities of the fluidized and suspension flows for all three avalanches. Nothing can be inferred about the impact pressures of the dense flows, however, because they did not encounter obstacles visible to us that could be damaged or destroyed.
Full-scale measurements on wet-snow avalanches [11,15,52,53] show clearly that the effective drag coefficient rises sharply with decreasing Froude number, in good agreement with laboratory experiments and simulations of dense granular flows [54]. If the definition of the Reynolds number is suitably adjusted to the conditions in dense granular flows, the Reynolds number dependence of the drag coefficient is at least qualitatively similar to that observed in molecular fluids. In the case of rapid dry-snow avalanches, field observations at a deflection dam in Iceland [55] and laboratory experiments with granular materials (e.g., [56,57,58]) have provided evidence for the occurrence of shocks that are the granular analogues of both hydraulic jumps (discontinuities in the flow depth and velocity) and gas-dynamic shocks (discontinuities in the density, temperature, and velocity). Along the deflection dam, flow marks from an oblique shock of the hydraulic-jump type were found, whereas two-dimensional simulations of granular flow around a cylinder show a bow shock along which the density and velocity change abruptly. (In three dimensional free-surface flows, one would expect both compression/rarefaction effects and splashing, i.e., a combined gas-dynamic and hydraulic shock.) In the present observations, however, no evidence of such shock effects was found.
The fundamental question to be considered when interpreting our damage observations is how the pressure exerted by a dilute granular flow impacting on some object relates to the flow properties (particle size and density, concentration, and velocity). The numerical study by Wassgren et al. [59] of dilute two-dimensional granular flow around a cylinder is directly relevant in this context. These authors find the drag force on the cylinder per unit flow depth, , to grow with the bulk density, , the square of the free-stream velocity, , and the effective cross-section, which is the sum of particle diameter, d, and cylinder diameter, D. This is captured by a slight extension of the well-known drag formula:
In the suspension layer, , the modification in Equation (5) is negligible. In the fluidized flow, a fraction of the particles has diameters approaching that of a tree trunk so that the force will be higher than expected on the basis of the conventional formula for molecular fluids.
The numerical experiments showed the drag coefficient, , to depend both on the Mach number (Ma, the ratio of fluid speed to speed of sound in the fluid) and the granular Knudsen number (Kn, the ratio of the mean free path of the particles to a characteristic length scale) rather than only on the Reynolds number as in molecular fluid dynamics. The situation in nature is even more complicated because the flow depth introduces another length scale (connected to shear effects in the flow), the particle-size distribution spans some three orders of magnitude, and the interstitial air plays an important role in suspension flow. Nevertheless, the results of Wassgren et al. [59] can give some guidance; their main findings can be summarized as follows:
- decreases significantly with increasing Mach number for , but is almost constant for supersonic speeds.
- The drag coefficient increases by about a factor of 2 from to and is about constant for .
- depends only mildly on the restitution and friction coefficients of inter-particle collisions.
- Except at very low Kn, for a cylinder in dilute granular flows is in the range 1.5–2.5 and thus roughly a factor 2 larger than in turbulent subsonic flows.
The definitions of Ma and Kn used in [59] do not readily apply to snow avalanches, and developing a suitable extension of those definitions is beyond the scope of this paper; the following estimates are therefore only provisional. The simplest case is the Knudsen number in suspension flow, where the volumetric particle concentration typically is and the particle diameter is . The definition given in [59],
indicates for the suspension flow. If snow grains dominate in the fluidized layer, we can set m and , which gives . However, for snow clods with m and a typical tree trunk diameter m, we find .
In [59], the (granular) speed of sound is defined in terms of the upstream granular temperature and volume concentration :
with the two-particle distribution function at contact given by . For , the expression in brackets is approximately and we get . Thus, the granular speed of sound in the suspension layer (fluidized layer) is roughly 2–4 (1–2) orders of magnitude larger than the fluctuation velocity of the particles. In suspension flow, the turbulent velocity determines the solid fluctuation velocity and should be in the range 5–20 m s, giving a granular Mach number far below 1. If the suspension is treated as a dense compressible fluid, the Mach number is found to be in the range 0.1–0.5, depending on the density and speed of the flow. We expect the fluctuation velocity in fluidized flows to be in a similar range as in suspension flows so that the flow is probably subsonic, possibly transonic.
Based on these estimates, estimated drag coefficients for small and large particles in fluidized flow and for suspension flow can be inferred from the numerical results in [59], with typical values listed in Table 2. Compared to typical values in turbulent air flow (e.g., in a storm), appears to be somewhat larger in a granular flow. This effect is rather pronounced for large snow clods in fluidized flow; for strongly polydisperse fluidized flow, one might expect . However, no firm conclusions are possible at this stage because the flow configuration—confined vs. free-surface flow—may play a decisive role: Experiments with a confined dense granular flow around a cylinder [54] show . In contrast, in free-surface dense flows at Froude number [58]. Thus, Table 2 primarily highlights the need for further research and should not be used in practical applications.

Table 2.
Estimates of volumetric particle concentration , Knudsen number, Mach number and drag coefficient of a tree trunk in fluidized and suspension flow based on numerical results from [59]. For comparison, typical values of for a turbulent air flow and the experimental results of Hauksson et al. [58] for a free-surface flow with Froude number around a cylinder are also listed (Kn, Ma: our estimates).
The non-dense parts of the Vilan avalanche broke several young spruce trees (without uprooting them) near the surface of the new-snow cover; trunk diameters were up to 20 cm. Such trees are typically 7–10 m high in this climate zone. We cannot say with certainty whether the fluidized flow or the suspension flow or both combined broke the trees, but two circumstances indicate that the former at least played a role in this: (i) Some of the broken trees were fairly small so that they were not strongly exposed to the suspension flow. (ii) Powder-snow avalanches often break spruce trees several meters above the ground (as observed at Albristhorn and Scex Rouge). Gales in strong storms, having stagnation pressures of 1–2 kPa, can destroy mature spruce stands, whereas younger trees are much less affected because their smaller height exposes them to less pressure, due to the wind speed growing monotonically with height. In contrast, powder-snow avalanches exhibit a pressure peak a few meters above ground and thus exert a lesser torque on a tree than a storm with the same peak pressure. One may therefore assume that the minimum pressure required for breaking or uprooting a spruce tree will be in the range 3–10 kPa. If the suspension flow was that powerful, it would likely have caused more damage to the mature trees at the lateral trim lines and further down along the path. Moreover, if our rough estimate of the front speed of the fluidized part also applies to the suspension flow, the internal velocity near the ground may have been in the range 40–50 m s. A stagnation pressure of 10 kPa would then require a suspension-layer density of the order of 10 kg m. This seems to be a rather high value for this avalanche of limited size. For the fluidized flow to break small spruce trees, the pressure should have been somewhat higher still, say 10–30 kPa. The corresponding density estimate of 10–30 kg m appears more in line with the other observations.
The damage observed at Albristhorn allows more detailed estimates. The fact that most, but not all, trees on the river bank were felled, gives both a lower bound of approximately 2 kPa and an upper bound around 5 kPa on the local maximum stagnation pressure in the suspension layer, averaged over the time scales of turbulence, i.e., over times smaller than about 1 s. The suspension-layer pressure diminished steadily with distance from the river bank, the perimeter of the potential damage area ([I], Figure S9) corresponding approximately to the 1 kPa isobar of the turbulence-averaged pressure distribution. A pressure of 2–5 kPa at the river bank is also compatible with the limited damage on the ski lift shed. It would then appear more likely that the door was pushed in (together with its frame) by the fluidized flow rather than by the suspension flow.
Some limits on the pressure in the fluidized flow follow from the circumstance that the ski lift shed did not suffer structural damage, nor was it pushed from its foundation. It was constructed as a traditional wood-frame building and presumably had fairly high strength thanks to its small size. In addition, it was oriented at roughly 45° to the direction of the avalanche flow and therefore subjected to a normal load about half of the stagnation pressure. Under these conditions, we estimate the near-ground pressure to have been at most 10–20 kPa (averaged over a time interval of 0.1–1 s and over the height of the shed), but hardly less than 5 kPa since the door was destroyed.
We can use the values inferred above to estimate the contributions of both flow layers to the horizontal force and overturning moment exerted on a spruce tree if we make some additional assumptions: Consider a tree of height m (from the snow surface) with a trunk diameter m at breast height above ground. The canopy reaches from the tip to about 2 m above ground, and we assume it not to be affected by the intermediate-density layer with flow depth . We approximate the tree as a triangle with a base width m. The effective drag coefficient of the trunk in the fluidized flow is because the snow particles (which we assume to carry a large fraction of the momentum) are stopped at impact. The canopy in contrast, has a drag coefficient due both to its partial permeability to the flow and to the essentially air-like behavior of the flow with small particles. Finally, we assume that the suspension-flow pressure diminishes linearly from ground to a height of , . With these assumptions, we obtain
for the horizontal forces on the tree and
for the moments. With typical values m, m, m, , –20 kPa, and –5 kPa, we get –32 kN, –225 kN, –32 kN m, and –1940 kN m. Despite all simplifications and the uncertainty of the pressure values, it is clear that the suspension flow is chiefly responsible for the damage to the forest. However, the situation would be different for smaller trees or closer to the apex of the alluvial fan, where the pressure in the fluidized flow was substantially larger than 20 kPa.
In the case of the Scex Rouge avalanche, absence of damage to the cabins suggests that the stagnation pressure at Grande Moilles was less than 10 kPa and likely below 5 kPa. The fact that the telephone and power line poles were pulled out of the ground rather than broken indicates that the flow had a substantial vertical velocity component; this is indeed the case in the frontal vortex of the suspension flow, where the upward velocity component is of the same order as the horizontal one. We crudely estimate the stagnation pressure needed to pull wooden telephone line poles as follows: The weight of a pole is in the range 1–2 kN. As the pole is pulled out, there may be friction in the range 0–5 kN, thus the aerodynamic forces on the wires and pole should exceed 1–7 kN per pole. If there are n wires with diameter d and the poles are spaced a distance l apart, we estimate the pull-out force on one line segment as
with the drag coefficient of a long cylinder at high Reynolds number. It thus appears plausible that the frontal vortex of the suspension flow was able to pull the poles of the telephone line out of the ground. Where trees were broken selectively, the average pressure should be in the range 2–5 kPa, a little larger than in a very strong storm that produces resembling damage. While none of these estimates by itself is conclusive, combined they indicate that the pressure was 5–10 kPa at Grande Moilles and diminished to 2–5 kPa further to the north and along the sides of the suspension flow. If the fluidized flow was at most 1–2 m deep, values as high as 10–20 kPa for averaged impact pressure would be compatible with the absence of substantial damage to the cabins. After an ascent of about 100 m, we expect the velocity of the fluidized flow to have been no more than 15–25 m s, which would allow plausible densities up to 30–50 kg m.
We estimated the fluidized-flow impact pressures of the 10 February 1999 and 25 February 1999 avalanches at the observation bunker of Vallée de la Sionne as about 20 and 50–70 kPa, respectively, based on the damage to doors and shutters and the perceived sudden pressure rise inside the bunker [27]. Combining these values with the estimates of the front velocity, density ranges of 20–30 kg m and 30–50 kg m, respectively, result. These values are compatible with our inferences from the three observed avalanches.
5. Possible Fluidization Mechanisms
Next, we examine whether constraints on the transportation mode and travel distance of snow clods can be extracted from the observations. In this context, comparison with other types of gravity mass flows with air as the interstitial fluid, i.e., rock avalanches and pyroclastic flows, is helpful. We adopt the conclusion from the preceding subsection that the head of dry-snow avalanches is in the fluidized flow regime, which is 1–2 orders of magnitude denser than air. Hence, the snow particles are not in constant contact with each other and the effective stress vanishes. We also surmise that particles between 5 and 30 cm in diameter represent a substantial fraction of the mass in this regime and that they are present even 3–5 m above the bed–flow interface in large avalanches [9].
5.1. Aerodynamic Forces in the Head of the Suspension Layer
One conceivable mechanism to achieve and maintain fluidization is by aerodynamic forces exerted by the ambient air or the highly turbulent suspension flow. In such a scenario, we have to assume that a suspension flow containing sub-millimeter particles has already formed and that particle collisions in the dense core copiously eject centimeter to decimeter-scale particles. We then ask whether this low-density turbulent flow is capable of maintaining a significant mass of large particles in a fluidized state over an extended period. Note, however, that there is strong evidence for fluidized flow in small avalanches without a substantial suspension layer [28,60]; this implies that aerodynamic forces cannot be the sole mechanism capable of fluidizing a snow avalanche.
With densities in the range –600 kg m and drag coefficients –1, the snow particles in the intermediate-density flow have masses from 0.02–0.04 kg (5 cm) to 4–8 kg (30 cm) and free-fall velocities in the range –70 m s. In steep paths, the slope-normal component of is 20–40% smaller than these values. In addition, hindered settling effects are expected to be non-negligible for the volume concentrations in a fluidized flow. Even then, the settling velocities are substantially larger than the mean turbulent velocity fluctuations in the suspension layer, which we may expect to be less than 10 m s even in large powder-snow avalanches. However, in the frontal vortex of the suspension layer, the uplift velocity is similar to the front velocity and should be sufficient to keep large particles in the air for a short while and to transport small particles to the back of the vortex. The transport competence of powder-snow avalanches is demonstrated by the accidents mentioned by Shimizu et al. [2] as well as credible reports of persons who were transported above ground over distances of tens of meters in the suspension layer [61].
However, when it comes to keeping a substantial mass of snow clods in the air, energetic considerations are important as well. To set the scale, we first estimate the input power per unit footprint area supplied by gravity to the suspension layer:
with –10 kg m the mean suspension-layer density near the front, kg m the air density, –20 m the suspension-layer height, and –70 m s the depth-averaged flow speed. The main resistive force is due to air entrainment at the upper surface; the associated power loss can be estimated as
Here, we used estimates of the entrainment speed from laboratory experiments on density currents and videos of powder-snow avalanches, . In steep terrain, the ratio tends to be near the upper limit so that .
The suspension flow expends turbulent kinetic energy to keep the small snow particles in suspension. The associated turbulent power loss is
with kg m the density of ice, the depth-averaged volume concentration of particles in suspension, and their average settling velocity. If turbulence were to keep the fluidized layer afloat in the same way, turbulent kinetic energy would be consumed at a rate , assuming –100 kg m, –5 m, and –30 m s. However, the mean free path between collisions in the fluidized flow is only of the order of one to a few particle diameters so that the free fall velocity will never be attained. It is difficult to give a plausible estimate for , but it is likely about two orders of magnitude smaller than the value indicated above and thus of the same order of magnitude as ,
This loss of turbulence energy together with viscous dissipation must be offset by turbulence production through shear—not necessarily locally, but on average over the frontal vortex. We estimate the turbulence production rate very crudely as
where approximates the shear rate and is the friction drag coefficient. This estimate must be considered very uncertain, but it is encouraging that is (possibly much) smaller than and so that generation of that much turbulent energy is plausible. At the same time, , indicating that the suspension layer can be maintained until the late stage of the PSA. It remains open whether suspension-layer turbulence is energetically sufficient for keeping the intermediate-density flow fluidized. However, as mentioned above, observations of small to medium avalanches with a clear Type 2 deposit, but without a developed suspension layer (see the reports at [60] for more details) lead us to conclude that the turbulence of the suspension layer cannot be the sole mechanism behind maintaining fluidization.
At the front of the dense core, the stagnation pressure is , with the front velocity. On the top surface slightly behind the front, there is underpressure of similar magnitude. The pressure gradient across the front, of the order of or about 0.5–1 kPa m, causes air to flow through the voids between snow particles. On videos from flume experiments on sand-rich flows in water [62], one can directly see how water flow through the front fluidizes and partly suspends the head of the flow. In air, the concomitant drag is not strong enough to achieve fluidization of an extended volume by itself, but it can assist other fluidization mechanisms. However, this effect is limited to the very front of the avalanche.
5.2. Dispersive Pressure Due to Collisions between Snow Clods
If a granular material is rapidly sheared while the volume is held constant, the shear and normal stresses grow as the square of the shear rate. In contrast, unconstrained flows, e.g., free-surface flows on an inclined plane, expand and the stresses grow more slowly with the shear rate. Fluidization results if the collisional stress normal to the glide plane equals the overburden and the effective stress borne by persistent particle contacts vanishes. Laboratory experiments with dry granular materials over a rough, non-erodible inclined bed have revealed that stationary dense flows are possible only within a finite range of inclination angles, which depends on the flow depth [63]. At more gentle inclinations, the flow comes to a halt, while, on steeper slopes, it accelerates. The empirical rheology (see, e.g., [64] for a review) successfully captures many features of the dense flow regime:
The inertial number I is a non-dimensionalized shear rate, depending on the particle diameter d, the intrinsic particle density , the pressure P, and the strain rate tensor through its second invariant (note that summation over repeated indices is implied throughout this paper):
Typical values for monodisperse granular materials used in experiments are , –0.7, , , and . For dry snow, the values of and may be expected to be somewhat higher due to the irregular shape of snow grains and snow clods. The effective friction coefficient is seen to approach the value as , but Equation (18) limits the inertial number to . Experimental support for this saturation comes from the study of the front of steady granular flows where [65]. If or , the model precludes stationary solutions in accordance with experiment. However, the model has only been tested for inertial numbers and cannot be used to predict the properties of the flow regime that lies beyond stationary dense flow. The fluidized flow regime that we believe to occur in snow avalanches is characterized by volume concentrations .
There are two relevant inferences to be made from the granular-flow experiments: (i) Substantial sections of numerous avalanche paths are steeper than the maximum slope angle permitting stationary flow of granular materials. In these cases, the experiments on granular flows indicate that a flow-regime transition is unavoidable. Moreover, most experiments were carried out in a regime where aerodynamic forces play a minor role. One may conclude from this that dispersive pressure due to particle collisions alone is sufficient for inducing fluidization on very steep slopes. (ii) Fluidized flow of snow avalanches is, however, also observed on slopes well below the lower limit . This implies that additional mechanisms play an important role in fluidizing snow avalanches. Novel experiments on granular flows on long, steep slopes would help in elucidating the role of granular collisions in the fluidization process.
In [20], the well-known Norem–Irgens–Schieldrop (NIS) rheology [66] was extended in an attempt to model transitions between the dense and fluidized flow regimes. The NIS rheology combines Coulomb friction (describing the quasi-static regime) and dispersive stresses due to granular collisions, proportional to the square of the shear rate. In the original formulation, the density and the model coefficients are assumed to be constant. The extended model allows the particle concentration and thus the density to vary and models the concentration dependence of the coefficients for normal and shear dispersive stresses, and , after the results of the kinetic theory of granular media [67] and of discrete-element simulations [68], both in two dimensions. For simple shear in the x-z plane, the relevant tensor components are (note that compressive normal stresses are considered positive here):
In the dense regime, Issler and Gauer [20] assumed a fixed density , disregarding the density variation in Equation (18). At the bottom of an avalanche flow of depth h, . At the critical shear rate , the effective pressure vanishes, the flow becomes fully fluidized, and the original NIS model ceases to apply. With , one obtains the equilibrium value of from the condition . Fluidization was found to have a strong effect on the velocity and run-out distance, but the simulated degree of fluidization in selected study cases was significantly less than observed. Functional forms for derived from a three-dimensional kinetic model for dense flows of inelastic spheres [69] facilitate fluidization to some degree [70], but likely the degree of fluidization will still be lower than observed in dry-snow avalanches.
While this suggests that another mechanism favoring fluidization should be at work in mixed snow avalanches, one may argue that the extremely high mobility of some large rock avalanches (sturzstroms) implies complete fluidization at least of the base of such flows—presumably due to dispersive pressure from particle collisions—and that fluidization of mixed snow avalanches should then also be achievable in this way. There are, however, a few differences between these phenomena that appear to be relevant in this context: First, increased mobility of sturzstroms is observed only for release volumes above (e.g., [71], Figure 1), whereas fluidized snow avalanches with volumes as small as 1000 m have been observed [28]. Second, the coefficient of restitution is much higher for rock fragments than for snow clods. Third, the path of a rock avalanche tends to be much rougher than the smoothed top of the snow cover over which an avalanche flows. The ensuing collisions between rock fragments and terrain irregularities in the path are an efficient way to convert translational energy to fluctuation energy, which in turn facilitates fluidization of sturzstroms. Such an explanation, termed acoustic fluidization, has been proposed for large rock avalanches [71,72], but it is contingent on persistent inter-particle contacts, i.e., high density, and does not explain the intermediate-density regime of snow avalanches. There are two other plausible mechanisms specific to very large rock avalanches that facilitate fluidization, namely release of stored elastic energy during fracturing [73] and frictional vaporization of water in the overflowed soil or in cracks of the rocks [74]. In addition, note that the extraordinary mobility of pyroclastic flows (nuées ardentes) is attributed to degassing of tephra [75,76]—possibly aided by vaporization of the water in the soil—creating large pressure at the base of the flow.
In summary, the dispersive stresses from particle collisions are instrumental in fluidizing the avalanche head and maintaining it in this regime, but most likely they are not sufficient by themselves, except on very steep slopes. However, a more detailed analysis of this problem is called for.
5.3. Fluidization by Compression of the Snow Pack?
We briefly sketch a possible fluidization mechanism—specific to dry-snow avalanches—that was proposed recently [77]. A dry-snow avalanche typically exerts a normal stress in the range 0.5–5 kPa on the snow cover over which it flows. This load is applied suddenly and in conjunction with shear stresses of similar magnitude. Cold, dry new snow has a volumetric concentration below 0.2 and thus is highly contractive. As the top layers of the snow cover collapse, the pore air pressure rises to some fraction of the overburden (the rest is borne by grain contacts in the collapsing snow layer). Most of the compressed air will flow upwards through the avalanche, see Figure 6. In doing so, it exerts a normal stress on the avalanche that is a fraction of the excess pore pressure inside the snow cover. Thus, the upward air flow through the avalanche supports a fraction of the overburden inside the flow, which amounts to partial fluidization.
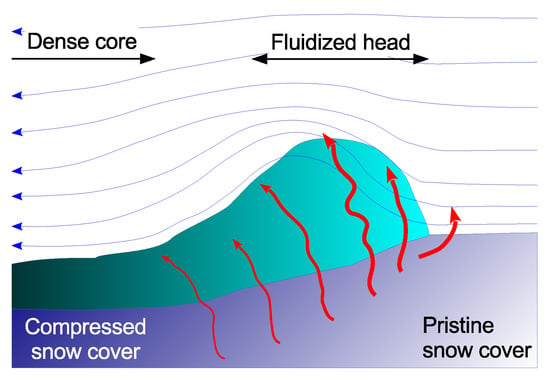
Figure 6.
Schematic representation of the proposed fluidization mechanism by air escaping from the snow cover under compression. The degree of shading indicates the relative densities. The ambient air flow around and partly through the avalanche head is also schematically indicated.
The fraction a varies along the avalanche path, decreasing with increasing density and depending also on the shape of the snow grains. b is less than 1 because the escaping air is accelerated to some degree. This acceleration in turn depends on the hydraulic conductivity of the avalanche body and thus on the density and particle size. There is a negative feed-back mechanism: As the avalanche density decreases, b diminishes and limits the density decrease.
The length of the fluidized part of the avalanche depends on how quickly the excess pore pressure dissipates. This process is governed on the one hand by the amount of compressed air, i.e., the depth of the new-snow layer, its density and compressive strength as well as the load from the avalanche. On the other hand, it depends on how easily the air can flow through the avalanche, thus on the pressure gradient and the hydraulic permeability. The latter in turn depends on the avalanche density and mean particle diameter. A preliminary estimate [77] yields dissipation times in the range 1–10 s for relatively soft snow packs. If this is confirmed, one may expect the fluidized head of avalanches to range from 10 to 500 m in length, in good agreement with what is observed. Similar to the dispersive pressure from particle collisions, the excess pore pressure by itself fails to achieve full fluidization, but the two mechanisms combined will likely succeed in many avalanches. However, the dynamical aspects and the dependence of a and b on the snow-cover and avalanche properties need to be understood quantitatively before firm conclusions can be drawn.
6. Inferences on Entrainment and Mass Balance
6.1. Entrainment by the Dense Flow
Despite large uncertainties, the mass balances of all three avalanches (Tables S1–S3 in the Supplementary Materials) show clearly that the dense flow eroded substantially—in some cases, all of the new snow along the trajectory that was left after passage of the fluidized flow.
Judging from photos taken from helicopter (Albristhorn, Figures S11 and S13) or from the counter-slope (Scex Rouge, Figure S18), we think that the dense flows of these two avalanches deposited little snow in the track, except perhaps along short, more gently inclined path segments. In contrast, the Vilan avalanche left a fairly uniform Type 1 deposit of considerable depth along the entire Däras gully, for a distance of close to 1 km. We did not closely investigate the distal end of the deposit, but it was not much deeper than 800 m upstream (Supplementary Materials, Figure S6). This implies that the deposition per unit area (i.e., the deposition rate integrated over the passage time) was nearly equal to the entrainment per unit area all along the channelized part of the path. The latter has an average inclination of about 20°. The detailed mass balance study of Sovilla et al. [78] at the Monte Pizzac site in northern Italy put the sequential occurrence of entrainment from the avalanche head and deposition from the tail at the same location in evidence. For those four events, the critical slope angle marking the upper limit for deposition was about 30. In the Vilan avalanche, this upper limit seems to have been between 20° and 30°, while the minimum slope angle for erosion was at most 20°.
We have not succeeded in determining the erosion mechanism(s) in the dense flows of the three avalanches described in the Supplementary Materials. In later field observations near Davos, Switzerland during the winters of 2004–2006, we found clear evidence for plowing erosion in some wet-snow avalanches [79] and continuous basal erosion in other wet-snow avalanches [29] (see [80] for a discussion of erosion mechanisms in snow avalanches). In dry-snow avalanches, we have not seen evidence for plowing, but we cannot exclude this mechanism either. All our observations are compatible with basal erosion (or perhaps ripping), but only in a single case did we find strong evidence for this mechanism: Topsoil was eroded in one small area in the track of a medium-size avalanche and could be traced in the deposits [28,81]. We found soil particles from several tens of meters downstream of the source area to a few tens of meters behind the distal end of the Type 1 deposit. Soil concentration was highest in an oblong area of the deposit, surrounded by a “halo” in which concentration diminished with distance. Incidentally, this also confirms that substantial mixing occurs in dense dry-snow avalanches.
6.2. Entrainment by the Fluidized Flow
At Albristhorn and Scex Rouge, our observations on the fluidized flow are limited to the run-out zone beyond the point where the dense flow stopped. At Vilan, however, we could study the fluidized deposit in the track part of the path. The two main observations are that: (i) the erosion depth varied between 0.7 m and all of the new snow (about 1 m); and (ii) at least in the surveyed area, erosion was followed by deposition. The area of strongest erosion was just below the upper bend of the Däras gully, after the fluidized flow had climbed up the gully bank. At the same location, at least as much snow was deposited, however. This indicates that there were substantial velocity or mobility differences even within the fluidized flow. There were also areas where 20–30% of the new-snow cover remained intact and the deposited snow mass was less than half of the mass eroded at the same location.
An interesting question for understanding and modeling the dynamics of fluidized flow is how far eroded snow travels on average: Long displacement would imply complete entrainment and strong mixing, while short displacement would indicate that the flow broke the snow cover at some level, e.g., along a weak layer, and dragged the eroded material some distance without truly incorporating it. The natural tracers provided by needles and twigs stripped from overflowed spruce trees in the path might have allowed such a study, but we were not yet aware of the interest of this question and also lacked time. However, the tracers in the snow pits P and P (see the Supplementary Materials, Section S2) could not come from the immediate vicinity. The random embedding of snow clods also points towards thorough mixing in the flow and a relatively long travel distance of eroded snow.
The fluidized flow in the much larger avalanches at Albristhorn and Scex Rouge eroded a (presumably harder) snow cover to a similar degree in the run-out zone on level or upwards sloping terrain. We may very roughly estimate the mean erosion rates for the three events if we make reasonable assumptions about the length, , and mean speed, , of (the eroding part of) the fluidized flows. Our assumptions and the resulting erosion rates are listed in Table 3.

Table 3.
Assumptions about the properties of the fluidized flows of the Vilan avalanche near the gully bend and the Albristhorn and Scex Rouge avalanches in the run-out zone (counter-slope, ↑) with Type 2 deposit, and the resulting mean erosion rates.
A first-order estimate of the entrainment capacity of a gravity mass flow is [82,83]
where (kg m s) is the erosion rate, is the depth-averaged flow speed, is the bed shear stress, (Pa) is the gravitational traction along the slope, and is the characteristic shear strength of the bed. This formula assumes that the flow speed is approximately constant and known. Clearly, the second approximate equality does not apply on a counter-slope; erosion during up-hill motion is also possible (and has been observed many times) as long as . For the Vilan avalanche, the erosion rate estimated in Table 3 requires in the range 0.3–1.5 kPa. We expect in the range 0.5–1 kPa, hence kPa. Only values near the lower limit of this range appear realistic for an avalanche of this size, e.g., , kg m. As with many other estimates in this paper, the uncertainty is very large, but useful bounds on the flow parameters emerge.
On the basis of data from profiling radar (see ([45] Figure 3), [46], and ([16] Figure 8b)), near-front erosion rates of 100–330 kg m s at Vallée de la Sionne are inferred. The front velocity ranged from 40 m s to about 70 m s. To fully entrain such massive amounts of snow, momentum conservation would require the frontal region of these avalanches to have an average gravitational traction of more than 5–15 kPa, depending on the event. On a slope of approximately 30°, this would require the avalanche to have a mass per unit footprint area of 1000–3000 kg m. These numbers are in clear disagreement with the measurements of flow depth and average pressure. The immediate conclusion is that the profiling radar measures, not the entrainment rate, but the erosion rate, i.e., the rate at which the texture of the snow cover is destroyed. The eroded mass is then only gradually set in motion and entrained by the avalanche.
This elementary application of momentum conservation to solid experimental data should have important consequences for the modeling of entrainment in numerical avalanche models. In the earliest continuum avalanche model, Eglit [84] modeled snow entrainment as a shock at the front, with the entrainment depth set beforehand by the user. If observed values of erosion depth and front velocity are assumed, the (dense) avalanche front must be unrealistically high to create the hydrostatic pressure gradient that is needed to accelerate the eroded snow across the shock front. Similar problems plague present-day models as well. See [83] for a theoretical analysis of the constraints imposed on models of erosion by scour.
6.3. Entrainment by the Suspension Flow
At Albristhorn, we were able to access the area of Type 3 deposit on the counter-slope. Beyond the Type 2 deposit, the deposited layer was only a few centimeters thick, implying that the sedimentation rate was low. We could not find evidence for erosion underneath the deposit, but our observations only exclude erosion depths of 0.1 m or more. On the basis of the visual appearance of the Type 3 deposit, we believe that erosion by plowing, ripping or eruption [85,86] can be excluded, and a generous upper limit for erosion by scour is 1 kg m s in this event on the counter-slope.
One should indeed expect the suspension flow to erode under the conditions that prevailed during the event. Near the ground, the pure suspension flow is then similar to blowing snow. From Figure 4 in [87], one can infer erosion rates of the order of kg m s for a particle-free strong breeze blowing over a level snow surface. The suspension layer is significantly faster and contains snow grains that are highly effective in ejecting snow grains from the snow cover upon impact. Erosion rates near the upper limit from our estimations therefore appear plausible.
7. Conclusions
Our study exemplifies how one may arrive at reasonably firm conclusions about important mechanisms in avalanche flow despite many ambiguities and large uncertainties in the underlying data. The key is to combine observations of different aspects of the same avalanche event and to apply simple physical reasoning to rule out alternative interpretations of the data or narrow down the ranges of flow variables. Our estimates are fraught with large uncertainties individually, but, when taken together, they reveal a coherent picture that is also supported by recent experimental findings [12,16]. Cross-comparison of estimates from different events may also increase the credibility of these inferences.
Some of the results that we believe to be novel are the bounds on the density of the suspension flow and the velocity of the fluidized flow from the run-up heights and the inference that the largest frontal entrainment rates inferred from profiling radar data [46,88] should be interpreted as erosion rates, while the corresponding entrainment rates often must be significantly smaller. Moreover, it seems that such a clear distinction between deposit types in mixed dry-snow avalanches and their association with different flow regimes has not been demonstrated in the literature yet. Another valuable result is that several avalanches had fluidized-layer densities in the same range of 30–100 kg m, which is compatible with the grain inertia regime of granular flows and experimental measurements.
Field observations such as ours cannot substitute for dedicated experiments at well-equipped test sites. However, those experiments are difficult, expensive, and limited to a few sites worlwide. Results of practical value as well as additional insight into the importance, variability, or scaling behavior of different processes can be gained by comparing avalanches from a larger number of sites, which comprise a wider range of path characteristics. The analysis methods of our study will need to be modified or supplemented by other types of estimates when analyzing other avalanche events. The examples presented may, however, serve as an indication as to which observations will be valuable and that one should approach the field work and the subsequent analysis from the perspective of the open flow-mechanical questions.
Supplementary Materials
A document describing the field observations of the three avalanches in detail can be accessed online at https://www.mdpi.com/2076-3263/10/1/2/s1.
Author Contributions
All authors participated in one or more of the field investigations. D.I. developed and applied the analysis methods and wrote the original report as well as the present text. D.I., P.G., and M.S. collaborated on the development of the concept of an intermediate flow regime. M.S. digitized the photographs, and he and P.G. created the figures and maps. P.G., M.S., and S.K. critically reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
Early work laying the ground for this paper was carried out while all authors were employed by the WSL Institute for Snow and Avalanche Research SLF. Later work was funded by the Swiss National Science Foundation (grant 200021-101911, 2004–2006) and the European Commission (5th Framework Programme, project SATSIE, EVG1-CT2002-00059, 2002–2006). A sabbatical fellowship from NGI to D.I. in 2014 allowed most of the analysis work to be completed. The final phase of the write-up was funded by the special grant for snow avalanche research from the Norwegian Ministry of Petroleum and Energy, administrated by the Directorate of Water Resources and Energy, and NGI’s general research grant from the Research Council of Norway.
Acknowledgments
D.I. thanks the Soil Dynamics Group at the Port and Airport Research Institute in Yokosuka, Japan, for their warm hospitality during his sabbatical leave, where much of this paper was written. We are grateful to numerous colleagues who helped us shape our view of the dynamics of snow avalanches through enjoyable discussions, in particular M. Barbolini, D. Berzi, M. E. Eglit, J.-T. Fischer, H. Gubler, F. Hermann, K. Hutter, F. Irgens, J. T. Jenkins, the late K. Lied, J. N. McElwaine, the late A. Moe, D. Mohrig, M. Naaim, H. Norem, J. Rajchenbach, F. Sandersen, B. Sovilla, and B. Teufen. D.I. furthermore thanks A. Errera, H. Gubler, B. Krummenacher, S. Priano and B. Teufen for their contributions to the field observations during 2004–2006 that were most useful in the present context. We are grateful to two anonymous reviewers for their careful reading of the manuscript and Supplementary Materials and their insightful comments, which have improved this paper.
Conflicts of Interest
The authors declare no conflict of interest. The funding agencies had no role in the design of the study or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Energy Balance of a Suspension Flow on a Counter-Slope
The main text obtains upper bounds on the mean particle concentration, , in the suspension layer at the lowest point of its trajectory from the run-up heights H and the initial and final mean velocities, and . Here, we derive Equation (4) from energy conservation and discuss the simplifying assumptions it contains.
Consider the energy balance of a suspension flow ascending a counter-slope, with z being the altitude. It is often observed that , where denotes the suspended snow mass and the velocity at the lowest point. This does not contradict energy conservation because the (neutrally buoyant) air inside the avalanche does not require net energy input during the ascent, but some of its kinetic energy is converted into potential energy of the snow particles in the process. Conversely, if H and are observed, an upper limit on the initial particle concentration in the flow can be derived from energy conservation. Effects complicating the energy balance are bed friction, turbulence, and the vortical motion of the head, entrainment and deposition of snow particles along the slope, and air entrainment. For simplicity, we neglect bed friction, thermal effects on buoyancy, and the generation of turbulence by shear in our simple estimate. Including them would lead to a more stringent upper bound on particle concentration.
At the valley bottom, the suspension flow, consisting of snow with mass and air with mass , has potential energy and translational kinetic energy . In addition, there is kinetic energy associated with the vortical motion of the head. Laboratory measurements [51] indicate that the velocity (in a reference frame fixed to the terrain) is close to 0 at the upper surface of the suspension layer and close to twice the average velocity near the bottom. This indicates that the stress due to turbulent entrainment of air is considerably larger than the bed shear stress—in contrast to dense flows, which tend to exhibit conveyor-belt-like motion. If the head vortex resembles a rigid rotation of a cylindrical body, its angular velocity is , h being the height of the cloud and u the local depth-averaged velocity. Integration of the kinetic energy of vortical motion gives . If the front vortex encompassed the entire cloud, would result; in a real avalanche, we expect . The total energy at the valley floor then becomes
During the ascent, the air mass increases to while the snow mass typically decreases due to deposition at a variable rate , hence . In some cases, can be obtained from field measurements. We set and and obtain the total potential energy of the suspended and deposited snow mass at the end of the ascent as
The value of B ranges from 0 to 1 and depends strongly on the situation.
The suspension layer often incorporates a large amount of air as it impacts the counter-slope and ascends, but again we have limited knowledge of the magnitude of this effect and simply write ; typical values of C might be in the range 3–10, increasing with H. The kinetic energy is written analogously to Equation (A1) as
The growth of the snow cloud raises the center-of-mass of the snow relative to the ground by some amount , but we neglect this effect.
A more important process is particle settling—it consumes turbulence energy, which in turn is replenished from translational kinetic energy via shear stresses generating turbulence. We assume the total turbulent energy in the cloud to remain approximately constant and estimate the contribution from settling as in terms of the mean particle settling speed and the ascent time ; here, is the mean front speed during the ascent and is the mean slope angle. We can absorb this term in the potential-energy term by replacing H by . Combining all elements, we obtain
Next, we express the masses in terms of the initial cloud volume , the volumetric particle concentration at the valley bottom, and the intrinsic densities of ice, kg m, and air, kg m, as and . Equating and , we arrive at
For the situation we consider, both the numerator and the denominator have to be positive. If multiplied by , the numerator represents the kinetic energy density of air converted into potential energy of the snow particles. Multiplied by the same factor, the denominator is the part of the potential energy (per unit volume of solid ice) that is not supplied by the kinetic energy of the snow. The resulting limit on tends to be small, i.e., the suspension layer is dilute and in or near the Boussinesq regime.
Incidentally, Equation (A5) may also describe another regime where both the numerator and the denominator are negative. In this case, air ingestion is so strong that a part of the snow kinetic energy must be used to accelerate the entrained air. Such a situation may occur during the formation of the powder-snow cloud (with ) or on relatively gentle counter-slopes combined with an obstacle (e.g., a catching dam) that intensifies turbulent mixing; furthermore, should be fairly large so that the flow is in the non-Boussinesq regime.
Typically, one has . The value of C is very uncertain, but, if can be estimated, is the upper bound in the dilute regime and the lower bound in the non-dilute regime. For avalanches with , the main uncertainty in evaluating Equation (A5) is due to the cloud growth factor C. The formula will not give meaningful results if the numerator of the second fraction on the right-hand side, , is significantly smaller than the denominator.
References
- Schaerer, P.A.; Salway, A.A. Seismic and impact-pressure monitoring of flowing avalanches. J. Glaciol. 1980, 26, 179–187. [Google Scholar] [CrossRef][Green Version]
- Shimizu, H.; Huzioka, E.; Akitaya, E.; Narita, H.; Nakagawa, M.; Kawada, K. A study on high-speed avalanches in the Kurobe canyon, Japan. J. Glaciol. 1980, 26, 141–151. [Google Scholar] [CrossRef][Green Version]
- McClung, D.M.; Schaerer, P.A. Characteristics of flowing snow and avalanche impact pressures. Ann. Glaciol. 1985, 6, 9–14. [Google Scholar] [CrossRef]
- Gubler, H.; Hiller, M.; Klausegger, G.; Suter, U. Messungen an Fliesslawinen. Zwischenbericht 1986; Mittlg. No. 41; Institut für Schnee- und Lawinenforschung: Davos, Switzerland, 1986. (In German) [Google Scholar]
- Norem, H. Discussion on the modelling of snow avalanche flow. In Proceedings of the Workshop on Avalanche Dynamics, Davos, Switzerland, 14–18 May 1990; Gubler, H.U., Ed.; Mittlg. No. 48. Institut für Schnee- und Lawinenforschung: Davos, Switzerland, 1991; pp. 57–72. [Google Scholar]
- Hopfinger, E.J. Snow avalanche motion and related phenomena. Annu. Rev. Fluid Mech. 1983, 15, 47–76. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Hutter, K. Avalanche Dynamics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Issler, D.; Gauer, P.; Schaer, M.; Keller, S. Staublawinenereignisse im Winter 1995: Seewis (GR), Adelboden (BE) und Col du Pillon (VD); SLF Internal Report 694; Institut für Schnee- und Lawinenforschung: Davos, Switzerland, 1996. (In German) [Google Scholar]
- Schaer, M.; Issler, D. Particle densities, velocities, and size distributions in large avalanches from impact-sensor measurements. Ann. Glaciol. 2001, 32, 321–327. [Google Scholar] [CrossRef]
- Sovilla, B.; Schaer, M.; Rammer, L. Measurements and analysis of full-scale avalanche impact pressure at the Vallée de la Sionne test site. Cold Reg. Sci. Technol. 2008, 51, 122–137. [Google Scholar] [CrossRef]
- Sovilla, B.; Schaer, M.; Kern, M.; Bartelt, P. Impact pressures and flow regimes in dense snow avalanches observed at the Valléée de la Sionne test site. J. Geophys. Res. 2008, 113, F01010. [Google Scholar] [CrossRef]
- Sovilla, B.; McElwaine, J.N.; Louge, M.Y. The structure of powder snow avalanches. C. R. Phys. 2015, 16, 97–104. [Google Scholar] [CrossRef]
- Köhler, A.; McElwaine, J.N.; Sovilla, B.; Ash, M.; Brennan, P. Surge dynamics of the 3 February 2015 avalanches in Vallée de la Sionne. J. Geophys. Res. 2016, F121, 2192–2210. [Google Scholar] [CrossRef]
- Köhler, A.; McElwaine, J.N.; Sovilla, B. GEODAR data and the flow regimes of snow avalanches. J. Geophys. Res. 2018, F123, 1272–1294. [Google Scholar] [CrossRef]
- Gauer, P.; Issler, D.; Lied, K.; Kristensen, K.; Iwe, H.; Lied, E.; Rammer, L.; Schreiber, H. On full-scale avalanche measurements at the Ryggfonn test site, Norway. Cold Reg. Sci. Technol. 2007, 49, 39–53. [Google Scholar] [CrossRef]
- Gauer, P.; Issler, D.; Lied, K.; Kristensen, K.; Sandersen, F. On snow avalanche flow regimes: Inferences from observations and measurements. In Proceedings of the International Snow Science Workshop ISSW ’08, Whistler, BC, Canada, 21–27 September 2008; pp. 717–723. [Google Scholar]
- Salm, B.; Gubler, H. Measurement and analysis of the motion of dense flow avalanches. Ann. Glaciol. 1985, 6, 26–34. [Google Scholar] [CrossRef]
- Gubler, H. Comparison of three models of avalanche dynamics. Ann. Glaciol. 1989, 13, 82–89. [Google Scholar] [CrossRef]
- Norem, H.; Irgens, F.; Schieldrop, B. A continuum model for calculating snow avalanche velocities. In Proceedings of the Davos Symposium, Avalanche Formation, Movement and Effects, Davos Switzerland, 14–19 September 1986; Salm, B., Gubler, H., Eds.; IAHS Press: Wallingford, UK, 1987; Volume 162, pp. 363–380. [Google Scholar]
- Issler, D.; Gauer, P. Exploring the significance of the fluidized flow regime for avalanche hazard mapping. Ann. Glaciol. 2008, 49, 193–198. [Google Scholar] [CrossRef]
- Issler, D. Modelling of snow entrainment and deposition in powder-snow avalanches. Ann. Glaciol. 1998, 26, 253–258. [Google Scholar] [CrossRef]
- Sampl, P.; Zwinger, T. Avalanche simulation with SAMOS. Ann. Glaciol. 2004, 38, 393–398. [Google Scholar] [CrossRef]
- Keshari, A.K.; Satapathy, D.P.; Kumar, A. The influence of vertical density and velocity distributions on snow avalanche runout. Ann. Glaciol. 2010, 51, 200–206. [Google Scholar] [CrossRef]
- Bartelt, P.; Meier, L.; Buser, O. Snow avalanche flow-regime transitions induced by mass and random kinetic energy fluxes. Ann. Glaciol. 2011, 52, 159–164. [Google Scholar] [CrossRef]
- Bartelt, P.; Bühler, Y.; Buser, O.; Christen, M.; Meier, L. Modeling mass-dependent flow regime transitions to predict the stopping and depositional behavior of snow avalanches. J. Geophys. Res. 2012, 117, F01015. [Google Scholar] [CrossRef]
- Issler, D.; Jenkins, J.T.; McElwaine, J.N. Comments on avalanche flow models based on extensions of the concept of random kinetic energy. J. Glaciol. 2018, 64, 148–164. [Google Scholar] [CrossRef]
- Gruber, U.; Bartelt, P.; Dufour, F.; Sovilla, B.; Kern, M.; Hiller, M.; Zimmerli, M. Zwischenbericht Vallée de la Sionne 1998/1999; SLF Internal Report 702; Swiss Federal Institute for Snow and Avalanche Research: Davos, Switzerland, 2002. [Google Scholar]
- Issler, D.; Errera, A.; Priano, S.; Gubler, H.; Teufen, B.; Krummenacher, B. Inferences on flow mechanisms from snow avalanche deposits. Ann. Glaciol. 2008, 49, 187–192. [Google Scholar] [CrossRef][Green Version]
- Issler, D.; Gubler, H. Dorfberg-Lawine (Davos Dorf), 20.03.2005/Dorfberg Avalanche (Davos Dorf), 20 March 2005. Available online: http://snf.ngi.no/dorfberg.050320.html (accessed on 31 October 2019).
- Issler, D.; Gubler, H. Salezertobel-Lawine (Davos Dorf), ca. 10.02.2005 / Salezertobel avalanche (Davos Dorf), around 10 February 2005. Available online: http://snf.ngi.no/salezertobel.050213.html (accessed on 31 October 2019).
- Issler, D.; Gubler, H.; Teufen, B. Trockenschneelawine auf der Inneralp (Monstein), 21.02.2004/Dry-Snow Avalanche at Inneralp (Monstein) on February 21, 2004. Available online: http://snf.ngi.no/inneralp.040224.html (accessed on 31 October 2019).
- Issler, D.; Errera, A. Gotschnawang-Lawine, 2006-03-12/Avalanche at Gotschnawang. 12 March 2006. Available online: http://snf.ngi.no/gotschnawang.060312.html (accessed on 31 October 2019).
- Mellor, M. Engineering properties of snow. J. Glaciol. 1977, 19, 15–66. [Google Scholar] [CrossRef]
- Steinkogler, W.; Gaume, J.; Löwe, H.; Sovilla, B.; Lehning, M. Granulation of snow: From tumbler experiments to discrete element simulations. J. Geophys. Res. 2015, F120, 1107–1126. [Google Scholar] [CrossRef][Green Version]
- Priano, S.; Errera, A.; Issler, D. The Rüchitobel Avalanche (Dischma Valley) of 18 January 2006. Available online: http://snf.ngi.no/reports/report_Ruechitobel_2006-01-18.pdf (accessed on 31 October 2019).
- Fischer, J.T.; Kaitna, R.; Heil, K.; Reiweger, I. The heat of the flow—Thermal equilibrium in gravitational mass flow. Geophys. Res. Lett. 2018, 45, 11219–11226. [Google Scholar] [CrossRef]
- Gauer, P.; Kristensen, K. Four decades of observations from NGI’s full-scale avalanche test site Ryggfonn—Summary of experimental results. Cold Reg. Sci. Technol. 2016, 125, 162–176. [Google Scholar] [CrossRef][Green Version]
- McClung, D.M. Superelevation of flowing avalanches around curved channel bends. J. Geophys. Res. 2001, 106, 16489–16498. [Google Scholar] [CrossRef]
- Issler, D. Dynamical Aspects of the 2017 Rigopiano Avalanche; NGI Technical Note 20170131-08-TN; Norwegian Geotechnical Institute: Oslo, Norway, 2019. [Google Scholar]
- Gauer, P. Comparison of avalanche front velocity measurements and implications for avalanche models. Cold Reg. Sci. Technol. 2014, 97, 132–150. [Google Scholar] [CrossRef]
- McClung, D.M.; Gauer, P. Maximum frontal speeds, alpha angles and deposit volumes of flowing snow avalanches. Cold Reg. Sci. Technol. 2018, 153, 78–85. [Google Scholar] [CrossRef]
- Rammer, L.; Kristensen, K.; Lied, K.; Schreiber, H.; Randeu, W.L. Radar measurements of snow avalanche full scale experiment in Ryggfonn. In 25 Years of Snow Avalanche Research, Voss, 12–16 May 1998; Hestnes, E., Ed.; Norges Geotekniske Institutt: Oslo, Norway, 1998; pp. 215–219. [Google Scholar]
- Gauer, P.; Kern, M.; Kristensen, K.; Lied, K.; Rammer, L.; Schreiber, H. On pulsed Doppler radar measurements of avalanches and their implication to avalanche dynamics. Cold Reg. Sci. Technol. 2007, 50, 55–71. [Google Scholar] [CrossRef]
- Gubler, H.; Hiller, M. The use of microwave FMCW radar in snow and avalanche research. Cold Reg. Sci. Technol. 1984, 9, 109–119. [Google Scholar] [CrossRef]
- Issler, D. Experimental information on the dynamics of dry-snow avalanches. In Dynamic Response of Granular and Porous Materials under Large and Catastrophic Deformations; Lecture Notes in Applied and Computational Mechanics; Hutter, K., Kirchner, N., Eds.; Springer: Berlin, Germany, 2003; Volume 11, pp. 109–160. [Google Scholar] [CrossRef]
- Sovilla, B. Field Experiments and Numerical Modelling of Mass Entrainment and Deposition Processes in Snow Avalanches. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2004. [Google Scholar] [CrossRef]
- Lied, K.; Bakkehøi, S. Empirical calculations of snow-avalanche run-out distance based on topographic parameters. J. Glaciol. 1980, 26, 165–177. [Google Scholar] [CrossRef][Green Version]
- Lied, K.; Moe, A.; Kristensen, K.; Issler, D. Ryggfonn. Full scale avalanche test site and the effect of the catching dam. Snow and avalanches test sites—Sites expérimentaux dédiés à l’étude de la neige et des avalanches. In Proceedings of the International Seminar on Snow and Avalanches Test Sites in the Memory of Philippe Revol, Grenoble, France, 22–23 November 2001; Naaim, M., Naaim-Bouvet, F., Eds.; Cemagref Editions: Antony, France, 2004; pp. 25–98. [Google Scholar]
- Gauer, P. Estimates on the reach of the powder part of avalanches. In Proceedings of the International Snow Science Workshop, Innsbruck, Austria, 7–12 October 2018; pp. 815–819. Available online: http://arc.lib.montana.edu/snow-science/objects/ISSW2018_P08.23.pdf (accessed on 31 October 2019).
- Beghin, P.; Olagne, X. Experimental and theoretical study of the dynamics of powder snow avalanches. Cold Reg. Sci. Technol. 1991, 19, 317–326. [Google Scholar] [CrossRef]
- Keller, S. Measurements of powder snow avalanches—Laboratory. Surv. Geophys. 1995, 16, 661–670. [Google Scholar] [CrossRef]
- Gauer, P.; Lied, K.; Kristensen, K. On avalanche measurements at the Norwegian full-scale test-site Ryggfonn. Cold Reg. Sci. Technol. 2008, 51, 138–155. [Google Scholar] [CrossRef]
- Sovilla, B.; Kern, M.; Schaer, M. Slow drag in wet-snow avalanche flow. J. Glaciol. 2010, 56, 587–592. [Google Scholar] [CrossRef]
- Chehata, D.; Zenit, R.; Wassgren, C.R. Dense granular flow around an immersed cylinder. Phys. Fluids 2003, 15, 1522–1531. [Google Scholar] [CrossRef]
- Jóhannesson, T. Run-up of two avalanches on the deflecting dams at Flateyri, northwest Iceland. Ann. Glaciol. 2001, 32, 350–354. [Google Scholar] [CrossRef]
- Tai, Y.C.; Gray, J.M.N.T.; Hutter, K.; Noelle, S. Flow of dense avalanches past obstructions. Ann. Glaciol. 2001, 32, 281–284. [Google Scholar] [CrossRef]
- Hákonardóttir, K.M.; Hogg, A.J. Oblique shocks in rapid granular flows. Phys. Fluids 2005, 17, 177101. [Google Scholar] [CrossRef]
- Hauksson, S.; Pagliardi, M.; Barbolini, M.; Jóhannesson, T. Laboratory measurements of impact forces of supercritical granular flow against mast-like obstacles. Cold Reg. Sci. Technol. 2007, 49, 54–63. [Google Scholar] [CrossRef]
- Wassgren, C.R.; Cordova, J.A.; Zenit, R.; Karion, A. Dilute granular flow around an immersed cylinder. Phys. Fluids 2003, 15. [Google Scholar] [CrossRef]
- Issler, D. Feldarbeiten/Measurement Campaigns 2004–2006. Available online: http://snf.ngi.no/kampagnen.html (accessed on 31 October 2019).
- Förster, M. Ausführliche Dokumentation ausgewählter Staublawinenereignisse und Bestimmung ihrer Eingangsparameter für die Verifikation von Staublawinenmodellen; SLF Internal Report 730; Institut für Schnee- und Lawinenforschung (SLF): Davos, Switzerland, 1999. [Google Scholar]
- Ilstad, T.; Marr, J.G.; Elverhø i, A.; Harbitz, C.B. Laboratory studies of subaqueous debris flows by measurements of pore-fluid pressure and total stress. Mar. Geol. 2004, 213, 403–414. [Google Scholar] [CrossRef]
- Pouliquen, O. Scaling laws in granular flows down rough inclined planes. Phys. Fluids 1999, 11, 542–548. [Google Scholar] [CrossRef]
- Forterre, Y.; Pouliquen, O. Granular Flows. Seminaire Poincaré 2009, XIII, 69–100. [Google Scholar]
- Pouliquen, O. On the shape of granular fronts down rough inclined planes. Phys. Fluids 1999, 11, 1956–1958. [Google Scholar] [CrossRef]
- Norem, H.; Irgens, F.; Schieldrop, B. Simulation of snow-avalanche flow in run-out zones. Ann. Glaciol. 1989, 13, 218–225. [Google Scholar] [CrossRef][Green Version]
- Pasquarell, G.C.; Ackermann, N.L.; Shen, H.H.; Hopkins, M.A. Collisional stress in granular flows: Bagnold revisited. J. Eng. Mech. 1988, 114, 59–64. [Google Scholar] [CrossRef]
- Campbell, C.S.; Gong, A. The stress-tensor in a two-dimensional granular shear flow. J. Fluid Mech. 1986, 164, 107–125. [Google Scholar] [CrossRef]
- Jenkins, J.T.; Berzi, D. Dense inclined flows of inelastic spheres: Tests of an extension of kinetic theory. Gran. Matter 2010, 12, 151–158. [Google Scholar] [CrossRef]
- Jenkins, J.T.; (Cornell University, Ithaca, NY, USA); Berzi, D.; (Politecnico di Milano, Milano, Italy). Personal communication. 2013. [Google Scholar]
- Collins, G.S.; Melosh, H.J. Acoustic fluidization and the extraordinary mobility of sturzstroms. J. Geophys. Res. 2003, 108, 2473. [Google Scholar] [CrossRef]
- Melosh, H.J. Acoustic fluidization. Am. Sci. 1983, 71, 158–165. [Google Scholar] [PubMed]
- Davies, T.R.; McSaveney, M.J. The role of rock fragmentation in the motion of large landslides. Eng. Geol. 2009, 109, 67–79. [Google Scholar] [CrossRef]
- De Blasio, F.V. Production of frictional heat and hot vapour in a model of self-lubricating landslides. Rock Mech. Rock Eng. 2008, 41, 219–226. [Google Scholar] [CrossRef]
- Sparks, R.S.J. Gas release rates from pyroclastic flows: An assessment of fluidization in their emplacement. Bull. Volcanol. 1978, 41, 1–9. [Google Scholar] [CrossRef]
- Gueugneau, V.; Kelfoun, K.; Roche, O.; Chupin, L. Effects of pore pressure in pyroclastic flows: Numerical simulation and experimental validation. Geophys. Res. Lett. 2017, 44, 2194–2202. [Google Scholar] [CrossRef]
- Issler, D. Notes on Fluidization of Snow Avalanches by Air Expulsion From the Snow Cover; NGI Technical Note 20140053-03-TN_rev0; Norwegian Geotechnical Institute: Oslo, Norway, 2017. [Google Scholar]
- Sovilla, B.; Sommavilla, F.; Tomaselli, A. Measurements of mass balance in dense snow avalanche events. Ann. Glaciol. 2001, 32, 230–236. [Google Scholar] [CrossRef]
- Issler, D.; Teufen, B. Nassschneelawine im Breitzug (Davos Glaris), 13.01.2004/Wet-Snow Avalanche in the Breitzug Gully (Davos Glaris) on 13 January 2004. Available online: http://snf.ngi.no/breitzug.040113.html (accessed on 31 October 2019).
- Gauer, P.; Issler, D. Possible erosion mechanisms in snow avalanches. Ann. Glaciol. 2004, 38, 384–392. [Google Scholar] [CrossRef]
- Priano, S.; Errera, A.; Issler, D.; Gubler, H. Avalanche in Sertig Valley on February 21, 2006. Available online: http://snf.ngi.no/reports/report_Sertig_2006-02-21.pdf (accessed on 31 October 2019).
- Issler, D.; Jóhannesson, T. Dynamically Consistent Entrainment and Deposition Rates in Depth-Averaged Gravity Mass Flow Models; NGI Technical Note 20110112-01-TN; Norwegian Geotechnical Institute: Oslo, Norway, 2011. [Google Scholar] [CrossRef]
- Issler, D. Dynamically consistent entrainment laws for depth-averaged avalanche models. J. Fluid Mech. 2014, 759, 701–738. [Google Scholar] [CrossRef]
- Eglit, M.E. Teoreticheskie podkhody k raschetu dvizheniia snezhnyk lavin. (Theoretical approaches to avalanche dynamics). Itogi Nauki. Gidrologiia Sushi. Gliatsiologiia 1967, 69–97, (In Russian. English translation in: Soviet Avalanche Research – Avalanche Bibliography Update: 1977–1983. Glaciological Data Report GD–16, pages 63–116. World Data Center A for Glaciology [Snow and Ice], 1984.). [Google Scholar]
- Louge, M.Y.; Carroll, C.S.; Turnbull, B. Role of pore pressure gradients in sustaining frontal particle entrainment in eruption currents: The case of powder snow avalanches. J. Geophys. Res. 2011, 116, 002065. [Google Scholar] [CrossRef]
- Carroll, C.S.; Louge, M.Y.; Turnbull, B. Frontal dynamics of powder snow avalanches. J. Geophys. Res. 2013, 118, 913–924. [Google Scholar] [CrossRef]
- Takeuchi, M. Vertical profile and horizontal increase of drift-snow transport. J. Glaciol. 1980, 26, 481–492. [Google Scholar] [CrossRef][Green Version]
- Sovilla, B.; Burlando, P.; Bartelt, P. Field experiments and numerical modeling of mass entrainment in snow avalanches. J. Geophys. Res. 2006, 111, F03007. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).