Vaccination Is a Suitable Tool in the Control of Aujeszky’s Disease Outbreaks in Pigs Using a Population Dynamics P Systems Model
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethical Statement
2.2. Farm Structure and Management Procedures
2.3. Population Dynamics P System (PDP) Model
2.4. Epidemiological Scenarios for Aujeszky Virus
2.5. Economic Impact
2.6. Statistical Analyses
3. Results
3.1. Descriptive Results
3.2. GLM Model
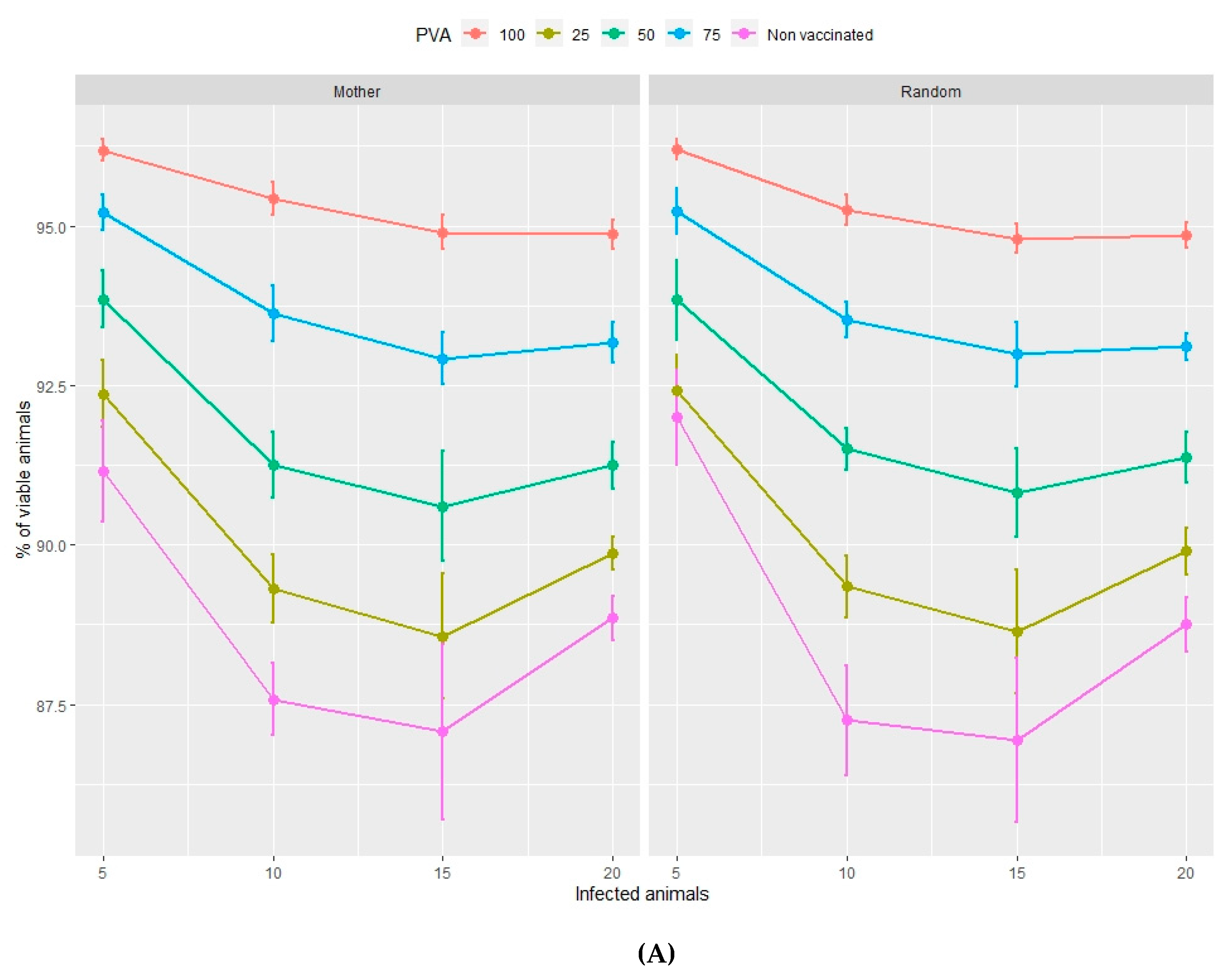
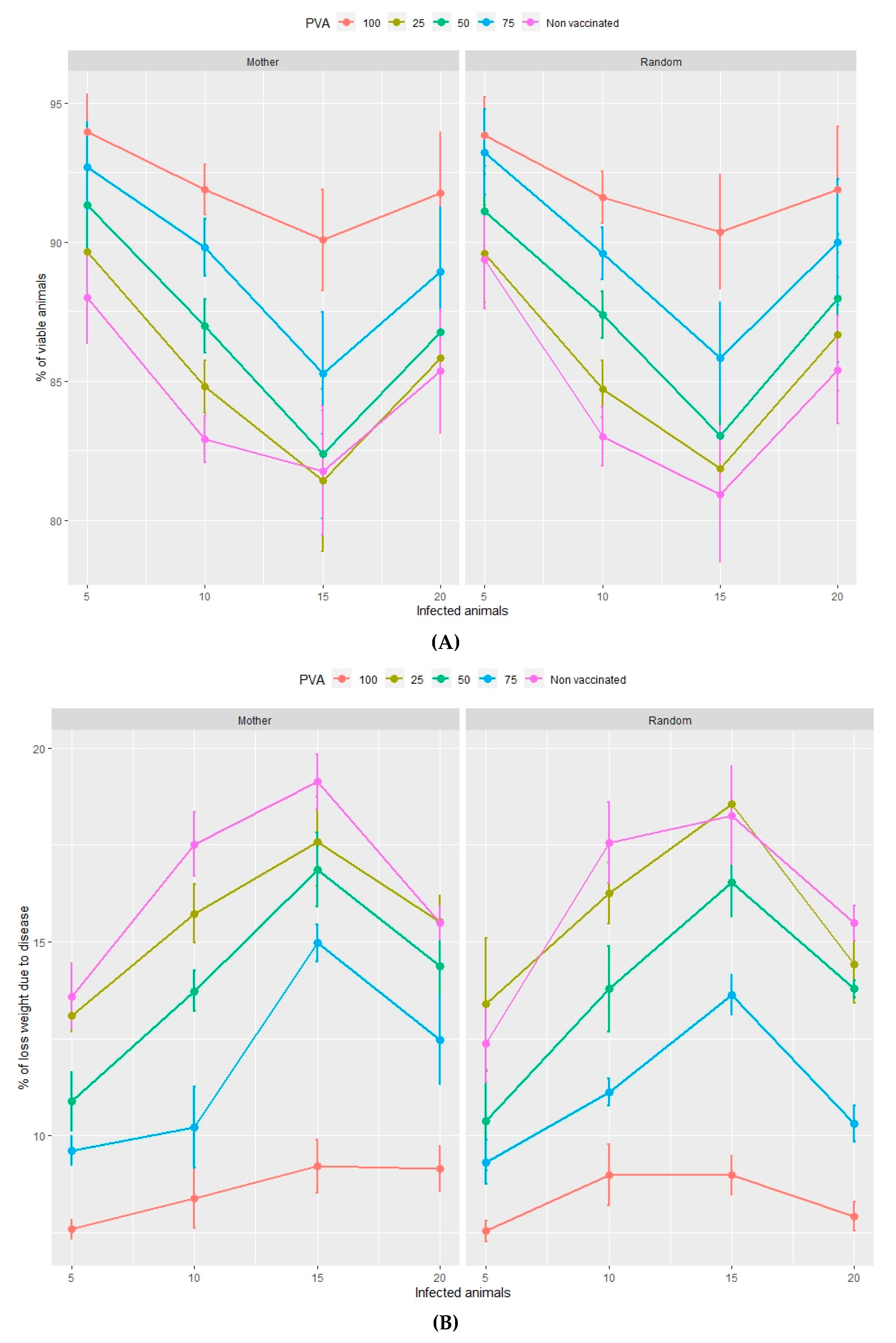
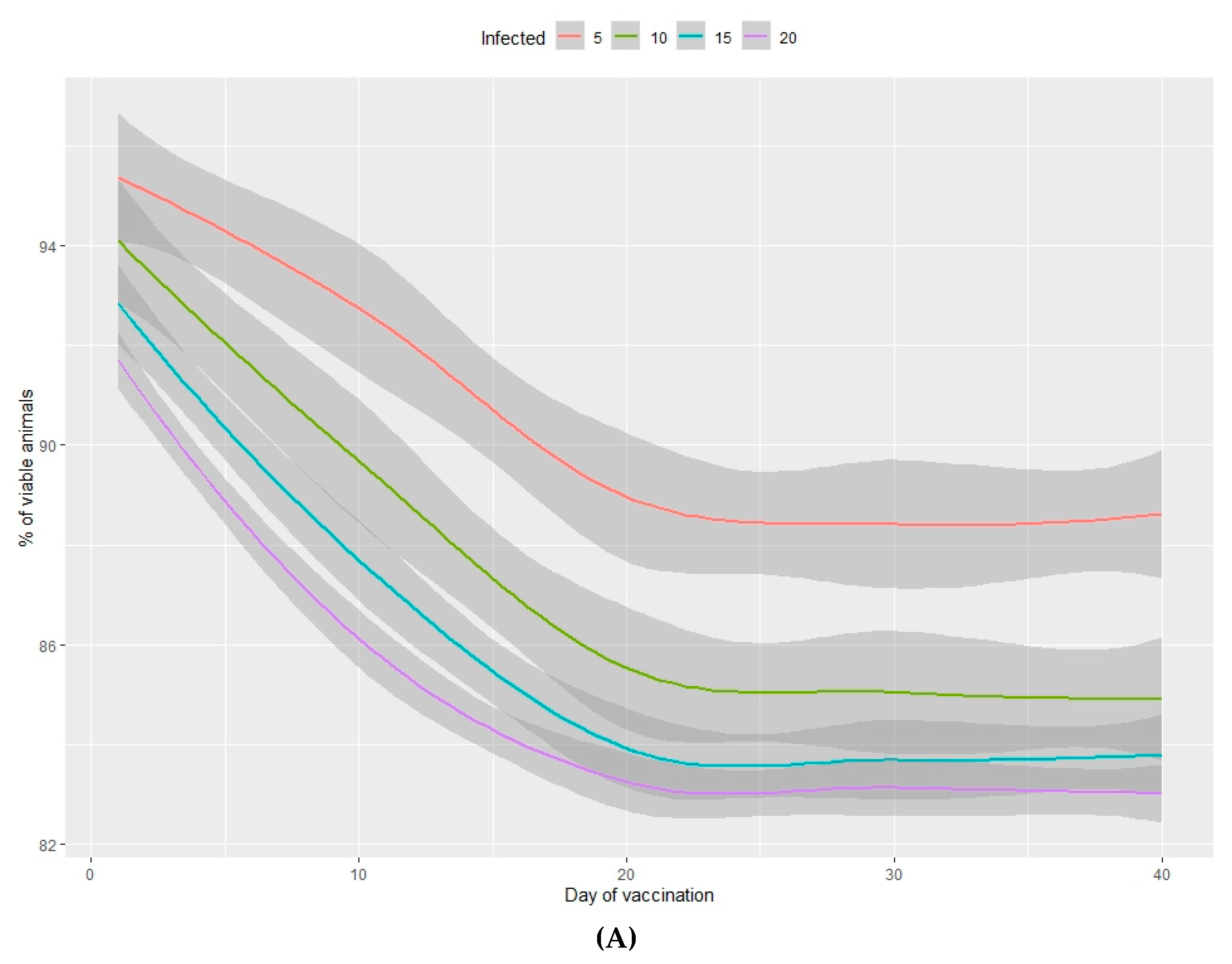
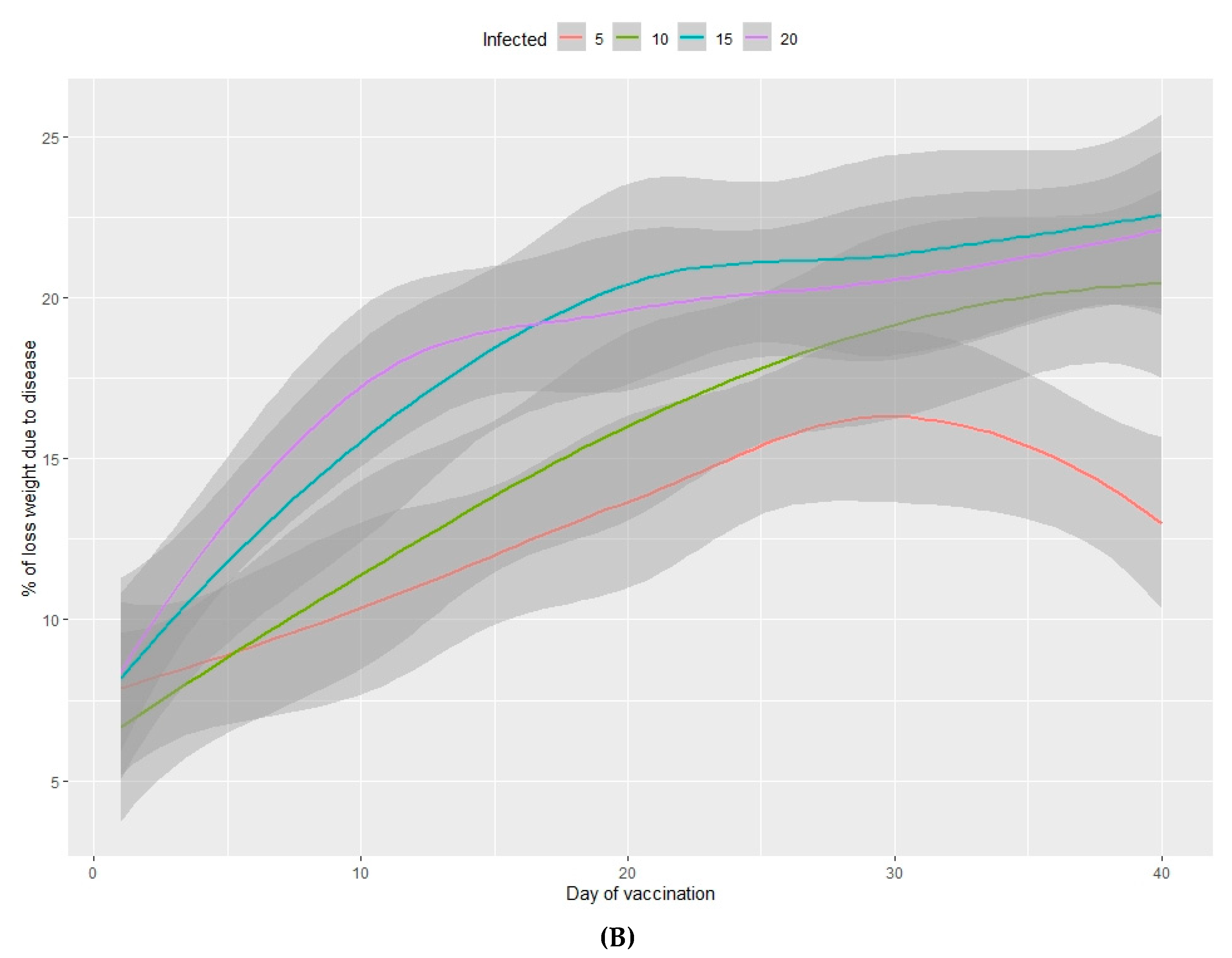
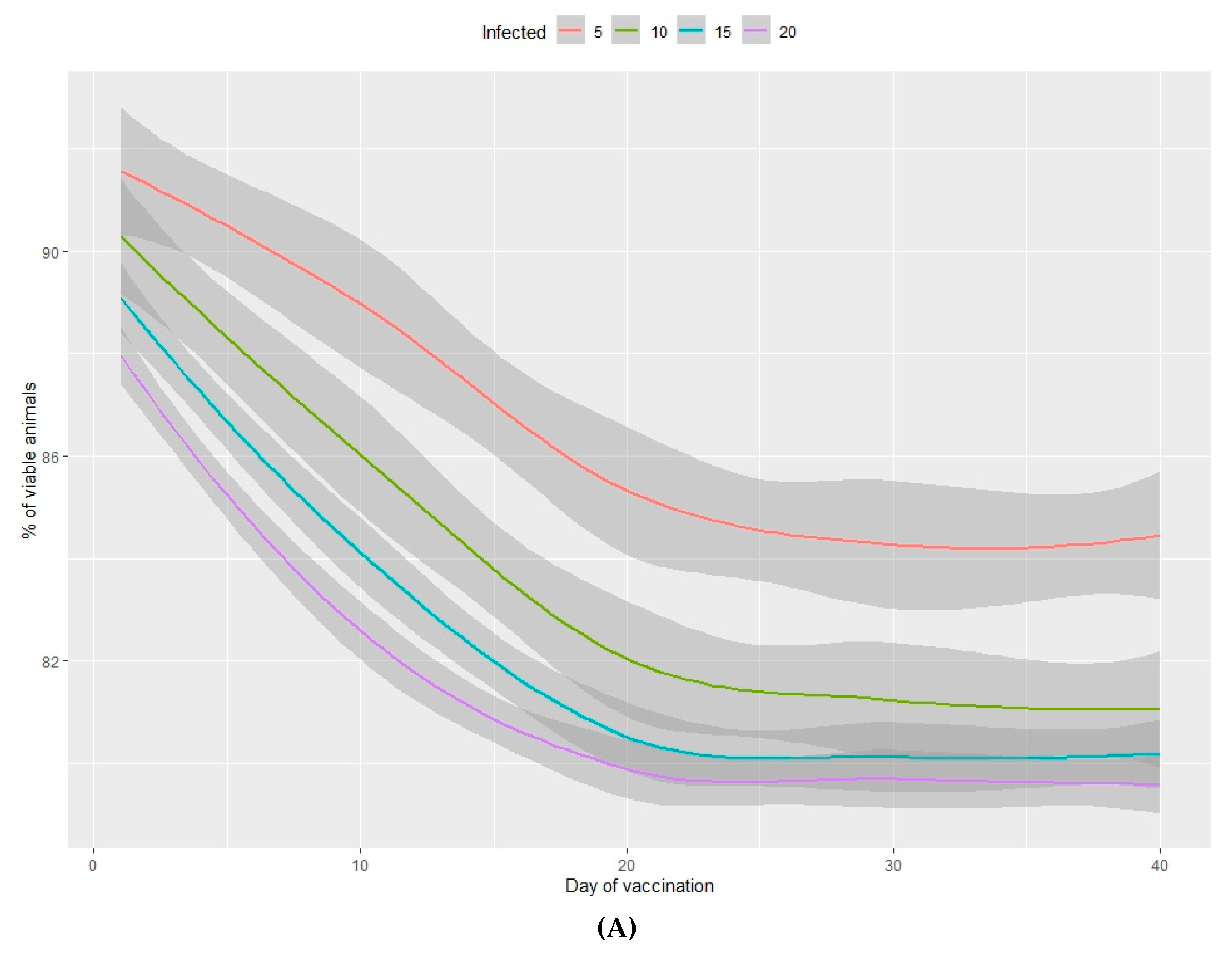
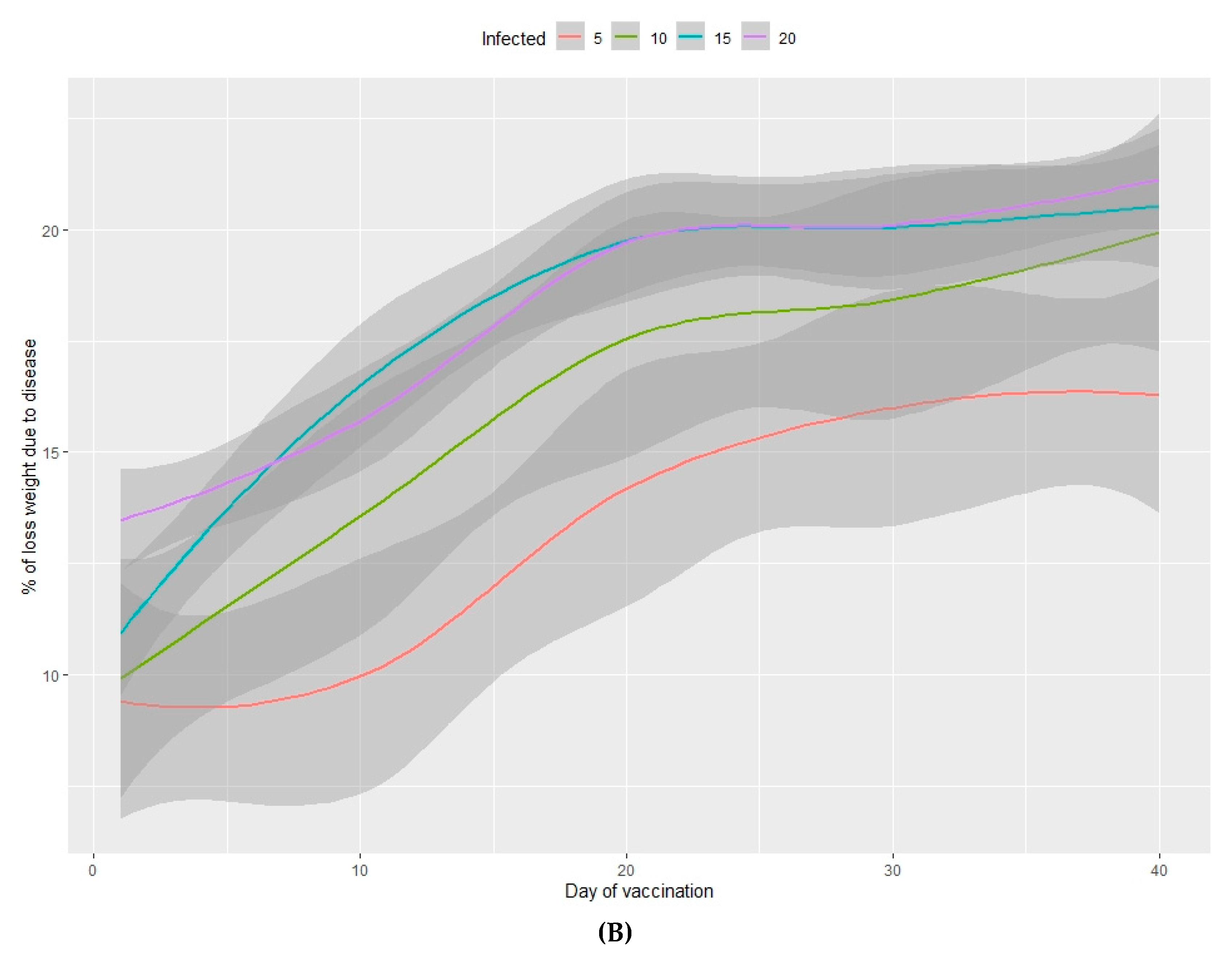
3.2.1. Viability of Animals
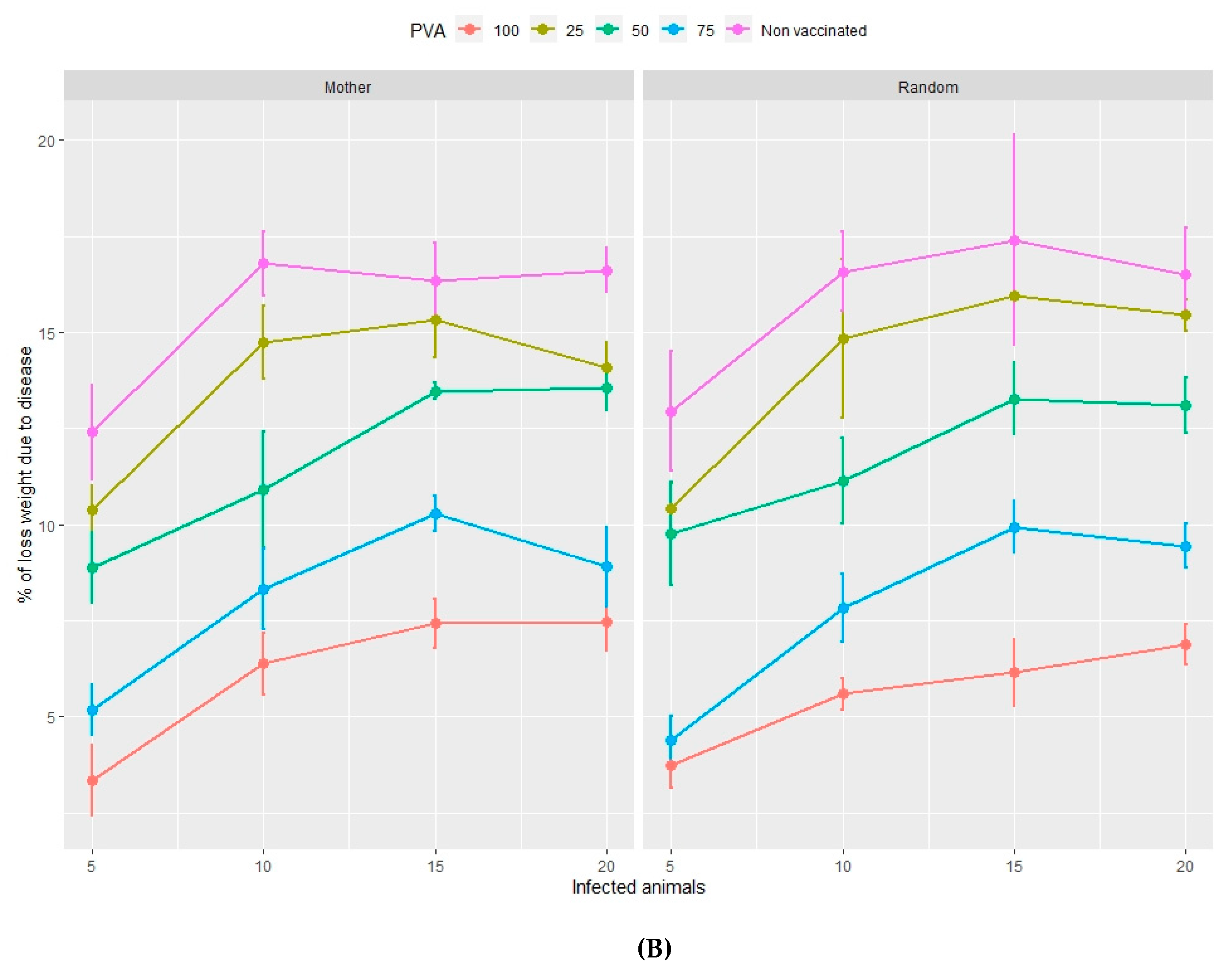
3.2.2. Loss of Total Weight Due to Disease
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, G.; Fanzo, J.; Miller, D.D.; Pingali, P.; Post, M.; Steiner, J.L.; Thalacker-Mercer, A.E. Production and supply of high-quality food protein for human consumption: Sustainability, challenges, and innovations. Ann. N. Y. Acad. Sci. 2014, 1321, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Rabobank: The Netherlands Will Lose Many Pig Producers. Available online: https://www.pigprogress.net/World-of-Pigs1/Articles/2018/10/Rabobank-The-Netherlands-will-lose-many-pig-producers-348896E/ (accessed on 1 May 2020).
- Rocadembosch, J.; Amador, J.; Bernaus, J.; Font, J.; Fraile, L. Production parameters and pig production cost: Temporal evolution 2010–2014. Porc. Health Manag. 2016, 2, 11. [Google Scholar] [CrossRef] [PubMed]
- Thrusfield, M. Veterinary Epidemiology, 3rd ed.; Blackwell Science Ltd.: Ames, IA, USA, 2005. [Google Scholar]
- Chand, R.J.; Trible, B.R.; Rowland, R.R. Pathogenesis of porcine reproductive and respiratory syndrome virus. Curr. Opin. Virol. 2012, 2, 256–263. [Google Scholar] [CrossRef]
- Fraile, L.; Alegre, A.; López-Jimenez, R.; Nofrarias, M.; Segalés, J. Risk factors associated with pleuritis and cranio-ventral pulmonary consolidation in slaughter-aged pigs. Vet. J. 2010, 184, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Postma, M.; Backhans, A.; Collineau, L.; Loesken, S.; Sjölund, M.; Belloc, C.; Emanuelson, U.; Beilage, E.G.; Stärk, K.D.C.; Dewulf, J. The biosecurity status and its associations with production and management characteristics in farrow-to-finish pig herds. Animal 2016, 10, 478–489. [Google Scholar] [CrossRef] [PubMed]
- Corzo, C.A.; Mondaca, E.; Wayne, S.; Torremorell, M.; Dee, S.A.; Davies, P.; Morrison, R.B. Control and elimination of porcine reproductive and respiratory syndrome virus. Virus Res. 2010, 154, 185–192. [Google Scholar] [CrossRef]
- Feng, H.; Segalés, J.; Fraile, L.; Lopez-Soria, S.; Sibila, M. Effect of high and low levels of maternally derived antibodies on porcine circovirus type 2 (PCV2) infection dynamics and production parameters in PCV2 vaccinated pigs under field conditions. Vaccine 2016, 34, 3044–3050. [Google Scholar] [CrossRef]
- Colomer, M.A.; Margalida, A.; Fraile, L. Improving the management procedures in farms infected with the Porcine Reproductive and Respiratory Syndrome virus using PDP models. Sci. Rep. 2019, 9, 9959. [Google Scholar] [CrossRef]
- Bouma, A. Determination of the effectiveness of Pseudorabies marker vaccines in experiments and field trials. Biologicals 2005, 33, 241–245. [Google Scholar] [CrossRef]
- Bitsouni, V.; Lycett, S.; Opriessnig, T.; Doeschl-Wilson, A. Predicting vaccine effectiveness in livestock populations: A theoretical framework applied to PRRS virus infections in pigs. PLoS ONE 2019, 14, e0220738. [Google Scholar] [CrossRef]
- Van Nes, A. Epidemiology: Mathematical modelling of pseudorabies virus (Syn. Aujeszky’s disease virus) outbreaks aids eradication programmes: A review. Vet. Q. 2001, 23, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Danon, L. Mathematical modelling of infectious diseases. Br. Med. Bull. 2009, 92, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Smith, J.O.; George, D.; Pepin, K.M.; Pitzer, V.E.; Pulliam, J.R.C.; Dobson, A.P.; Hudson, P.J.; Grenfell, B.T. Epidemic Dynamics at the Human-Animal Interface. Science 2009, 326, 1362–1367. [Google Scholar] [CrossRef] [PubMed]
- Garner, M.G.; Beckett, S.D. Modelling the spread of foot-and-mouth disease in Australia. Aust. Vet. J. 2008, 83, 758–766. [Google Scholar] [CrossRef] [PubMed]
- Giraldo, J.O.; Palacio, D.H. Deterministic SIR (Susceptible–Infected–Removed) models applied to varicella outbreaks. Epidemiol. Infect. 2007, 136, 679–687. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Aly, S.S.; Cano, J.P.; Polson, D.; Kass, P.H.; Perez, A.M. Stochastic model of porcine reproductive and respiratory syndrome virus control strategies on a swine farm in the United States. Am. J. Vet. Res. 2014, 75, 260–267. [Google Scholar] [CrossRef] [PubMed]
- Barongo, M.B.; Bishop, R.P.; Fèvre, E.M.; Knobel, D.L.; Ssematimba, A. A Mathematical Model that Simulates Control Options for African Swine Fever Virus (ASFV). PLoS ONE 2016, 11, e0158658. [Google Scholar] [CrossRef]
- White, L.A.; Torremorell, M.; Craft, M.E. Influenza A virus in swine breeding herds: Combination of vaccination and biosecurity practices can reduce likelihood of endemic piglet reservoir. Prev. Vet. Med. 2017, 138, 55–69. [Google Scholar] [CrossRef]
- Colomer, M.A.; Margalida, A.; Pérez-Jiménez, M.J. Population Dynamics P System (PDP) Models: A Standardized Protocol for Describing and Applying Novel Bio-Inspired Computing Tools. PLoS ONE 2013, 8, e60698. [Google Scholar] [CrossRef]
- Stegeman, J.A.; Kimman, T.G.; Van Oirschot, J.T.; Tielen, M.J.; Hunneman, W.A. Spread of Aujeszky’s disease virus within pig herds in an intensively vaccinated region. Vet. Rec. 1994, 134, 327–330. [Google Scholar] [CrossRef]
- Stegeman, A.; Elbers, A.R.; De Jong, M.C.M.; Oosterlaak, B.; Dijkhuizen, A. Estimating the rate of pseudorabies virus introduction into pig-finishing herds at regional level. Vet. Q. 1997, 19, 5–9. [Google Scholar] [CrossRef] [PubMed]
- De Jong, M.C.M.; Kimman, T.G. Experimental quantification of vaccine-induced reduction in virus transmission. Vaccine 1994, 12, 761–766. [Google Scholar] [CrossRef]
- Indicadores de Porcino. 2018. Available online: https://www.mapa.gob.es/es/ganaderia/temas/produccion-y-mercados-ganaderos/indicadoresbdporc2018_tcm30-440329.pdf (accessed on 1 May 2020).
- Miller, G.Y.; Gale, S.B.; Eshelman, C.E.; Wells, S.J. Emergency vaccination use in a modelled foot and mouth disease outbreak in Minnesota. Rev. Sci. Tech. 2015, 34, 729–740. [Google Scholar] [CrossRef] [PubMed]
- Pileri, E.; Gibert, E.; Soldevila, F.; García-Saenz, A.; Pujols, J.; Díaz, I.; Darwich, L.; Casal, J.; Martín, M.; Mateu, E. Vaccination with a genotype 1 modified live vaccine against porcine reproductive and respiratory syndrome virus significantly reduces viremia, viral shedding and transmission of the virus in a quasi-natural experimental model. Vet. Microbiol. 2015, 175, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Qiu, L.; Yang, Z.; Dang, R.; Wang, X. Emergency vaccination alleviates highly pathogenic porcine reproductive and respiratory syndrome virus infection after contact exposure. BMC Vet. Res. 2013, 9, 26. [Google Scholar] [CrossRef]
- Brosig, J.; Traulsen, I.; Krieter, J. Control of Classical Swine Fever Epidemics Under Varying Conditions—With Special Focus on Emergency Vaccination and Rapid PCR Testing. Transbound. Emerg. Dis. 2012, 61, 258–265. [Google Scholar] [CrossRef]
- Kooij, D. Economic aspects of the control of Aujeszky’s disease in the European Community. Acta Vet. Hung. 1994, 42, 405–408. [Google Scholar]
- Miller, J.S.; Tsai, G.Y.; Forster, D.L. Benefit-cost analysis of the national pseudorabies virus eradication program. J. Am. Vet. Med. Assoc. 1996, 208, 208–213. [Google Scholar]
- Andersson, H.; Lexmon, A.; Robertsson, J.A.; Lundeheim, N.; Wierup, M. Agricultural policy and social returns to eradication programs: The case of Aujeszky’s disease in Sweden. Prev. Vet. Med. 1997, 29, 311–328. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Q.; Rao, X.; Diao, X.; Yang, L.; Fang, X.; Hogeveen, H. An economic assessment of pseudorabies (Aujeszky’ disease) elimination on hog farms in China. Prev. Vet. Med. 2019, 163, 24–30. [Google Scholar] [CrossRef]
| Non-Vaccinated | |||
| Parameter | Lactation period | Nursery | Fattening |
| Basic reproductive ratio (Ro) | NA | 10 | 10 |
| Incubation period (days) | NA | 4 | 4 |
| Infectious period (days) | NA | 15 | 15 |
| Lethality | NA | 15 | 10 |
| Reduction of weight at the end of the period (gr) | 1000 | 4000 | |
| Vaccinated | |||
| Parameter | Lactation period | Nursery | Fattening |
| Basic reproductive ratio (Ro) | NA | 0.5 | 0.5 |
| Incubation period (days) | NA | 4 | 4 |
| Infectious period (days) | NA | 10 | 10 |
| Lethality | NA | 6 | 3 |
| Reduction of weight at the end of the period (gr) | 500 | 2000 | |
| GLM Models | Estimate | p-Value | Estimate | p-Value |
|---|---|---|---|---|
| % of viable animals | Nursery | Fattening | ||
| (Intercept) | 4.578 | <0.001 | 4.559 | <0.001 |
| Infected 10 | −0.026 | 0.0892 | −0.045 | 0.004 |
| Infected 15 | −0.033 | 0.0350 | −0.080 | <0.001 |
| Infected 20 | −0.024 | 0.1178 | −0.036 | 0.022 |
| 25% of vaccinated animals | −0.057 | 0.0011 | −0.072 | <0.001 |
| 50% of vaccinated animals | −0.037 | 0.0300 | −0.054 | 0.002 |
| 75% of vaccinated animals | −0.017 | 0.327 | −0.028 | 0.115 |
| Non vaccinated | −0.072 | <0.001 | −0.083 | <0.001 |
| Random management | 0.0004 | 0.971 | 0.003 | 0.770 |
| Deviance of model | 89.99% | 69.79% | ||
| % of sick animals | Nursery | Fattening | ||
| (Intercept) | 2.303 | <0.001 | 0.107 | 0.412 |
| Infected 10 | 0.364 | <0.001 | 0.063 | 0.073 |
| Infected 15 | 0.485 | <0.001 | −1.650 | <0.001 |
| Infected 20 | 0.5601 | <0.001 | −0.547 | <0.001 |
| 25% of vaccinated animals | 1.774 | <0.001 | 3.051 | <0.001 |
| 50% of vaccinated animals | 1.576 | <0.001 | 3.091 | <0.001 |
| 75% of vaccinated animals | 0.998 | <0.001 | 2.531 | <0.001 |
| Non vaccinated | 1.829 | <0.001 | 2.807 | <0.001 |
| Random management | 0.002 | 0.905 | 0.143 | <0.001 |
| Deviance of model | 96.06% | 75.45% | ||
| % of loss weight due to disease | Nursery | Fattening | ||
| (Intercept) | 1.464 | <0.001 | 1.9545 | <0.001 |
| Infected 10 | 0.328 | <0.001 | 0.2126 | <0.001 |
| Infected 15 | 0.433 | <0.001 | 0.3552 | <0.001 |
| Infected 20 | 0.404 | <0.001 | 0.1792 | <0.001 |
| 25% of vaccinated animals | 0.862 | <0.001 | 0.6088 | <0.001 |
| 50% of vaccinated animals | 0.695 | <0.001 | 0.4875 | <0.001 |
| 75% of vaccinated animals | 0.314 | <0.001 | 0.3019 | <0.001 |
| Non vaccinated | 0.984 | <0.001 | 0.6465 | <0.001 |
| Random management | 0.002 | 0.939 | −0.0249 | 0.393 |
| Deviance of model | 88.38% | 88.45% | ||
| GLM Models | Estimate | p-Value | Estimate | p-Value |
|---|---|---|---|---|
| % of viable animals | Nursery | Fattening | ||
| (Intercept) | 4.560 | <0.001 | 4.518 | <0.001 |
| Infected 10 | −0.033 | 0.483 | −0.033 | 0.501 |
| Infected 15 | −0.050 | 0.292 | −0.048 | 0.319 |
| Infected 20 | −0.061 | 0.200 | −0.059 | 0.227 |
| Day of vaccination | −0.002 | 0.049 | −0.003 | 0.043 |
| Management | −0.006 | 0.854 | −0.006 | 0.863 |
| Deviance of model | 83.37% | 84.63% | ||
| % of sick animals | Nursery | Fattening | ||
| (Intercept) | 3.285 | <0.001 | 0.654 | 0.014 |
| Infected 10 | 0.319 | <0.001 | −0.446 | 0.045 |
| Infected 15 | 0.438 | <0.001 | −0.989 | <0.001 |
| Infected 20 | 0.508 | <0.001 | −1.503 | <0.001 |
| Day of vaccination | 0.026 | <0.001 | 0.044 | <0.001 |
| Management | 0.047 | 0.214 | −0.140 | 0.454 |
| Deviance of model | 74.95% | 79.12% | ||
| % of loss weight due to disease | Nursery | Fattening | ||
| (Intercept) | 2.072 | <0.001 | 2.272 | <0.001 |
| Infected 10 | 0.186 | 0.129 | 0.193 | 0.102 |
| Infected 15 | 0.364 | 0.002 | 0.273 | 0.019 |
| Infected 20 | 0.362 | 0.002 | 0.322 | 0.005 |
| Day of vaccination | 0.019 | <0.001 | 0.013 | <0.001 |
| Management | 0.017 | 0.832 | 0.031 | 0.694 |
| Deviance of model | 74.34% | 79.62% | ||
| Day of Vaccine Application | Percentage of Sick Animals | |||
|---|---|---|---|---|
| 5% | 10% | 15% | 20% | |
| 1 | 352,173 ± 29,500 | 370,655 ± 32,632 | 409,303 ± 2301 | 504,044 ± 26,193 |
| 10 | 372,651 ± 7247 | 506,993 ± 10,497 | 616,843 ± 17049 | 587,593 ± 28,184 |
| 20 | 530,288 ± 60,536 | 655,955 ± 38,887 | 738,466 ± 16,356 | 736,997 ± 12,592 |
| 30 | 598,236 ± 33,832 | 689,390 ± 65,294 | 749,734 ± 37,314 | 752,063 ± 27,830 |
| 40 | 608,803 ± 85,860 | 745,715 ± 79,878 | 768,040 ± 40137 | 790,447 ± 4899 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colomer, M.A.; Margalida, A.; Fraile, L. Vaccination Is a Suitable Tool in the Control of Aujeszky’s Disease Outbreaks in Pigs Using a Population Dynamics P Systems Model. Animals 2020, 10, 909. https://doi.org/10.3390/ani10050909
Colomer MA, Margalida A, Fraile L. Vaccination Is a Suitable Tool in the Control of Aujeszky’s Disease Outbreaks in Pigs Using a Population Dynamics P Systems Model. Animals. 2020; 10(5):909. https://doi.org/10.3390/ani10050909
Chicago/Turabian StyleColomer, Maria Angels, Antoni Margalida, and Lorenzo Fraile. 2020. "Vaccination Is a Suitable Tool in the Control of Aujeszky’s Disease Outbreaks in Pigs Using a Population Dynamics P Systems Model" Animals 10, no. 5: 909. https://doi.org/10.3390/ani10050909
APA StyleColomer, M. A., Margalida, A., & Fraile, L. (2020). Vaccination Is a Suitable Tool in the Control of Aujeszky’s Disease Outbreaks in Pigs Using a Population Dynamics P Systems Model. Animals, 10(5), 909. https://doi.org/10.3390/ani10050909







