Next Article in Journal
Removal of Chemical Oxygen Demand (COD) from Swine Farm Wastewater by Corynebacterium xerosis H1
Previous Article in Journal
The Characterization of a Gonococcal HicAB Toxin–Antitoxin System Capable of Causing Bacteriostatic Growth Arrest
Previous Article in Special Issue
Human Echinococcosis in the Russian Federation in the 21st Century: A Systematic Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Microorganisms
Volume 13
Issue 7
10.3390/microorganisms13071620
microorganisms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

In Silico Approach for Early Antimalarial Drug Discovery: De Novo Design of Virtual Multi-Strain Antiplasmodial Inhibitors

by
Valeria V. Kleandrova
,
M. Natália D. S. Cordeiro
and
Alejandro Speck-Planche
*
LAQV@REQUIMTE/Department of Chemistry and Biochemistry, Faculty of Sciences, University of Porto, 4169-007 Porto, Portugal
*
Author to whom correspondence should be addressed.
Microorganisms 2025, 13(7), 1620; https://doi.org/10.3390/microorganisms13071620
Submission received: 15 May 2025 / Revised: 28 June 2025 / Accepted: 8 July 2025 / Published: 9 July 2025
(This article belongs to the Special Issue Infectious Diseases: New Approaches to Old Problems, 3rd Edition)
Browse Figures
Versions Notes

Abstract

Plasmodium falciparum is the causative agent of malaria, a parasitic disease that affects millions of people in terms of prevalence and is associated with hundreds of thousands of deaths. Current antimalarial medications, in addition to exhibiting moderate to serious adverse reactions, are not efficacious enough due to factors such as drug resistance. In silico approaches can speed up the discovery and design of new molecules with wide-spectrum antimalarial activity. Here, we report a unified computational methodology combining a perturbation theory machine learning model based on multilayer perceptron networks (PTML-MLP) and the fragment-based topological design (FBTD) approach for the prediction and design of novel molecules virtually exhibiting versatile antiplasmodial activity against diverse P. falciparum strains. Our PTML-MLP achieved an accuracy higher than 85%. We applied the FBTD approach to physicochemically and structurally interpret the PTML-MLP, subsequently extracting several suitable molecular fragments and designing new drug-like molecules. These designed molecules were predicted as multi-strain antiplasmodial inhibitors, thus representing promising chemical entities for future synthesis and biological experimentation. The present work confirms the potential of combining PTML modeling and FBTD for early antimalarial drug discovery while opening new horizons for extended computational applications for antimicrobial research and beyond.

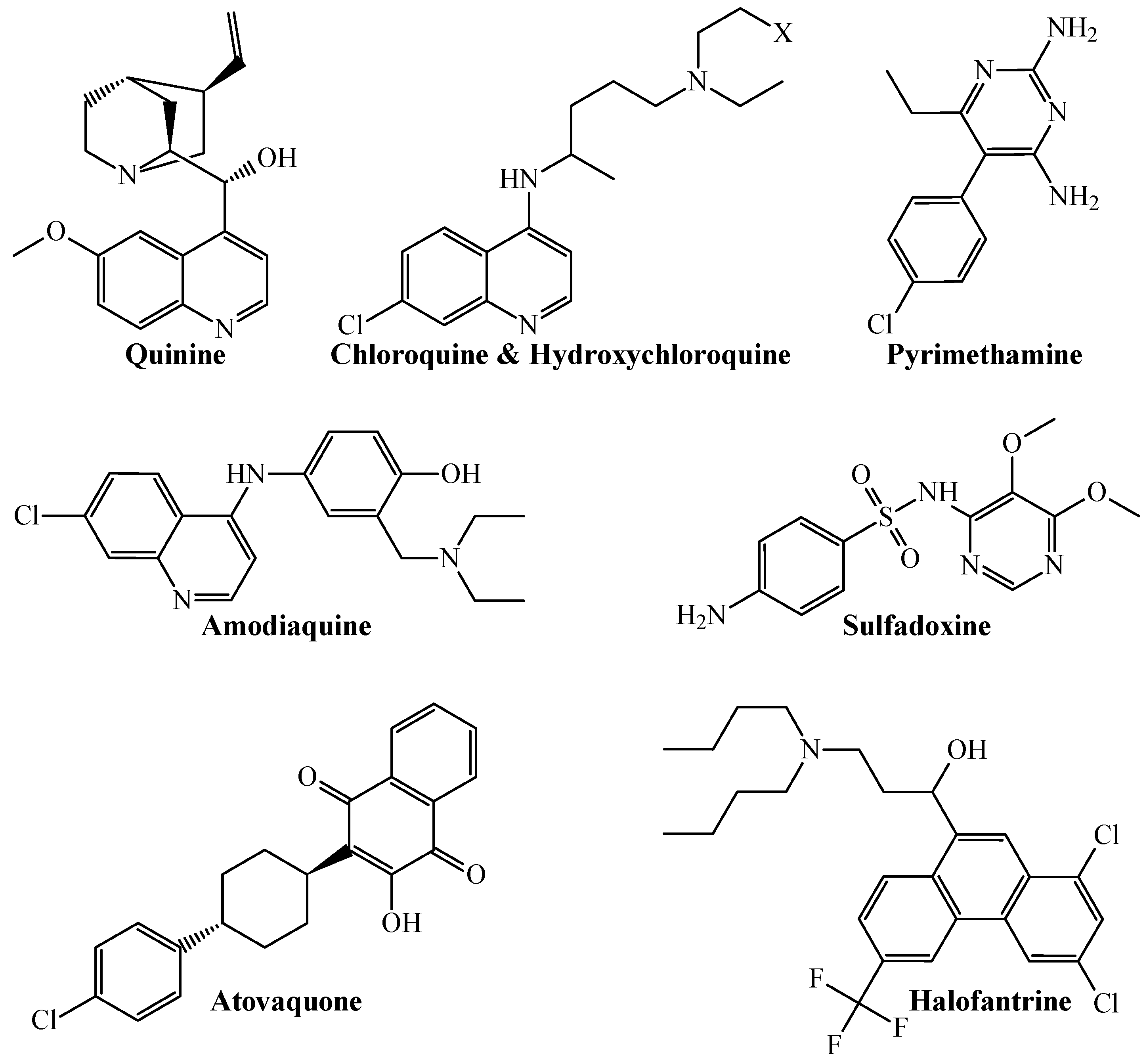
1. Introduction

Malaria constitutes an incredibly serious medical condition characterized by a deadly impact on the human population. This mosquito-borne infectious disease was responsible for about 247 million malaria cases and 619,000 malaria deaths [1]. Among the causative agents of malaria, Plasmodium falciparum accounts for the majority of incidence and mortality cases, representing the most concerning parasitic pathogen [2,3]. In addition, current antimalarial drugs have become less effective due to the development of and increase in drug resistance, including multidrug-resistant (MDR) strains [4,5,6]. All of these factors, together with the adverse effects associated with current antimalarial medications [7,8], indicate that the search for new antiplasmodial agents against P. falciparum continues to be a highly active field of research, as well as a need to tackle malaria.
Over time, antimalarial drug discovery has evolved to accelerate the identification of a variety of new chemical entities, with some of them being in late-stage clinical development [1,9,10]. Although experimental methods constitute the benchmark to deliver and validate antiplasmodial agents against P. falciparum malaria [11], they are associated with a great expenditure of time and financial resources. In this sense, discovering antiplasmodial agents against P. falciparum can be rationalized through in silico approaches, with complex network analysis [12], pharmacophore modeling [12,13,14], quantum mechanical calculations [13,15,16], structure-based drug design methods (e.g., molecular docking alone or in combination with molecular dynamics) [12,13,14,15,16,17,18,19,20], and machine learning [20,21,22]. Nevertheless, one or more limitations, such as the use of reduced dataset of chemicals (impeding an appropriate prioritization of the vast chemical space), the prediction of activity against only one protein or strain related to P. falciparum (thus affecting the search for antiplasmodial molecules capable of simultaneously targeting different strains), and insufficient physicochemical or structural interpretability (preventing the rational design of novel chemical entities with multi-strain antiplasmodial activity), are present in the aforementioned computational approaches, preventing their full exploitation for the discovery of antiplasmodial compounds against P. falciparum.
Advanced models based on perturbation theory machine learning (PTML) have been able to overcome the disadvantages mentioned above [23,24]. In terms of applications, PTML models have been successfully employed in antimicrobial research [25,26,27,28,29,30], neurological diseases [31,32,33,34,35], immunology [36,37,38], nanocarriers [39,40,41], and antineoplastic discovery [39,42,43,44,45,46]. Furthermore, PTML models have been directly interpreted by applying the fragment-based topological design (FBTD) approach, thus enabling the de novo design of molecules virtually exhibiting the desired bioactivity profiles [30,46].
Despite the pivotal role of all the aforementioned in silico methods in prioritizing drug discovery, there have been no studies focused on guiding the de novo rational design of multi-strain antiplasmodial inhibitors at the phenotypic level. Here, we set the theoretical bases for the applications of PTML modeling to early-stage antimalarial discovery. In particular, we demonstrate that the computational framework combining a PTML model based on a multiplayer perceptron network (PTML-MLP) and the FBTD approach can be used to enable the interpretation-driven de novo design of new drug-like molecules with predicted multi-strain antiplasmodial activity to be considered for future synthesis and biological experimentation.

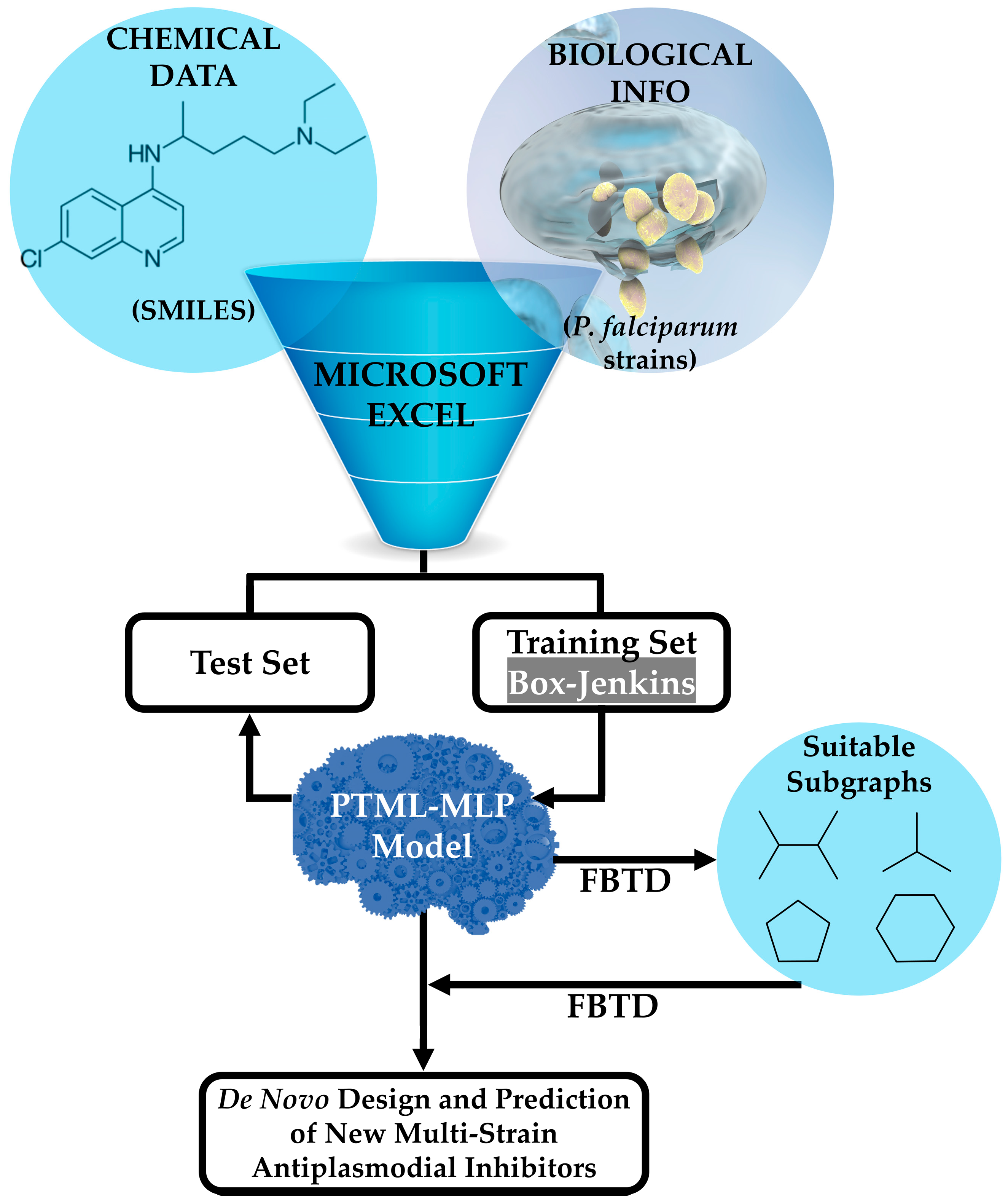
2. Materials and Methods

2.1. Data Curation and Topological Indices

The general steps associated with the joint use of the PTML-MLP and the FBTD approach are illustrated in Figure 1. Details will be given throughout this entire Materials and Methods section, as well as some key aspects regarding the application of FBTD in Section 3. In this sense, a single tabular file compatible with Microsoft Excel was downloaded from the public online database known as ChEMBL [47,48,49]. The file contained both the chemical data in the form of Simplified Molecular Input Line Entry System (SMILES) codes and the biological information, represented by the half-maximal inhibitory concentration (IC50) expressed in nanomolar (nM) against P. falciparum. The IC50 values considered in this study were measured over a time of either 48 or 72 h, since a recent report demonstrated that the IC50 values do not show a significant difference when measured by considering the aforementioned periods [50,51]. Consequently, as part of the curation process (containing steps such as deleting entries lacking SMILES codes, units of measurement, and IC50 values), when a molecule was assayed more than once against the same P. falciparum strain, we kept only the entry corresponding to the lowest IC50 value of that molecule. It is important to highlight that after the curation process, the dataset contained 6513 molecules, where each of them was experimentally assayed against at least 1 out of 9 P. falciparum strains (tg). Not all of the molecules were tested against all the P. falciparum strains (tg), and thus the dataset reported in this study ended up containing 9595 cases.
Each case of molecules in the dataset was classified as active or inactive. If a molecule had IC50 ≤ 500 nM against a specific P. falciparum strain, then the molecule was labeled as active [APi(ej) = 1], while molecules with IC50 ≥ 2000 nM were noted as inactive [APi(ej) = –1]. The selection of these cutoffs prevented any imbalance between the number of active and inactive cases, while the non-inclusion of molecules with intermediate activity (500 nM < IC50 < 2000 nM) guaranteed a sufficiently clear demarcation between the aforementioned activity classes [52]. Notice that APi(ej) is a two-category variable accounting for the antiplasmodial activity of the ith case under the experimental condition ej. At the same time, ej contains two aspects, namely tg (containing 9 labels, each of them belonging to a specific type of P. falciparum strain) and ds, with the latter containing two labels indicating whether a defined P. falciparum strain was sensitive or resistant to well-established antimalarial drugs (chloroquine, quinine, pyrimethamine, sulfadoxine, and cycloguanil).
The SMILES codes of the 9595 cases of molecules were deposited in a .txt file. This file was used as input by the software MODESLAB version 1.5 [53], where the topological indices (TIs) known as bond-based spectral moments [SM(PP)o], degree-based connectivity indices from the vertices’ valences [Xv(SG)m] and edges [e(SG)m], and the Kier–Hall shape index [K(Alpha)m] were calculated [54,55]. Notice that in the case of SM(PP)o, the notation “o” indicated the order (maximum number of bonds that a fragment can have, with o being between 1 and 7), while “PP” referred to any physicochemical property, such as the standard bond distance and bond dipole moment, or atomic contributions to hydrophobicity, the polar surface area, molar refractivity, Gasteiger-Marsili charges, and atomic weight. Regarding Xv(SG)m and e(SG)m, the order “m” reflects the specific size (exact number of bonds, with m in the range from 1 to 6) of a subgraph or fragment SG. Furthermore, the fragment SG was present in four types, namely path (linear fragment), cluster (ramification), path-cluster (combination of linear portion and ramification), and cycle (ring). Lastly, for the case of K(Alpha)m, this considers m = 3 for only path subgraphs, while “Alpha” is a factor considering the presence of heteroatoms (non-hydrogen atoms other than carbon) [54,55]. We also calculated a new set of normalization-like topological indices (NTIs). Each NTI was obtained as the ratio of a TI to nBO, with the latter representing the number of bonds in a molecule without counting bond multiplicity.
The dataset containing the 9595 cases of molecules (Supplementary Information S1) was divided into training (~75%) and test (~25%) sets according to the following procedure. First, the 9595 cases were ordered in terms of their increasing IC50 values. Then, the first three cases were annotated to belong to the training set, while the fourth was designated to be in the test set. The procedure was repeated until all the cases were assigned to the training or the test sets. After assigning all the cases to the training and test sets, we applied the Box–Jenkins approach through the following mathematical steps [30,46,56]:
a v g G B I e j = 1 n e j × ∑ a = 1 n e j G B I a
D G B I e j = G B I − a v g G B I e j s d v G B I × p e j
In Equation (1), GBI represents any of the original TIs (or their normalized counterparts (NTIs)) calculated for each case or molecule in the dataset. The term n(ej) indicates the number of cases annotated as active, which were experimentally tested against the same element of ej. Because ej depends on the aspects tg and ds, Equation (1) was applied to each of them separately. The same assumption was valid for the average term avg[GBI]ej. On the other hand, Equation (2) was also applied to the aspects tg and ds separately. Thus, the a priori probability p(ej) followed the same assumption as n(ej) and avg[GBI]ej, being calculated as the ratio of n(ej) to the total number of cases tested against the same aspect of ej (tg or ds). Furthermore, sdv[GBI] reflected the standard deviation of all the GBI values. The D[GBI]ej term is a multi-label graph index accounting for both the chemical structure of a case or molecule and a specific aspect of the experimental condition ej (tg or ds). Notice that n(ej), avg[GBI]ej, and p(ej) were calculated from cases of molecules labeled as belonging to the training set.

2.2. PTML Modeling: Assessment of Performance and Applicability Domain

The next step after calculating the D[GBI]ej indices was to rank them in terms of significance or information content. For this, we employed the computer program IMMAN version 1.0 [57]. In this sense, for each D[GBI]ej index, we calculated the geometric mean value (GMV) of three information-based metrics, namely the differential Shannon entropy [58], gain ratio [59], and symmetric uncertainty [60]. The D[GBI]ej indices with the greatest information content (and potentially the greatest discriminatory power) were those exhibiting the largest GMVs. Following the sorting of the D[GBI]ej indices according to their decreasing GMVs, we performed a correlation analysis, calculating the pair-wise Pearson’s correlation coefficient (PCC) values. The software STATISTICA version 13.5.0.17 was employed to perform the correlation analysis [61]. We only chose those D[GBI]ej indices satisfying the condition −0.7 < PCC < 0.7; the other D[GBI]ej indices were discarded.
The last step was to find the PTML-MLP, using the D[GBI]ej indices as its inputs. Through this procedure, we employed the artificial neural network menu of the software STATISTICA version 13.5.0.17. When searching for the most appropriate MLP network (PTML-MLP), we configured the values of the key hyperparameters. Thus, the number of input nodes (Ni) was set to be 25, and the minimum and maximum numbers of hidden neurons (Hn) were 30 and 80, respectively. The logistic and hyperbolic tangents were used as the activation functions in both the hidden and output layers. The number of output nodes (On) was set to 2 (number of predicted categories, i.e., active and inactive).
We configured the procedure to train 1000 MLP networks, with 300 of them being retained. The values of the different aforementioned hyperparameters selected by us were based on our extensive experience in PTML modeling, which allowed us to compare the dataset used in the present study with the datasets reported in previous PTML-MLPs [30,46,56]. Thus, we could estimate the hyperparameters mentioned above. The parameter ρ was calculated to assess whether the MLP networks could lead to overfitting:
ρ = C t N i + 1 H n + ( H n + 1 O n ]
In Equation (3), the meanings of Ni, Hn, and On were explained above. The number of cases in the training set (Ct) is also considered in this equation. To avoid overfitting, the condition ρ > 3 must be complied with [62,63]. In the end, we checked the performance of 300 retained MLP networks utilizing the global metrics (in both the training and test sets) known as sensitivity (Sn), specificity (Sp), and the normalized Matthew’s correlation coefficient (nMCC) [64]. However, the most suitable MLP network (the PTML-MLP) was the one exhibiting the highest values of local sensitivities [Sn(tg) and Sn(ds)] and specificities [Sp(tg) and Sp(ds)]. These local metrics depended on the two aspects of the experimental condition ej (tg and ds). Last, the applicability domain (AD) of the PTML-MLP was assessed according to a recent variation of the descriptors’ space approach [30,46,56].

3. Results and Discussion

3.1. Analyzing the Performance of the PTML-MLP Model

Details on the D[GBI]ej indices used as inputs by the PTML-MLP are present in Table 1. These include definitions based on the physicochemical and structural aspects.
The PTML-MLP found by us can be expressed in the form MLP 25-78-2. This notation means that the number of input nodes is Ni = 25 (equal to the number of D[GBI]ej indices), the number of neurons in the hidden layer is Hn = 78, the number of output nodes is On = 2, and the number of cases is Ct = 7197 (Supplementary Information S1). Substitution of the Ni, Hn, On, and Ct values into Equation (3) yielded a value of ρ = 3.292. Such a value confirms that our PTML-MLP did not overfit the data.
We analyzed the performance of the PTML-MLP at the global and local levels. In terms of global metrics (Table 2), the PTML-MLP exhibited Sn values above 93% and 89% in the training and test sets, respectively. This indicates a high number of true positive (TP) cases relative to the number of cases annotated as active (NActive). A similar trend was observed in the Sp values, where the number of true negative (TN) cases relative to the number of cases labeled as inactive (NInactive) was also high. For the training set, Sp > 90% was obtained, while Sp > 86% was achieved in the test set.
The Sn and Sp values indicate that our PTML-MLP has great statistical quality and predictive power when classifying antiplasmodial chemicals. This affirmation is further corroborated by the high nMCC values; the closeness of these nMCC values to one shows the strong convergence between the observed APi(ej) and predicted Pred[APi(ej)] values of antiplasmodial activity. More information regarding the classification and predictions performed by the PTML-MLP can be found in the Supplementary Information S2 File. Aside from achieving extremely good values for Sn, Sp, and nMCC, our PTML-MLP displayed quite good values for the local metrics. In this sense, Sn(tg) was in the interval 88–98% in the training set; in the test set, Sn(tg) was in the range of 80–93%. At the same time, Sp(tg) exhibited values in the intervals of 80–97% and 81–96% in the training and test sets, respectively. On the other hand, when considering the drug sensitivity aspect (ds) of the different P. falciparum strains, Sn(ds) and Sp(ds) showed values between 90% and 94% in the training set, while Sn(ds) > 88% and Sp(ds) > 85% were reported for the test set. All the values of these local statistical metrics demonstrate that the PTML-MLP can accurately predict antiplasmodial activity across multiple P. falciparum strains and drug sensitivity labels (Supplementary Information S2).
In terms of the AD of the PTML-MLP, we previously mentioned (see Section 2.2) that a modification of the descriptors’ space approach was applied. In this sense, for each molecule present in the dataset and a defined D[GBI]ej index present in the PTML-MLP (see Table 1), a categorical value known as the local score of applicability domain (LSAD_D[GBI]ej) was calculated by comparing the D[GBI]ej value of that molecule with the maximum and minimum D[GBI]ej values. If the D[GBI]ej value for the molecule was within the boundaries of the maximum and minimum D[GBI]ej values, then the LSAD_D[GBI]ej associated with that molecule and considering that particular D[GBI]ej index was equal to one. If this condition was not satisfied, then the value LSAD_D[GBI]ej = 0 was obtained. Notice that this procedure was applied to each of the 25 D[GBI]ej indices in the PTML-MLP, which means that for each molecule, 25 LSAD_D[GBI]ej values were calculated. Then, for each molecule, the total score (TSAD) was determined. TSAD = 25 indicated that a molecule was within the AD of the PTML-MLP, while TSAD < 25 showed that the molecule was outside the AD, thus constituting an unreliable prediction. In the end, out of the 9595 cases of molecules in our dataset used to create the PTML-MLP, 9583 cases were within the AD (Supplementary Information S2).
From a more chemical-oriented point of view, our PTML-MLP also demonstrated that it can correctly predict and classify the multi-strain antiplasmodial activity of well-established antimalarial drugs (Figure 2).
The antimalarial drugs with multi-strain antiplasmodial activity correctly predicted by the PTML-MLP include (but are not limited to) those labeled in our dataset as ChEMBL170 (quinine), ChEMBL76 (chloroquine), ChEMBL1535 (hydroxychloroquine), ChEMBL36 (pyrimethamine), ChEMBL682 (amodiaquine), ChEMBL1539 (sulfadoxine), ChEMBL1450 (atovaquone), and ChEMBL1107 (halofantrine). Furthermore, our PTML-MLP was quite useful in identifying and predicting new molecular patterns (Figure 3), which are different from those present in the aforementioned antimalarial drugs.
Notice that Figure 3 presents a non-exhaustive list of molecules with different chemical structures. Because such molecules appear in the dataset, this means that they were experimentally assayed as multi-strain antiplasmodial agents and were also predicted by our PTML-MLP. We would like to highlight that some of these molecules are drugs approved by the Food and Drug Administration (FDA) with different therapeutic applications other than antimalarial activity. This is the case for the molecules labeled ChEMBL34259 and ChEMBL58, which are the FDA-approved drugs methotrexate and mitoxantrone, respectively. These are antineoplastic agents used in chemotherapies against different types of cancer. Furthermore, CHEMBL539947 (known as tyrphostin Ag-879) is a molecule with known anticancer activity [65,66]. Also, other FDA-approved drugs include ChEMBL1448 (niclosamide, an anthelmintic) and ChEMBL567 (perphenazine, an antipsychotic drug). All of this demonstrates that our PTML-MLP, in addition to having the capability to correctly identify and predict diverse molecular patterns with multi-strain antiplasmodial activity, can also be used as a computational tool in virtual screening scenarios to repurpose FDA-approved drugs.

3.2. The FBTD Approach: Interpretation of the PTML-MLP

The physicochemical and structural interpretation of the D[GBI]ej indices present in the PTML-MLP is crucial to designing new molecules with the desired versatile inhibitory profile [30,46,56]. We considered four aspects; the first was the assessment of the significance of the D[GBI]ej indices (Figure 4) through the sensitivity values (SVs).
This means that the D[GBI]ej indices with the highest SVs were the ones for which, in addition to having a greater discriminatory power [67], the physicochemical properties and structural features characterized by them were most important in both the molecules of the dataset used to the build the PTML-MLP and any new molecule to be designed.
The second aspect is that each of the 25 D[GBI]ej indices present in the PTML-MLP characterized the presence of different generic fragments (Figure 5), which are known as subgraphs (SGs).
Notice that each SG represents a generic fragment related to substructural moieties such as polar functional groups, aliphatic portions, and aliphatic and aromatic rings of different sizes.
The third aspect is the physicochemical information encoded by the D[GBI]ej indices; they maintain the same physicochemical and structural content as the topological indices from which they were calculated (see Equation (2)). Thus, the D[GBI]ej indices derived from SM(PP)o (see Section 2) describe how a defined physicochemical property is concentrated in different regions of a molecule while also being expressed as the number of times diverse SGs are present in that molecule [68,69,70,71,72,73]. The D[GBI]ej indices obtained from Xv(SG)m measure the molecular accessibility [74,75,76,77,78,79,80], i.e., the ability of the diverse SGs or fragments to effectively participate in both polar and non-polar interactions with other surrounding molecules (e.g., solvent molecules or components of a cellular membrane). The D[GBI]ej indices calculated from e(SG)m are quantitative contributions of the molecular volume of the different SGs and fragments [81,82,83,84,85].
Lastly, Table 3 illustrates the fourth aspect, i.e., how the value of each D[GBI]ej index should vary in the PTML-MLP to enhance the biological activity profile under study (in this study, the multi-strain antiplasmodial activity).
For each D[GBI]ej index, two average values were computed: one for the cases annotated and correctly classified as active and the other for the cases labeled and correctly classified as inactive [30,46,56]. When comparing the two averages, if the value considered active is higher, then this means that the value of that particular D[GBI]ej index should be increased to enhance the multi-strain antiplasmodial activity; otherwise, the value of that D[GBI]ej index will have to be decreased. We would like to emphasize that only correctly annotated and classified cases were used to compute the aforementioned D[GBI]ej-based averages. This ensured a clean and reliable interpretation of the trends in the D[GBI]ej indices, tightly aligned with the actual statistical quality and predictive performance of the PTML-MLP.
There were 12 D[GBI]ej indices derived from SM(PP)o in our PTML-MLP. In this sense, DGB01 and DGB03 characterized the increase in polarizability. Notice that DGB01 focuses on the SG-04 and SG-06 subgraphs; SG-04 represented the presence of sulfur or a halogen (with Cl, Br, and I being preferred over F) attached to a ring, as well as two rings connected by a single bond or forming a condensed aromatic system. For SG-06, this involved CZ3 and OCZ3 moieties, where Z can be a methyl or a halogen (with Cl, Br, and I preferred over F). Notice that SG-06 contains several SG-04 subgraphs. In contrast, DGB03 is a measure of the global polarizability of a molecule (SG-01), favoring the presence of aromatic rings and heteroaromatic rings, as well as sulfur, nitrogen from secondary and tertiary aromatic amines, halogens other than fluorine, and heteroaliphatic rings. We would like to highlight that in terms of importance in the PTML-MLP, DGB01 and DGB03 ranked 20th and 4th, respectively.
On the other hand, DGB02 and DGB17 indicate the augmentation of the hydrophobicity. Notice that DGB02 describes this property in the SG-04 subgraphs (e.g., the CZ3 and OCZ3 moieties mentioned above, tertiary amines, two rings connected by a single bond or forming a condensed aromatic system, and any sulfur and halogen atom attached to rings or as part of an aliphatic ramification) as well as the SG-05 subgraphs (three-membered rings, particularly oxirane and thiirane). In the case of DGB17, this measures the global hydrophobicity (SG-01 subgraph, with each bond of a molecule being hydrophobically favored by the presence of sulfur and halogen atoms, as well as aromatic carbons (except those containing nitrogen or bound to a nitrogen or oxygen atom)). DGB02 and DGB17 ranked 6th and 12th, respectively, among the D[GBI]ej indices in the PTML-MLP.
In the case of DGB04, this indicates the increase in the value of the charge through each bond of the molecule (SG-01 subgraph), meaning that functional groups having a high electronic density (e.g., hydroxyl or amino) should be reduced, thus favoring the presence of halogens such as Cl, Br, and I. Simultaneously, DGB04 (ranking as 21st most important among the D[GBI]ej indices) favors heteroaromatic rings with pyridinic nitrogen atoms (particularly pyridine, pyridazine, and pyrimidine). Heteroaliphatic rings lacking nitrogen and oxygen (e.g., tetrahydro-2H-thiopyran) are also quite suitable.
The D[GBI]ej indices DGB09 and DGB18 characterized the diminution of the polar surface area. In the case of DGB09 (the 19th most influential D[GBI]ej index), this focuses on the SG-04 and SG-06 subgraphs. For SG-04, the number of carbonyl, amide, urea, and sulfoxide groups should be reduced as much as possible; alkoxy, phenoxy, alkylamino, pyridine-3-olate, and arylamino are more suitable due to their lower polar surface areas. The same line of thinking applies to polar groups represented by the SG-06 subgraph; the previously described functional groups CZ3 and OCZ3 (Z can be only halogen or methyl) should be present only once when possible. The D[GBI]ej index DGB18 (ranking 11th) focused on the diminution of the global polar surface area of each bond (SG-01 subgraph) of a molecule. Thus, the number of functional groups with high polar surface areas (e.g., amide, sulfone, sulfonamide, and sulfoxide) should be decreased.
The decrease in the atomic weight is described in the PTML-MLP by DGB10 and DGB19. It should be highlighted that DGB10 (ranking 25th among the D[GBI]ej indices) characterized the presence of many fragments in which the atomic weight of the atoms should be diminished. This was the case for the subgraphs of SG-04 (presence of two rings connected by a single bond or forming a condensed aromatic system ring systems and containing mainly carbon, nitrogen, and oxygen, as well as fluorine and, to a lesser degree, chlorine), SG-05 (three-membered rings, mainly cyclopropane), SG-06 (favoring the CZ3 and OCZ3 groups, with Z being preferably fluorine or methyl, respectively), SG-07 (e.g., trifluoromethoxy or tert-butoxy groups attached to any atom), SG-08 (focused on two rings connected by a single bond or forming a condensed aromatic system containing only carbon and nitrogen), and SG-09 (five-membered rings containing only carbon, nitrogen, and oxygen). Regarding DGB19 (being the 17th most important D[GBI]ej index), this is a measure of the molecular weight. Therefore, to favorably decrease its value, the number of atoms different from carbon, nitrogen, oxygen, and fluorine should be greatly reduced.
The D[GBI]ej index DGB14, which ranked 16th in the PTML-MLP model, described the increase in the bond distance in each bond of the molecule, where the presence of atoms such as halogens (other than fluorine) and sulfur is favorable. At the same time, the D[GBI]ej indices DGB15 and DGB16 described the diminution of the dipole moment. In the case of DGB15, which is the most important D[GBI]ej index in the PTML-MLP, this described the same subgraph (SG-01) as explained for DGB18 above. However, while DGB18 gave priority to the decrease in polar groups to diminish the potential interactions via hydrogen bonds, DGB15 focused more on decreasing the number of polar groups to favor non-polar interactions (London dispersion forces through carbons and halogens). Thus, the presence of any moiety containing a carbonyl, amide, thiocarbonyl, nitrile, sulfoxide, sulfone, sulfonamide, thioether, or nitro group should be avoided. At the same time, DGB16 (ranking ninth) characterized the same subgraphs and fragments as DGB10. For this reason, to favorably diminish the dipole moment, the D[GBI]ej index DGB16 prioritized the increment of the number of rings (both aliphatic or aromatic) connected through a single bond or forming a condensed system (SG-04). For this same subgraph, nitrogen (both as amino group and as part of a ring), as well as the hydroxyl, alkoxy, phenoxy, and pyridine-3-olate groups, are also suitable. Through the D[GBI]ej index DGB16, the dipole moment could also be favorably diminished in other subgraphs such as SG-05 (three-membered rings, e.g., cyclopropane), SG-06 (priority is given to tert-butyl and tert-butoxy), SG-07 (tert-butoxy is preferred), SG-08 (condensed heteroaromatic system), and SG-09 (five-membered rings with low polarity, e.g., cyclopentane and pyrrole).
The D[GBI]ej indices DGB11, DGB12, DGB20, DGB21, and DGB22 measured the influence of molecular accessibility based on the occurrence of polar and non-polar interactions in different regions of a molecule, and they ranked 23rd, 10th, 3rd, 15th, and 14th, respectively. In this sense, DGB11 indicated the decrease in the number of five-membered rings. If present, then an aromatic five-membered ring (e.g., pyrrole or imidazole) would be preferred over its aliphatic counterparts, and it should have substitutions in more than two positions. Simultaneously, DGB12 characterized the diminution of the number of many large fragments or subgraphs (SG-13, SG-14, SG-15, SG-16, SG-17, and SG-18). Because these fragments and subgraphs are quite common, they should be based on polar functional groups and moieties that are formed only by carbon, nitrogen, and oxygen. In all of these fragments, aliphatic chains are preferred the least, while structural moieties containing aromatic rings (whether fused or connected through a single bond) are favored. The diminution of linear fragments formed by three bonds (SG-03 subgraph) was described by DGB20, and therefore, when present, such fragments should contain only carbon, nitrogen, and oxygen. In the case of DGB21, this characterized the diminution of fragments or functional groups based on the SG-04 subgraph. Notice that the SG-04 subgraph representing ramifications (and substitution in rings) should also be reduced. If present, SG-04 subgraphs should appear in the form of hydroxyl, alkoxy, phenoxy, amino, alkylamino, and arylamino groups attached to rings (or secondary carbons). When considering DGB22, it should be pointed out that in the case of the SG-11 subgraphs, the presence of six-membered rings is highly desirable, where six-membered aliphatic rings (including those containing heteroatoms) are preferred over their aromatic counterparts.
The D[GBI]ej indices DGB05, DGB06, DGB07, DGB08, DGB13, DGB23, and DGB24, which were graded 13th, 24th, 8th, 5th, 2nd, 22nd, and 7th among the most influential indices in the PTML-MLP, respectively, represent steric aspects, constituting measures of the volume in different regions of a molecule. In the case of DGB05, this described the decrease in the global molecular volume (SG-01 subgraph, each bond of the molecule), thus supporting the presence of ramifications and polysubstituted rings. In contrast, DGB06 favored an increment in the volume by increasing the number of linear fragments in a molecule (SG-02 subgraph), while DGB07 exerted a similar effect to DGB06 but focused on linear fragments based on the SG-12 subgraphs. Notice that DGB06 and DGB07 did not favor the presence of ramifications. Therefore, if ramifications are present, then they are preferred in the periphery of a molecule. Furthermore, DGB08 indicated the increase in the number of six-membered rings, with emphasis on those where the number of substituents was low (not more than two). In the case of DGB13, this involved the increase in the number of ramifications based on the SG-06 subgraph. This means that the presence of the aforementioned functional groups CZ3 and OCZ3 (with Z being mainly methyl or halogen) is favorable. For the case of DGB23, this indicated the decrease in the number of moieties containing the SG-10 subgraph. Notice that SG-10 is composed of SG-02 and SG-06, which means that if SG-06 is present, then the functional groups of the type OCZ3 (with Z being methyl or halogen) are highly suitable. The D[GBI]ej index DGB24 characterized the diminution of the number of the same types of fragments as discussed above for DGB12. However, DGB24 described the influence of the volume of those fragments (instead of the molecular accessibility characterized by DGB12). Finally, the D[GBI]ej index DGB25, which ranked 18th in the PTML-MLP, described the shape of a molecule by decreasing the number of SG-03 subgraphs, which should be part of rings, particularly two or three rings interconnected by single bonds or forming a condensed or fused aromatic system.

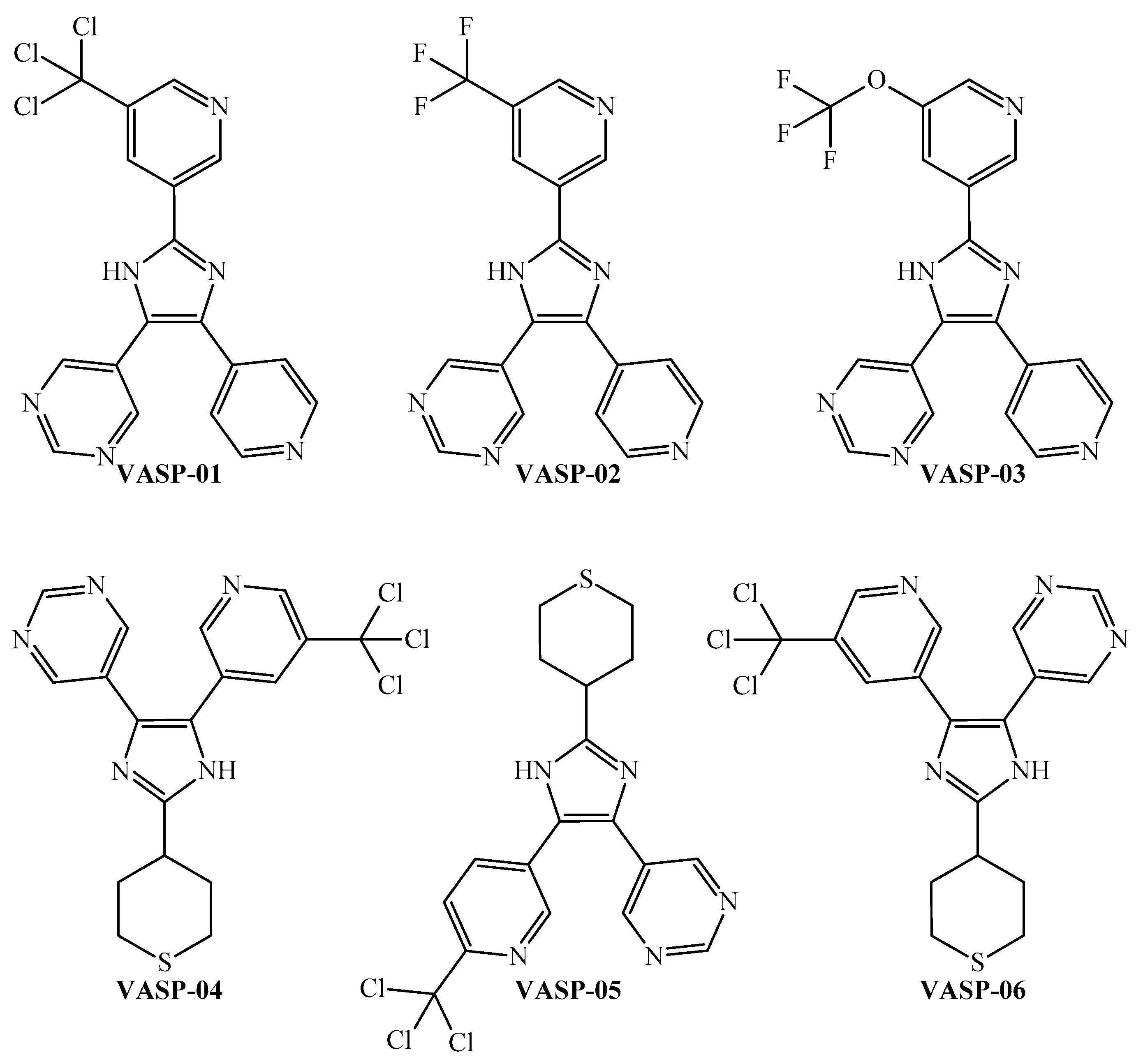
3.3. Combining the PTML-MLP and FBTD to Enable the Design of Multi-Strain Antiplasmodial Inhibitors

Only the joint interpretation of the D[GBI]ej indices in the PTML-MLP model allowed us to design new molecules. In this sense, we would like to point out that, in its essence, the joint interpretation of all the D[GBI]ej indices is to design molecules that maximize the effect of all the physicochemical properties and structural features in the PTML-MLP. This means that the design molecule will contain a series of fragments and moieties whose presences favorably and simultaneously vary (either increasing or decreasing) the values of several D[GBI]ej indices in the PTML-MLP. Thus, the joint interpretations used to design the molecules indicated that several six-membered rings (probably three or four) should be present in the chemical structure of a molecule, either forming a fused ring system or one connected through a single- or a two-bond fragment containing a heteroatom (nitrogen or oxygen). Also, these six-membered rings should be polysubstituted.
The peripheral parts of the molecule are incredibly important. Notice that although most of these six-membered rings in a molecule should be heteroaromatic (pyridine, pyridazine, and pyrimidine), a polysubstituted aromatic ring may also be suitable. In the case of an aliphatic ring (preferably a sulfur-containing cycle), when present, this should be in the periphery of the molecule. The peripheral part of the molecule is also the region where halogens (the sum should not be more than four) or sulfur (not more than one) should be placed. For ramifications, functional groups such as CZ3 and OCZ3 (where Z is methyl, fluorine, or chlorine) are expected to also appear in the peripheral part of the molecule. On the other hand, the presence of a five-membered ring is desirable when this ring is heteroaromatic (pyrrole, imidazole, oxazole, etc.). By rigorously following the joint interpretation as a guideline, we designed six molecules (Figure 6) and predicted their multi-strain antiplasmodial activity using the PTML-MLP.
Notice that if a molecule is predicted by the PTML-MLP to be active with a probability (ProbAct) value higher than 50% against a given P. falciparum strain, then this molecule can be considered to exhibit antiplasmodial activity against that particular strain. Almost all of the predictions for the six designed molecules fell within the AD of the PTML-MLP (Supplementary Information S3). The only exception was the prediction of the molecule VASP-03 against the P. falciparum (FCB), which yielded TSAD = 24 (instead of the ideal value of TSAD = 25). In any case, the results from Table 4 indicate that all of the designed molecules satisfied this condition against several P. falciparum strains. This means that the six designed molecules were predicted by the PTML-MLP to be multi-strain antiplasmodial inhibitors, thus virtually displaying IC50 ≤ 500 nM (the activity cutoff used to develop the PTML-MLP) against three or more P. falciparum strains. It is also important to point out that despite the relatively subtle structural differences among the designed molecules, there was great variation in the ProbAct values across different P. falciparum strains. This confirms the great discriminatory power and meaningful chemistry-driven information of the D[GBI]ej indices in the PTML-MLP, favorably enabling them to capture relevant structural differences not only among heterogenous groups of chemicals (as demonstrated by the statistical performance of the PTML-MLP in Section 3.1, including Figure 2 and Figure 3) but also within a series of structurally related chemicals (as in the case of the six designed molecules).
A simple inspection of Table 4 and Figure 6 indicates that the six designed molecules are divided into two subfamilies of 2,4,5-trisubstituted imidazoles. In the first subfamily, composed of VASP-01, VASP-02, and VASP-03, all of the rings are heteroaromatic, and the main chemical variation is the substitution of the 5-(substituted)pyridin-3-yl moiety, where the order of suitability to enhance the multi-strain antiplasmodial activity is trichloromethyl > trifluoromethoxy > trifluoromethyl. In this sense, the key role of the trichloromethyl fragment in the discovery and design of antiplasmodial molecules has been strongly supported by experimental evidence [86,87]. Likewise, biological assays for determination of the antiplasmodial activity have permitted experimentally corroborating the relative superiority of trifluoromethoxy over trifluoromethyl [88].
Therefore, for the design of the second subfamily of 2,4,5-trisubstituted imidazoles (formed by VASP-04, VASP-05, and VASP-06), we maintained the trichloromethyl group while introducing the tetrahydro-2H-thiopyran moiety in a peripheral part of the molecules. By performing these two chemical modifications, the designed molecules of the second subfamily exhibit higher ProbAct values than those from the first subfamily, with the former being predicted to display multi-strain antiplasmodial activity against the nine P. falciparum strains reported in this work.
Notice that we are not considering all of the possible chemical variations or modifications of the chemical structures within the two subfamilies of 2,4,5-trisubstituted imidazoles; we are focusing only on specific modifications through the use of certain functional groups to demonstrate the ability of the PTML model (through the D[GBI]ej indices) to efficiently discriminate between even small chemical modifications. In any case, the six designed molecules exhibited great potential to inhibit different P. falciparum strains with different degrees of resistance to current antimalarial drugs.
We wanted to assess whether the six designed molecules had some novelty from a chemistry-based point of view. For this, the chemical structures of the designed molecules were searched for in several well-known large databases such as ChEMBL [47,48,89], ZINC [90], and eMolecules [91]. These online repositories, in addition to containing chemical (and, in some cases, bioactivity profile) information on organic molecules, allow searching for chemical similarity by assessing the Tanimoto coefficient (T) [92]. Although the widely accepted cutoff of chemical similarity is T ≥ 0.85 [92,93], here we used a slightly more rigorous cutoff (T ≥ 0.8) to consider potential chemical similarity when comparing the structures of our six designed molecules with the structures of the molecules present in the aforementioned databases.
None of the chemical structures of the designed molecules were reported in these databases. This means that no exact matches were found. Furthermore, the similarity searches using T ≥ 0.8 failed to retrieve any molecules structurally related to our designed molecules (from VASP-01 to VASP-06) in these databases. This strongly supports the chemical novelty and scaffold uniqueness of these designed molecules. At the same time, given that the designed molecules fell into the 2,4,5-trisubstituted imidazole class but with non-reported, multi-substituted heteroaromatic moieties and trichloromethyl and tetrahydrothiopyran fragments, their novelty is not only structural but also pharmacologically contextual, as no such combinations have been reported in the antiplasmodial or wider bioactivity domains.
All of this suggests that the combined use of our PTML-MLP FBTD approach can lead to new scaffolds and scaffold-based chemicals virtually displaying multi-strain antiplasmodial activity which can be considered for future organic synthesis and bioactivity evaluation (in this case, antiplasmodial activity).

3.4. Druglikeness of the Designed Molecules

Regarding the six designed molecules, in addition to assessing their chemistry-based novelty and their encouraging virtual multi-strain antiplasmodial profiles against different P. falciparum strains, we explored the druglikeness. For this, we used the software AlvaDesc v1.0.22 [94], and we computed a series of physicochemical properties (Table 5).
It is important to highlight that physicochemical properties such as the molecular weight (MW), total number of atoms (TNA), number of rotatable bonds (NRB), numbers of atoms behaving as hydrogen bond donors (HBDs) or acceptors (HBAs), molar refractivity (MR), polar surface area (PSA), and the logarithm of the n-octanol-water partition coefficient (MLOGP and ALOGP) are closely related to druglikeness-based standards such as the Lipinski rule of five [95], Ghose’s guidelines [96], and Veber’s filter [97]. In this sense, MW < 500 Da, HBD ≤ 5, and HBA ≤ 10, in addition to the MLOGP and ALOGP being below 5, should be property values that a molecule should have to comply with Lipinski’s rule of five. Furthermore, for the case of Ghose’s guidelines, a molecule should possess an MLOGP and ALOGP in the range from −0.4 to +5.6, with 40 ≤ MR ≤ 130, 180 ≤ MW ≤ 480, and 20 ≤ TNA ≤ 70. To satisfy Veber’s filter, a molecule should exhibit PSA ≤ 140 and NRB ≤ 10. The examination of all these physicochemical property values depicted in Table 5 shows that the six designed molecules complied with these three druglikeness-based standards, thus highlighting their adequate druglikeness.
To further expand our discussion in terms of druglikeness, we predicted many absorption, distribution, metabolism, elimination, and toxicity (ADMET) endpoints of the six designed molecules. For this, we employed the ADMETLab web server [98], which allowed us to estimate 31 ADMET endpoints (Supplementary Information S4). In summary, the six designed molecules demonstrated favorable pharmacokinetic and safety profiles. Despite being predicted to exhibit a relatively low solubility, the six designed molecules displayed acceptable predicted values for Caco-2 cell permeability, human intestinal absorption, and oral bioavailability. Regarding the distribution phase, most of them were predicted to have plasma protein binding (PPB) levels below 90%, and their volumes of distribution fell within the optimal range of 0.04–20 L/kg. The designed molecules were predicted to be able to penetrate the blood–brain barrier (BBB), a critical trait for therapeutic agents targeting cerebral malaria.
Regarding metabolism, the designed molecules showed varying degrees of interaction potential with the major cytochrome P450 (CYP) enzymes (particularly CYP1A2, CYP3A4, CYP2C9, CYP2C19, and CYP2D6). These compounds were mainly estimated as CYP inhibitors and non-CYP substrates. As for the elimination profiles, the predicted clearance rates for the six designed molecules were low, and the half-lives were relatively high.
When assessing toxicity, one concern was the potential for inhibition of the hERG channel, which may lead to cardiotoxic effects. However, we should highlight that the ADMET web server used a stringent threshold (IC50 < 40 µM), which is more conservative than the commonly used cutoff of IC50 ≤ 10 µM for defining significant hERG inhibition. At the same time, some caution should be taken since the designed molecules were predicted to exhibit hepatotoxicity. With regard to mutagenicity, skin sensitization, and acute in vivo toxicity, the compounds were generally considered safe.
Altogether, the predicted ADMET profiles suggest that the six designed molecules possess a sufficiently promising pharmacokinetic and safety profile, justifying future synthesis and experimental investigation in the context of early-stage antimalarial discovery.

4. Conclusions

Despite the current intensive search for novel antiplasmodial agents, new chemicals capable of fighting against P. falciparum malaria are presently needed. Consequently, in silico methodologies should focus more efforts on the early discovery of molecules exhibiting great versatility when inhibiting multiple P. falciparum strains, thus contributing to avoiding drug resistance issues, including MDR strains. The findings presented in this study indicate that the integrated use of a PTML-MLP and the FBTD approach can enable a deeper interpretation of the diverse physicochemical properties and structural aspects associated with the appearance and enhancement of multi-strain antiplasmodial activity. This led to the computational design of new molecules seemingly exhibiting both chemical novelty and multi-strain antiplasmodial profile. The unified application of PTML modeling and FBTD opens new horizons for the chemistry-driven in silico generation of new scaffolds and scaffold-based compounds with multi-strain antiplasmodial activity, which could be expanded to other microbial diseases beyond malaria.

Supplementary Materials

The following supporting information can be downloaded at. https://www.mdpi.com/article/10.3390/microorganisms13071620/s1. Supplementary Information S1: Graph-based indices (GBIs) (including different families of topological indices (TIs) and their normalization-like counterparts (NTIs)), averages avg[GBI]ej, and standard deviation values sdv[GBI]. Supplementary Information S2: D[GBI]ej indices, classification results, local metrics, and applicability domain. Supplementary Information S3: Graph-based indices (GBIs) (including different families of topological indices (TIs) and their normalization-like counterparts (NTIs)), D[GBI]ej indices, classification results, and applicability domain for the designed molecules. Supplementary Information S4: Predicted ADMET endpoints of the designed molecules.

Author Contributions

Conceptualization, A.S.-P.; methodology, A.S.-P.; software, A.S.-P. and V.V.K.; validation, A.S.-P.; formal analysis, A.S.-P.; investigation, A.S.-P., V.V.K., and M.N.D.S.C.; resources, A.S.-P., V.V.K., and M.N.D.S.C.; data curation, A.S.-P. and V.V.K.; writing—original draft preparation, A.S.-P., V.V.K., and M.N.D.S.C.; writing—review and editing, A.S.-P.; visualization, A.S.-P. and V.V.K.; supervision, A.S.-P.; project administration, A.S.-P. and V.V.K.; funding acquisition, M.N.D.S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work received financial support from PT national funds (FCT/MCTES, Fundação para a Ciência e Tecnologia and Ministério da Ciência, Tecnologia e Ensino Superior) through the project UID/50006–Laboratório Associado para a Química Verde–Tecnologias e Processos Limpos.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Siqueira-Neto, J.L.; Wicht, K.J.; Chibale, K.; Burrows, J.N.; Fidock, D.A.; Winzeler, E.A. Antimalarial drug discovery: Progress and approaches. Nat. Rev. Drug Discov. 2023, 22, 807–826. [Google Scholar] [CrossRef]
  2. Xia, J.; Wu, D.; Wu, K.; Zhu, H.; Sun, L.; Lin, W.; Li, K.; Zhang, J.; Wan, L.; Zhang, H.; et al. Epidemiology of Plasmodium falciparum Malaria and Risk Factors for Severe Disease in Hubei Province, China. Am. J. Trop. Med. Hyg. 2020, 103, 1534–1539. [Google Scholar] [CrossRef] [PubMed]
  3. Deutsch-Feldman, M.; Brazeau, N.F.; Parr, J.B.; Thwai, K.L.; Muwonga, J.; Kashamuka, M.; Tshefu Kitoto, A.; Aydemir, O.; Bailey, J.A.; Edwards, J.K.; et al. Spatial and epidemiological drivers of Plasmodium falciparum malaria among adults in the Democratic Republic of the Congo. BMJ Glob. Health 2020, 5, e002316. [Google Scholar] [CrossRef] [PubMed]
  4. Schafer, T.M.; Pessanha de Carvalho, L.; Inoue, J.; Kreidenweiss, A.; Held, J. The problem of antimalarial resistance and its implications for drug discovery. Expert Opin. Drug Discov. 2024, 19, 209–224. [Google Scholar] [CrossRef] [PubMed]
  5. Masserey, T.; Lee, T.; Golumbeanu, M.; Shattock, A.J.; Kelly, S.L.; Hastings, I.M.; Penny, M.A. The influence of biological, epidemiological, and treatment factors on the establishment and spread of drug-resistant Plasmodium falciparum. Elife 2022, 11, e77634. [Google Scholar] [CrossRef]
  6. Dhorda, M.; Amaratunga, C.; Dondorp, A.M. Artemisinin and multidrug-resistant Plasmodium falciparum—A threat for malaria control and elimination. Curr. Opin. Infect. Dis. 2021, 34, 432–439. [Google Scholar] [CrossRef]
  7. Saadeh, K.; Nantha Kumar, N.; Fazmin, I.T.; Edling, C.E.; Jeevaratnam, K. Anti-malarial drugs: Mechanisms underlying their proarrhythmic effects. Br. J. Pharmacol. 2022, 179, 5237–5258. [Google Scholar] [CrossRef]
  8. Lewis, J.; Gregorian, T.; Portillo, I.; Goad, J. Drug interactions with antimalarial medications in older travelers: A clinical guide. J. Travel Med. 2020, 27, taz089. [Google Scholar] [CrossRef]
  9. Umumararungu, T.; Nkuranga, J.B.; Habarurema, G.; Nyandwi, J.B.; Mukazayire, M.J.; Mukiza, J.; Muganga, R.; Hahirwa, I.; Mpenda, M.; Katembezi, A.N.; et al. Recent developments in antimalarial drug discovery. Bioorg. Med. Chem. 2023, 88–89, 117339. [Google Scholar] [CrossRef]
  10. Pandey, S.K.; Anand, U.; Siddiqui, W.A.; Tripathi, R. Drug Development Strategies for Malaria: With the Hope for New Antimalarial Drug Discovery—An Update. Adv. Med. 2023, 2023, 5060665. [Google Scholar] [CrossRef]
  11. Sakura, T.; Ishii, R.; Yoshida, E.; Kita, K.; Kato, T.; Inaoka, D.K. Accelerating Antimalarial Drug Discovery with a New High-Throughput Screen for Fast-Killing Compounds. ACS Infect. Dis. 2024, 10, 4115–4126. [Google Scholar] [CrossRef] [PubMed]
  12. Das, A.; Rajkhowa, S.; Sinha, S.; Zaki, M.E.A. Unveiling potential repurposed drug candidates for Plasmodium falciparum through in silico evaluation: A synergy of structure-based approaches, structure prediction, and molecular dynamics simulations. Comput. Biol. Chem. 2024, 110, 108048. [Google Scholar] [CrossRef]
  13. Elamin, E.M.; Eshage, S.E.; Mohmmode, S.M.; Mukhtar, R.M.; Mahjoub, M.; Sadelin, E.; Shoaib, T.H.; Edris, A.; Elshamly, E.M.; Makki, A.A.; et al. Discovery of dual-target natural antimalarial agents against DHODH and PMT of Plasmodium falciparum: Pharmacophore modelling, molecular docking, quantum mechanics, and molecular dynamics simulations. SAR QSAR Environ. Res. 2023, 34, 709–728. [Google Scholar] [CrossRef] [PubMed]
  14. Mafethe, O.; Ntseane, T.; Dongola, T.H.; Shonhai, A.; Gumede, N.J.; Mokoena, F. Pharmacophore Model-Based Virtual Screening Workflow for Discovery of Inhibitors Targeting Plasmodium falciparum Hsp90. ACS Omega 2023, 8, 38220–38232. [Google Scholar] [CrossRef]
  15. Almasoudi, H.H.; Nahari, M.H. Targeting Plasmodium falciparum Schizont Egress Antigen-1 in Infected Red Blood Cells: Docking-Based Fingerprinting, Density Functional Theory, Molecular Dynamics Simulations, and Binding Free Energy Analysis. Pharmaceuticals 2025, 18, 237. [Google Scholar] [CrossRef]
  16. Oduselu, G.O.; Elebiju, O.F.; Ogunnupebi, T.A.; Akash, S.; Ajani, O.O.; Adebiyi, E. Employing Hexahydroquinolines as PfCDPK4 Inhibitors to Combat Malaria Transmission: An Advanced Computational Approach. Adv. Appl. Bioinform. Chem. 2024, 17, 83–105. [Google Scholar] [CrossRef]
  17. Withers-Martinez, C.; George, R.; Ogrodowicz, R.; Kunzelmann, S.; Purkiss, A.G.; Kjaer, S.; Walker, P.A.; Kovada, V.; Jirgensons, A.; Blackman, M.J. Structural plasticity of Plasmodium falciparum plasmepsin X to accommodate binding of potent macrocyclic hydroxyethylamine inhibitors. J. Mol. Biol. 2025, 437, 169062. [Google Scholar] [CrossRef]
  18. Morcoss, M.M.; Saddik, J.N.; Amin, M.E.; Mohamed, F.A.M.; El-Rashedy, A.A.; Almutairi, T.M.; Youssif, B.G.M.; Lamie, P.F. Design, synthesis, antimalarial activity, and in-silico studies of new benzimidazole/pyridine hybrids as dihydrofolate reductase inhibitors. Bioorg. Chem. 2025, 156, 108171. [Google Scholar] [CrossRef]
  19. Yasir, M.; Park, J.; Han, E.T.; Han, J.H.; Park, W.S.; Chun, W. Identification of Malaria-Selective Proteasome beta5 Inhibitors Through Pharmacophore Modeling, Molecular Docking, and Molecular Dynamics Simulation. Int. J. Mol. Sci. 2024, 25, 11881. [Google Scholar] [CrossRef]
  20. Costa, E.B.; Silva, R.C.; Espejo-Roman, J.M.; Neto, M.F.A.; Cruz, J.N.; Leite, F.H.A.; Silva, C.; Pinheiro, J.C.; Macedo, W.J.C.; Santos, C.B.R. Chemometric methods in antimalarial drug design from 1,2,4,5-tetraoxanes analogues. SAR QSAR Environ. Res. 2020, 31, 677–695. [Google Scholar] [CrossRef]
  21. Roche-Lima, A.; Rosado-Quinones, A.M.; Feliu-Maldonado, R.A.; Figueroa-Gispert, M.D.M.; Diaz-Rivera, J.; Diaz-Gonzalez, R.G.; Carrasquillo-Carrion, K.; Nieves, B.G.; Colon-Lorenzo, E.E.; Serrano, A.E. Antimalarial Drug Combination Predictions Using the Machine Learning Synergy Predictor (MLSyPred(c)) tool. Acta Parasitol. 2024, 69, 415–425. [Google Scholar] [CrossRef] [PubMed]
  22. van Heerden, A.; Turon, G.; Duran-Frigola, M.; Pillay, N.; Birkholtz, L.M. Machine Learning Approaches Identify Chemical Features for Stage-Specific Antimalarial Compounds. ACS Omega 2023, 8, 43813–43826. [Google Scholar] [CrossRef] [PubMed]
  23. Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Perturbation-Theory Machine Learning for Multi-Objective Antibacterial Discovery: Current Status and Future Perspectives. Appl. Sci. 2025, 15, 1166. [Google Scholar] [CrossRef]
  24. Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Optimizing drug discovery using multitasking models for quantitative structure-biological effect relationships: An update of the literature. Expert Opin. Drug Discov. 2023, 18, 1231–1243. [Google Scholar] [CrossRef]
  25. Velasquez-Lopez, Y.; Ruiz-Escudero, A.; Arrasate, S.; Gonzalez-Diaz, H. Implementation of IFPTML Computational Models in Drug Discovery Against Flaviviridae Family. J. Chem. Inf. Model. 2024, 64, 1841–1852. [Google Scholar] [CrossRef]
  26. Santiago, C.; Ortega-Tenezaca, B.; Barbolla, I.; Fundora-Ortiz, B.; Arrasate, S.; Dea-Ayuela, M.A.; Gonzalez-Diaz, H.; Sotomayor, N.; Lete, E. Prediction of Antileishmanial Compounds: General Model, Preparation, and Evaluation of 2-Acylpyrrole Derivatives. J. Chem. Inf. Model. 2022, 62, 3928–3940. [Google Scholar] [CrossRef] [PubMed]
  27. Dieguez-Santana, K.; Casanola-Martin, G.M.; Torres, R.; Rasulev, B.; Green, J.R.; Gonzalez-Diaz, H. Machine Learning Study of Metabolic Networks vs ChEMBL Data of Antibacterial Compounds. Mol. Pharm. 2022, 19, 2151–2163. [Google Scholar] [CrossRef]
  28. Barbolla, I.; Hernandez-Suarez, L.; Quevedo-Tumailli, V.; Nocedo-Mena, D.; Arrasate, S.; Dea-Ayuela, M.A.; Gonzalez-Diaz, H.; Sotomayor, N.; Lete, E. Palladium-mediated synthesis and biological evaluation of C-10b substituted Dihydropyrrolo[1,2-b]isoquinolines as antileishmanial agents. Eur. J. Med. Chem. 2021, 220, 113458. [Google Scholar] [CrossRef]
  29. Vasquez-Dominguez, E.; Armijos-Jaramillo, V.D.; Tejera, E.; Gonzalez-Diaz, H. Multioutput Perturbation-Theory Machine Learning (PTML) Model of ChEMBL Data for Antiretroviral Compounds. Mol. Pharm. 2019, 16, 4200–4212. [Google Scholar] [CrossRef]
  30. Speck-Planche, A.; Kleandrova, V.V. Multi-Condition QSAR Model for the Virtual Design of Chemicals with Dual Pan-Antiviral and Anti-Cytokine Storm Profiles. ACS Omega 2022, 7, 32119–32130. [Google Scholar] [CrossRef]
  31. Baltasar-Marchueta, M.; Llona, L.; M-Alicante, S.; Barbolla, I.; Ibarluzea, M.G.; Ramis, R.; Salomon, A.M.; Fundora, B.; Araujo, A.; Muguruza-Montero, A.; et al. Identification of Riluzole derivatives as novel calmodulin inhibitors with neuroprotective activity by a joint synthesis, biosensor, and computational guided strategy. Biomed. Pharmacother. 2024, 174, 116602. [Google Scholar] [CrossRef]
  32. Sampaio-Dias, I.E.; Rodriguez-Borges, J.E.; Yanez-Perez, V.; Arrasate, S.; Llorente, J.; Brea, J.M.; Bediaga, H.; Vina, D.; Loza, M.I.; Caamano, O.; et al. Synthesis, Pharmacological, and Biological Evaluation of 2-Furoyl-Based MIF-1 Peptidomimetics and the Development of a General-Purpose Model for Allosteric Modulators (ALLOPTML). ACS Chem. Neurosci. 2021, 12, 203–215. [Google Scholar] [CrossRef] [PubMed]
  33. Diez-Alarcia, R.; Yanez-Perez, V.; Muneta-Arrate, I.; Arrasate, S.; Lete, E.; Meana, J.J.; Gonzalez-Diaz, H. Big Data Challenges Targeting Proteins in GPCR Signaling Pathways; Combining PTML-ChEMBL Models and [(35)S]GTPgammaS Binding Assays. ACS Chem. Neurosci. 2019, 10, 4476–4491. [Google Scholar] [CrossRef]
  34. Ferreira da Costa, J.; Silva, D.; Caamano, O.; Brea, J.M.; Loza, M.I.; Munteanu, C.R.; Pazos, A.; Garcia-Mera, X.; Gonzalez-Diaz, H. Perturbation Theory/Machine Learning Model of ChEMBL Data for Dopamine Targets: Docking, Synthesis, and Assay of New l-Prolyl-l-leucyl-glycinamide Peptidomimetics. ACS Chem. Neurosci. 2018, 9, 2572–2587. [Google Scholar] [CrossRef] [PubMed]
  35. Kleandrova, V.V.; Speck-Planche, A. PTML Modeling for Alzheimer’s Disease: Design and Prediction of Virtual Multi-Target Inhibitors of GSK3B, HDAC1, and HDAC6. Curr. Top. Med. Chem. 2020, 20, 1661–1676. [Google Scholar] [CrossRef] [PubMed]
  36. Tenorio-Borroto, E.; Castanedo, N.; Garcia-Mera, X.; Rivadeneira, K.; Vazquez Chagoyan, J.C.; Barbabosa Pliego, A.; Munteanu, C.R.; Gonzalez-Diaz, H. Perturbation Theory Machine Learning Modeling of Immunotoxicity for Drugs Targeting Inflammatory Cytokines and Study of the Antimicrobial G1 Using Cytometric Bead Arrays. Chem. Res. Toxicol. 2019, 32, 1811–1823. [Google Scholar] [CrossRef]
  37. Vazquez-Prieto, S.; Paniagua, E.; Solana, H.; Ubeira, F.M.; Gonzalez-Diaz, H. A study of the Immune Epitope Database for some fungi species using network topological indices. Mol. Divers. 2017, 21, 713–718. [Google Scholar] [CrossRef]
  38. Martinez-Arzate, S.G.; Tenorio-Borroto, E.; Barbabosa Pliego, A.; Diaz-Albiter, H.M.; Vazquez-Chagoyan, J.C.; Gonzalez-Diaz, H. PTML Model for Proteome Mining of B-Cell Epitopes and Theoretical-Experimental Study of Bm86 Protein Sequences from Colima, Mexico. J. Proteome Res. 2017, 16, 4093–4103. [Google Scholar] [CrossRef]
  39. Santana, R.; Zuluaga, R.; Ganan, P.; Arrasate, S.; Onieva, E.; Montemore, M.M.; Gonzalez-Diaz, H. PTML Model for Selection of Nanoparticles, Anticancer Drugs, and Vitamins in the Design of Drug-Vitamin Nanoparticle Release Systems for Cancer Cotherapy. Mol. Pharm. 2020, 17, 2612–2627. [Google Scholar] [CrossRef]
  40. Santana, R.; Zuluaga, R.; Ganan, P.; Arrasate, S.; Onieva, E.; Gonzalez-Diaz, H. Predicting coated-nanoparticle drug release systems with perturbation-theory machine learning (PTML) models. Nanoscale 2020, 12, 13471–13483. [Google Scholar] [CrossRef]
  41. Urista, D.V.; Carrue, D.B.; Otero, I.; Arrasate, S.; Quevedo-Tumailli, V.F.; Gestal, M.; Gonzalez-Diaz, H.; Munteanu, C.R. Prediction of Antimalarial Drug-Decorated Nanoparticle Delivery Systems with Random Forest Models. Biology 2020, 9, 198. [Google Scholar] [CrossRef] [PubMed]
  42. Munteanu, C.R.; Gutierrez-Asorey, P.; Blanes-Rodriguez, M.; Hidalgo-Delgado, I.; Blanco Liverio, M.J.; Castineiras Galdo, B.; Porto-Pazos, A.B.; Gestal, M.; Arrasate, S.; Gonzalez-Diaz, H. Prediction of Anti-Glioblastoma Drug-Decorated Nanoparticle Delivery Systems Using Molecular Descriptors and Machine Learning. Int. J. Mol. Sci. 2021, 22, 11519. [Google Scholar] [CrossRef]
  43. Cabrera-Andrade, A.; Lopez-Cortes, A.; Munteanu, C.R.; Pazos, A.; Perez-Castillo, Y.; Tejera, E.; Arrasate, S.; Gonzalez-Diaz, H. Perturbation-Theory Machine Learning (PTML) Multilabel Model of the ChEMBL Dataset of Preclinical Assays for Antisarcoma Compounds. ACS Omega 2020, 5, 27211–27220. [Google Scholar] [CrossRef]
  44. Cabrera-Andrade, A.; Lopez-Cortes, A.; Jaramillo-Koupermann, G.; Gonzalez-Diaz, H.; Pazos, A.; Munteanu, C.R.; Perez-Castillo, Y.; Tejera, E. A Multi-Objective Approach for Anti-Osteosarcoma Cancer Agents Discovery through Drug Repurposing. Pharmaceuticals 2020, 13, 409. [Google Scholar] [CrossRef]
  45. Bediaga, H.; Arrasate, S.; Gonzalez-Diaz, H. PTML Combinatorial Model of ChEMBL Compounds Assays for Multiple Types of Cancer. ACS Comb. Sci. 2018, 20, 621–632. [Google Scholar] [CrossRef]
  46. Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. Perturbation Theory Machine Learning Model for Phenotypic Early Antineoplastic Drug Discovery: Design of Virtual Anti-Lung-Cancer Agents. Appl. Sci. 2024, 14, 9344. [Google Scholar] [CrossRef]
  47. Mendez, D.; Gaulton, A.; Bento, A.P.; Chambers, J.; De Veij, M.; Felix, E.; Magarinos, M.P.; Mosquera, J.F.; Mutowo, P.; Nowotka, M.; et al. ChEMBL: Towards direct deposition of bioassay data. Nucleic Acids Res. 2019, 47, D930–D940. [Google Scholar] [CrossRef]
  48. Gaulton, A.; Bellis, L.J.; Bento, A.P.; Chambers, J.; Davies, M.; Hersey, A.; Light, Y.; McGlinchey, S.; Michalovich, D.; Al-Lazikani, B.; et al. ChEMBL: A large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. [Google Scholar] [CrossRef] [PubMed]
  49. Mok, N.Y.; Brenk, R. Mining the ChEMBL database: An efficient chemoinformatics workflow for assembling an ion channel-focused screening library. J. Chem. Inf. Model. 2011, 51, 2449–2454. [Google Scholar] [CrossRef]
  50. Quadros, H.C.; Herrmann, L.; Manaranche, J.; Paloque, L.; Borges-Silva, M.C.; Dziwornu, G.A.; D’Alessandro, S.; Chibale, K.; Basilico, N.; Benoit-Vical, F.; et al. Characterization of antimalarial activity of artemisinin-based hybrid drugs. Antimicrob. Agents Chemother. 2024, 68, e0014324. [Google Scholar] [CrossRef]
  51. Herrmann, L.; Leidenberger, M.; Sacramento de Morais, A.; Mai, C.; Capci, A.; da Cruz Borges Silva, M.; Plass, F.; Kahnt, A.; Moreira, D.R.M.; Kappes, B.; et al. Autofluorescent antimalarials by hybridization of artemisinin and coumarin: In vitro/in vivo studies and live-cell imaging. Chem. Sci. 2023, 14, 12941–12952. [Google Scholar] [CrossRef] [PubMed]
  52. Kore, M.; Acharya, D.; Sharma, L.; Vembar, S.S.; Sundriyal, S. Development and experimental validation of a machine learning model for the prediction of new antimalarials. BMC Chem. 2025, 19, 28. [Google Scholar] [CrossRef]
  53. Estrada, E.; Gutiérrez, Y. MODESLAB, v1.5; Santiago de Compostela, Spain. 2004. Available online: https://insilicomoleculardesign.com/software-databases/ (accessed on 10 May 2025).
  54. Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; WILEY-VCH Verlag GmbH: Hoboken, NJ, USA, 2000. [Google Scholar]
  55. Todeschini, R.; Consonni, V. (Eds.) Molecular Descriptors for Chemoinformatics; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009; Volumes I and II. [Google Scholar]
  56. Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. In Silico Approach for Antibacterial Discovery: PTML Modeling of Virtual Multi-Strain Inhibitors Against Staphylococcus aureus. Pharmaceuticals 2025, 18, 196. [Google Scholar] [CrossRef] [PubMed]
  57. Urias, R.W.; Barigye, S.J.; Marrero-Ponce, Y.; Garcia-Jacas, C.R.; Valdes-Martini, J.R.; Perez-Gimenez, F. IMMAN: Free software for information theory-based chemometric analysis. Mol. Divers. 2015, 19, 305–319. [Google Scholar] [CrossRef]
  58. Stahura, F.L.; Godden, J.W.; Bajorath, J. Differential Shannon entropy analysis identifies molecular property descriptors that predict aqueous solubility of synthetic compounds with high accuracy in binary QSAR calculations. J. Chem. Inf. Comput. Sci. 2002, 42, 550–558. [Google Scholar] [CrossRef] [PubMed]
  59. Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
  60. Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C: The art of Scientific Computing, 1st ed.; Cambridge University Press: New York, NY, USA, 1988. [Google Scholar]
  61. STATISTICA (Data Analysis Software System); v13.5.0.17; TIBCO-Software-Inc.: Palo Alto, CA, USA, 2018.
  62. Schneider, G.; Wrede, P. Artificial neural networks for computer-based molecular design. Prog. Biophys. Mol. Biol. 1998, 70, 175–222. [Google Scholar] [CrossRef]
  63. Manallack, D.T.; Livingstone, D.J.; A-Razzak, M.; Glen, R.C. Neural Networks and Expert Systems in Molecular Design. In Advanced Computer––Assisted Techniques in Drug Discovery; van de Waterbeemd, H., Ed.; Methods and Principles in Medicinal Chemistry; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1994; pp. 293–331. [Google Scholar]
  64. Chicco, D.; Jurman, G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification. BioData Min. 2023, 16, 4. [Google Scholar] [CrossRef]
  65. Rende, M.; Pistilli, A.; Stabile, A.M.; Terenzi, A.; Cattaneo, A.; Ugolini, G.; Sanna, P. Role of nerve growth factor and its receptors in non-nervous cancer growth: Efficacy of a tyrosine kinase inhibitor (AG879) and neutralizing antibodies antityrosine kinase receptor A and antinerve growth factor: An in-vitro and in-vivo study. Anti-Cancer Drugs 2006, 17, 929–941. [Google Scholar] [CrossRef]
  66. He, H.; Yumiko, H.; Aviv, G.; Yoshihiro, Y.; Hiroyuki, M.; Yuko, K.; Toshiaki, K.; Ching-Yi, H.; Hsing-Jien, K.; Guillaume, L.; et al. The Tyr-Kinase Inhibitor AG879, that Blocks the ETK-PAK1 Interaction, Suppresses the RAS-induced PAK1 Activation and Malignant Transformation. Cancer Biol. Ther. 2004, 3, 96–101. [Google Scholar] [CrossRef]
  67. Zhou, X.; Lin, H.; Lin, H. Global Sensitivity Analysis. In Encyclopedia of GIS; Shekhar, S., Xiong, H., Eds.; Springer: Boston, MA, USA, 2008; pp. 408–409. [Google Scholar]
  68. Estrada, E. Spectral moments of the edge adjacency matrix in molecular graphs. 1. Definition and applications for the prediction of physical properties of alkanes. J. Chem. Inf. Comput. Sci. 1996, 36, 844–849. [Google Scholar] [CrossRef]
  69. Estrada, E. Spectral moments of the edge adjacency matrix in molecular graphs. 2. Molecules containing heteroatoms and QSAR applications. J. Chem. Inf. Comput. Sci. 1997, 37, 320–328. [Google Scholar] [CrossRef]
  70. Estrada, E. Spectral moments of the edge adjacency matrix in molecular graphs. 3. Molecules containing cycles. J. Chem. Inf. Comput. Sci. 1998, 38, 23–27. [Google Scholar] [CrossRef]
  71. Estrada, E. How the parts organize in the whole? A top-down view of molecular descriptors and properties for QSAR and drug design. Mini Rev. Med. Chem. 2008, 8, 213–221. [Google Scholar] [CrossRef]
  72. Estrada, E.; Patlewicz, G.; Gutierrez, Y. From knowledge generation to knowledge archive. A general strategy using TOPS-MODE with DEREK to formulate new alerts for skin sensitization. J. Chem. Inf. Comput. Sci. 2004, 44, 688–698. [Google Scholar] [CrossRef] [PubMed]
  73. Estrada, E.; Molina, E. Automatic extraction of structural alerts for predicting chromosome aberrations of organic compounds. J. Mol. Graph. Model. 2006, 25, 275–288. [Google Scholar] [CrossRef]
  74. Estrada, E. Physicochemical Interpretation of Molecular Connectivity Indices. J. Phys. Chem. A 2002, 106, 9085–9091. [Google Scholar] [CrossRef]
  75. Kier, L.B.; Murray, W.J.; Hall, L.H. Molecular connectivity. 4. Relationships to biological activities. J. Med. Chem. 1975, 18, 1272–1274. [Google Scholar] [CrossRef]
  76. Kier, L.B.; Hall, L.H. Molecular connectivity VII: Specific treatment of heteroatoms. J. Pharm. Sci. 1976, 65, 1806–1809. [Google Scholar] [CrossRef]
  77. Hall, L.H.; Kier, L.B. Structure-activity studies using valence molecular connectivity. J. Pharm. Sci. 1977, 66, 642–644. [Google Scholar] [CrossRef]
  78. Kier, L.B.; Hall, L.H. Derivation and significance of valence molecular connectivity. J. Pharm. Sci. 1981, 70, 583–589. [Google Scholar] [CrossRef] [PubMed]
  79. Kier, L.B.; Hall, L.H. Intermolecular accessibility: The meaning of molecular connectivity. J. Chem. Inf. Comput. Sci. 2000, 40, 792–795. [Google Scholar] [CrossRef]
  80. Kier, L.B.; Hall, L.H. Molecular connectivity: Intermolecular accessibility and encounter simulation. J. Mol. Graph. Model. 2001, 20, 76–83. [Google Scholar] [CrossRef]
  81. Estrada, E. Edge adjacency relationship and a novel topological index related to molecular volume. J. Chem. Inf. Comput. Sci. 1995, 35, 31–33. [Google Scholar] [CrossRef]
  82. Estrada, E. Edge adjacency relationships in molecular graphs containing heteroatoms: A new topological index related to molar volume. J. Chem. Inf. Comput. Sci. 1995, 35, 701–707. [Google Scholar] [CrossRef]
  83. Estrada, E.; Rodríguez, L. Edge-Connectivity Indices in QSPR/QSAR Studies. 1. Comparison to Other Topological Indices in QSPR Studies. J. Chem. Inf. Comput. Sci. 1999, 39, 1037–1041. [Google Scholar] [CrossRef]
  84. Estrada, E. Edge-Connectivity Indices in QSPR/QSAR Studies. 2. Accounting for Long-Range Bond Contributions. J. Chem. Inf. Comput. Sci. 1999, 39, 1042–1048. [Google Scholar] [CrossRef]
  85. Estrada, E.; Guevara, N.; Gutman, I. Extension of Edge Connectivity Index. Relationships to Line Graph Indices and QSPR Applications. J. Chem. Inf. Comput. Sci. 1998, 38, 428–431. [Google Scholar] [CrossRef]
  86. Amrane, D.; Gellis, A.; Hutter, S.; Prieri, M.; Verhaeghe, P.; Azas, N.; Vanelle, P.; Primas, N. Synthesis and Antiplasmodial Evaluation of 4-Carboxamido- and 4-Alkoxy-2-Trichloromethyl Quinazolines. Molecules 2020, 25, 3929. [Google Scholar] [CrossRef]
  87. Desroches, J.; Kieffer, C.; Primas, N.; Hutter, S.; Gellis, A.; El-Kashef, H.; Rathelot, P.; Verhaeghe, P.; Azas, N.; Vanelle, P. Discovery of new hit-molecules targeting Plasmodium falciparum through a global SAR study of the 4-substituted-2-trichloromethylquinazoline antiplasmodial scaffold. Eur. J. Med. Chem. 2017, 125, 68–86. [Google Scholar] [CrossRef]
  88. Amrane, D.; Primas, N.; Arnold, C.S.; Hutter, S.; Louis, B.; Sanz-Serrano, J.; Azqueta, A.; Amanzougaghene, N.; Tajeri, S.; Mazier, D.; et al. Antiplasmodial 2-thiophenoxy-3-trichloromethyl quinoxalines target the apicoplast of Plasmodium falciparum. Eur. J. Med. Chem. 2021, 224, 113722. [Google Scholar] [CrossRef] [PubMed]
  89. Overington, J. ChEMBL. An interview with John Overington, team leader, chemogenomics at the European Bioinformatics Institute Outstation of the European Molecular Biology Laboratory (EMBL-EBI). Interview by Wendy A. Warr. J. Comput. Aided Mol. Des. 2009, 23, 195–198. [Google Scholar] [CrossRef]
  90. Irwin, J.J.; Shoichet, B.K. ZINC—A free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005, 45, 177–182. [Google Scholar] [CrossRef] [PubMed]
  91. Hersey, A.; Chambers, J.; Bellis, L.; Patricia Bento, A.; Gaulton, A.; Overington, J.P. Chemical databases: Curation or integration by user-defined equivalence? Drug Discov. Today Technol. 2015, 14, 17–24. [Google Scholar] [CrossRef] [PubMed]
  92. Maggiora, G.; Vogt, M.; Stumpfe, D.; Bajorath, J. Molecular similarity in medicinal chemistry. J. Med. Chem. 2014, 57, 3186–3204. [Google Scholar] [CrossRef]
  93. Martin, Y.C.; Kofron, J.L.; Traphagen, L.M. Do structurally similar molecules have similar biological activity? J. Med. Chem. 2002, 45, 4350–4358. [Google Scholar] [CrossRef]
  94. Mauri, A. alvaDesc: A Tool to Calculate and Analyze Molecular Descriptors and Fingerprints. In Ecotoxicological QSARs; Roy, K., Ed.; Springer: New York, NY, USA, 2020; pp. 801–820. [Google Scholar]
  95. Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 2001, 46, 3–26. [Google Scholar] [CrossRef]
  96. Ghose, A.K.; Viswanadhan, V.N.; Wendoloski, J.J. A knowledge-based approach in designing combinatorial or medicinal chemistry libraries for drug discovery. 1. A qualitative and quantitative characterization of known drug databases. J. Comb. Chem. 1999, 1, 55–68. [Google Scholar] [CrossRef]
  97. Veber, D.F.; Johnson, S.R.; Cheng, H.Y.; Smith, B.R.; Ward, K.W.; Kopple, K.D. Molecular properties that influence the oral bioavailability of drug candidates. J. Med. Chem. 2002, 45, 2615–2623. [Google Scholar] [CrossRef]
  98. Dong, J.; Wang, N.N.; Yao, Z.J.; Zhang, L.; Cheng, Y.; Ouyang, D.; Lu, A.P.; Cao, D.S. ADMETlab: A platform for systematic ADMET evaluation based on a comprehensively collected ADMET database. J. Cheminformatics 2018, 10, 29. [Google Scholar] [CrossRef]
Microorganisms 13 01620 g001
Figure 1. Combination of a PTML-MLP and the FBTD approach to enable the prediction and de novo design of versatile antiplasmodial chemicals. The training and test sets are used to find the best PTML-MLP and assess the predictive power, respectively. Microsoft Excel, as a math editor and tabulator, enables the use of different mathematical formulas related to the Box–Jenkins approach (see Equations (1) and (2)). The FBTD approach is applied to perform two tasks, namely the physicochemical and substructural interpretation of the PTML-MLP with the subsequent extraction of the subgraphs (in the form of molecular fragments such as functional groups or rings) responsible for the multi-strain antiplasmodial activity and the fusion and connection of different suitable fragments, yielding new drug-like molecules virtually exhibiting multi-strain antiplasmodial activity. More details on the application of the FBTD approach will be given in Section 3.
Figure 1. Combination of a PTML-MLP and the FBTD approach to enable the prediction and de novo design of versatile antiplasmodial chemicals. The training and test sets are used to find the best PTML-MLP and assess the predictive power, respectively. Microsoft Excel, as a math editor and tabulator, enables the use of different mathematical formulas related to the Box–Jenkins approach (see Equations (1) and (2)). The FBTD approach is applied to perform two tasks, namely the physicochemical and substructural interpretation of the PTML-MLP with the subsequent extraction of the subgraphs (in the form of molecular fragments such as functional groups or rings) responsible for the multi-strain antiplasmodial activity and the fusion and connection of different suitable fragments, yielding new drug-like molecules virtually exhibiting multi-strain antiplasmodial activity. More details on the application of the FBTD approach will be given in Section 3.
Microorganisms 13 01620 g001
Microorganisms 13 01620 g002
Figure 2. Chemical structures of different antimalarial drugs whose multi-strain antiplasmodial profile was correctly predicted by the PTML-MLP. Notice that X = H for chloroquine, while X = OH for hydroxychloroquine.
Figure 2. Chemical structures of different antimalarial drugs whose multi-strain antiplasmodial profile was correctly predicted by the PTML-MLP. Notice that X = H for chloroquine, while X = OH for hydroxychloroquine.
Microorganisms 13 01620 g002
Microorganisms 13 01620 g003
Figure 3. Chemicals containing different molecular patterns, which were predicted by the PTML-MLP to be versatile inhibitors against different P. falciparum strains.
Figure 3. Chemicals containing different molecular patterns, which were predicted by the PTML-MLP to be versatile inhibitors against different P. falciparum strains.
Microorganisms 13 01620 g003
Microorganisms 13 01620 g004
Figure 4. Sensitivity values (SVs): measures of the influence or discriminatory power of each of the D[GBI]ej indices present in the PTML-MLP model.
Figure 4. Sensitivity values (SVs): measures of the influence or discriminatory power of each of the D[GBI]ej indices present in the PTML-MLP model.
Microorganisms 13 01620 g004
Microorganisms 13 01620 g005
Figure 5. Most common subgraphs (SGs) characterized by the D[GBI]ej indices of the PTML-MLP. These generic fragments represent a wide variety of substructural moieties in the molecules.
Figure 5. Most common subgraphs (SGs) characterized by the D[GBI]ej indices of the PTML-MLP. These generic fragments represent a wide variety of substructural moieties in the molecules.
Microorganisms 13 01620 g005
Microorganisms 13 01620 g006
Figure 6. New molecules designed through the application of the FBTD approach to the PTML-MLP.
Figure 6. New molecules designed through the application of the FBTD approach to the PTML-MLP.
Microorganisms 13 01620 g006
Table 1. The D[GBI]ej indices: symbols and concepts.
Table 1. The D[GBI]ej indices: symbols and concepts.
Codes a,b,cSymbolsConcepts
DGB01D[SM(Mol)4]tgMulti-label graph index derived from the bond-based spectral moment of the 4th order, weighted by atom-based molar refractivities.
DGB02D[NSM(Hyd)3]tgMulti-label graph index derived from the normalized bond-based spectral moment of the 3rd order, weighted by atom-based hydrophobicities.
DGB03D[NSM(Mol)1]tgMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by atom-based molar refractivities.
DGB04D[NSM(Gas)1]tgMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by Gasteiger-Marsili atomic charges.
DGB05D[Ne(P)1]tgMulti-label graph index derived from the normalized bond-based connectivity of the 1st order, containing only path subgraphs.
DGB06D[Ne(P)2]tgMulti-label graph index derived from the normalized bond-based connectivity of the 2nd order, containing only path subgraphs.
DGB07D[Ne(P)6]tgMulti-label graph index derived from the normalized bond-based connectivity of the 6th order, containing only path subgraphs.
DGB08D[Ne(Ch)6]tgMulti-label graph index derived from the normalized bond-based connectivity of the 6th order, containing only cycle (ring) subgraphs.
DGB09D[SM(Psa)4]dsMulti-label graph index derived from the bond-based spectral moment of the 4th order, weighted by atom-based polar surface areas.
DGB10D[SM(Ato)7]dsMulti-label graph index derived from the bond-based spectral moment of the 7th order, weighted by atomic weights.
DGB11D[Xv(Ch)5]dsMulti-label graph index derived from the atom-based valence connectivity of the 5th order, containing only cycle (ring) subgraphs.
DGB12D[Xv(PC)6]dsMulti-label graph index derived from the atom-based valence connectivity of the 6th order, containing only path-cluster subgraphs.
DGB13D[e(C)4]dsMulti-label graph index derived from the bond-based connectivity of the 4th order, containing only cluster subgraphs.
DGB14D[NSM(Std)1]dsMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by the standard bond distances.
DGB15D[NSM(Dip)1]dsMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by the bond dipole moments.
DGB16D[NSM(Dip)7]dsMulti-label graph index derived from the normalized bond-based spectral moment of the 7th order, weighted by the bond dipole moments.
DGB17D[NSM(Hyd)1]dsMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by atom-based hydrophobicities.
DGB18D[NSM(Psa)1]dsMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by atom-based polar surface areas.
DGB19D[NSM(Ato)1]dsMulti-label graph index derived from the normalized bond-based spectral moment of the 1st order, weighted by atomic weights.
DGB20D[NXv(P)3]dsMulti-label graph index derived from the normalized atom-based valence connectivity of the 3rd order, containing only path subgraphs.
DGB21D[NXv(C)3]dsMulti-label graph index derived from the normalized atom-based valence connectivity of the 3rd order, containing only cluster subgraphs.
DGB22D[NXv(Ch)6]dsMulti-label graph index derived from the normalized atom-based valence connectivity of the 6th order, containing only cycle (ring) subgraphs.
DGB23D[Ne(C)6]dsMulti-label graph index derived from the normalized bond-based connectivity of the 6th order, containing only cluster subgraphs.
DGB24D[Ne(PC)6]dsMulti-label graph index derived from the normalized bond-based connectivity of the 6th order, containing only path-cluster subgraphs.
DGB25D[NK(Alpha)3]dsMulti-label graph index derived from the normalized alpha-modified shape descriptor of the 3rd order, containing only path subgraphs.
a The codes for the D[GBI]ej indices will be used throughout the entire manuscript. b For the D[GBI]ej indices containing the symbol “SM”, the order (mentioned above with the notation “o”) is the maximum number of bonds that a fragment can have without considering bond multiplicity. For the D[GBI]ej indices containing the symbols “Xv” and “e”, the order (mentioned above with the notation “m”) is the exact number of bonds (without considering multiplicity) present in a fragment. c The notation tg indicates that the D[GBI]ej indices depend on the chemical structure and the specific P. falciparum strain. Likewise, ds indicates that the D[GBI]ej indices depend on the chemical structure and whether a P. falciparum strain is sensitive or resistant to current antimalarial drugs.
Table 2. Global metrics of performance associated with the PTML-MLP.
Table 2. Global metrics of performance associated with the PTML-MLP.
SYMBOLS aTraining SetTest Set
NActive36131204
TP33931074
Sn93.91%89.20%
NInactive35841194
TN32601029
Sp90.96%86.18%
nMCC0.9250.877
aNActive = number of cases annotated as active; NInactive = number of cases annotated as inactive; TP = true positive; TN = true negative; Sn = sensitivity (percentage of cases correctly predicted as active); Sp = specificity (percentage of cases correctly predicted as inactive); nMCC = normalized Matthews correlation coefficient.
Table 3. Variation in the values of the different D[GBI]ej indices.
Table 3. Variation in the values of the different D[GBI]ej indices.
Codes aAverage ValuesTendency b
ActiveInactive
DGB018.220 × 10−3−1.054 × 10−1Increase
DGB021.195 × 10−2−5.387 × 10−2Increase
DGB03−2.959 × 10−4−1.455 × 10−2Increase
DGB045.718 × 10−3−6.431 × 10−2Increase
DGB05−9.300 × 10−31.488 × 10−1Decrease
DGB063.953 × 10−3−2.272 × 10−1Increase
DGB076.967 × 10−3−2.938 × 10−1Increase
DGB08−7.765 × 10−3−8.953 × 10−2Increase
DGB093.773 × 10−31.589 × 10−1Decrease
DGB101.687 × 10−41.049 × 10−1Decrease
DGB11−4.437 × 10−42.400 × 10−2Decrease
DGB124.613 × 10−31.039 × 10−2Decrease
DGB131.253 × 10−2−4.819 × 10−2Increase
DGB142.450 × 10−4−1.427 × 10−1Increase
DGB15−1.374 × 10−32.750 × 10−1Decrease
DGB162.155 × 10−31.896 × 10−1Decrease
DGB174.187 × 10−3−1.435 × 10−1Increase
DGB185.651 × 10−52.241 × 10−1Decrease
DGB198.620 × 10−31.171 × 10−1Decrease
DGB202.873 × 10−34.588 × 10−2Decrease
DGB214.693 × 10−31.153 × 10−1Decrease
DGB224.674 × 10−3−1.728 × 10−1Increase
DGB232.511 × 10−31.447 × 10−1Decrease
DGB241.987 × 10−32.057 × 10−3Decrease
DGB251.196 × 10−38.020 × 10−2Decrease
a The codes are the same as those present in Table 1. b This refers to the variation (decrease or increase in the value of a defined D[GBI]ej index).
Table 4. Predictions of multi-strain antiplasmodial activity for the six designed molecules.
Table 4. Predictions of multi-strain antiplasmodial activity for the six designed molecules.
tgadsbProbAct (%) c,d
VASP-01VASP-02VASP-03VASP-04VASP-05VASP-06
P. falciparum (7G8)Drug-resistant56.8344.1146.1474.2473.7074.24
P. falciparum (Dd2)Drug-resistant56.9145.8349.8182.2681.0082.26
P. falciparum (D6)Drug-sensitive64.4559.4365.3683.9182.5883.91
P. falciparum (3D7)Drug-sensitive64.3849.0057.7582.2181.1282.21
P. falciparum (W2)Drug-resistant66.4238.1645.5980.3379.0880.33
P. falciparum (D10)Drug-sensitive69.3444.9151.0474.3072.8674.30
P. falciparum (FCB)Drug-resistant61.3687.0687.1464.4466.6764.44
P. falciparum (K1)Drug-resistant69.6041.7047.3478.6977.9978.69
P. falciparum (NF54)Drug-sensitive66.9851.0155.7179.9879.1879.98
a The element tg refers to a specific P. falciparum strain. b The element ds indicates whether a defined P. falciparum strain is sensitive or resistant to current antimalarial drugs. c The symbol “VASP-” is the code associated with each designed molecule. d The term “ProbAct” represents the probability value (expressed as a percentage) predicted by the PTML-MLP to classify a molecule as active.
Table 5. Druglikeness-related physicochemical properties calculated for the designed molecules.
Table 5. Druglikeness-related physicochemical properties calculated for the designed molecules.
IDPhysicochemical Properties a
MWTNANRBHBDHBAMRPSAMLOGPALOGP
VASP-01417.7038315106.2680.242.90412.8515
VASP-02368.353831891.76080.242.5682.2614
VASP-03384.353941993.36189.471.80883.439
VASP-04440.8143314113.1792.653.63013.4394
VASP-05440.8143314112.8092.653.63013.8679
VASP-06440.8143314113.1792.653.63013.4394
a The symbols used for the different physicochemical properties are as follows: MW = molecular weight (expressed in daltons); TNA = total number of atoms in a molecule (including hydrogen atoms); NRB = number of rotatable bonds; HBD = number of atoms participating in hydrogen bonds as donors; HBA = number of atoms participating in hydrogen bonds as acceptors; MR = molar refractivity (expressed in cm3/mol), estimated according to the Ghose–Crippen atomic and fragment contributions; PSA = topological polar surface area (expressed in Å2), estimated from atomic and fragment contributions for functional groups containing nitrogen, oxygen, fluor, sulfur, and phosphorus; MLOGP = logarithm of the n-octanol-water partition coefficient, estimated according to Moriguchi’s method; ALOGP = logarithm of the n-octanol-water partition coefficient, estimated according to the Ghose–Crippen atomic and fragment contributions.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kleandrova, V.V.; Cordeiro, M.N.D.S.; Speck-Planche, A. In Silico Approach for Early Antimalarial Drug Discovery: De Novo Design of Virtual Multi-Strain Antiplasmodial Inhibitors. Microorganisms 2025, 13, 1620. https://doi.org/10.3390/microorganisms13071620

AMA Style

Kleandrova VV, Cordeiro MNDS, Speck-Planche A. In Silico Approach for Early Antimalarial Drug Discovery: De Novo Design of Virtual Multi-Strain Antiplasmodial Inhibitors. Microorganisms. 2025; 13(7):1620. https://doi.org/10.3390/microorganisms13071620

Chicago/Turabian Style

Kleandrova, Valeria V., M. Natália D. S. Cordeiro, and Alejandro Speck-Planche. 2025. "In Silico Approach for Early Antimalarial Drug Discovery: De Novo Design of Virtual Multi-Strain Antiplasmodial Inhibitors" Microorganisms 13, no. 7: 1620. https://doi.org/10.3390/microorganisms13071620

APA Style

Kleandrova, V. V., Cordeiro, M. N. D. S., & Speck-Planche, A. (2025). In Silico Approach for Early Antimalarial Drug Discovery: De Novo Design of Virtual Multi-Strain Antiplasmodial Inhibitors. Microorganisms, 13(7), 1620. https://doi.org/10.3390/microorganisms13071620

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop