A Crawling Soft Robot Driven by Pneumatic Foldable Actuators Based on Miura-Ori
Abstract
1. Introduction
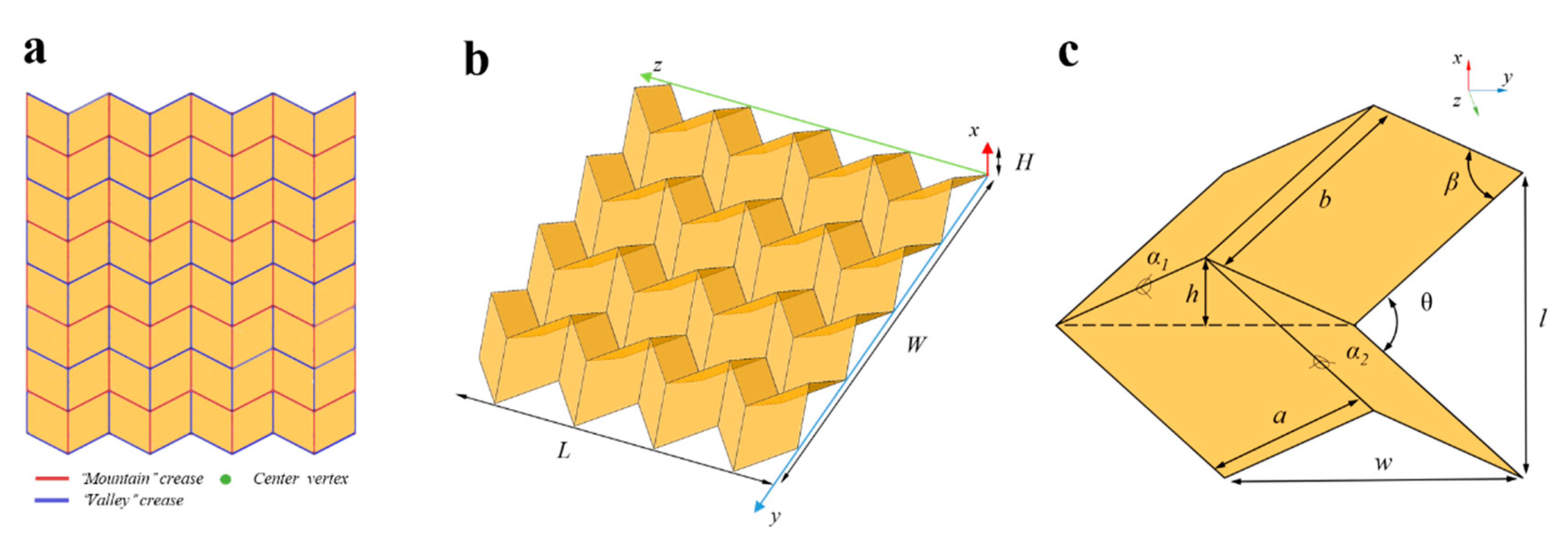
2. Inspiration from Miura-Ori
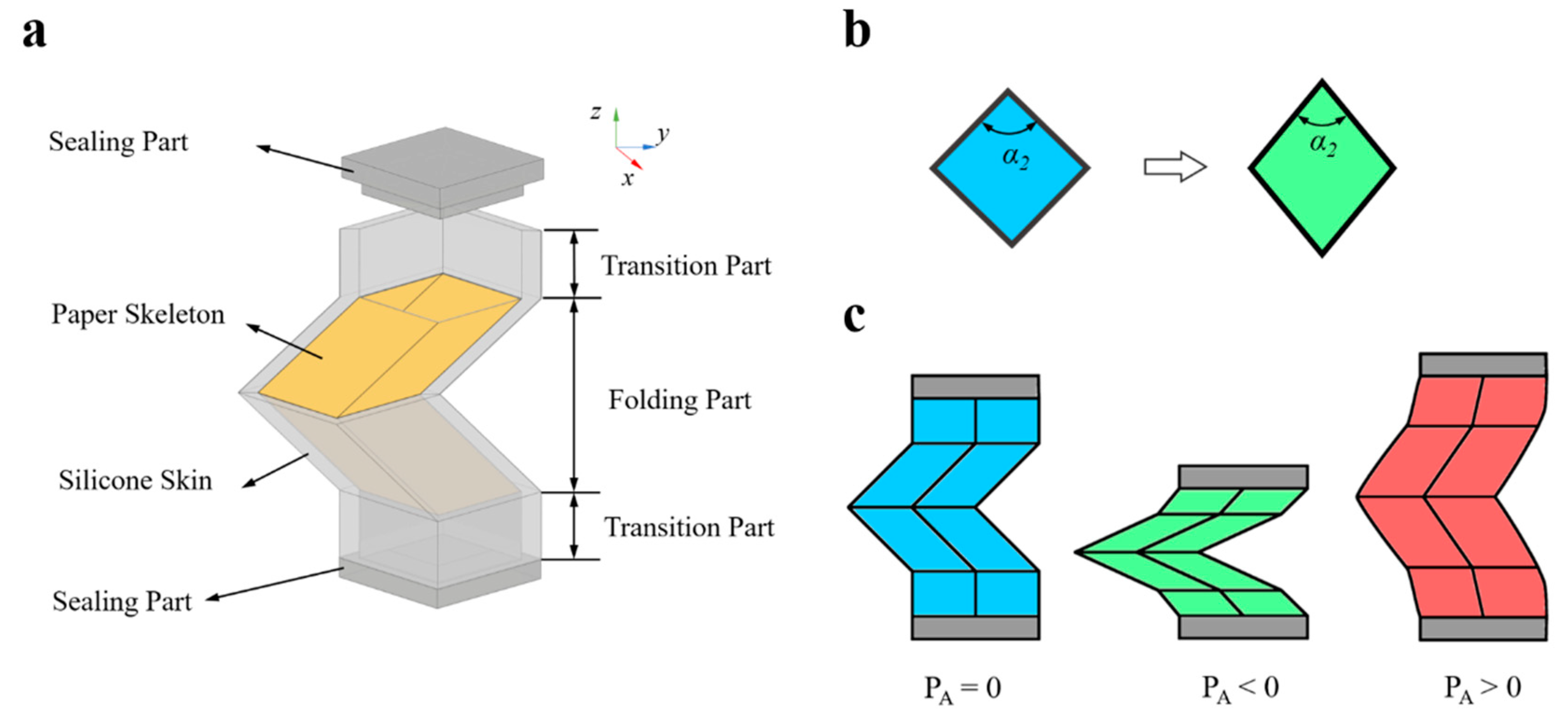
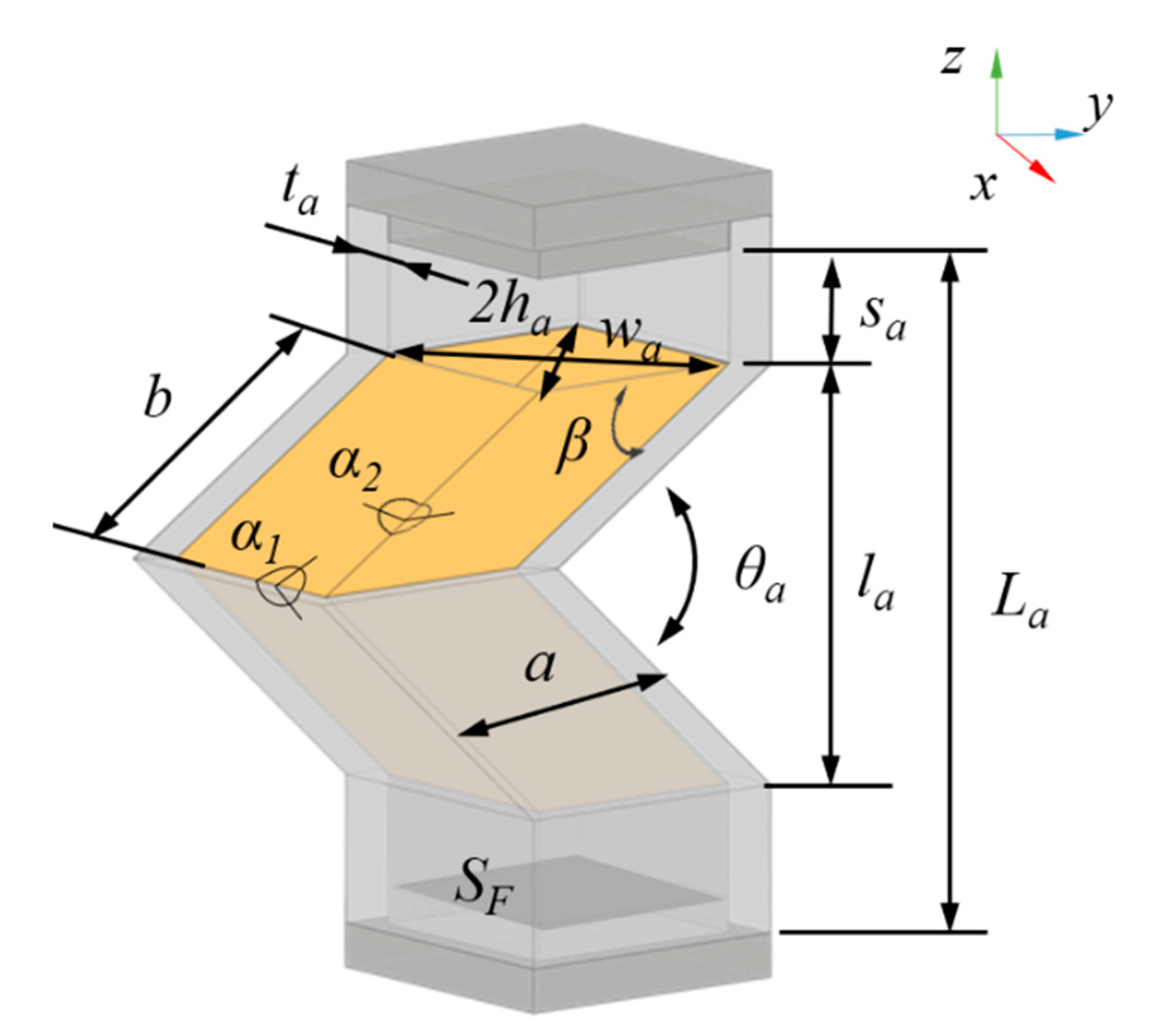
2.1. Design of the Pneumatic Foldable Actuator
2.2. Theoretical Modeling of the PFA
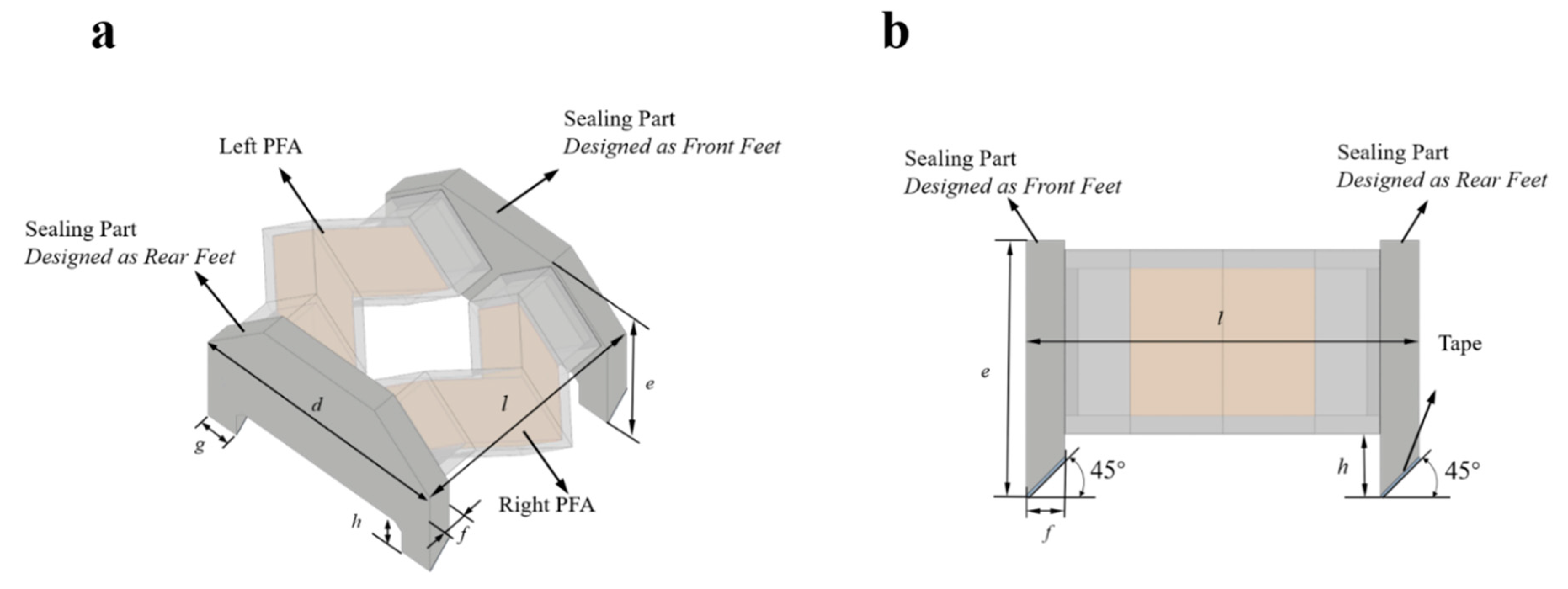
2.3. Design of the Crawling Robot Composed of the Two PFAs
2.4. The Movement Patterns
3. Materials and Fabrication
4. Experiments and Results
4.1. The Pressure–Displacement and Volume–Pressure Curves
4.2. Determining the Working Pressure for the Crawling Robot
4.3. The Movement of the Crawling Robot
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef]
- Hawkes, E.W.; Blumenschein, L.H.; Greer, J.D.; Okamura, A.M. A soft robot that navigates its environment through growth. Sci. Robot. 2017, 2, 1–8. [Google Scholar] [CrossRef]
- Ge, J.Z.; Calderón, A.A.; Chang, L.; Pérez-Arancibia, N.O. An earthworm-inspired friction-controlled soft robot capable of bidirectional locomotion. Bioinspir. Biomim. 2019, 14, 036004. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Niiyama, R.; Kawahara, Y. Design and Development of a Soft Robotic Earthworm with Hydrostatic Skeleton. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1–6. [Google Scholar]
- Zou, J.; Lin, Y.; Ji, C.; Yang, H. A Reconfigurable Omnidirectional Soft Robot Based on Caterpillar Locomotion. Soft Robot. 2018, 5, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Rafsanjani, A.; Zhang, Y.; Liu, B.; Rubinstein, S.M.; Bertoldi, K. Kirigami skins make a simple soft actuator crawl. Sci. Robot. 2018, 3, eaar7555. [Google Scholar] [CrossRef]
- Luo, M.; Agheli, M.; Onal, C.D. Theoretical Modeling and Experimental Analysis of a Pressure-Operated Soft Robotic Snake. Soft Robot. 2014, 1, 136–146. [Google Scholar] [CrossRef]
- Fras, J.; Noh, Y.; Macias, M.; Wurdemann, H.; Althoefer, K. Bio-Inspired Octopus Robot Based on Novel Soft Fluidic Actuator. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–4 June 2018; pp. 1583–1588. [Google Scholar]
- Laschi, C.; Cianchetti, M.; Mazzolai, B.; Margheri, L.; Follador, M.; Dario, P. Soft Robot Arm Inspired by the Octopus. Adv. Robot. 2012, 26, 709–727. [Google Scholar] [CrossRef]
- Cianchetti, M.; Calisti, M.; Margheri, L.; Kuba, M.; Laschi, C. Bioinspired locomotion and grasping in water: The soft eight-arm OCTOPUS robot. Bioinspir. Biomim. 2015, 10, 035003. [Google Scholar] [CrossRef]
- Li, T.; Zou, Z.; Mao, G.; Yang, X.; Liang, Y.; Li, C.; Qu, S.; Suo, Z.; Yang, W. Agile and Resilient Insect-Scale Robot. Soft Robot. 2019, 6, 133–141. [Google Scholar] [CrossRef]
- Qin, L.; Liang, X.; Huang, H.; Chui, C.K.; Yeow, R.C.H.; Zhu, J. A Versatile Soft Crawling Robot with Rapid Locomotion. Soft Robot. 2019, 6, 455–467. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Jiangbei, W.; Yanqiong, F. The Structure, Design, and Closed-Loop Motion Control of a Differential Drive Soft Robot. Soft Robot. 2018, 5, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Qin, L.; Liu, J.; Ren, Q.; Foo, C.C.; Wang, H.; Lee, H.P.; Zhu, J. Untethered soft robot capable of stable locomotion using soft electrostatic actuators. Extrem. Mech. Lett. 2018, 21, 9–16. [Google Scholar] [CrossRef]
- Tolley, M.T.; Shepherd, R.F.; Mosadegh, B.; Galloway, K.C.; Wehner, M.; Karpelson, M.; Wood, R.J.; Whitesides, G.M. A Resilient, Untethered Soft Robot. Soft Robot. 2014, 1, 213–223. [Google Scholar] [CrossRef]
- Li, T.; Li, G.; Liang, Y.; Cheng, T.; Dai, J.; Yang, X.; Liu, B.; Zeng, Z.; Huang, Z.; Luo, Y.; et al. Fast-moving soft electronic fish. Sci. Adv. 2017, 3, e1602045. [Google Scholar] [CrossRef]
- Bartlett, N.W.; Tolley, M.T.; Overvelde, J.T.B.; Weaver, J.C.; Mosadegh, B.; Bertoldi, K.; Whitesides, G.M.; Wood, R.J. A 3D-printed, functionally graded soft robot powered by combustion. Science 2015, 349, 161–165. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Q.; Lin, G.; Yin, J. Switchable Adhesion Actuator for Amphibious Climbing Soft Robot. Soft Robot. 2018, 5, 592–600. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of origami robots. Nat. Rev. Mater. 2018, 3, 101–112. [Google Scholar] [CrossRef]
- Pagano, A.; Yan, T.; Chien, B.; Wissa, A.; Tawfick, S. A crawling robot driven by multi-stable origami. Smart Mater. Struct. 2017, 26, 094007. [Google Scholar] [CrossRef]
- Jeong, D.; Lee, K. Design and analysis of an origami-based three-finger manipulator. Robotica 2018, 36, 261–274. [Google Scholar] [CrossRef]
- Fang, H.; Zhang, Y.; Wang, K.W. Origami-based earthworm-like locomotion robots. Bioinspir. Biomim. 2017, 12, 065003. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.-Y.; Kim, S.-R.; Kim, J.-S.; Park, J.-J.; Cho, K.-J. Origami Wheel Transformer: A Variable-Diameter Wheel Drive Robot Using an Origami Structure. Soft Robot. 2017, 4, 163–180. [Google Scholar] [CrossRef] [PubMed]
- Martinez, R.V.; Fish, C.R.; Chen, X.; Whitesides, G.M. Elastomeric origami: Programmable paper-elastomer composites as pneumatic actuators. Adv. Funct. Mater. 2012, 22, 1376–1384. [Google Scholar] [CrossRef]
- Miura, K. Method of Packaging and Deployment of Large Membranes in Space. Inst. Sp. Astronaut. Sci. Rep. 1985, 618, 1–9. [Google Scholar]
- Schenk, M.; Guest, S.D. Geometry of Miura-folded metamaterials. Proc. Natl. Acad. Sci. USA 2013, 110, 3276–3281. [Google Scholar] [CrossRef]
- Nishiyama, Y. Miura folding: Applying origami to space exploration. Int. J. Pure Appl. Math. 2012, 79, 269–279. [Google Scholar]
- Zhou, X.; Zang, S.; You, Z. Origami mechanical metamaterials based on the Miura-derivative fold patterns. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160361. [Google Scholar] [CrossRef]
- Lv, C.; Krishnaraju, D.; Konjevod, G.; Yu, H.; Jiang, H. Origami based Mechanical Metamaterials. Sci. Rep. 2015, 4, 5979. [Google Scholar] [CrossRef]
- Grey, S.W.; Schenk, M.; Scarpa, F.L. Local Actuation of Tubular Origami. In Proceedings of the seventh meeting of Origami, Science, Mathematics and Education, Oxford, UK, 4–7 September 2018. [Google Scholar]




| Parameters | Value |
|---|---|
| a | 10 mm |
| b | 10 mm |
| β | 60° |
| α2 | 90° |
| θ | 90° |
| w | 7.07 mm |
| l | 14.14 mm |
| Parameters | Value |
|---|---|
| The length of the crawling robot l (mm) | 32 |
| The width of the crawling robot d (mm) | 31 |
| The height of the crawling robot e (mm) | 20 |
| The thickness of the front and rear feet f (mm) | 3 |
| The width of the front and rear feet g (mm) | 4 |
| The height of the front and rear feet h (mm) | 4 |
| Soft Crawling Robot | Actuation Method | Body Length (mm) | Turning Speed (°/s) | Linear Speed (mm/s) | LS/BL |
|---|---|---|---|---|---|
| Our robot | Pneumatic | 32 | ~15 | ~5 | ~0.15 |
| Zou et al. [6] | Pneumatic | 154 | ~1.63 | ~5 | ~0.032 |
| Qin et al. [13] | Pneumatic | 135 | 15.09 | 16 | 0.11 |
| Wu et al. [14] | Pneumatic | ~110 | ~1.23 | 9.85 | 0.089 |
| Tolley et al. [16] | Pneumatic | 650 | ~0.2 | ~5 | ~0.007 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Yang, W.; Yu, Y.; Cheng, X.; Jiao, Z. A Crawling Soft Robot Driven by Pneumatic Foldable Actuators Based on Miura-Ori. Actuators 2020, 9, 26. https://doi.org/10.3390/act9020026
Yu M, Yang W, Yu Y, Cheng X, Jiao Z. A Crawling Soft Robot Driven by Pneumatic Foldable Actuators Based on Miura-Ori. Actuators. 2020; 9(2):26. https://doi.org/10.3390/act9020026
Chicago/Turabian StyleYu, Meng, Weimin Yang, Yuan Yu, Xiang Cheng, and Zhiwei Jiao. 2020. "A Crawling Soft Robot Driven by Pneumatic Foldable Actuators Based on Miura-Ori" Actuators 9, no. 2: 26. https://doi.org/10.3390/act9020026
APA StyleYu, M., Yang, W., Yu, Y., Cheng, X., & Jiao, Z. (2020). A Crawling Soft Robot Driven by Pneumatic Foldable Actuators Based on Miura-Ori. Actuators, 9(2), 26. https://doi.org/10.3390/act9020026






