A Novel Framework for a Systematic Integration of Pneumatic-Muscle-Actuator-Driven Joints into Robotic Systems Via a Torque Control Interface
Abstract
1. Introduction
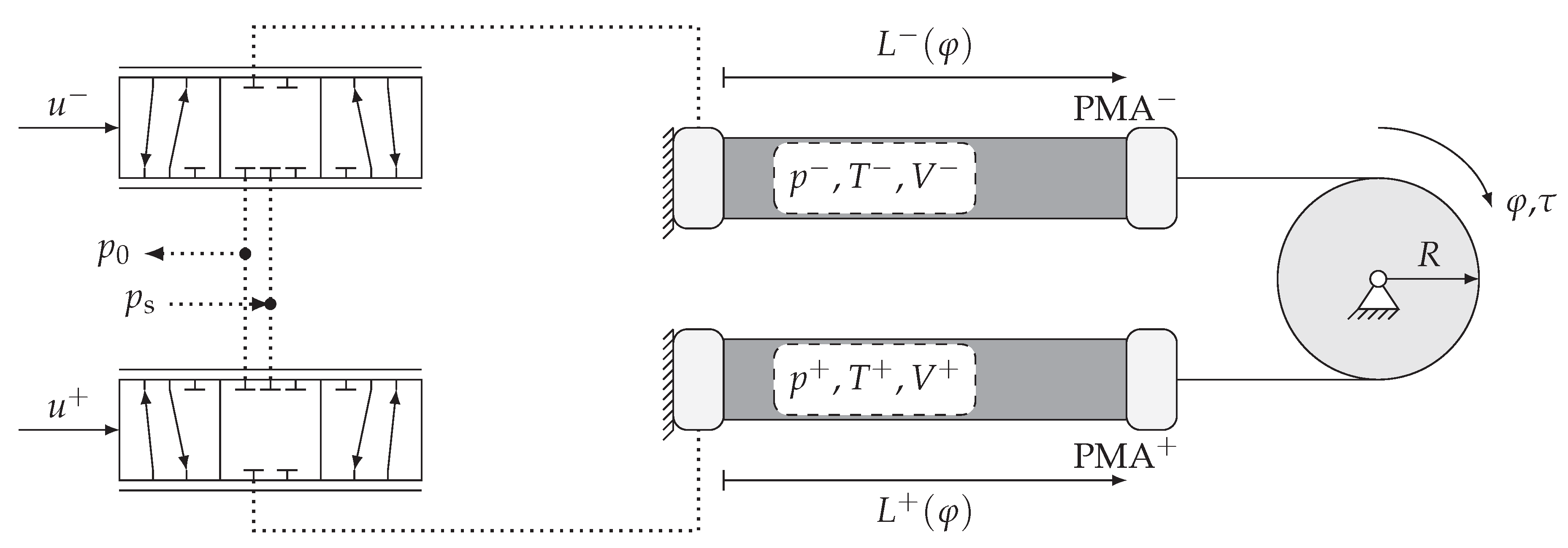
2. The PMA-Driven Joint
2.1. An Overview
2.2. Torque Characteristic
2.2.1. PMA Force
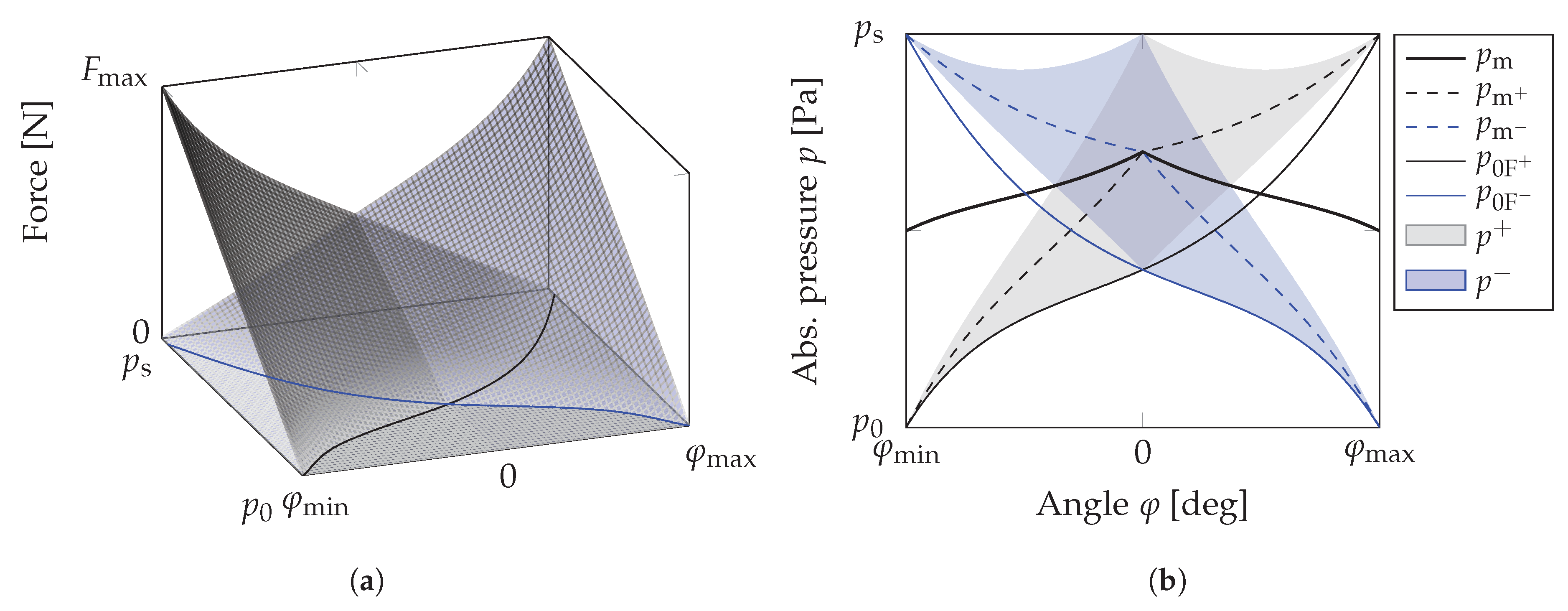
2.2.2. Pressure Trajectory Generation by Mean Pressure Definition—”PM-Approach”
- For every angle the upper individual mean pressure— (blue dashed) respectively (black dashed)—is set to be in the middle of and the supply pressure .
- The lower individual mean pressure is calculated such that the forces of both PMAs are equal, if both PMAs are filled with their individual mean pressure.
- For any time the pressure has to be inside the black, the pressure inside the blue area. The pressures are limited by the supply pressure and the pressure of zero force , because otherwise the rope would hang loose. Furthermore, both pressures are always equidistant to the mean pressure and the smaller force range, defined by the pressure range around the individual mean pressures limits both pressure ranges.
- The common mean pressure (bold black line) is a result of (10).
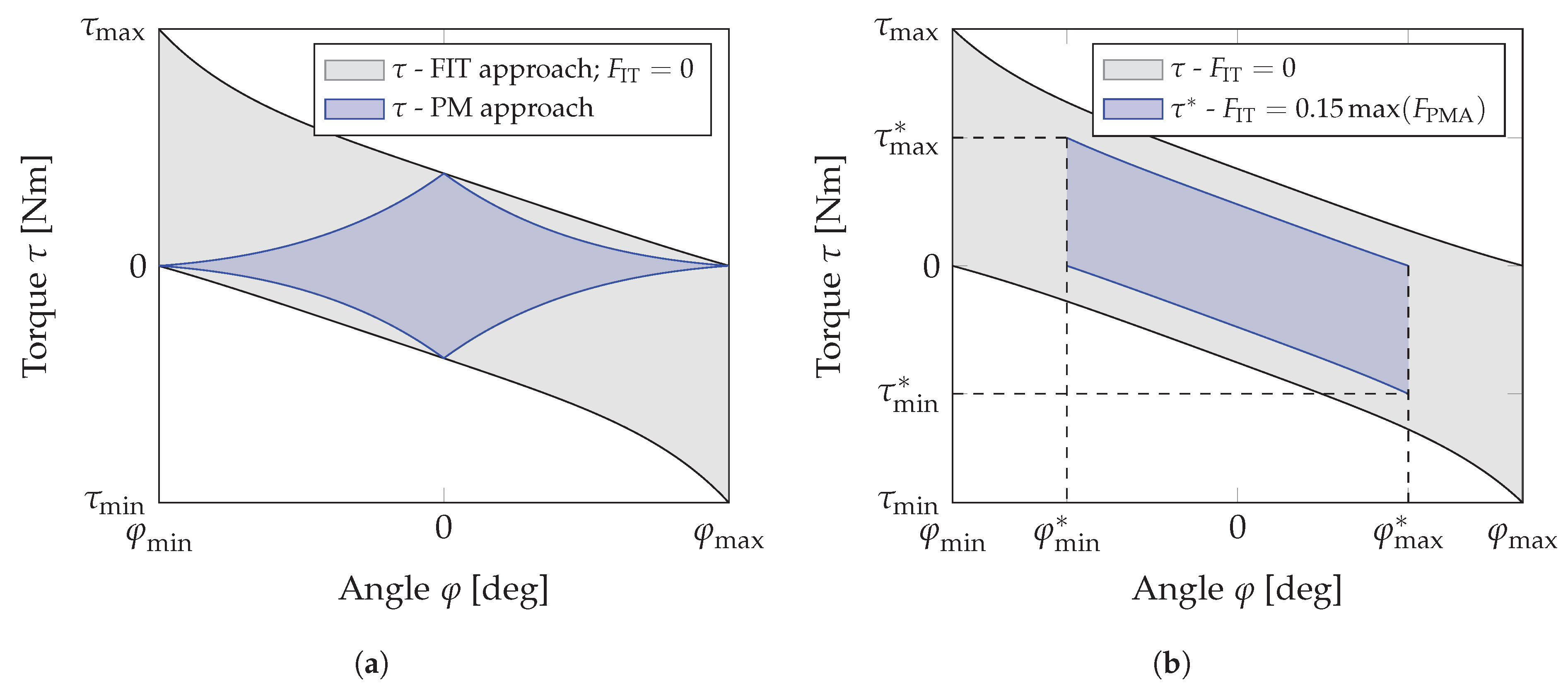
2.2.3. Pressure Trajectory Generation by Force Separation—“FIT-Approach”
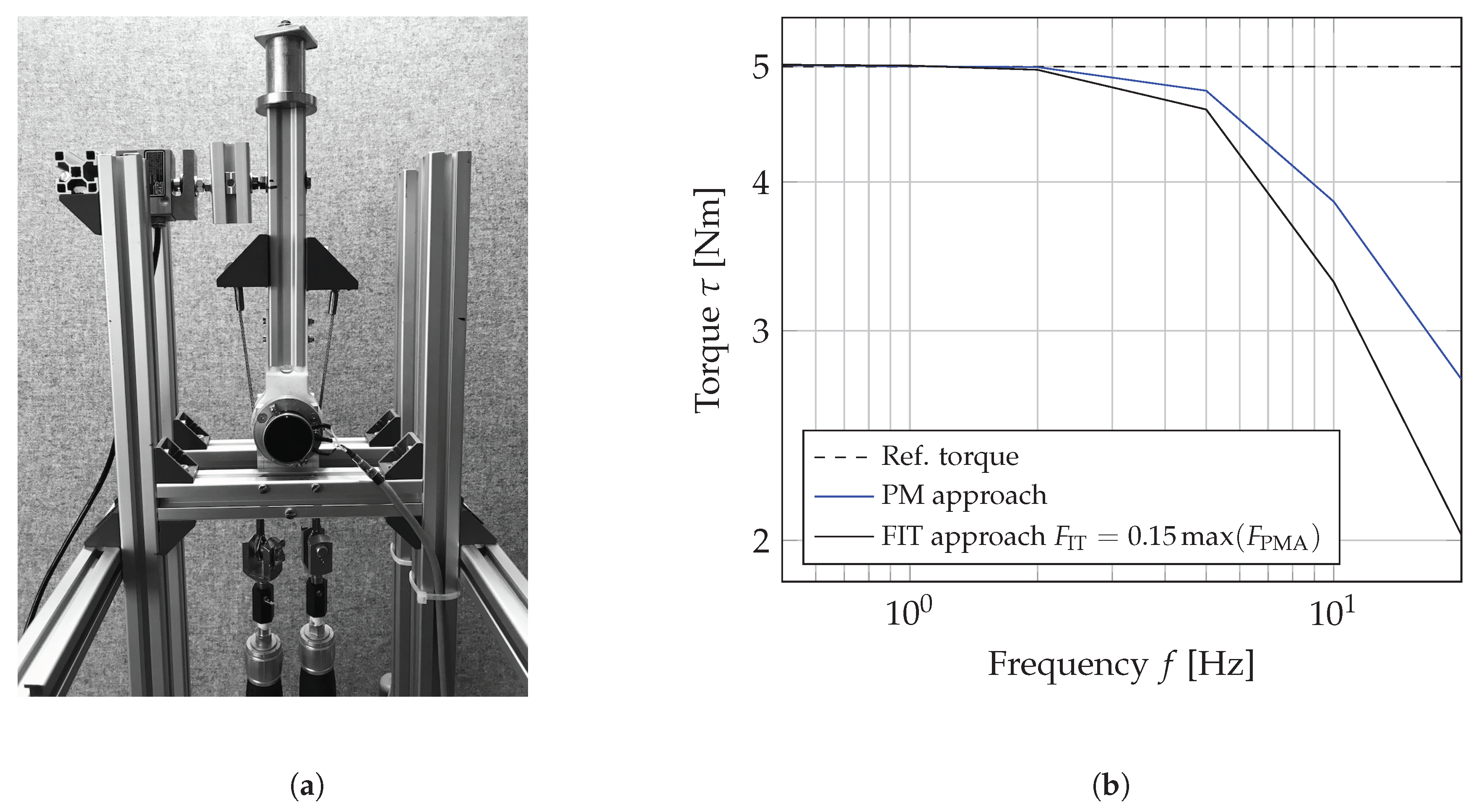
2.2.4. A Comparison of Two Torque Characteristics
2.3. Bandwidth of the Torque Controller
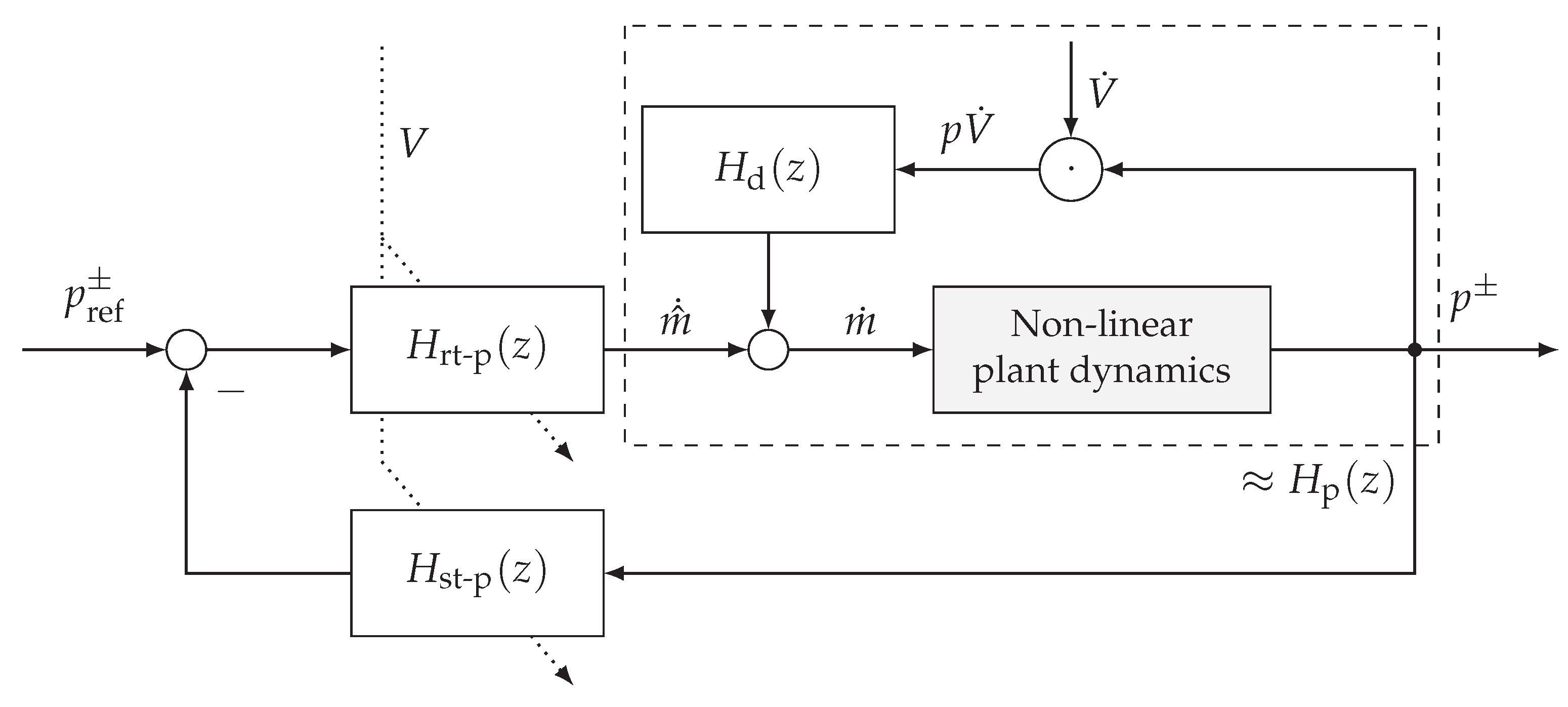
2.3.1. Pressure Dynamics
2.3.2. Controller Design
Mass Flow as Virtual Input
Interpreting the Plant as a Linear Time-Invariant System
2.3.3. Pressure Controller Design
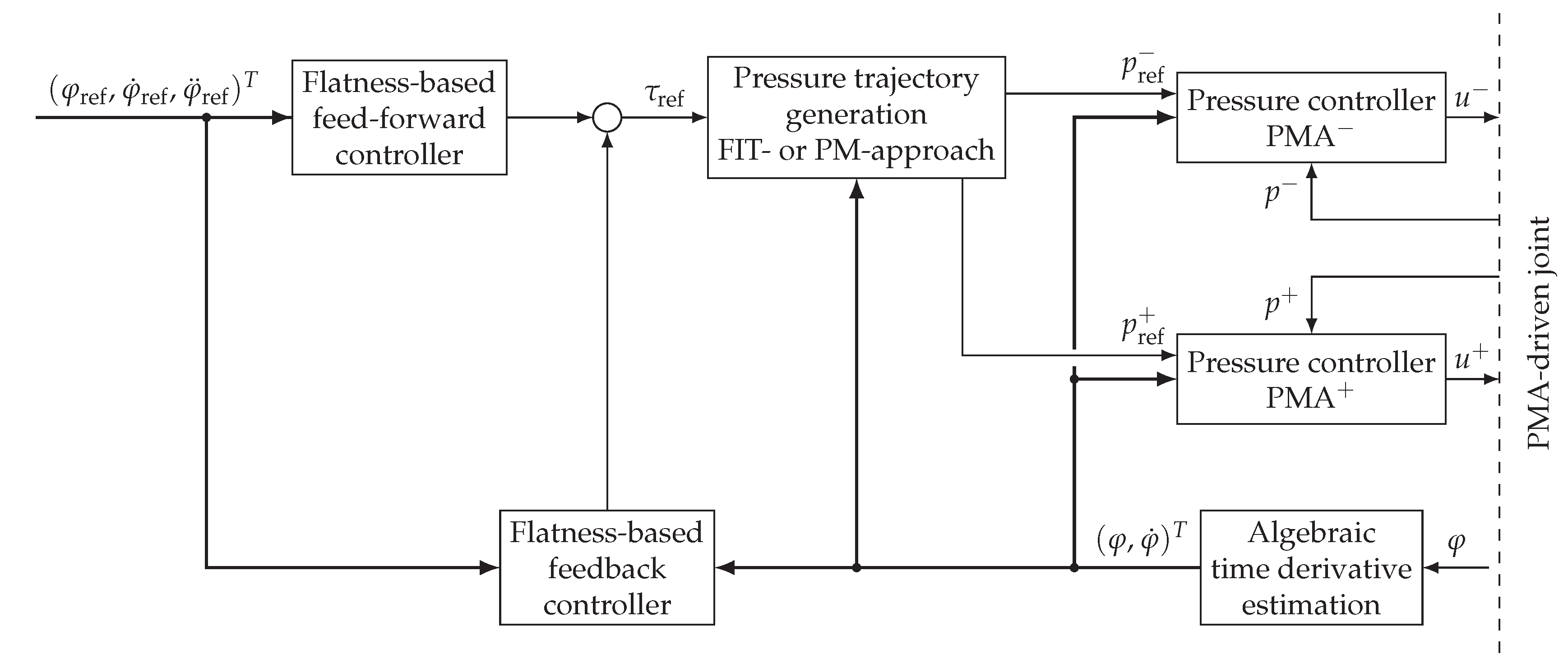
3. Angular Position Controller for an Exemplary Robotic Arm
3.1. Inner Torque Control Loop
3.2. Outer Angular Position Controller
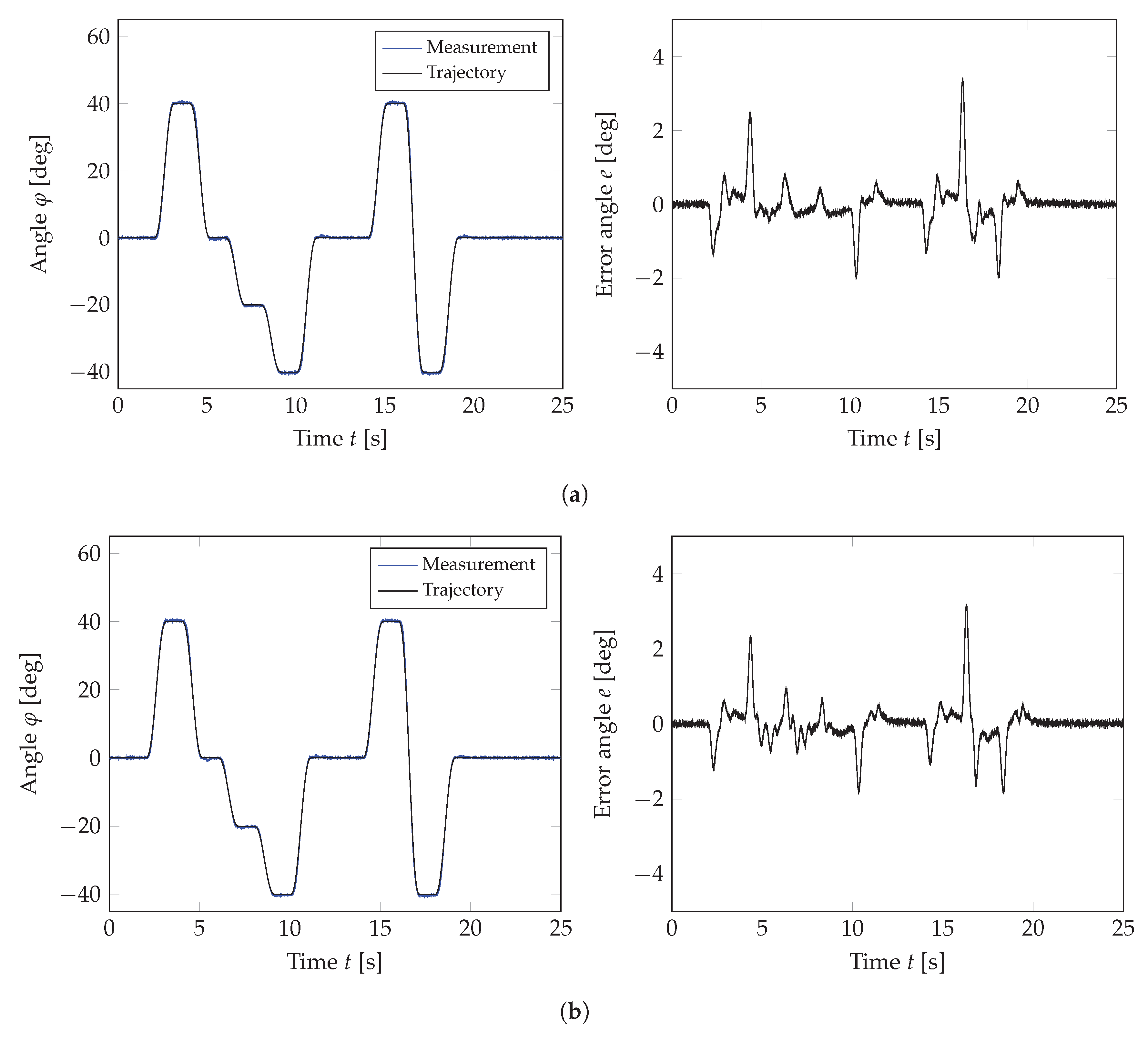
3.3. Experimental Investigation of the Trajectory Following Behavior
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof A(L) ≠ 0 and A(L+) + A(L−) ≠ 0
Appendix B. Force Map Festo DMSP-20-300
| Force [N] | ||||||||||||||||||||||||
| Length [mm] | 224 | 226 | 227 | 229 | 231 | 232 | 234 | 235 | 238 | 240 | 243 | 245 | 250 | 253 | 260 | 264 | 276 | 278 | 289 | 290 | 296 | 297 | 299 | |
| Rel. Pressure [Pa] | ||||||||||||||||||||||||
| 10,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 9 | |
| 50,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −3 | 11 | 91 | 96 | |
| 100,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −7 | 0 | 13 | 101 | 125 | 209 | 216 | |
| 150,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 83 | 12 | 123 | 212 | 245 | 331 | 343 | |
| 200,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 69 | 12 | 176 | 112 | 236 | 325 | 370 | 456 | 471 | |
| 250,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 60 | 12 | 141 | 91 | 270 | 212 | 353 | 440 | 495 | 580 | 599 | |
| 300,000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 47 | 12 | 119 | 76 | 214 | 170 | 365 | 313 | 470 | 556 | 622 | 706 | 729 | |
| 350,000 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 43 | 12 | 96 | 67 | 178 | 140 | 287 | 249 | 460 | 413 | 588 | 671 | 748 | 831 | 857 | |
| 400,000 | 0 | 0 | 0 | 0 | 1 | 0 | 40 | 10 | 86 | 58 | 145 | 121 | 237 | 204 | 360 | 329 | 555 | 513 | 705 | 787 | 874 | 955 | 986 | |
| 450,000 | 0 | 0 | 0 | 0 | 35 | 10 | 78 | 52 | 129 | 105 | 193 | 174 | 295 | 268 | 433 | 409 | 649 | 613 | 822 | 902 | 1000 | 1080 | 1115 | |
| 500,000 | 0 | 0 | 1.5 | 22 | 70 | 47 | 116 | 93 | 171 | 151 | 242 | 228 | 354 | 332 | 505 | 488 | 744 | 713 | 939 | 1018 | 1125 | 1204 | 1243 | |
| 550,000 | 0 | 6 | 21.5 | 54.5 | 105 | 84 | 154 | 134 | 214 | 198 | 291 | 281 | 413 | 396 | 578 | 566 | 838 | 813 | 1056 | 1132 | 1250 | 1328 | 1371 | |
| 590,000 | 0 | 28 | 46 | 80.5 | 132 | 114 | 184 | 166 | 248 | 235 | 329 | 324 | 460 | 447 | 636 | 629 | 913 | 892 | 1149 | 1224 | 1348 | 1427 | 1472 | |
Appendix C. Sonic Conductance Festo MPYE-5-1/8-LF-010-B
| x | C(x) | x | C(x) | x | C(x) |
| 0 | |||||
| 1 |
References
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. A survey on applications of pneumatic artificial muscles. In Proceedings of the 2011 19th Mediterranean Conference on Control & Automation (MED), Corfu, Greece, 20–23 June 2011; pp. 1439–1446. [Google Scholar]
- Caldwell, D.G.; Tsagarakis, N.G.; Kousidou, S.; Costa, N.; Sarakoglou, I. “Soft” exoskeletons for upper and lower body rehabilitation—Design, control and testing. Int. J. Humanoid Robot. 2007, 4, 549–573. [Google Scholar] [CrossRef]
- Cao, J.; Xie, S.Q.; Das, R. MIMO sliding mode controller for gait exoskeleton driven by pneumatic muscles. IEEE Trans. Control Syst. Technol. 2018, 26, 274–281. [Google Scholar] [CrossRef]
- Noritsugu, T.; Tanaka, T. Application of rubber artificial muscle manipulator as a rehabilitation robot. IEEE/ASME Trans. Mechatron. 1997, 2, 259–267. [Google Scholar] [CrossRef]
- Hošovskỳ, A.; Pitel’, J.; Židek, K.; Tóthová, M.; Sárosi, J.; Cveticanin, L. Dynamic characterization and simulation of two-link soft robot arm with pneumatic muscles. Mech. Mach. Theory 2016, 103, 98–116. [Google Scholar] [CrossRef]
- Schindele, D.; Aschemann, H. Trajectory tracking of a pneumatically driven parallel robot using higher-order SMC. In Proceedings of the 2010 15th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 23–26 August 2010; pp. 387–392. [Google Scholar]
- Schindele, D.; Aschemann, H. P-type ILC with phase lead compensation for a pneumatically driven parallel robot. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 5484–5489. [Google Scholar]
- Andrikopoulos, G.; Nikolakopoulos, G. HUmanoid Robotic Leg via pneumatic muscle actuators: Implementation and control. Meccanica 2018, 53, 465–480. [Google Scholar] [CrossRef]
- Dirven, S.; McDaid, A. A Systematic Design Strategy for Antagonistic Joints Actuated by Artificial Muscles. IEEE/ASME Trans. Mechatron. 2017, 22, 2524–2531. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L. Robotics—Modelling, Planning and Control; Springer: London, UK, 2012. [Google Scholar]
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Boblan, I.; Maschuw, J.; Engelhardt, D.; Schulz, A.; Schwenk, H.; Bannasch, R.; Rechenberg, I. A human-like robot hand and arm with fluidic muscles: Modelling of a muscle driven joint with an antagonistic setup. In Proceedings of the 3rd International Symposium on Adaptive Motion in Animals and Machines, Ilmenau, Germany, 25–30 September 2005. [Google Scholar]
- Shen, X. Nonlinear model-based control of pneumatic artificial muscle servo systems. Control Eng. Pract. 2010, 18, 311–317. [Google Scholar] [CrossRef]
- Hildebrandt, A.; Sawodny, O.; Neumann, R.; Hartmann, A. Cascaded control concept of a robot with two degrees of freedom driven by four artificial pneumatic muscle actuators. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 1, pp. 680–685. [Google Scholar] [CrossRef]
- Vitiello, N.; Lenzi, T.; De Rossi, S.M.M.; Roccella, S.; Carrozza, M.C. A sensorless torque control for Antagonistic Driven Compliant Joints. Mechatronics 2010, 20, 355–367. [Google Scholar] [CrossRef]
- Lin, C.J.; Lin, C.R.; Yu, S.K.; Chen, C.T. Hysteresis modeling and tracking control for a dual pneumatic artificial muscle system using Prandtl–Ishlinskii model. Mechatronics 2015, 28, 35–45. [Google Scholar] [CrossRef]
- Aschemann, H.; Schindele, D. Comparison of Model-Based Approaches to the Compensation of Hysteresis in the Force Characteristic of Pneumatic Muscles. IEEE Trans. Ind. Electron. 2014, 61, 3620–3629. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. Incorporation of thermal expansion in static force modeling of Pneumatic Artificial Muscles. In Proceedings of the 2015 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015; pp. 414–420. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. Novel Considerations on Static Force Modeling of Pneumatic Muscle Actuators. IEEE/ASME Trans. Mechatron. 2016, 21, 2647–2659. [Google Scholar] [CrossRef]
- Kerscher, T.; Albiez, J.; Zollner, J.; Dillmann, R. Evaluation of the dynamic model of fluidic muscles using quick-release. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, 2006. BioRob 2006, Pisa, Italy, 20–22 February 2006; pp. 637–642. [Google Scholar]
- Schindele, D.; Aschemann, H. Model-based compensation of hysteresis in the force characteristic of pneumatic muscles. In Proceedings of the 2012 12th IEEE International Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia-Herzegovina, 25–27 March 2012; pp. 1–6. [Google Scholar]
- Hildebrandt, A.; Sawodny, O.; Neumann, R.; Hartmann, A. A cascaded tracking control concept for pneumatic muscle actuators. In Proceedings of the 2003 European Control Conference (ECC), Cambridge, UK, 1–4 September 2003; pp. 2517–2522. [Google Scholar]
- Aschemann, H.; Hofer, E.P. Nonlinear trajectory control of a high-speed linear axis driven by pneumatic muscle actuators. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 3857–3862. [Google Scholar]
- Schindele, D.; Aschemann, H. Nonlinear model predictive control of a high-speed linear axis driven by pneumatic muscles. In Proceedings of the American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3017–3022. [Google Scholar]
- Martens, M.; Boblan, I. Modeling the static force of a Festo pneumatic muscle actuator: A new approach and a comparison to existing models. Actuators 2017, 6, 33. [Google Scholar] [CrossRef]
- Martens, M.; Passon, A.; Boblan, I. A sensor-less approach of a torque controller for pneumatic muscle actuator driven joints. In Proceedings of the 2017 3rd International Conference on Control, Automation and Robotics (ICCAR), Nagoya, Japan, 24–26 April 2017; pp. 477–482. [Google Scholar] [CrossRef]
- Wickramatunge, K.C.; Leephakpreeda, T. Study on mechanical behaviors of pneumatic artificial muscle. Int. J. Eng. Sci. 2010, 48, 188–198. [Google Scholar] [CrossRef]
- Sárosi, J.; Biro, I.; Nemeth, J.; Cveticanin, L. Dynamic modeling of a pneumatic muscle actuator with two-direction motion. Mech. Mach. Theory 2015, 85, 25–34. [Google Scholar] [CrossRef]
- Martens, M.; Boblan, I. Erratum: Modeling the Static Force of a Festo Pneumatic Muscle Actuator: A New Approach and a Comparison to Existing Models. Actuators 2018, 7, 9. [Google Scholar] [CrossRef]
- Chou, C.P.; Hannaford, B. Static and dynamic characteristics of McKibben pneumatic artificial muscles. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; Volume 1, pp. 281–286. [Google Scholar] [CrossRef]
- Festo, A.G. Datasheet–Fluidic Muscle DMSP/MAS. Available online: https://www.festo.com/rep/en_corp/assets/pdf/info_501_en.pdf (accessed on 27 November 2018).
- Martens, M.; Seel, T.; Boblan, I. A Decoupling Servo Pressure Controller for Pneumatic Muscle Actuators. In Proceedings of the 2018 23rd International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2018; pp. 286–291. [Google Scholar]
- Beater, P. Pneumatic Drives; Springer: Berlin, Germany, 2007. [Google Scholar]
- KG, F.V.G.C. Datasheet–Proportional Directional Control Valves MPYE; Festo Vertrieb GmbH Co. KG, Festo Campus: Esslingen, Germany, 2017. [Google Scholar]
- Rager, D.; Neumann, R.; Murrenhoff, H. Simplified Fluid Transmission Line Model. In Proceedings of the 14th Scandinavian International Conference on Fluid Power (SICFP15), Tampere, Finland, 20–22 May 2015. [Google Scholar]
- Åström, K.J.; Wittenmark, B. Computer-Controlled Systems: Theory and Design, 3rd ed.; Dover Publication, Inc.: New York, NY, USA, 2013. [Google Scholar]
- Zehetner, J.; Reger, J.; Horn, M. Echtzeit-Implementierung eines algebraischen Ableitungsschätzverfahrens (Realtime Implementation of an Algebraic Derivative Estimation Scheme). at-Automatisierungstechnik 2007, 55, 553–560. (In German) [Google Scholar] [CrossRef]
- Zehetner, J.; Reger, J.; Horn, M. A derivative estimation toolbox based on algebraic methods-theory and practice. In Proceedings of the IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 331–336. [Google Scholar]
- Adamy, J. Nichtlineare Systeme und Regelungen; Springer: Berlin, Germany, 2018. [Google Scholar]


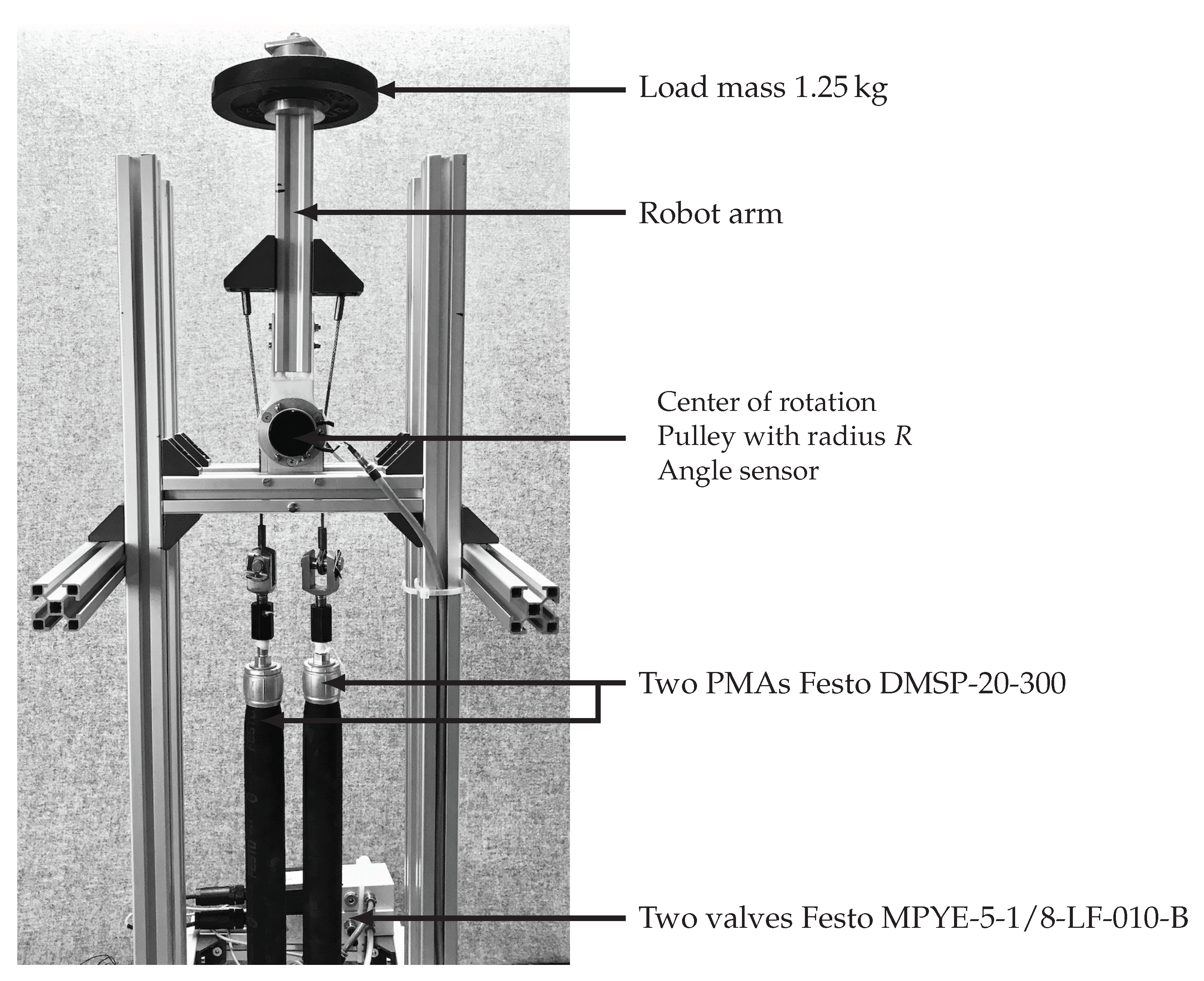
| DMSP-20-300 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martens, M.; Seel, T.; Zawatzki, J.; Boblan, I. A Novel Framework for a Systematic Integration of Pneumatic-Muscle-Actuator-Driven Joints into Robotic Systems Via a Torque Control Interface. Actuators 2018, 7, 82. https://doi.org/10.3390/act7040082
Martens M, Seel T, Zawatzki J, Boblan I. A Novel Framework for a Systematic Integration of Pneumatic-Muscle-Actuator-Driven Joints into Robotic Systems Via a Torque Control Interface. Actuators. 2018; 7(4):82. https://doi.org/10.3390/act7040082
Chicago/Turabian StyleMartens, Mirco, Thomas Seel, Johannes Zawatzki, and Ivo Boblan. 2018. "A Novel Framework for a Systematic Integration of Pneumatic-Muscle-Actuator-Driven Joints into Robotic Systems Via a Torque Control Interface" Actuators 7, no. 4: 82. https://doi.org/10.3390/act7040082
APA StyleMartens, M., Seel, T., Zawatzki, J., & Boblan, I. (2018). A Novel Framework for a Systematic Integration of Pneumatic-Muscle-Actuator-Driven Joints into Robotic Systems Via a Torque Control Interface. Actuators, 7(4), 82. https://doi.org/10.3390/act7040082





