Abstract
Synthetic jet actuators (SJA) are emerging in various engineering applications, from flow separation and noise control in aviation to thermal management of electronics. A SJA oscillates a flexible membrane inside a cavity connected to a nozzle producing vortices. A complex interaction between the cavity pressure field and the driving electronics can make it difficult to predict performance. A reduced-order model (ROM) has been developed to predict the performance of SJAs. This paper applies this model to a canonical configuration with applications in flow control and electronics cooling, consisting of a single SJA with a rectangular orifice, emanating perpendicular to the surface. The practical implementation of the ROM to estimate the relationship between cavity pressure and jet velocity, jet velocity and diaphragm deflection and applied driving voltage is explained in detail. Unsteady Reynolds-averaged Navier Stokes computational fluid dynamics (CFD) simulations are used to assess the reliability of the reduced-order model. The CFD model itself has been validated with experimental measurements. The effect of orifice aspect ratio on the ROM parameters has been discussed. Findings indicate that the ROM is capable of predicting the SJA performance for a wide range of operating conditions (in terms of frequency and amplitude).
1. Introduction
Synthetic jet actuators (SJAs) generate a train of vortices which are formed by periodic suction and ejection of the same amount of fluid across an orifice. This establishes a directional flow with zero net mass input, formed from the ambient fluid surrounding the orifice, hence “synthetic” jet [1,2]. These types of actuators have been used to control flow separation and noise, e.g., in aviation applications, as well as more recently in the thermal management of electronics.
An SJA typically consists of a piezoelectric or electromagnetic driver deflecting a flexible membrane inside a cavity, which is connected to an external body of fluid through a short nozzle or orifice (The terms ‘nozzle’ and ‘orifice’ will be used interchangeably in this paper). An oscillation of the internal membrane causes a cavity pressure fluctuation and, thus, an oscillatory flow through the orifice. At a sufficiently high stroke length [3], a stable vortex detaches from the orifice and propagates into the surrounding flow field, thereby imparting momentum to a boundary layer.
A basic synthetic jet flow emanating into quiescent ambient fluid is characterized by a few parameters: (i) the jet Reynolds number , where is the hydraulic diameter of the orifice, is the fluid kinematic viscosity and is a characteristic velocity scale representing the average nozzle ejection velocity, defined as , where is the actuation frequency. The stroke length is defined as the average distance a fluid slug is expelled during the ejection phase, assuming a harmonic velocity profile in the orifice which is positive during ejection () and negative during the suction phase ():
where represents the spatially averaged orifice or nozzle velocity, hence subscript ‘n’. The dimensionless stroke length is the reciprocal of a Strouhal number or . Usually the actuator diaphragm is excited by a sine wave, in which case the characteristic velocity where is the peak (spatially averaged) orifice velocity, or the amplitude of the sine wave .
For sharp-edged orifices, threshold values for a vortex to detach, and thus for a synthetic jet flow to form, are for a circular orifice and for a two-dimensional slot orifice with infinite aspect ratio , where is defined as the span-to-width ratio of a rectangular slot or . The stroke length is a characteristic for the flow structure [4].
For flow control purposes, the SJA is usually embedded within a streamlined or bluff body, with the jet emanating from a surface at an angle [5,6]. For electronics cooling purposes, the synthetic jet flow is usually directed at a surface, impinging onto the object to be cooled [7]. In both cases however, the orifice can be circular or rectangular in shape, and the jet can issue at an oblique angle. Moreover, the use of dual adjacent SJAs can be used to achieve flow vectoring, determined by the phase difference in the driving signals for adjacent actuators [8].
Each of these configurations leads to quite different and complicated pressure fields, making it hard to predict SJA performance a priori. Since the jet flow structure is determined by the aforementioned dimensionless groups and , information is needed about the synthetic jet orifice velocity , or for sine wave actuation, simply the velocity amplitude . Hence:
However, the orifice velocity cannot be inferred directly from the driving voltage . Nor can the orifice velocity be measured easily in typical applications, requiring either intrusive techniques (e.g., hot-wire anemometry) or more expensive optical velocity measurements. A calibration correlating actuator voltage with orifice velocity can be performed; however, this may be subject to degradation or drift in actuator characteristics. A calibration of cavity acoustic pressure with orifice velocity is, therefore, preferred [9,10,11]. For instance, when changing the phase difference between adjacent SJAs, only a pressure-velocity calibration approach can maintain a constant jet Reynolds number [8].
For a synthetic jet issuing into an external boundary layer, the combined flow field is further characterized by the velocity ratio or the dimensionless frequency , where is the freestream velocity and represents the streamwise location of the SJA from a leading edge, or the length of a separated zone.
Three main types of actuating mechanisms have been used to generate synthetic jet flows in academic research, (i) an oscillating piston, (ii) an electromagnetic loudspeaker or (iii) a piezoelectric bending element. Both air and liquid have been used as working fluids. It will be shown in Section 2 that the type of driver (i, ii or iii) does not affect the relationship between the nozzle velocity and cavity pressure , only the relationship between input power and diaphragm motion. Hence, a general reduced-order model (ROM) will incorporate a so-called ‘fluidic model’ relating to which does not depend on the actuator type, and a ‘driver model’ relating driver input to diaphragm deflection, . The cavity pressure is the physical linking variable between both parts of the model.
Table 1 gives an overview of different types of actuators, orifices, and SJA operating conditions for a selection of experimental studies in the scientific literature. The list is not exhaustive, since the purpose is merely to convey the range of actuator types and typical parameter ranges encountered. The final table entry represents the current study.

Table 1.
List of experimental synthetic jet investigations with details of the type of orifice and actuator used.
The objectives of this paper are threefold: (i) to provide a clear but concise overview of an analytical ROM for a generic SJA, which would be useful both for early stage design and for controlling SJA operation; (ii) to validate this ROM for a typical lab-scale SJA with rectangular orifice, using both experimental calibration data as well as 2D and 3D transient CFD simulation results; (iii) to compare CFD and experimental results and illustrate the potential challenges associated with the comparison of 2D and 3D geometries for SJA in the frequency domain.
2. Analytical Reduced-Order Model (ROM)
The SJA ROM used in this paper is a lumped parameter analytical model, combining (i) a second-order equivalent representation of the driving element (i.e., a piezoelectric diaphragm or a loudspeaker) with (ii) a zeroth-order gas dynamics approximation of the fluid motion in the orifice, with fluid compressibility in the cavity. The main mechanical degrees of freedom represent the motion of the diaphragm and fluid slug in the nozzle , respectively.
The overall system response function can be broken down into its constituent parts as follows:
where and are the fluid density and speed of sound, and are the cross-section and surface areas of the nozzle and diaphragm, respectively, and is the electrical impedance of the driver. All variables in bold () in Equation (3) represent complex quantities in the frequency domain, dependent on the Laplace variable which has been omitted in Equation (3) for brevity.
2.1. Brief Description of the ROM
The operational fluidic model was described by Persoons and O’Donovan [11] and can be used to estimate the SJA velocity from a measured cavity pressure. It can be simplified to a closed form analytical expression, and thus is easily implemented in a data acquisition or control system, as described in this section. The coupling between the electromechanical driver model and fluidic model is described in full detail by Persoons [16]. Comparable reduced-order models, also referred to as lumped element models (LEM), are presented and discussed by other researchers [17,18,19,20,21]. Thus for the sake of brevity and clarity, only the basic elements are described here and the reader is referred to other works for more details on the derivations of the equations [11,16].
Figure 1 shows a schematic diagram and equivalent electrical networks for this ROM with a piezoelectric actuator (Figure 1b) and electromagnetic (e.g., loudspeaker) actuator (Figure 1c). The diaphragm and nozzle slug velocities and displacements are related as and .
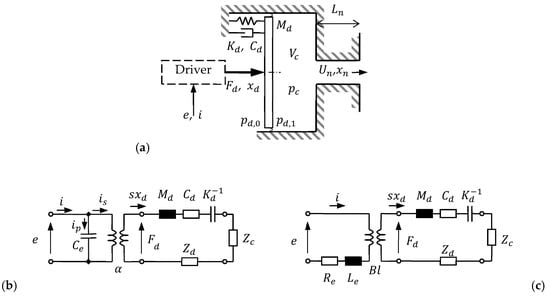
Figure 1.
(a) Schematic diagram and equivalent electrical networks of a reduced-order model of a synthetic jet actuator (SJA) with (b) piezoelectric and (c) electromagnetic driver: from driving voltage to diaphragm deflection , cavity pressure and nozzle velocity [16].
Most parameters can be determined from known dimensions and manufacturer’s specifications for the driver. Only two parameters ( and ) should be determined by calibration: relates to the non-linear nozzle damping and relates to the added nozzle inertia due to acoustic radiation.
The mechanical/fluidic behavior can be described by combining two second-order models, one relating to the oscillating diaphragm and one relating to the compressible gas dynamics:
where are the equivalent mass, damping and stiffness of the driver, is the motive force applied by the actuator and and are the pressures on either side of the diaphragm, which are governed by acoustic radiation impedances and the cavity impedance . Equation (4) can be thus rewritten as:
where is an electromechanical coupling coefficient. In case of a piezoelectric actuator, where is the piezoelectric modulus relating electric field and volumetric extension. This case is represented in Figure 1b.
In Equation (5), and are the geometric length and cross-sectional area of the nozzle, represents the damping force related to fluid oscillating through the orifice, and the two terms correspond to acoustic impedances on both ends of the nozzle. and are directly related to the aforementioned parameters and , as explained below.
Firstly, the frequency-dependent acoustic radiation impedance is described in detail by Beranek [22] for some canonical geometries. Appendix A in Persoons [16] describes the radiation impedance for a circular and rectangular orifice of aspect ratio , based on tabulated data by Burnett and Soroka [23]. A low-frequency approximation for of this impedance where represents a mass of fluid adjacent to one side of the orifice which adds to the oscillating inertia. This approximation thus leads to the introduction of the added mass coefficient . When applied to both sides of the orifice equally, this can be recast into an equivalent (end-corrected) nozzle length :
With the total equivalent (quantities with a prime (‘) indicate the inclusion of an added mass correction) oscillating fluid mass and the cavity compressibility where is the cavity volume, the Helmholtz resonance frequency emerges from the Equation:
Secondly, the nozzle damping force can be represented by a combination of first-order (viscous) and second-order (inertial) damping. The relative dominance of first or second-order damping depends on the Stokes number (); however, for short nozzles and moderate frequencies the first-order term can typically be ignored [16], leaving only:
Equation (5) can thus be recast as the non-linear cavity impedance relating SJA cavity pressure to orifice velocity:
The reciprocal of in Equation (10) describes the operational SJA model in the frequency domain. Appendix C in Persoons [16] explains how this expression can be simplified for sine wave actuation to the following closed-form expression to estimate the nozzle velocity amplitude from the cavity pressure amplitude :
Using a microphone, the cavity pressure amplitude can easily be measured [11,16] and Equation (11) thus allows for to be directly calculated, once values for and are known for the orifice. The following section describes the procedure for determining these parameters.
Other useful expressions relating nozzle velocity to diaphragm deflection and actuator voltage can be derived from the above set of equations. The reader is referred to Persoons [16] for the full derivation. The following relates nozzle velocity to diaphragm deflection :
Based on derivations in Persoons [16], the relationship between nozzle velocity and piezoelectric actuator voltage is given by:
For an electromagnetic actuator (see Figure 1c), a similar expression can be obtained [16]:
where and are the voice coil resistance and inductance, respectively, is the electromagnetic force factor (), and .
Equations (12)–(14) are only provided here in complex notation, yet these can easily be implemented in a data acquisition software such as NI LabVIEW or MATLAB (sample code is available upon request from the corresponding author (Tim Persoons)) to infer the amplitude and phase lag of as a function of either or .
The two system resonance frequencies and are related to, but not equal to, the Helmholtz resonance frequency and driver resonance frequency , and are determined as:
The equivalent diaphragm mass appears here in its modified form [16], including an added mass correction on one side of the diaphragm, .
Persoons [16] gives more details about the physical interpretation of and , and further confirmation for these resonance frequencies can also be found in Gallas et al. [18], Kordik et al. [19] and Kooijman and Ouweltjes [24].
2.2. Estimating ROM Parameters and
The non-linear damping coefficient and added mass coefficient can be determined by least-squares fitting the model expression in a calibration procedure, as described by Persoons [16]. This will tend to over predict as the fit includes acoustic effects from the diaphragm, which are only implicitly included in the ROM while only the acoustic effects at the nozzle are explicitly used. Alternatively, can be determined analytically, as described below.
As mentioned in the brief description of the SJA ROM, arises from acoustic radiation impedance and affects the inertia of the nozzle in the same manner that adding additional mass would. For a rectangular nozzle, such as the one used in this work, acoustic impedance can be interpolated from the tabulated data given by Burnett and Soroka [23] or analytically determined from the equation provided therein [23] and reproduced below. For a circular nozzle, the acoustic impedance can be determined by using a Struve H function of the first kind [16]. For a rectangular nozzle, can be determined as a function of frequency and aspect ratio as follows:
where is the imaginary part of the acoustic impedance and is the wave number () which is normalized by the nozzle cross-sectional area as . The function can be determined as:
where parameters and are defined as and , and the function is defined as:
Note that Equations (16)–(18) for determining are a low-frequency approximation, and only valid for values of . Alternatively, the following equation is an empirical fit for that is valid for and , with a mean error of 1.9% and a maximum error of 7.9% for :
In the limit for infinite aspect ratio (), the low-frequency approximation of obtained from Equations (16)–(19) is zero. Thus, for a two-dimensional CFD model with an inherent aspect ratio of infinity, tends to zero and thus no end correction is needed for a ROM representing that case. In Equation (7), the apparent nozzle length for a 2D CFD simulation thus reduces to the geometric length , which is used in Section 3.3 to explain how to compare the performance of 2D and 3D SJA cavity geometries.
3. Validation Methodologies
3.1. Numerical Validation Using Transient Computational Fluid Dynamics (CFD) Modelling
Two-dimensional (2D) unsteady compressible CFD simulations are carried out using Ansys CFX software. For a selected number of cases, three-dimensional (3D) simulations have been carried out using the same package (see Section 3.1.1). Figure 2 displays the 2D computational domain and the generated mesh used in the simulations. To achieve the most realistic computation of the flow induced by the synthetic jet, Alimohammadi et al. [25] reported on the importance of diaphragm deformation and the inclusion of the cavity and deforming diaphragm as a part of the simulation. This approach stands in contrast to the traditional assumption of an oscillating boundary condition at the exit of the orifice slot which leads to an over-simplification of boundary conditions. As a result, the oscillating wall of the cavity is simulated in the developed CFD model here by means of dynamic mesh techniques. The diaphragm deformation applied in the CFD model is different from the deformation of the loudspeaker cone used for the experiments (see Section 3.2), however the maximum deflection for all cases considered in this study does not exceed 4% of the cavity height , and therefore the difference in impact on the internal cavity flow is deemed negligible.

Figure 2.
2D computational domain and mesh (the diaphragm deformation is exaggerated and only indicative. The full solution domain is not shown for the sake of clarity).
The computational domain consists of three distinct regions, namely cavity, nozzle (length mm, width mm), and the near-orifice region where the synthetic jet develops. The cavity dimensions for the simulations are mm and mm, to mimic the experimental validation geometry as best as possible.
The far-field boundaries at atmospheric pressure are placed at a distance of in the direction and in the direction from the orifice outlet. The simulation of synthetic jets consists of intricate fluid mechanics featuring flow separation, unsteadiness, and vortex dynamics. Alimohammadi et al. [25] have suggested the shear stress transport (SST) model coupled with modified curvature correction and also the Gamma-Theta transition model as the most suitable Reynolds Averaged Navier Stokes (RANS) turbulence model to be utilized. As such, the 2D domain is composed of nearly 100,000 cells in a structured mesh, and the near wall refinement assures the value (i.e., the non-dimensional distance of the first grid point from the wall) does exceed unity.
The numerical uncertainty is quantified by the grid convergence index () method which represents the discretization error, the method recommended by the Journal of Fluids Engineering [26]. Through several mesh refinements to study the independency of the mesh generation, the maximum numerical uncertainties () are calculated for different grids, reporting that solutions are within the asymptotic range of convergence. The based on the peak nozzle velocity is calculated as 0.8%.
3.1.1. Complementary 3D Simulations
For some selected cases, 3D CFD simulations are performed on a mesh with 1.46 million cells for the same solver settings and conditions. For the 3D simulations, the exact experimental dimensions are taken (see Section 3.2). By choosing similar linear cavity dimensions, it is anticipated that internal vortex formation in the cavity would be reasonably similar in 2D and 3D cases. However, Section 3.3 explains important consequences for the comparison of results from 2D and 3D geometries in the frequency domain.
3.2. Experimental Validation
The experimental validation approach is identical to the description in Persoons [16], to which the reader is referred for full details. Similar to the CFD simulations, the orifice slot measures mm by mm (aspect ratio ) with a length mm, while the cavity volume cm3 and cm2, corresponding to a 75 mm circular diaphragm representing a Visaton FR8 (4 Ohm, 10 W) loudspeaker [16].
Figure 3 shows a schematic diagram identifying the primary instrumentation used: (i) a hot-wire sensor (e.g., Dantec 55P11, Pt-plated tungsten wire, 5 m diameter by 1.25 mm in length), operated in a constant temperature anemometer (Dantec 54T30, bridge ratio 20:1, resistance overheat ratio 1.8, 10 kHz low pass filter) measures the approximate centerline nozzle velocity which is taken to represent the mean nozzle velocity in the assumption that the profile is reasonably uniform for a short orifice. The probe is less than 0.5 mm away from the orifice outlet plane to avoid velocity decay. The off-angle positioning of the probe, away from the main jet formation region, minimizes its flow disturbance. The hot-wire was calibrated in this same orientation in a low-turbulence wind tunnel, using a pitot-static probe as reference, for a range of air velocities between 0.6 m/s and 48 m/s. A King’s law relation was least-squares fitted to the calibration data, resulting in a coefficient of determination of 99.9%. The probe reading is insensitive to flow direction, yet due to the probe body orientation being nearly perpendicular to the jet flow (see Figure 3), the reading can be inverted during the suction stroke. The transitions between suction and ejection strokes are determined by locating the local minima in the hot-wire reading (in absolute value). During these transitions, wherever the velocity reading falls below the lower limit of the calibration range (<0.6 m/s), readings are ignored. (ii) The cavity acoustic pressure is measured relative to atmosphere using a low sensitivity microphone (G.R.A.S., Hole, Demark. 40BD with 26CB constant current power (CCP) preamplifier, 1.6 mV/Pa, 40–174 dB, 4 Hz–70 kHz). (iii) The deflection of the diaphragm is measured with a laser displacement sensor (e.g., Keyence LK-G157, range mm, linearity ). These quantities are read into a data acquisition system along with the driver voltage and current . The data is phase-averaged over 16 periods to achieve an uncertainty level below 5% based on a 95% confidence level on the phase-averaged velocity, pressure and diaphragm deflection waveforms.
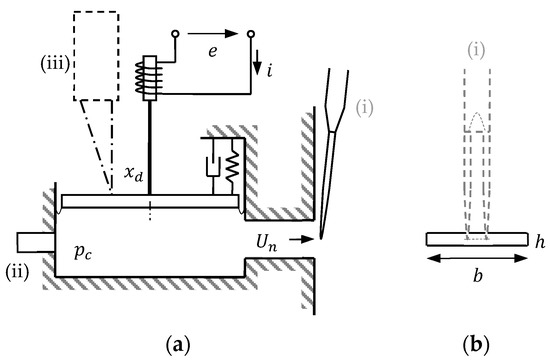
Figure 3.
(a) Schematic diagram of an instrumented SJA with (b) rectangular orifice (not to scale), instrumented with (i) a hot-wire anemometer probe for nozzle velocity , (ii) microphone for cavity pressure and (iii) laser displacement sensor for [16].
3.3. Comparing Synthetic Jet Actuator Performance for 2D and 3D Geometries
As mentioned in Section 2.1, the Helmholtz resonance frequency and driver resonance frequency are two important quantities that characterize the performance of an SJA in the temporal or frequency domain. The Helmholtz resonance frequency defined by Equation (8) is the primary parameter, since typically the driver and cavity resonance frequencies are chosen to be of similar magnitudes for optimal performance.
For 3D geometries such as the actuator used for the experimental validation, the Helmholtz resonance frequency can be estimated based on the cavity volume, nozzle cross-sectional area end-corrected nozzle length (which requires an estimate of the added mass coefficient ):
For a 2D geometry used for the CFD simulations in this study, the added mass coefficient , as explained in Section 2.2. Thus the 2D equivalent of the Helmholtz resonance frequency is defined slightly differently as:
In this paper, the Helmholtz resonance frequencies for the 2D and 3D CFD simulations and experiments are Hz, Hz and Hz, respectively. In the following section, the frequency domain results are plotted as a function of the normalized frequency , where takes the aforementioned values for 2D and 3D data.
4. Results and Discussion
Table 2 shows an overview of the cases studied in this paper. All cases represent experiments and matching CFD simulations for an SJA with a rectangular orifice, however as specified above, there are inevitable physical differences in the systems, more specifically the 2D CFD geometry having an infinite orifice aspect ratio , whereas the aspect ratio for the experiments and 3D CFD results is finite ().

Table 2.
List of cases included in this investigation. Cases A and B are indicated respectively as red and blue markers in subsequent figures. Values in parenthesis are reduced-order model (ROM) predictions at the operating conditions.
Table 2 also summarizes the velocity-to-pressure ratio values, representing the fluidic SJA model defined in Equation (11). The values are provided in dimensionless form as , where the amplitudes and are obtained from the (i) experiments, (ii) 2D CFD and (iii) 3D CFD simulations, respectively. For each condition, the corresponding reduced-order model value obtained using Equation (11) is also provided in brackets.
Figure 4 provides a graphical representation of the agreement between the experimental values (markers) and the ROM (solid lines) in terms of the ratio of nozzle velocity to cavity pressure , referred to as the fluidic model and defined in Equation (11). Because the model is non-linear, four lines are shown for four different cavity pressure amplitudes ranging from 100 Pa to 1000 Pa. The markers represent experimental measurement points at corresponding pressure amplitudes, as listed in Table 2. Cases A and B (see Table 2) are indicated with red and blue markers, respectively.
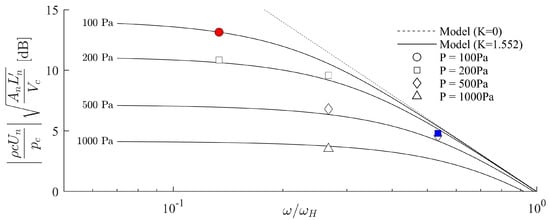
Figure 4.
ROM validation in terms of the fluidic model (Equation (11) with and ) (lines) versus experimental data (markers) for a synthetic jet actuator with rectangular orifice of aspect ratio 30:1. Markers represent cavity pressure magnitudes (⚪) 100 Pa, (☐) 200 Pa, (◇) 500 Pa, (△) 1000 Pa. Cases A and B (see Table 2) are indicated with red and blue markers, respectively.
The higher the pressure amplitude, the more the damping term featuring in Equation (11) dominates, and the less sensitive the velocity-to-pressure ratio becomes to frequency. The frequency on the horizontal axis is normalized by the Helmholtz resonance frequency. For frequencies exceeding the Helmholtz resonance by a factor of 3–5, the velocity-to-pressure ratio is no longer quasi constant and increasingly tends towards the dashed line. This represents an undamped model (), corresponding to .
Regarding the procedure for determining the parameters and through calibration, this is described in detail in Persoons [16]. In short, once a given dataset of cavity pressure and nozzle velocity waveforms are provided, whether through experimental measurements or numerical simulations, the amplitudes and are determined to calculate the velocity-to-pressure ratio as listed in Table 2. Then a least-squares fitting procedure is applied to determine and such that Equation (11) best fits the experimental or numerically determined ratios. Because of the non-linearity, it is convenient for plotting purposes if the data are taken at predefined cavity pressure amplitudes, which explains why the data in Table 2 have cavity pressure amplitudes that are approximately 100 Pa, 200 Pa, 500 Pa and 1000 Pa. During the experiments, this can be done by monitoring the cavity pressure microphone readings, although admittedly this is somewhat more cumbersome to achieve for the CFD simulations using the dynamic meshing approach. However, this is merely a small inconvenience from the perspective of plotting results to collapse onto a small number of lines representing Equation (11).
The nozzle velocity, cavity pressure and diaphragm deflection waveforms that were used to determine the amplitudes in Figure 4 and Table 2 are shown for two selected cases A and B in Figure 5 and Figure 6. These cases are chosen for the following reasons: Case A (red marker in Figure 4) is relatively low frequency and has a small cavity pressure amplitude (approximately 100 Pa), and thus also a small velocity amplitude, which makes for challenging measurement conditions. Case B (blue marker in Figure 4) is obtained at a higher frequency closer to the Helmholtz resonance frequency, which makes for increasingly more challenging conditions to obtain reliable convergence of the CFD simulations. Due to the significant computational cost involved in performing transient 3D CFD simulations, only cases A and B were simulated in 3D. 2D CFD simulations were carried out for the entire set of cases.
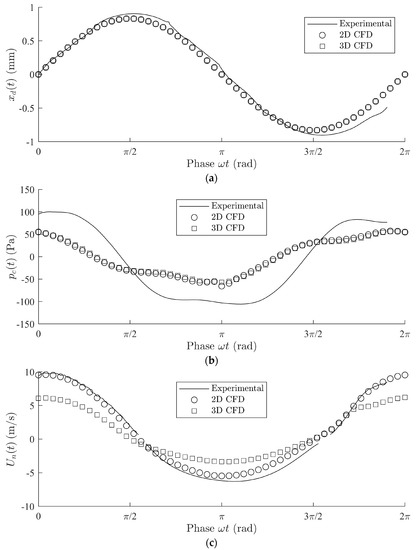
Figure 5.
(a) Diaphragm deflection , (b) cavity pressure and (c) nozzle velocity as a function of phase angle for case A (see Table 2), comparing experimental results (─), 2D CFD results (⚪), and 3D CFD results (☐).
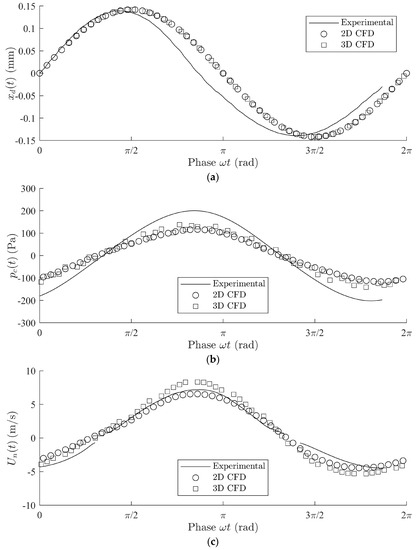
Figure 6.
(a) Diaphragm deflection , (b) cavity pressure and (c) nozzle velocity as a function of phase angle for case B (see Table 2), comparing experimental results (─), 2D CFD results (⚪), and 3D CFD results (☐).
For Case A, Figure 5 shows plots of the phase-resolved (a) diaphragm deflection , (b) cavity pressure and (c) nozzle velocity determined from experimental measurements, 2D CFD simulations and 3D CFD simulations, where the phase angle is given by . Phase angle is arbitrarily chosen as the zero crossing of the diaphragm deflection during the ejection stroke. For the experiments, the waveforms are ensemble-averaged over 16 cycles, as explained in Section 3.2. For the CFD simulations, the waveforms are extracted after periodic conditions were reached. The threshold for reaching periodicity is defined such that the root-mean-squared deviation on the instantaneous values of velocity and pressure between two successive cycles does not exceed 1%.
Since the diaphragm deflection is a user-defined input in the CFD simulations, perfect sine waveforms are observed for the CFD implementation of in Figure 5a. The simulated cavity pressure in Figure 5b broadly resembles the measured pressure waveform; however, some phase lag can be seen in some of the higher order fluctuations. With respect to the ROM, however, it only considers first order effects and neglects any higher order acoustics, thus these discrepancies are of minor importance in that regard. The difference in pressure magnitude in Figure 5b between experiments and CFD simulations has been verified to be independent of mesh density, turbulence model, and numerical discretization method. Furthermore, 2D and 3D CFD simulations yield similar pressure amplitudes. However, it is the ratio of velocity to pressure amplitude that matters for the fluidic model validation, not the cavity pressure amplitude itself.
In terms of the nozzle velocity , it is important to note that the measured velocity is obtained by means of a hot-wire anemometer probe, placed in close proximity to the outlet of the jet nozzle (see Section 3.2). Because a hot-wire anemometer is insensitive to flow direction, the original velocity waveform is unfolded during the suction stroke to produce the directional velocity waveform shown in Figure 5a. Furthermore, because of the asymmetry in the near-orifice flow fields for a synthetic jet during ejection and suction, there is a small but significant difference in the positive and negative peak velocity magnitudes during ejection and suction, respectively.
Furthermore, as mentioned in Section 3.2, the hot-wire measures the approximate centerline nozzle velocity . Therefore, the velocity at the same location is extracted from the CFD results to provide a fair comparison. In Figure 5c and 6c, hot-wire readings below the calibration range (<0.6 m/s) are omitted from the graphs.
Overall, Figure 5c shows a reasonable agreement between the experimental and numerical velocity waveforms, faithfully reproducing a minor peak during the startup of the ejection phase, visible at phase angle . The difference in magnitude between the experimental and CFD results should be interpreted as follows: although the 2D CFD results show a good agreement with the experiments in terms of velocity, the 2D CFD cavity pressure is underestimated. For the 3D CFD results, the predicted velocity magnitude is smaller yet the ratio of velocity to pressure amplitude is much closer to the experimental data, giving a stronger confirmation of the validity of the fluidic model in Equation (11).
Similar to Figure 5, Figure 6 shows the corresponding waveforms for case B at a greater frequency, closer to the Helmholtz resonance frequency. Again, a reasonable general agreement is observed between experimental and numerical data. Because it is approaching the resonance frequency, a significant phase shift is observed for case B between the diaphragm deflection and nozzle velocity, compared to the low frequency case A.
In terms of the 2D CFD simulations, it was found that the results are not particularly sensitive to changes in the modelling approach. Different discretization schemes and turbulence models were used for the 2D CFD simulations during the initial exploratory simulations for this study, and even the 3D CFD simulation results do not appreciably alter the shape of the pressure and velocity waveforms. A notable improvement in the velocity-to-pressure ratio prediction was observed for 3D CFD simulations compared to 2D simulations (see Figure 5).
Furthermore, it was found that there was no need to match exactly the location of the cavity pressure probe in the CFD pressure field to the location of the microphone used in the experiments. Thus it seems that, at least in first approximation, the physics relating bulk cavity pressure to nozzle velocity can indeed be captured reliably by a reduced-order model.
Figure 7 demonstrates this more clearly by plotting the experimental and numerical values for the velocity-to-pressure ratio on the vertical axis against the corresponding ROM prediction on the horizontal axis. As before, cases A and B are indicated by red and blue markers, respectively, and the other cases listed in Table 2 are also included (only 2D CFD and experimental data). As mentioned previously, because of the difference in geometry for the 2D versus 3D geometries, different values are used. In Figure 7, the ROM predictions corresponding to the experimental and numerical data are produced using Equation (11) with . For the experimental results, . For the 3D CFD results, and for the 2D CFD results, as explained in Section 2.2. The reason for the difference in between the 3D CFD and experimental results can be attributed to the different acoustic radiation impedance boundary conditions; the experiments feature radiation from the rear of the diaphragm, which is not included in the CFD simulation. Furthermore, the far field radiation and reflective properties of the lab environment are difficult to reproduce faithfully in CFD at a reasonable computational cost.
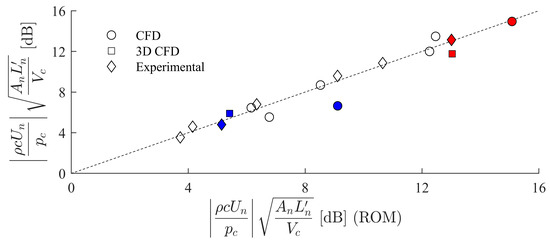
This study has revealed the challenges in reliably matching up experimental and numerical conditions for this type of phenomenon. Further research including more detailed pressure and velocity field quantification will be required to fully understand these aspects.
5. Conclusions
In this paper, the underlying physics and methodology behind a physics-based reduced-order model (ROM) with two degrees of freedom for a synthetic jet actuator (SJA) has been explained. The ROM combines (i) a fluidic model relating jet velocity amplitude to cavity pressure amplitude and (ii) an electromechanical driver model relating the driver input to the diaphragm deflection amplitude and cavity pressure amplitude .
The fluidic model provides the velocity-to-pressure amplitude ratio as a function of the fluid speed of sound, SJA dimensions and the operating frequency . It is a non-linear model which accounts for fluid damping and inertia effects in the nozzle—these effects are captured by the two empirical model parameters, the pressure loss coefficient and added mass coefficient . Guidelines are provided for evaluating and , and a closed form expression for the added mass coefficient is given for rectangular slot orifices as a function of orifice aspect ratio and frequency .
The simplified version of the fluidic model equation (assuming sine wave actuation) is described by Equation (11) which is generally applicable to any SJA operating in any gas or liquid medium, as long as the fluid compressibility outweighs the mechanical compliance of the cavity and surrounding structure [27]. The electromechanical driver model is established in Equations (13) and (14) for the most common actuation methods used, i.e., a piezoelectric diaphragm and loudspeaker, respectively.
The paper has presented both experimental and numerical results using transient computational fluid dynamics (CFD) simulations, using both 2D and 3D geometries. Important aspects related to the comparison of 2D and 3D geometries are discussed in Section 3.3 and Section 4.
A satisfactory agreement is achieved with the ROM predictions for both experimental measurements as well as 2D and 3D numerical simulations, as summarized by Figure 7. This demonstrates the validity of this fairly simple analytical ROM for a variety of conditions, for a range of frequencies approaching the Helmholtz resonance frequency.
Author Contributions
T.P., R.C. and S.A. wrote the paper; T.P. developed the original reduced-order model; R.C. carried out additional analytical work to refine the reduced-order model; S.A. performed the numerical simulation work.
Funding
The paper was supported by the Naughton Foundation under grant number NGF/1617/TCD/01, and the Irish Research Council (IRC) under grant number GOIPD/2016/216. This publication has emanated from research conducted with the financial support of the Science Foundation Ireland under the SFI Strategic Partnership Programme Grant Number SFI/15/SPP/E3125.
Acknowledgments
The authors acknowledge the support of the DJEI/DES/SFI/HEA Irish Centre for High-End Computing (ICHEC) for the provision of computational facilities and support.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Nomenclature
| Cross-sectional area, m2 | |
| Orifice aspect ratio () | |
| Electromagnetic force factor () | |
| Spanwise length of slot orifice, m | |
| Linear damping coefficient, N/(m*s) or capacitance, F | |
| Speed of sound, m/s | |
| Hydraulic diameter, m | |
| Actuator voltage, V | |
| Dimensionless frequency () | |
| Actuator driving force, N | |
| Actuation frequency, Hz | |
| Orifice slot width, m | |
| Actuator current, A | |
| Imaginary unit ( | |
| Nozzle non-linear damping coefficient or stiffness, N/m | |
| Length, m or inductance, H | |
| Synthetic jet stroke length, m | |
| Mass, kg | |
| Cavity acoustic pressure, Pa | |
| Resistance, Ohm | |
| Reynolds number () | |
| Laplace variable (), s−1 | |
| Time, s | |
| Velocity, m/s | |
| Characteristic velocity (), m/s | |
| Volume, m3 | |
| Displacement, m | |
| Impedance, Ω | |
| Subscripts | |
| 0 | Characteristic synthetic jet scale |
| c | Actuator cavity |
| d | Actuator diaphragm |
| e | Electrical (referring to the actuator driver) |
| emf | Electromotive force |
| H | Helmholtz resonance |
| n | Actuator nozzle or orifice |
| p | Parallel |
| s | Series |
| Free stream | |
| Greek symbols | |
| Electromechanical coupling coefficient, N/V | |
| Nozzle added mass coefficient | |
| Density, kg/m3 | |
| Kinematic viscosity, m2/s | |
| Abbreviations | |
| CFD | Computational fluid dynamics |
| ROM | Reduced-order model |
| SJA | Synthetic jet actuator |
References
- Smith, B.L.; Glezer, A. The formation and evolution of synthetic jets. Phys. Fluids 1998, 10, 2281–2297. [Google Scholar] [CrossRef]
- Glezer, A.; Amitay, M. Synthetic jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Holman, R.; Utturkar, Y.; Mittal, R.; Smith, B.L.; Cattafesta, L. Formation criterion for synthetic jets. AIAA J. 2005, 43, 2110–2116. [Google Scholar] [CrossRef]
- McGuinn, A.; Farrelly, R.; Persoons, T.; Murray, D.B. Flow regime characterisation of an impinging axisymmetric synthetic jet. Exp. Therm. Fluid Sci. 2013, 47, 241–251. [Google Scholar] [CrossRef]
- You, D.; Moin, P. Active control of flow separation over an airfoil using synthetic jets. J. Fluids Struct. 2008, 24, 1349–1357. [Google Scholar] [CrossRef]
- Dandois, J.; Garnier, E.; Sagaut, P. Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 2007, 574, 25–58. [Google Scholar] [CrossRef]
- Persoons, T.; McGuinn, A.; Murray, D.B. A general correlation for the stagnation point Nusselt number of an axisymmetric impinging synthetic jet. Int. J. Heat Mass Transf. 2011, 54, 3900–3908. [Google Scholar] [CrossRef]
- Fanning, E.; Persoons, T.; Murray, D.B. Heat transfer and flow characteristics of a pair of adjacent impinging synthetic jets. Int. J. Heat Fluid Flow 2015, 54, 153–166. [Google Scholar] [CrossRef]
- Smith, B.L.; Glezer, A. Jet vectoring using synthetic jets. J. Fluid Mech. 2002, 458, 1–34. [Google Scholar] [CrossRef]
- Smith, B.L.; Glezer, A. Vectoring of adjacent synthetic jets. AIAA J. 2005, 43, 2117–2124. [Google Scholar] [CrossRef]
- Persoons, T.; O’Donovan, T.S. A pressure-based estimate of synthetic jet velocity. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Shuster, J.M.; Smith, D.R. Experimental study of the formation and scaling of a round synthetic jet. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Smith, B.L.; Swift, G.W. A comparison between synthetic jets and continuous jets. Exp. Fluids 2003, 34, 467–472. [Google Scholar] [CrossRef]
- Crittenden, T.M.; Glezer, A. A high-speed, compressible synthetic jet. Phys. Fluids 2006, 18. [Google Scholar] [CrossRef]
- Kordík, J.; Trávníček, Z. Novel nozzle shapes for synthetic jet actuators intended to enhance jet momentum flux. Actuators 2018, 7. [Google Scholar] [CrossRef]
- Persoons, T. General reduced-order model to design and operate synthetic jet actuators. AIAA J. 2012, 50, 916–927. [Google Scholar] [CrossRef]
- McCormick, D. Boundary layer separation control with directed synthetic jets. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar]
- Gallas, Q.; Holman, R.; Nishida, T.; Carroll, B.; Sheplak, M.; Cattafesta, L. Lumped element modeling of piezoelectric-driven synthetic jet actuators. AIAA J. 2003, 41, 240–247. [Google Scholar] [CrossRef]
- Kordík, J.; Trávníček, Z.; Safarik, P. Experiments on resonance frequencies of synthetic jet actuators. J. Flow Vis. Image Proc. 2010, 17, 203–214. [Google Scholar] [CrossRef]
- Chiatto, M.; Capuano, F.; Coppola, G.; Luca, L.D. LEM characterization of synthetic jet actuators driven by piezoelectric element: A review. Sensors 2017, 17, 1216. [Google Scholar] [CrossRef] [PubMed]
- Kordík, J.; Trávníček, Z. Optimal diameter of nozzles of synthetic jet actuators based on electrodynamic transducers. Exp. Therm. Fluid Sci. 2017, 86, 281–294. [Google Scholar] [CrossRef]
- Beranek, L.L. Acoustics; McGraw-Hill: New York, NY, USA, 1954; pp. 116–128. [Google Scholar]
- Burnett, D.S.; Soroka, W.W. Tables of rectangular piston radiation impedance functions, with application to sound transmission loss through deep apertures. J. Acoust. Soc. Am. 1972, 51, 1618–1623. [Google Scholar] [CrossRef]
- Kooijman, G.; Ouweltjes, O. Finite difference time domain electroacoustic model for synthetic jet actuators including nonlinear flow resistance. J. Acoust. Soc. Am. 2009, 125, 1911–1918. [Google Scholar] [CrossRef] [PubMed]
- Alimohammad, S.; Fanning, E.; Persoons, T.; Murray, D.B. Characterization of flow vectoring phenomenon in adjacent synthetic jets using CFD and PIV. Comput. Fluids 2016, 140, 232–246. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130. [Google Scholar] [CrossRef]
- Persoons, T.; Saenen, T.; Oevelen, T.V.; Baelmans, M. Effect of flow pulsation on the heat transfer performance of a minichannel heat sink. J. Heat Transf. 2012, 134. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).