Polymer Microgripper with Autofocusing and Visual Tracking Operations to Grip Particle Moving in Liquid
Abstract
:1. Introduction
2. System Design and Installation
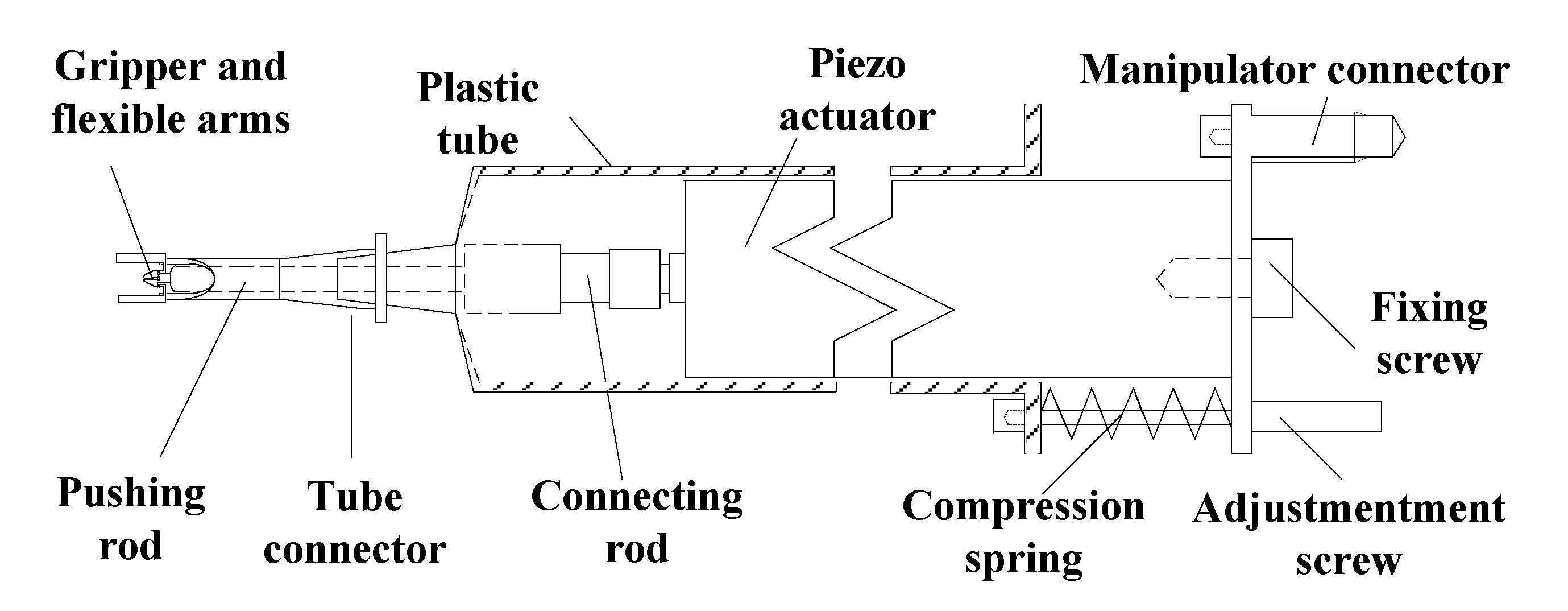
2.1. Micro Gripper System and Moving Manipulator System
2.2. Object Platform
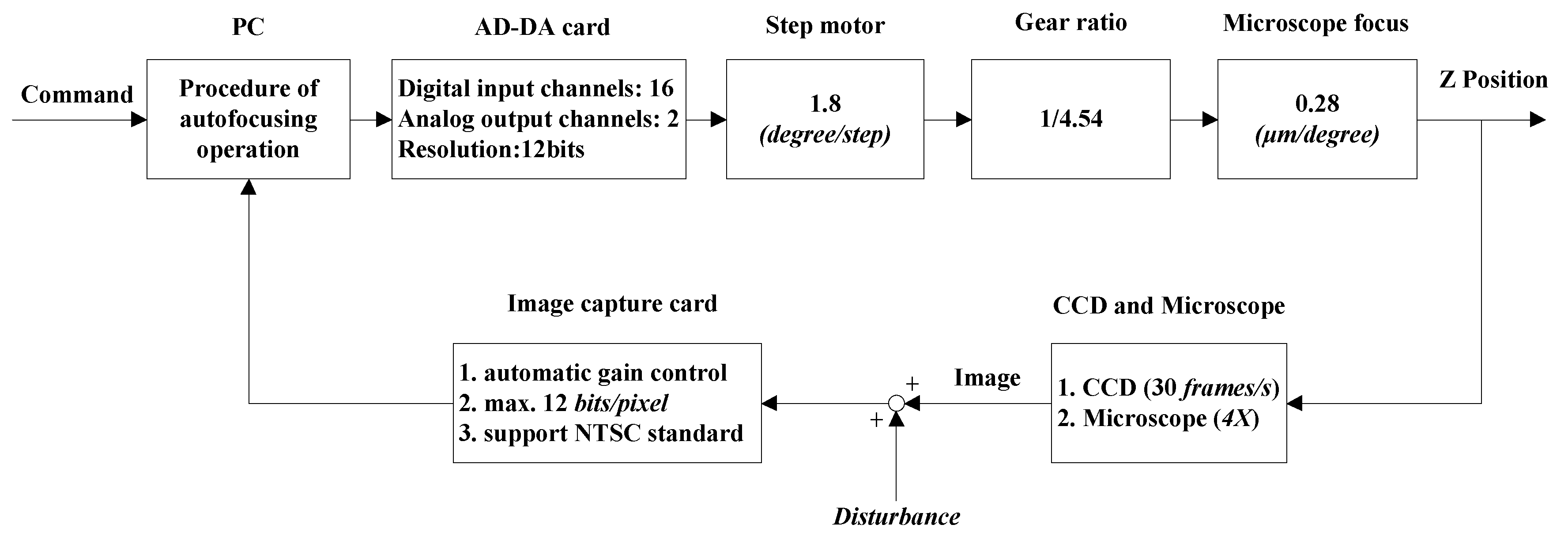
2.3. Autofocusing Stage
3. Autofocusing Operations
3.1. Wavelet-Entropy Focusing Function
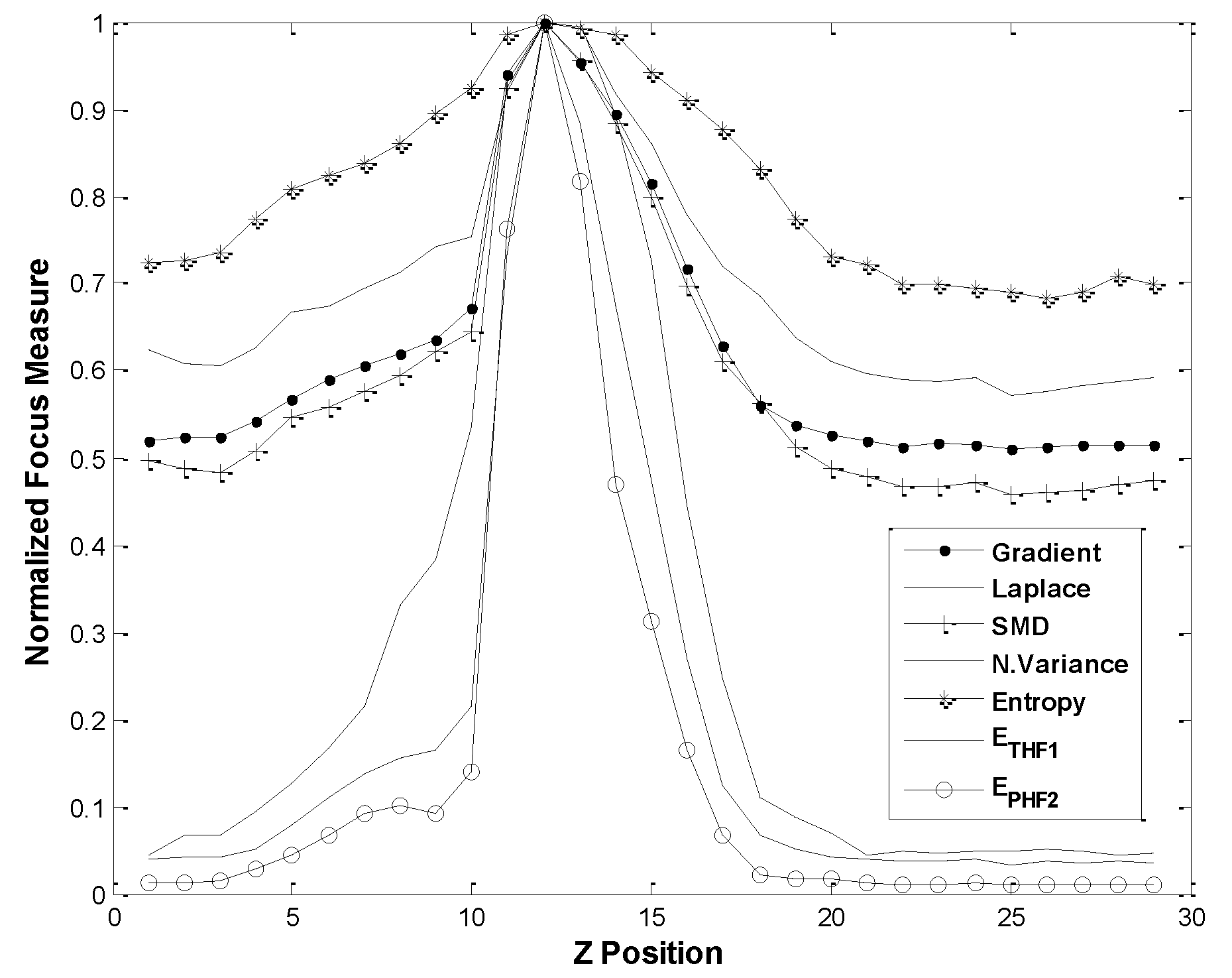
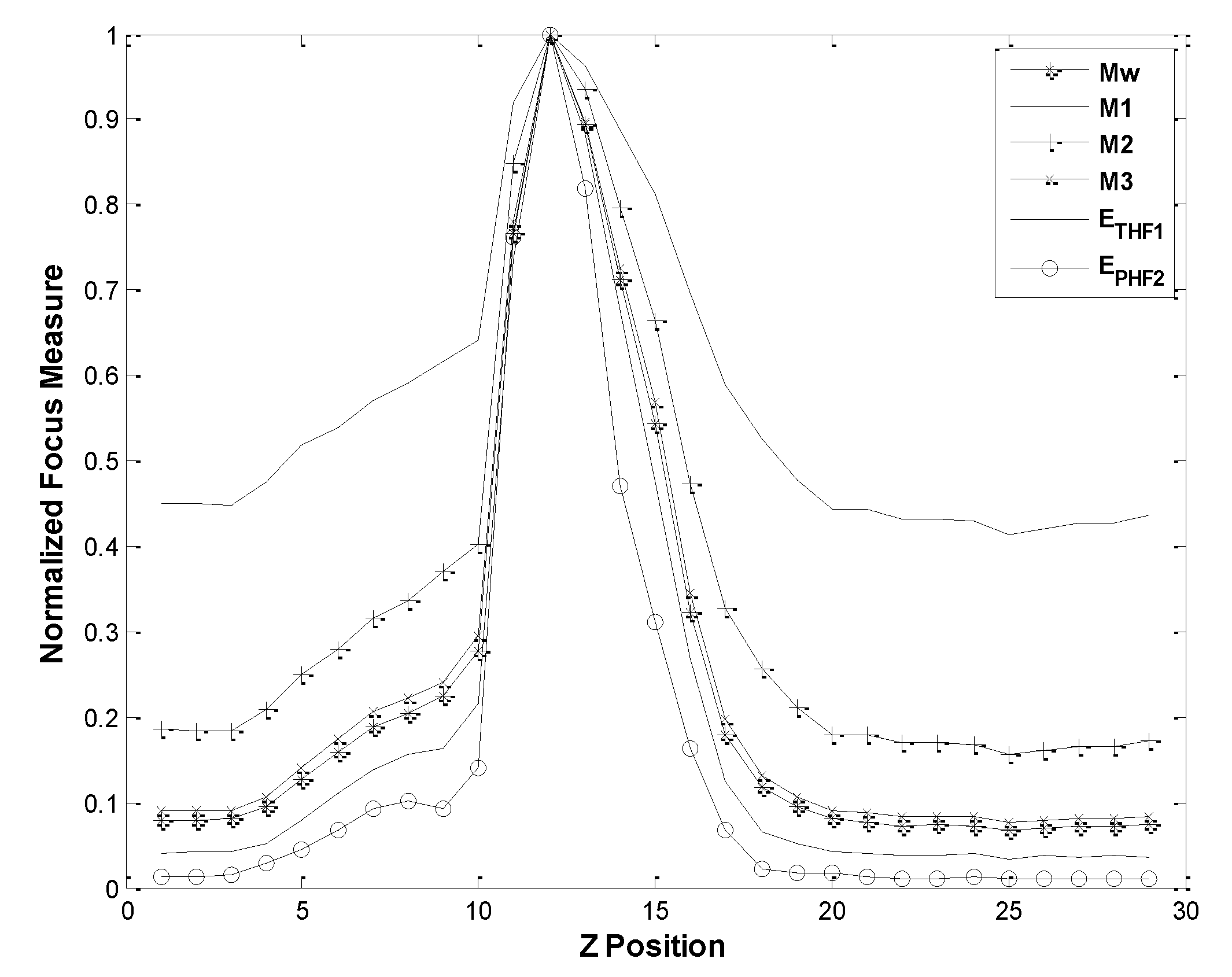
3.2. Experimental Test and Comparison with Other Focusing Functions
3.2.1. Comparison with Common Focusing Functions
3.2.2. Comparison of Wavelet-Based Focusing Functions
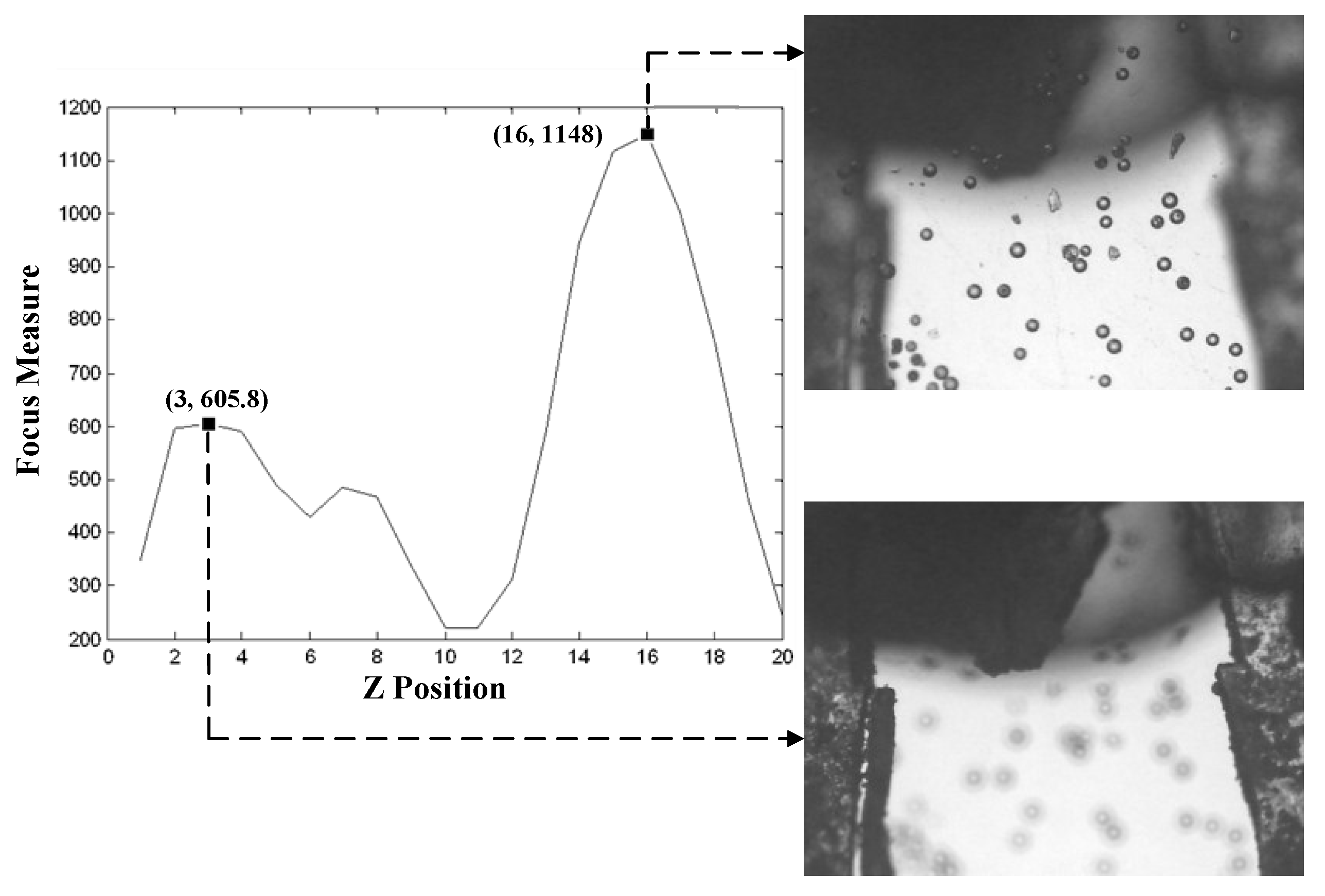
3.3. Peak Position Identification and Depth Estimation in Visual Servo
3.3.1. Peak Position Identification
3.3.2. Depth Estimation
4. Particle Tracking Process
4.1. PCSS Algorithm
- Step 1.
- Set an interrogation pattern I centered on the object particle i with radius of R. In the pattern I, the other particles are , where
- Step 2.
- Establish a polar coordinate system with the identified centroid of the particle i as the pole. The relative positions of to i is obtained by their polar radii and angles
- Step 3.
- Repeat Steps 1 and 2 for another interrogation pattern J centered on the object particle j with radius of R. In the pattern J, the other particles are , where and the relative positions of to j is obtained by their polar radii and angles
- Step 4.
- Define a similarity coefficient between patterns I and J aswhere is a step function. and are thresholds of the polar radius and angle, respectively.
- Step 5.
- Calculate the Sij for all candidate particles in the patterns I and J, and find the matched candidate particle i which gives the maximum value of Sij.
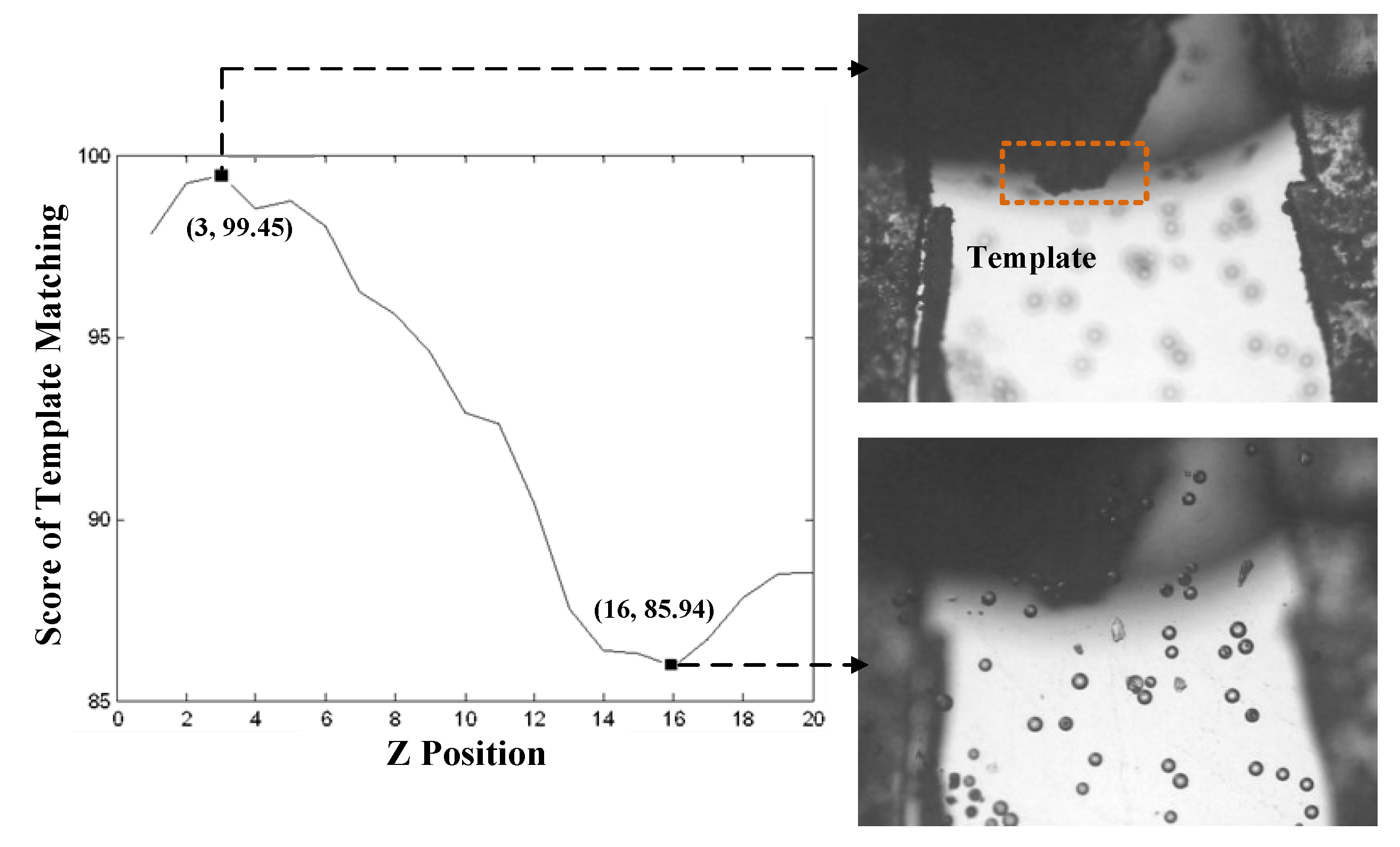
4.2. Template Matching
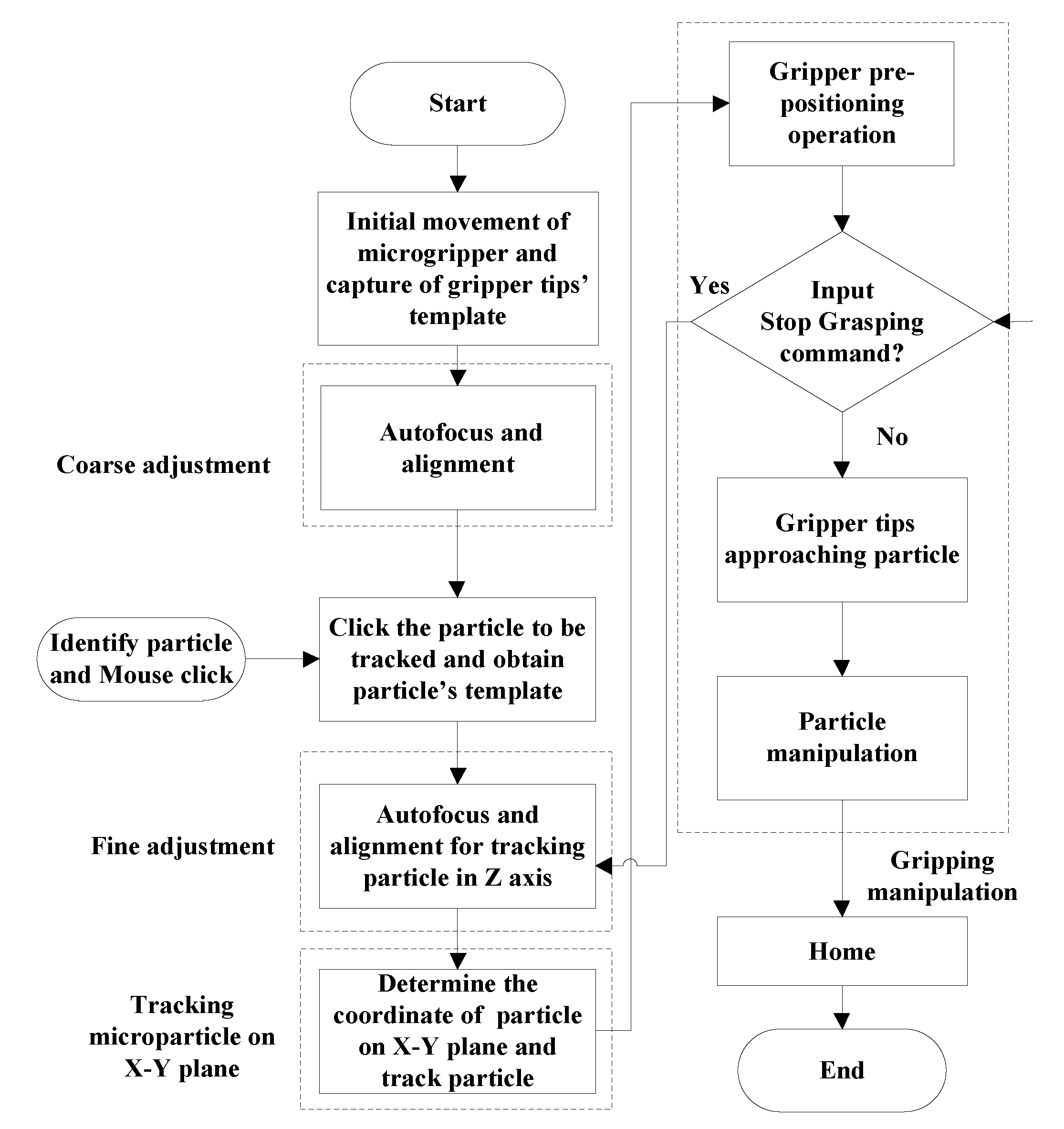
5. Gripping Microparticle Tests
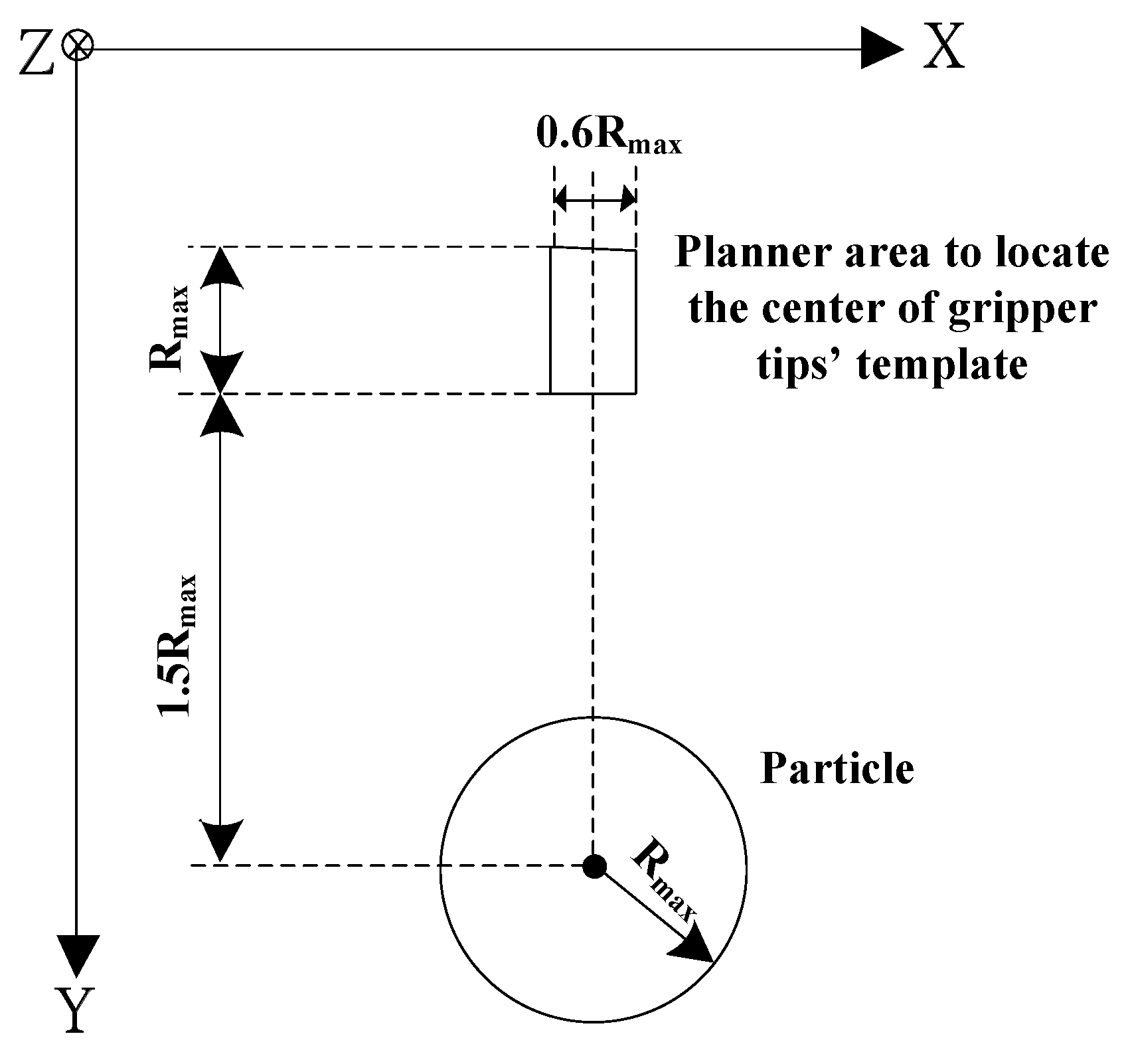
5.1. Working Space in Gripping Operation
5.2. Fine Adjustment of Tracking in Z axis
5.3. Pre-Positioning and Approaching Operations
5.4. Gripping and Releasing Operations
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jager, E.W.H.; Inganas, O.; Lundstrom, I. Microrobots for micrometer-size objects in aqueous media: Potential tools for single-cell manipulation. Science 2000, 288, 2335–2338. [Google Scholar] [CrossRef] [PubMed]
- Desai, J.P.; Pillarisetti, A.; Brooks, A.D. Engineering approaches to biomanipulation. Annu. Rev. Biomed. Eng. 2007, 9, 35–53. [Google Scholar] [CrossRef] [PubMed]
- Carrozza, M.C.; Dario, P.; Menciassi, A.; Fenu, A. Manipulating biological and mechanical micro-objects using LIGA-microfabricated end-effectors. In Proceedings of the IEEE International Conference on Robotics & Automation, Leuven, Belgium, 16–20 May 1998; Volume 2, pp. 1811–1816. [Google Scholar]
- Ok, J.; Chu, M.; Kim, C.J. Pneumatically driven microcage for micro-objects in biological liquid. In Proceedings of the Twelfth IEEE International Conference on Micro Electro Mechanical Systems, Orlando, FL, USA, 17 January 1999; pp. 459–463. [Google Scholar]
- Arai, F.; Sugiyama, T.; Luangjarmekorn, P.; Kawaji, A.; Fukuda, T.; Itoigawa, K.; Maeda, A. 3D Viewpoint Selection and Bilateral Control for Bio-Micromanipulation. In Proceedings of the IEEE International Conference on Robotics & Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 947–952. [Google Scholar]
- Beyeler, F.; Neild, A.; Oberti, S.; Bell, D.J.; Sun, Y. Monolithically fabricated microgripper with integrated force sensor for manipulating microobjects and biological cells aligned in an ultrasonic field. J. Microelectromech. Syst. 2007, 16, 7–15. [Google Scholar] [CrossRef]
- Feng, L.; Wu, X.; Jiang, Y.; Zhang, D.; Arai, F. Manipulating Microrobots Using Balanced Magnetic and Buoyancy Forces. Micromachines 2018, 9, 50. [Google Scholar] [CrossRef]
- Potrich, C.; Lunelli, L.; Bagolini, A.; Bellutti, P.; Pederzolli, C.; Verotti, M.; Belfiore, N.P. Innovative Silicon Microgrippers for Biomedical Applications: Design, Mechanical Simulation and Evaluation of Protein Fouling. Actuators 2018, 7, 12. [Google Scholar] [CrossRef]
- Chronis, N.; Lee, L.P. Electrothermally activated SU-8 microgripper for single cell manipulation in solution. J. Microelectromech. Syst. 2005, 14, 857–863. [Google Scholar] [CrossRef]
- Hériban, D.; Agnus, J.; Gauthier, M. Micro-manipulation of silicate micro-sized particles for biological applications. In Proceedings of the 5th International Workshop on Microfactories, Becanson, France, 25–27 October 2006; p. 4. [Google Scholar]
- Solano, B.; Wood, D. Design and testing of a polymeric microgripper for cell manipulation. Microelectron. Eng. 2007, 84, 1219–1222. [Google Scholar] [CrossRef]
- Han, K.; Lee, S.H.; Moon, W.; Park, J.S.; Moon, C.W. Design and fabrication of the microgripper for manipulation the cell. Integr. Ferroelectr. 2007, 89, 77–86. [Google Scholar] [CrossRef]
- Colinjivadi, K.S.; Lee, J.B.; Draper, R. Viable cell handling with high aspect ratio polymer chopstick gripper mounted on a nano precision manipulator. Microsyst. Technol. 2008, 14, 1627–1633. [Google Scholar] [CrossRef]
- Kim, K.; Liu, X.; Zhang, Y.; Sun, Y. Nanonewton force-controlled manipulation of biological cells using a monolithic MEMS microgripper with two-axis force feedback. J. Micromech. Microeng. 2008, 18, 055013. [Google Scholar] [CrossRef]
- Kim, K.; Liu, X.; Zhang, Y.; Cheng, J.; Xiao, Y.W.; Sun, Y. Elastic and viscoelastic characterization of microcapsules for drug delivery using a force-feedback MEMS microgripper. Biomed. Microdevices 2009, 11, 421–427. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Chu, J.; Wang, H.; Chen, Z. A multipurpose electrothermal microgripper for biological micro-manipulation. Microsyst. Technol. 2013, 89, 89–97. [Google Scholar] [CrossRef]
- Di Giamberardino, P.; Bagolini, A.; Bellutti, P.; Rudas, I.J.; Verotti, M.; Botta, F.; Belfiore, N.P. New MEMS tweezers for the viscoelastic characterization of soft materials at the microscale. Micromachines 2018, 9, 15. [Google Scholar] [CrossRef]
- Cauchi, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. Analytical, numerical and experimental study of a horizontal electrothermal MEMS microgripper for the deformability characterisation of human red blood cells. Micromachines 2018, 9, 108. [Google Scholar] [CrossRef]
- Malachowski, K.; Jamal, M.; Jin, Q.R.; Polat, B.; Morris, C.J.; Gracias, D.H. Self-folding single cell grippers. Nano Lett. 2014, 14, 4164–4170. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Yoon, C.; Ongaro, F.; Scheggi, S.; Selaru, F.M.; Misra, S.; Gracias, D.H. Stimuli-responsive soft untethered grippers for drug delivery and robotic surgery. Front. Mech. Eng. 2017, 3, 7. [Google Scholar] [CrossRef]
- Wang, W.H.; Lin, X.Y.; Sun, Y. Contact detection in microrobotic manipulation. Int. J. Robot. Res. 2007, 26, 821–828. [Google Scholar] [CrossRef]
- Inoue, K.; Tanikawa, T.; Arai, T. Micro-manipulation system with a two-fingered micro-hand and its potential application in bioscience. J. Biotechnol. 2008, 133, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yang, Z.; Sun, L. Three-dimensional tracking at micro-scale using a single optical microscope. In Proceedings of the International Conference on Intelligent Robotics and Applications, Wuhan, China, 15–17 October 2008; pp. 178–187. [Google Scholar]
- Duceux, G.; Tamadazte, B.; Fort-Piat, N.L.; Marchand, E.; Fortier, G.; Dembele, S. Autofocusing-based visual servoing: Application to MEMS micromanipulation. In Proceedings of the 2010 International Symposium on Optomechatronic Technologies (ISOT), Toronto, ON, Canada, 25–27 October 2010; p. 11747002. [Google Scholar]
- Subbarao, M.; Tyan, J.K. Selecting the optimal focus measure for autofocusing and depth-from-focus. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 864–870. [Google Scholar] [CrossRef] [Green Version]
- Brenner, J.F.; Dew, B.S.; Horton, J.B.; King, T.; Neurath, P.W.; Selles, W.D. An automated microscope for cytologic research, a preliminary evaluation. J. Histochem. Cytochem. 1976, 24, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Groen, F.C.A.; Young, I.T.; Ligthart, G. A comparison of different focus functions for use in autofocus algorithms. Cytometry 1985, 6, 81–91. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Firestone, L.; Cook, K.; Culp, K.; Talsania, N.; Preston, K., Jr. Comparison of autofocus methods for automated microscopy. Cytometry 1991, 12, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Santos, A.; De Solorzano, C.O.; Vaquero, J.J.; Peña, J.M.; Malpica, N.; Del Pozo, F. Evaluation of autofocus functions in molecular cytogenetic analysis. J. Microsc. 1997, 188, 264–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Duthaler, S.; Nelson, B.J. Autofocusing in computer microscopy: Selecting the optimal focus algorithm. Microsc. Res. Tech. 2004, 65, 139–149. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Rong, W.B.; Sun, L.N. Construction and Evaluation of a Wavelet-Based Focus Measure for Microscopy Imaging. Microsc. Res. Tech. 2007, 70, 987–995. [Google Scholar] [CrossRef] [PubMed]
- Shindler, L.; Moroni, M.; Cenedese, A. Spatial–temporal improvements of a two-frame particle-tracking algorithm. Meas. Sci. Technol. 2010, 21, 1–15. [Google Scholar] [CrossRef]
- Chang, R.J.; Lai, Y.H. Design and implementation of micromechatronic systems: SMA drive polymer microgripper. In Design, Control and Applications of Mechatronic Systems in Engineering; Sahin, Y., Ed.; InTechOpen: London, UK, 2017. [Google Scholar]
- Yao, Y.; Abidi, B.; Doggaz, N.; Abidi, M. Evaluation of sharpness measures and search algorithms for the auto focusing of high-magnification images. Proc. SPIE 2006, 6246, 62460G. [Google Scholar] [CrossRef] [Green Version]
- Kou, C.J.; Chiu, C.H. Improved auto-focus search algorithms for CMOS image-sensing module. J. Inf. Sci. Eng. 2011, 27, 1377–1393. [Google Scholar]
- Mendelsohn, M.L.; Mayall, B.H. Computer-oriented analysis of human chromosomes-III focus. Comput. Biol. Med. 1972, 2, 137–150. [Google Scholar] [CrossRef]
- Krotkov, E. Focusing. Int. J. Comput. Vis. 1987, 1, 223–237. [Google Scholar] [CrossRef]
- Subbarao, M.; Choi, T.S.; Nikzad, A. Focusing techniques. J. Opt. Eng. 1993, 32, 2824–2836. [Google Scholar] [CrossRef]
- Yeo, T.T.E.; Ong, S.H.; Jayasooriah; Sinniah, R. Autofocusing for tissue microscopy. Image Vis. Comput. 1993, 11, 629–639. [Google Scholar] [CrossRef]
- Nayar, S.K.; Nakagawa, Y. Shape from Focus. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 824–831. [Google Scholar] [CrossRef]
- Vollath, D. Automatic focusing by correlative methods. J. Microsc. 1987, 147, 279–288. [Google Scholar] [CrossRef]
- Vollath, D. The influence of the scene parameters and of noise on the behavior of automatic focusing algorithms. J. Microsc. 1988, 151, 133–146. [Google Scholar] [CrossRef]
- Yang, G.; Nelson, B.J. Wavelet-based autofocusing and unsupervised segmentation of microscopic images. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 2143–2148. [Google Scholar]
- Ruan, X.D.; Zhao, W.F. A novel particle tracking algorithm using polar coordinate system similarity. Acta Mech. Sin. 2005, 21, 430–435. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Use of the Hough Transformation to detect lines and curves in pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, R.-J.; Chien, Y.-C. Polymer Microgripper with Autofocusing and Visual Tracking Operations to Grip Particle Moving in Liquid. Actuators 2018, 7, 27. https://doi.org/10.3390/act7020027
Chang R-J, Chien Y-C. Polymer Microgripper with Autofocusing and Visual Tracking Operations to Grip Particle Moving in Liquid. Actuators. 2018; 7(2):27. https://doi.org/10.3390/act7020027
Chicago/Turabian StyleChang, Ren-Jung, and Yu-Cheng Chien. 2018. "Polymer Microgripper with Autofocusing and Visual Tracking Operations to Grip Particle Moving in Liquid" Actuators 7, no. 2: 27. https://doi.org/10.3390/act7020027
APA StyleChang, R.-J., & Chien, Y.-C. (2018). Polymer Microgripper with Autofocusing and Visual Tracking Operations to Grip Particle Moving in Liquid. Actuators, 7(2), 27. https://doi.org/10.3390/act7020027



