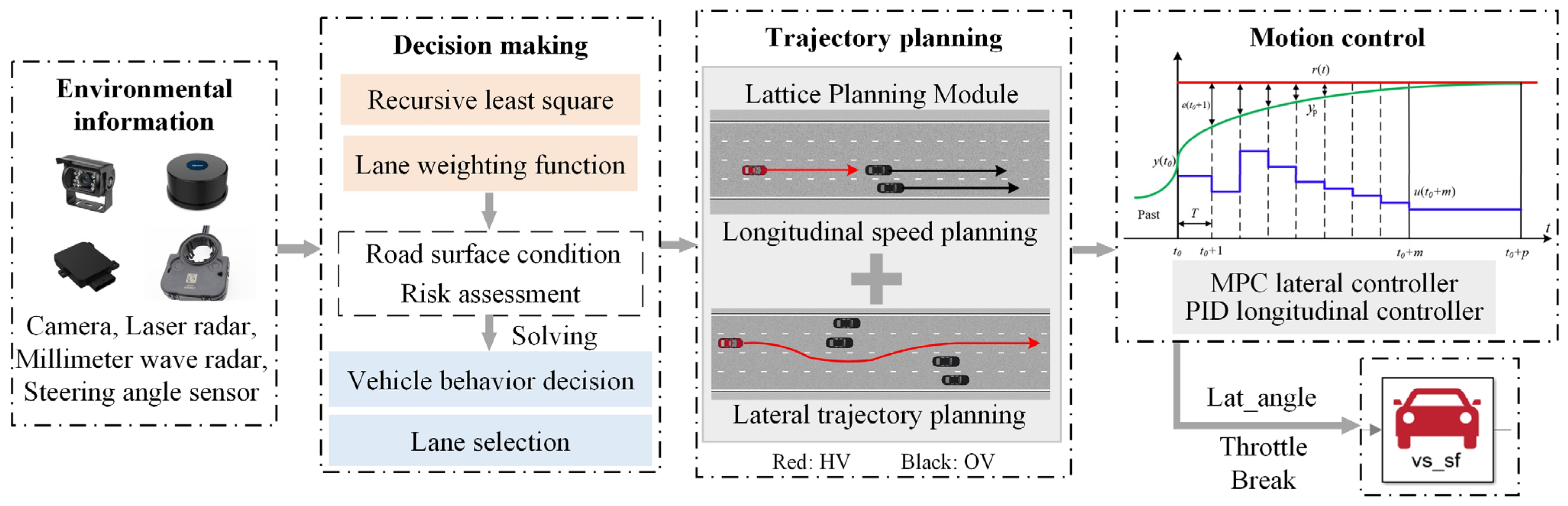
1. Introduction
An autonomous driving system typically consists of four basic modules: perception, decision-making, planning, and control. Driving decisions and trajectory planning are the key bridge connecting perception and execution control [
1]. Road conditions, lane infrastructure, and surrounding vehicles influence the process of vehicle driving decisions and trajectory planning [
2]. Road friction, damage, or water accumulation limit the available adhesion, affecting braking and acceleration strategies. Lane width, marking, and guardrail deformation define lateral driving space, left and right lane changes, and obstacle avoidance feasibility, and the speed and intention of the surrounding vehicles form a dynamic constraint, which prompts the system to switch between lane keeping, overtaking, or longitudinal driving in real time. The decision-making and trajectory planning module must integrate this information to generate an executable path that is both safe, compliant, efficient, and smooth [
3]. Most current research obtains accurate road layout and lane infrastructure information through high-definition maps and self-positioning, and acquires dynamic obstacle information through onboard sensors [
4]. At the same time, it assumes that road adhesion conditions (
the tire–road friction coefficient) can be provided by high-definition maps or empirical values [
5], while ignoring the direct impact of real-time road changes (snow accumulation, water accumulation, wear, etc.) on the vehicle’s dynamic limits and safety indicators [
6]. In fact, the road adhesion coefficient determines the maximum force that the tire can exert during acceleration, braking, and steering. If the adhesion coefficient is overestimated, it may cause the control system to request excessive power output, leading to tire slipping, skidding, and even vehicle loss of control. If the estimated value is too conservative, it will limit the vehicle’s dynamic performance and reduce traffic efficiency and maneuverability [
7]. Therefore, considering real-time road changes at the front end of the planning–control link and designing a reasonable and efficient driving decision mechanism can help vehicles reasonably plan a driving path in highly dynamic scenarios such as emergency braking, obstacle avoidance, lane changing, and high-speed steering, and ensure that the motion control strategy is safely and effectively executed. This is of great significance for improving the safety, comfort, and traffic efficiency of intelligent vehicles in complex environments [
8,
9].
Current methods for estimating road adhesion coefficients can be classified into those based on causes, effects, and data-driven and hybrid approaches [
10]. Effect-based methods typically establish the longitudinal and lateral dynamics of the vehicle and design filters or observers to measure and analyze the vehicle response caused by road changes to estimate the road adhesion coefficient [
11,
12]. This method does not require expensive sensor equipment and has better real-time performance and higher accuracy compared to other methods. It is widely used in vehicles [
13,
14]. An expectation maximization robust extended Kalman filter, which considers the influence of sensor data loss on the estimation accuracy of sideslip angle, yaw rate and vehicle speed, was proposed by Wang [
15]. A method based on model learning, combined with an event-triggered cubature Kalman filter and extended Kalman neural network, was proposed by Wang to identify the road adhesion coefficient [
16]. Liu proposed a method for estimating vehicle state parameters and road adhesion coefficients by integrating sliding mode theory, trigonometric function group fitting, and cubic spline interpolation within an extended Kalman filter framework [
17]. A strong tracking unscented Kalman filtering method [
18] with faster convergence speed and ability to dynamically estimate the road adhesion coefficient on time-varying roads was designed by Ping. RLS is one of the effect-based methods, converting the complex nonlinear adhesion coefficient estimation of the vehicle into a linear model parameter tracking problem [
19]. It achieves efficient calculation and real-time updates through recursive characteristics and adapts to sudden road changes through forgetting factors. Compared to traditional offline algorithms or complex nonlinear methods such as Kalman filtering, the RLS method demonstrates strong practical value on resource-constrained on-board ECUs [
20]. The least squares method was employed by Chen to perform multivariate fitting on the relationship curve between slip rate and adhesion coefficient, thereby estimating the road status [
21]. A three-dimensional mapping model of slip rate, road adhesion coefficient, and road peak adhesion coefficient was established by He, and the road status was estimated based on the slope of the curve of the surface model [
22].
Recently, research on intelligent vehicle driving decision-making has been evolving from rule-driven to data-driven game decision-making, with the core being to achieve multi-objective dynamic balance within a safety framework [
23]. A driving operation diagram was utilized by Zhang to implicitly represent the driving styles of a self–driving vehicle and other vehicles. Through supervised learning, decision-making strategies were learned from human driving data and rule-based indicators were explicitly introduced to achieve adaptive lane-changing decisions based on driving styles [
24]. Yang proposed a human–machine collaborative continuous learning framework. The driver provided demonstration data through the takeover mechanism, dynamically corrected the AV’s decision deviations, designed an anti-forgetting learning algorithm, and combined behavior cloning with Q-value optimization to generate personalized strategies [
25]. Trajectory planning research has evolved multiple technical routes at “global–local” levels: traditional graph search, sampling-, optimization-, and learning-based methods [
26,
27]. The traditional graph search method demonstrates stability in structured environments due to its determinism and explainability, making it suitable for global path planning. However, when dealing with dynamic obstacles, unstructured roads, or uncertain behaviors of traffic participants, its adaptability is poor [
28]. The sampling-based method, relying on the discretization approach, quickly forms in unknown environments, but has the bottleneck of rough trajectories and inability to meet vehicle kinematic constraints [
29] directly. The optimization-based method obtains smooth trajectories and differentiable control instructions through continuous optimization. However, it is prone to falling into computational bottlenecks or local optima when the obstacle complexity or search space dimensionality is high [
30]. To balance the efficiency of discrete search and the feasibility of continuous optimization, the academic community proposed the state lattice trajectory planning: first, design offline a set of motion primitives that comply with vehicle kinematics and form a “gridded” state lattice in the pose space, then use online heuristic searching to concatenate the primitives between grid points to generate a fully dynamic and feasible trajectory [
31]. The lattice method benefits from its prior kinematic feasibility, discrete search convergence, real-time heuristic cost, offline optimization for comfort, and easy integration with vehicle dynamic models and constraints, and has become the mainstream solution in scenarios such as highway lane changing, urban road overtaking, and multi-vehicle formation, which combines real-time performance and trajectory quality [
32]. Currently, the lattice method mainly performs a gridded search in the lateral direction. It is often used for lateral trajectory planning, ignoring the dynamic coupling effect of the longitudinal dimension in the trajectory generation process. In complex dynamic environments such as variable obstacle avoidance, emergency braking, or low-adhesion road surfaces, the longitudinal behavior is closely coupled with the lateral path, and relying solely on lateral search makes it difficult to exactly reflect overall dynamic feasibility and safety [
33]. To address this issue, this paper improves the lattice method.
The primary innovations of this paper are:
In the motion decision and trajectory planning module, the influence of road conditions (adhesion coefficient, curvature) is considered to improve the safety of the autonomous driving system.
A longitudinal and lateral coupled lattice trajectory planning method is proposed, which can improve the dynamic feasibility of the trajectory and ensure longitudinal–lateral consistency under complex working conditions.
The rest of this article is arranged as follows. In the
Section 2, the overall research framework of this article is introduced. In the
Section 3, vehicle–road comprehensive influencing factors are considered to aid in designing the vehicle driving decision mechanism. In the
Section 4, the lattice method is improved, the longitudinal and lateral coupled trajectory planning algorithm for vehicles is studied, and the trajectory tracking module is constructed to achieve intelligent vehicle motion control. In the
Section 5, Simulink–CarSim–Prescan joint simulation verification is carried out. In the
Section 6, the entire article is summarized and future work is presented.
4. Coupled Longitudinal and Lateral Trajectory Planning of Vehicles Based on the Lattice Method
This paper improves the traditional lattice method and designs a trajectory planning framework with both longitudinal and lateral coupling capabilities. This method can dynamically switch between joint longitudinal and lateral trajectory planning and the single longitudinal planning mode based on the behavioral instructions issued by the upper-level decision module and the current environmental perception results. It enables a smooth transition between lateral trajectory planning and longitudinal speed planning, enhancing the consistency and robustness of the decision-making and planning in complex scenarios such as slippery roads and dense obstacles. The key variables in the planning algorithm are summarized as
Table 1.
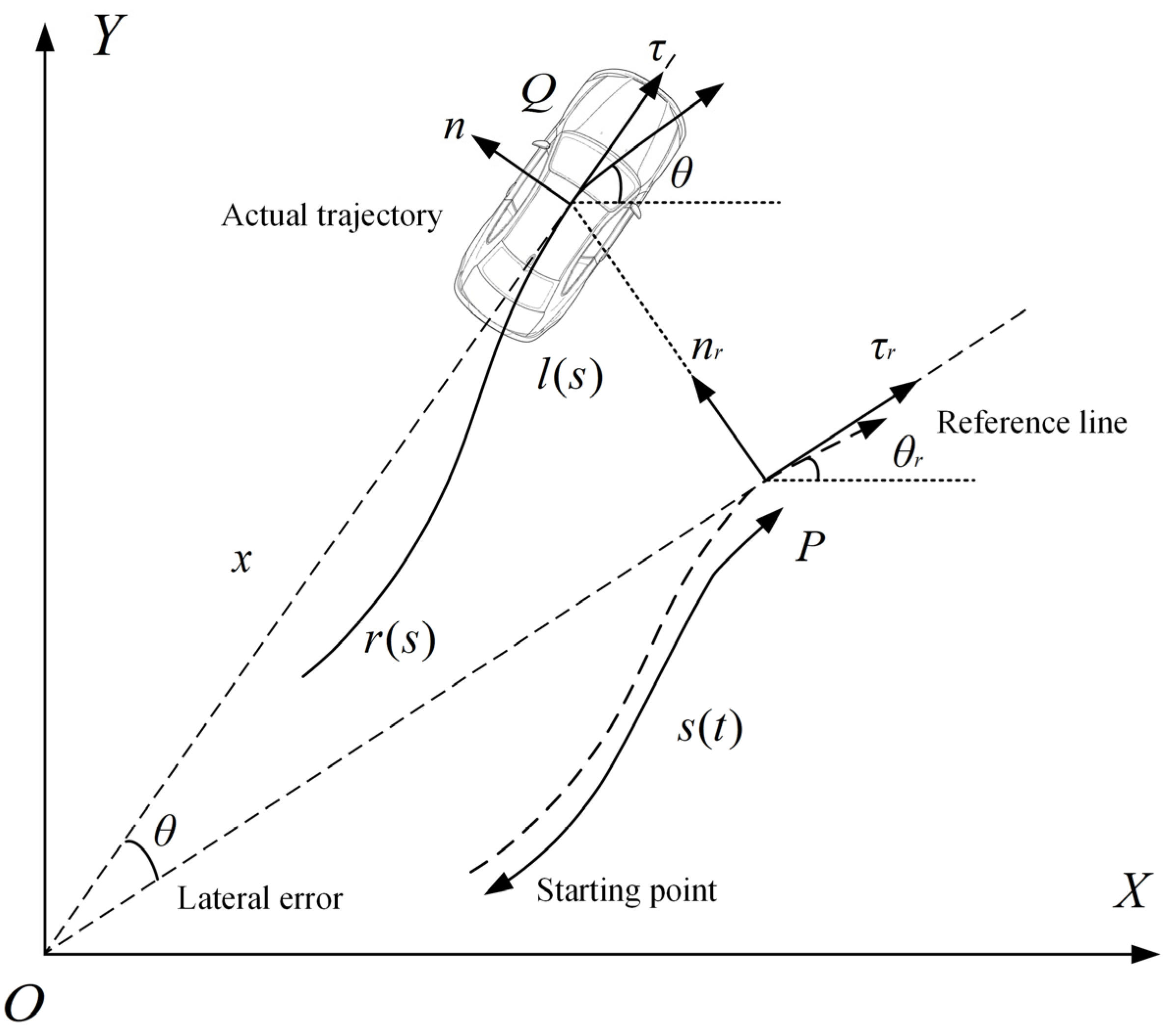
4.1. Coordinate Transformation
In intelligent vehicle trajectory planning and control, the Frenet coordinate system is based on the reference line and represents the vehicle position as the arc length
along the path direction and the lateral offset
which can effectively simplify the trajectory generation problem and make the planning more efficient and compliant with road constraints [
36]. The Cartesian coordinate system
reflects the actual position of the vehicle in the global environment and is necessary for perception data processing, map interaction, and control execution. The conversion between the two coordinate systems is shown in
Figure 2. During the planning process, global coordinate systems are constructed to record road information, including lanes and road curvatures, and a global reference path is generated, as shown in
Figure 3.
According to
Figure 2, the position coordinates of the vehicle at the current moment are:
where
represents the position vector of the HV,
represents the point
obtained by projecting the vehicle onto the reference line,
is the curve distance from the starting point to point
represents the position vector of the vehicle on the reference line, and
represents the normal unit vector at point
.
After conversion, the vehicle motion state is represented as while in the Frenet system, it is expressed as represents the heading angle, represents the curvature in the current state, represents the vehicle speed, and represents the acceleration. represent the derivatives of the lateral displacement with respect to time, and represent the derivatives of the lateral displacement with respect to the longitudinal displacement. is the distance between adjacent points.
The tangential and normal unit vectors at the projection point of the vehicle position on the reference line are expressed as:
Course angle and curvature calculation:
The conversion relationship between the two coordinate systems is summarized as follows.
4.2. Lateral Trajectory Planning
In order to take into account the feasibility of the path and the smoothness of the trajectory, this paper adopts a two-stage trajectory generation structure combining dynamic programming (DP) and quadratic programming (QP), conducting path search and trajectory optimization separately. This achieves a balance between search efficiency and trajectory quality. Firstly, from the obstacle information in the global coordinate system, obstacles existing in the forward field of view and the lateral perceptible area are selected. The obstacle information is classified and the static obstacle position, dynamic obstacle position, and velocity vector are output, which are used as input for local path planning. The position vector and longitudinal–lateral relative distance of the obstacle relative to the host vehicle are calculated:
For the square of the distance between each obstacle point and each trajectory point:
Based on the starting position of the vehicle and the position of static obstacles, a dynamic programming method is used to search for a lateral trajectory path with the minimum cost within the prescribed lateral grid, and the
sequence of the optimal trajectory is output. A quintic polynomial trajectory function is constructed, with the initial state
and the target state
. For the lateral motion of the vehicle:
When
:
where coefficient vector
is obtained by solving the system of equations.
Separately construct the trajectory smoothing cost term and the obstacle avoidance cost term:
where
are weighting coefficients,
is the Euclidean distance between the vehicle trajectory point and the obstruction,
is the set collision penalty coefficient, indicating a strong penalty, and
serves as a progressive penalty function, with a closer distance resulting in a greater cost. By constructing a trajectory smoothness cost term and an obstacle avoidance cost term, the degree of fluctuation of the trajectory is minimized, preventing the trajectory from approaching or crossing the obstacle and achieving a balance between safety and feasibility during driving.
In order to further enhance the continuity and dynamic controllability of the trajectory, this paper introduces a quadratic programming optimization module based on the DP dynamic programming path. The QP module takes the output of DP as the reference path, constructs a cubic derivative smoothing objective function, optimizes the lateral offset
of the vehicle and its first-order, second-order, and third-order derivative terms, and optimizes the variable vector:
The cost function is defined as follows:
where
is a symmetric positive definite cost weight matrix, including the centerline deviation cost
the lateral velocity penalty term
the lateral acceleration penalty term
and the jerk penalty term (rate of change of acceleration)
is a linear term.
Establishing dynamic continuity constraints:
Establishing constraints on the variation range of derivatives:
Establishing the lateral boundary of the obstacle, taking into account the vehicle width
and the offset positions
of the front axles:
4.3. Longitudinal Speed Planning
To achieve the integration and smooth transition of lateral trajectory planning and longitudinal speed planning, in this section, the longitudinal speed distribution is optimized and designed, and the longitudinal speed is independently planned to generate a complete time sequence trajectory. Given the position sequence under the reference line, continuous curves for time parameter speed and acceleration are generated to realize the integration from a spatial trajectory to a spatial–temporal trajectory.
Establish boundary conditions:
Based on the integral constraints of first-order and second-order derivatives, the continuity of the vehicle’s position and velocity and acceleration are ensured at each time period:
Based on the end position
of the dynamic planning path and the recommended planning duration
an initial longitudinal velocity trajectory consisting of three dimensions—position, speed, and acceleration—is constructed. A minimum jerk trajectory optimization model with position constraints, speed limits, and acceleration constraints is adopted, and the objective function is:
where
represents the acceleration at the
moment, the second term constrains the jerk smoothness, and
is the weighting coefficient.
Using as the index, interpolate the lateral trajectory as the function . According to the Frenet transformation formula, restore it to the Cartesian trajectory and generate the final complete trajectory . Finally, concatenate the current frame’s trajectory with the remaining trajectory from the previous frame to construct a complete prediction trajectory queue, ensuring smoothness, continuity, and control tracking performance of the trajectory.
4.4. Trajectory Tracking
In this paper, the MPC algorithm is employed to achieve high-precision lateral trajectory control for vehicles. By optimizing the vehicle’s future short-term motion trajectory in real time, considering vehicle dynamic constraints and road boundary conditions, it effectively improves the path tracking accuracy and stability of the vehicle in complex conditions such as cornering and lane changing. The vehicle dynamic prediction model is as follows:
where
represents the quantity of state,
represents the control input, and
represent the system matrices obtained through the linearization of vehicle dynamics.
MPC cost function:
where
represents the length of the prediction time domain,
represents the length of the control time domain, and
represent the weight matrices, which are used to balance the trajectory error and the smoothness of the control input.
In longitudinal trajectory tracking, a dual-closed-loop PID control strategy based on position loop and speed loop is designed and implemented. The outer-loop position controller generates the expected speed command based on the longitudinal position information of the target path, while the inner-loop speed controller adjusts the throttle and braking system to rapidly converge the actual vehicle speed to the expected value, ensuring the rapid response characteristic of longitudinal tracking and effectively suppressing the speed overshoot phenomenon, enabling the vehicle to smoothly follow the longitudinal changes of the target path.
Definition of error:
where
represents the vehicle’s expected trajectory and
represents the actual vehicle trajectory.
The collaborative application of these two control algorithms provides a reliable guarantee for the safe and efficient driving of intelligent vehicles in complex traffic environments. More details can be found in [
37].
5. Simulink–CarSim–Prescan Joint Experimental Verification
To verify the validity and stability of the intelligent vehicle trajectory planning and control method proposed in this paper, experiments were conducted based on a Simulink–CarSim–Prescan joint simulation environment. The main parameters of the simulated vehicles are shown in
Table 2.
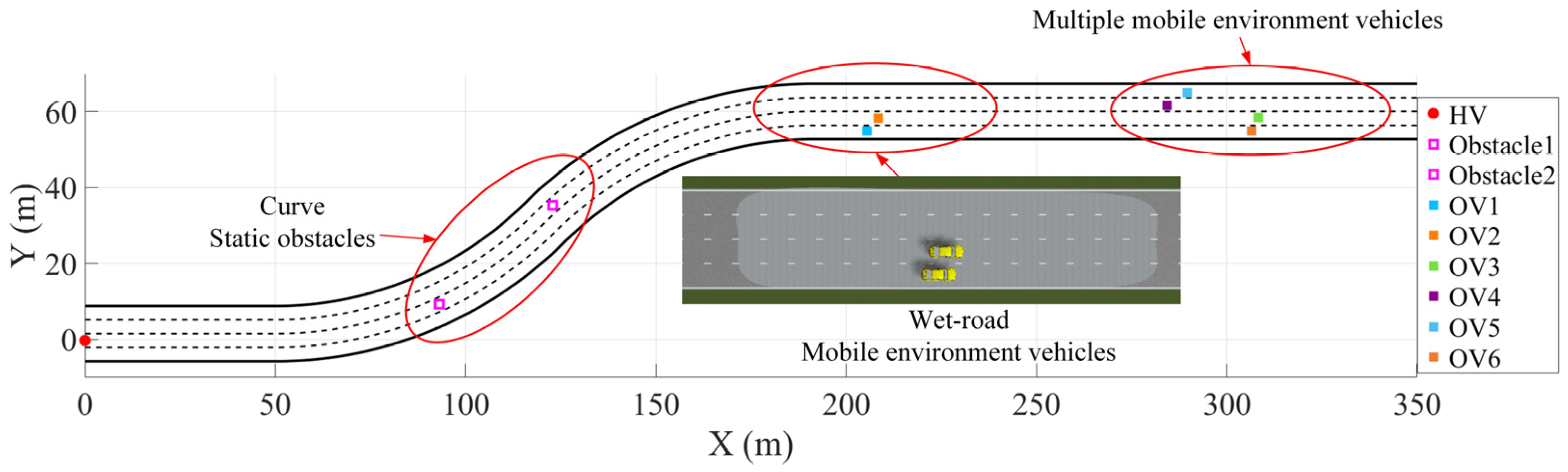
Three scenarios were designed for a highway with four lanes on each carriageway: avoiding stationary obstacles on the curve, wet road conditions, and multiple moving vehicles. The width of each lane is 3.5 m. The simulated environment in global coordinates is shown in
Figure 4. The X and Y axes represent the global coordinates. Additionally, a comparison was made between the results from the traditional lattice method, which does not consider changes in the road adhesion coefficient, and those from the proposed method under the same simulation environment. The simulation result videos, including the comparison of the proposed method that accounts for vehicle–road interaction factors, have been uploaded to bilibili. The links are
https://www.bilibili.com/video/BV172tqz9E8b/ (accessed on 7 August 2025) and
https://www.bilibili.com/video/BV1E1tqzsEJd/ (accessed on 7 August 2025).
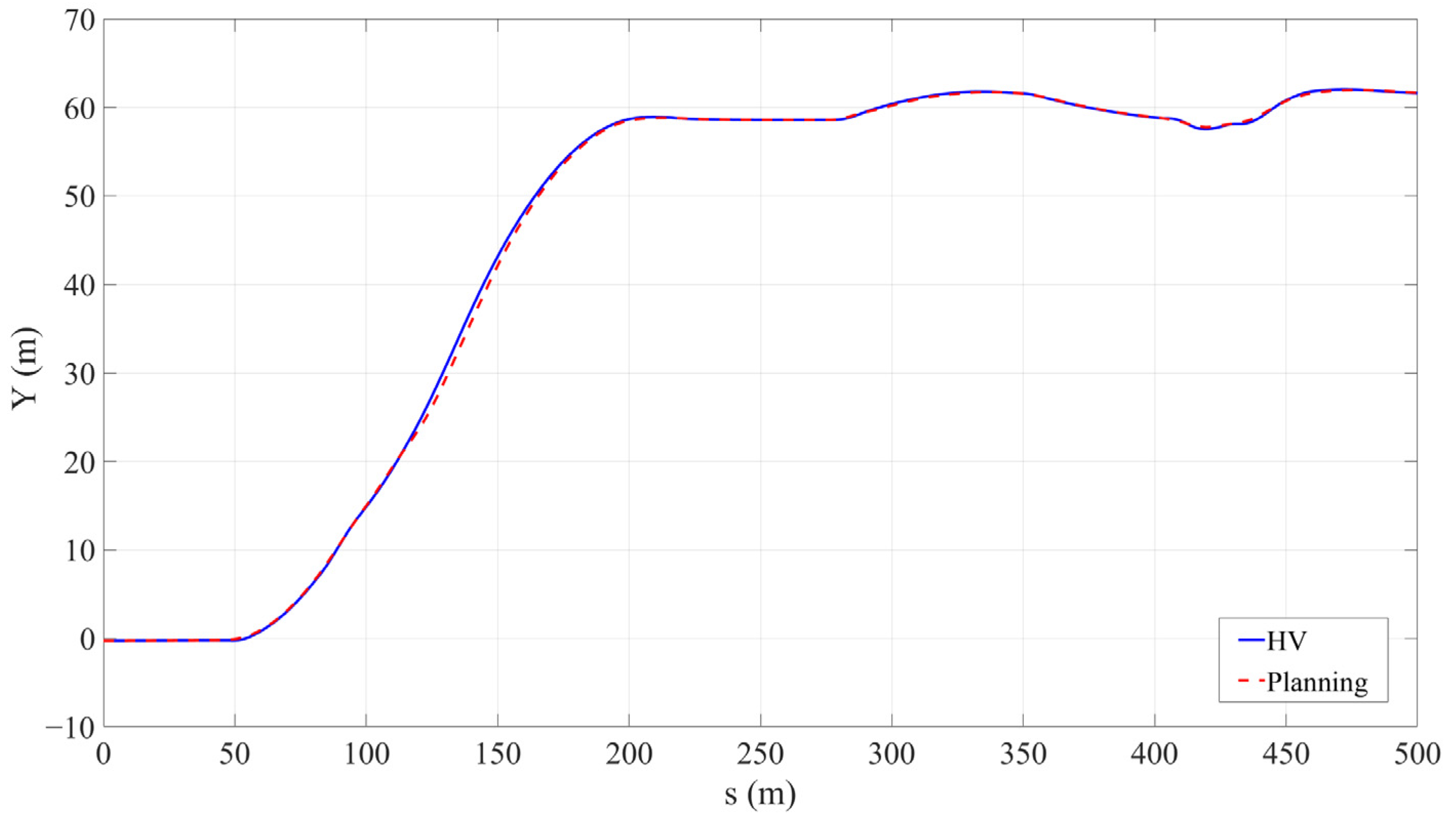
Scene 1 consists of a straight 50 m section connected to two circular arc sections with a total length of 78.5 m, each having a curvature radius of 100 m, and no transition curves were set between each section of the road. The initial speed of the host vehicle (HV) is 0. In each of the second and third lanes, there is a static obstacle with a volume of 1 cubic meter. The vehicle trajectory is shown in
Figure 5. In the initial stationary state of the HV, based on the lattice trajectory planning algorithm, it achieved safe passage around multiple obstacles on the continuous curved sections. By calculating the Euclidean distance between each trajectory point and the obstacles, the minimum distances between the vehicle trajectory and the two obstacles are 3.03 m and 2.97 m, respectively, meeting the vehicle safety envelope. By directly incorporating the curvature constraint as an optimization condition to limit the lateral acceleration and the vehicle’s optimal speed curve, a moderate increase in speed in long-radius curves and more uniform longitudinal and lateral control are achieved. The vehicle’s driving trajectory always remains between the road boundary and the lane lines, and the obstacle avoidance process is continuous, smooth, and without sudden changes. This verifies the effectiveness and feasibility of the proposed method in the mixed scenarios of curved roads and obstacles. The overall trajectory exhibits good trajectory continuity, dynamic feasibility, and obstacle safety margin, which can meet the requirements of safety and real-time performance in high-speed scenarios.
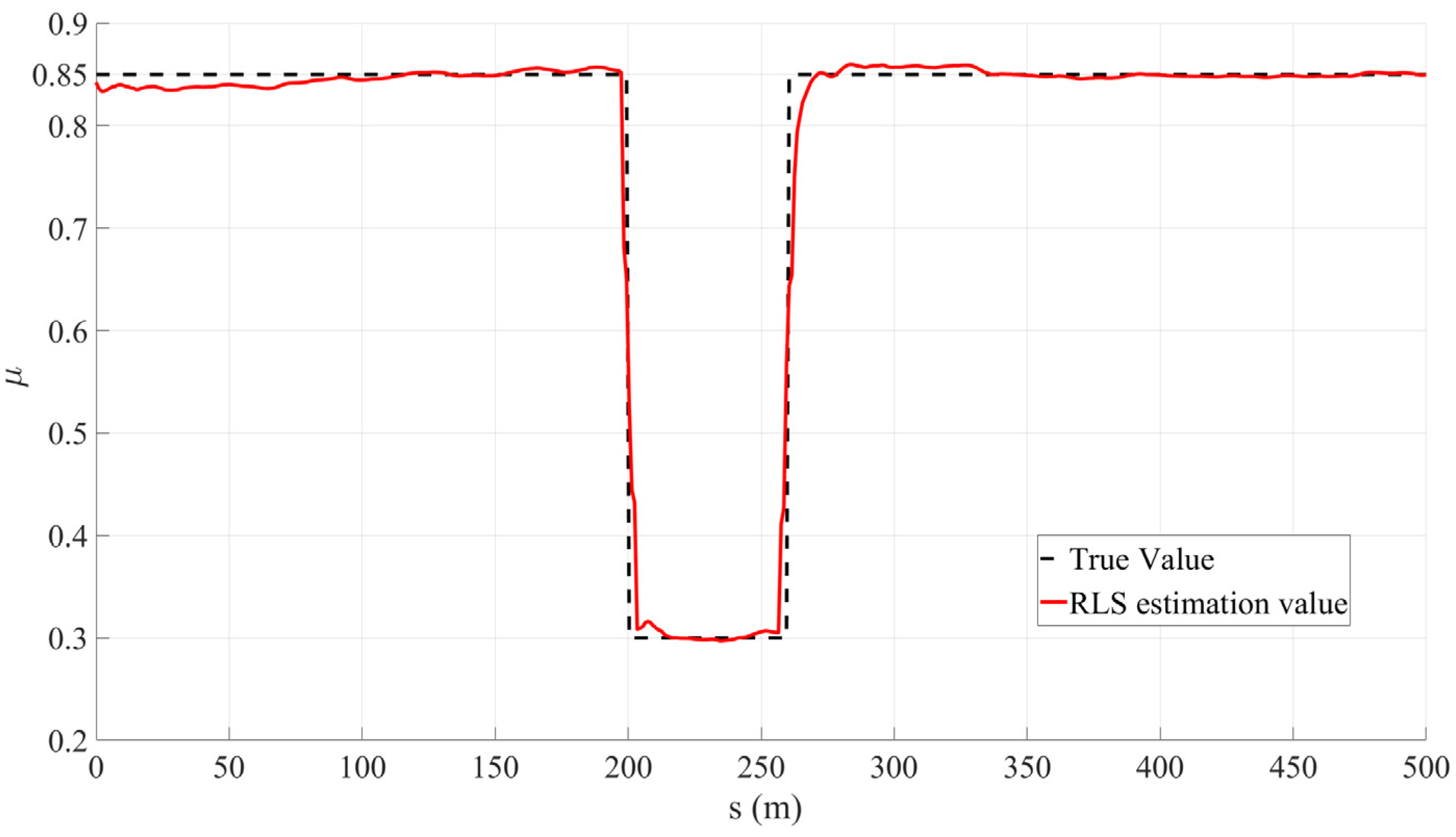
In this study, an RLS observer was built on the Simulink simulation platform, and the longitudinal road adhesion coefficient estimation model was simulated and verified jointly with CarSim. The simulation results are shown in
Figure 6. Between the driving distances of 200 to 260 m, the road adhesion coefficient suddenly changed from 0.85 to 0.3. Through the RLS algorithm, the estimated curve tracked the changes in the adhesion conditions, with good real-time performance. The average estimated error was 0.0124, and the estimation accuracy was relatively high.
In Scene 2, there is a slippery road surface and moving obstacle vehicles in the first and second lanes. In
Figure 7, based on the comprehensive framework for driving decision-making and trajectory planning constructed in this paper, the system can accurately identify sudden changes in road conditions. According to the simulation results in
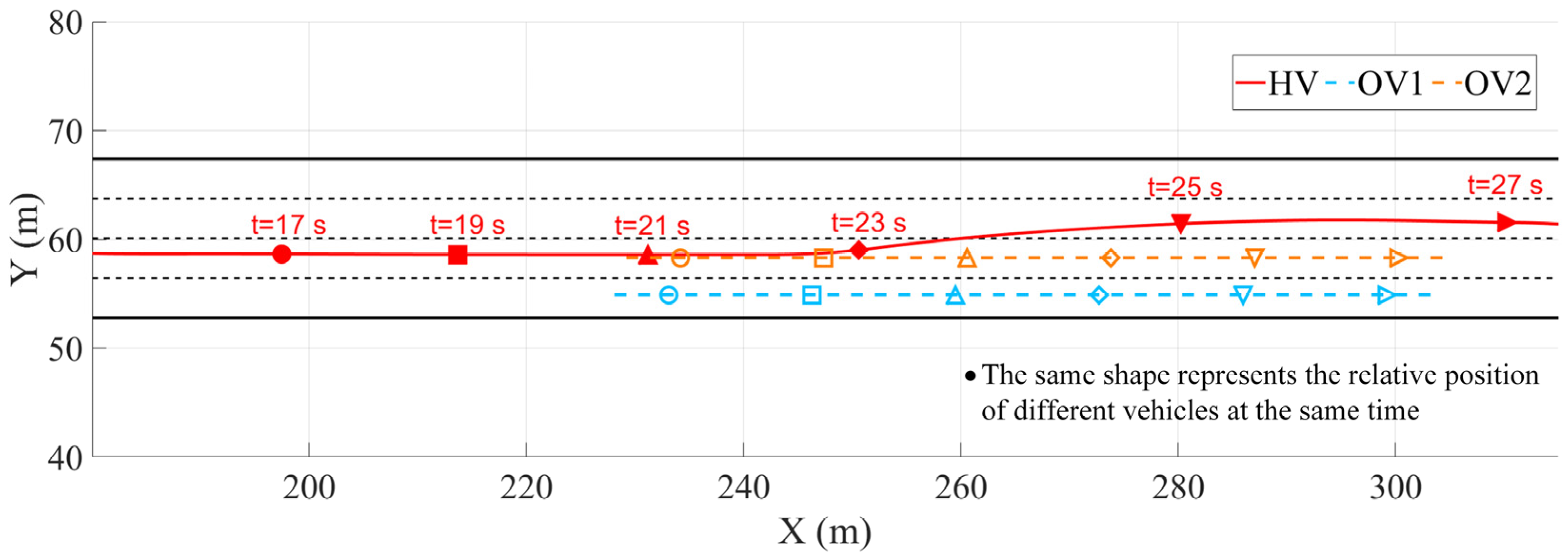
Section 3.1, when the HV reaches 200 m, the road adhesion coefficient suddenly changes from 0.85 to 0.3. At this point, the action instructions are issued by the decision-making layer, and the longitudinal and lateral coupling planning is smoothly converted to longitudinal speed planning. The HV slows down and maintains a safe distance from the preceding vehicle. After leaving the slippery road surface, the system switches back to the longitudinal and lateral coupling trajectory planning mode. Based on the environmental perception results, the decision module triggers the lane change and acceleration–overtaking actions and the HV accelerates and overtakes, effectively avoiding dynamic targets. Through the wet road–moving vehicle scenario, the intelligent decision-making and trajectory planning framework proposed in this paper has been verified to be able to coordinate multiple sources of information, reasonably switch planning modes, and effectively avoid high-risk situations such as skidding and rollover caused by insufficient adhesion under sudden road changes, thereby improving the environmental adaptability, safety, and stability of the autonomous driving system.
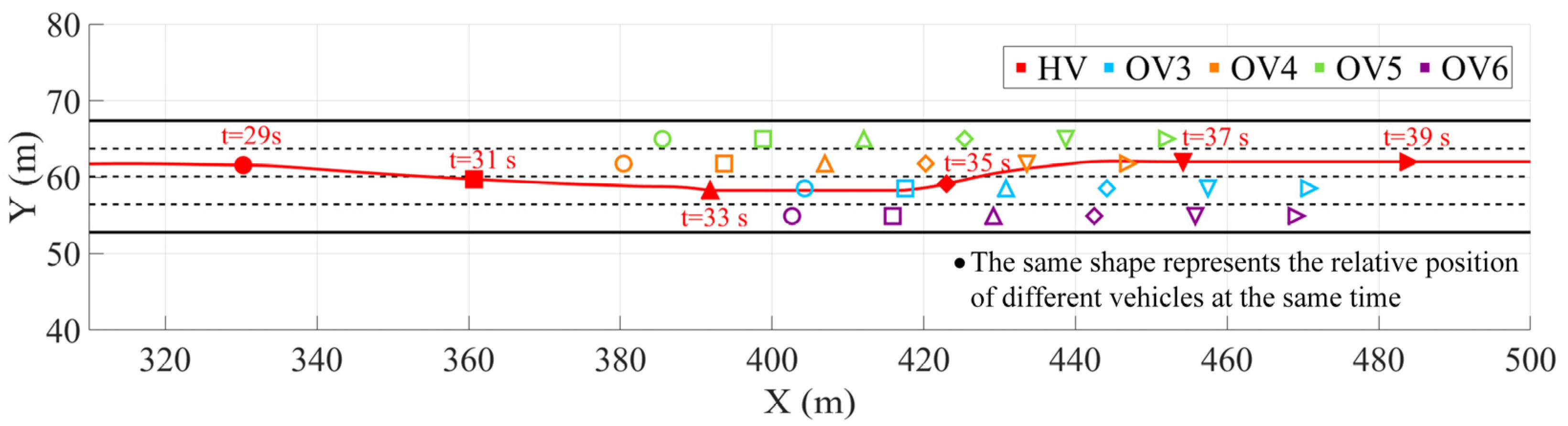
Scene 3 is a complex scenario involving multiple moving vehicles. The HV is faced with multiple moving vehicles (ov3 to ov6) distributed continuously across different lanes, and needs to dynamically complete multiple lane changes and overtaking maneuvers. In
Figure 8, the HV is traveling in the third lane. After detecting ov4 in the same lane ahead, the decision-making module actively plans the lane change strategy based on the surrounding traffic conditions and autonomously changes lanes to the second lane to complete the overtaking. During the continued driving process, the HV again recognizes ov3 in the current lane, and the system promptly completes the second right lane change, successfully returning to the third lane to complete the overtaking operation. Throughout the process, the trajectory planning module generates paths that maintain good continuity and feasibility, with smooth trajectory curves, timely obstacle avoidance behaviors, and no sudden changes or dangerous deviations. The system effectively integrates the results of multi-vehicle situation awareness and lateral dynamic constraints, achieving coordinated avoidance of multiple dynamic targets in dense traffic flows and demonstrating the advantages of the decision-making and planning framework proposed in this paper in terms of security.
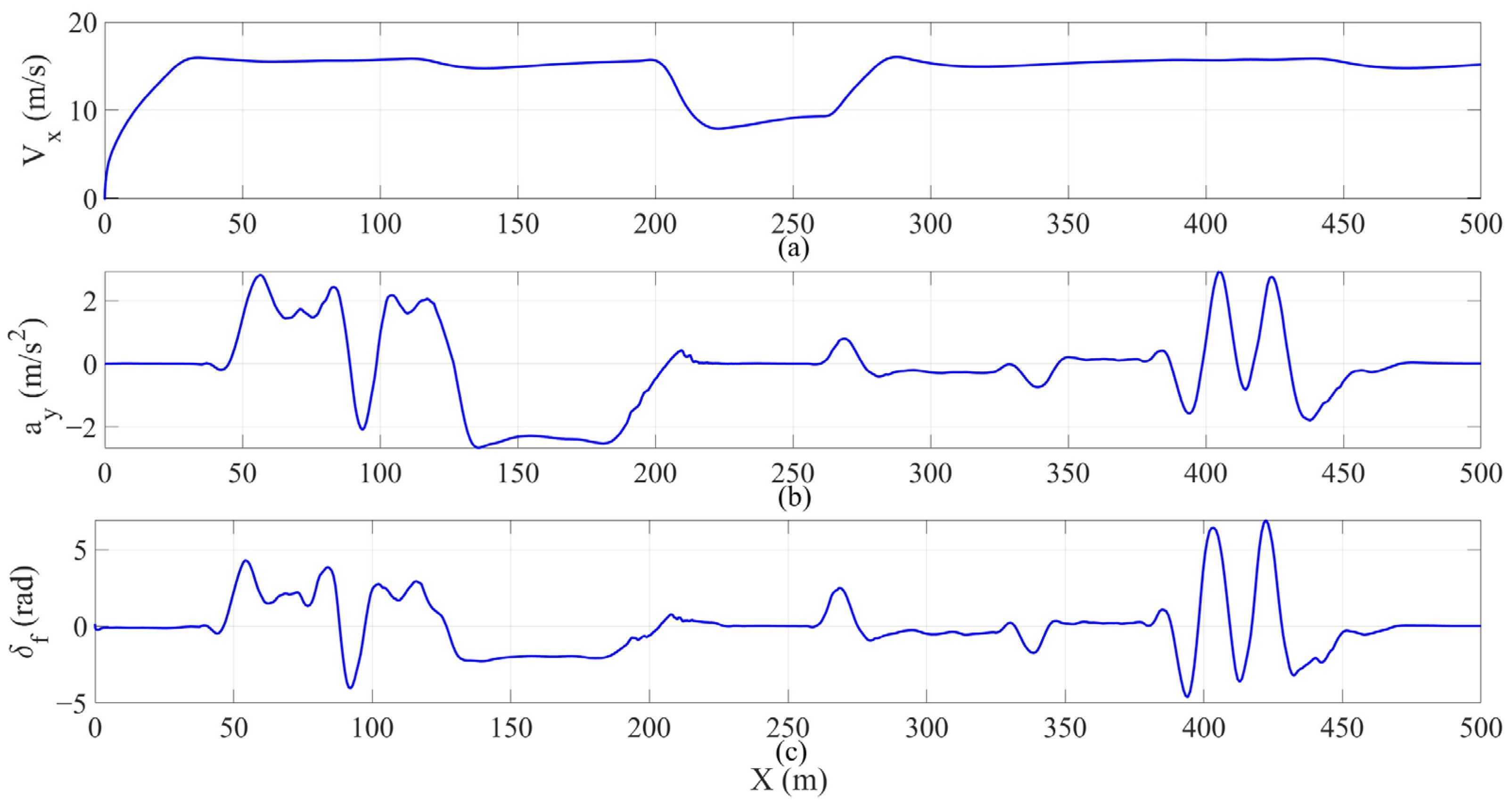
To further verify the physical feasibility and security of the generated trajectories, the curves of longitudinal velocity, lateral acceleration, and front wheel angle changing with driving distance
are extracted. These three parameters are extracted from the whole simulation process, including all three scenarios, as shown in
Figure 9.
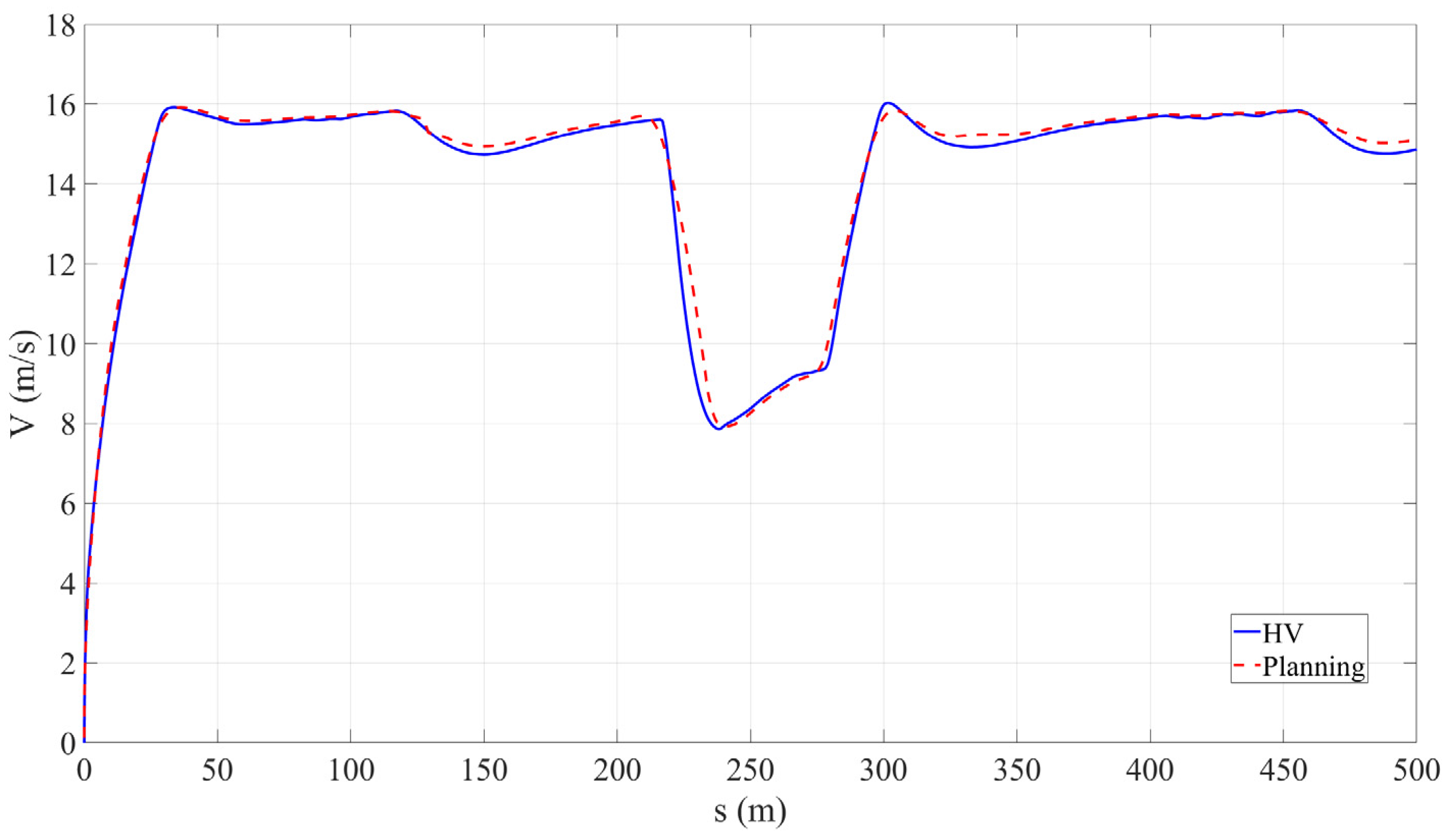
In
Figure 9a, the longitudinal velocity of the HV is shown. The initial speed is 0 m/s, and it accelerates smoothly to the desired speed of 16 m/s. During the obstacle avoidance process, there is a slight fluctuation. When it reaches 200 m, due to a sudden change in the road surface condition, the vehicle speed drops to 8 m/s. It maintains a safe distance and continues driving, then accelerates to overtake after leaving the slippery road surface. This verifies that the intelligent vehicle driving decisions and trajectory planning framework proposed in this paper fully considers the influence of road surface conditions, which is of great significance for improving driving safety.
The lateral acceleration curve of the HV is shown in
Figure 9b. When HV is traveling in the curve in Scenario 1, the curvature radii of both sections of the curve are 100. Therefore, there are downward and upward centrifugal accelerations of 2.56 m/s
2 in the lateral direction. On the first section of the curve, due to the lane change to the third lane to avoid obstacles, the lateral acceleration is pulled back. On the second section of the curve, there is no lane change behavior, and the lateral acceleration fluctuates slightly. In Scenario 3, multiple obstacle vehicles are interlaced in adjacent lanes, forming a dynamic dense traffic environment. The HV needs to perform multiple consecutive lane changes and obstacle avoidance actions. The lateral acceleration curve in this section shows high-frequency fluctuations, with the maximum value being ±2.8 m/s
2. This mainly reflects the continuous lateral maneuvering behavior of the vehicle in complex traffic scenarios, but it has never exceeded the adhesion limit allowed range (
), and there is a certain safety margin without exceeding the physical limit of vehicle stability.
In
Figure 9c, there is a curve showing the variation of the front wheel angle. The vehicle maintains excellent steering control performance during the driving process. There are obvious fluctuations when encountering the high-density dynamic obstacle targets in Scenario 3, but the maximum angle amplitude is controlled within a range of ±7°, not exceeding the physical limitations of lateral control. The system responds quickly and acts reasonably during the lane changing–obstacle avoidance process, verifying the controllability and stability of the proposed planning framework in complex dynamic environments.
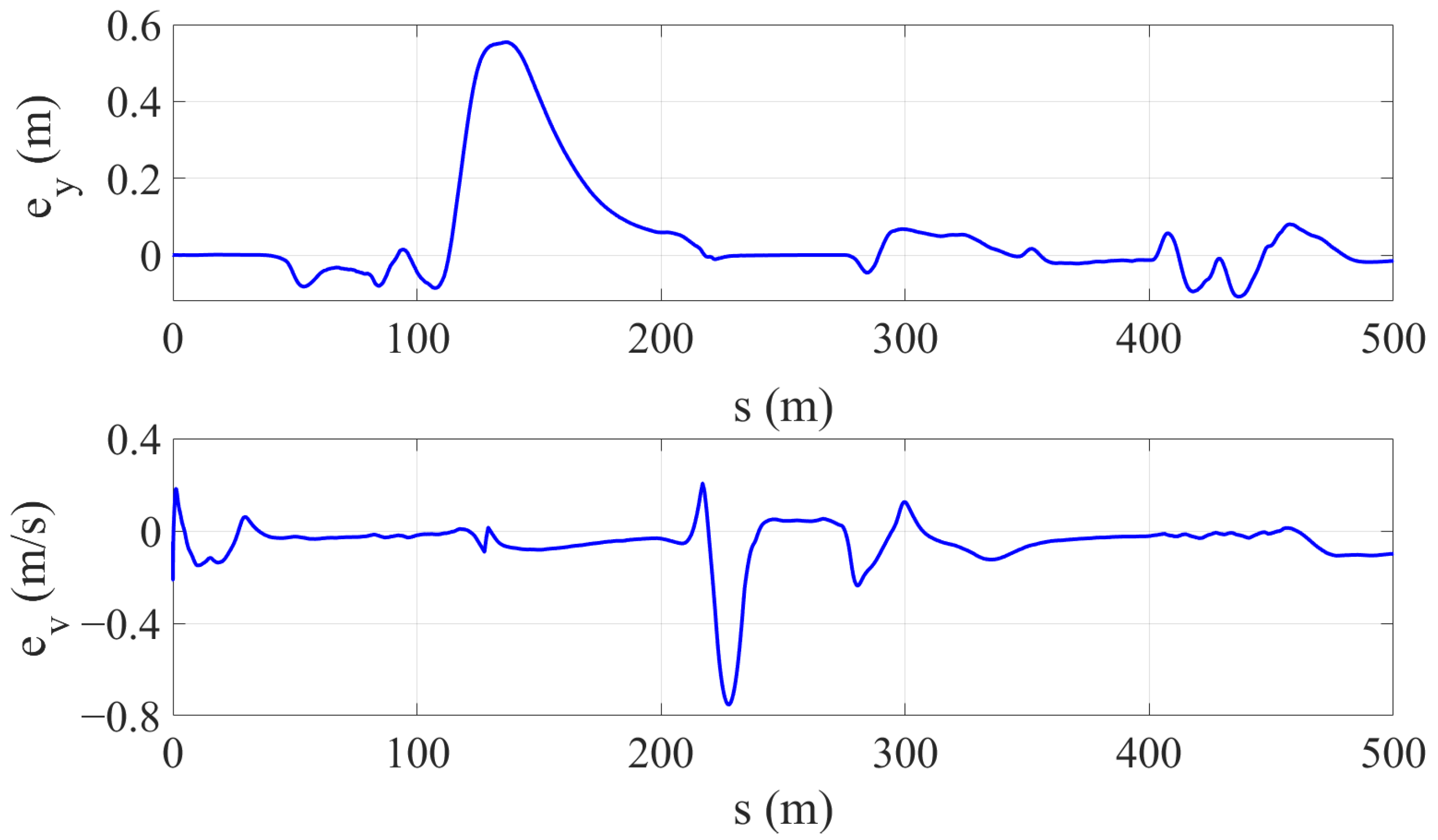
To verify the control method used in this paper, the lateral position and speed data were extracted from the planning results, and corresponding data were also obtained from the control results. The lateral position error and speed error were calculated. The parameter comparison and error results are shown in
Figure 10,
Figure 11 and
Figure 12.
To present the accuracy of the control algorithm more intuitively, the root mean square errors of the lateral displacement and longitudinal velocity are calculated. The maximum errors of the lateral displacement and longitudinal velocity are shown in
Table 3.
In this table, it can be seen that in Scenario 1, due to the main vehicle avoiding obstacles in consecutive curves, the peak value of the lateral position error is 0.516 m. However, through calculation, the root mean square error is 0.125 m per second, proving that the overall lateral position error is relatively small. In Scenario 2, there is a slippery road surface, and the main vehicle needs to slow down and follow closely during driving. The peak value of the speed tracking error is 0.781 m, and the root mean square error is 0.230 m per second, still at an excellent level. This confirms that the tracking method adopted in this paper has good tracking accuracy.
6. Summary and Future Work
This paper focuses on the key issues of vehicle decision-making and trajectory planning in intelligent driving systems, and proposes a vehicle driving decision-making and trajectory planning framework that comprehensively considers the influencing factors of vehicles and roads. Various scenarios were constructed for experimental verification. The main work included a lane-level driving decision-making mechanism based on environmental perception information, fully considering key factors such as surrounding vehicle information, lane boundaries, and road adhesion conditions. The lattice longitudinal–lateral coupling trajectory planning method was improved, generating fifth-order polynomial lateral trajectories based on the decision results and planning longitudinal speed based on a cubic acceleration model, ensuring consistency of longitudinal and lateral movements while meeting obstacle avoidance and stability requirements. The MPC algorithm and dual PID algorithm were used to achieve precise trajectory tracking and stable control of intelligent vehicles in different scenarios. Finally, a complex traffic scene including continuous obstacle avoidance in curves, slippery road surfaces, and multiple moving vehicles was constructed through the joint simulation platform to verify the comprehensive capabilities of the proposed method in dynamic decision-making, environmental adaptability, and safety control.
In future research, we will consider enhancing the dynamic traffic scenario adaptability of the autonomous driving system. By introducing multi-vehicle interaction game modeling mechanisms and other methods, we will strengthen the multi-agent coordination and conflict avoidance capabilities in complex traffic scenarios. At the same time, we will introduce driver style modeling methods to conduct personalized trajectory optimization for different driving behavior patterns such as aggressive and conservative types, thereby improving the human–vehicle collaboration experience and the explainability of driving behaviors. Finally, we will consider conducting hardware-in-the-loop verification and real road vehicle tests. We will build an HIL platform including ECU, IMU, GPS, and onboard Ethernet communication to test the performance and timeliness of the algorithm in a real-time closed loop and conduct road experiments under different adhesion coefficients (slippery, icy), multi-sensor error injection, and external disturbance scenarios to systematically evaluate the stability and safety margin of the method.