A Novel Laminar Jamming Mechanism for Variable-Stiffness Robotic Arms

Abstract

A central problem in human–robot interaction is the risk of severe injury in humans in the event of a collision with a rigid robot arm. The introduction of variable stiffness into a robot arm mitigates the effects of impact and generates a safe interaction in its compliant state. An approach to vary the stiffness of members in a robotic arm is Laminar Jamming. In this article, a new lock/unlock mechanism for Laminar Jamming is proposed. The solution consists of a pneumatic actuator that drives a trapezoidal pin to interfere mechanically with the layers, and, in turn, changing the stiffness of the Laminar Jamming Structure. Additionally, frames are placed along the structure to avoid local buckling of the layers. Experiments and finite element simulations were carried out to study the mechanical performance of this new mechanism. Experiments show that the proposed mechanism reached a maximum stiffness ratio of 3.65, which is 15% higher than the stiffness ratio of an equivalent flat clamp mechanism. Experiments also demonstrate that the proposed mechanism does not show the stick-slip phenomenon that exists in the flat clamp mechanism. Computational case studies were carried out to investigate the effects of the angle of the trapezoidal pin, the number of frames, the direction of the transverse force and the behavior at high deflections. Simulations show that the 30° trapezoidal pin has the highest stiffness for pressures larger than 500 kPa, three frames placed along the Laminar Jamming generate the maximum stiffness ratio, the stiffness slightly varies when the transverse force changes direction, and the stiffness decreases with increasing deflection.

1. Introduction

Robots and humans have traditionally been kept isolated due to safety concerns. Only in recent years, collaborative robots (cobots) that can work alongside humans have come to market. This has raised an important problem in Human–Robot Interaction which is the reduction of damage during an impact between a robot and a human being. This problem is critical because humans could suffer serious or even fatal injuries if they received a rigid impact from a robot. Furthermore, the impact could cause serious damage to the mechanical adjustment of the robot. A practical solution to reduce these negative consequences is for manipulators to have variable stiffness.

Variable stiffness in robot arms can be implemented through two strategies: Variable-Stiffness Joints (VSJ) and Variable-Stiffness Links (VSL). VSJ has been extensively investigated in human–robot interaction [1,2,3], while VSL has been recently studied [4,5,6]. In addition, one of the applications of variable stiffness in robotics is the attenuation of collisions between human beings and robots. There are two strategies in this regard. The first approach is active compliance, which consists of detecting the collision and then controlling the stiffness of the arm appropriately [7,8]. This strategy involves using various types of sensors to detect the collision [9], and actuation mechanisms to dynamically respond to the impact. The second strategy is passive compliance, which consists of mechanical components that absorb the excessive collision force. Examples of passive components are springs, dampers, and soft covers. Passive compliance provides fast and reliable responses to collisions, but the response cannot be controlled during the impact because the stiffness of these components is usually tuned before the operation of the robot, or it is a permanent property of the component [4,5].

Various technologies have been studied to modulate the stiffness of members in the robotic fields of Medical Devices [10] and Soft Robotics [11]. Laminar Jamming (LJ) is one of these technologies that has been investigated since 2002 [12]. In addition, LJ structures have been implemented to build VSLs [13,14,15,16], which demonstrate a considerable potential to reduce the impact between robot arms and human beings.

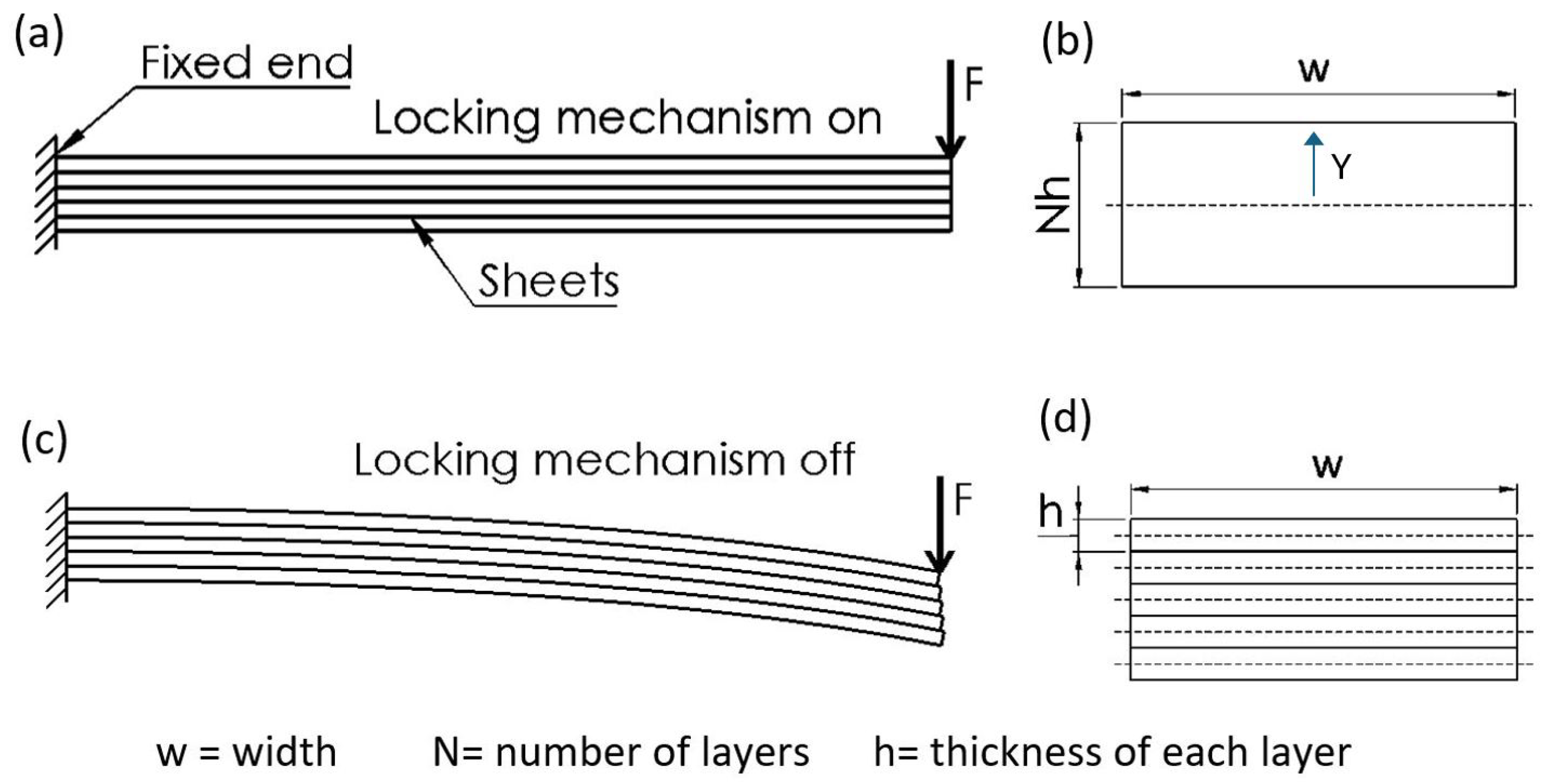
A LJ structure consists of a beam that is made of a stack of thin sheets and a mechanism to lock/unlock the sheets. When the mechanism locks the sheets, the bending stiffness is high and the whole beam resembles the behavior of a rigid member. When the mechanism unlocks the layers, sliding can occur between them, the bending stiffness reduces, and the LJ structure becomes flexible. Figure 1a,b illustrate the rigid and flexible states of a LJ structure that is formed by 5 sheets (N = 5). It can be observed that, in the flexible state, the layers are not coupled and there is slip between them.

The fundamental phenomenon that allows the variation in bending stiffness of the LJ structure is the change in the area moment of inertia I. The bending stiffness k depends linearly on I, in the case of a cantilever beam of length L and Young’s modulus E, this relation is given by Equation (1) [18].

$$k={\displaystyle \frac{3EI}{L^3}}$$

(1)

Figure 1b,d illustrate the cross-sectional area (A) of a LJ structure, w is the width of the beam, h is the thickness of each layer, and N is the numbers of layers. When the mechanism locks the layers, they form a solid beam as illustrated in Figure 1b, all the layers bend around the neutral axis of the stack and the beam has maximum bending stiffness, or in other words, the LJ structure is stiff. The I of the beam in this case is defined by Equation (2).

$$I_{rigid}={\int }_{{\displaystyle \frac{-Nh}{2}}}^{{\displaystyle \frac{Nh}{2}}}{y}^{2}dA=N^3{\displaystyle \frac{w{h}^3}{12}}$$

(2)

When the mechanism unlocks the layers, each individual layer bends around its own neutral axis, the whole beam has the minimum bending stiffness, and the layers slide freely as it can be seen in Figure 1c. In other words, the beam is in a flexible state. The I of the beam in this case is defined by Equation (3).

$$I_{flexible}=N{\int }_{{\displaystyle \frac{-h}{2}}}^{{\displaystyle \frac{h}{2}}}{y}^{2}dA=N{\displaystyle \frac{w{h}^3}{12}}$$

(3)

It can be observed in Equation (2), that I of the LJ structure in the rigid state depends on the number of layers raised to the 3rd power ($N^3$). In contrast, Equation (3) shows that I of the beam in the flexible state depends on the number of layers (N). The stiffness ratio or the stiffness variation can be calculated by comparing the area moments of inertia in the flexible and rigid state, which yields:

$${\displaystyle \frac{I_{rigid}}{I_{flexible}}}={\displaystyle \frac{N^3}{N}}=N^2$$

(4)

As Equation (4) shows, the stiffness ratio in a LJ structure depends on the number of layers raised to the second power [12,17]. This generates, at least in theory, the possibility of obtaining very high stiffness variation by only adding more layers to the beam [17]. For the case of the LJ presented in Section 2, the number of sheets is 10 (N= 10), which implies that the maximum stiffness ratio that could be reached is 100. However, this is a theoretical value because other factors, such as friction and efficacy of the lock/unlock mechanism, would reduce significantly the stiffness ratio that can be achieved.

Common mechanisms to lock/unlock the LJ structures are based on friction, mechanical interference, or miscellaneous principles [19]. In general, these mechanisms have demonstrated to be effective in achieving the variation of stiffness. The first two principles are relevant for the mechanism proposed in this article.

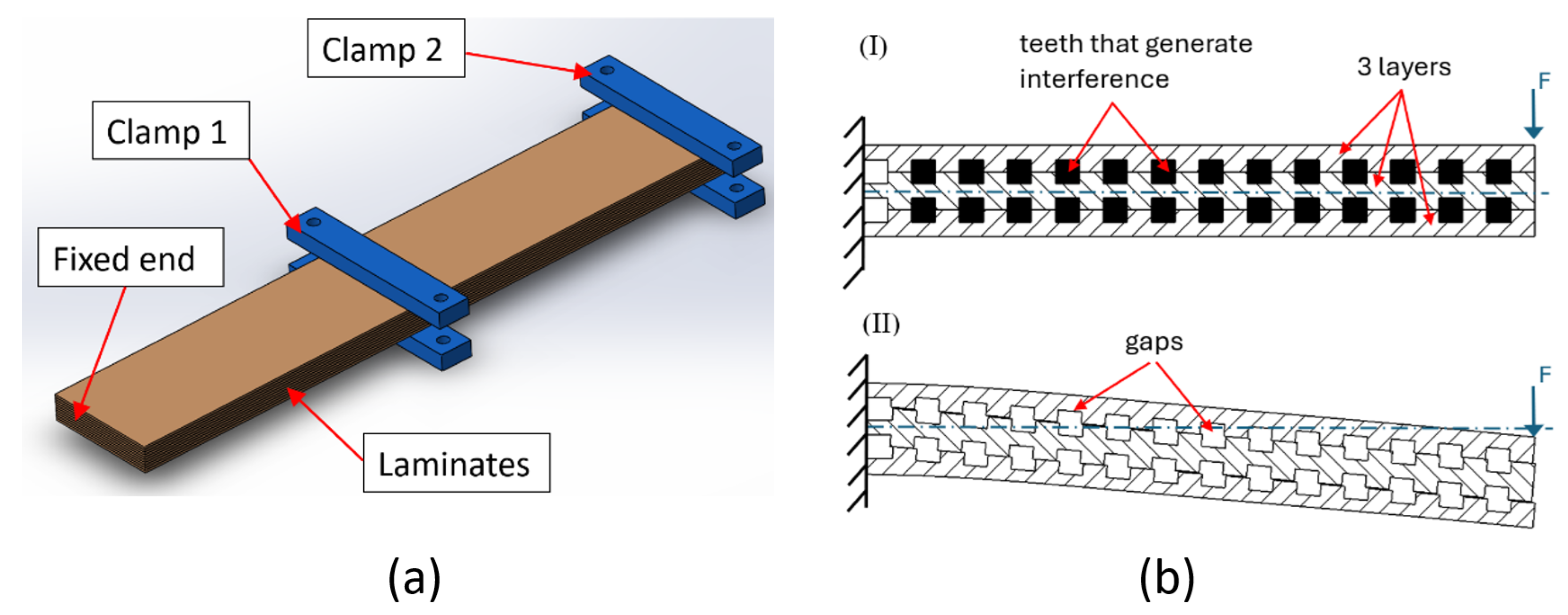
The principle of friction-based mechanisms consists on modifying factors that determine friction forces. One of these friction mechanisms is known as Discrete Laminar Jamming (DLJ), which consists of many variable pressure clamps placed discretely along the LJ structure [14,15] as can be seen in Figure 2a. The clamps apply normal force to the stack of layers in that specific section which increases the friction between the sheets, leading to the locking of the layers and increasing the bending stiffness of the LJ structure.

The principle of mechanical interference consists on preventing the relative slip between the layers. This principle is usually implemented by introducing an object that passes through the layers of the LJ structure. There is an actuator that thrusts the object into the sheets to increase the stiffness and pulls the object out of the layers to reduce the stiffness. The sheets often have a slot or cutout to accommodate the object that goes through them. Figure 2b illustrates an example of a mechanism based on mechanical interference. The mechanism consists of layers with teeth that are aligned and form gaps between them, as can be seen in Figure 2b(II). A mechanism driven by Shape Memory Allowy wires [20], or a mechanism based on electroactive polymers [21] introduces teeth inside the gaps of the layers. This generates a mechanical interference that prevents slipping between the sheets and, therefore, increases bending stiffness, as Figure 2b(I) illustrates. The same mechanism can remove the teeth that generate the interference, allowing slip between the layers, which, in turn, generates the minimum bending stiffness, as illustrated in Figure 2b(II). Intermediate values of bending stiffness can be achieved by varying the location and number of the teeth that are introduced in the gaps along the LJ structure.

In the last years, vacuum pressure has become the predominant lock/unlock mechanism of LJ applied in robots with VSLs. This mechanism consists of an airtight chamber that envelops the sheet stack, and a vacuum pump that applies negative pressure inside the chamber. When the vacuum is activated, atmospheric pressure compresses the chamber and the stack of sheets that is inside. As a result, friction between the layers increases, leading to the locking of the sheets and the corresponding increase in bending stiffness [22].

The main advantages of LJ with vacuum pressure are the highest speeds of stiffening and destiffening in comparison with other lock/unlock mechanisms [11,17], and the possibility to reach stiffness ratios as high as 180 [23]. However, this mechanism is still too slow to be applied in the reduction of an impact between a human being and a robot arm. For example, a LJ structure with vacuum pressure has a measured time constant about 0.5 s to change its stiffness [24], which is too slow when taking into account that the damage due to impacts between humans and industrial robotic arms takes about 0.1 s [25]. Moreover, the transition of LJ structures from the rigid state to the flexible state may not be complete nor immediate, as was demonstrated in experiments where, after each test, the LJ sample was disconnected from the vacuum regulator and flexed multiple times to speed up its return to ambient pressure [22]. Another problem of this mechanism is the sealing of the airtight chamber because it uses an elastic membrane that could be damaged due to contact or impact against rough edges [14,15].

The new lock/unlock mechanism for LJ proposed in this work has the prospect of achieving a fast change from high stiffness to low stiffness in order to be useful during an impact between a human being and a robot link. Furthermore, this mechanism does not have the sealing limitations of LJ with vacuum pressure.

This article is a revised and expanded version of a paper entitled “Laminar Jamming with Trapezoidal Pin Mechanism for Variable Stiffness Robotic Arms” [26], which was presented at ROBIO 2022, Xishuangbanna, China, and the paper entitled “A Novel Multi-Layer Beam Mechanism for Variable Stiffness Robotic Arms” [27], which was presented at ACRA 2021, Melbourne, Australia. This article presents a novel mechanism to lock/unlock a LJ structure, as well as experiments and finite element (FE) simulations that were conducted to evaluate the performance of this new mechanism as a potential method to modulate the stiffness of a robot link arm. This article is organized as follows: the concept is presented in Section 2; Section 3 describes the experiments and their result; Section 4 discusses the finite element simulations and their results; Section 5 describes the computational studies; and conclusions and future work are provided in Section 6.

2. Trapezoidal Pin Mechanism

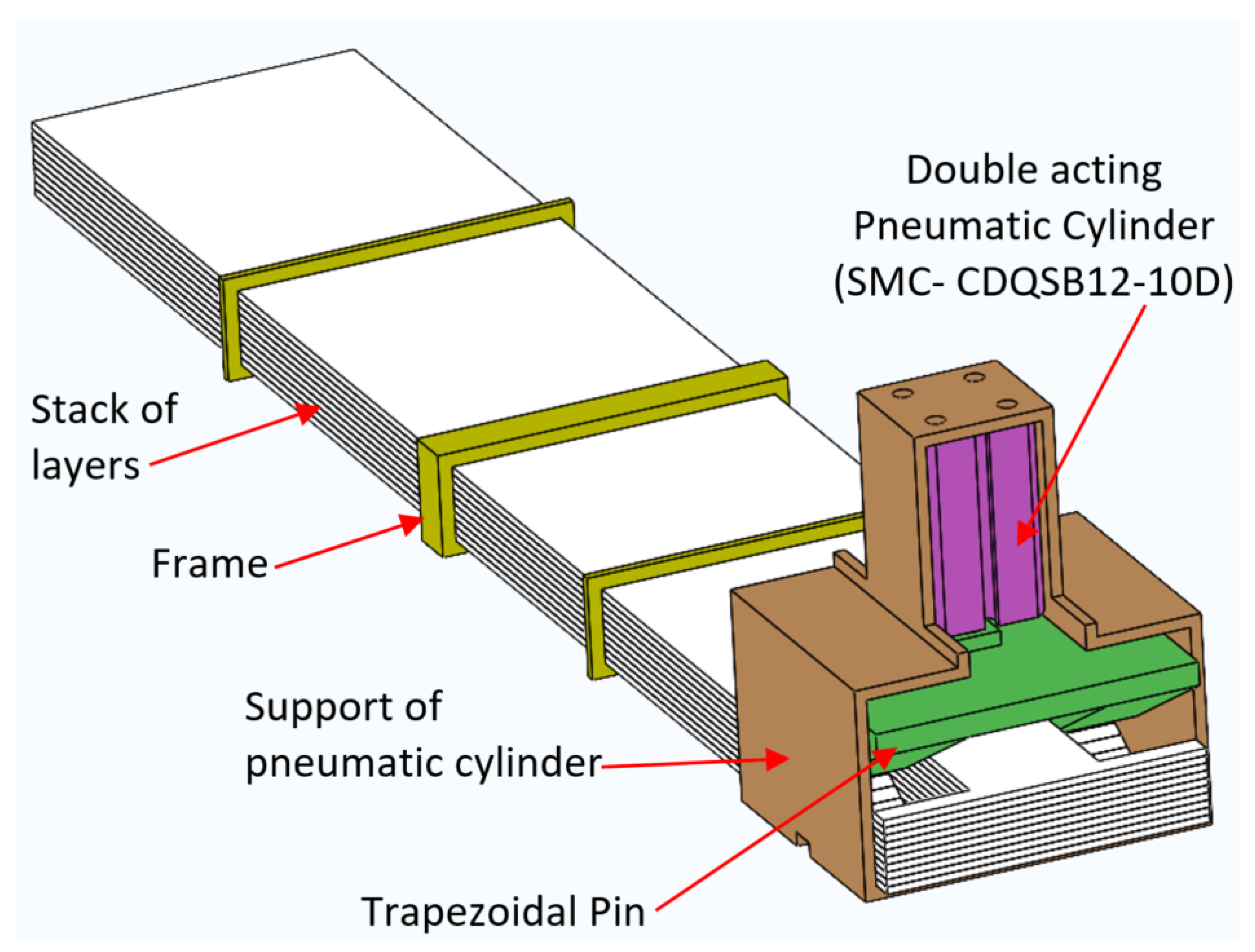
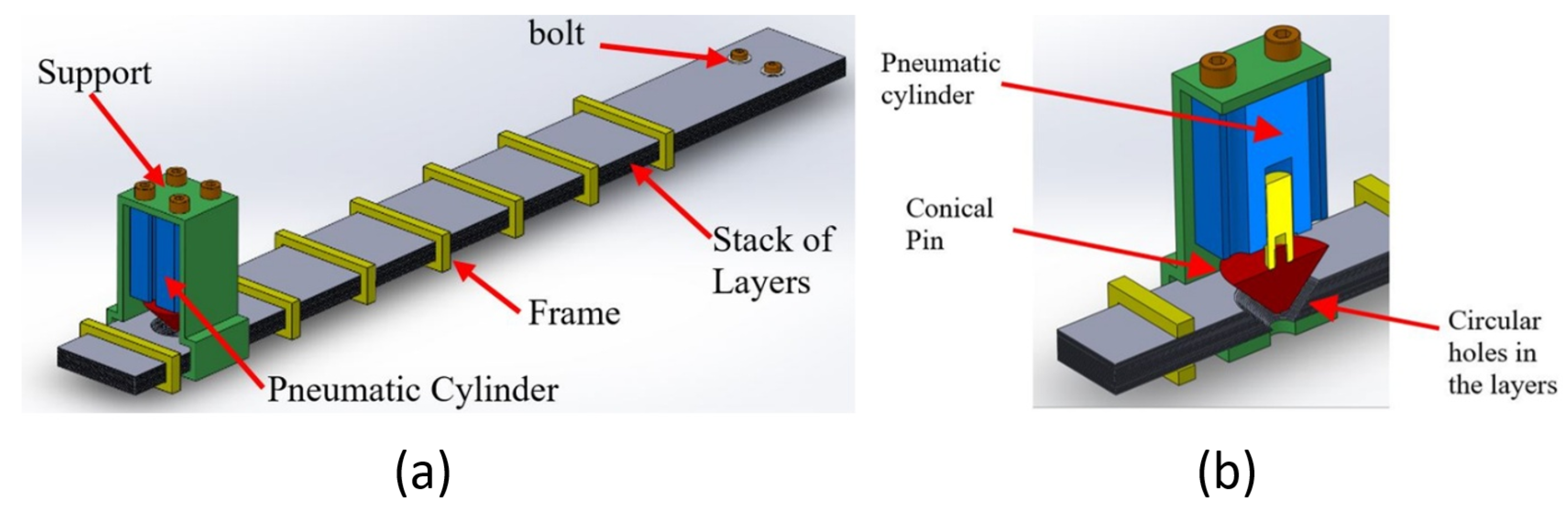
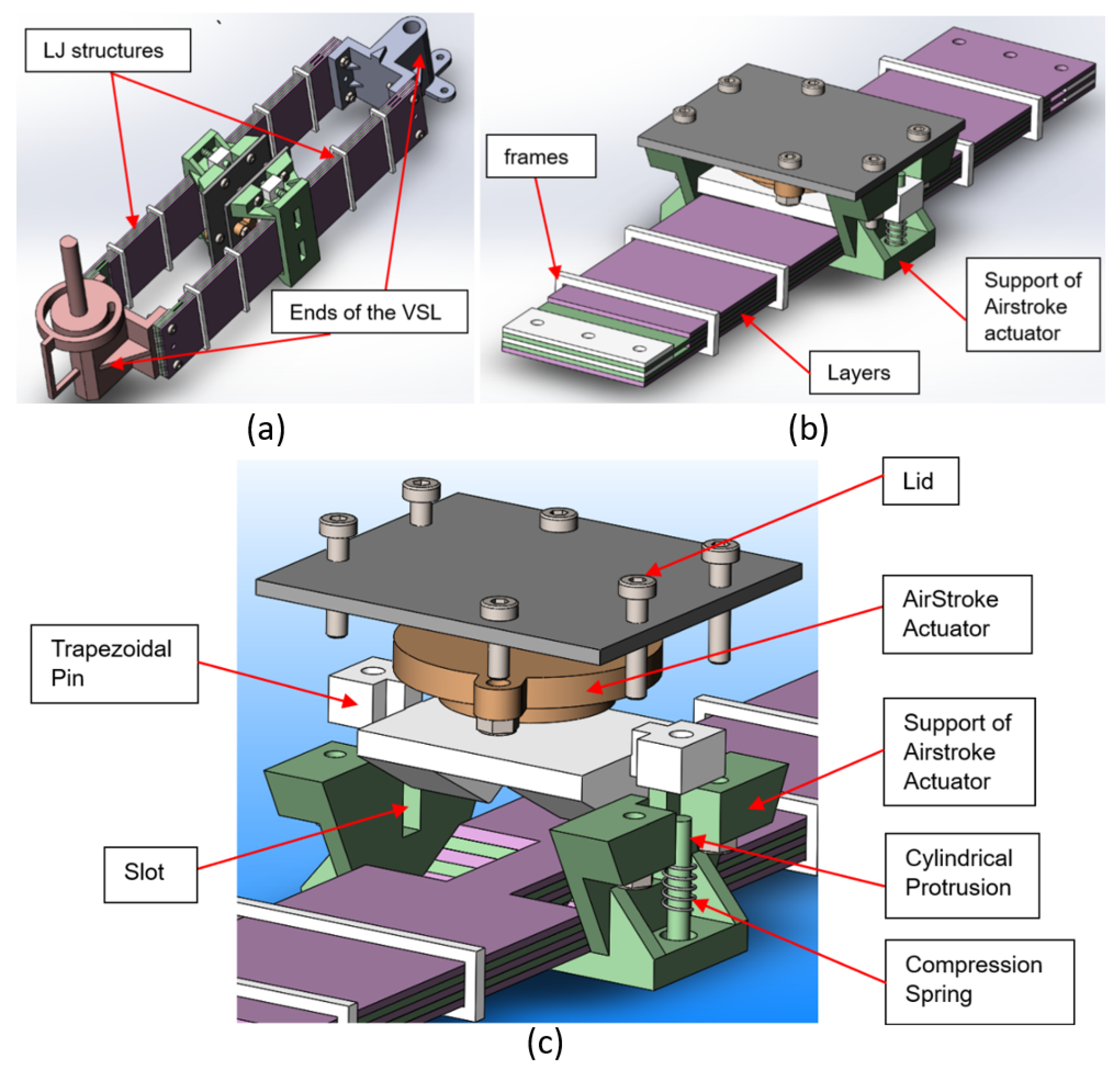
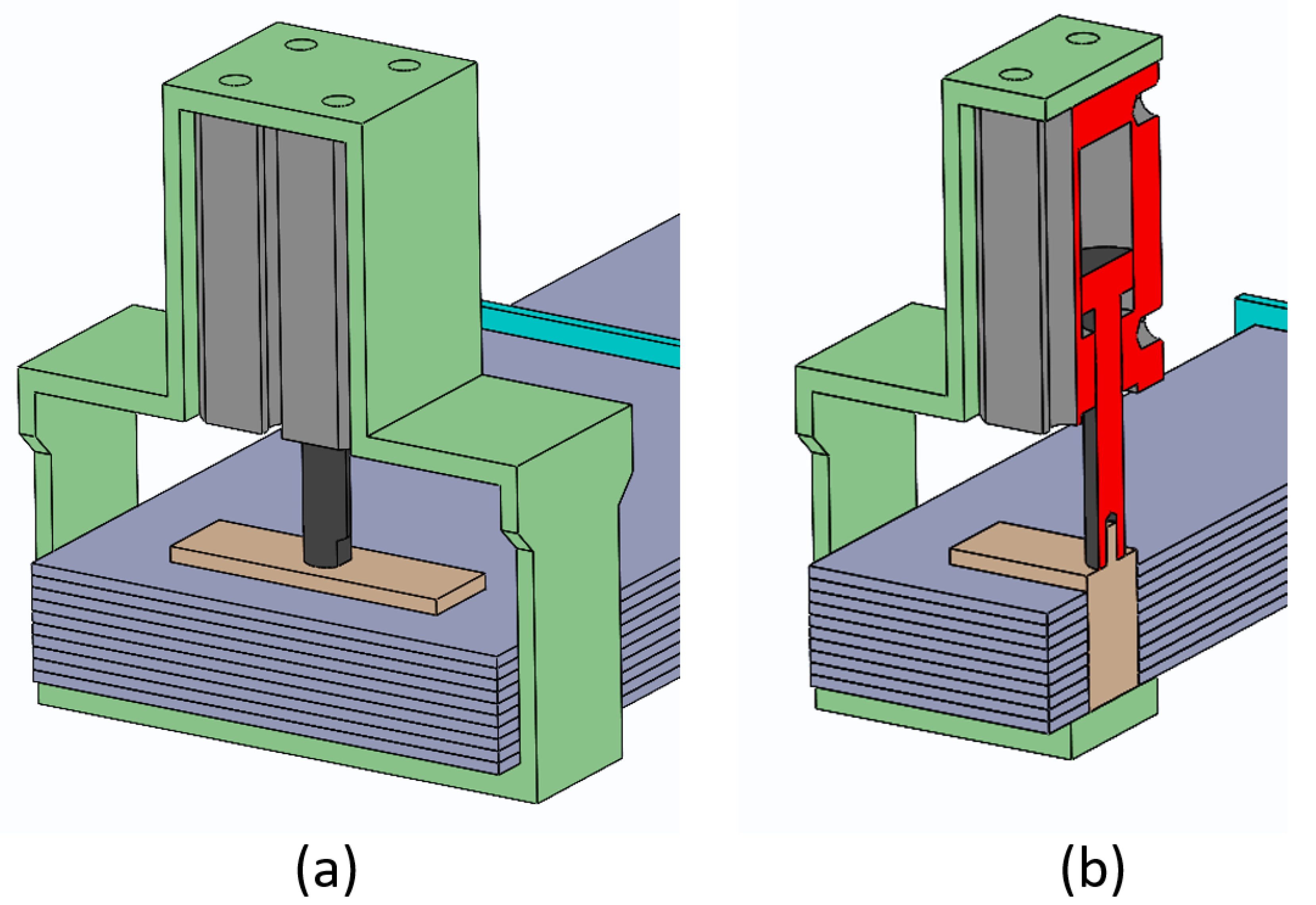
The lock/unlock mechanism of LJ structures presented in this work is based on a combination of the principles of mechanical interference and friction. The components of this mechanism can be seen in Figure 3. It consists of a trapezoidal pin that is coupled to the rod of a pneumatic actuator. Figure 4a shows that when the pneumatic cylinder is pressurized, the trapezoidal pin is thrust into the trapezoidal slots formed in the sheets. The trapezoidal pin compresses the layers and raises the friction force between them in that section. The fact that the pin comes in and out of the LJ structure produces mechanical interference. When the trapezoidal pin is disengaged, the LJ structure has the lowest stiffness (Figure 3). When the trapezoidal pin is engaged, the stiffness of the LJ structure depends on the force that is applied to the pin, which in turn depends on the air pressure in the pneumatic actuator (Figure 4a).

When the LJ structure is bent, the slip between the layers pushes the pin out due to its trapezoidal shape. This phenomenon, which is described in Section 5.4, makes a fast transition from a high stiffness state to a low stiffness state easier. In contrast, a straight pin or cylindrical pin tends to get stuck by the layers when the LJ structure is deformed by bending as was noticed in preliminary qualitative tests.

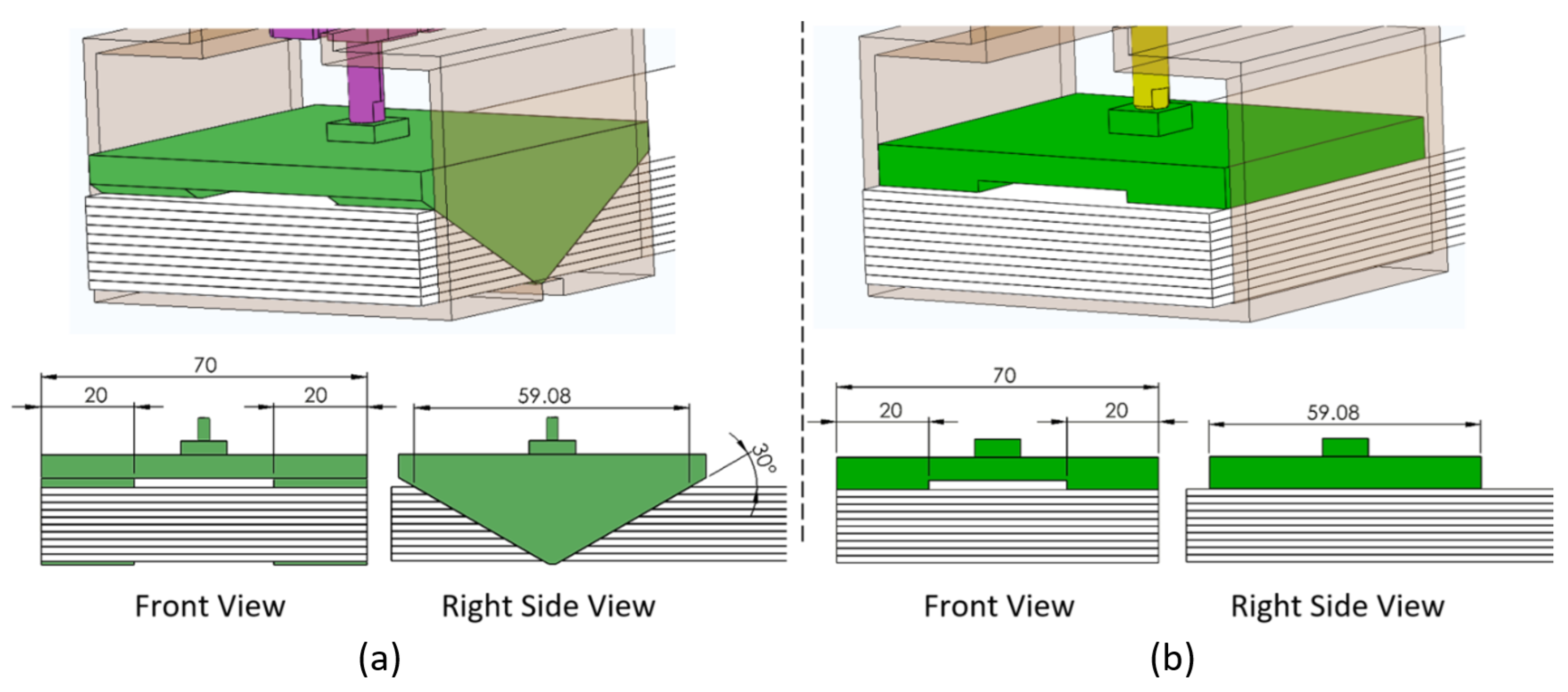
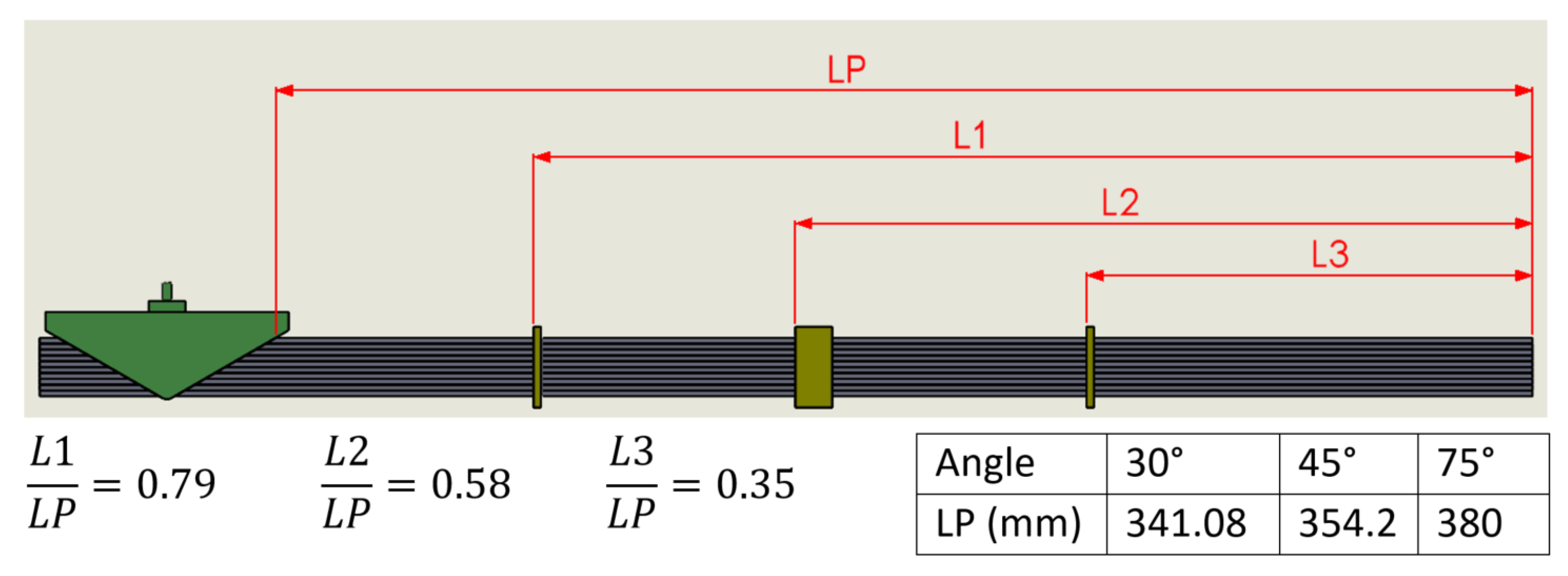
The LJ with trapezoidal pin was compared to an LJ with a flat clamp that is illustrated in Figure 4b. Both LJ structures have the same parts and dimensions and were simulated and tested under the same conditions. The concept of the flat clamp is similar to the concept of DLJ. The main difference between these two LJ mechanisms is the width of the clamp. The clamps in DLJ have the same width of the stack of layers and make contact with them along the whole width. Instead, the flat clamp presented in this article has two contact areas whose width (20 mm) and length (59.08 mm) in the horizontal plane are identical to the projected contact areas in the trapezoidal pin to enable a fair comparison, as shown in Figure 4.

2.1. Description of the Components of the LJ

The general characteristics of each component of the proposed LJ mechanism are described as follows.

Frames: Three frames were placed along the LJ structure. Their main function is to avoid independent buckling of the sheets by keeping them together in one stack. The frame in the middle is notably longer than the other two frames. This feature was implemented to resemble the DLJ design that has a clamp of similar length in the same position [14,15]. The frames do not constrain the relative slipping of the sheets because some of the frames are bonded to the top layer and others to the bottom layer, but none are bonded to both. In addition, a small clearance between the frames and the stack of sheets ensures that they do not apply pressure to the LJ structure.

Layers: The LJ structure has 10 layers made of Acrylonitrile Butadiene Styrene (ABS) plastic with a thickness of 1.5 mm, length of 405 mm, and width of 70 mm. The material has a density of 1030 Kg/m³ and a Young’s Modulus of 180 GPa. Each sheet has a cutout with a different length to accommodate the trapezoidal pin.

Pneumatic Cylinder (SMC-CDQSB12-10D): This double-acting pneumatic cylinder was selected because of its high force per weight output compared to other actuators, such as solenoids. This pneumatic cylinder was manufactured by SMC (Tokyo-Japan).

Trapezoidal Pin: The trapezoidal pin sits in the trapezoidal cutouts of the layers in such a way that it comes into contact with all the layers of the LJS. The pin has two trapezoidal protrusions that come in contact with the stack of layers in two areas that have a width of 20 mm each, as can be seen in Figure 4. The rod of the pneumatic cylinder is attached to the trapezoidal pin with a threaded connection.

Support of Pneumatic Cylinder: This support, which is attached to the bottom layer with an adhesive, has enough height to let the trapezoidal pin completely emerge from the stack of sheets. Thus, it does not prevent the slip between the sheets.

The trapezoidal pin, the support of the pneumatic cylinder, and the frames were manufactured by 3D printing (fused deposition modeling technology), and the material was polylactic acid (PLA).

2.2. Manufacturing

The layers are the components that require the most work and attention. The external shape of the layers was cut with a saw/router machine in the LJ structure with flat clamp and the LJ structure with the trapezoidal pin. In the case of the LJ structure with flat clamp mechanism, there is no other manufacturing process required.

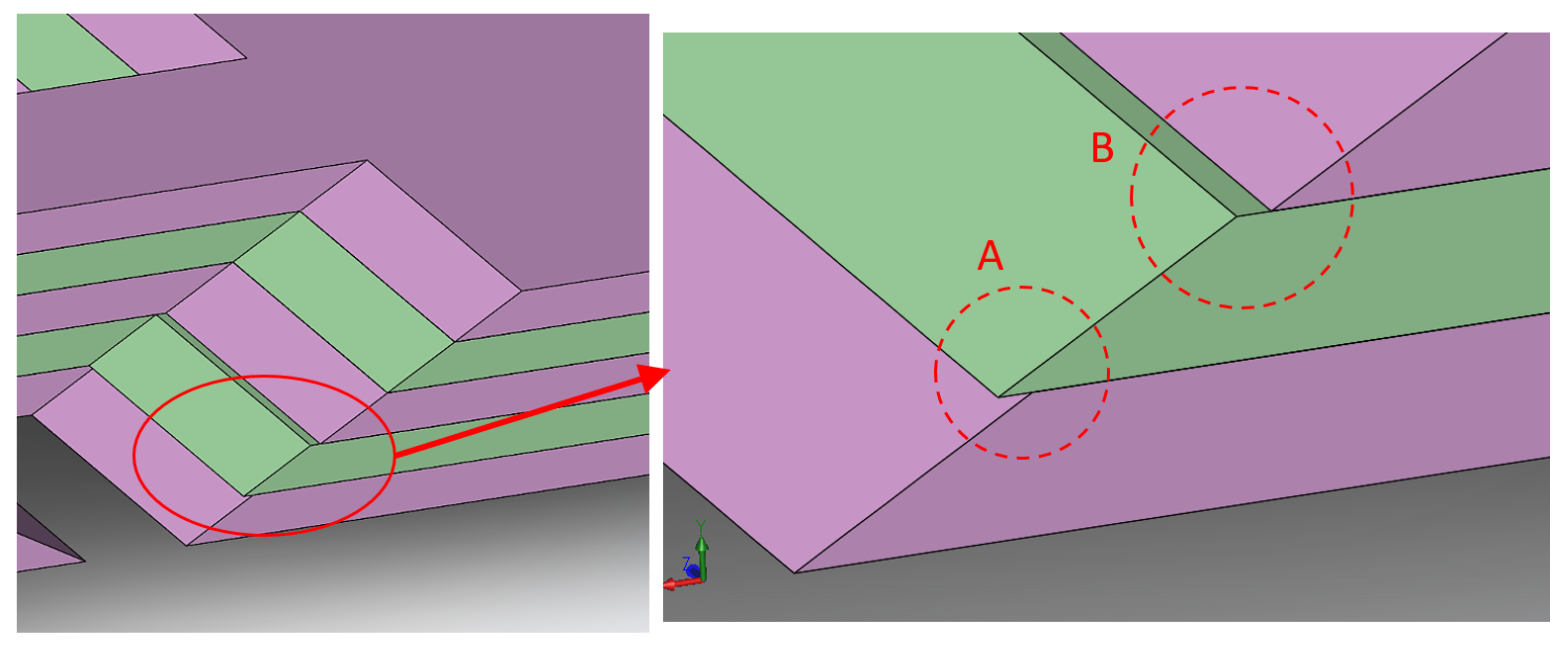
In the case of the LJ structure with the trapezoidal pin mechanism, the machining of trapezoidal cutouts in the layers is a critical task. Milling the trapezoidal slot in each layer separately was not a viable solution since any variation in the machining process of each layer would generate a step or a zig-zag pattern in the trapezoidal slots, as can be seen in Figure 5, which in turn would generate contact with the trapezoidal pin that occurs only in one specific layer instead of contact occurring in all the layers.

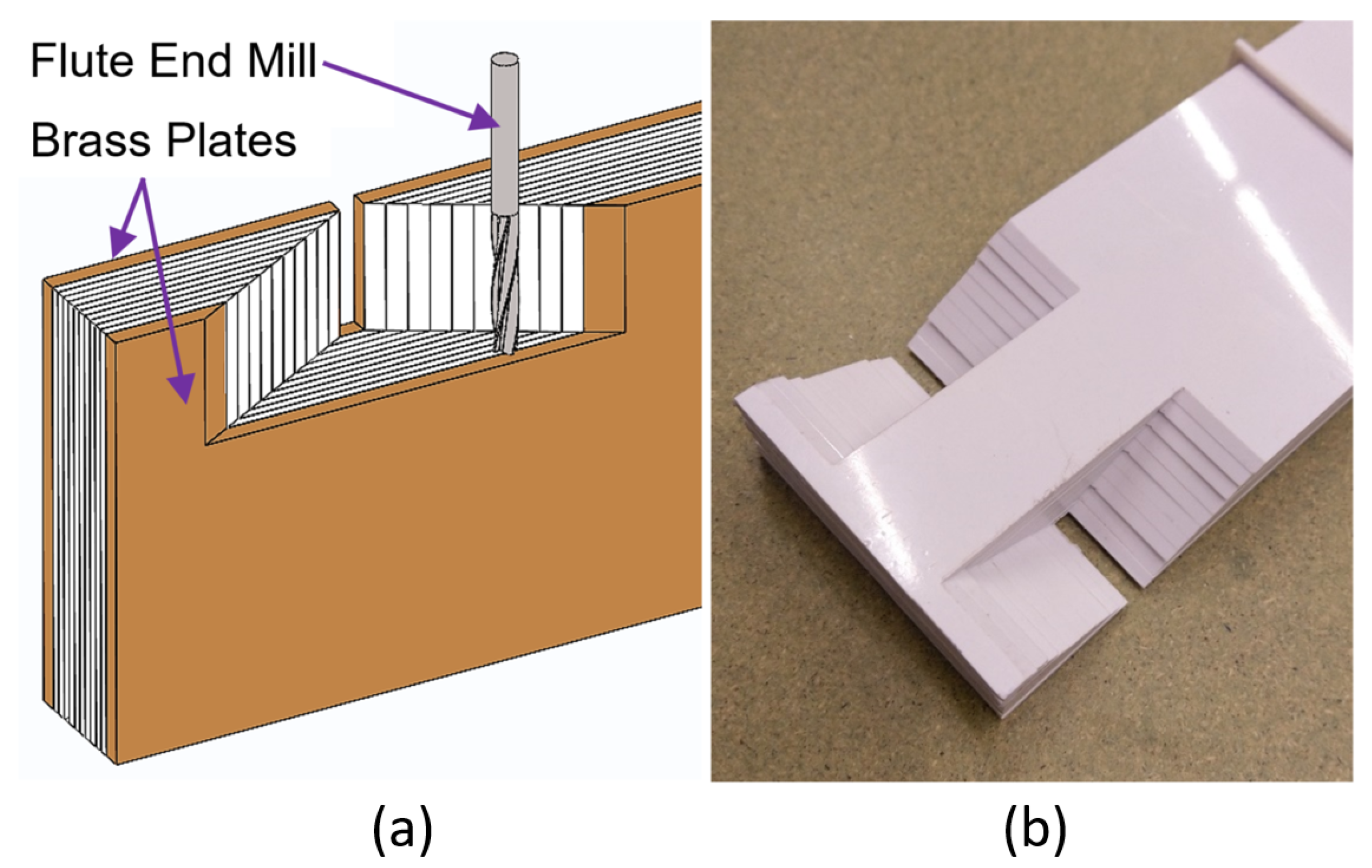
The solution to cut the trapezoidal slot in the LJ structure consisted on machining all the layers at the same time, as can be seen in Figure 6. A fixture comprising two sacrificial brass plates was implemented to achieve this purpose, and all the layers and the brass plates are joined by bolts on one end of the LS structure. These plates have two functions. First, they keep the sheets together during the machining. Second, it allows to fix the LJ structure on the milling machine or the machining center. As a result, there was no flutter or vibration of the ABS layers when the milling tool cut the trapezoidal slot.

Machining was preferred over laser cutting for layer manufacture because laser machines are not usually able to cut a chamfer since the laser is always perpendicular to the sheets. In addition, laser cutting produces toxic fumes when cutting ABS. Furthermore, machining would be more appropriate for manufacturing the layers in metallic materials, which is one of the directions of future work that is envisioned for LJ structures with a trapezoidal pin mechanism.

3D printing for layer manufacture was not selected due to insufficient dimensional accuracy, rough surface finish, and low repeatability of material and mechanical properties that characterize most of the 3D printing technologies of plastic materials [28], which does not give the researchers good confidence to replicate the results through experiments or FE simulations.

2.3. Novelty of the Trapezoidal Pin Mechanism

The novelty of the trapezoidal pin mechanism consists of four aspects that were defined according to the Function–Behavior–Structure Model [29]. The first aspect is its working principle applied to the development of VSLs. The trapezoidal pin mechanism combines the principles of friction force and mechanical interference that were explained in Section 1. The proposed mechanism is based on the conical pin mechanism that also combines the principles of friction and mechanical interference with the purpose of being applied in VSLs [27]. Only another LJ structure with the same combination of working principles has been found in the literature, but it was developed for providing variable stiffness in haptic gloves [30].

The second novel aspect of the trapezoidal pin mechanism is its structure or design. The combination of the friction principle and the mechanical interference principle occurs in the same structural element, which is the trapezoidal pin, rather than having two separate mechanisms with different working principles placed at different locations along the LJ structure. The trapezoidal pin generates normal friction between the layers and simultaneously interferes mechanically with the layers, preventing their relative slip. The intensity of the effects generated by each principle depends on the angle of the trapezoidal pin, this behavior will be explicitly described in Section 5.1. It should be noted that the specific friction mechanism that is combined in the trapezoidal pin mechanism is the DLJ while the friction mechanism that is combined in the application of haptic gloves is the vacuum pressure mechanism [31].

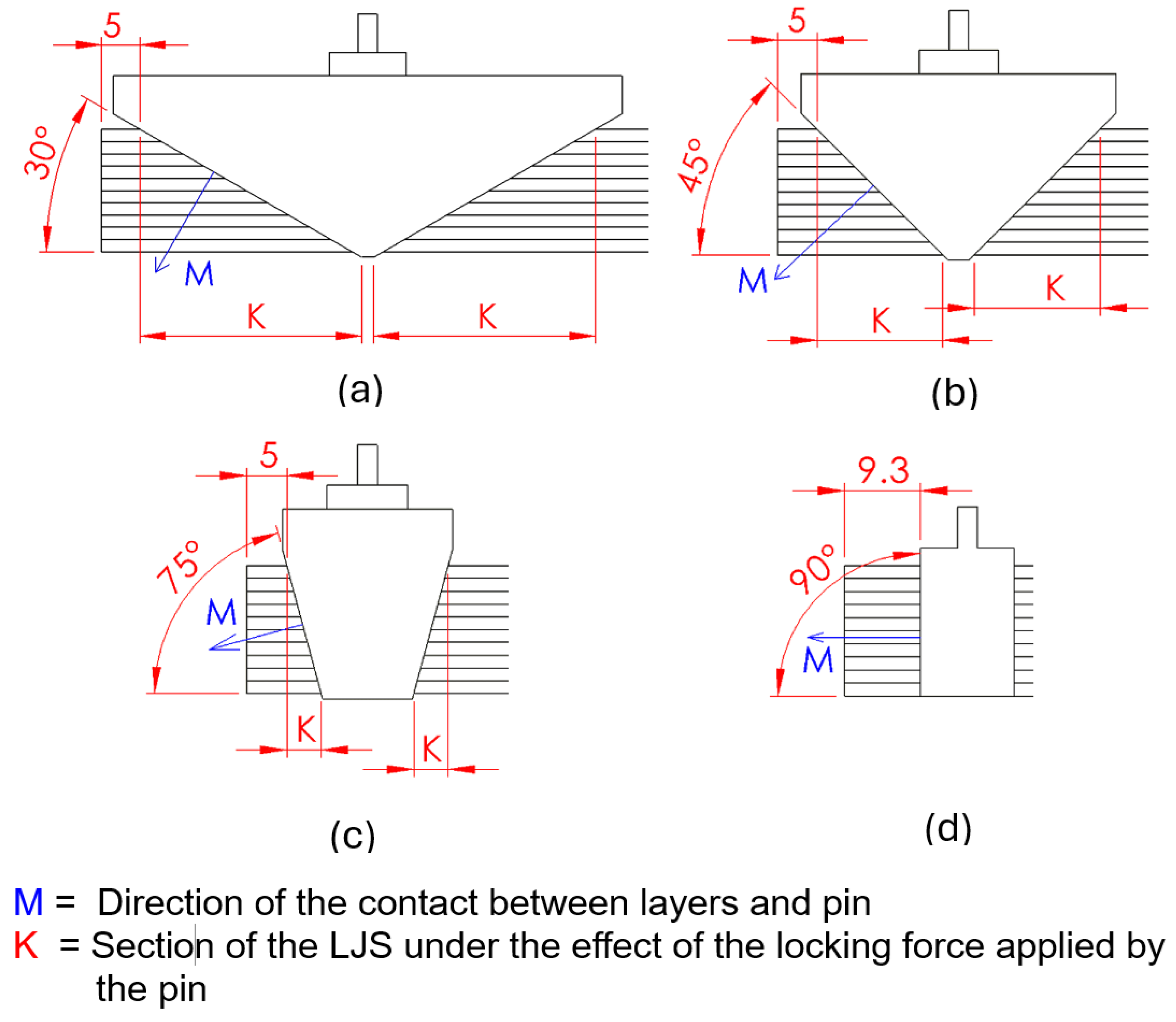
The third novel aspect of the trapezoidal pin mechanism is its structure compared to the conical pin mechanism. As can be seen in Figure 7, the conical pin mechanism is essentially the same mechanism as the trapezoidal pin mechanism, the difference between them is the shape of the pin and the cavity shape in the stack of layers where the pin fits. The trapezoidal pin was developed as an evolution of the conical pin because the manufacturing of the trapezoidal pin mechanism offers more flexibility in terms of the geometry than can be generated in comparison with the manufacturing of the conical pin mechanism. The limitation lies in the manufacturing of the cavity in the layers where the pin fits rather than the manufacturing of the pin. In the trapezoidal pin mechanism, the trapezoidal slots can be machined at any angle, as can be seen in Figure 6. In contrast, in the conical pin mechanism, the machining of the conical holes in the layers is limited by the angle of the countersink drill bit; this is a significant limitation because cutting tools manufacturers do not produce more than six different angles of countersink drill bits. Laser cutting could also be used to cut the conic cavity in the stack of sheets, which would allow any angle angle of the conic cavity, but the hole in each sheet would not be conical but cylindrical, which would reduce the contact with the conical pin to a single point rather than a contact area.

The fourth novel aspect of the trapezoidal pin mechanism is the presence of frames placed along the LJ structure. This structural component was also used in the conical pin mechanism [27] and is described in Section 2.1. It should be noted that frames are different from the clamps used in DLJ because frames are passive elements while the clamps in DLJ have actuators. The effect of frames is investigated in Section 5.2.

3. Experiment Set Up

The objective of the experiment was to determine the variation in stiffness of the LJ structure as a function of the air pressure in the pneumatic actuator. Figure 8 shows the components of the experimental setup. The LJ structure was fixed by a clamp at one end and deflected at the other end in the horizontal direction by a ZHIQU ZQ-21A-10 Tensile Testing Machine (manufactured by ZHIQU-mainland China). The load applied at the free end was measured by a ZHIQU DS2-20N force gauge that has an accuracy of ±0.2% FS and a resolution of 0.01 N (manufactured by ZHIQU-mainland China) The tip deflection was measured by a digital caliper that has a resolution of 0.01 mm.

The pneumatic cylinder is controlled by a pneumatic circuit that has a 5/2-way valve with manual actuation, as can be seen in Figure 8. The circuit also has a pressure regulator that controls the pressure in the whole circuit, including the pneumatic actuator.

3.1. Experimental Procedure

The experiment of force vs deflection consisted on the application of a complete load-unload cycle at 800, 600, 400, 200, 50, and 0 kPa of pressure in the pneumatic actuator. In the LJ structure with trapezoidal pin, the experiment starts with the loading procedure, where the deflection rises every 4 mm, from 0 mm to 40 mm, which is about 10% of the total length of the LJ structure. Then, the unloading procedure starts by diminishing the deflection in steps of 2 mm, from 40 mm until a deflection where the force gauge measures 0 N. The experimental procedure for the LJ with flat clamp was the same, except for the loading procedure where the deflection is incremented every 2 mm from 0 mm to 12 mm, and then every 4 mm up to 40 mm. When the pressure in the pneumatic cylinder is zero, the cylinder rod is manually retracted so that the flat clamp or the trapezoidal pin is not in contact with the stack of layers.

For both LJ structures, the values were recorded after the force had reached a stable value. For this reason, it can be considered that the LJ structures are loaded and unloaded quasi-statically.

3.2. Results of Experiments

Figure 9a illustrates the results of the experiments for the LJ structure with trapezoidal pin at 50 kPa in the pneumatic cylinder. The loading procedure is represented by the upper branch of the curve. The unloading procedure is represented by the lower branch of the curve. Three trials were carried out at each pressure value. Similar experiments on DLJ [15] and LJ based on vacuum pressure [32] also carried out three trials at each pressure value. The average force obtained for a given deflection is represented by the points in Figure 9, and the error is illustrated through the error bars that reflect the range of force values obtained for a given deflection. A similar procedure to illustrate the error in stiffness experiments was implemented in robots with leg locomotion [33].

Figure 9 shows the presence of the hysteresis phenomenon in the LJ structure. The presence of hysteresis is likely due to the friction forces between the LJ components. The friction force is a non-conservative force that dissipates energy during the loading cycle. This phenomenon is also present in other lock/unlock mechanisms of LJ structures [15,17,22,27].

The stiffness of the LJ structure is the slope of the force vs deflection curve. For the purpose of comparing the stiffness of the LJ at different air pressures in the pneumatic cylinder, the results of the experiment at each pressure value were linearized using the least squares method to generate a straight line whose slope is the stiffness k [12,15,17]. Figure 10 shows that the linearization includes only the points from 0 mm to 20 mm in the loading part of the cycle, which was the same range that was considered in the linearization of the DLJ experiments [14,15].

The stiffness calculated from the linearization of the results at each state of pressure is illustrated in

Table 1. Stiffness for each state of air pressure from the experiments. Table adapted from [26].

Stiffness (N/mm)	Pressure (kPa)
	800	600	400	200	50	0
Flat clamp	0.0886	0.0731	0.0582	0.0407	0.0313	0.0279
Trapezoidal pin	0.1008	0.0887	0.0788	0.0646	0.0406	0.0276

. It can be observed that the maximum stiffness and minimum stiffness correspond to 800 kPa and 0 kPa, respectively. The maximum stiffness ratio is calculated as the ratio between the maximum stiffness and the minimum stiffness [14], which yields 3.17 for the LJ structure with flat clamp and 3.65 for the LJ structure with trapezoidal pin.

3.3. Discussion

The stiffness ratio of the LJ structure with trapezoidal pin (3.65) is much less than the theoretical maximum that could be reached if all the layers were joined to form one solid beam (100 for N = 10). The limitation to reach a higher stiffness ratio in this test is purely technical. In this case, the stiffness ratio is limited by the maximum pressure that the air compressor is able to supply (800 kPa). If the air compressor is able to supply 1000 kPa, which is the maximum operative pressure of the pneumatic actuator, the stiffness ratio may be higher. In addition, the difference in the stiffness ratio between the experiment and the theoretical value exists because of multiple factors that affect the effectiveness of the trapezoidal pin mechanism. Some of these factors are discussed later on in this section and in Section 5. In particular, the combination of other values of coefficient of friction, air pressure in the pneumatic cylinder, and the number of frames along the LJ structure has a significant effect in the stiffness ratio. This effect was investigated in the FE simulations presented in Section 5.2, which demonstrates that the stiffness ratio can reach values between 4.2 and 4.7 if the coefficient of friction between the layers is 0.6 and the pressure in the pneumatic cylinder is 1000 kPa.

Figure 9b,c shows an important difference in the loading part of the cycle between the flat clamp and the trapezoidal pin. The LJ with trapezoidal pin has a nearly constant stiffness (slope of the curve), whereas the LJ with flat clamp has sections where the stiffness declines and then rises again as it can be observed in the encircled areas in Figure 9c. This behavior demonstrates that the phenomenon of stick-slip intermittent motion is present in the LJ with flat clamp. In this case, the layers stick together for a while, then they slip suddenly, and then stick again repeating this cycle. When the layers slip abruptly, the LJ stiffness decreases. Then, when the layers stick again, the LJ stiffness increases. This stick-slip motion was also observed visually during the flat clamp experiment and is present in other LJ with friction mechanisms applied to VSLs [14,34]. No stick-slip was noticed during experiments utilizing the trapezoidal pin.

Table 1 and Figure 11 show that the LJ structure with trapezoidal pin reaches larger stiffness values than the LJ structure with flat clamp for almost all the pressure states in the pneumatic cylinder. Thus, the maximum stiffness ratio for the LJ structure with trapezoidal pin is about 15% larger than the stiffness ratio of the LJ structure with flat clamp.

In terms of manufacturing, the LJ structure with trapezoidal pin mechanism requires a more complex manufacturing process than the LJ structure with flat clamp mechanism. As discussed in Section 2.2, the LJ structure with trapezoidal pin mechanism requires a milling operation and a fixture to ensure the correct machining of the trapezoidal slots while the LJ structure with flat clamps only requires a saw/router operation to cut the external shape.

Table 2. Comparison between LJ structure with flat clamp mechanism and trapezoidal pin mechanism.

Variable Stiffness Mechanism	Flat Clamp	Trapezoidal Pin
Working Principle	Friction	Friction + mechanical interference
Manufacturing Method	Saw/router for external shape	saw/router for external shape, end milling for the trapezoidal slots
Stiffness Ratio	3.17	3.65
Presence of Stick-Slip Phenomenon	yes	No

summarizes the differences between the trapezoidal pin mechanism and the flat clamp mechanism in terms of their working principle, manufacturing, and mechanical performance. It can be observed that the trapezoidal pin mechanism is better than the flat clamp mechanism in terms of mechanical performance because the trapezoidal pin mechanism has a higher stiffness ratio and does not present the stick-slip phenomenon. However, the trapezoidal pin mechanism is also more difficult to manufacture.

The behavior of the LJ with trapezoidal pin also depends on other parameters such as the number of layers, the location of the actuators, the number of actuators, and the coefficient of friction (COF). These parameters were not included in this research because they have been extensively investigated in DLJ [14,15]. The conclusions obtained in DLJ studies can be applied to the trapezoidal pin mechanism because both mechanisms have in common the concept of discrete actuators placed in particular locations of the LJ structure. For example, the stiffness ratio of DLJ increases when the number of clamps placed along the beam increases. Similarly, if multiple trapezoidal pin mechanisms are placed along the LJ structure, the stiffness will increase significantly.

DLJ reaches a stiffness ratio of 5 when only the end clamp is implemented [14]. This mechanism surpasses the stiffness ratio of the LJ with trapezoidal pin and the LJ with flat clamps. However, it is necessary to take into account that there are important differences between these LJ mechanisms such as the contact areas between the clamp and the layers, and the presence of frames along LJ structure. Therefore, it is not possible to definitely conclude that the LJ mechanisms presented in this article are less effective than the DLJ.

The speed of the stiffness change in LJ with trapezoidal pin mechanism depends on various characteristics of the pneumatic system and it was not measured in this study. However, the time that the piston rod takes to enter the cylinder at 1000 kPa is roughly estimated at 0.02 s based on the speed of the piston (500 mm/s) and the stroke (10 mm). This time is shorter than 0.1 s which is the duration in the human body of the dynamic effects caused by an impact against a robot manipulator [25], showing that this pneumatic system has the potential to attenuate the effects of this type of collisions. In addition, subsequent studies implemented variations of the trapezoidal pin mechanism in a robot arm with VSLs [35]. The impact tests carried out in these studies demonstrated that the trapezoidal pin mechanism can achieve an impact force reduction of approximately 33% of the impact force variation (difference in the impact force between the rigid case and the flexible case) within a period of 100 ms. The impact test also demonstrated that VSL robot arm was able to completely transition from its rigid to flexible state within a period of 173 ms.

It should be noted that the LJ structure with trapezoidal pin mechanism presented in this study is an approach to the design and construction of a VSL. It does not incorporate all the functions and requirements that a completely functional VSL must have, such as joints at the ends to be attached to other links. In addition, the investigation of the mechanical performance of the proposed mechanism is limited to bending stiffness. However, the design of a completely functional VSL that is based on the trapezoidal pin mechanism has been developed and investigated in a subsequent study [35]. This VSL is illustrated in Figure 12 and has the capacity to support axial loads, a bending stiffness ratio up to 2.54, and the capability to vary the torsional stiffness characterized by a torsional stiffness ratio of 1.56.

4. Finite Element Simulation of the Trapezoidal Pin and Flat Pin

Other lock/unlock mechanisms of LJ structures have been modeled by analytical methods or by finite element (FE) methods [15,17,20,22,36,37]. In the case of LJ with many sheets, FE simulations would be favored over analytical methods since analytical methods are algebraically taxing [22]. This section presents FE simulations of the trapezoidal pin and the flat clamp as lock/unlock mechanisms.

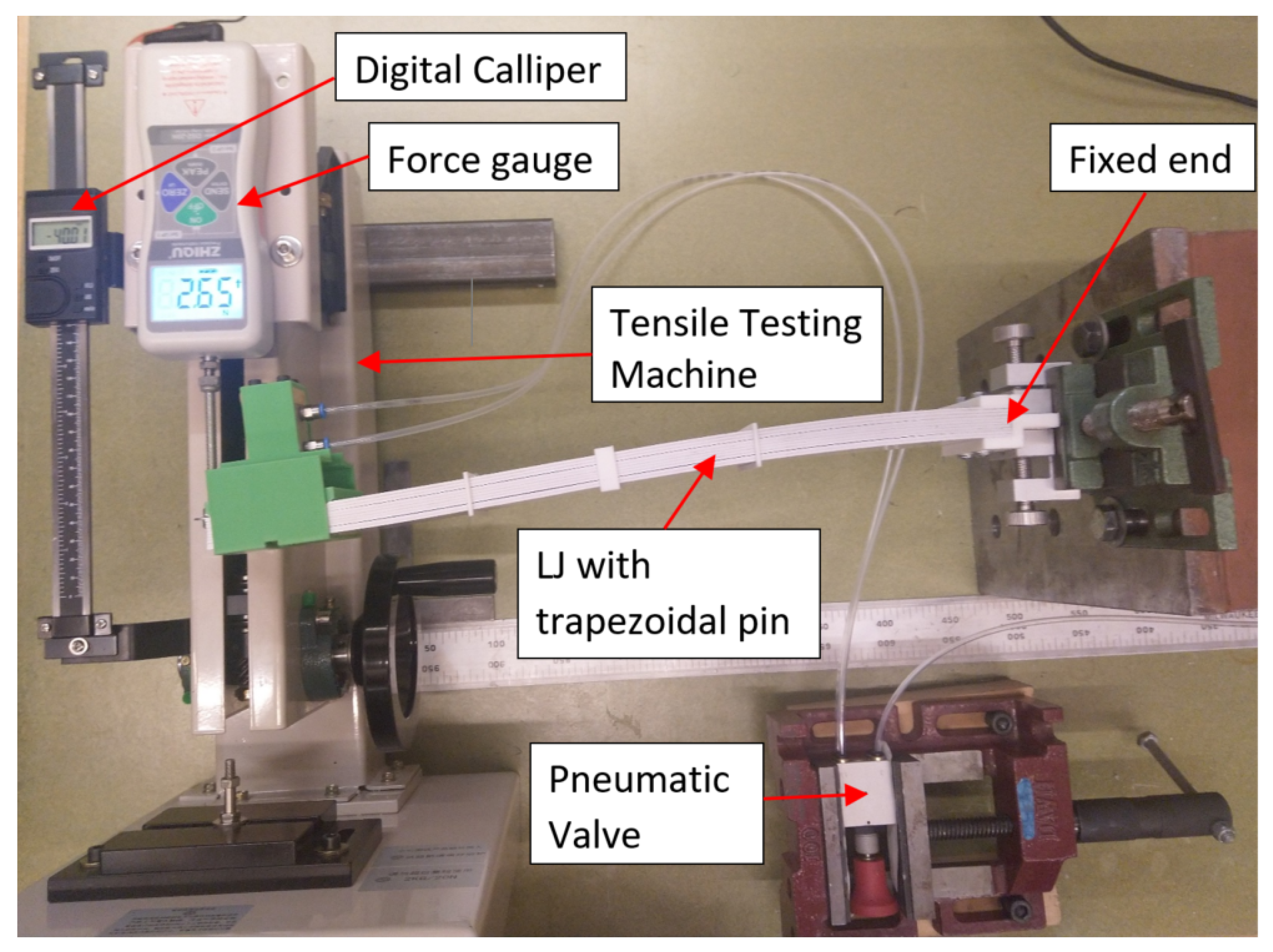
The FE models were developed in Ansys with the same components and dimensions as the experimental set up presented in Section 2 and Section 3. The FE model has the same geometry, materials, boundary conditions, and load conditions that were implemented in the experiment. This means that the LJ model is fixed in one of its ends, deflection was applied at the free end following the same values that were imposed in the test, the pressure in the pneumatic cylinder is implemented as a pair of forces that are applied to the cylinder body and the cylinder rod, and the value of these forces correspond to the forces applied by the cylinder when it is pressurized at the same values of pressure of the experiment. The result of the simulations was the force associated with each value of the applied deflection.

The coefficient of friction (COF) between the sheets was measured by using an inclined-plane friction device [38]. The same experiment was conducted between the layers and trapezoidal pin, and between the sheets and flat clamp. The results of these tests indicate that the COF between the sheets is 0.253, and the COF between the layers and flat clamp, and the COF between the layers and trapezoidal pin is 0.126. These COF values were used in the FE simulations.

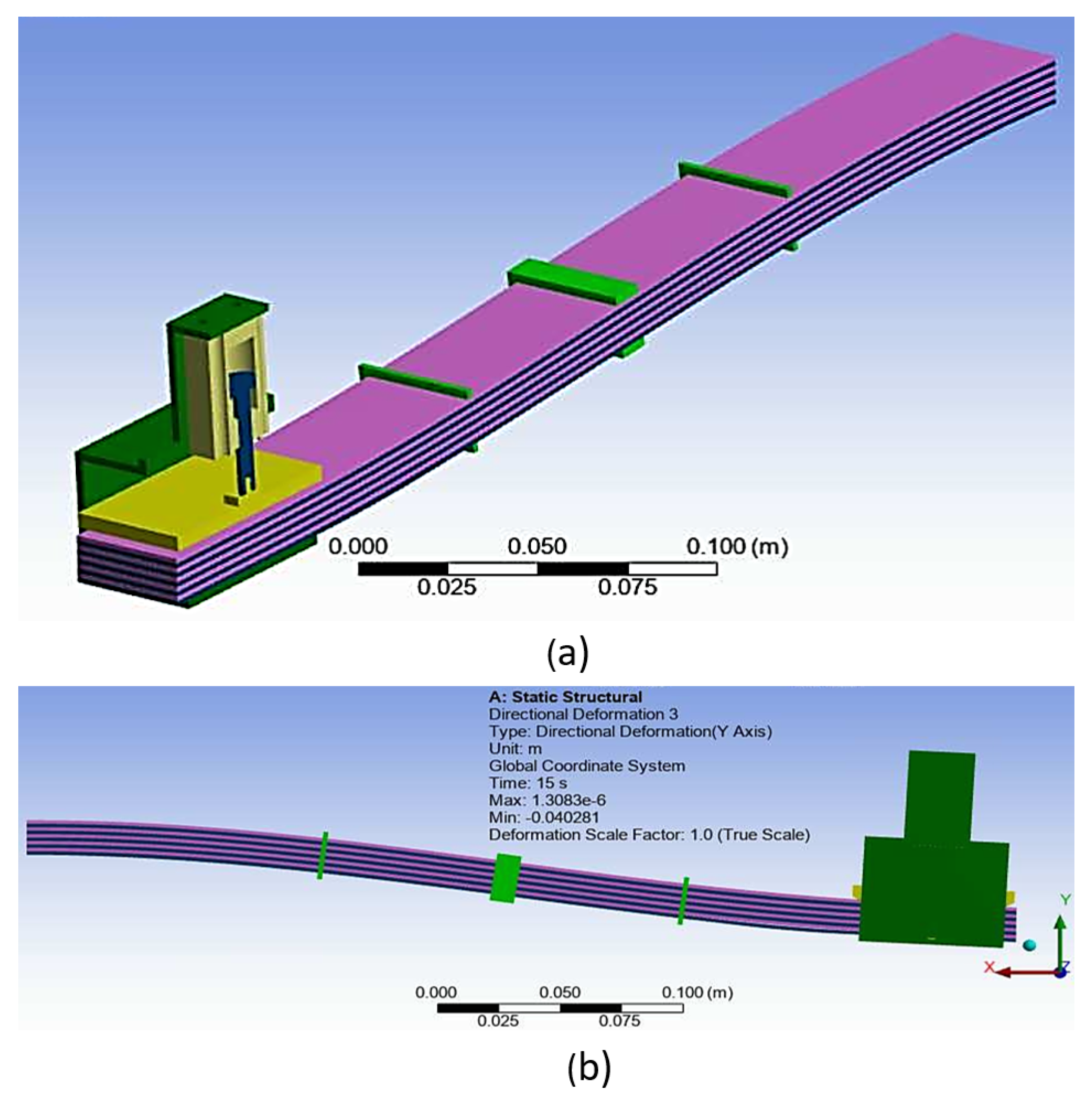
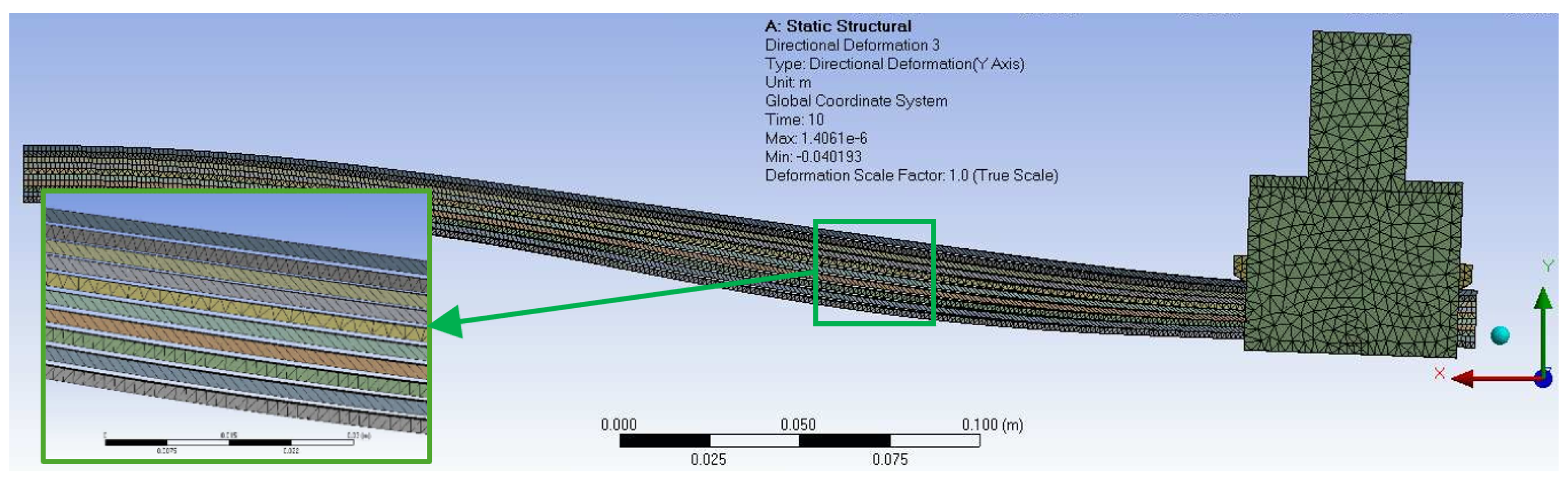
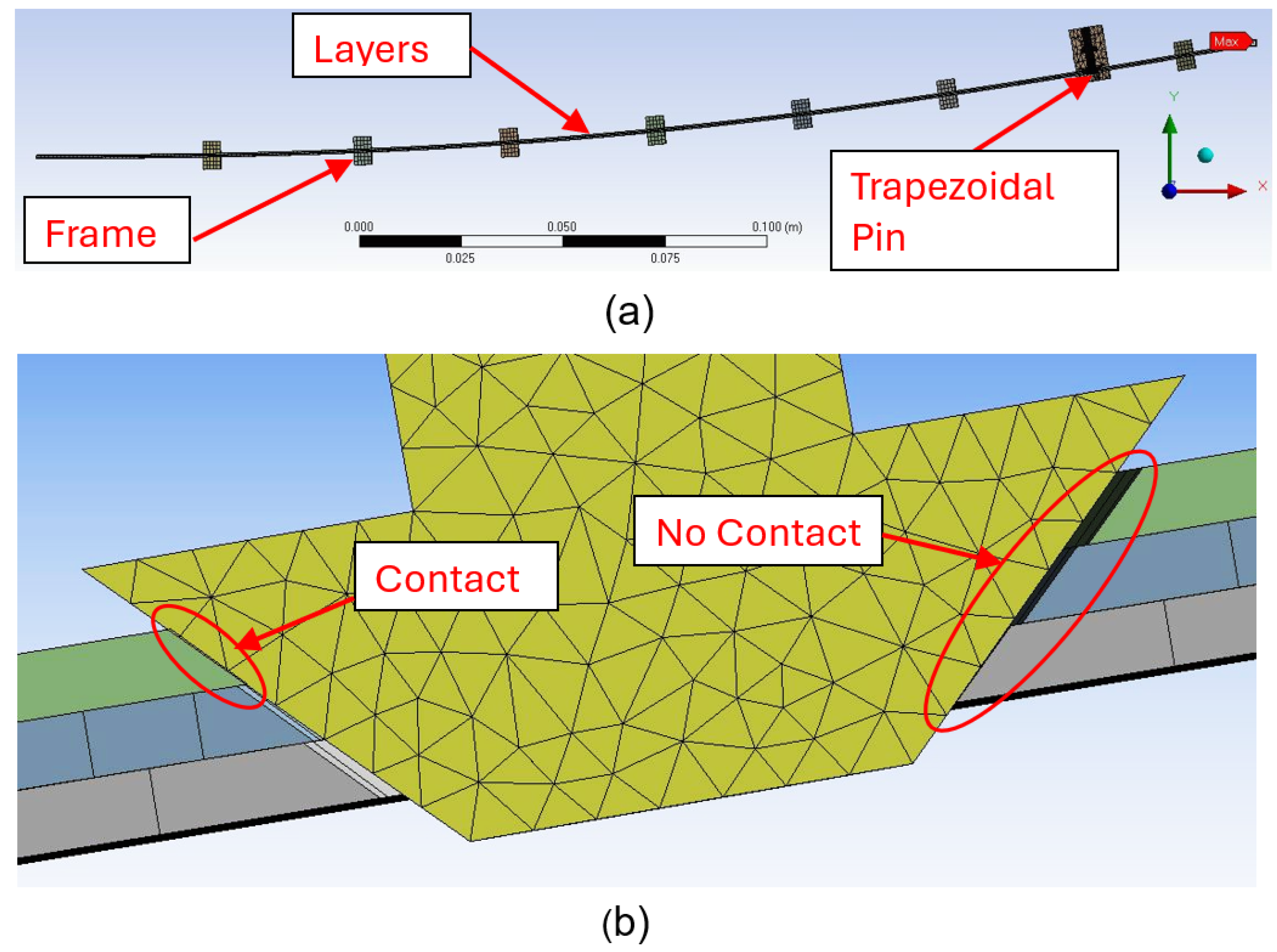
The most relevant details about the pre-process of the simulation are as follows. Only one half of the LJ structure is modeled and symmetry along the longitudinal plane was imposed as can be observed in Figure 13a. The mesh of the sheets is composed of elements of quadratic order and all the layers have one element across the thickness. The Static Structural Solver was selected to carry out the simulation because the experiment was conducted in quasi-static conditions. Large deflection is turned on considering that the maximum deflection in the experiment was about 10 % of the length of the LJ structure. The setup of the contact among the sheets, and between the sheets and the pin had a critical role in the convergence of the solution. In this aspect, the most relevant parameters are the Contact Formulation, which was selected as Augmented Lagrange, the stiffness, which is updated in each iteration, and the normal stiffness factor, which is set up as 0.01. The maximum number of equilibrium iterations per solution step is 50 and was defined through the command NEQIT.

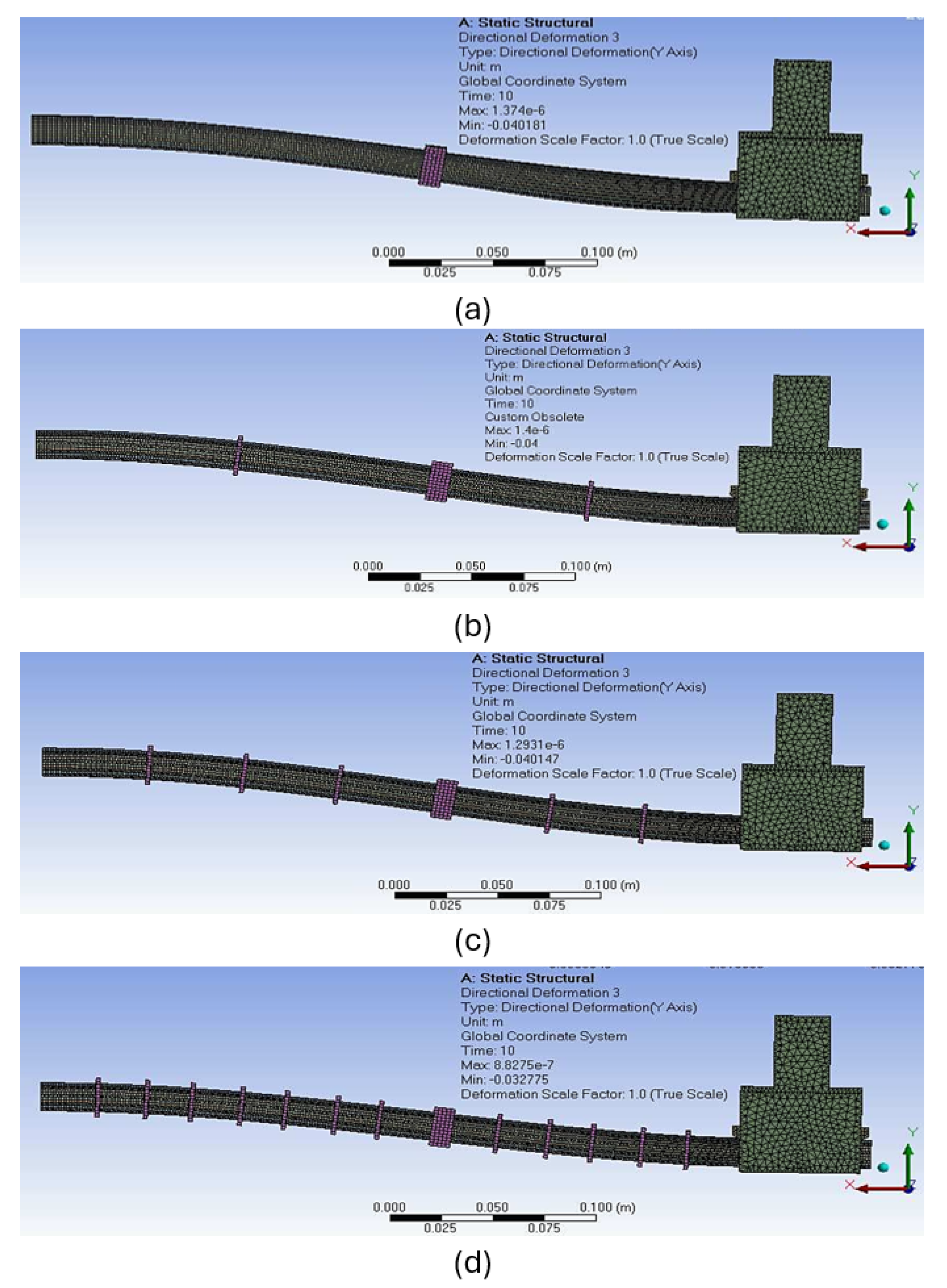
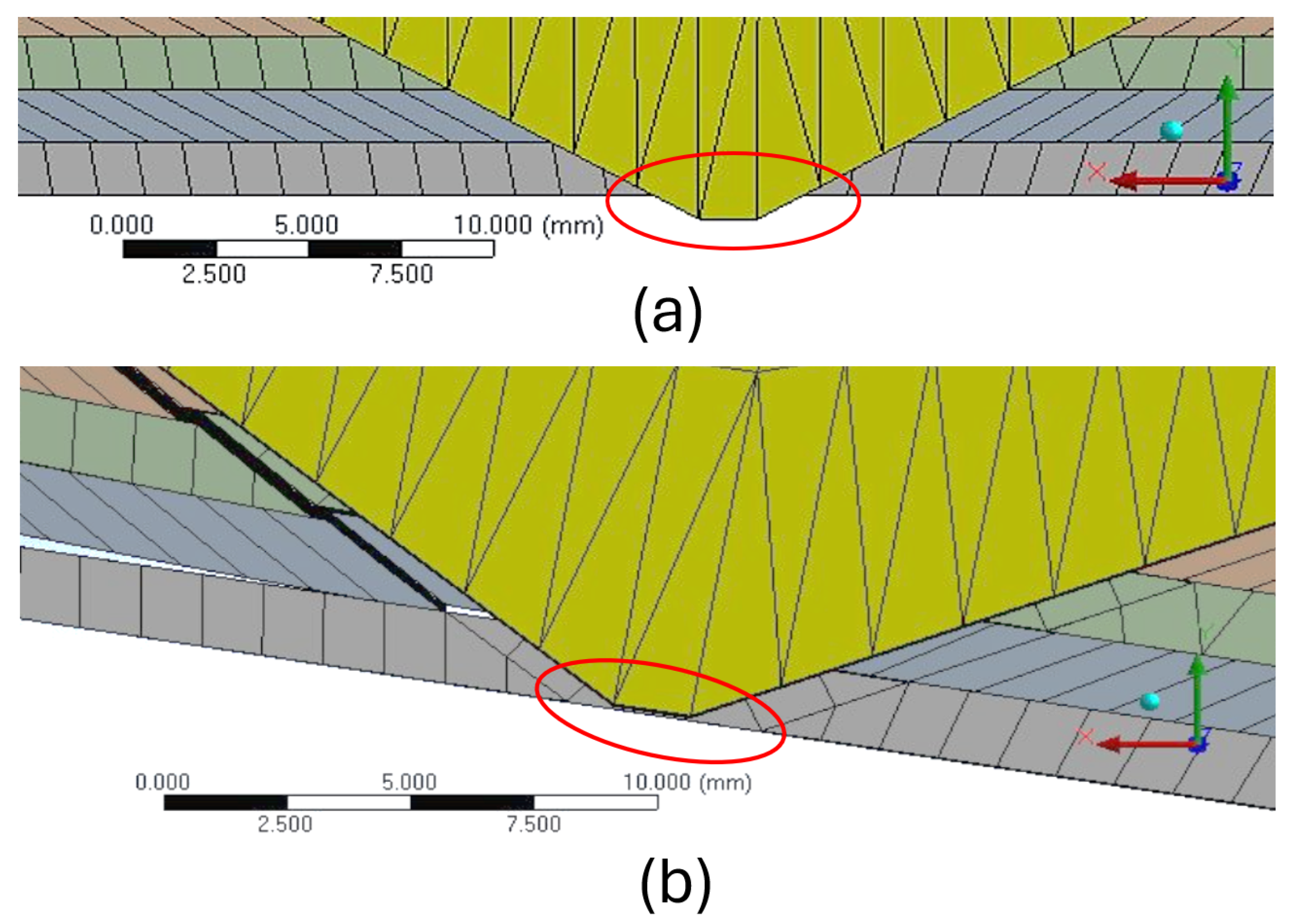
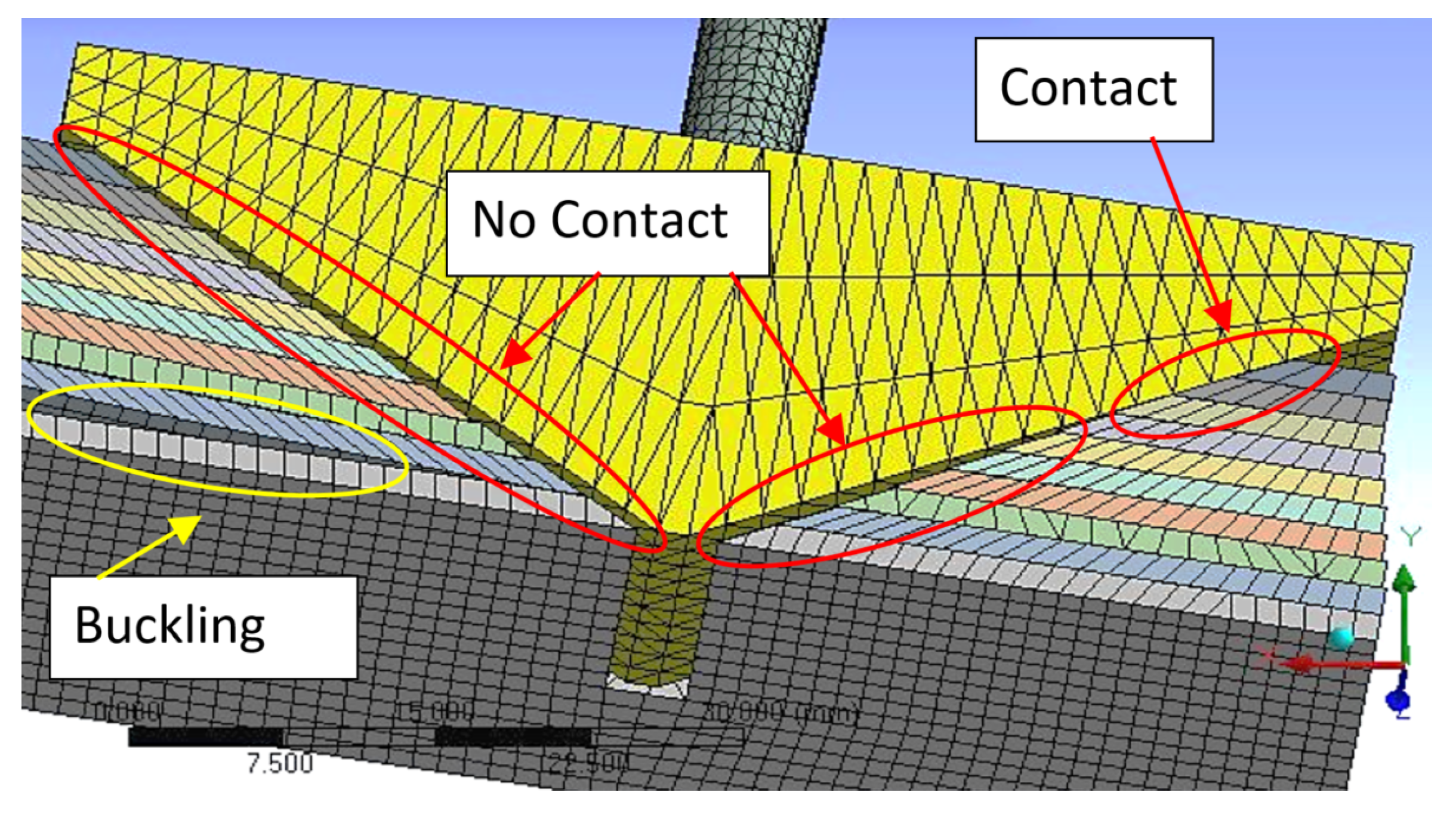
Figure 13b shows the shape of the LJ with trapezoidal pin at a locking pressure of 800 kPa when it reaches 40 mm of deflection, which is the maximum deflection of the free end that was applied in the experiment and replicated in the simulation. It can be seen that the curvature of the LJ structure is very low in the segment that is near to the trapezoidal pin mechanism. Basically, the action of the trapezoidal pin makes that segment of the LJ structure straight.

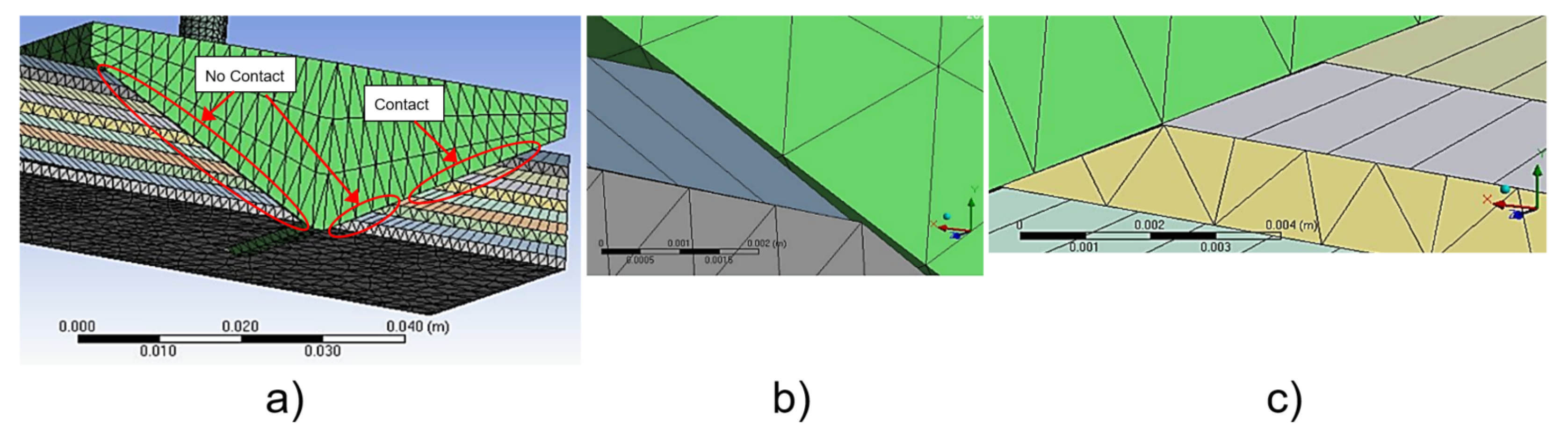
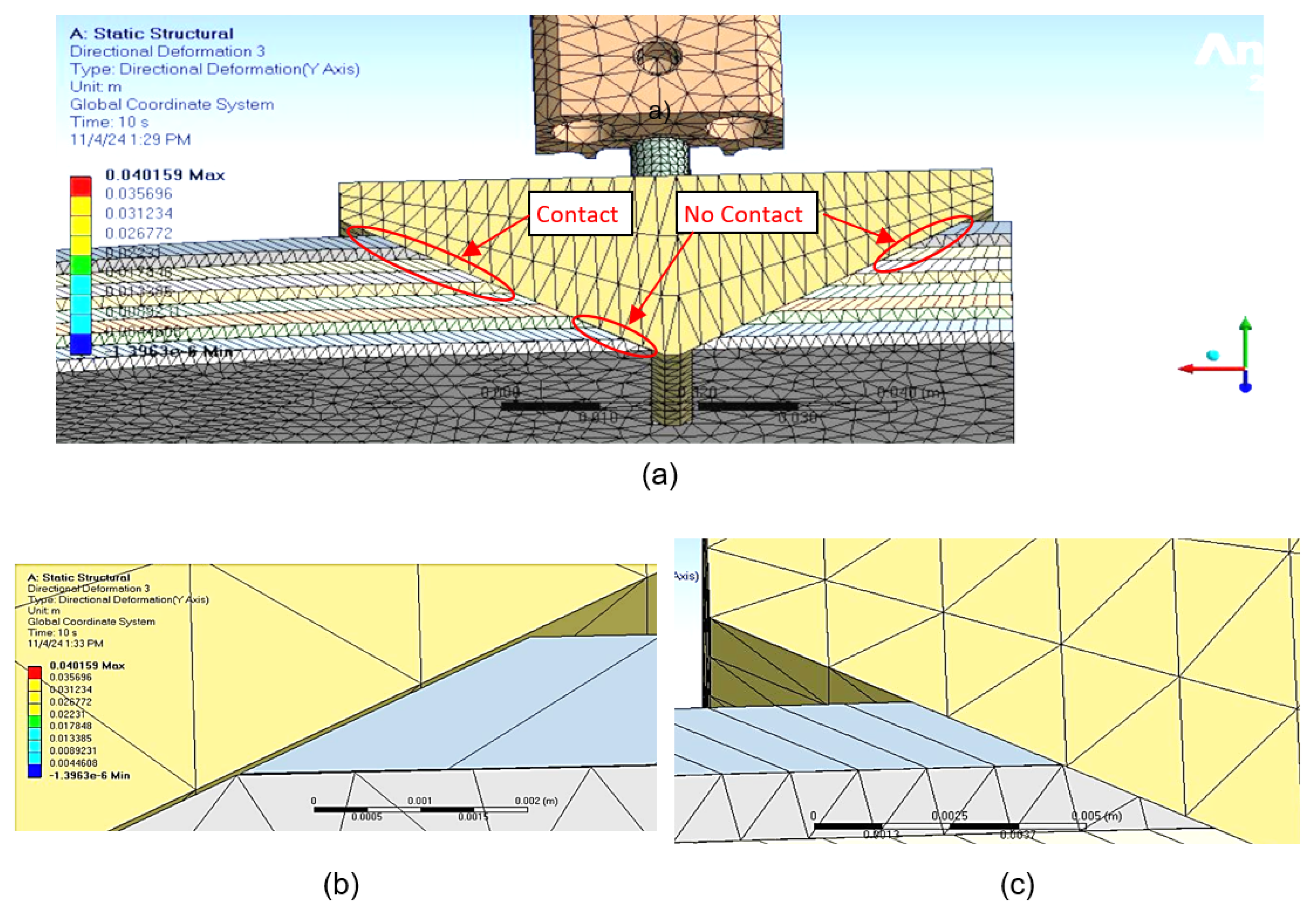
Figure 14 illustrates some details that were not possible to observe in the bending test. Figure 14a,c show that the trapezoidal pin only keeps contact with some of the top sheets in the front of the pin. Figure 14b illustrates how the contact between the layers and the trapezoidal pin is missing in the back part of the pin. This figure also shows the relative slip between the sheets. The areas of contact and no-contact are more evident in Figure 31. The consequences of the existence of these areas are also explained in the Section 5.4.

The cause for the existence of the contact and no-contact zones is the fact that slip between the layers depends on the distance from the clamp end to the position of analysis along the LJ structure. When the laminar jamming is bent, the slip between the layers in the clamp end is zero, then the slip differs from zero as the point of analysis moves along the beam [22]. In addition, the slip between the layers also depends on the position of the layers in relation to the bottom layer. It is necessary to remember that trapezoidal pin is ultimately attached to the bottom layer. In other words, the trapezoidal pin can move perpendicularly to the bottom layer, but both components remain in the same position along the beam. Therefore, when the LJ structure is bent, all the layers move or try to move in relation to trapezoidal pin, except for the bottom layer.

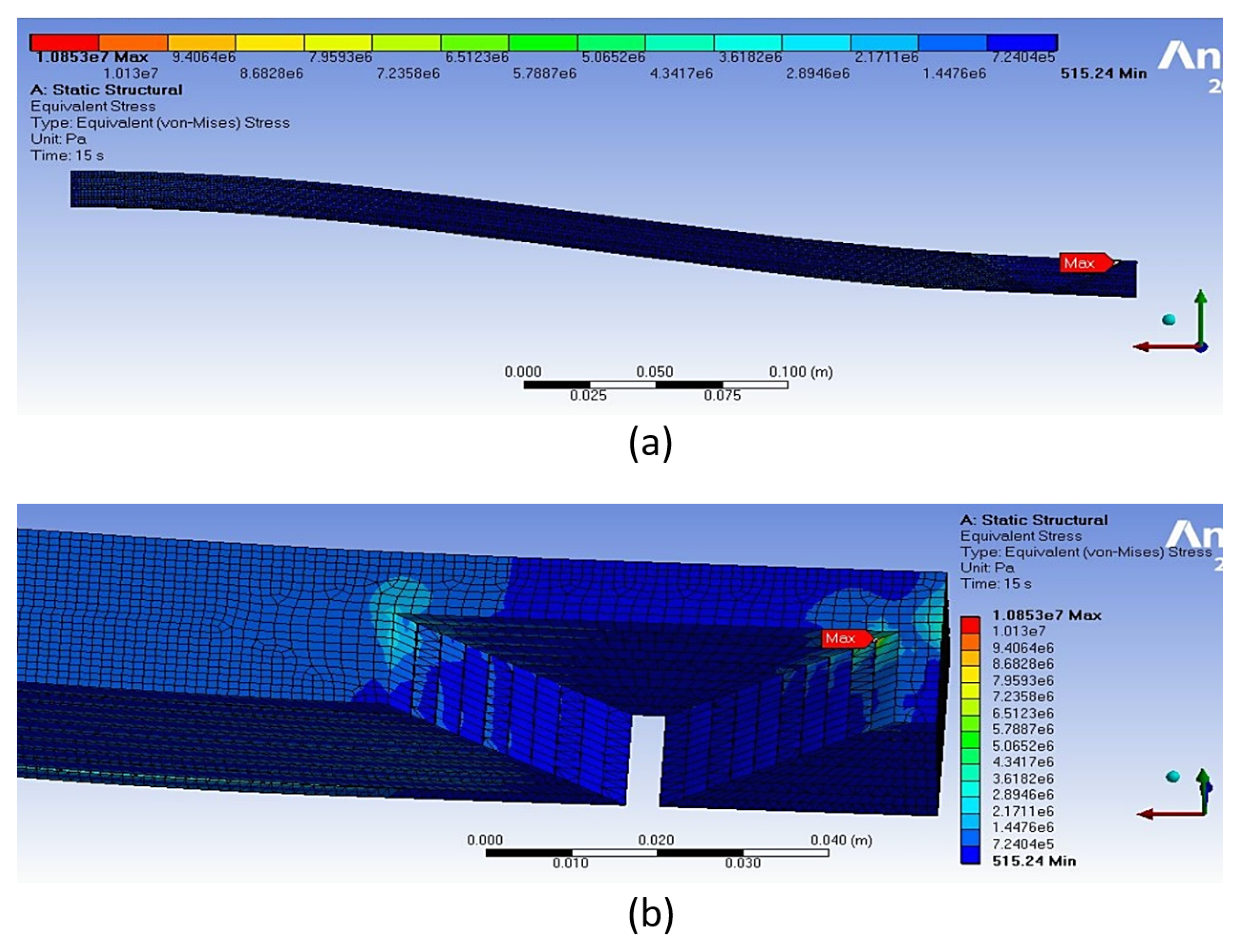
Another aspect that was investigated through the FE simulations is the possibility of plastic deformation of the ABS sheets during the bending experiments. Figure 15 illustrates the Von-Mises stresses of the ABS laminates when air pressure in the cylinders is 800 kPa and the deflection in the free end of the LJ structure is 40 mm (the same simulation as Figure 13), which was the maximum deflection in the experiment. It can be seen that the maximum stress in the sheets is 10.8 MPa and occurs in the trapezoidal slots in the top layers. The maximum stress at this point is probably caused by the contact between the trapezoidal pin and the top layers. Another cause of the maximum stress in this location is the proximity to the edge where the trapezoidal slot starts, which generates a stress concentration factor. This stress value is less than the yield strength of ABS (39 MPa according with the sheets manufacturer). Therefore, plastic deformation does not occur in the ABS sheets. This result matches the experiment where no damage or plastic deformation in the ABS sheets was observed after the bending tests.

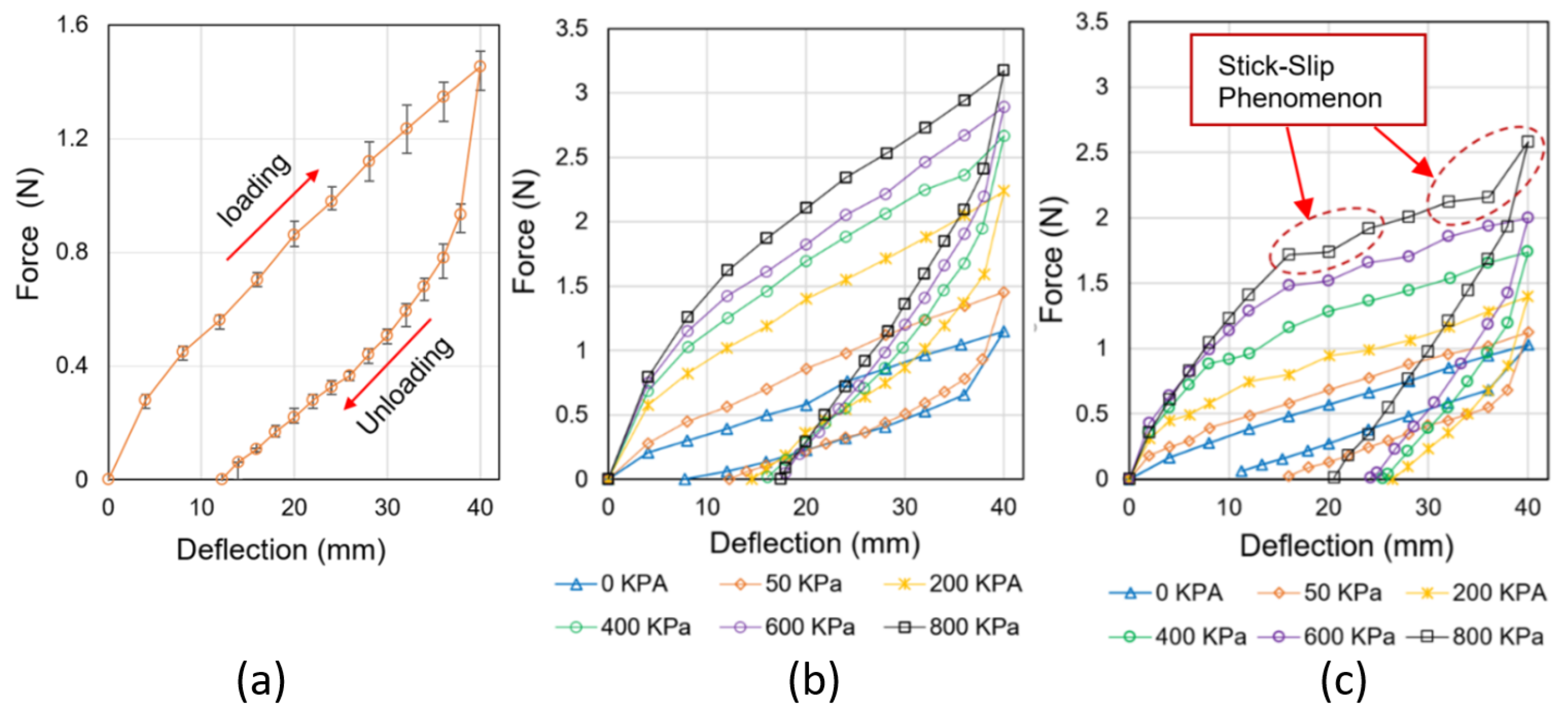
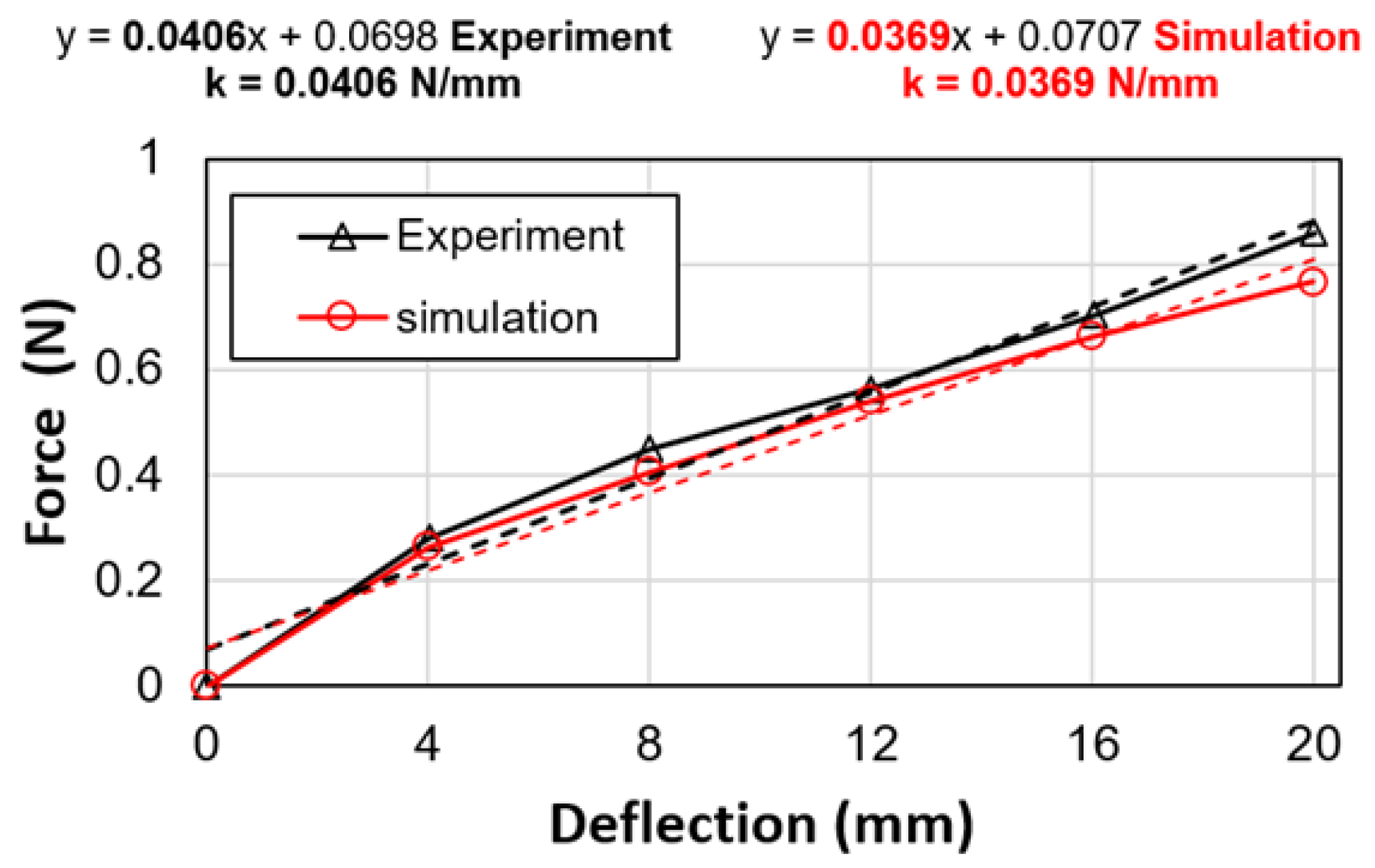
Experiments Versus Simulations

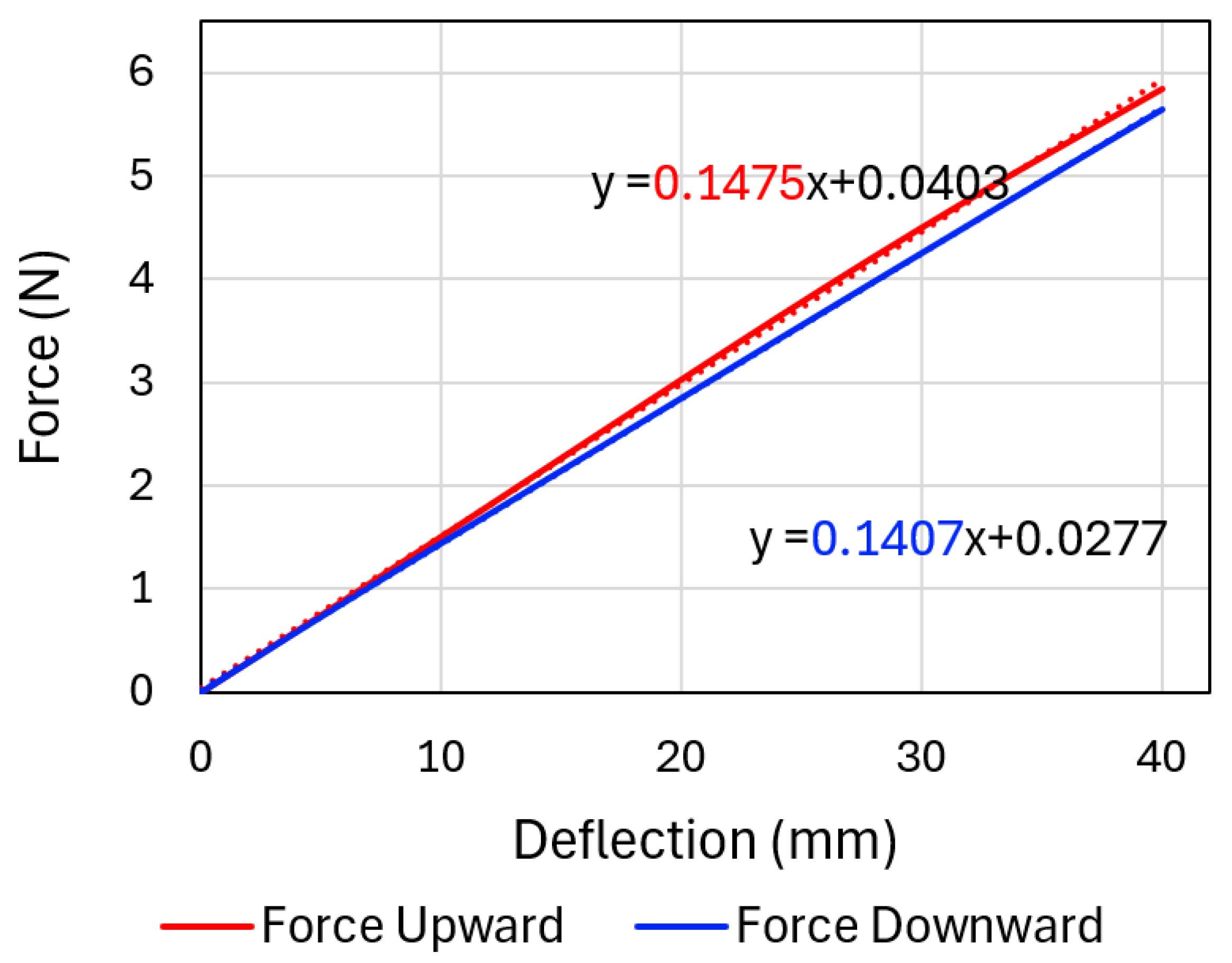
Figure 10 shows the results of the experiment compared with results from the FE simulations for the LJ structure with trapezoidal pin at 50 kPa. It can be seen that the simulation results agree well with the experimental results. The results are compared from 0 mm to 20 mm in the loading part of the cycle, as the same range was considered in the studies about DLJ [14,15]. The results were a stiffness of k = 0.0369 N/mm in the simulation, and a stiffness of k = 0.0406 N/mm in the experiment. Thus, the simulation error with respect to the test is about 9.1% in this case.

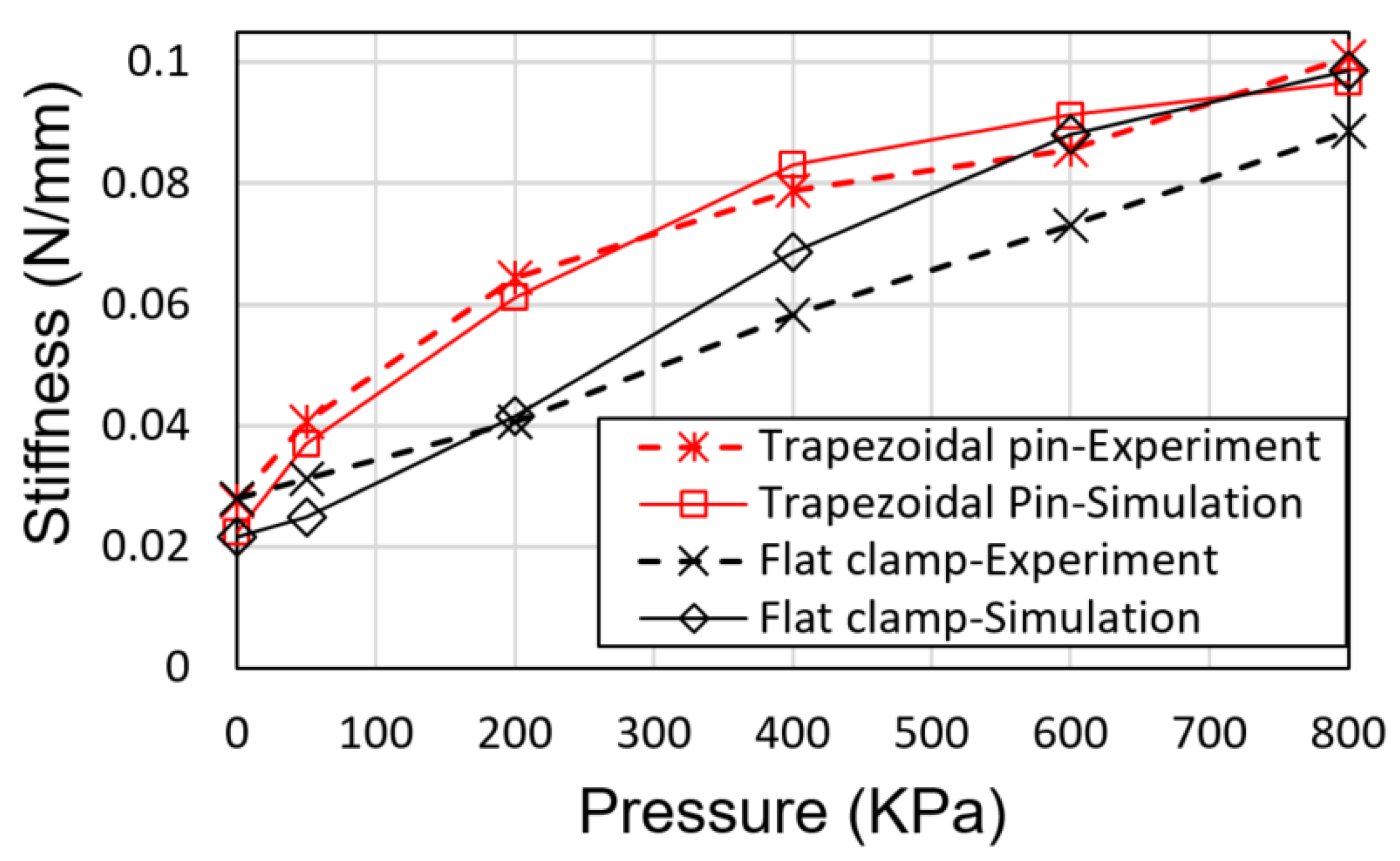
Figure 11 shows a comparison of the simulation and the experimental stiffness values for all pressure states that were tested in the experiments. For the case of the LJ structure with trapezoidal pin, it can be seen that the results of the simulations match well the results of the experiment. The maximum difference is about 10% and occurs at 0 kPa. This difference occurs because the ABS layers are not totally flat, which results in gaps between the sheets when there is not any locking force that keeps them together. On the other hand, the ABS layers in the simulations are modeled as totally flat and they remain together even when there is not any locking force on them. For the case of the LJ structure with flat clamp, it can be seen that the results of the simulation follow the same trend of the experiment but with a maximum error about 20%. The FE simulations do not present the stick-slip phenomenon that occurs in the tests of the LJ structure with flat clamp, which may be the cause of the difference between the experimental and the simulation results in this case.

5. Computational Studies

A series of computational studies were carried out in order to optimize the design of the LJ with trapezoidal pin and develop an understanding of how some design parameters affect the bending stiffness. The key parameters that were analyzed through FE simulations were the angle of the trapezoidal pin and the number of frames. In addition, the behavior of the LJ structure with trapezoidal pin when it is bent upward and its behavior at high deflections were also analyzed through FE simulations.

5.1. Vary the Angle of the Trapezoidal Pin

To study the effect of the angle of the trapezoidal pin on the beam stiffness, FE simulations with various tip angles were performed. The setup of this case study is illustrated in Figure 16. The overall dimensions of the beam, the number of sheets, the materials, the load conditions, and the settings of the FE simulations for all trapezoidal pins are equal to the LJ structure described in Section 2 and Section 4.

As it will be explained in Section 5.2, three frames generate the maximum stiffness ratio in the LJ with trapezoidal pin. Therefore, all of the LJ structures that were studied have three frames. The frames are placed along the beam at lengths that keep the same proportion in relation to the distance LP that is illustrated in Figure 17.

Figure 16 shows four different angles that have been studied, including 30°, 45°, 75°, and the straight pin. The straight pin is considered as a trapezoidal pin with an angle of 90°. It is clear that the angle of the trapezoidal pin and the contact area between the pin and the layers are related. Therefore, they can not be changed independently. The parameters that remain unchanged between the cases are the position of the pin and the width of the contact areas of the pin. All the pins were located at 5 mm from the free end of the LJ, except for the straight pin, which can not be placed at that position because there would not be enough space to place the support of the pneumatic cylinder. In relation to the width of the pins, they have the same two contact zones whose widths are 20 mm each and separated by a gap as illustrated in Figure 4. The only exception is the straight pin that only has one contact area for reasons of simplicity as can be seen in Figure 18. The flat clamp was not included because its FE simulation was not accurate enough according to Figure 11.

Figure 19 illustrates the results of the simulations for each pin. It can be seen in this figure that the trapezoidal pins at 30°, 45°, and 75° present a growing trend between the pressure and the stiffness. The increment of the stiffness is larger at low pressures (less than 200 kPa), and then the stiffness increments are lower at large pressures (more than 400 kPa). It is important to note that the stiffness at 0 kPa corresponds to the situation when the pin is disengaged from the layers.

As explained in Section 2 the trapezoidal pin mechanisms are based on a combination of the principles of friction and mechanical interference. The angle of the trapezoidal pin affects the amount of friction force versus mechanical interference generated by the pin. In relation to the friction force, it should be noted that the size of the beam section where the locking force is applied depends on the angle of the trapezoidal pin as can be seen in Figure 16, where the dimension K represents the section of the LJ structure that is affected by the trapezoidal pin. In particular, as the angle of the trapezoidal pin decreases, the pin becomes flatter and the section of the beam under the effect of the pin increases. Thus, the friction force between the layers is larger. In relation to mechanical interference, as the angle of the trapezoidal pin increases, the pin becomes steeper and the interference phenomenon grows because the direction of the contact between the layers and the pin gets close to the parallel direction to the layer as shown in Figure 16 where vector M is the direction of the contact between the layers and the pin. Therefore, as the angle of the pin increases, the effect of the mechanical interference becomes stronger while the effect of the friction force fades. It can be inferred that the flat clamp (angle 0°) is the extreme case where there is only friction force and no mechanical interference. In contrast, the straight pin (angle 90°) is the extreme case where there is only mechanical interference and no friction force.

While trapezoidal pins of 30°, 45°, and 75° have a growing trend between the stiffness and the pressure, the straight pin reaches its maximum stiffness at the lowest non-zero pressure tested (50 kPa), and then the stiffness remains constant for higher pressures because there is only mechanical interference and the increase in pressure does not generate additional friction force between the layers. This behavior indicates that the straight pin works as an on-off mechanism, whereas the other trapezoidal pins work as continuous mechanisms that are able to modulate the stiffness. These observations make it clear how the interference mechanism differs from the friction force mechanism. The straight pin, which is a pure interference mechanism, can not compress the layers. Instead, it prevents the relative slip of the layers, which combined with the action of the frames that will be explained in the Section 5.2, block the independent bending of each layer, and force them to bend as a whole beam, increasing the bending stiffness.

Figure 19 shows that the 30° trapezoidal pin has the largest stiffness for pressures higher than 500 kPa. In contrast, the 75° trapezoidal pin and the straight pin have the largest stiffness at pressures lower than 200 kPa. This behavior shows that the effect of friction force is dominant at high pressures (more than 500 kPa) and the effect of mechanical interference is dominant at low pressures (less than 200 kPa). At low pressures, the 75° trapezoidal pin has the highest stiffness because most of its stiffness comes from mechanical interference, while the stiffness of the 30° trapezoidal pin is the lowest because its mechanical interference is scarce and the friction between the layers is low because the pressure is low as well. At higher pressures, the 30° trapezoidal pin has the maximum stiffness, which comes mainly from the friction force that is high due to high pressure and the large area of the layers that are under the effect of the pin. In contrast, the stiffness of the 75° trapezoidal pin is lower because most of its stiffness comes from mechanical interference that does not grow significantly at higher pressures, while the generated friction force is low due to the small area of the layers under the effect of the pin.

The behavior of the LJ with trapezoidal pin and DLJ differs considerably in terms of the relation between the contact area and the stiffness. It was explained above that the contact area increases when the angle of trapezoidal pin decreases. However, It should be noted that the increase in the contact area between the trapezoidal pin and the layers does not generate a larger stiffness at all pressures. In the DLJ, the stiffness of the LJ structure raises when the contact area increases by making the clamps longer [15].

5.2. Effect of Frames in the LJ Structure

The LJ solution proposed in this article utilizes frames, which are a novel component compared to other LJ mechanisms. For this reason, this section focuses only on the study of the effect of the number of frames in the LJ structure through FE simulations.

FE simulations were carried out on an LJ structure with a trapezoidal pin at the free end and with 13, 6, 3, 1, and 0 frames distributed along the LJ structure. The overall dimensions of the beam, the number of sheets, the materials, the load conditions, and the settings of the FE simulations for all trapezoidal pins are equal to the LJ structures described in Section 2 and Section 4, and only the values of the COF between the layers and the Young’s Modulus of ABS have changed to 0.6 and 2.2 GPa, respectively. The distribution of the frames can be seen in Figure 20.

For each number of frames, the simulations were run at 10 kPa and 0 kPa of pressure in the pneumatic cylinder to calculate the maximum and minimum stiffness, respectively. The results are illustrated in Figure 21. It can be seen that the main effect of the number of frames is the displacement of the stiffness range of the LJ. As the number of frames increases; the maximum, the minimum, and the average values of stiffness rises. For example, the comparison of the stiffness range between 0 frames and 13 frames, demonstrates that there are increments of 33.6% in the minimum stiffness and 39.3% in the maximum stiffness.

Figure 22 shows the behavior of the stiffness ratio as a function of the number of frames. The maximum stiffness ratio occurs when there are 3 frames in the LJ structure and represents an increase of about 11.3% in relation to the minimum stiffness ratio that occurs when there are no frames. Figure 21 and Figure 22 indicate that raising the number of frames beyond 3 frames increases the average stiffness of the LJ structure but decreases its stiffness ratio.

The frames avoid buckling of the sheets when the LJ structure is bent by transverse forces, as can be seen in Figure 13. When there are no frames, the layers buckle as transverse load is applied and deflects the LJ structure. Because the sheets do not have any constraint and the trapezoidal pin opposes the relative slip between the layers at the free end, the sheets buckle independently and contact between them is lost (Figure 23). When there are frames in the LJ structure, the sheets are restricted from separating, leading to a significant diminution of the buckling of the layers, as can be seen in Figure 13.

The manipulation of the stiffness range of the LJ structure by modifying the number of frames has two advantages. First, frames are passive elements that do not need any actuator to be effective. Second, it is a very convenient method that does not need the total disassembly of the LJ structure. In the context of the use of the LJ in a cobot, this method will enable variation of the stiffness range without interrupting the operation of the cobot for lengthy periods of time. Furthermore, the utilization of frames is also possible in LJ structures with other lock/unlock mechanisms, such as shape-memory alloy wires [17] and clamps [14,15]. Other methods to variate the stiffness of the LJ, such as changing the number of layers, require the complete disassembly of the LJ structure, which could cause long interruptions in the operation of the cobot.

5.3. Bending of the LJ Structure When Transverse Force Points Upwards

The bending experiment and the FE simulations presented in Section 3, Section 4 and Section 5.2 are characterized by a transverse force that points downward. This section explores the behavior of the LJ structure when the transverse force is applied upward. A FE simulation was used to carry out this study. It must be noted that the terms “upward” and “downward” are relative to the page and it does not mean that the simulations were carried out in the vertical plane. Therefore, gravity force is not included in these simulations.

The LJ structure, the boundary conditions and the FE simulation settings are the same as the simulation of the LJ structure with three frames presented in Section 5.2. The only difference is that the deflection applied at the free end points upward. The result of the simulations was the force associated with the applied deflection.

Figure 24 illustrates the resulting shape of the LJ structure when the deflection at the free end was 40 mm. The LJ structure has an “S” shape that is very similar to the shape of the LJ structure when the deflection is applied downward.

Figure 25 illustrates the details of the contact between the trapezoidal pin and the sheets of the LJ structure. It should be noted that the contact and no-contact areas flip sides in comparison to the LJ structure when it is bent downward (see Figure 14 and Figure 31). In this case, the contact between the top layers and the pin occurs at the back of the pin while the front part of the pin loses contact with the layers. This distribution of contact is more evident in Figure 26, which illustrates a LJ structure that is also deflected upwards and has only three sheets and a 45° trapezoidal pin.

The results of the FE simulation of the LJ structure when it is bent upward are illustrated in Figure 27. The same figure also shows the result of the LJ structure that was presented in Section 5.2 and illustrated in Figure 20b, which corresponds to the transverse force applied downward. The results were linearized by the method of the least squares to calculate the stiffness. It can be observed that the stiffness of the LJ structure when it is bent upward (0.1475 N/mm) is slightly higher than the stiffness when the LJ structure is bent downward (0.1407 N/mm). This variation can be explained by the difference in the location of contact between the trapezoidal pin and the layers along the LJ structure. As was explained above, the contact occurs behind the pin when the LJ structure is bent upward, while the contact occurs in front of the pin when it is bent downward. A similar effect was present in the DLJ, where the effect of the location of the flat clamp along the LJ structure was studied, showing that the stiffness increases when the clamp is closer to the middle of the beam and decreases as the clamp is located closer to the ends [15].

5.4. Large Deflections

The maximum deflection at the free end that was enforced in the experiments and FE simulations was 10% of the length of the LJ structure. In the case of a collision between the VSL and human operator, it is expected that the maximum acceleration and impact forces occur during the first part of the impact when the deflection is less than 10% of the length of the link. However, VSL may present larger deflections during an impact with a human being, particularly at high collision velocities. Therefore, a simulation with a maximum deflection of 100 mm is presented with the purpose of investigating the behavior of the stiffness for higher deflections.

Figure 28 illustrates the LJ structure under 100 mm deflection pointing downward at the free end. The LJ structure has the dimensions of the samples presented in Section 2 and the load conditions and simulation settings are the same as those described in Section 4 with the exception of the number of frames that is 13, the pressure in the pneumatic cylinder that is 500 kPa, the COF between the sheets that is 0.6, and the COF between the layers and the trapezoidal pin that is 0.6 as well.

The results of the simulation are illustrated in Figure 29. It can be observed that the slope of the curves decreases as the deflection grows, which means that the stiffness varies significantly during the deformation of the LJ structure. The graph can be divided into three regions with distinctive stiffness values. The stiffness in Region I is 0.1578 N/mm while the stiffness in Region III is 0.0854N/mm. The results show that the reduction of the stiffness is significant since the stiffness in Region III is almost half of the stiffness in Region I.

These simulations also show some details that are difficult to note in the previous simulations. One of them is the fact that the layers push the pin upwards as the LJ structure bends. Figure 30a shows the pin sticks out from the bottom layer when the LJ is straight due to no transverse load. Figure 30b shows the LJ structure when the deflection is 100 mm in the free end due to the action of the transverse load, and it can be seen that the pin does not stick out from the bottom layer anymore. According to Figure 30, the pin moves about 0.8 mm upward. It is important to note that the pressure in the pneumatic cylinder is 500 kPa in both cases.

Another fact that is evident in this simulation is how the contact between the pin and the layers concentrates in the top layers as the deflection increases. Figure 31 shows that only the three top layers are in contact with the pin when the deflection is 100 mm, while Figure 14 shows that about 6 layers are in contact with the pin when the deflection is 40 mm. This behaviour may also explain the reduction in beam stiffness as deflection increases, as the contact area between the pin and the LJ structure reduces significantly. Another detail that is evident in Figure 31 is that the bottom layer buckles despite having 13 frames distributed along the beam. Therefore, the buckling in the LJ with trapezoidal pin cannot be completely avoided despite using a large number of frames.

6. Conclusions and Future Work

In this article, we presented a novel mechanism to lock/unlock the sheets of a LJ structure with the purpose of modifying its stiffness and making it useful for the construction of VSL robots. The mechanism consists of a pneumatic actuator that drives a trapezoidal pin to interfere mechanically with the layers and, in turn, modulating the stiffness of the LJ structure. Another LJ with a flat clamp mechanism is presented for the purpose of comparing the mechanical behavior of both mechanisms.

The trapezoidal pin mechanism has some significant advantages over the vacuum pressure mechanism, as the proposed mechanism does not require an airtight chamber. Therefore, it is not vulnerable to sealing damage due to contact with rough edges. In addition, the proposed mechanism can reach higher values of stiffness since it applies a positive pressure that could reach up to 7.9 atm (800 kPa), which is the standard pressure of industrial pneumatic installations, while the vacuum pressure mechanism is limited to a maximum pressure of 1 atm (101.3 kPa). Another advantage of the trapezoidal mechanism is that the transition from rigid state to flexible state or vise-versa does not require additional manipulations while the vacuum pressure mechanism may require to be disconnected from the vacuum regulator and flexed multiple times to return to ambient pressure. Furthermore, the trapezoidal pin mechanism has the potential to change the stiffness faster than the vacuum pressure mechanism, making the proposed mechanism adequate for mitigating impacts between robot arms and human beings.

Force-deflection tests were conducted to characterize variations of bending stiffness in the LJ structures due to changes in air pressure in the pneumatic cylinder. The results demonstrated that the maximum stiffness ratio of the trapezoidal pin is about 15% larger than the maximum stiffness ratio of the flat clamp. In addition, the experiments showed that the stick-slip phenomenon occurs in the flat clamp mechanism, but it is not present in the trapezoidal pin mechanism.

Both lock/unlock mechanisms were simulated by finite element (FE) methods. The results of the FE simulations match well the test results in the case of the trapezoidal pin mechanism. In the case of the flat clamp mechanism, the FE simulations differ considerably from the experiments. This difference may happen because the FE simulations do not replicate the stick-slip phenomenon that happens in the tests of the LJ structure with flat clamp.

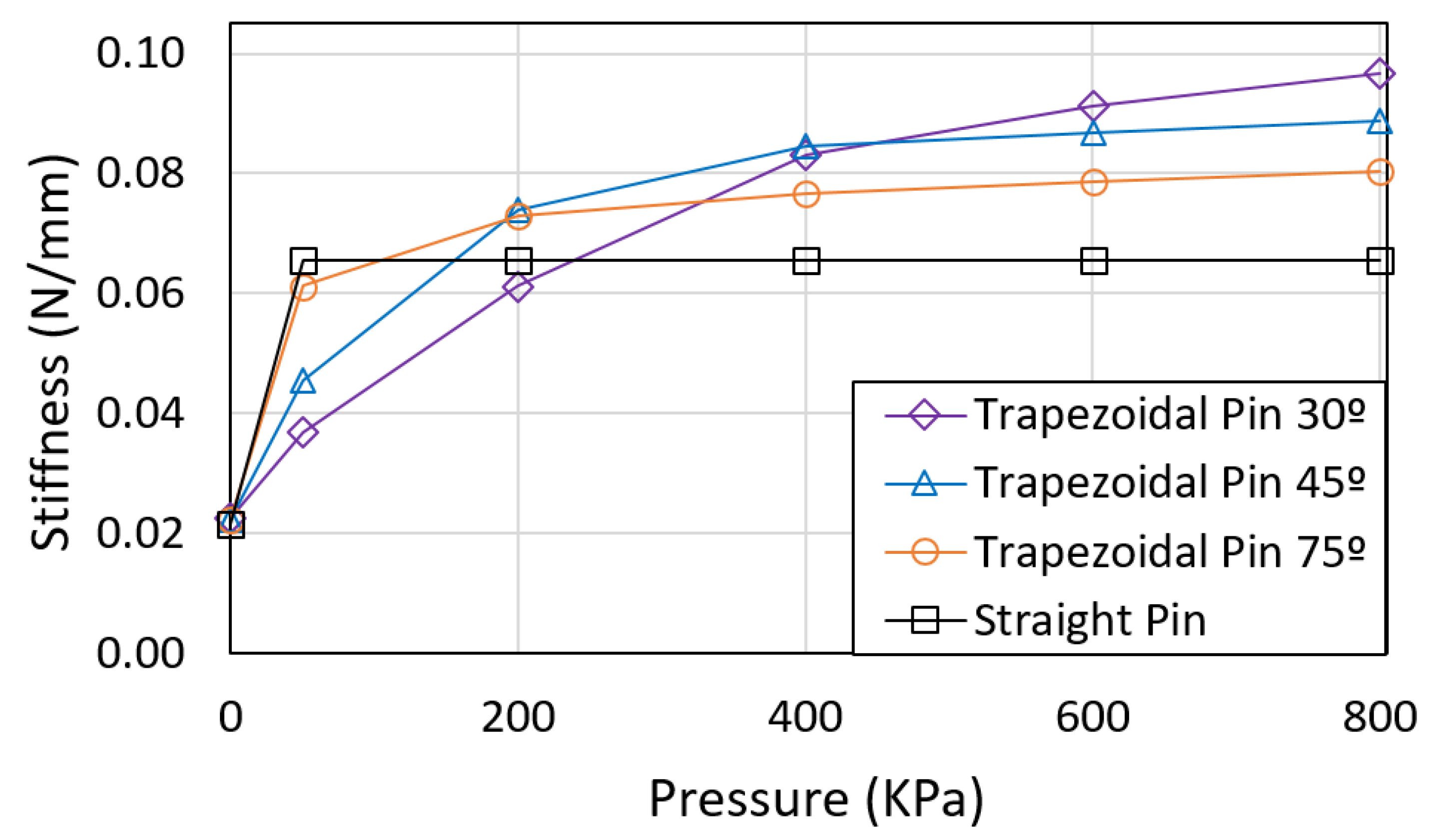
Computational case studies were carried out using FE simulations to study the effect of the angle of the trapezoidal pin in the LJ. The simulations show that the 30° trapezoidal pin has the highest stiffness for pressures greater than 500 kPa, while the 75° and 90° trapezoidal pins have the highest stiffness for pressures lower than 200 kPa.

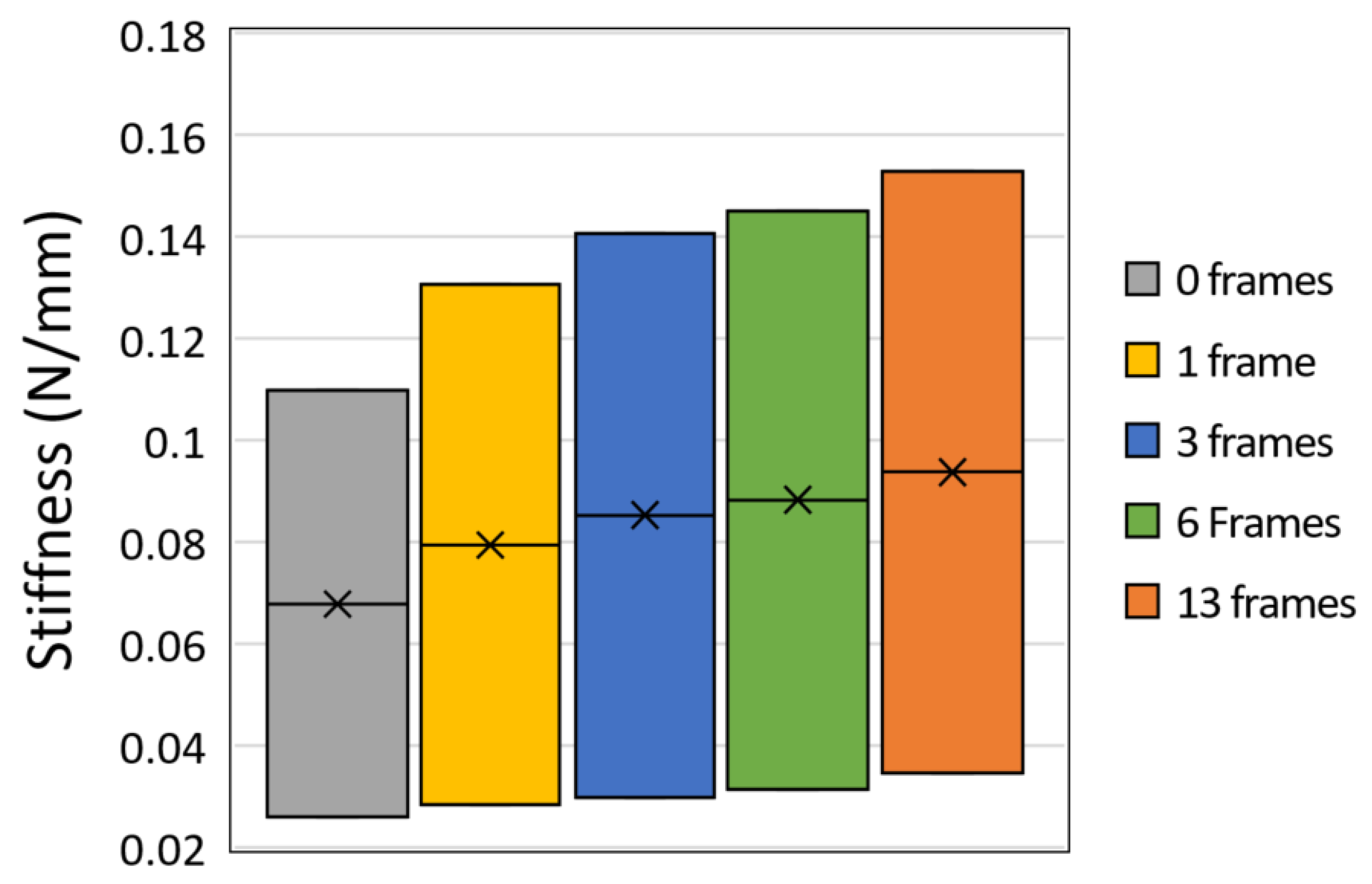
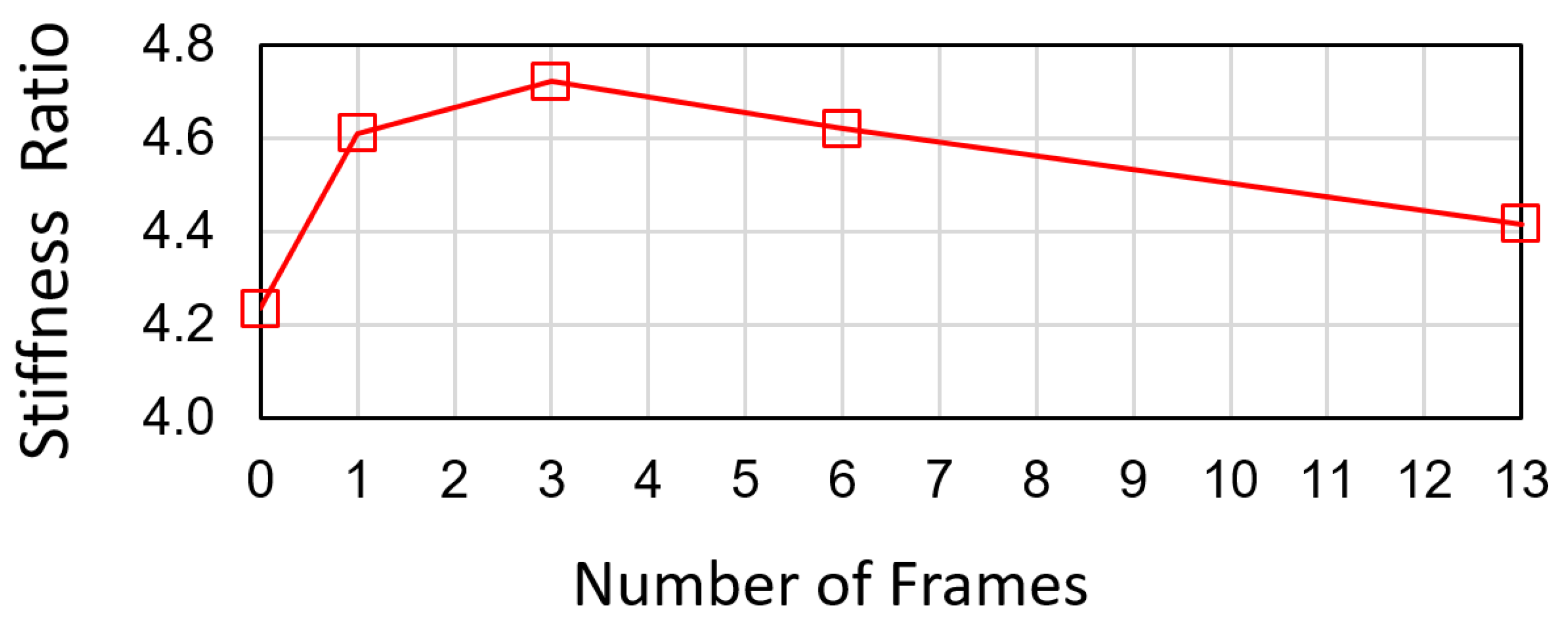
Another computational study was carried out to investigate the effect of the number of frames placed along the LJ with trapezoidal pin. FE simulations show that the increment of the number of frames results in an increased average of the stiffness range. Furthermore, the stiffness ratio reaches a maximum value when there are three frames in the LJ structure, showing an increase of about 11.5% in relation to the minimum stiffness ratio. Overall, altering the number of frames is a practical and novel method of modulating the stiffness range without including more actuators in the LJ structure.

The behavior of the LJ structure with a trapezoidal pin when it is bent upward was also studied through FE simulations. The simulations demonstrate that the contact areas between the trapezoidal pin and the layers flip sides in comparison to the LJ structure when it is bent downward. The results of the simulation also show that the stiffness of the LJ structure when it is bent upward is slightly higher than the stiffness of the LJS when it is bent downward. This difference in the results occurs because of the variation in the location of the contact zones between the pin and the sheets of the LJS.

The behavior of the proposed mechanism when deflections are large was also analyzed through FE analysis. The simulations demonstrate that the stiffness of the LJ structure diminishes when the deflection increases beyond 10% of the length of the LJ structure. In addition, it is evident that at large deflections, the layers of the LJ structure push the pin upwards and the pin keeps contact only in the first top layers.

Future work should focus on the formulation of new designs of VSLs that are based on LJ structures activated by trapezoidal pin mechanisms and the investigation of impact between those VSLs and human beings to evaluate the potential reduction in injury severity in human operators. The design of VSLs that incorporate LJ structures has some challenges that have not been addressed in the literature such as ensuring that the VSL properly supports all load conditions (axial force, bending, and torsion) and reducing the volume of the VSL. Furthermore, the proposed mechanism should be evaluated in terms of performance to carry out the tasks of typical cobots in order to determine how possible it is to apply it in such applications.

Reducing the volume of the actuators and increasing the lock/unlock force is desirable if this type of mechanism is implemented in VSL robots. The combination of trapezoidal pin and pneumatic actuator could be improved in order to achieve this objective. Pneumatic cylinders are easy to couple with the trapezoidal pin but they become bulky if more force is required. Other types of pneumatic actuators, such as air bellow actuators, can provide larger forces while they are smaller than pneumatic cylinders. In addition, other types of actuators could be explored to drive the trapezoidal. For instance, piezoelectric actuators could be used to drive the trapezoidal pin and achieve high speeds of stiffening and destiffening. In the case of DLJ, piezoelectric actuators are also being considered to drive the flat clamp mechanism [15]. Part of the future work proposed in this section has been carried out and presented in a subsequent study [35].