Master Cylinder Pressure Control Based on Piecewise-SMC in Electro-Hydraulic Brake System
Abstract
1. Introduction
- (1)
- A novel position–velocity–pressure (P–V–P) relationship is formulated to provide a more accurate dynamic model of the system.
- (2)
- An Extended Sliding Mode Observer (ESMO) is designed to robustly estimate pressure against nonlinearities, disturbances, and uncertainties.
- (3)
- A Piecewise-SMC is developed, which leverages a piecewise linear model to significantly mitigate chattering and enhance control performance.
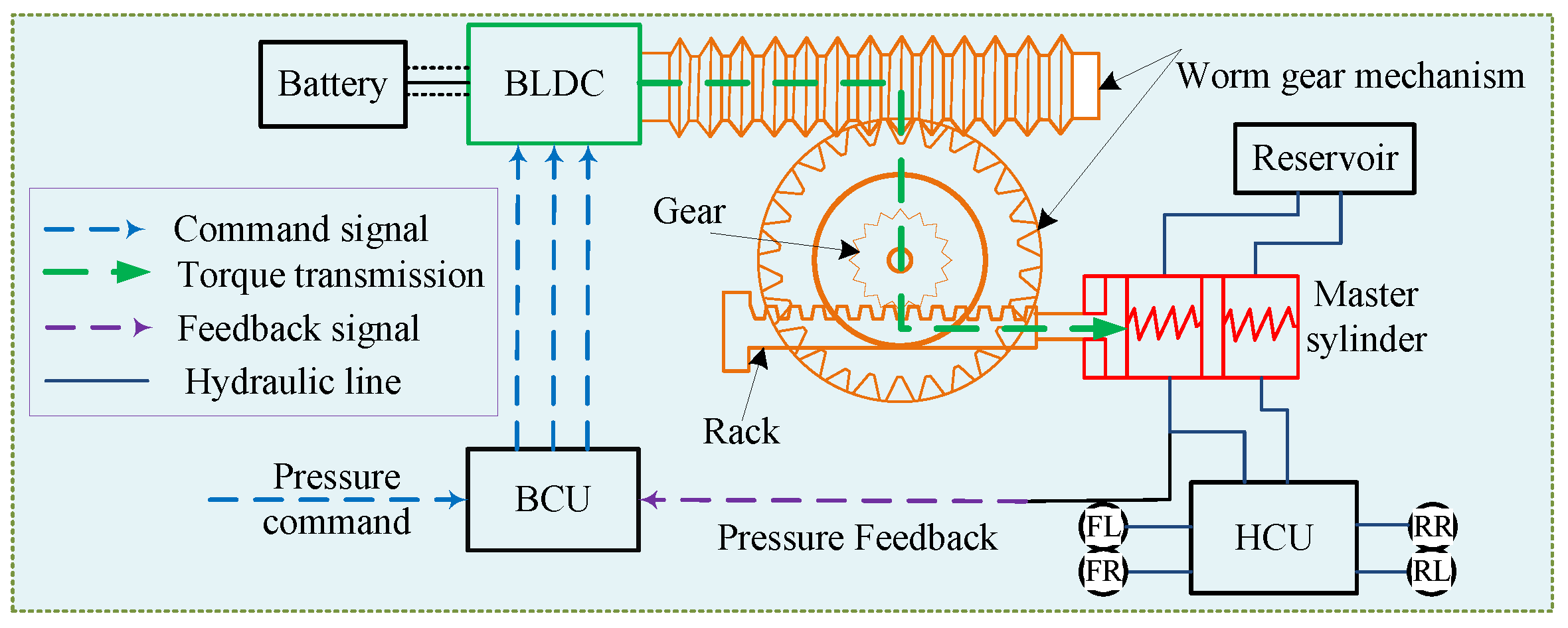
2. Analysis and Modeling of the EHB System
2.1. Novel P–X–V Pressure Model
2.2. Model Validation
3. Master Cylinder Pressure Estimation of EHB Based on an Extended Sliding Mode Observer
4. Design of Piecewise-SMC
5. Results and Analysis
5.1. Simulation Results of Master Cylinder Pressure Estimation
5.2. Simulation Results of Pressure Control Strategy
5.3. Results of Experimental Verification
6. Conclusions
- (1)
- A dynamic model incorporating piston velocity is established, enhancing pressure representation beyond traditional displacement-only models and improving dynamic response.
- (2)
- An ESMO is designed based on this model to estimate pressure without sensors, effectively handling nonlinearities and uncertainties with high accuracy and robustness under realistic braking.
- (3)
- Building on the model and observer, a Piecewise-SMC controller is proposed. Experiments under step braking scenarios show the Piecewise-SMC reduces RMSE by up to 9.6%, response time by 31.8%, and overshoot by 35.8% compared to conventional SMC, demonstrating notable gains in tracking accuracy and dynamic performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Jin, L.; Zhang, Y.; Li, J. Research on Estimation and Precise Control of Wheel Cylinder Pressure for Integrated Electronic Hydraulic Brake System. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; IEEE: New York, NY, USA, 2021; pp. 4590–4594. [Google Scholar]
- Wei, L.; Liu, Y.; Zhu, Z.; Wang, X.; Li, L. Parameters self-learning of solenoid valve for wheel pressure estimation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 3109–3120. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, H.; Li, H.; Li, Y.; Ding, Z.; Chen, J. Development of crawler steering gearbox for combine harvester straight forward and steering in situ. Int. J. Agric. Biol. Eng. 2020, 13, 120–126. [Google Scholar] [CrossRef]
- Chen, J.; Zong, H.; Song, H.; Wu, Y.; Liang, H.; Su, Z. Closed-loop plasma flow control of a turbulent cylinder wake flow using machine learning at Reynolds number of 28,000. Phys. Fluids 2024, 36, 015123. [Google Scholar] [CrossRef]
- Wei, L.; Liu, Y.; Wang, X.; Li, L. Estimation of Wheel Pressure for Hydraulic Braking System by Interacting Multiple Model Filter. IEEE Trans. Veh. Technol. 2024, 73, 463–472. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Wang, R.; Xu, X.; Shen, Y.; Liu, Y. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar]
- Chen, Y.; Chen, L.; Huang, C.; Lu, Y.; Wang, C. A dynamic tire model based on HPSO-SVM. Int. J. Agric. Biol. Eng. 2019, 12, 36–41. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Xiong, L.; Han, W. Hydraulic Control of Integrated Electronic Hydraulic Brake System Based on Lugre Friction Model; Technical Report; SAE Technical Paper; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Zheng, J.; Nie, S.; Jing, H.; He, Y.; Li, M.; Ma, Y.; Ding, Z. Potential and electro-mechanical coupling analysis of a novel HTS maglev system employing double-sided homopolar linear synchronous motor. IEEE Trans. Intell. Transp. Syst. 2024, 25, 13573–13583. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, Q.; Wei, Y.; He, Y.; He, Z.; He, L. Electro-hydraulic braking dynamics for pressure demand control of brake-by-wire system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 238, 735–748. [Google Scholar] [CrossRef]
- Xiong, L.; Han, W.; Yu, Z. Adaptive sliding mode pressure control for an electro-hydraulic brake system via desired-state and integral-antiwindup compensation. Mechatronics 2020, 68, 102359. [Google Scholar] [CrossRef]
- Shi, B.; Xiong, L.; Yu, Z. Master Cylinder Pressure Estimation of the Electro-Hydraulic Brake System Based on Modeling and Fusion of the Friction Character and the Pressure-Position Character. IEEE Trans. Veh. Technol. 2022, 72, 1748–1762. [Google Scholar] [CrossRef]
- Shi, Q.; He, L. A model predictive control approach for electro-hydraulic braking by wire. IEEE Trans. Ind. Inform. 2022, 19, 1380–1388. [Google Scholar] [CrossRef]
- Todeschini, F.; Corno, M.; Panzani, G.; Fiorenti, S.; Savaresi, S.M. Adaptive cascade control of a brake-by-wire actuator for sport motorcycles. IEEE/ASME Trans. Mechatron. 2014, 20, 1310–1319. [Google Scholar] [CrossRef]
- Wang, X.; Wu, X.; Cheng, S.; Shi, J.; Ping, X.; Yue, W. Design and experiment of control architecture and adaptive dual-loop controller for brake-by-wire system with an electric booster. IEEE Trans. Transp. Electrif. 2020, 6, 1236–1252. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Liu, X.; Bai, X.; Liu, J. Sensorless Control Based on Discrete Fractional-Order Terminal Sliding Mode Observer for High-Speed PMSM with LCL Filter. IEEE Trans. Power Electron. 2025, 40, 1654–1668. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, X.; Zhu, Z.; Zhai, Z.; Liu, Y. Dual-microphone active noise cancellation paved with Doppler assimilation for TADS. Mech. Syst. Signal Process. 2023, 184, 109727. [Google Scholar] [CrossRef]
- Shi, B.; Xiong, L.; Yu, Z. Pressure estimation of the electro-hydraulic brake system based on signal fusion. Actuators 2021, 10, 240. [Google Scholar] [CrossRef]
- Wei, H.; Xiong, L.; Yu, Z. Braking Pressure Tracking Control of a Pressure Sensor Unequipped Electro-Hydraulic Booster Based on a Nonlinear Observer; Technical Report; SAE Technical Paper; SAE: Warrendale, PA, USA, 2018. [Google Scholar]
- Chen, G.; Wu, W.; Yang, C.; Hu, H.; Zhang, J.; Shi, J.; Wu, C.; Ma, Y. Practical Finite-Time Observer-Based Adaptive Backstepping Super-Twisting Sliding Mode Control for Deep-Sea Hydraulic Manipulator. IEEE Trans. Ind. Electron. 2025, 72, 9569–9579. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Strano, S.; Tordela, C. Development of sliding mode observers for estimating sideslip angle and lateral forces in road vehicles. Trans. Inst. Meas. Control 2025, 01423312251326643. [Google Scholar] [CrossRef]
- Wang, K.; Liu, X.; Wang, G. Self-scheduled direct thrust control for gas turbine engine based on EME approach with bounded parameter variation. Chin. J. Aeronaut. 2025, 38, 103392. [Google Scholar] [CrossRef]
- Ding, S.; Liu, C.; Fan, Z.; Hang, J. Lumped Parameter Adaptation-Based Automatic MTPA Control for IPMSM Drives by Using Stator Current Impulse Response. IEEE Trans. Energy Convers. 2025, 40, 2108–2118. [Google Scholar] [CrossRef]
- Zhang, S.; He, Y.; Gu, Y.; He, Y.; Wang, H.; Wang, H.; Yang, R.; Chady, T.; Zhou, B. UAV based defect detection and fault diagnosis for static and rotating wind turbine blade: A review. Nondestruct. Test. Eval. 2025, 40, 1691–1729. [Google Scholar] [CrossRef]
- Han, W.; Xiong, L.; Yu, Z. Interconnected pressure estimation and double closed-loop cascade control for an integrated electrohydraulic brake system. IEEE/ASME Trans. Mechatron. 2020, 25, 2460–2471. [Google Scholar] [CrossRef]
- Han, W.; Xiong, L.; Yu, Z.; Zhuo, G.; Leng, B.; Xu, S. Integrated pressure estimation and control for electro-hydraulic brake systems of electric vehicles considering actuator characteristics and vehicle longitudinal dynamics. IEEE/ASME Trans. Mechatron. 2022, 28, 197–209. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, Y.; Chen, G.; Yuan, L.; Zhou, J.; Zhang, J. Adaptative Pressure Estimation and Control Architecture for Integrated Electro-Hydraulic Brake System. Chin. J. Mech. Eng. 2025, 38, 28. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, C.; Liu, Z.; Liu, Y.; Wang, X.; Shi, B.; Li, L. An Offset-Free Explicit Model Predictive Pressure Controller for Integrated Braking System. IEEE Trans. Transp. Electrif. 2024, 10, 2355–2366. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Ding, L. A Brief Overview of Recent Advances in Distributed Accelerated Secondary Control for Islanded AC Microgrids. IEEE Trans. Ind. Inform. 2025. [Google Scholar] [CrossRef]










| Approach | Representative Works | Key Strengths | Core Limitations | Contributions of This Study |
|---|---|---|---|---|
| Advanced Sensor-Based Control | Jiang et al. [11], Xiong et al. [12], Chen et al. [13] | Effectively addresses nonlinearities, such as friction and saturation, enhancing dynamic response and tracking accuracy. | Fundamentally relies on physical pressure sensors, making the system susceptible to noise and drift, which limits long-term reliability and adaptability. | Eliminates the dependency on physical sensors from the ground up through a sensorless estimation-and-control framework. |
| MC Pressure Estimation Models | Shi et al. [19], Wei et al. [20] | Established initial master cylinder pressure estimation models, verifying the feasibility of a sensorless approach. | 1. Limited to the estimation level, lacking integration with a closed-loop control system. 2. Insufficient robustness against system uncertainties and disturbances. | Achieves high-fidelity estimation for closed-loop control by designing a robust ESMO observer grounded in a more accurate P–V–P physical model. |
| Integrated Estimation and Control Strategies | Han’s group [26,27], Zhao et al. [28] | Achieved estimation–control integration, validating the feasibility of an integrated framework and introducing modern control theories. | Robust adaptation under severe parameter uncertainties or actuator degradation remains an open challenge. | Proposes a Piecewise Sliding Mode Controller that embeds a piecewise model into the control law, enhancing robustness and adaptability while significantly mitigating chattering. |
| Conditions | Indices | Piecewise-SMC | SMC | Piecewise-PID |
|---|---|---|---|---|
| Sinusoidal | RMSE (bar) | 4.63 | 7.69 | 9.06 |
| MAE (bar) | 9.51 | 14.23 | 19.23 | |
| Step | RMSE (bar) | 6.45 | 7.13 | 7.95 |
| Average Overshoot (%) | 4.37% | 6.81% | 10.01% | |
| Average Response Time (s) | 0.15 | 0.22 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, C.; Xu, X.; Deng, H.; He, C.; Chen, L.; Wang, Y. Master Cylinder Pressure Control Based on Piecewise-SMC in Electro-Hydraulic Brake System. Actuators 2025, 14, 416. https://doi.org/10.3390/act14090416
Liang C, Xu X, Deng H, He C, Chen L, Wang Y. Master Cylinder Pressure Control Based on Piecewise-SMC in Electro-Hydraulic Brake System. Actuators. 2025; 14(9):416. https://doi.org/10.3390/act14090416
Chicago/Turabian StyleLiang, Cong, Xing Xu, Hui Deng, Chuanlin He, Long Chen, and Yan Wang. 2025. "Master Cylinder Pressure Control Based on Piecewise-SMC in Electro-Hydraulic Brake System" Actuators 14, no. 9: 416. https://doi.org/10.3390/act14090416
APA StyleLiang, C., Xu, X., Deng, H., He, C., Chen, L., & Wang, Y. (2025). Master Cylinder Pressure Control Based on Piecewise-SMC in Electro-Hydraulic Brake System. Actuators, 14(9), 416. https://doi.org/10.3390/act14090416







