Event-Triggered Fixed-Time Consensus Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Dead-Zone Input

Abstract

This study explores the issue of fixed-time dynamic event-triggered consensus control for uncertain nonlinear multi-agent systems (MASs) within directed graph frameworks. In practical applications, the system encounters multiple constraints such as unknown time-varying parameters, unknown external disturbances, and input dead zones, which may increase the communication burden of the system. Therefore, achieving fixed-time consensus tracking control under the aforementioned conditions is challenging. To address these issues, an adaptive fixed-time consensus tracking control method based on boundary estimation and fuzzy logic systems (FLSs) is proposed to achieve online compensation for the input dead zone. Additionally, to optimize the utilization of communication resources, a periodic adaptive event-triggered control (PAETC) is designed. The mechanism dynamically adjusts the frequency at which the trigger is updated in real time, reducing communication resource usage by responding to changes in the control signal. Finally, the efficacy of the proposed approach is confirmed via theoretical evaluation and simulation.

1. Introduction

Consensus control is a crucial cooperative control strategy in MASs, where multiple agents achieve a unified decision or state through local communication and coordination. Within the topological network framework constructed using graph theory, consensus control problems are classified into leaderless consensus [1] and leader–follower consensus [2]. The latter introduces a leader to provide a clear objective, enabling followers to adjust their behaviors flexibly and thus achieve tracking goals more efficiently. As consensus control theory progresses, its application to the MAS control domain is becoming increasingly prevalent, yielding substantial outcomes [3,4,5,6]. For instance, Chen et al. introduced a consensus control scheme for MASs, allowing follower agents to track the trajectory of the leader [3]. Yao et al. explored the application of consensus control in nonlinear uncertain MASs, designing an adaptive controller by using a backstepping technique [4].

Furthermore, multi-agent systems such as unmanned aerial vehicles (UAVs) and mobile robots frequently encounter various constraints in actual engineering systems [7,8]. These constraints include unknown nonlinear characteristics and input dead zones, both of which can adversely affect system performance. Addressing these constraints may significantly increase the communication burden [9]. It is important to note that each agent has limited communication resources. Given that event-triggered control schemes can conserve resources and reduce communication burdens, this method has been extensively applied in MASs [10,11,12,13]. Although traditional event-triggered mechanisms show great potential in resource-constrained applications, they have limitations in handling complex systems. These mechanisms rely on fixed thresholds or conditions to trigger events, making it challenging to adapt to the dynamic changes in system states. To address this issue, researchers have proposed dynamic event-triggered mechanisms. By introducing internal dynamic variables, these mechanisms can dynamically adjust trigger conditions based on changes in system states [14,15,16,17]. Ju et al. designed a dynamic event-triggered protocol (DETP) for multi-agent consensus tracking control, further improving the efficiency with which communication resources are utilized. [18]. Liu et al. proposed a dynamic event-triggered scheme to address multi-agent consensus control problems, with event-triggering conditions that avoid Zeno behavior [19]. In these studies, the dynamic event-triggered control mechanism not only ensures system stability but also significantly enhances the efficiency of communication resource savings. However, existing event-triggered mechanisms require frequent monitoring of input signals, which is often difficult to achieve in practical applications.

On the other hand, Lyapunov stability theory provides a solid foundation for the stability analysis of control systems [20]. It should be noted that the uncertainty of convergence time can be a limitation in practical applications that require rapid response. Finite-time control, as a convergence control strategy, has garnered attention for its faster convergence speed, stronger robustness, and resistance to disturbances [21,22]. For example, Qin et al. presented a finite-time consensus tracking method for higher-order nonlinear MASs, effectively compensating for the nonlinear effects caused by input dead zones [23]. Wang et al. combined fuzzy adaptive control technology with finite-time control theory and applied it to higher-order nonlinear MASs [24]. Although finite-time stability offers a rapid and certain convergence mechanism, its inherent limitation is that the convergence time fails to be independent of the initial states [25]. To overcome this issue, fixed-time control has emerged as a special form of finite-time control, gaining wide attention due to its unique advantages [26,27,28]. Xu et al. addressed the fixed-time consensus tracking control problem for first-order nonlinear MASs [29]. Furthermore, the research scope of fixed-time consensus control protocols has expanded from first-order systems to second-order systems [30] and higher-order systems [31,32]. These control protocols enable rapid convergence while eliminating the dependency of convergence time on the initial states, ensuring that systems converge within a predetermined time, thereby enhancing the robustness of the system. Nevertheless, in practical systems, constraints such as time-varying control gains, strong external disturbances, and input dead zones can adversely affect control performance and lead to instability.

Drawing inspiration from the previously mentioned literature, this study examines the fixed-time event-triggered consensus control issue for uncertain high-order nonlinear multi-agent systems featuring input dead zones. The major innovations are outlined as follows:

• For MASs under constraints including time-varying control gains, external disturbances, and input dead zones, the demand for communication resources increases significantly. To address these challenges, a periodic adaptive event-triggered control (PAETC) is proposed, integrating boundary estimation techniques and fuzzy logic systems. This approach does not require frequent monitoring of input signals and enables dynamic compensation for input dead zones while minimizing communication resource usage.
• A fixed-time periodic adaptive event-triggered consensus tracking control method is investigated by the backstepping technique. In contrast to the aforementioned FTC approaches, where the time required for convergence relies on the system’s initial conditions, this control method ensures that the system converges to the specified trajectory within a fixed time, despite unknown external disturbances, time-varying control gains, and input dead zones. Moreover, the upper bound of convergence duration remains fixed and is not influenced by the system’s initial conditions.

2. Preliminaries

2.1. Graph Theory

In a directed communication topology for a multi-agent system, the matrix $\mathcal{A}=\left[a_{i,j}\right]\in {\mathbb{R}}^{n\times n}\left(i,j\in \left\{\left.1,2,\dots ,n\right\}\right.\right)$ represents the communication weights between agents, where each entry indicates the weight of communication between agent i and agent j. The set $\mathcal{C}=0,1,2,\dots ,n$ includes both leaders and followers, while $\mathcal{H}\subseteq \mathcal{C}\times \mathcal{C}$ defines the set of edges within the topology. If $\left(j,i\right)\in \mathcal{H}$, with $j\ne i$ and $a_{i,j}>0$, agent i receives state information from agent j. Conversely, if $a_{i,j}=0$, it indicates the absence of information exchange between the agents. The vector $\mathcal{V}=\left\{h_1,h_2,\dots ,h_n\right\}\in {\mathbb{R}}^n$ serves as a weighted adjacency vector, reflecting the strength of the connections between leaders and followers. The in-degree matrix is denoted as $\mathcal{B}=diag\{d_1,d_2,\dots ,d_n\}\in {\mathbb{R}}^{n\times n}$, where each $d_i={\sum }_{j=1}^n{a}_{i,j}$ represents the sum of the communication weights for agent i. The Laplacian matrix can be then defined as $L=\mathcal{B}-\mathcal{A}$.

2.2. Preliminaries

Lemma 1 

([33]). Consider the system $\dot{x}=f\left(x\right)$, where $x\in {\mathbb{R}}^n$. Given the existence of a continuous positive-definite function $V\left(x\right)$, the following formulation is satisfied:

$$\begin{array}{c}\dot{V}\left(x\right)\le -\Phi V^{q1}\left(x\right)-\Psi V^{q2}\left(x\right)+\Gamma \end{array}$$

(1)

where $\Phi >0$, $\Psi >0$, $0<q_1<1$, $q_2>1$, and $\Gamma >0$ are constants; it can be obtained that the system $\dot{x}=f\left(x\right)$ exhibits practical fixed-time stability. The compact set of the solution is denoted by Θ, and the predefined convergence time by $T_m$:

$$\Theta =\left\{x|V\left(x\right)\le min\left\{{\left({\displaystyle \frac{\Gamma }{\left(1-\lambda \right)\Psi }}\right)}^{\frac{1}{q_1}},{\left({\displaystyle \frac{\Gamma }{\left(1-\lambda \right)\Phi }}\right)}^{\frac{1}{q_2}}\right\}\right\}$$

(2)

$$\begin{array}{c}{T}_m\le {\displaystyle \frac{1}{\Psi \lambda \left(1-q_1\right)}}+{\displaystyle \frac{1}{\Phi \lambda \left(q_2-1\right)}}\end{array}$$

(3)

where $0<\lambda <1$.

Lemma 2 

([34]). For $\chi \in$ and $\delta >0$, one has

$$\begin{array}{c}0\le \left|\chi \right|-\chi tan\mathrm{h}\left(\frac{\chi }{\delta }\right)\le 0.2785\delta \end{array}$$

(4)

Lemma 3 

([35]). For ${\chi }_1\in$, ${\chi }_2\in$, ${\delta }_1>0$, ${\delta }_2>0$, and $k>0$, one has

$${\left|{\chi }_1\right|}^{{\delta }_1}{\left|{\chi }_2\right|}^{{\delta }_2}\le {\displaystyle \frac{{\delta }_1}{{\delta }_2+{\delta }_1}}k{\left|{\chi }_1\right|}^{{\delta }_1+{\delta }_2}+{\displaystyle \frac{{\delta }_2}{{\delta }_2+{\delta }_1}}{k}^{-{\displaystyle \frac{{\delta }_1}{{\delta }_2}}}{\left|{\chi }_2\right|}^{{\delta }_1+{\delta }_2}$$

(5)

Lemma 4 

([36]). Given that $k_i>0$ for $i=1,2,\dots ,n$, $0<b_1<1$, and $1<b_2<\infty$, one has

$$\begin{array}{c}{\left({\displaystyle \sum _{i=1}^n}{k}_i\right)}^{b_1}\le \end{array}{\displaystyle \sum _{i=1}^n}{k}_i^{b_1}$$

(6)

$$\begin{array}{c}{\left({\displaystyle \sum _{i=1}^n}{k}_i\right)}^{b_2}\le {\displaystyle \frac{1}{n^{1-b_2}}}\end{array}{\displaystyle \sum _{i=1}^n}{k}_i^{b_2}$$

(7)

Lemma 5 

(Young’s inequality [37]). For $\forall x_1\in \mathbb{R}$ and $\forall x_2\in \mathbb{R}$, one has

$$x_1{x}_2\le {\displaystyle \frac{{\kappa }^b}{b}}{\left|x_1\right|}^b+{\displaystyle \frac{1}{\mu {\kappa }^{\mu }}}{\left|x_2\right|}^{\mu }$$

(8)

where $b>1$, $\mu >1$, $\kappa >0$, and $\mu -1={\displaystyle \frac{1}{b-1}}$.

Lemma 6 

([38]). For ${\chi }_3\in$ and any constant $b_4>0$, one has

$$\begin{array}{c}0\le \left|{\chi }_3\right|<b_4+{\displaystyle \frac{{\chi }_3^2}{\sqrt{{\chi }_3^2+{\kappa }_1^2}}}\end{array}$$

(9)

Lemma 7 

([39]). When $\overline{Y}={\left[y_1,y_2,\dots ,y_N\right]}^T$, $\overline{e}={\left[e_1,e_2,\dots ,e_N\right]}^T$, and ${\overline{Y}}_a={\left[y_a,y_a,...,y_a\right]}^T\in {\mathbb{R}}^N$, the following expression holds:

$$∥\overline{Y}-{\overline{Y}}_a∥\le {\displaystyle \frac{∥\overline{e}∥}{{\beta }_{min}}}$$

(10)

where $\overline{Y}-{\overline{Y}}_a$ represents the tracking error, and β denotes the smallest eigenvalue of $L+\mathcal{V}$.

Assumption 1. 

Each follower is connected to the leader through at least one path. The leader’s output $y_a$ is continuous and bounded, with a computable second-order derivative ${\ddot{y}}_a$.

Assumption 2. 

For the time-varying parameters $M_i\left(t\right)$, which are positive definite and bounded, there exist unknown positive constants ${{\displaystyle \underline{M}}}_i$ and ${\overline{M}}_i$ satisfied by $0<{{\displaystyle \underline{M}}}_i<M_i\left(t\right)<{\overline{M}}_i$. Similarly, for the bounded external disturbances $d_i\left(t\right)$, there exist constants such that $\left|d_i\left(t\right)\right|\le {\overline{d}}_i$.

2.3. Fuzzy Logic Systems

FLSs have the ability to estimate unknown nonlinear continuous functions. The corresponding mathematical expression is as follows [40]:

$$y\left(S\right)={\displaystyle \frac{{\displaystyle \sum _{P=1}^N}{\overline{y}}_l{\displaystyle \prod _{i=1}^n}{K}_{F_i^P}\left(x_i\right)}{{\displaystyle \sum _{P=1}^N}{\displaystyle \prod _{i=1}^n}{K}_{F_i^P}\left(x_i\right)}}$$

(11)

where $x={\left[x_1,x_2,...,x_n\right]}^T$ represents the input variable, ${\overline{y}}_l={max}_{y\in V}{K}_{U^P}\left(y\right)$, and $K_{F_i^P}$ denotes the fuzzy membership functions. The sets $F_i^P$ and $U^P$ correspond to the fuzzy membership functions $K_{F_i^P}\left(x_i\right)$ and $K_{U^P}\left(x_i\right)$, respectively. Additionally, N indicates the total number of fuzzy rules.

FLSs are defined as follows:

$$y\left(x\right)={\theta }^T\xi \left(x\right)$$

(12)

where $\theta ={\left[{\overline{y}}_1,{\overline{y}}_2,...,{\overline{y}}_N\right]}^T={\left[{\theta }_1,{\theta }_2,..,{\theta }_N\right]}^T$ and ${\xi }^T\left(x\right)=\left[{\xi }_1\left(x\right),{\xi }_2\left(x\right),\dots ,{\xi }_N\left(x\right)\right]$.

Lemma 8 

([41]). Given an unknown continuous function $f\left(x\right)$, where $x\in {\mathbb{R}}^n$, processed by a fuzzy logic system, the following result is obtained:

$${\displaystyle \underset{x\in \Omega }{sup}}\left|f\left(x\right)-{\theta }^T\xi \left(x\right)\right|\le \Re$$

(13)

where for any given constant $\Re >0$.

3. Controller Design and Stability Analysis

This section develops a fixed-time consensus tracking control framework with fuzzy periodic adaptive event-triggered mechanisms, synthesized through integration of backstepping methodology, boundary estimation algorithms, and fuzzy inference systems. Subsequent rigorous investigation systematically validates the fixed-time convergence properties and stability guarantees.

3.1. Problem Formulation

The uncertain nonlinear MASs under consideration comprise one leader and several followers. The leader is designated as a, while the followers are labeled as $i(i=1,2,\dots ,n)$. The dynamic characters of the i-th follower can be expressed by the following formulation [42,43,44]:

$$\left\{\begin{array}{c}{\dot{x}}_{i,\zeta }=p_{i,\zeta }\left({\overline{x}}_{i,\zeta }\right)x_{i,\zeta +1}\left(\zeta =1,2,\dots ,n-1\right)\hfill \\ M_{\mathrm{i}}\left(t\right){\dot{x}}_{i,n}=p_{i,n}\left({\overline{x}}_{i,n}\right){\mathcal{D}}_i\left(u_i\right)+{\partial }_i\left({\overline{x}}_{i,n}\right)+w_i\left(t\right)\hfill \\ y_i=x_{i,1}\hfill \end{array}\right.$$

(14)

where $p_{i,\zeta }\left({\overline{x}}_{i,\zeta }\right)$ represents an unknown nonlinear gain function, while $M_i\left(t\right)$ and ${\partial }_i\left({\overline{x}}_{i,n}\right)$ are unknown time-varying functions; $w_i\left(t\right)$ accounts for an unknown external disturbance; ${\mathcal{D}}_i\left(u_i\right)$ represents the input dead-zone nonlinearity; and $x_{i,\zeta }$ represents the condition of the i-th follower, where ${\overline{x}}_{i,\zeta }={\left[x_{i,1},x_{i,2},\dots ,x_{i,\zeta }\right]}^T\in {\mathbb{R}}^{\zeta }\left(\zeta =1,2,\dots ,n\right)$. The control input is denoted by $u_i$, and the system output is given by $y_i(i=1,2,\dots ,n)$.

As illustrated in Figure 1, the input dead-zone model ${\mathcal{D}}_i\left(u_i\right)$ can be mathematically expressed as follows:

$${\mathcal{D}}_i\left(u_i\right)=s_i{u}_i+z_i$$

(15)

where $s_{i,1}>0$ and $s_{i,2}>0$ represent the unknown slopes of the curve on the negative and positive axes, respectively, while $z_{i,1}<0$ and $z_{i,2}>0$ denote the unknown inflection points.

$$s_i=\left\{\begin{array}{c}{s}_{i,1},u_i<{\mathrm{z}}_{i,1}\hfill \\ 0,{\mathrm{z}}_{i,1}\le u_i\le z_{i,2}\hfill \\ s_{i,2},u_i>z_{i,2}\hfill \end{array}\right.$$

(16)

$$z_i=\left\{\begin{array}{c}-s_{i,1}{z}_{i,1},u_i<{\mathrm{z}}_{i,1}\hfill \\ 0,{\mathrm{z}}_{i,1}\le u_i\le z_{i,2}\hfill \\ -s_{i,2}{z}_{i,2},u_i>z_{i,2}\hfill \end{array}\right.$$

(17)

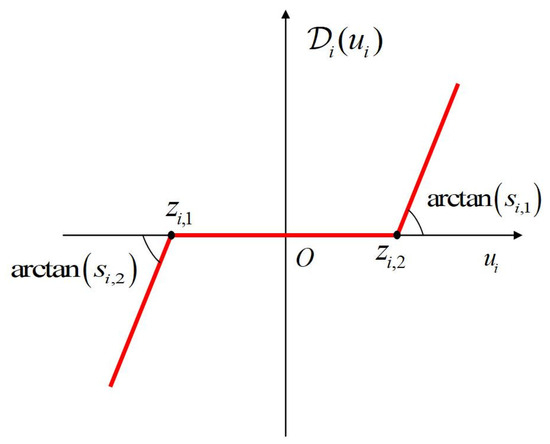
Figure 1. Input dead zone.

3.2. Design of the Adaptive Fixed-Time Consensus Tracking Controller

Firstly, the coordinate transformation for the followers i is defined as follows:

$$\left\{\begin{array}{c}{e}_{i,1}={\mathcal{F}}_i(y_i-y_a)+{\displaystyle \sum _{j\in M_i}}{a}_{ij}(y_i-y_j)\hfill \\ e_{i,\zeta }=x_{i,\zeta }-{\alpha }_{i,\zeta -1}\hfill \end{array}\right.$$

(18)

where $\mathcal{F}i>0$ indicates that the followers acquire messages from the leader; otherwise, $\mathcal{F}i=0$. The variable $y_a$ denotes the leader’s output, $e_{i,1}$ is the synchronization error, $e_{i,\zeta }\left(\zeta =1,2,\dots ,n\right)$ represents the virtual error, and ${\alpha }_{i,\zeta -1}$ is the virtual controller that needs to be specified.

Step 1: The Lyapunov function $V_{i,1}$ is chosen as follows:

$$V_{i,1}={\displaystyle \frac{1}{2}}{e}_{i,1}^2+{\displaystyle \frac{1}{2{\ell }_{i,1}}}{\tilde{\vartheta }}_{i.1}^2$$

(19)

where ${\tilde{\vartheta }}_{i,1}={\vartheta }_{i,1}-{\hat{\vartheta }}_{i,1}$, ${\hat{\vartheta }}_{i,1}$ is the estimated value of ${\vartheta }_{i,1}$.

Differentiating $V_{i,1}$ yields

$$\begin{array}{c}\hfill {\dot{V}}_{i,1}=e_{i,1}[({\mathcal{F}}_i+d_i)p_{i,1}{x}_{i,2}+{\overline{\Omega }}_{i,1}\left({\mathcal{X}}_{i,1}\right)]-{\displaystyle \frac{{\tilde{\vartheta }}_{i,1}}{{\ell }_{i,1}}}{\dot{\hat{\vartheta }}}_{i,1}\end{array}$$

(20)

where ${\overline{\Omega }}_{i,1}\left({\mathcal{X}}_{i,1}\right)=-{\displaystyle \sum _{j\in M_i}}{a}_{i,j}{p}_{j,1}{x}_{j,2}-{\mathcal{F}}_i{\dot{y}}_a$, ${\mathcal{X}}_{i,1}={[x_{i,1},x_{j,1},x_{j,2}]}^T$, then ${\mathcal{F}}_i>0$ also includes.

According to the FLS and Lemma 8, as ${\overline{\Omega }}_{i,1}\left({\mathcal{X}}_{i,1}\right)$ is a continuous function, it can be estimated by the FLS to represent the unknown nonlinear function. It is assumed that

$${\overline{\Omega }}_{i,1}\left({\mathcal{X}}_{i,1}\right)={\theta }_{i,1}^T{\xi }_{i,1}\left({\mathcal{X}}_{i,1}\right)+{\hslash }_{i,1}\left({\mathcal{X}}_{i,1}\right)$$

(21)

where ${\hslash }_{i,1}\left({\mathcal{X}}_{i,1}\right)$ represents the estimation error, and it satisfies ${\hslash }_{i,1}\left({\mathcal{X}}_{i,1}\right)<{\overline{\hslash }}_{i,1}$, with ${\overline{\hslash }}_{i,1}>0$.

Based on Lemma 5, the following results are obtained:

$$\begin{array}{c}\begin{array}{c}\hfill e_{i,1}{\overline{\Omega }}_{i,1}\left({\mathcal{X}}_{i,1}\right)\le {\displaystyle \frac{1}{2{\tau }_{i,1}^2}}{e}_{i,1}^2{\vartheta }_{i,1}{\xi }_{i,1}^T{\xi }_{i,1}+{\displaystyle \frac{e_{i,1}^2}{2}}+{\displaystyle \frac{{\tau }_{i,1}^2}{2}}+{\displaystyle \frac{{\hslash }_{i,1}^2}{2}}\end{array}\hfill \end{array}$$

(22)

where ${\vartheta }_{i,1}={∥{\overline{\theta }}_{i,1}∥}^2$, and ${\tau }_{i,1}>0$.

The virtual control law ${\alpha }_{i,1}$ is formulated as follows:

$${\alpha }_{i,1}=-{\displaystyle \frac{e_{i,1}{\overline{\alpha }}_{i,1}^2}{{{\displaystyle \underline{p}}}_{i,1}({\mathcal{F}}_i+d_i)\sqrt{e_{i,1}^2{\overline{\alpha }}_{i,1}^2+{\nu }_{i,1}^2}}}$$

(23)

$${\overline{\alpha }}_{i,1}=r_{i,1}{e}_{i,1}^3+b_{i,1}{e}_{i,1}^{2q-1}+{\displaystyle \frac{e_{i,1}}{2}}+{\displaystyle \frac{1}{2{\tau }_{i,1}^2}}{e}_{i,1}{\xi }_{i,1}^T{\xi }_{i,1}{\hat{\vartheta }}_{i,1}$$

(24)

where $b_{i,1}>0$ and $r_{i,1}>0$, and ${\nu }_{i,1}>0$, ${{\displaystyle \underline{p}}}_{i,1}$ represents the lower boundary of the gain function $p_{i,1}$, with $p_{i,1}>{{\displaystyle \underline{p}}}_{i,1}>0$.

According to Lemma 6, one has

$$e_{i,1}({\mathcal{F}}_i+d_i)p_{i,1}{\alpha }_{i,1}\le -{\displaystyle \frac{e_{i,1}^2{\overline{\alpha }}_{i,1}^2}{\sqrt{e_{i,1}^2{\overline{\alpha }}_{i,1}^2+{\nu }_{i,1}^2}}}\le {\nu }_{i,1}-e_{i,1}{\overline{\alpha }}_{i,1}$$

(25)

Combining Equations (19)–(25), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_{i,1}\le & -r_{i,1}{e}_{i,1}^4-b_{i,1}{e}_{i,1}^{2q}+{\displaystyle \frac{1}{2{\tau }_{i,1}^2}}{e}_{i,1}^2{\xi }_{i,1}^T{\xi }_{i,1}{\tilde{\vartheta }}_{i,1}-{\displaystyle \frac{{\tilde{\vartheta }}_{i,1}}{{\ell }_{i,1}}}{\dot{\hat{\vartheta }}}_{i,1}\hfill \\ & +e_{i,1}({\mathcal{F}}_i+d_i)p_{i,1}{e}_{i,2}+{\displaystyle \frac{{\tau }_{i,1}^2}{2}}+{\displaystyle \frac{{\overline{\hslash }}_{i,1}^2}{2}}+{\nu }_{i,1}\hfill \end{array}$$

(26)

Step k (k = 2, 3,…, n − 1): In a similar way, the Lyapunov function $V_{i,k}$ is constructed as follows:

$$V_{i,k}=V_{i,k-1}+{\displaystyle \frac{1}{2}}{e}_{i,k}^2+{\displaystyle \frac{1}{2{\ell }_{i,k}}}{\tilde{\vartheta }}_{i,k}^2$$

(27)

where ${\tilde{\vartheta }}_{i,k}={\vartheta }_{i,k}-{\hat{\vartheta }}_{i,k}$, ${\ell }_{i,k}>0$.

By differentiating $V_{i,k}$, one has

$${\dot{V}}_{i,k}={\dot{V}}_{i,k-1}+e_{i,k}(p_{i,k}{e}_{i,k+1}+p_{i,k}{\alpha }_{i,k}+{\overline{\Omega }}_{i,k})-{\displaystyle \frac{{\tilde{\vartheta }}_{i,k}}{{\ell }_{i,k}}}{\dot{\hat{\vartheta }}}_{i,k}$$

(28)

where ${\overline{\Omega }}_{i,2}\left({\mathcal{X}}_{i,2}\right)=-{\dot{\alpha }}_{i,1}+({\mathcal{F}}_i+b_i)p_{i,1}{e}_{i,1}$, with ${\mathcal{X}}_{i,2}={[x_{i,1},x_{j,1},x_{j,2}]}^T$, and $j\in M_i,k=2$. Similarly, ${\overline{\Omega }}_{i,k}\left({\mathcal{X}}_{i,k}\right)=-{\dot{\alpha }}_{i,k-1}+p_{i,k-1}{e}_{i,k-1}$, with $X_{i,k}=\left[x_{i,1},\dots ,x_{i,k},x_{j,1},\dots ,x_{j,k},\right.$$\left.{\hat{\vartheta }}_{i,1},\dots ,{\hat{\vartheta }}_{i,k-1}\right]$, $j\in M_i,k\ge 3$. Additionally, if ${\mathcal{F}}_i>0$, ${\mathcal{X}}_{i,2}$ and ${\mathcal{X}}_{i,k}$ also incorporate ${\dot{y}}_d$ and $y_d$.

Similar to (22), one has

$$\begin{array}{c}\begin{array}{c}\hfill e_{i,k}{\overline{\Omega }}_{i,k}\le {\displaystyle \frac{1}{2{\tau }_{i,k}^2}}{e}_{i,k}^2{\vartheta }_{i,k}{\xi }_{i,k}^T{\xi }_{i,k}+{\displaystyle \frac{e_{i,k}^2}{2}}+{\displaystyle \frac{{\tau }_{i,k}^2}{2}}+{\displaystyle \frac{{\hslash }_{i,k}^2}{2}}\end{array}\hfill \end{array}$$

(29)

where ${\vartheta }_{i,k}={∥{\theta }_{i,k}∥}^2$, ${\tau }_{i,k}>0$.

The virtual control law can formulated as follows:

$${\alpha }_{i,k}=-{\displaystyle \frac{e_{i,k}{\overline{\alpha }}_{i,k}^2}{{{\displaystyle \underline{p}}}_{i,k}\sqrt{e_{i,k}^2{\overline{\alpha }}_{i,k}^2+{\nu }_{i,k}^2}}}$$

(30)

$${\overline{\alpha }}_{i,k}=r_{i,k}{e}_{i,k}^3+b_{i,k}{e}_{i,k}^{2q-1}+{\displaystyle \frac{e_{i,k}}{2}}+{\displaystyle \frac{1}{2{\tau }_{i,k}^2}}{e}_{i,k}{\xi }_{i,k}^T{\xi }_{i,k}{\hat{\vartheta }}_{i,k}$$

(31)

where ${{\displaystyle \underline{p}}}_{i,k}$ denotes the lower bound of the gain function $p_{i,k}$, with $p_{i,k}>{{\displaystyle \underline{p}}}_{i,k}>0$. Additionally, $c_{i,k}>0$, $b_{i,k}>0$, and ${\nu }_{i,k}>0$.

Combining the above equations, we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_{i,k}\le & -{\displaystyle \sum _{m=1}^k}{r}_{i,m}{e}_{i,m}^4-{\displaystyle \sum _{m=1}^k}{b}_{i,m}{e}_{i,m}^{2q}+{\displaystyle \sum _{m=1}^k}{\displaystyle \frac{1}{2{\tau }_{i,m}^2}}{e}_{i,m}^2{\xi }_{i,m}^T{\xi }_{i,m}{\tilde{\vartheta }}_{i,m}\hfill \\ & -{\displaystyle \sum _{m=1}^k}{\displaystyle \frac{{\tilde{\vartheta }}_{i,m}}{{\ell }_{i,m}}}{\dot{\hat{\vartheta }}}_{i,m}+{\displaystyle \sum _{m=1}^k}({\displaystyle \frac{{\tau }_{i,m}^2}{2}}+{\displaystyle \frac{{\overline{\hslash }}_{i,m}^2}{2}}+{\nu }_{i,m})+e_{i,k}{p}_{i,k}{e}_{i,k+1}\hfill \end{array}$$

(32)

From (14), we derive ${\dot{x}}_{i,n}={\displaystyle \frac{p_{i,n}}{M_i}}\left(s_i{u}_i+z_i+{\partial }_i+w_i\right)$. Subsequently, we define the functions ${\sigma }_i={\displaystyle \frac{p_{i,n}}{M_i}}(w_i+z_i)$ and ${\gamma }_i={\displaystyle \frac{p_{i,n}{s}_i}{M_i}}$. According to the assumptions, ${\sigma }_i$ and ${\gamma }_i$ are bounded. We further define ${\overline{\sigma }}_i={sup}_{t\ge 0}\left\{\left.\left|{\sigma }_i\right|\right\}\right.>0$ and ${\overline{\gamma }}_i={\displaystyle \frac{1}{{{\displaystyle \underline{\gamma }}}_i}}>0$; ${\overline{\gamma }}_i={inf}_{t\ge 0}\left\{\left.{\gamma }_i\right\}\right.>0$.

To deal with the challenges posed by input dead zones, control gain variations, and external disturbances, FLSs and adaptive control techniques are utilized to estimate the unknown time-varying parameters. This method aims to clarify the influence of these parameters on the system’s behavior. Two adaptive numbers, ${\hat{\sigma }}_i$ and ${\hat{\gamma }}_i$, are introduced to estimate ${\overline{\sigma }}_i$ and ${\overline{\gamma }}_i$, respectively. Consequently, the estimation errors’s are defined as ${\tilde{\sigma }}_i={\overline{\sigma }}_i-{\hat{\sigma }}_i$ and ${\tilde{\gamma }}_i={\overline{\gamma }}_i-{\hat{\gamma }}_i$.

Step n: The Lyapunov function $V_{i,n}$ is constructed as follows:

$$V_{i,n}=V_{i,n-1}+{\displaystyle \frac{1}{2}}{e}_{i,n}^2+{\displaystyle \frac{1}{2{\ell }_{i,n}}}{\tilde{\vartheta }}_{i,n}^2++{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{2{\eta }_{i,n}}}{\tilde{\gamma }}_i^2+{\displaystyle \frac{1}{2{\upsilon }_{i,n}}}{\tilde{\sigma }}_i^2$$

(33)

where the parameters ${\ell }_{i,n}>0$, ${\eta }_{i,n}>0$, and ${\upsilon }_{i,n}>0$ are defined, and ${\tilde{\vartheta }}_{i,n}={\vartheta }_{i,n}-{\hat{\vartheta }}_{i,n}$, with ${\hat{\vartheta }}_i$ representing the estimation of ${\vartheta }_{i,n}$.

The derivative of $V_{i,n}$ can be obtained as follows:

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}=& {\dot{V}}_{i,n-1}+e_{i,n}({\gamma }_i{u}_i+{\sigma }_i+{\displaystyle \frac{{\partial }_i}{M_{\mathrm{i}}}}-{\dot{\alpha }}_{i,n-1})-{\displaystyle \frac{1}{{\ell }_{i,n}}}{\tilde{\vartheta }}_{i,n}{\dot{\hat{\vartheta }}}_{i,n}-{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{{\eta }_{i,n}}}{\tilde{\gamma }}_i{\dot{\hat{\gamma }}}_i-{\displaystyle \frac{1}{{\upsilon }_{i,n}}}{\tilde{\sigma }}_i{\dot{\hat{\sigma }}}_i\hfill \end{array}$$

(34)

Combining (32) and (34) yields

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _{m=1}^{n-1}}{r}_{i,m}{e}_{i,m}^4-{\displaystyle \sum _{m=1}^{n-1}}{b}_{i,m}{e}_{i,m}^{2q}-{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\tilde{\vartheta }}_{i,m}}{{\ell }_{i,m}}}{\dot{\hat{\vartheta }}}_{i,m}\hfill \\ & +{\displaystyle \sum _{m=1}^{n-1}}({\displaystyle \frac{{\tau }_{i,m}^2}{2}}+{\displaystyle \frac{{\overline{\hslash }}_{i,m}^2}{2}}+{\nu }_{i,m})+e_{i,n}({\gamma }_i{u}_i+{\overline{\sigma }}_i)\hfill \\ & +e_{i,n}{\overline{\Omega }}_{i,n}\left({\mathcal{X}}_{i,n}\right)-{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{{\eta }_{i,n}}}{\tilde{\gamma }}_i{\dot{\hat{\gamma }}}_i-{\displaystyle \frac{1}{v_{i,n}}}{\tilde{\sigma }}_i{\dot{\hat{\sigma }}}_i\hfill \end{array}$$

(35)

where ${\overline{\Omega }}_{i,n}\left({\mathcal{X}}_{i,n}\right)=e_{i,n-1}{p}_{i,n-1}+{\displaystyle \frac{{\partial }_i}{M_{\mathrm{i}}}}-{\dot{\alpha }}_{i,n-1}$.

According to the fuzzy logic system and Lemma 5, one has

$$\begin{array}{c}\begin{array}{cc}\hfill e_{i,n}{\overline{\Omega }}_{i,n}\left({\mathcal{X}}_{i,n}\right)\le & {\displaystyle \frac{1}{2{\tau }_{i,n}^2}}{e}_{i,n}^2{\vartheta }_{i,n}{\xi }_{i,n}^T{\xi }_{i,n}+{\displaystyle \frac{e_{i,n}^2}{2}}+{\displaystyle \frac{{\tau }_{i,n}^2}{2}}+{\displaystyle \frac{{\hslash }_{i,n}^2}{2}}\hfill \end{array}\hfill \end{array}$$

(36)

where ${\vartheta }_{i,n}={∥{\theta }_{i,n}∥}^2$, ${\tau }_{i,n}>0$.

3.3. Design of the Periodic Adaptive Event-Triggered Fixed-Time Controller

To minimize communication costs, a periodic adaptive event-triggered mechanism is implemented in the communication channel between the controller and the actuator. This approach deviates from traditional fixed-threshold event-driven control methods by incorporating a dynamic adjustment mechanism. This mechanism shortens the information update interval when the control signal $u_i$ undergoes significant changes, enabling adaptive updates of the trigger period and thereby accelerating system stability. Conversely, when the control signal $u_i$ exhibits minimal variation, indicating that the system is nearing stability, the update interval is lengthened. This strategy effectively reduces communication frequency, thereby conserving communication resources:

$$t_{i,c+1}=t_{i,c}+{\displaystyle \frac{{\Xi }_i\left|u\left(t_{i,c}\right)\right|+{\mathrm{Z}}_i}{max\left\{G_i,\left|\dot{u}\left(t_{i,c}\right)\right|\right\}}}$$

(37)

$$\begin{array}{c}\hfill {\omega }_i\left(t\right)=\left\{\begin{array}{c}-{\alpha }_{i,n}tanh\left({\displaystyle \frac{e_{i,n}{\alpha }_{i,n}}{{\omega }_i}}\right)\left(1+{\Xi }_i\right)\hfill \\ -{\displaystyle \frac{\left(1+{\Xi }_i\right)e_{i,n}}{2{\left(1-{\Xi }_i\right)}^2}},\left|u_i\right|\le {\Lambda }_i\hfill \\ {\alpha }_{i,n}-{\displaystyle \frac{1}{2}}{e}_{i,n},\left|u_i\right|>{\Lambda }_i\hfill \end{array}\right.\end{array}$$

(38)

$$u_i\left(t\right)={\omega }_{i,c}\left(t_{i,c}\right),\forall t\in \left[\left.t_{i,c},t_{i,c+1}\right)\right.$$

(39)

where the controller update time is given by $u_i\left(t\right)={\omega }_i\left(t_{i,c}\right)$ for all t within the interval $[\left.t_{i,c},t_{i,c+1}\right)$; $t_{i,1}$ is the initial time. The constants $Z_i$, $G_i$, ${\omega }_i$, and ${\Lambda }_i$ are positive design parameters. The control signal intervals between consecutive triggering instants are defined as ${\Xi }_i\left|u\left(t_{i,c}\right)\right|+{\mathrm{Z}}_i$, with $0<{\Xi }_i<1$. Here, $\left|\dot{u}\left(t_{i,c}\right)\right|$ represent the rates of change in the control signal intervals.

Remark 1. 

Upon each triggering event, the control signal $u_i\left(t_{i,c}\right)={\omega }_i\left(t_{i,c}\right)$ is immediately applied to the actuator, and the subsequent trigger point $t_{i,c+1}$ is calculated based on the current state. Throughout the interval $\left[\left.t_{i,c},t_{i,c+1}\right)\right.$ the control signals remain constant. This update mechanism effectively reduces the frequency of updates, thus conserving communication resources.

Based on the event-triggering formula, for $\forall t\in \left[\left.t_{i,c},t_{i,c+1}\right)\right.$, there is $\left|{\omega }_i\left(t\right)-u_i\left(t\right)\right|<{\Xi }_i\left|u_i\left(t\right)\right|+{\mathrm{Z}}_i$. Furthermore, we can obtain

$$u_i\left(t\right)={\displaystyle \frac{{\omega }_i\left(t\right)-{\mathrm{Z}}_i{o}_{i,1}\left(t\right)}{1+{\Xi }_i{o}_{i,2}\left(t\right)}}$$

(40)

where $0<o_{i,1}\left(t\right)\le 1$ and $0<o_{i,2}\left(t\right)\le 1$.

When $\left|u_i\right|\le {\Lambda }_i$, it can be obtained as follows:

$$\begin{array}{cc}\hfill {\gamma }_i{u}_i{e}_{i,n}=& -{\gamma }_i{e}_{i,n}\left[{\displaystyle \frac{\left(1+{\Xi }_i\right){\alpha }_{i,n}}{1+{\Xi }_i{o}_{i,2}\left(t\right)}}tanh\left({\displaystyle \frac{e_{i,n}{\alpha }_{i,n}\left(t\right)}{{\omega }_i}}\right)\right.\hfill \\ & +{\displaystyle \frac{\left(1+{\Xi }_i\right)e_{i,n}}{2\left(1+{\Xi }_i{o}_{i,n}\left(t\right)\right){\left(1-{\Xi }_i\right)}^2}}\left.+{\displaystyle \frac{{\mathrm{Z}}_i{o}_{i,1}\left(t\right)}{1+{\Xi }_i{o}_{i,2}\left(t\right)}}\right]\hfill \end{array}$$

(41)

Utilizing the results from Lemma 2 and Lemma 5, one has

$$\begin{array}{cc}\hfill {\gamma }_i{u}_i{e}_{i,n}& \le {\gamma }_i\left[\left|e_{i,n}{\alpha }_{i,n}\right|-e_{i,n}{\alpha }_{i,n}tanh\left({\displaystyle \frac{e_{i,n}{\alpha }_{i,n}}{{\omega }_i}}\right)\right.\left.-\left|e_{i,n}{\alpha }_{i,n}\right|-{\displaystyle \frac{e_{i,n}^2}{2{\left(1-{\Xi }_i\right)}^2}}+\left|{\displaystyle \frac{{\mathrm{Z}}_i{e}_{i,n}}{1-{\Xi }_i}}\right|\right]\hfill \\ & \begin{array}{c}\le {\gamma }_i{e}_{i,n}{\alpha }_{i,n}+{\displaystyle \frac{1}{2}}{\overline{\gamma }}_i{\mathrm{Z}}_i^2+0.2785{\overline{\gamma }}_i{\omega }_i\end{array}\hfill \end{array}$$

(42)

When $\left|u_i\right|>{\Lambda }_i$, one has

$$\begin{array}{cc}\hfill {\gamma }_i{u}_i{e}_{i,n}=& {\gamma }_i{e}_{i,n}\left[{\displaystyle \frac{{\alpha }_{i,n}}{1+{\Xi }_i{o}_{i,2}\left(t\right)}}-{\displaystyle \frac{e_{i,n}}{2\left(1+{\Xi }_i{o}_{i,2}\left(t\right)\right)}}\right.\left.-{\displaystyle \frac{{\mathrm{Z}}_i{o}_{i,1}\left(t\right)}{1+{\Xi }_i{o}_{i,2}\left(t\right)}}\right]\hfill \end{array}$$

(43)

Similarly to (42), one has

$$\begin{array}{cc}\hfill {\gamma }_i{u}_i{e}_{i,n}& \le {\gamma }_i\left[e_{i,n}{\alpha }_{i,n}-{\displaystyle \frac{e_{i,n}^2}{2{\left(1+{\Xi }_i{o}_{i,2}\left(t\right)\right)}^2}}+\left|{\displaystyle \frac{{\mathrm{Z}}_i{e}_{i,n}}{1+{\Xi }_i{o}_{i,2}\left(t\right)}}\right|\right]\hfill \\ \hfill & \le {\gamma }_i{e}_{i,n}{\alpha }_{i,n}+\begin{array}{c}{\displaystyle \frac{1}{2}}{\overline{\gamma }}_i{\mathrm{Z}}_i^2\end{array}\hfill \end{array}$$

(44)

Based on the derivation under the two conditions, the following result holds:

$${\gamma }_i{u}_i{e}_{i,n}\le {\gamma }_i{e}_{i,n}{\alpha }_{i,n}+{\displaystyle \frac{1}{2}}{\overline{\gamma }}_i{\mathrm{Z}}_i^2+0.2785{\overline{\gamma }}_i{\omega }_i$$

(45)

The virtual control law is formulated as follows:

$${\alpha }_{i,n}=-{\displaystyle \frac{e_{i,n}{\hat{\gamma }}_i^2{\overline{\alpha }}_{i,n}^2}{\sqrt{e_{i,n}^2{\hat{\gamma }}_i^2{\overline{\alpha }}_{i,n}^2+{\nu }_{i,n}^2}}}$$

(46)

Substituting (46) into (35), we obtain

$$\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _{m=1}^{n-1}}{r}_{i,m}{e}_{i,m}^4-{\displaystyle \sum _{m=1}^{n-1}}{b}_{i,m}{e}_{i,m}^{2q}+{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{1}{2{\tau }_{i,m}^2}}{e}_{i,m}^2{\xi }_{i,m}^T{\xi }_{i,m}{\tilde{\vartheta }}_{i,m}-{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\tilde{\vartheta }}_{i,m}}{{\ell }_{i,m}}}{\dot{\hat{\vartheta }}}_{i,m}\hfill \\ & +{\displaystyle \sum _{m=1}^{n-1}}({\displaystyle \frac{{\tau }_{i,m}^2}{2}}+{\displaystyle \frac{{\overline{\hslash }}_{i,m}^2}{2}}+{\nu }_{i,m})-{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{{\eta }_{i,n}}}{\tilde{\gamma }}_i{\dot{\hat{\gamma }}}_i-{\displaystyle \frac{1}{v_{i,n}}}{\tilde{\sigma }}_{i,n}{\dot{\hat{\sigma }}}_{i,n}+{\gamma }_{i,n}{e}_{i,n}{\alpha }_{i,n}+{\displaystyle \frac{1}{2}}{\overline{\gamma }}_{i,n}{\mathrm{Z}}_i^2\hfill \\ & +0.2785{\overline{\gamma }}_{i,n}{\omega }_i+e_{i,n}{\overline{\sigma }}_{i,n}+{\displaystyle \frac{e_{i,n}^2}{2}}+{\displaystyle \frac{{\tau }_{i,n}^2}{2}}+{\displaystyle \frac{{\hslash }_{i,n}^2}{2}}\hfill \end{array}$$

(47)

Utilizing the virtual control law in conjunction with Lemma 7, one has

$$\begin{array}{cc}\hfill {\gamma }_i{e}_{i,n}{\alpha }_{i,n}& \le -{\displaystyle \frac{{\gamma }_i{e}_{i,n}^2{\hat{\gamma }}_i^2{\overline{\alpha }}_{i,n}^2}{\sqrt{e_{i,n}^2{\hat{\gamma }}_i^2{\overline{\alpha }}_{i,n}^2+{\nu }_{i,n}^2}}}\le {{\displaystyle \underline{\gamma }}}_i{\nu }_{i,n}-{{\displaystyle \underline{\gamma }}}_i{\hat{\gamma }}_i{\overline{\alpha }}_{i,n}{e}_{i,n}\hfill \end{array}$$

(48)

From the above equation, one has

$$\begin{array}{cc}\hfill & {{\displaystyle \underline{\gamma }}}_i{e}_{i,n}\left({\hat{\gamma }}_i+{\tilde{\gamma }}_i\right){\overline{\alpha }}_{i,n}={{\displaystyle \underline{\gamma }}}_i{e}_{i,n}{\overline{\gamma }}_i{\overline{\alpha }}_{i,n}=e_{i,n}{\overline{\alpha }}_{i,n}\hfill \end{array}$$

(49)

The ${\overline{\alpha }}_{i,n}$ is constructed as

$$\begin{array}{cc}\hfill {\overline{\alpha }}_{i,n}=& r_{i,n}{e}_{i,n}^3+b_{i,n}{e}_{i,n}^{2q-1}+{\displaystyle \frac{e_{i,n}}{2}}+{\hat{\sigma }}_{i}tanh\left({\displaystyle \frac{e_{i,n}}{l_{i,n}}}\right)+{\displaystyle \frac{1}{2{\tau }_{i,n}^2}}{e}_{i,n}^2{\hat{\vartheta }}_{i,n}{\xi }_{i,n}^T{\xi }_{i,n}\hfill \end{array}$$

(50)

where the specified parameters are $r_{i,n}>0$, $b_{i,n}>0$, and $l_{i,n}>0$.

From Equation (50), one has

$$\begin{array}{c}\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _{m=1}^n}{r}_{i,m}{e}_{i,m}^4-{\displaystyle \sum _{m=1}^n}{b}_{i,m}{e}_{i,m}^{2q}+{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\tilde{\vartheta }}_{i,m}}{{\ell }_{i,m}}}\left({\displaystyle \frac{{\ell }_{i,m}}{2{\tau }_{i,m}^2}}{e}_{i,m}^2{\xi }_{i,m}^T{\xi }_{i,m}-{\dot{\hat{\vartheta }}}_{i,m}\right)\hfill \\ & +{\overline{\sigma }}_i\left|\left.e_{i,n}\right|\right.-{\overline{\sigma }}_i{e}_{i,n}tanh\left({\displaystyle \frac{e_{i,n}}{l_{i,n}}}\right)-{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{{\eta }_{i,n}}}{\tilde{\gamma }}_i\left({\dot{\hat{\gamma }}}_i-{\eta }_{i,n}{e}_{i,n}{\overline{\alpha }}_{i,n}\right)\hfill \\ & -{\displaystyle \frac{{\tilde{\sigma }}_i}{v_{i,n}}}\left({\dot{\hat{\sigma }}}_i-v_{i,n}{e}_{i,n}tanh\left({\displaystyle \frac{e_{i,n}}{l_{i,n}}}\right)\right)+\Gamma \hfill \end{array}\hfill \end{array}$$

(51)

where $\Gamma ={{\displaystyle \underline{\gamma }}}_i{\nu }_{i,n}+{\displaystyle \frac{1}{2}}{\overline{\gamma }}_i{\mathrm{Z}}_i^2+0.2785{\overline{\gamma }}_i{\omega }_i+{\displaystyle \sum _{m=1}^{n-1}}{\nu }_{i,m}+{\displaystyle \sum _{m=1}^n}({\displaystyle \frac{{\tau }_{i,m}^2}{2}}+{\displaystyle \frac{{\overline{\hslash }}_{i,m}^2}{2}})$.

Three adaptive laws are designed as follows:

$${\dot{\hat{\vartheta }}}_{i,m}={\displaystyle \frac{{\ell }_{i,m}}{2{\tau }_{i,m}^2}}{e}_{i,m}^2{\xi }_{i,m}^T{\xi }_{i,m}-{\mu }_{i,m}{\hat{\vartheta }}_{i,m}-{\displaystyle \frac{{\mu }_{i,m}}{{\ell }_{i,m}}}{\hat{\vartheta }}_{i,m}^3$$

(52)

$${\dot{\hat{\gamma }}}_i={\eta }_{i,n}{e}_{i,n}{\overline{\alpha }}_{i,n}-g_{i,n}{\hat{\gamma }}_i-{\displaystyle \frac{g_{i,n}}{{\eta }_{i,n}}}{\hat{\gamma }}_i^3$$

(53)

$${\dot{\hat{\sigma }}}_i=v_{i,n}{e}_{i,n}tanh\left({\displaystyle \frac{e_{i,n}}{l_{i,n}}}\right)-h_{i,n}{\hat{\sigma }}_i-{\displaystyle \frac{h_{i,n}}{v_{i,n}}}{\hat{\sigma }}_i^3$$

(54)

where the parameters ${\mu }_{i,m}$, $g_{i,n}$, and $h_{i,n}$ are all positive values.

According to Equations (51)–(54) and Lemma 2, the following result holds:

$$\begin{array}{c}\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _{m=1}^n}{r}_{i,m}{e}_{i,m}^4-{\displaystyle \sum _{m=1}^n}{b}_{i,m}{e}_{i,m}^{2q}+{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\tilde{\vartheta }}_{i,m}}{{\ell }_{i,m}}}\left({\mu }_{i,m}{\hat{\vartheta }}_{i,m}+{\displaystyle \frac{{\mu }_{i,m}}{{\ell }_{i,m}}}{\hat{\vartheta }}_{i,m}^3\right)\hfill \\ & +{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{{\eta }_{i,n}}}{\tilde{\gamma }}_i\left(g_{i,n}{\hat{\gamma }}_i+{\displaystyle \frac{g_{i,n}}{{\eta }_{i,n}}}{\hat{\gamma }}_i^3\right)+{\displaystyle \frac{{\tilde{\sigma }}_i}{v_{i,n}}}\left(h_{i,n}{\hat{\sigma }}_i+{\displaystyle \frac{h_{i,n}}{v_{i,n}}}{\hat{\sigma }}_i^3\right)+{\Gamma }_1\hfill \end{array}\hfill \end{array}$$

(55)

where ${\Gamma }_1=\Gamma +0.2785{\overline{\sigma }}_i{l}_{i,n}$.

According to Lemma 5 and Lemma 3, one has

$${\displaystyle \frac{{\mu }_{i,m}}{{\ell }_{i,m}}}{\tilde{\vartheta }}_{i,m}{\hat{\vartheta }}_{i,m}\le {\displaystyle \frac{{\mu }_{i,m}}{2{\ell }_{i,m}}}{\vartheta }_{i,m}^2-{\left({\displaystyle \frac{{\mu }_{i,m}}{2{\ell }_{i,m}}}{\tilde{\vartheta }}_{i,m}^2\right)}^q+\psi$$

(56)

$${\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}}{{\eta }_{i,n}}}{\tilde{\gamma }}_i{\hat{\gamma }}_i\le {\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}}{2{\eta }_{i,n}}}{\overline{\gamma }}_i^2-{\left({\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}}{2{\eta }_{i,n}}}{\tilde{\gamma }}_i^2\right)}^q+\psi$$

(57)

$${\displaystyle \frac{h_{i,n}}{v_{i,n}}}{\tilde{\sigma }}_i{\hat{\sigma }}_i\le {\displaystyle \frac{h_{i,n}}{2v_{i,n}}}{\overline{\sigma }}_i^2-{\left({\displaystyle \frac{h_{i,n}}{2v_{i,n}}}{\tilde{\sigma }}_i^2\right)}^q+\psi$$

(58)

where $\psi =-(q-1)q^{{\displaystyle \frac{q}{1-q}}}$.

Substituting from (56) to (58) into (55), one has

$$\begin{array}{c}\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\displaystyle \sum _{m=1}^n}{r}_{i,m}{e}_{i,m}^4-{\displaystyle \sum _{m=1}^n}{b}_{i,m}{e}_{i,m}^{2q}\hfill \\ & -{\left({\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\mu }_{i,m}}{2{\ell }_{i,m}}}{\tilde{\vartheta }}_{i,m}^2\right)}^q+{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\mu }_{i,m}}{{\ell }_{i,m}^2}}{\tilde{\vartheta }}_{i,m}{\hat{\vartheta }}_{i,m}^3\hfill \\ & -{\left({\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}}{2{\eta }_{i,n}}}{\tilde{\gamma }}_i^2\right)}^q+{\displaystyle \frac{g_{i,n}{{\displaystyle \underline{\gamma }}}_i}{{\eta }_i^2}}{\tilde{\gamma }}_i{\hat{\gamma }}_i^3-{\left({\displaystyle \frac{h_{i,n}}{2v_{i,n}}}{\tilde{\sigma }}_i^2\right)}^q\hfill \\ & +{\displaystyle \frac{h_{i,n}}{v_{i,n}^2}}{\tilde{\sigma }}_i{\hat{\sigma }}_i^3+{\Gamma }_2\hfill \end{array}\hfill \end{array}$$

(59)

where ${\Gamma }_2={\Gamma }_1+3\psi +{\displaystyle \sum _{m=1}^n}{\displaystyle \frac{{\mu }_{i,m}}{2{\ell }_{i,m}}}{\vartheta }_{i,m}^2+{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}}{2{\eta }_{i,n}}}{\overline{\gamma }}_i^2+{\displaystyle \frac{h_{i,n}}{2v_{i,n}}}{\overline{\sigma }}_i^2$.

According to the definitions of ${\tilde{\vartheta }}_{i,m}$, ${\tilde{\gamma }}_i$ and ${\tilde{\sigma }}_i$, one has

$${\tilde{\vartheta }}_{i,m}{\hat{\vartheta }}_{i,m}^3={\tilde{\vartheta }}_{i,m}({\overline{\vartheta }}_{i,m}^3+3{\overline{\vartheta }}_{i,m}{\tilde{\vartheta }}_{i,m}^2-3{\overline{\vartheta }}_{i,m}^2{\tilde{\vartheta }}_{i,m}-{\tilde{\vartheta }}_{i,m}^3)$$

(60)

$${\tilde{\gamma }}_i{\hat{\gamma }}_i^3={\tilde{\gamma }}_i({\overline{\gamma }}_i^3+3{\overline{\gamma }}_i{\tilde{\gamma }}_i^2-3{\overline{\gamma }}_i^2{\tilde{\gamma }}_i-{\tilde{\gamma }}_i^3)$$

(61)

$${\tilde{\sigma }}_i{\hat{\sigma }}_i^3={\tilde{\sigma }}_i({\overline{\sigma }}_i^3+3{\overline{\sigma }}_i{\tilde{\sigma }}_i^2-3{\overline{\sigma }}_i^2{\tilde{\sigma }}_i-{\tilde{\sigma }}_i^3)$$

(62)

According to Lemma 6, one has

$${\tilde{\vartheta }}_{i,m}{\overline{\vartheta }}_{i,m}^3\le {\displaystyle \frac{{\overline{\vartheta }}_{i,m}^4}{12}}+3{\tilde{\vartheta }}_{i,m}^2{\overline{\vartheta }}_{i,m}^2$$

(63)

$$3{\overline{\vartheta }}_{i,m}{\tilde{\vartheta }}_{i,m}^3\le {\displaystyle \frac{9f_{i,m}^{\frac{4}{3}}{\tilde{\vartheta }}_{i,m}^4}{4}}+{\displaystyle \frac{3{\overline{\vartheta }}_{i,m}^4}{4f_{i,m}^4}}$$

(64)

$${\tilde{\gamma }}_i{\overline{\gamma }}_i^3={\displaystyle \frac{{\overline{\gamma }}_i^4}{12}}+3{\tilde{\gamma }}_i^2{\overline{\gamma }}_i^2$$

(65)

$$3{\overline{\gamma }}_i{\tilde{\gamma }}_i^3\le {\displaystyle \frac{9f_{i,n}^{\frac{4}{3}}{\tilde{\gamma }}_i^4}{4}}+{\displaystyle \frac{3{\overline{\gamma }}_i^4}{4f_{i,n}^4}}$$

(66)

$${\tilde{\sigma }}_i{\overline{\sigma }}_i^3={\displaystyle \frac{{\overline{\sigma }}_i^4}{12}}+3{\tilde{\sigma }}_i^2{\overline{\sigma }}_i^2$$

(67)

$$3{\overline{\sigma }}_i{\tilde{\sigma }}_i^3\le {\displaystyle \frac{9f_{i,n}^{\frac{4}{3}}{\tilde{\sigma }}_i^4}{4}}+{\displaystyle \frac{3{\overline{\sigma }}_i^4}{4f_{i,n}^4}}$$

(68)

where $f_{i,n}>0$.

Combining the above equations from (63) to (68), the following can be obtained:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mu }_{i,m}}{{\ell }_{i,m}^2}}{\tilde{\vartheta }}_{i,m}{\hat{\vartheta }}_{i,m}^3\le & -(4{\mu }_{i,m}-9{\mu }_{i,m}{f}_{i,m}^{{\displaystyle \frac{4}{3}}}){({\displaystyle \frac{1}{2{\ell }_{i,m}}}{\tilde{\vartheta }}_{i,m}^2)}^2+{\displaystyle \frac{{\mu }_{i,m}{\overline{\vartheta }}_{i,m}^4}{12{\ell }_{i,m}^2}}+{\displaystyle \frac{3{\mu }_{i,m}{\overline{\vartheta }}_{i,m}^4}{4f_{i,m}^4{\ell }_{i,m}^2}}\hfill \end{array}$$

(69)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{\mathrm{g}}_{i,n}}{{\eta }_{i,n}}}{\tilde{\gamma }}_i{\hat{\gamma }}_i^3\le & -(4{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}-9{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}{f}_{i,n}^{{\displaystyle \frac{4}{3}}}){({\displaystyle \frac{1}{2{\eta }_{i,n}}}{\tilde{\gamma }}_i^2)}^2+{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}{\overline{\gamma }}_i^4}{12{\eta }_{i,n}^2}}+{\displaystyle \frac{3{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}{\overline{\gamma }}_i^4}{4f_{i,n}^4{\eta }_{i,n}^2}}\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill {\displaystyle \frac{h_{i,n}}{v_{i,n}}}{\tilde{\sigma }}_i{\hat{\sigma }}_i^3\le & -(4h_{i,n}-9h_{i,n}{f}_{i,n}^{{\displaystyle \frac{4}{3}}}){({\displaystyle \frac{1}{2v_{i,n}}}{\tilde{\sigma }}_i^2)}^2+{\displaystyle \frac{h_{i,n}{\overline{\sigma }}_i^4}{12v_{i,n}^2}}+{\displaystyle \frac{3h_{i,n}{\overline{\sigma }}_i^4}{4f_{i,n}^4{v}_{i,n}^2}}\hfill \end{array}$$

(71)

Applying Lemma 4, the following expression holds:

$$\begin{array}{c}\begin{array}{cc}\hfill {\dot{V}}_{i,n}\le & -{\Phi }_{i,1}{\left({\displaystyle \sum _{m=1}^n}{\displaystyle \frac{e_{i,m}^2}{2}}\right)}^2-{\Psi }_{i,1}{\left({\displaystyle \sum _{m=1}^n}{\displaystyle \frac{e_{i,m}^2}{2}}\right)}^q\hfill \\ & -{\Phi }_{i,2}{\left({\displaystyle \sum _{m=1}^n}{\displaystyle \frac{1}{2{\ell }_{i,m}}}{\tilde{\vartheta }}_{i,m}^2\right)}^2-{\Psi }_{i,2}{\left({\displaystyle \sum _{m=1}^n}{\displaystyle \frac{1}{2{\ell }_{i,m}}}{\tilde{\vartheta }}_{i,m}^2\right)}^q\hfill \\ & -{\Phi }_{i,3}{\left({\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{2{\eta }_{i,n}}}{\tilde{\gamma }}_i^2\right)}^2-{\Psi }_{i,3}{\left({\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i}{2{\eta }_{i,n}}}{\tilde{\gamma }}_i^2\right)}^q\hfill \\ & -{\Phi }_{i,4}{\left({\displaystyle \frac{1}{2v_{i,n}}}{\tilde{\sigma }}_i^2\right)}^2-{\Psi }_{i,4}{\left({\displaystyle \frac{1}{2v_{i,n}}}{\tilde{\sigma }}_i^2\right)}^q+{\Gamma }_3\hfill \end{array}\hfill \end{array}$$

(72)

where ${\Phi }_{i,1}={\displaystyle \frac{4min\{r_{i,1},r_{i,2},\dots ,r_{i,n}\}}{n}}$, ${\Phi }_{i,2}={\displaystyle \frac{min\left\{4{\mu }_{i,m}-9{\mu }_{i,m}{f}_{i,m}^{\frac{4}{3}}\right\}}{n}}$, ${\Phi }_{i,3}={\displaystyle \frac{\left(4g_{i,n}-9g_{i,n}{f}_{i,n}^{\frac{4}{3}}\right)}{{{\displaystyle \underline{\gamma }}}_i}}$, ${\Phi }_{i,4}=(4h_{i,n}-9h_{i,n}{f}_{i,n}^{{\displaystyle \frac{4}{3}}})$, ${\Psi }_{i,4}=h_{i,n}^q$, ${\Psi }_{i,3}=g_{i,n}^q$, ${\Psi }_{i,2}=min\{{\mu }_{i,1}^q,{\mu }_{i,2}^q,\dots ,{\mu }_{i,n}^q\}$, ${\Psi }_{i,1}=2^{q}min\{b_{i,1},b_{i,2},\dots ,b_{i,n}\}$, ${\Gamma }_3={\Gamma }_2+{\displaystyle \frac{{\mu }_{i,m}{\overline{\vartheta }}_{i,m}^4}{12{\ell }_{i,m}^2}}+{\displaystyle \frac{3{\mu }_{i,m}{\overline{\vartheta }}_{i,m}^4}{4f_{i,m}^4{\ell }_{i,m}^2}}+{\displaystyle \frac{{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}{\overline{\gamma }}_i^4}{12{\eta }_{i,n}^2}}+{\displaystyle \frac{3{{\displaystyle \underline{\gamma }}}_i{g}_{i,n}{\overline{\gamma }}_i^4}{4f_{i,n}^4{\eta }_{i,n}^2}}+{\displaystyle \frac{h_{i,n}{\overline{\sigma }}_i^4}{12v_{i,n}^2}}+{\displaystyle \frac{3h_{i,n}{\overline{\sigma }}_i^4}{4f_{i,n}^4{v}_{i,n}^2}}$.

Finally, according to Lemma 1 and the expression of $V_{i,n}$, one has

$$\begin{array}{c}{\dot{V}}_{i,n}\le -{\Psi }_i{V}_{i,n}^q-{\Phi }_i{V}_{i,n}^2+{\Gamma }_3\end{array}$$

(73)

where ${\Psi }_i$ $=min\left\{{\Psi }_{i,1},\right.{\Psi }_{i,2},$${\Psi }_{i,3},\left.{\Psi }_{i,4}\right\}$, ${\Phi }_i=min\left\{{\Phi }_{i,1},\right.{\Phi }_{i,2},{\Phi }_{i,3},\left.{\Phi }_{i,4}\right\}$.

3.4. Stability Analysis

Given Assumptions 1–2, the proposed control protocol guarantees that the nonlinear MASs exhibit the following characteristics:

• In the multi-agent system, all closed-loop signals are bounded and the tracking error can be limited to a small range within a fixed time.
• The Zeno phenomenon will not occur.

Proof. 

According to Lemma 1 and the fixed-time inequality, the error signal $E_i=\left[E_1^T,E_2^T,\dots E_n^T\right]$ will converge to the following residual set.

$$\begin{array}{c}{\Theta }_i=\left\{E_i|V_{i,n}\left(E_i\right)\le \left\{{\left({\displaystyle \frac{{\Gamma }_3}{\left(1-\lambda \right){\Psi }_i}}\right)}^{{\displaystyle \frac{1}{q}}},\right.\right.\left.\left.{\left({\displaystyle \frac{{\Gamma }_3}{\left(1-\lambda \right){\Phi }_i}}\right)}^{{\displaystyle \frac{1}{2}}}\right\}\right\}\hfill \end{array}$$

(74)

$$\begin{array}{c}{T}_i\le {\displaystyle \frac{1}{{\Psi }_i\lambda \left(1-q\right)}}+{\displaystyle \frac{1}{{\Phi }_i\lambda }}\hfill \end{array}$$

(75)

Therefore, the error signal ${\mathrm{E}}_i$ will converge to the set specified by (75) within the fixed time $T_i$. Based on $e_{i,1}$ and Lemma 1, it follows that $y_i=x_{i,1}\left(i=1,2,\dots ,n\right)$ remains bounded.

Furthermore, considering the definitions of ${\tilde{\vartheta }}_{i,1}$, ${\tilde{\gamma }}_{i,1}$, and ${\tilde{\sigma }}_{i,1}$, it can be inferred that ${\hat{\vartheta }}_{i,1}$, ${\hat{\gamma }}_{i,1}$, and ${\hat{\sigma }}_{i,1}$ are bounded. By analyzing Equations (18), (23) and (24), it can also be established that ${\alpha }_{i,1}$ and $x_{i,2}$ remain bounded. Similarly, it is satisfied that $x_{i,k}$, $u_i\left(t\right)$ and ${\omega }_i\left(t\right)$ are bounded for all $\left(i=1,2,\dots ,n,1\le k\le n\right)$. Thus, all closed-loop signals are bounded.

On the basis of Lemma 7, the tracking error meets these constraints:

$$\begin{array}{cc}\hfill {∥Y_i-Y_d∥}^2& \le min\left\{{\displaystyle \frac{\sqrt{2}}{{\lambda }_{max}\left(L+\mathcal{V}\right)}}{\left({\displaystyle \frac{{\Gamma }_3}{\left(1-\lambda \right){\Phi }_i}}\right)}^{{\displaystyle \frac{1}{4}}},\right.\left.{\displaystyle \frac{\sqrt{2}}{{\lambda }_{max}\left(L+\mathcal{V}\right)}}{\left({\displaystyle \frac{{\Gamma }_3}{\left(1-\lambda \right){\Psi }_i}}\right)}^{{\displaystyle \frac{1}{2q}}}\right\}\hfill \end{array}$$

(76)

where $Y_i={\left[y_1,y_2,\dots ,y_n\right]}^T$, and $Y_a={\left[y_a,y_a,\dots ,y_a\right]}^T\in {\mathbb{R}}^n$. ${\lambda }_{max}\left(L+\mathcal{V}\right)$ represents the maximum eigenvalue of the matrix $\left(L+\mathcal{V}\right)$. □

Remark 2. 

From Equations (37) to (39), it can be observed that since the value of ${\omega }_i\left(t\right)$ depends on the virtual control law ${\alpha }_{i,n}$ and the error $e_{i,n}$, the derivative ${\dot{\omega }}_i\left(t\right)$ remains bounded. This implies the existence of constants such that $\left|{\dot{\omega }}_i\left(t\right)\right|\le {\overline{\omega }}_i\left(t\right)$ with ${\overline{\omega }}_i\left(t\right)>0$, ensuring that ${\dot{\omega }}_i\left(t\right)$ is finite. Furthermore, the interval between trigger times satisfies $t_i^{*}=t_{i,c+1}-t_{i,c}\ge {\displaystyle \frac{{\Xi }_i\left|u_i\left(t\right)\right|+{\mathrm{Z}}_i}{{\overline{\omega }}_i}}$, effectively preventing Zeno behavior.

Remark 3. 

By carefully choosing the design parameters, the system can reach stability within a predetermined time frame. Notably, as indicated by (76), the stabilization time is independent of the system’s initial states.

4. Simulation

4.1. Simulation Example

Figure 2 illustrates a communication topology network that comprises one leader UAV (denoted as a) and four follower UAVs (labeled 1, 2, 3, and 4), each with uncertain nonlinear dynamics and input dead zones. The dynamic model for follower UAV i ($i=1,2,3,4$) is described as follows [45,46]:

$$\left\{\begin{array}{c}{\dot{x}}_{i,1}=p_{i,1}\left({\overline{x}}_{i,1}\right)x_{i,2}\hfill \\ M_{\mathrm{i}}\left(t\right){\dot{x}}_{i,2}=p_{i,2}\left({\overline{x}}_{i,2}\right){\mathcal{D}}_i\left(u_i\right)+{\partial }_i\left({\overline{x}}_i\right)+w_i\left(t\right)\hfill \\ y_i=x_{i,1}\hfill \end{array}\right.$$

(77)

where $x_{i,1}={\left[x_{i,1}^X,x_{i,1}^Y,x_{i,1}^Z\right]}^T$ and $x_{i,2}={\left[x_{i,2}^X,x_{i,2}^Y,x_{i,2}^Z\right]}^T$ demonstrate the position and velocity vectors of the follower UAV, respectively. The term $M_i\left(t\right)=\mathrm{diag}\left[M_i^X,M_i^Y,M_i^Z\right]$ represents the UAV mass matrix. The control input vector is denoted as $u_i={\left[u_i^X,u_i^Y,u_i^Z\right]}^T$. The centripetal and Coriolis forces are captured by the vector $\partial i={\left[{\partial }_i^X,{\partial }_i^Y,{\partial }_i^Z\right]}^T$, in which ${\partial }_i^X=\left(Q_i+W_i\left|x_{i,2}^X\right|\right)x_{i,2}^X-M_i^Y{x}_{i,2}^Z{x}_{i,2}^Y$, ${\partial }_i^Y=M_i^X{x}_{i,2}^Z{x}_{i,2}^X+\left(R_i+F_i\left|x_{i,2}^Y\right|\right)x_{i,2}^Y$, and ${\partial }_i^Z=\left(H_i+J_i\left|x_{i,2}^Z\right|\right)x_{i,2}^Z$. The external, unknown, time-varying disturbances are represented by $w_i={\left[w_i^X,w_i^Y,w_i^Z\right]}^T$. The system output is given by $y_i={\left[y_{i,1}^X,y_{i,1}^Y,y_{i,1}^Z\right]}^T$.

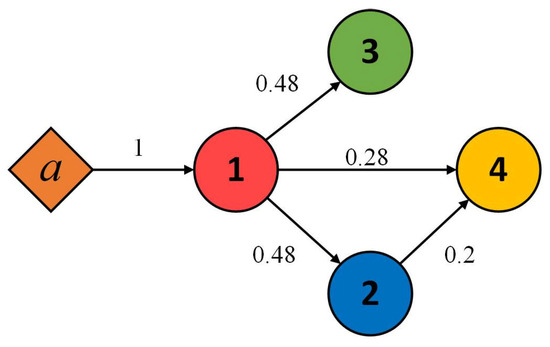
Figure 2. Communication topology diagram of UAVs.

The radial basis functions in the X-axis direction are provided as follows:

$$K_{F_i^P}=exp\left[-{\displaystyle \frac{{\left({\mathcal{X}}_i-3+P\right)}^2}{2}}\right]$$

(78)

where $P=1,2,3,4,5$. Given the communication topology, the state vectors are defined as follows: ${\mathcal{X}}_1={\left[x_{1,1}^X,x_{1,2}^X,{\mathrm{y}}_a,{\dot{\mathrm{y}}}_a\right]}^T$, $n_1=8$; ${\mathcal{X}}_2={\left[x_{2,1}^X,x_{2,2}^X,x_{1,1}^X,x_{1,2}^X\right]}^T$, $n_2=8$; ${\mathcal{X}}_3={\left[x_{3,1}^X,x_{3,2}^X,x_{1,1}^X,x_{1,2}^X\right]}^T$, $n_3=8$; ${\mathcal{X}}_4={\left[x_{4,1}^X,x_{4,2}^X,x_{1,1}^X,x_{1,2}^X,x_{2,1}^X,x_{2,2}^X\right]}^T$, $n_4=10$. Furthermore, the radial basis functions along the Y- and Z-axes demonstrate analogous characteristics to those established for the X-axis direction.

The fuzzy basis function is expressed as

$${\xi }_i={\displaystyle \frac{{\prod }_{=1}^{n_m}{K}_{F_i^P}\left({\mathcal{X}}_{\mathrm{i}}\right)}{{\sum }_{\aleph =1}^5{\prod }_{=1}^{n_m}{K}_{F_i^P}\left({\mathcal{X}}_{\mathrm{i}}\right)}}$$

(79)

The developed PAETC method is as follows:

$${\alpha }_{i,1}=-{\displaystyle \frac{e_{i,1}{\overline{\alpha }}_{i,1}^2}{{{\displaystyle \underline{p}}}_{i,1}({\mathcal{F}}_i+d_i)\sqrt{e_{i,1}^2{\overline{\alpha }}_{i,1}^2+{\nu }_{i,1}^2}}}$$

(80)

$${\overline{\alpha }}_{i,1}=r_{i,1}{e}_{i,1}^3+b_{i,1}{e}_{i,1}^{2q-1}+{\displaystyle \frac{e_{i,1}}{2}}+{\displaystyle \frac{1}{2{\tau }_{i,1}^2}}{e}_{i,1}{\xi }_{i,1}^T{\xi }_{i,1}{\hat{\vartheta }}_{i,1}$$

(81)

$$t_{i,c+1}=t_{i,c}+{\displaystyle \frac{{\Xi }_i\left|u\left(t_{i,c}\right)\right|+{\mathrm{Z}}_i}{max\left\{G_i,\left|\dot{u}\left(t_{i,c}\right)\right|\right\}}}$$

(82)

$$\begin{array}{c}\hfill {\omega }_i\left(t\right)=\left\{\begin{array}{c}-{\alpha }_{i,n}tanh\left({\displaystyle \frac{e_{i,n}{\alpha }_{i,n}}{{\omega }_i}}\right)\left(1+{\Xi }_i\right)\hfill \\ -{\displaystyle \frac{\left(1+{\Xi }_i\right)e_{i,n}}{2{\left(1-{\Xi }_i\right)}^2}},\left|u_i\right|\le {\Lambda }_i\hfill \\ {\alpha }_{i,n}-{\displaystyle \frac{1}{2}}{e}_{i,n},\left|u_i\right|>{\Lambda }_i\hfill \end{array}\right.\end{array}$$

(83)

$$u_i\left(t_i\right)={\omega }_i\left(t_{i,c}\right),\forall t\in \left[\left.t_{i,c},t_{i,c+1}\right)\right.$$

(84)

$${\alpha }_{i,2}=-{\displaystyle \frac{e_{i,2}{\hat{\gamma }}_i^2{\overline{\alpha }}_{i,2}^2}{\sqrt{e_{i,2}^2{\hat{\gamma }}_i^2{\overline{\alpha }}_{i,2}^2+{\nu }_{i,2}^2}}}$$

(85)

$$\begin{array}{cc}\hfill {\overline{\alpha }}_{i,2}=& r_{i,2}{e}_{i,2}^3+b_{i,2}{e}_{i,2}^{2q-1}+{\displaystyle \frac{e_{i,2}}{2}}+{\hat{\sigma }}_{i}tanh\left({\displaystyle \frac{e_{i,2}}{l_{i,2}}}\right)+{\displaystyle \frac{1}{2{\tau }_{i,2}^2}}{e}_{i,2}^2{\hat{\vartheta }}_{i,2}{\xi }_{i,2}^T{\xi }_{i,2}\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill {\dot{\hat{\vartheta }}}_{i,m}=& {\displaystyle \frac{{\ell }_{i,m}}{2{\tau }_{i,m}^2}}{e}_{i,m}^2{\xi }_{i,m}^T{\xi }_{i,m}-{\mu }_{i,m}{\hat{\vartheta }}_{i,m}\hfill \\ & -{\displaystyle \frac{{\mu }_{i,m}}{{\ell }_{i,m}}}{\hat{\vartheta }}_{i,m}^3,(m=1,2)\hfill \end{array}$$

(87)

$${\dot{\hat{\gamma }}}_i={\eta }_{i,2}{e}_{i,2}{\overline{\alpha }}_{i,2}-g_{i,2}{\hat{\gamma }}_i-{\displaystyle \frac{g_{i,2}}{{\eta }_{i,2}}}{\hat{\gamma }}_i^3$$

(88)

$${\dot{\hat{\sigma }}}_i=v_{i,2}{e}_{i,2}tanh\left({\displaystyle \frac{e_{i,2}}{{\epsilon }_{i,2}}}\right)-h_{i,2}{\hat{\sigma }}_i-{\displaystyle \frac{h_{i,2}}{v_{i,2}}}{\hat{\sigma }}_i^3$$

(89)

In the simulation, the nonlinear input dead zone is modeled by ${\mathcal{D}}_i\left(u_i\right)$, where the initial parameters are set as $\left[s_{i,1},s_{i,2},z_{i,1},z_{i,2}\right]=\left[1,1,-1,1\right]$. The unknown functions are defined as $p_{i,1}=1.5+0.01sin\left(x_{i,1}\right)$ and $p_{i,2}=1.5+0.01cos\left(x_{i,1}{x}_{i,2}\right)$. The trajectory of the leader is as follows: $x_a={\left[sint,cost,t\right]}^T$. The initial states of the three adaptive parameters are set to ${\hat{\vartheta }}_i=0$, ${\hat{\gamma }}_i=0$, and ${\hat{\sigma }}_i=0$. The fuzzy membership function is selected as $x_{1,1}={\left[0.05,1.05,0.05\right]}^T$, $x_{2,1}={\left[-0.1,1.1,0.1\right]}^T$, $x_{3,1}={\left[0.1,1.2,-0.1\right]}^T$, $x_{4,1}=[-0.15,0.9,$${-0.05]}^T$, $x_{1,2}=x_{2,2}=x_{3,2}=x_{4,2}=0_{3\times 1}$. The designed controller parameters are presented in Table 1.

Table 1. The design parameters.

Parameters

$r_{1,1}=b_{1,1}=10$, $r_{i,2}=b_{i,2}=2$, $r_{2,1}=b_{2,1}=22$, $r_{3,1}=b_{3,1}=22$, $q=\frac{4}{5}$, $r_{4,1}=b_{4,1}=22$, $v_{i,1}=1$, ${\Xi }_i=0.15$, $Z_i=100$, $K_i=0.1$, ${\eta }_i=1$, $M_i=10+0.1sin\left(0.01t\right)$, $Q_i=-0.02+0.002{\left(-1\right)}^i$, ${\mu }_i=0.1$, $W_i=-0.5+0.05{\left(-1\right)}^i$, $R_i=-0.2+0.02{\left(-1\right)}^i$, $F_i=-4+0.4{\left(-1\right)}^i$, $H_i=-0.01+0.001{\left(-1\right)}^i$, $J_i=-30+3{\left(-1\right)}^i$, $w_i^X=0.6+0.02{\left(-1\right)}^{i}sin\left(0.02t\right)$, $w_i^Y=0.6+0.01{\left(-1\right)}^{i}sin\left(0.02t\right)$, $w_i^Z=0.6+0.02{\left(-1\right)}^{i}sin\left(0.02t\right)$, ${\tau }_{i,1}={\tau }_{i,2}=0.15$, $g_i=0.5$, $h_i=0.01$, ${\Lambda }_i=10$, ${\ell }_i=0.1$, $l_i=0.5$, $v_{i,2}=0.2$, $G_{i,1}=4500$, $G_{i,2}=4500$, $G_{i,3}=3500$, $G_{i,4}=5500$

The results of the simulation are illustrated in Figure 3, Figure 4 and Figure 5, providing a detailed illustration of the proposed method’s performance. Specifically, Figure 3a,c,e present the output signals of the virtual leader and each follower, showing that all follower UAVs accurately track the leader’s trajectory. As can be seen from the figures, all signals remain bounded, demonstrating the effective regulation capability of the control strategy on system outputs. Figure 3b,d,f depict the synchronization errors among the followers. From the figure, it can be observed that all error values are consistently controlled within a range of 5.0%, reflecting the system’s strong robustness and consistent tracking performance. Moreover, the followers achieve rapid error convergence within a short time, indicating the system’s fast stability and high response efficiency. Even though the input dead zones and external disturbances exist, the multi-UAV system maintains stable and effective consensus tracking under the proposed controller.

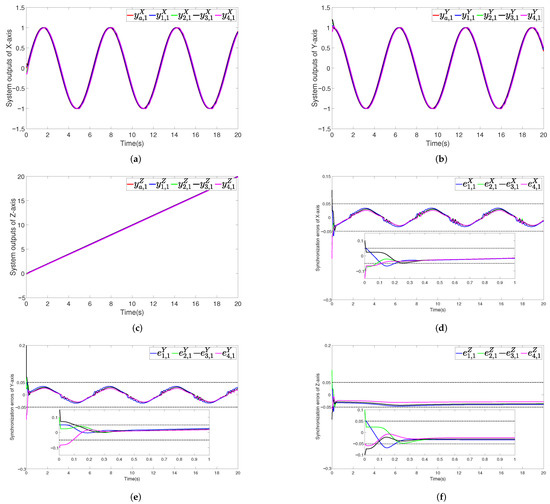
Figure 3. (a–c) The X/Y/Z-axis output trajectory of virtual leaders and the corresponding tracking results of follower UAVs. (d–f) The X/Y/Z-axis synchronization errors.

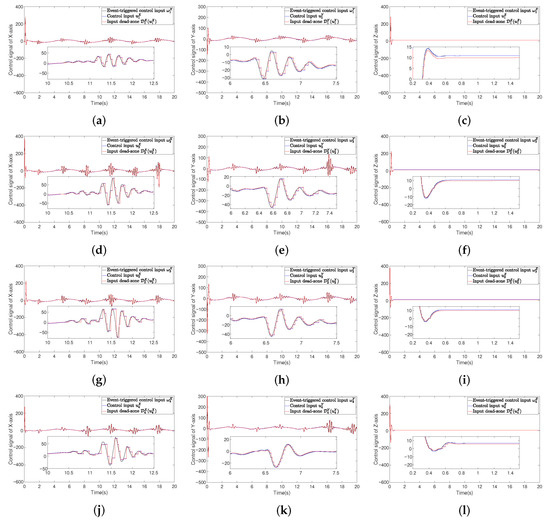
Figure 4. (a–c) The X/Y/Z-axis control inputs ${\omega }_1$, $u_1$, and ${\mathcal{D}}_1\left(u_1\right)$. (d–f) The X/Y/Z-axis control inputs ${\omega }_2$, $u_2$, and ${\mathcal{D}}_2\left(u_2\right)$. (g–i) The X/Y/Z-axis control inputs ${\omega }_3$, $u_3$, and ${\mathcal{D}}_3\left(u_3\right)$. (j–l) The X/Y/Z-axis control inputs ${\omega }_4$, $u_4$, and ${\mathcal{D}}_4\left(u_4\right)$.

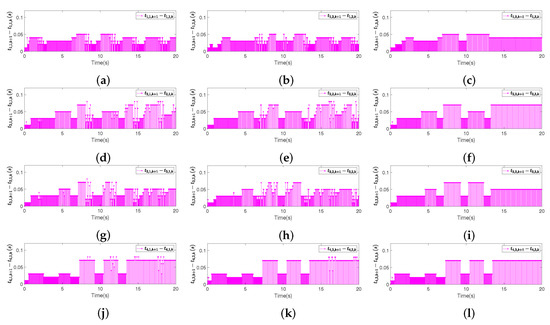
Figure 5. (a–c) The X/Y/Z-axis event triggering of actuator on UAV 1. (d–f) The X/Y/Z-axis event triggering of actuator on UAV 2. (g–i) The X/Y/Z-axis event triggering of actuator on UAV 3. (j–l) The X/Y/Z-axis event triggering of actuator on UAV 4.

Figure 4 illustrates the control signal responses of the followers. It can be seen that the proposed control scheme can effectively compensate for the input dead zone dynamically and does not require continuous updates, which further validates the effectiveness of the designed control method and its adaptability to input dead zones. Figure 5 shows that the maximal triggered time intervals of each UAV are 0.05 s, 0.08 s, 0.08 s, 0.08 s, respectively. Figure 6 and Table 2 quantify the communication resource savings, showing the percentage of bandwidth resources reduction: 70.4%, 73.4%, 71.2%, and 72.2% of communication resources are saved on each UAV, respectively. It can be observed that, compared to the conventional time-trigger control method, the proposed strategy significantly reduces the number of triggering events, verifying its superiority in lowering communication frequency. Additionally, the data reveal that the proposed event-triggered control scheme can significantly reduce the consumption of communication resources while ensuring system stability and consistent tracking performance.

Figure 6. (a) The number of triggering events in the X-axis; (b) the number of triggering events in the Y-axis; (c) the number of triggering events in the Z-axis.

Table 2. Percentage of communication bandwidth resources saved.

Description	UAV1	UAV2	UAV3	UAV4
Number of continuous-time triggers	2000	2000	2000	2000
Number of PAETC triggers ($u_k^X$)	598	561	611	559
Number of PAETC triggers ($u_k^Y$)	607	534	588	555
Number of PAETC triggers ($u_k^Z$)	571	488	527	552
Average of PAETC triggers	592	528	575	555
Resource savings rate ($u_k^X$)	70.10%	71.95%	69.45%	72.05%
Resource savings rate ($u_k^Y$)	69.65%	73.30%	70.60%	72.25%
Resource savings rate ($u_k^Z$)	71.45%	75.60%	73.65%	72.40%
Average resource savings rate	70.4%	73.4%	71.2%	72.2%

4.2. Comparison with Related Work

A comparison to related studies is shown in Table 3. Compared with the asymptotic stability or finite-time frameworks used in [47,48], fixed-time frameworks enhance robustness in practical applications by ensuring the convergence time is independent of the initial conditions. Compared with [5], with a similar purpose of fixed-time control, considering the impact of input dead zones within a fixed-time framework, as well as dynamically compensating for input dead zones, can improve the applicability of the proposed method in practical situations. Moreover, in constant to time-triggered and event-triggered control, the proposed PAETC enables adaptive updates of the trigger period, accelerating system stability while saving communication resource usage, making it more effective in practical applications.

Table 3. Comparison with related works.

Scheme	Convergence Framework	Trigger Strategy	Input Dead Zone
In [47]	AS	ET	Yes
In [48]	Finite-T	ET	Yes
In [5]	Fixed-T	ET	No
In [49]	Fixed-T	TT	Yes
Proposed	Fixed-T	PAET	Yes

AS: asymptotic stability; Fixed-T: fixed time; Finite-T: finite time; ET: event-triggered; TT: time-triggered; PAET: periodic adaptive event-triggered.

From the above analysis and simulation results, the proposed method demonstrates not only significant advantages in stability and dynamic performance but also the ability to preserve communication resource in practical applications.

5. Conclusions

A fixed-time event-triggered consensus control is proposed for uncertain nonlinear MASs with input dead zones, time-varying control gains, and external disturbances. By using a fuzzy logic system to compensate for unknown time-varying parameters and combining it with an adaptive controller, a PAETC strategy is developed. This strategy ensures the boundedness of MAS signals and achieves trajectory tracking convergence within a fixed time. Moreover, by using an adaptive-update event-triggered period, the proposed strategy effectively conserves system resources and avoids Zeno behavior. Ultimately, a theoretical analysis and simulation experiments verify the effectiveness and fixed-time stability of the designed strategy. In the future, the authors will focus on the control of MASs when dealing with actuator saturation issues and input time delay.