Abstract
Langevin ultrasonic transducers, also known as Tonpilz transducers, are widely used in high-power ultrasonic applications, including underwater sonar arrays, ultrasonic cleaning, and sonication devices. Traditionally designed for narrowband operation centered on a fundamental longitudinal resonance mode, their performance has been limited by structural constraints that tie resonance frequency to overall transducer length and mass. However, technical demands in biomedical, industrial, and underwater technologies have driven the development of broadband Langevin transducers capable of operating over wider frequency ranges. Lower frequencies are desirable for deep penetration and cavitation effects, while higher frequencies offer improved resolution and directivity. Recent design innovations have focused on modifications to the three key components of the transducer: the head mass, piezoelectric drive stack, and tail mass. Techniques such as integrating flexural or edge-resonance modes, adopting piezocomposite stacks, and tailoring structural geometry have shown promising improvements in bandwidth and transmitting efficiency. This review examines broadband Langevin transducer designs over the past three decades, offering detailed insights into design strategies for future development of high-power broadband ultrasonic transducers.
Keywords:
transducer; underwater; ultrasonics; Langevin; Tonpilz; broadband; piezoelectric; multi-mode 1. Introduction
A Langevin ultrasonic transducer, also known as a Tonpilz transducer, is a widely used high-power piezoelectric transducer, particularly suited for the elements of underwater ultrasound array projectors, ultrasonic cleaning devices, and benchtop sonicators [1,2,3]. In the Langevin configuration, the piezoelectric drive stack is sandwiched between a head mass at the front end (which radiates acoustic pressure into the water medium) and a tail mass at the back end (which serves as an inertial reaction mass to enhance forward acoustic output) [4,5]. Typically, multiple piezoelectric disks with a center hole, with the entire stack operating in longitudinal mode, are stacked with alternating poling directions to form a longitudinal piezoelectric resonator. In addition to bonding stacked non-piezoelectric layers with a central piezoelectric layer [6,7], this stack is prestressed by applying compressive force through a central tie-rod and bolt assembly [8,9].
Langevin transducer is a resonant-type, narrowband device originally designed for high-power applications rather than broadband operation [10]. Its operating frequency is primarily determined by the fundamental longitudinal resonance mode, which involves the entire length of the transducer [11,12]. Consequently, the resonance frequency is largely governed by the transducer’s longitudinal dimensions and total mass. For instance, achieving a lower single-mode operating frequency typically requires a larger and heavier overall structure, whereas smaller Langevin transducers exhibit higher resonance frequencies [13].
Langevin transducers with wide frequency bandwidths are advantageous for biomedical, industrial, and underwater applications. Lower frequencies are often preferred for acoustic transmission with reduced propagation losses, and acoustic cavitation generation for subsequent mechanochemical effects [14,15,16], while higher frequencies offer greater beam directivity and controllability [17,18,19]. Accordingly, a variety of broadband Langevin transducer designs have been developed to meet these demands [20,21]. These designs typically involve significant modifications to the three main components: the head mass, piezoelectric drive stack, and tail mass [8,20]. For example, the traditional cylindrical head mass has been replaced with tapered geometries to harness head-edge-flexural resonance modes, thereby extending the −3 dB or −6 dB transmitting voltage response (TVR) bandwidth alongside the fundamental longitudinal mode [9,22]. Additionally, piezoelectric composite drive stacks have demonstrated wider bandwidths due to their lower mechanical quality factor (QM) and higher electromechanical coupling coefficient (kt) compared to conventional ceramic stacks [23,24]. As a result, modern broadband Langevin designs require more sophisticated analysis and optimization procedures to select appropriate design parameters for various high-power ultrasound applications. We expect that a detailed technical review of these broadband Langevin transducer designs provides useful, in-depth insight for designers and engineers aiming to develop high-performance, broadband Langevin transducers for biomedical, industrial, and underwater applications.
While a few recent review articles broadly surveyed underwater sensing techniques and various ultrasonic transducer types including Tonpilz, flextensional, Moonie, and Cymbal transducers [13,25], further details of the key design strategies for achieving broadband characteristics should provide informative design guidelines for designing broadband Langevin transducers. In this review, we aim to provide a technical review of broadening frequency band approaches focusing specifically on advancements over the past three decades in broadband Langevin transducer designs, organized around the three main transducer components: the piezoelectric drive stack, head mass, and tail mass, each discussed in dedicated chapters to summarize current developments and design approaches (Figure 1).
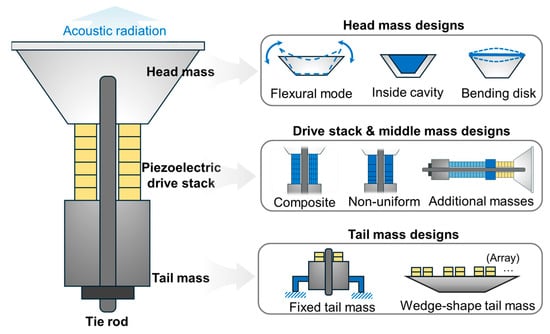
Figure 1.
Schematic of a Langevin transducer design and summary of key component strategies for broadband frequency response.
This review focuses specifically on broadband Tonpilz transducer designs based on piezoceramic materials, which remain the predominant choice for high-power applications. While magnetostrictive and piezoelectric polymer are important alternative transducer materials, their design principles are beyond the scope of this article. Additionally, the scope of this review is confined to transmitting (projector) applications, particularly those requiring broadband output under high-power operating conditions.
2. Head Mass Designs
The head mass of a Langevin transducer plays a crucial role in shaping its acoustic response [8,26]. Early designs typically featured traditional head masses optimized for narrowband operation, focusing solely on the fundamental longitudinal resonance mode. In these designs, other nearby vibration modes, such as flexural modes, were initially regarded as spurious, as they were believed to degrade the transducer’s transmission performance [4,27]. Thus, early strategies for bandwidth enhancement were limited to lower the QM by using light head mass material (e.g., aluminum and heavy-particle/epoxy composite) which stores less inertial energy (causing the Langevin transducer to damp out more quickly) together with the application of multiple acoustic matching layers on the front face of the head mass to improve transmission over a broader frequency range [21,28].
However, significant advancement was made when light head mass designs demonstrated the ability to broaden the frequency bandwidth by effectively utilizing additional flexural vibration modes [27]. These modes could be coupled with the primary longitudinal resonance, enabling enhanced performance across a wider frequency range [9]. This finding led to the development of various head mass modification strategies, building the foundation for modern broadband Langevin transducer designs, such as inside cavity or penetrating hole designs [29,30], additional bending disk design [31], and head filling design [32].
Table 1 summarizes different head mass design approaches aimed at achieving broadband performance. It should be noted that the frequency bandwidth, TVR, resonance frequency (fr), anti-resonance frequency (fa), and central frequency (fc) values were summarized based on the final reported results or estimated from graphs in each referenced paper, following the priority order of (1) experimental data, (2) finite element analysis (FEA) results, and (3) theoretical modeling data. Although some surveyed papers include interesting Langevin transducer designs focusing on head mass modifications [26,33,34], papers lacking explicit frequency bandwidth information were excluded from the table. Based on the reviewed literature, two principal design approaches were dominant: (1) the utilization of flexural vibration modes and (2) the introduction of additional central bending modes in the head mass structure. These strategies reflect the ongoing effort to broaden operational bandwidth while maintaining or improving acoustic performance.

Table 1.
Reported head mass design strategies contributing to broadband performance in Langevin transducers, where fr, and fc mean the first peak frequency and the central frequency, respectively.
2.1. Flexural Mode of a Tappered Head Mass
In comparison with classical head masses with uniform geometry, tapered head mass designs introduce gradients in stiffness and mass distribution, naturally supporting flexural resonance modes at frequencies near the fundamental longitudinal resonance [27,40]. These flexural modes can constructively couple with the primary longitudinal mode, resulting in a dual-peak response and significantly broadening the overall bandwidth of the Langevin transducer [9].
To effectively harness this flexural edge mode, careful selection of the head mass material and geometric parameters is essential. An approximate expression for the head mass flexural resonance frequency is given by Equation (1), where ch, th, Dh, and νh denote the wave speed, thickness, diameter, and Poisson’s ratio of the head mass, respectively [8]. Due to the nature of coupled mode vibration, the mode coupling with a flexural mode typically lowers the fundamental longitudinal resonance frequency [19,27].
According to this expression, a thinner head mass with a larger diameter shifts the flexural resonance frequency lower, bringing it closer to the fundamental longitudinal resonance. Applying a taper (where the edge thickness is reduced) can further lower the flexural mode frequency. However, the frequency alignment is not the only consideration; the transmitting voltage response (TVR) amplitude of the flexural mode is also important.
An optimal design achieves a close frequency spacing between the longitudinal and flexural modes (e.g., 1.5–2.0fr, where fr s the longitudinal resonance frequency), with minimal TVR difference between the peaks (ideally <1 dB). As illustrated in Figure 2A, a well-designed tapered head mass produces a dual-peak TVR spectrum (blue), while a conventional single-mode design shows only one dominant peak (black). Conversely, if the head mass is made too light or has an excessively thin edge, the flexural mode may become overly dominant, resulting in a higher-frequency resonance peak and a pronounced null in the TVR between modes (Figure 2A, red spectrum). This phase cancelation arises because roughly half the outer region of the head mass vibrates out of phase with the inner region [8], leading to degradation in broadband response. Therefore, optimizing both the frequency gap and the TVR magnitude difference between the two modes is essential. To incorporate additional structural resonance modes with the fundamental longitudinal resonance mode, various head mass design optimization strategies have been implemented to meet this goal, achieving −6 dB fractional bandwidths (FBWs) exceeding 80% in some previous studies [9,38].
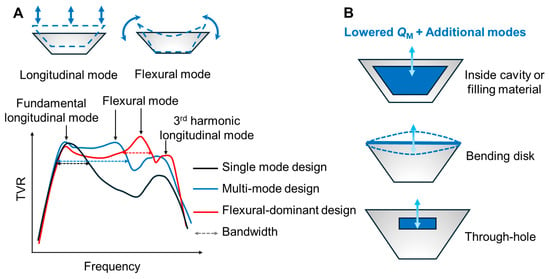
Figure 2.
Representative head mass design modifications to enhance broadband performance: (A) tapered edge designs utilizing flexural modes, with representative TVR spectra (illustrated); (B) broadband models incorporating cavities or holes in the head mass.
2.2. Hole, Cavity, and Filling Materials Inside the Head Mass
An important design guideline for broadband Tonpilz transducers is that the head mass should be lighter than the tail mass to achieve a lower QM [8]. A lower QM is directly associated with broader bandwidth as a lighter head mass stores less inertial energy, resulting in the Langevin transducer damping out more quickly, which makes a lightweight head mass a fundamental strategy for broadband design. Thus, various innovative head mass configurations have been developed, primarily incorporating internal cavities or through-holes to reduce mass [29,30,37]. These air-filled cavities significantly decrease the effective mass of the head, contributing to enhanced broadband performance. Additionally, some designs utilize lightweight filler materials to further optimize mass without compromising structural integrity.
Beyond simple mass reduction, cavities and holes in the head mass also influence vibrational behavior. In particular, the flexural edge (or flapping) mode is sensitive to the cavity geometry [37]. Properly designed cavities can enable an additional front-end surface vibration mode that couples with the flexural resonance. This coupling enhances bandwidth by shifting the flexural mode closer to the fundamental longitudinal resonance, which is otherwise too distant in frequency for solid tapered head designs (see Figure 2A, red TVR spectrum). As a result, cavity-based designs allow more effective utilization of flexural modes at higher frequencies.
This beneficial effect of cavity-induced center bending has been demonstrated in several head mass configurations, including internal cavities, through-hole designs, and added flexible bending disks. These approaches have achieved remarkable −6 FBWs, exceeding 100% in some cases [30,31,37].
2.3. Combined Effects with a Piezoelectric Composite Drive Section
The aforementioned recent advances in Tonpilz transducer head mass designs are often closely integrated with innovations in the drive section as well. In particular, the use of piezoelectric composite materials, especially 1–3 piezoelectric composites, as the drive section has emerged as a powerful approach to enhance broadband performance. These composites exhibit both high electromechanical coupling coefficients (kt) and low QM, which are highly favorable for achieving broad frequency bandwidths in high-power ultrasonic transducers.
Several of the surveyed works in this chapter highlight the synergistic combination of two key strategies: (1) the utilization of flexural modes enabled by lightweight or cavity-based head mass designs, and (2) the adoption of piezoelectric composites in the drive stack. This dual approach allows the transducer to benefit simultaneously from structural and material-based bandwidth enhancement mechanisms. For instance, one reported design that combines a cavity-type head mass with a 1–3 composite drive section achieved a remarkable −6 dB FBW of 129%, significantly outperforming the conventional Tonpilz designs [37].
The interplay between flexural resonance in the head mass and the broader frequency response facilitated by composite materials effectively expands the operational bandwidth while maintaining acoustic output performance. The piezoelectric composite’s low QM enables a more damped response, allowing energy to spread across a wider frequency range, while the cavity or through-hole in the head mass brings in higher-order flexural modes closer to the primary longitudinal mode. This combination not only widens the useful bandwidth but also smooths the TVR spectrum, which is crucial for high-fidelity broadband applications.
Further details on the design principles and material choices for piezoelectric composite stacks will be explored in the next chapter, Piezoelectric Drive Stack and Middle Mass, where their advantages and limitations will be discussed.
3. Piezoelectric Drive Stack and Middle Mass
The piezoelectric drive stack is the most critical component in a Tonpilz transducer, as it governs the overall electromechanical transduction efficiency and strongly influences the operational bandwidth [8]. A high electromechanical coupling coefficient k33 is typically desirable for the drive stack of Langevin transducers. However, the QM of the piezoelectric material also plays a vital role in determining broadband performance. In this context, lead magnesium niobate–lead titanate (PMN-PT) single crystals have attracted attention due to their combination of high piezoelectric coefficients and low QM (<50) compared to soft piezoelectric ceramics like PZT-5H, which typically exhibit QM around 60–100 [42,43].
Despite their superior electromechanical properties, PMN-PT single crystals are brittle and expensive, which limits their practical use in Langevin transducers that require high prestressing forces via a central tie rod. As an alternative, piezoelectric composites, such as 2–2 or 1–3 piezocomposites, offer a favorable balance of high electromechanical coupling and low QM while maintaining cost-efficiency and manufacturability [44,45]. These composites have been utilized as useful materials for the drive sections of broadband Langevin transducers.
In addition to material choice, the drive stack positioning and the inclusion of intermediate (middle) masses have been explored to further broaden the frequency response. By increased eigenmodes in the operating frequency range, properly designed drive stack and middle mass configurations can support multiple resonance modes, making them effective strategies for multimode or broadband operation. The summarized findings related to the drive section and middle mass configurations are presented in Table 2.

Table 2.
Reported drive stack and middle mass design strategies contributing to broadband performance in Langevin transducers, where fr, and fc mean the first peak frequency and the central frequency, respectively.
3.1. Piezoelectric Composite Drive Stacks
The intrinsic properties of piezoelectric materials dictate that the electromechanical coupling coefficient for the longitudinal mode (k33) is generally higher than that for the thickness mode (kt), primarily due to differences in boundary conditions [52]. However, by dicing a thickness-mode sample into multiple narrow columns to form a 1–3 piezoelectric composite, the effective kt can surpass that of the bulk material with the same overall dimensions [45]. In addition, the epoxy matrix that surrounds the piezoelectric columns in a 1–3 composite introduces mechanical damping due to its soft, lossy nature, resulting in a significantly lower QM compared to pure piezoelectric ceramics, although the 1–3 piezoelectric composite structure is less robust than pure ceramics under high pre-stress conditions imposed by the tie-rod and bolt assembly, and more susceptible to excessive heating during high-power operation. These two advantages, i.e., enhanced electromechanical coupling and reduced QM, have been actively exploited in the development of broadband piezo-composite ultrasonic transducers, including Langevin transducers.
Among composite configurations, a volume fraction of 60–70% piezoelectric material has been shown to yield the highest electromechanical coupling coefficient, and is thus commonly used in drive section design [53,54]. Early implementations of 2–2 and 1–3 composites in single-mode Tonpilz transducers produced modest improvements in bandwidth [23,46]. However, significant bandwidth enhancement was achieved when 1–3 composites were combined with multi-mode transducer architectures. Unlike conventional ceramics, 1–3 composites exhibit a broader and flatter frequency response due to the less pronounced resonance peak at the fundamental longitudinal mode [9]. This characteristic facilitates smoother transitions between the longitudinal and flexural modes, enabling the realization of dual-mode or broadband operation.
By integrating 1–3 composite drive stacks with multi-mode cavity-type head masses, recent designs have demonstrated exceptional bandwidth performance, achieving −6 dB fractional bandwidths exceeding 120% in experimental validations [37].
3.2. Additional Masses in the Middle
In general piezoelectric device designs, vibration characteristics, such as resonance frequency, mode shape, and amplitude, can be passively tuned by stacking additional non-piezoelectric layers [55,56]. Similarly, incorporating additional masses and compliant elements into Tonpilz transducer structures has proven to be a highly effective strategy for achieving broadband, multi-mode performance. These multiple-mass configurations typically consist of a tail mass, an active piezoelectric drive section, one or more center (middle) masses, passive compliant members, and a head mass. This structure forms a mass–spring–mass–spring–mass system, capable of supporting multiple coupled resonance modes [8,12].
By carefully tuning the placement, mass ratios, and stiffness of these elements, the transducer can exhibit three or more distinct resonance frequencies. For example, broadband performance is enhanced when the center and tail masses are of equal weight, and the head mass and matching layer each comprise approximately half the weight of the tail mass. Such designs have demonstrated significant bandwidth improvements, with operational frequency ranges expanding from 13 kHz to ~25 kHz, substantially wider than those of conventional Tonpilz transducers of similar size and weight [12].
Recent studies have further demonstrated the benefits of multiple middle masses for broadband operation [47]. By optimizing the length and position of dual drive stacks, the first three longitudinal modes can be effectively activated, yielding a broader and flatter TVR. In continued work, they extended this concept by incorporating three drive stacks and multiple internal masses, enabling the excitation of four consecutive longitudinal resonances. Through the combination of finite element analysis and simulated annealing optimization, they developed an ultra-wideband transducer with an operating range from 19.5 kHz to 90 kHz. Notably, this was achieved without compromising the transducer’s structural simplicity [48], and the approach also shares similarities with the non-uniform stack driving effect [49].
These findings indicate the effectiveness of using multiple center masses and drive stacks to facilitate multi-resonance behavior in Tonpilz transducers. By utilizing the coupling of higher-order longitudinal modes and maintaining a balanced mechanical structure, transducer developers can achieve significantly widened bandwidths while preserving the compact and robust characteristics.
4. Tail Mass Designs
For broadband or multi-resonance mode operation, tail mass design is generally more straightforward compared to other key components such as the head mass and piezoelectric drive stack. The primary design parameter is the mass of the tail, which is governed by its thickness, lateral dimensions, and material density [57]. Traditionally, tail mass tuning has involved adjusting the volume and selecting different metal materials, following the classical design approach of making the tail mass heavier than the head mass [8]. Due to this relatively simple and conventional strategy, few innovative tail mass design concepts have been explored for achieving broadband performance in Langevin transducers.
Recent developments have introduced novel tail mass design strategies aimed at generating additional resonance modes. These include using supporting materials attached to or embedded within the tail mass, shaping the tail mass to influence wave reflection and propagation direction, and incorporating asymmetric liquid cavities, particularly in Janus–Helmholtz (JH) transducer designs. The results from these design approaches, focusing on tail mass modifications for broadband or multi-mode operations, are summarized in Table 3.

Table 3.
Reported tail mass design strategies contributing to multi-mode performance in Langevin transducers, where ft, fr, and fc mean the fixed tail resonance frequency, the longitudinal peak frequency, and the central frequency, respectively.
4.1. Rear-Mounted Tail Mass Designs for Low-Frequency Resonance
As a resonant-type, narrowband transducer, its operating frequency is primarily governed by the fundamental longitudinal resonance mode, which is inversely related to the transducer’s axial length. Consequently, achieving lower resonance frequencies necessitates larger and heavier transducer assemblies. Low-frequency operation is especially desirable for underwater wave transmission due to its lower attenuation in the medium [62]. To deliver the required acoustic intensity and beam directivity at these frequencies, large-scale array systems are typically employed. However, the size and weight of conventional Tonpilz transducers present practical limitations for use in array platforms with constrained payload capacity [11,63].
To overcome these challenges, compact transducer designs that support low-frequency operation were realized by novel fixed tail mass Tonpilz configuration [11,58,59]. This design features a tail mass suspended by an elastomeric support, introducing an additional resonance mode due to the compliance of the suspension system. As a result, a whole-body oscillation mode occurs below the standard longitudinal resonance, enabling dual-band operation (Figure 3).
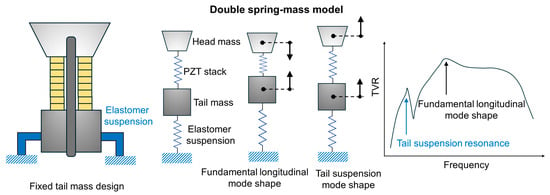
Figure 3.
Summary of the fixed tail mass design with representative TVR spectrum (illustrated): an elastomer suspension supports the tail mass, introducing an additional resonance mode at a frequency lower than the fundamental longitudinal resonance mode.
The concept of a fixed tail mass was initially proposed through a preliminary design study using finite element analysis (FEA). Utilizing 2D axisymmetric FEA models, the study identified useful trends in parameter effects across a limited number of cases [58]. To enable a more comprehensive parametric investigation, a theoretical framework based on equivalent circuit models (both lumped and distributed) was subsequently developed [11,59]. Through these 1-D equivalent circuit models, several key findings were revealed: (1) increasing the suspension stiffness reduces the frequency ratio between the sub-fundamental and fundamental modes, thereby enhancing the low-frequency TVR; (2) decreasing the tail mass thickness improves the TVR at the sub-fundamental mode, which contrasts with conventional designs that favor heavier tail masses; and (3) increasing the head mass thickness yields a slight improvement in sub-fundamental TVR, although its effect is less significant than the other parameters [11]. The suspension structure stiffness can be tailored by either dimension or a synthesis process of metal-particle/epoxy composites [64,65]. While experimental validation is still pending, the rear-mounted transducer design with optimized parameters demonstrates promising dual-mode transmission characteristics, offering a compact and effective solution for broadband underwater applications [11].
4.2. Wedge-Shaped, Shared Tail Mass Block for Tonpilz Array Elements
Another distinctive tail mass configuration involves a wedge-shaped shared tail mass block designed for Tonpilz array elements (Figure 4). This approach was introduced to enhance the acoustic performance of linear Tonpilz array transducers, in conjunction with electrical compensation, with the primary objective of improving the Figure of Merit (FOM), a critical metric that reflects the balance between TVR, power consumption, and overall system size.
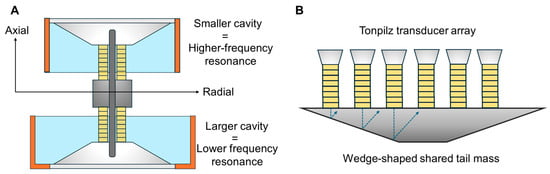
Figure 4.
Schematics of broadband Janus–Helmholtz (JH) transducer design (A) and wedge-shaped shared tail mass design (B).
The design integrates 12 Tonpilz elements arranged linearly, all mechanically coupled to a single, wedge-shaped tail mass structure. In contrast to traditional designs employing flat, parallel tail masses, the wedge geometry offers both mechanical and acoustic advantages. Most notably, it aims to suppress backward-propagating acoustic waves, which are known to induce inter-element crosstalk, energy loss, and undesirable modal coupling in densely packed transducer arrays [60,63].
Although the original paper did not explicitly explain the backward wave suppression mechanism, the underlying rationale can be inferred. The tapered geometry of the wedge-shaped tail mass is expected to gradually redirect backward-traveling acoustic energy away from the transducer axis, promoting refraction and scattering along non-axial paths [66]. This reduces constructive interference and minimizes acoustic reflections toward the drive stack, thereby preserving forward radiation and enhancing overall efficiency [60].
4.3. Multi-Cavity Janus–Helmholtz Transducer
A slight modification of the conventional Langevin transducer leads to the development of the JH transducer, which typically consists of a shared tail mass and two back-to-back piezoelectric hemispheres or disks that expand and contract in the radial direction [67]. A recently introduced design presents an innovative enhancement to JH transducers by integrating multiple liquid-filled cavities of varying dimensions (Figure 4A). This approach aims to achieve broadband acoustic radiation, particularly in the low-frequency range, which is critical for applications such as underwater communication and sonar systems. Specifically, the use of two liquid cavities of different sizes enables the coupling of multiple resonance modes, effectively broadening the operational frequency range. Results from equivalent circuit modeling, finite element analysis (FEM), and experimental measurements demonstrate the emergence of distinct resonance peaks due to the asymmetric cavity configuration, as well as a significantly broader operating bandwidth compared to traditional JH transducer designs [61].
5. Summary and Future Perspectives
5.1. Discussion
This review has examined recent advancements in the design of broadband Langevin (Tonpilz-type) ultrasonic transducers, with a focus on the three critical components: the head mass, piezoelectric drive stack, and tail mass. The head mass has emerged as the most impactful element for enhancing bandwidth. Its direct role in acoustic radiation makes it highly sensitive to geometric modifications, flexural mode integration, and impedance tuning, all of which have been shown to substantially broaden the transducer’s operational bandwidth [40,57,68].
The piezoelectric drive stack is another area of active innovation, particularly with the adoption of piezoelectric composites and intermediate mass-coupled structures. These approaches introduce multiple resonant modes and improve electromechanical coupling, both of which contribute to broadband performance. In contrast, the tail mass has received comparatively little attention in the literature, with limited contribution to bandwidth enhancement in most reviewed designs. In summary, these studies reflect consistent attention toward engineering Langevin transducers for both broadband and high-power applications. They provide valuable design insights and highlight the potential of emerging technologies to shape future generations of transducers.
One limitation in this review is the gap between simulated predictions and experimentally validated results. Langevin transducers are most commonly employed in low-frequency (<100 kHz) ultrasonic applications, where longer wavelengths present experimental challenges. Reflections from surrounding boundaries in test setups often interfere with accurate measurements, complicating empirical validation. Consequently, many researchers rely heavily on FEM simulations to explore design options and predict performance. While FEM offers robust modeling capabilities, inconsistencies in simulation setups, material parameters, and boundary conditions can make cross-study comparisons difficult. To maintain clarity, this review distinguished between results obtained from simulations, theoretical models, and experimental measurements. It is encouraged to critically evaluate the source and methodology of each reported metric when benchmarking transducer performance.
5.2. Applications of Broadband Langevin Transducer and Future Perspectives
Current applications of broadband Tonpilz transducers are primarily found in underwater sonar projector systems. Compared to narrowband alternatives, broadband projectors offer several advantages: (1) enhanced target discrimination enabled by complex, frequency-modulated signals, which improve range resolution and object identification, (2) improved multipath suppression through short-duration pulses and higher pulse repetition rates, and (3) multi-functionality, allowing operation in multiple modes to support various ranging and detection tasks with a single device [8,12,14,40].
In biomedical applications, high-power broadband Langevin transducers show strong potential for versatile cavitation-enhanced biosample processing. Unlike conventional commercial Langevin transducers operating at a single frequency (typically 20–40 kHz), broadband devices support higher frequency modes and a wider operating range, enabling more flexible and effective pulsing strategies. This is especially beneficial for activating diverse cavitation agents such as perfluorocarbon microbubbles, phase-change nanodroplets, and nanostructured cavitation enhancers, tailored to specific therapeutic or treatment purposes [15,69,70,71].
Several promising research directions could further expand the performance and design versatility of broadband Langevin transducers. (1) Integration of acoustic metamaterials: Embedding metamaterials or metastructures within the head or tail mass could enable tailored impedance characteristics, additional resonant modes, and optimized QM. These innovations may unlock new performance levels in bandwidth and efficiency, particularly when implemented via additive manufacturing (AM) [66,72]. (2) Advances in piezoelectric materials: Next-generation single-crystal and high-coupling composite piezoelectric materials hold potential for superior electromechanical transduction with enhanced frequency response. These materials could offer broader operational bandwidths while maintaining structural reliability. (3) High-fidelity 3D printing: AM can drastically accelerate the prototyping and testing of complex Langevin transducer geometries. It may facilitate novel structural designs and facilitate the development of compact or high-frequency Langevin transducers [73], including those for biomedical or micro-scale applications [74]. (4) Material characterization for AM: Realizing the full potential of 3D printing in functional transducer design will require systematic characterization of printable materials. Detailed databases on the acoustic and mechanical properties of common AM materials, such as PLA, photopolymers, metal composites, and high-density resins, are crucial for reliable and repeatable design outcomes for Tonpilz transducer assembly. (5) Lastly, the key features of Tonpilz transducer assemblies, specifically, the use of additional resonance modes enabled by stacked mass structures, can also be applied to other electro-thermo-mechanical engineering applications with the broad operational frequency bandwidth, such as acoustic levitation devices, energy harvesters, and biosample sonicators [15,75,76,77].
5.3. Conclusions
In conclusion, this review has examined recent advancements in broadband Langevin transducer designs, with a focus on multi-mode operation strategies involving the head mass, piezoelectric drive stack, and tail mass. Each component plays a critical role in the generation, coupling, and separation of resonance modes, and precise control of these modes has enabled –6 dB fractional bandwidths of up to 80% in some designs. The future of broadband Langevin transducer design lies in the convergence of multiple disciplines, electrical engineering, materials science, acoustics, mechanical design, and additive manufacturing. These collaborative advances may promise technical innovation of high-performance ultrasonic transducers for underwater, industrial, and biomedical applications.
Author Contributions
Conceptualization, J.K. (Jinwook Kim); writing—original draft preparation, J.K. (Jinwook Kim); writing—review and editing, J.K. (Jinwook Kim), J.K. (Jinwoo Kim) and J.K. (Juwon Kang); Visualization, J.K. (Jinwook Kim), J.K. (Jinwoo Kim) and J.K. (Juwon Kim). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Kyungpook National University Research Fund, 2024.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, S. Study on the Multifrequency Langevin Ultrasonic Transducer. Ultrasonics 1995, 33, 445–448. [Google Scholar] [CrossRef]
- Escoffre, J.-M.; Bouakaz, A. (Eds.) Therapeutic Ultrasound; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-22535-7. [Google Scholar]
- Su, S.; Wang, Y.; Zheng, L.; Sun, M.; Tang, Q.; Huang, H. Study on the Cooling Performance of a Focused Ultrasonic Radiator for Electrical Heating Elements. Micromachines 2024, 15, 116. [Google Scholar] [CrossRef] [PubMed]
- Safari, A.; Akdogan, E.K. Piezoelectric Transducers and Acoustic Materials for Transducer Aplications; Springer Science & Business Media: New York, NY, USA, 2008; ISBN 978-0-387-76538-9. [Google Scholar]
- Alvarez, N.P.; Cardoni, A.; Cerisola, N.; Riera, E.; Andrade, M.A.; Adamowski, J.C. Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers. Actuators 2015, 4, 255–266. [Google Scholar] [CrossRef]
- Mieczkowski, G.; Borawski, A.; Szpica, D. Static Electromechanical Characteristic of a Three-Layer Circular Piezoelectric Transducer. Sensors 2020, 20, 222. [Google Scholar] [CrossRef] [PubMed]
- Mieczkowski, G. Optimization and Prediction of Durability and Utility Features of Three-Layer Piezoelectric Transducers. Mechanika 2018, 24, 335–342. [Google Scholar] [CrossRef]
- Sherman, C.H.; Butler, J.L. Transducers and Arrays for Underwater Sound; Springer: New York, NY, USA, 2007; ISBN 0387329404. [Google Scholar]
- Kim, J.; Kim, H.; Roh, Y. Design and Fabrication of Multi-Mode Wideband Tonpilz Transducers. J. Acoust. Soc. Korea 2013, 32, 191–198. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, X.; Chen, Y.; Zhang, Z.; Zheng, H. Modeling of High-Power Tonpilz Terfenol-D Transducer Using Complex Material Parameters. Sensors 2022, 22, 3781. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Roh, Y. Modeling and Design of a Rear-Mounted Underwater Projector Using Equivalent Circuits. Sensors 2020, 20, 7085. [Google Scholar] [CrossRef] [PubMed]
- Butler, S.C. Triple-Resonant Transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1292–1300. [Google Scholar] [CrossRef] [PubMed]
- Pyun, J.Y.; Kim, Y.H.; Park, K.K. Design of Piezoelectric Acoustic Transducers for Underwater Applications. Sensors 2023, 23, 1821. [Google Scholar] [CrossRef] [PubMed]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Snaders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Kasoji, S.K.; Pattenden, S.G.; Malc, E.P.; Jayakody, C.N.; Tsuruta, J.K.; Mieczkowski, P.A.; Janzen, W.P.; Dayton, P.A. Cavitation Enhancing Nanodroplets Mediate Efficient DNA Fragmentation in a Bench Top Ultrasonic Water Bath. PLoS ONE 2015, 10, e0133014. [Google Scholar] [CrossRef] [PubMed]
- O’Daly, B.J.; Morris, E.; Gavin, G.P.; O’Byrne, J.M.; McGuinness, G.B. High-Power Low-Frequency Ultrasound: A Review of Tissue Dissection and Ablation in Medicine and Surgery. J. Mater. Process. Technol. 2008, 200, 38–58. [Google Scholar] [CrossRef]
- Wu, H.; Hossain, M.M.; Kim, H.; Gallippi, C.M.; Jiang, X. A 1.5-D Array for Acoustic Radiation Force (ARF)-Induced Peak Displacement-Based Tissue Anisotropy Assessment with a Row-Column Excitation Method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1278–1287. [Google Scholar] [CrossRef] [PubMed]
- Kurusingal, V. Tonpilz Transducer Array for Wideband Sonar Applications. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Scotland, UK, 6–9 October 2019; pp. 1750–1752. [Google Scholar]
- Noh, E.; Lee, H.; Chun, W.; Ohm, W.-S.; Been, K.; Moon, W.; Chang, W.; Yoon, H. Iterative Solutions of the Array Equations for Rapid Design and Analysis of Large Projector Arrays. J. Acoust. Soc. Am. 2018, 144, 2434–2446. [Google Scholar] [CrossRef] [PubMed]
- Yao, Q.; Bjorno, L. Broadband Tonpilz Underwater Acoustic Transducers Based on Multimode Optimization. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 1060–1066. [Google Scholar] [CrossRef]
- VanCrombrugge, M.; Thompson, W., Jr. Optimization of the Transmitting Characteristics of a Tonpilz-type Transducer by Proper Choice of Impedance Matching Layers. J. Acoust. Soc. Am. 2005, 75, S16. [Google Scholar] [CrossRef]
- Hawkins, D.W.; Gough, P.T. Multiresonance Design of a Tonpilz Transducer Using the Finite Element Method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 782–790. [Google Scholar] [CrossRef]
- Pei, D.L.; Roh, Y. Design of an Underwater Tonpilz Transducer with 1–3 Piezocomposite Materials. Jpn. J. Appl. Phys. 2008, 47, 4003. [Google Scholar] [CrossRef]
- Kim, J.; Roh, Y. Equivalent Properties of 1–3 Piezocomposites of PMN-PT Single Crystals for Transducers. In Proceedings of the SPIE Smart Structures and Materials+ Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 6–10 March 2011; Volume 7978, pp. 797826–797828. [Google Scholar]
- Sun, K.; Cui, W.; Chen, C. Review of Underwater Sensing Technologies and Applications. Sensors 2021, 21, 7849. [Google Scholar] [CrossRef] [PubMed]
- Roh, Y.; Afzal, M.S.; Kwon, S.R. Analysis of the Effect of Radiating Surface Geometry on the Beam Pattern of Underwater Acoustic Transducers. Sens. Actuators A Phys. 2021, 330, 112843. [Google Scholar] [CrossRef]
- Butler, J.L.; Cipolla, J.R.; Brown, W.D. Radiating Head Flexure and Its Effect on Transducer Performance. J. Acoust. Soc. Am. 1981, 70, 500–503. [Google Scholar] [CrossRef]
- Douglas, G.R.; Wilson, C.R. Tonpilz Head Mass Studies. J. Acoust. Soc. Am. 1982, 72, S9. [Google Scholar] [CrossRef]
- Chhith, S.; Roh, Y. Wideband Tonpilz Transducer with a Cavity inside a Head Mass. Jpn. J. Appl. Phys. 2010, 49. [Google Scholar] [CrossRef]
- He, X.; Zhu, X.; Wu, Z.; Kang, X.; Wang, Y. A Wideband Tonpilz Transducer with a Transverse Through-Hole in the Radiating Head. J. Acoust. Soc. Am. 2021, 150, 2655–2663. [Google Scholar] [CrossRef] [PubMed]
- Saijyou, K.; Okuyama, T. Design Optimization of Wide-Band Tonpilz Piezoelectric Transducer with a Bending Piezoelectric Disk on the Radiation Surface. J. Acoust. Soc. Am. 2010, 127, 2836–2846. [Google Scholar] [CrossRef] [PubMed]
- Gou, Y.; Ye, S.; Fu, X.; Zheng, F.; Zha, X.; Li, C. Optimizing Tonpilz Transducer Transmission Through Impedance Matching and Head Mass Structure. Micromachines 2025, 16, 352. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, M. Acoustic Characteristic Analysis of a Langevin Transducer Attached with a Circular Plate Supported on a Concentric Circle. Jpn. J. Appl. Phys. 2025, 64, 28006. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, G.; Zhang, X. A Low-Frequency Longitudinal Vibration Transducer with a Helical Slot Structure. J. Acoust. Soc. Am. 2019, 145, 2948–2954. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Hu, J. Study on the Broadband Tonpilz Transducer with a Single Hole. Ultrasonics 2009, 49, 419–423. [Google Scholar] [CrossRef] [PubMed]
- Afzal, M.S.; Lim, Y.; Lee, S.; Yoon, H.; Roh, Y. Optimization and Characterization of a Wideband Multimode Tonpilz Transducer for Underwater Acoustical Arrays. Sens. Actuators A Phys. 2020, 307, 112001. [Google Scholar] [CrossRef]
- Kim, H.; Roh, Y. Design and Fabrication of a Wideband Tonpilz Transducer with a Void Head Mass. Sens. Actuators A Phys. 2016, 239, 137–143. [Google Scholar] [CrossRef]
- Pyo, S.; Lim, Y.; Roh, Y. Analysis of the Transmitting Characteristics of an Acoustic Conformal Array of Multimode Tonpilz Transducers by the Equivalent Circuit Method. Sens. Actuators A Phys. 2021, 318, 112507. [Google Scholar] [CrossRef]
- Kurt, P.; Şansal, M.; Tatar, İ.; Duran, C.; Orhan, S. Vibro-Acoustic Design, Manufacturing and Characterization of a Tonpilz-Type Transducer. Appl. Acoust. 2019, 150, 27–35. [Google Scholar] [CrossRef]
- Abdullah, Z.; Naz, S.; Raja, M.A.Z.; Zameer, A. Design of Wideband Tonpilz Transducers for Underwater SONAR Applications with Finite Element Model. Appl. Acoust. 2021, 183, 108293. [Google Scholar] [CrossRef]
- Lin, S. Analysis of Multifrequency Langevin Composite Ultrasonic Transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1990–1998. [Google Scholar] [CrossRef] [PubMed]
- Yalcin, E.; Ankut, M.; Sungur, S.M.; Turgut, H.I.; Kar, K.S.; Alkoy, S.; Aykac, A.; Boz, M.; Aydin, E.; Gozuacik, N.K.; et al. Comparison of the Performance Characteristics of the Tonpilz Transducers Fabricated from 0.60PMN-0.40PT & PZT Piezoceramics. Ferroelectrics 2021, 586, 82–92. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Yuan, F. Guided Wave Generation, Sensing and Damage Detection Using in-Plane Shear Piezoelectric Wafers. Smart Mater. Struct. 2014, 23, 015014. [Google Scholar] [CrossRef]
- Gururaja, T.R.; Schulze, W.A.; Cross, L.E.; Newnham, R.E.; Auld, B.A.; Wang, Y.J. Piezoelectric Composite Materials for Ultrasonic Transducer Applications. Part I: Resonant Rod-Polymer Composites. IEEE Trans. Sonics Ultrason. 1985, SU-32, 481–498. [Google Scholar] [CrossRef]
- Li, X.; Ma, T.; Tian, J.; Han, P.; Zhou, Q.; Shung, K.K. Micromachined PIN-PMN-PT Crystal Composite Transducer for High-Frequency Intravascular Ultrasound (IVUS) Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1171–1178. [Google Scholar] [CrossRef] [PubMed]
- Roh, Y.; Lu, X. Design of an Underwater Tonpilz Transducer with 2–2 Mode Piezocomposite Materials. J. Acoust. Soc. Am. 2006, 119, 3734–3740. [Google Scholar] [CrossRef]
- Ji, B.; Hong, L.; Lan, Y. Influences of Length and Position of Drive-Stacks on the Transmitting-Voltage-Response of the Broadband Tonpilz Transducer. J. Acoust. Soc. Am. 2021, 150, 4140–4150. [Google Scholar] [CrossRef] [PubMed]
- Ji, B.; Lan, Y.; Qiao, G.; Wang, M. Bandwidth Extension of the Tonpilz Transducer Using High-Order Longitudinal Vibrations. J. Acoust. Soc. Am. 2023, 154, 3709–3725. [Google Scholar] [CrossRef] [PubMed]
- Pyo, S.; Afzal, M.S.; Lim, Y.; Lee, S.; Roh, Y. Design of a Wideband Tonpilz Transducer Comprising Non-Uniform Piezoceramic Stacks with Equivalent Circuits. Sensors 2021, 21, 2680. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Huang, D.; Chen, B.; Tang, Y. Wideband Single Crystal Longitudinal Transducer for Underwater Sound. In Proceedings of the 2019 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019; pp. 1–3. [Google Scholar]
- Thompson, S.C.; Meyer, R.J.; Markley, D.C. Performance of Tonpilz Transducers with Segmented Piezoelectric Stacks Using Materials with High Electromechanical Coupling Coefficient. J. Acoust. Soc. Am. 2014, 135, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.L.W.; Unsworth, J.; Bui, T. Mode Coupling in Modified Lead Titanate/Polymer 1–3 Composites. J. Appl. Phys. 1989, 65, 1754–1758. [Google Scholar] [CrossRef]
- Smith, W.A.; Auld, B.A. Modeling 1–3 Composite Piezoelectrics: Thickness-Mode Oscillations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1991, 38, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.L.W.; Unsworth, J. Simple Model for Piezoelectric Ceramic/Polymer 1–3 Composites Used in Ultrasonic Transducer Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1989, 36, 434–441. [Google Scholar] [CrossRef] [PubMed]
- Szpica, D.; Mieczkowski, G.; Borawski, A.; Koten, H. Numerical Evaluation of the Influence of the Outlet Nozzle Diameter of a Piezoelectric Gas Injector on Its Flow Properties. Math. Probl. Eng. 2022, 2022, 2199890. [Google Scholar] [CrossRef]
- Mieczkowski, G.; Szpica, D.; Borawski, A. Analytical and Numerical Modelling of Deflection of Circular Three-Layer Piezoelectric Transducer. Eng. Rural Dev. 2020, 19, 555–564. [Google Scholar] [CrossRef]
- Thompson, S.C.; Hess, S. Preliminary Design Rationale for Tonpilz Transducer Elements. J. Acoust. Soc. Am. 2005, 75, S16. [Google Scholar] [CrossRef]
- Kim, J.-W.; Kim, W.-H.; Joh, C.-Y.; Roh, Y.-R. A Study on the Resonant Characteristics of a Tonpilz Transducer with a Fixed Tail Mass. J. Acoust. Soc. Korea 2010, 29, 439–447. [Google Scholar]
- Kim, J.-W.; Kim, W.-H.; Joh, C.-Y.; Roh, Y.-R. Analysis of the Resonant Characteristics of a Tonpilz Transducer with a Fixed Tail Mass by the Equivalent Circuit Approach. J. Acoust. Soc. Korea 2011, 30, 344–352. [Google Scholar] [CrossRef]
- Lee, D. Improved FOM (Figure of Merit) Performance Characteristics of a Linear Array Underwater Acoustic Transducer with a Gradual Wedge-Shaped Tail Mass Characteristics of a Linear Array Underwater Acoustic Transducer with a Gradual Wedge-Shaped Tail Mass. Korean J. Fish. Aquat. Sci. 2021, 54, 1036–1044. [Google Scholar]
- Liu, W.; Mo, X.; Chai, Y.; Wu, T.; Zhang, X. Broadband Janus-Helmholtz Transducer with Various Liquid Cavity Resonances. Appl. Acoust. 2024, 221, 110032. [Google Scholar] [CrossRef]
- Sheehy, M.J.; Halley, R. Measurement of the Attenuation of Low-Frequency Underwater Sound. J. Acoust. Soc. Am. 1957, 29, 464–469. [Google Scholar] [CrossRef]
- Lee, J.; Seo, I.; Han, S.M. Radiation Power Estimation for Sonar Transducer Arrays Considering Acoustic Interaction. Sens. Actuators A Phys. 2001, 90, 1–6. [Google Scholar] [CrossRef]
- Zhou, Q.; Cha, J.H.; Huang, Y.; Zhang, R.; Cao, W.; Shung, K.K. Alumina/Epoxy Nanocomposite Matching Layers for High-Frequency Ultrasound Transducer Application. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 213–219. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Ma, J.; Qi, X.; Shen, B.; Liu, Y.; Sun, E.; Zhang, R. Enhancement of Ultrasonic Transducer Bandwidth by Acoustic Impedance Gradient Matching Layer. Sensors 2022, 22, 8025. [Google Scholar] [CrossRef] [PubMed]
- Rojas, S.S.; Tridandapani, S.; Lindsey, B.D. A Thin Transducer with Integrated Acoustic Metamaterial for Cardiac CT Imaging and Gating. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1064–1076. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Mo, X.; Chai, Y.; Wu, T.; Pan, R. A Distributed Parameter Model of the Janus–Helmholtz Transducer. J. Acoust. Soc. Am. 2024, 155, 681–694. [Google Scholar] [CrossRef] [PubMed]
- Hadeed, M.; Siddique Bhatti, H.; Afzal, M.S.; Epin, V.; Abdullah, M.; Ali asghar, M. Design and Development of a High-Power Wideband Multimode Tonpilz Transducer for Underwater Applications. J. Mech. Eng. Sci. 2024, 18, 10161–10170. [Google Scholar] [CrossRef]
- Blum, N.T.; Gyorkos, C.M.; Narowetz, S.J.; Mueller, E.N.; Goodwin, A.P. Phospholipid-Coated Hydrophobic Mesoporous Silica Nanoparticles Enhance Thrombectomy by High-Intensity Focused Ultrasound with Low Production of Embolism-Inducing Clot Debris. ACS Appl. Mater. Interfaces 2019, 11, 36324–36332. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, K.; Pollard, R.; Borden, M. Ultrasound Microbubble Contrast Agents: Fundamentals and Application to Gene and Drug Delivery. Annu. Rev. Biomed. Eng. 2007, 9, 415–447. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, B.D.; Rojas, J.D.; Dayton, P.A. On the Relationship between Microbubble Fragmentation, Deflation and Broadband Superharmonic Signal Production. Ultrasound Med. Biol. 2015, 41, 1711–1725. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, Z.; Yang, D.Q.; Liu, S.L.; Yu, S.Y.; Lu, M.H.; Zhu, J.; Zhang, S.T.; Zhu, M.W.; Guo, X.S.; Wu, H.D.; et al. Broadband Gradient Impedance Matching Using an Acoustic Metamaterial for Ultrasonic Transducers. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Cannata, J.M.; Meyer, R.J.; Van Tol, D.J.; Tadigadapa, S.; Hughes, W.J.; Shung, K.K.; Trolier-McKinstry, S. Fabrication and Characterization of Micromachined High-Frequency Tonpilz Transducers Derived by PZT Thick Films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 350–357. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.H.; Jeong, J.-W.; Liu, Y.; Zhang, Y.; Shi, Y.; Kang, S.-K.; Kim, J.; Kim, J.S.; Lee, N.Y.; Kim, B.H.; et al. Materials and Wireless Microfluidic Systems for Electronics Capable of Chemical Dissolution on Demand. Adv. Funct. Mater. 2015, 25, 1338–1343. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, S.; Xu, X.; Liu, W.; Zhang, S.; Li, G.; He, J. Dynamic Piezo-Thermoelectric Generator for Simultaneously Harvesting Mechanical and Thermal Energies. Nano Energy 2020, 69, 104397. [Google Scholar] [CrossRef]
- Baac, H.W.; Lee, T.; Guo, L.J. Micro-Ultrasonic Cleaving of Cell Clusters by Laser-Generated Focused Ultrasound and Its Mechanisms. Biomed. Opt. Express 2013, 4, 1442–1450. [Google Scholar] [CrossRef] [PubMed]
- Marzo, A.; Drinkwater, B.W. Holographic Acoustic Tweezers. Proc. Natl. Acad. Sci. USA 2019, 116, 84–89. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).