Coordinating the Redundant DOFs of Humanoid Robots

Abstract

The new generation of robots (Industry 5.0 and beyond) is expected to be accompanied by the massive introduction of autonomous and cooperative agents in our society, both in the industrial and service sectors. Cooperation with humans will be simplified by humanoid robots with a similar kinematic outline and a similar kinematic redundancy, which is required by the diversity of tasks that will be performed. A bio-inspired approach is proposed for coordinating the redundant DOFs of such agents. This approach is based on the ideomotor theory of action, combined with the passive motion paradigm, to implicitly address the degrees of freedom problem, without any kinematic inversion, while producing coordinated motor patterns structured according to the typical features of biological motion. At the same time, since the approach is force-field-based, it allows us to integrate the computational loop parallel modules that exploit the redundancy of the system for satisfying geometric or kinematic constraints implemented by appropriate repulsive force fields. Moreover, the model is expanded to include dynamic constraints associated with the Lagrangian dynamics of the humanoid robot to improve the energetic efficiency of the generated actions.

1. Introduction

By definition, a humanoid robot resembles the human body in shape. Still, such similarity must be fully integrated with human-like functional purposes to cooperate with humans in many practical applications by learning to use human tools and understand environments. This is a field that, after science fiction, is becoming a topic of technological interest, with an expected Compound Annual Growth Rate of over 50% in the period 2024–2032 (Market Research Future^®). The conventional wisdom of such expectation is based on the belief that it will be driven by AI technologies, extrapolating the surprising performance of recent foundation models, such as large language models (LLMs) or vision language models (VLMs) [1,2]. The problem is that AI methodologies are intrinsically disembodied, despite the marginal attempt by EAI to define a mildly embodied form of AI. In contrast, the human cognitive system is essentially embodied [3,4,5], and this motivates a bio-inspired approach to humanoid robotics that is based on developmental principles [6] and aimed at mutual human–robot understanding [7,8].

A bio-inspired approach to humanoid robotics must first address, in computational terms, the organization of actions of a complex body. Humanoid robots share with humans the issue of how to deal with the redundancy of a complex, articulated body for the coordination of purposive actions. The first researcher to address the problem scientifically was probably Nikolai Bernstein [9], who observed the performance of professional workers in repetitive tasks, such as hammering blacksmiths, and found that precise hammer trajectories across repetitive trials were produced by the highly variable rotation patterns of the redundant set of joints recruited for the task. From such observations, Bernstein [10] formulated the general problem of motor redundancy to be solved by the worker’s brain, observing that the motor system must produce many more control signals than the variables that characterize and constrain typical skilled actions, and proposed that the solution consists in the elimination of redundant degrees of freedom, allowing the brain to focus only on the essential elements.

The issue of motor redundancy, focused on the problem of how to coordinate the excessive number of DOFs (Degrees of Freedom), is intertwined with the empirical evidence that human multi-joint movements are characterized by spatio-temporal invariants in the motion of the end-effector, whatever the number of recruited DOFs; this includes the bell-shaped speed profile in reaching movements or the anticorrelation of the speed and curvature profiles in general gestures of the hand, like in cursive handwriting [11]. As a matter of fact, the spatio-temporal invariances express the smoothness of biological motion in general full-body actions [12]. They can be explained by the minimum jerk model [13], within the framework of a remarkable feature of the energetic frugality of biological motion, which has been demonstrated in human motor control [14] as well as in industrial robotics [15].

The general rationale of the smoothness of biological motion in connection with the emergence of figural-kinematic invariances can be linked to the ideomotor theory, already formulated by psychologists of the 19th century, such as William James [16], and recently reviewed with more solid neurophysiological support [17,18]. According to this theory, the brain of a skilled person initiates the computational process that will lead to the performance of a purposive action by formulating the idea of the relevant sensory consequences (as the expected trajectory of the end-effector) rather than the detailed coordination of the DOFs recruited for the actual execution of the action and the corresponding muscle activation patterns. Shortly, an action idea mediates between the intention to act and the generation of detailed motor control patterns. The problem is how to computationally express such a process that requires the broad imbalance between the numerosity of the DOFs of the body and the number of parameters that characterize the action idea to be faced. Such an imbalance is already high in the human case. Still, it pales compared with other species such as the elephant trunk and octopus tentacles, i.e., muscular hydrostats with infinite DOFs. On the other hand, it is remarkable that the invariant features of the elephant’s purposive actions [19] are quite similar to those of human biological motion.

The approaches developed to deal with DOF imbalance reveal a wide range of opposite evaluations. For example, some researchers designate it (negatively) as redundancy [20], whereas others [21] describe it (positively) as motor abundance, emphasizing a range of affordances that include flexibility and adaptability to various ancillary aspects of skilled behavior.

The issue of kinematic redundancy in robotic manipulators is well established and formulated mainly as a problem of inverse kinematics. This is a complex problem, in contrast with direct kinematics (the mapping of joint rotation patterns into the corresponding law of motion of different body parts, i.e., different end-effectors): direct kinematics is a well-defined problem with a unique solution, whichever the number of DOFs, whereas inverse kinematics is an ill-posed problem which may involve infinite solutions or no solution at all. The number of methods proposed in robotics is very large. Most focus on the Jacobian matrix, with various forms of pseudo-inversion whose computational robustness decreases with an increase in the degree of redundancy in the robot architecture, as in humanoid robots. In particular, many proposals are based on the null space projection technique developed in the 1980s [22,23,24]. However, most robotic redundancy resolution schemes do not enable the integration of the inverse kinematic process with the issue of smoothness, which is typical of biological motion, or the various constraints that the coordinated joint rotation patterns are supposed to satisfy, such as the range of motion of the DOFs, the range of torque of the actuators, or the range of stability in bipedal standing.

The proposed approach is bio-inspired, in the general sense that it is built upon the recognition of the already cited bliss of motor abundance, articulated in such a way to include the basic elements of the ideomotor theory and the intrinsic smoothness of biological motion, integrated with the capability of multiple constraint satisfaction. The main module is a computational model, named Passive Motion Paradigm (PM) [25,26,27], which is based on the Jacobian matrix of the body schema, as in many robotic formulations, but without any attempt to invert it or the explicit utilization of the associated null space. The basic concept, implicit in the ideomotor theory, is to shift the focus from primitive motions to primitive force fields: this means that if our brain is requested to carry out the ill-posed task of coordinating the multiple DOFs of the body in order to “push” the end-effector towards a designated target, it may instead imagine “pulling” the end-effector to the target and then allowing the body to follow, i.e., the whole kinematic chain will passively yield to the pulling field, thus producing a coordinate rotation pattern of the redundant DOFs. This is equivalent to using the transpose Jacobian for mapping a pulling force field, defined in the low-dimensional task space, into an equivalent torque field, operating in the high-dimensional joint space. The “passivity” of the planning paradigm is modulated by a compliance matrix that maps the torque field into incremental joint rotations and then, via the same Jacobian matrix, into the incremental motion of the end-effector, attracted to the target according to the ideomotor theory by an attractive force field.

The attractive dynamics of the PMP can be integrated with the repulsive dynamics of additional modules, which express geometric or structural constraints, as the RoM (limited Range of Motion) of the different DOFs or the constraint of bipedal stability that implies a RoM in the position of the center of mass of the body on the support area. Such constraints can generate online repulsive torque fields combined additively with the attractive torque field for a coordinated synergy formation process that implicitly exploits the null space for a trade-off between the competing requirements of the different modules. In this paper, the PMP approach to motor redundancy is extended with the motor adaptation of the compliance matrix related to a number of other dynamic constraints involving the torque requirements of the different actuators.

2. Methods

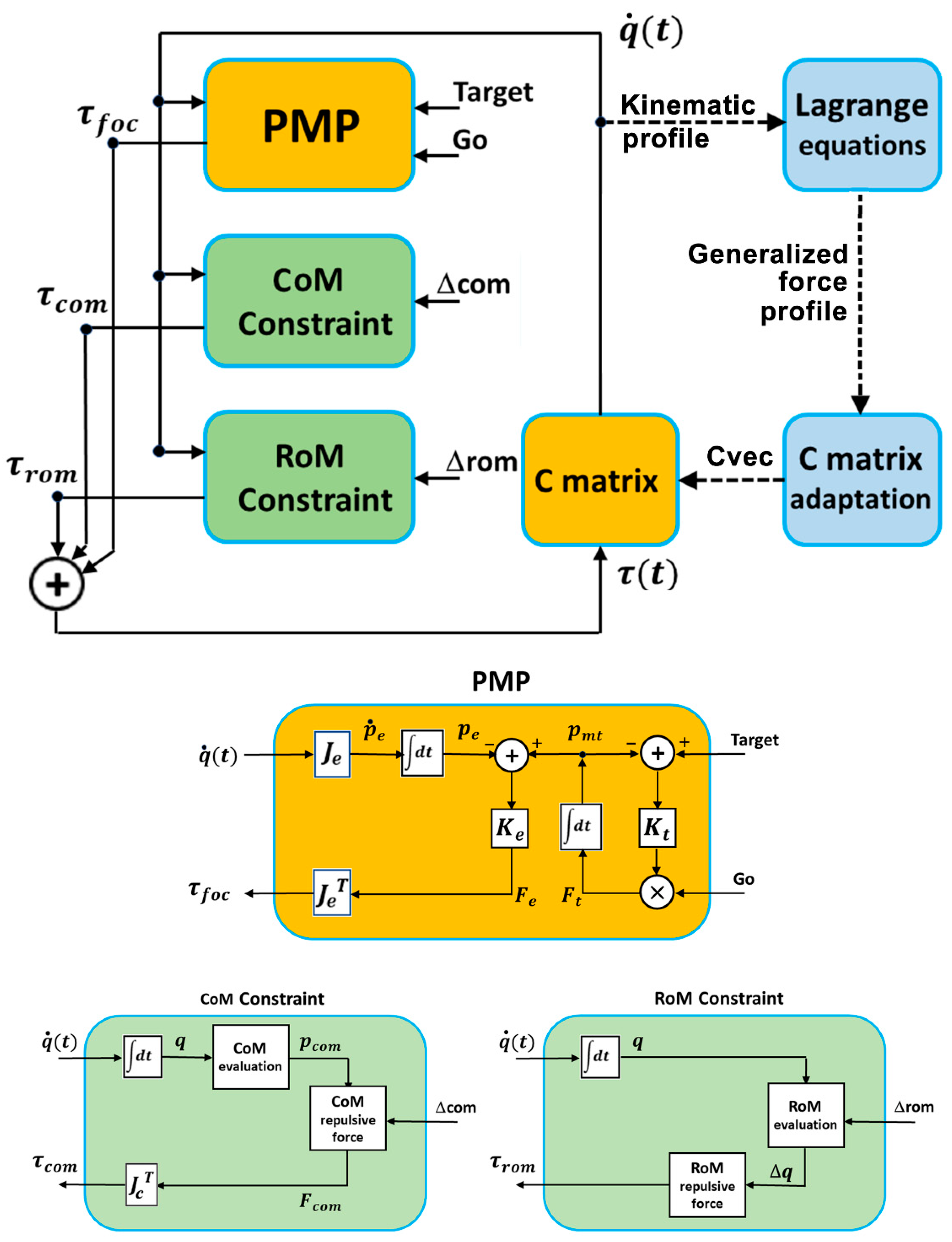
The proposed model of coordination for the redundant DOFs of full-body robots is illustrated in Figure 1. The top panel is the general block diagram built around the PMP (Passive Motion Paradigm) module, which implements the ideomotor theory, in parallel with two blocks which implement the geometric and kinematic constraints to be satisfied on-line during the simulation of the model in order to drive the full-body synergy formation process: (a) the CoM constraint for the postural stability of the standing robot, i.e., the requirement of constraining the projection of the CoM (Center of Mass) inside the convex hull of the support area between the feet, and (b) the RoM constraint, for the structural integrity of the body model, i.e., the requirement to keep the rotation angle of each DOF inside the Range of Motion of each joint. Additional blocks can be integrated to express other specific postural constraints.

All these blocks are driven by the current kinematic state vector, which includes the DOF angular vector $q$ and the corresponding angular speed $\dot{q}$; the blocks interact during the execution of a movement by combining specific torque fields: (1) the focal torque field ${\tau }_{foc}$, determined by the attraction force of the end-effector to the target, (2) the postural torque field ${\tau }_{com}$, induced by a virtual force applied to the pelvis of the body as a function of the position of the projected body CoM on the support base in order to repulse it from the boundary, (3) the RoM torque field ${\tau }_{rom}$, applied to each DOF to repulse it from the limits of the structural Range of Motion. The combined torque field $\tau \left(t\right)$ closes the loop of the PMP model by mapping the torque field into a motion field $\dot{q}\left(t\right)$ of the whole body through the compliance matrix $C$. For simplicity, we may assume that there are no multi-joint actuators (as it occurs in the human body for multi-joint muscles). Thus, the compliance matrix is diagonal, and is identified by a compliance vector $Cvec$ whose elements express the relative degree of participation of each DOF in a planned coordinated action. In particular, setting all the components of the vector to 1 means that all the DOFs share the same availability to contribute to the coordinated action: thus, for a 7-DOF model, $Cvec=[1 1 1 1 1 1 1]$.

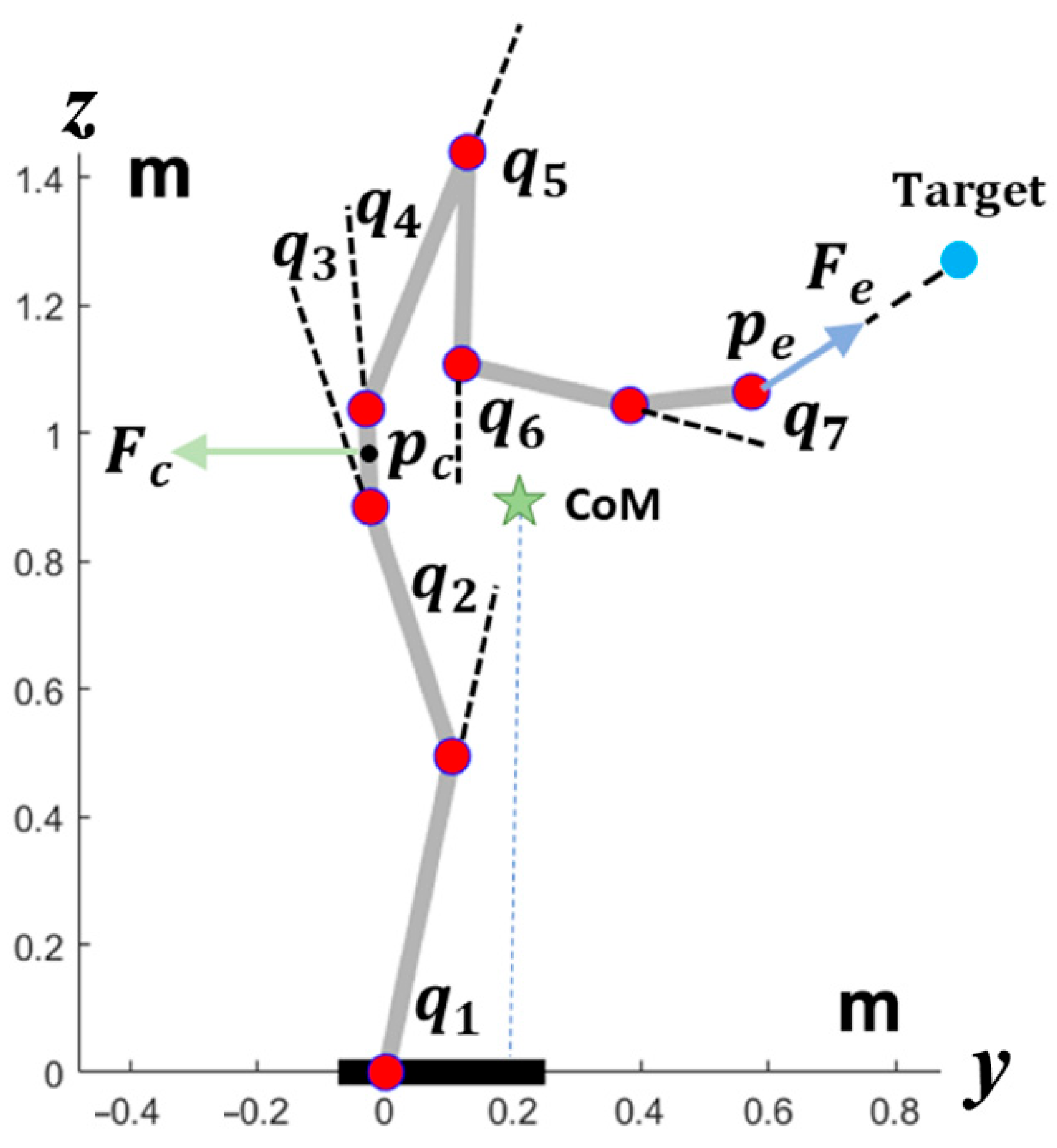
The robot body model is a single planar kinematic chain with eight segments and seven joints, as illustrated in Figure 2. By assigning different patterns to $Cvec$, we obtain different kinematic patterns. Still, all these movements share the same spatio-temporal invariant features of the end-effector, including the trajectory and the speed profile. At the same time, the oscillation of the projection of the CoM on the support base remains inside a safety margin, and the oscillations of each DOF remain inside the corresponding RoM. Such kinematic invariance in the model is equivalent to a trade-off among the three different kinematic requirements defined above by some path planning in the null space of the kinematic structure. In general, the higher the dimensionality of the null space, the easier it is to identify a good trade-off. For example, the simulations reported in the next section are related to a planar robot with 7 DOFs and a 2-dimensional task space: this means that the null-space is 5-dimensional, with good room for maneuver for constraint satisfaction. Moreover, while the coordination paradigm illustrated above allows one to simultaneously satisfy multiple geometric/kinematic requirements on-line, it is possible to exploit the modulation of the $Cvec$ parameter vector for additional dynamics constraints. In particular, the graph of Figure 1 is related to the modulation of the vector in such a way as to constrain the torque requirement of each DOF for the given action plan. For example, the simulations illustrate an adaptation procedure that minimizes the worst actuator’s peak torque. For simplicity, the robot model is planar, with seven joints and eight corresponding links (see Figure 2): the geometric and structural parameters are listed in

Table 1. Robot links.

Segment	1	2	3	4	5	6	7	8
Name	foot	leg	thigh	pelvis	trunk	arm	forearm	hand
Length (m)	0.3	0.505	0.411	0.153	0.432	0.332	0.271	0.192
Weight (kg)		7.6	19.6	11.8	27.3	4.2	2.8	2.2
Inertia Moment (kg m2)		0.1615	0.2759	0.0230	0.4236	0.0367	0.0171	0.0061

and

Table 2. Robot joints.

Joint	1	2	3	4	5	6	7
Name	ankle	knee	hip	lumbar	shoulder	elbow	wrist
RoM min (deg)	+45	−10	−30	−140	−210	0	−15
RoM max (deg)	+100	+120	+45	+15	+10	+120	+45

.

Now, let us describe in detail the different modules used in the synergy formation process of the redundant robot.

2.1. PMP Module

The PMP module activates a force field that attracts the moving target $p_{mt}$ to the designated Target:

$$\left\{\begin{array}{l}{F}_t=K_t\left(Target-p_{mt}\right)\times Go\left(t\right)\\ {\dot{p}}_{mt}=F_t\end{array}\right.$$

(1)

The moving target is initially located in the same position as the end-effector, $p_{mt}\left(t_0\right)=p_e\left(t_0\right)$, where $t_0$ is the activation time of the Go-signal, a non-linear gain function with a limited duration $T$ and a quickly rising profile diverging to infinity at $t=t_0+T$, in agreement with the terminal attractor theory [28]:

$$\left\{\begin{array}{c}Go=0 0\ge t-t_0\ge T\\ Go={\displaystyle \frac{\dot{\rho }}{1-\rho }} \rho =6 {\delta }^5-15 {\delta }^4+10 {\delta }^3 \delta ={\displaystyle \frac{t-t_0}{T}} 0<t-t_0<T \end{array}\right.$$

(2)

In brief, integrating Equation (1) with the non-linear gain of Equation (2) generates a straight trajectory for the moving target that reaches the designated target at time T after the start, whatever the initial distance and with a bell-shaped velocity profile, thus meeting the ideomotor theory’s rationale and the biological motion’s smoothness. The structure of the PMP module in Figure 2 shows that, simultaneously with the generation of the moving target described above, the end-effector of the robot, reconstructed by integrating over time the direct kinematic equation

$${\dot{p}}_e=J_e \dot{q}$$

(3)

is attracted to the moving target by the following elastic force field:

$$F_e=K_e \left(p_{mt}-p_e\right)$$

(4)

Thus, there are two interacting force fields: the former field $F_{mt}$ attracts the moving target to the final target, and the latter field $F_e$ attracts the end-effector to the moving target. This field is then mapped from the task space to the joint space by the following equation, which is dual to Equation (3):

$${\tau }_{foc}={J_e}^T F_e$$

(5)

The loop of the PMP module is then closed through the compliance matrix:

$$\dot{q}=C \tau$$

(6)

In summary, the two interacting force fields of the PMP module generate two trajectories for the moving target end and the end-effector, respectively, which in most cases are almost coincident, unless the CoM constraint module and/or the RoM constraint module induce some deviation to comply with the constraint in the null space.

The Jacobian matrix of the end-effector has two rows and seven columns: $J_e=\left[J_1 J_2\dots J_7\right]$. The columns are computed recursively in a backward order, from the wrist to the ankle:

$$\left\{\begin{array}{c}{J}_7=L_7\times \left[\begin{array}{c}-S_7\\ +C_7\end{array}\right] \\ \dots . \\ J_i=J_{i+1}+L_i\times \left[\begin{array}{c}-S_i\\ +C_i\end{array}\right] \\ \dots . \\ J_1=J_2+L_1\times \left[\begin{array}{c}-S_1\\ +C_1\end{array}\right] \end{array}\right.\mathrm{where} \left\{\begin{array}{c}{C}_i=cos\left({\sum }_{k=1}^i{q}_k\right)\\ S_i=sin \left({\sum }_{k=1}^i{q}_k\right)\end{array}\right.$$

(7)

2.2. CoM-Constraint Module

The purpose of this module is to apply a virtual force to the pelvis area to contrast the danger of falling, induced indirectly by the focal reaching movement. An index of such a threat is the closeness of the projection of the CoM on the support base from the corresponding borders. In the specific case of the simulations reported in this paper, the support base is a segment whose length is the foot length (30 cm), connected to the ankle joint at a point that is the origin of the Cartesian reference system. The range of motion of the projection of the CoM must be constrained between $y_{min}=-5 \mathrm{c}\mathrm{m}$ and $y_{max}=25 \mathrm{c}\mathrm{m}$ (the $\Delta com$ input of Figure 1).

This module is driven by the ongoing law of motion of the whole body, i.e., $q\left(t\right)$ and $\dot{q}\left(t\right)$, which allows for the reconstruction of the current position of the CoM $p_{com}$ by combining the CoMs of each body segment ($p_c\left(i\right), i=1:7)$, including a load hold by the end-effector:

$$P_{com}=\left[\begin{array}{c}{y}_{com}\\ z_{com}\end{array}\right]={\displaystyle \frac{{\sum }_{i=1}^7{p}_c\left(i\right)\times M_i+p_e\times load}{{\sum }_{i=1}^7{M}_i+Load}}$$

(8)

Supposing that the CoM of each link is in the middle of the link, the corresponding coordinate vectors of the previous equation can be computed as follows, where $(p_J\left(i\right), i=1:7)$ are the vectors of the seven joints, with $p_J\left(1\right)=0$:

$$\left\{\begin{array}{c}{p}_J\left(i+1\right)=p_J\left(i\right)+L_i\times \left[\begin{array}{c}{C}_i\\ S_i\end{array}\right]\\ p_c\left(i+1\right)=p_J\left(i\right)+{0.5\times L}_i\times \left[\begin{array}{c}{C}_i\\ S_i\end{array}\right]\end{array}\right. \mathrm{where} \left\{\begin{array}{c}{C}_i=cos\left({\sum }_{k=1}^i{q}_k\right)\\ S_i=sin \left({\sum }_{k=1}^i{q}_k\right)\end{array}\right.$$

(9)

The projection of the CoM on the support base is the y coordinate of $p_{com}$, i.e., $y_{com},$ and the purpose of this module is to ensure that it remains in the range of values defined above while the attractive force of the PMP module applied to the end-effector, i.e., $F_e$, might induce the CoM to violate the constraint. In order to achieve this task, a virtual force field $F_c$ is applied to the central part of the pelvis: this force should be directed backward if $y_{com}$ is closer to $y_{max}$ than to $y_{min},$ and forward in the opposite case. In particular, $F_c$ is computed according to the following field as a function of the position of $y_{com}$ inside the safe interval ($y_{min}\to y_{max}$):

$$F_c=f\left(y_{com}\right)=K_{com}\left(e^{\frac{\left(y_{com}-y_{max}\right)}{\Delta }}-e^{\frac{{(y}_{min}-ycom)}{\Delta }}\right)$$

(10)

The field is null in the middle of the interval, positive and exponentially increasing in the right part, and negative and exponentially decreasing in the left part. The parameter $\Delta$, defined as a small part of the safe interval ($\Delta ={\displaystyle \frac{y_{max}-y_{min}}{k}}$), modulates the sharpness of the generated force profiles; this is sharper and sharper as $k$ increases: for $k>10$ all the torque profiles cross the limits of the safe interval with the same value: $F_e=+K_{com}$ for the right limit and $F_e=-K_{com}$ for the left limit. In the simulations reported in the next section, $k=50$ and $K_{com}=400 N$. The force field is mapped into the corresponding torque field, similarly to Equation (5):

$${\tau }_{com}={J_c}^T F_c$$

(11)

The employed Jacobian matrix is defined for a part of the whole kinematic chain (from the ankle to the hip), which includes 3 DOFs. The three columns of the Jacobian are computed as follows:

$$\left\{\begin{array}{c}{J}_c(3)=0.5\times L_3\times \left[\begin{array}{c}-S_3\\ +C_3\end{array}\right] \\ J_c(2)=J_c(3)+L_2\times \left[\begin{array}{c}-S_2\\ +C_2\end{array}\right] \\ J_c(1)=J_c(2)+\times \left[\begin{array}{c}-S_1\\ +C_1\end{array}\right] \end{array}\right.\mathrm{where} \left\{\begin{array}{c}{C}_i=cos\left({\sum }_{k=1}^i{q}_k\right)\\ S_i=sin \left({\sum }_{k=1}^i{q}_k\right)\end{array}\right.$$

(12)

2.3. RoM-Constraint Module

The RoM of each DOF is an interval between a minimum and maximum angular value; thus, the input to this module is $\Delta rom:\left(q_{min}\left(i\right)\to q_{max}\left(i\right)\right) i=1:7$. The goal is to repulse each DOF from either joint limit, and this is implemented in a similar way to the CoM module by activating the following repulsive torque field:

$${\tau }_{RoM}(i)=-K_{RoM }\times \left(e^{\frac{q\left(i\right)-q_{max}\left(i\right)}{\Delta \left(i\right)}}-e^{\frac{q_{min}-q\left(i\right)}{\Delta \left(i\right)}}\right) i=1:7.$$

(13)

The parameter $\Delta \left(i\right)$ is defined as a small part of the safe interval of each DOF, and it determines the sharpness of the generated torque profiles: $\Delta (i)={\displaystyle \frac{q_{max}\left(i\right)-q_{min}\left(i\right)}{k}}$. In the simulations reported in the next section, $k=50$ and $K_{RoM}=300 \mathrm{N}\mathrm{m}$ for all the DOFs of the model; the related RoMs are listed in Table 2.

2.4. C-Matrix Adaptation Module

By combining the torque fields generated by the three modules described above and mapping the torque field into a motion field through the compliance matrix, the model coordinates the redundant DOFs, selecting a path in the null space that satisfies all the requirements instant by instant, i.e., on-line, while keeping the same spatio-temporal structure. Additional modules can be integrated into this architecture to express additional constraints of the generated synergy; these are either on-line constraints that operate on the instantaneous value of the kinematic state or off-line constraints that aim to achieve the modulation of the compliance matrix for affecting features of the overall generated action. In particular, the off-line module implemented in this simulation study illustrates a dynamic rather than a kinematic constraint, as do the two modules described above. In particular, the dynamic constraint is related to the torque requirements for the robot actuators, given a family of kinematically equivalent coordinated movements.

As shown in the picture, the following kinematic action profile of the planned coordinated action is saved:

$$\left[q_i=q_i\left(t\right) i=1:7 t\in t_o\leftrightarrow t_f\right]$$

(14)

This kinematic action profile is transformed into the corresponding generalized force profile that expresses the time course of the torques requested for each actuator:

$$\left[Q_i=Q_i\left(t\right) i=1:7 t\in t_o\leftrightarrow t_f\right]$$

(15)

The transformation is carried out by using the Lagrange formulation of the equations of motion for robotic arms:

$$\left\{\begin{array}{l}{Q}_i={\displaystyle \frac{d}{dt}}\left({\displaystyle \frac{\partial K}{\partial {\dot{q}}_i}}\right)-{\displaystyle \frac{\partial U}{\partial q_i}} i=1:7\\ U\left(q\right)={\sum }_{k=1}^7{M}_k g z_k+M_{load} z_7\\ K\left(q,\dot{q}\right)={\sum }_{k=1}^7\left({\displaystyle \frac{1}{2}}{M}_k{v_k}^2+{\displaystyle \frac{1}{2}}{{I_k\omega }_k}^2\right)+{\displaystyle \frac{1}{2}}{I}_{load}{{\omega }_7}^2\end{array}\right.$$

(16)

$U$ and $K$ are, respectively, the potential and kinetic energy functions of the robot; $\left(z_k, k=1:7\right)$ are the vertical coordinates of the CoM of each link; $\left(v_k, k=1:7\right)$ are the velocities of the CoM; and $\left({\omega }_k, k=1:7\right)$ are the corresponding angular velocities. The analysis of the generalized force profile is used to adapt the $C_{vec}$ parameter vector with the purpose of optimizing some dynamic indicator of the stress faced by the actuators. In particular, the simulations reported in the next section used the following indicator, namely the maximum peak value of the torque for the whole ensemble of actuators and the given kinematic profile:

$$Q_{peak}=\underset{\begin{array}{c}i=1:7\\ t\in t_0-t_f\end{array}}{\mathit{max}}⌈Q_i=Q_i\left(t\right)⌉$$

(17)

This goal is achieved by a simple gradient descent procedure for the minimization of $Q_{peak}$:

$${\widehat{C}}_{vec}=\underset{C_{\mathit{vec}}}{\mathit{min}}{Q}_{peak}\left(C_{vec}\right)$$

(18)

The optimization procedure (Appendix A) initiates with the default assignment of unitary values to all the components of the vector, the simulation of the model, and the estimation of $Q_{peak}$; it proceeds with repeated simulations, updating the vectors according to the gradient of $Q_{peak}$.

From a computational point of view, the simulation model is an explicit system of first-order differential equations of high dimensionality. The simulations illustrated in the results were carried out using MATLAB^® (MathWorks, MATLAB R2023b), adopting the forward Euler method or the 4th-order Runge–Kutta method for integrating the differential equation system, with a time step of 0.1 ms. The simulation software is available on demand.

3. Results

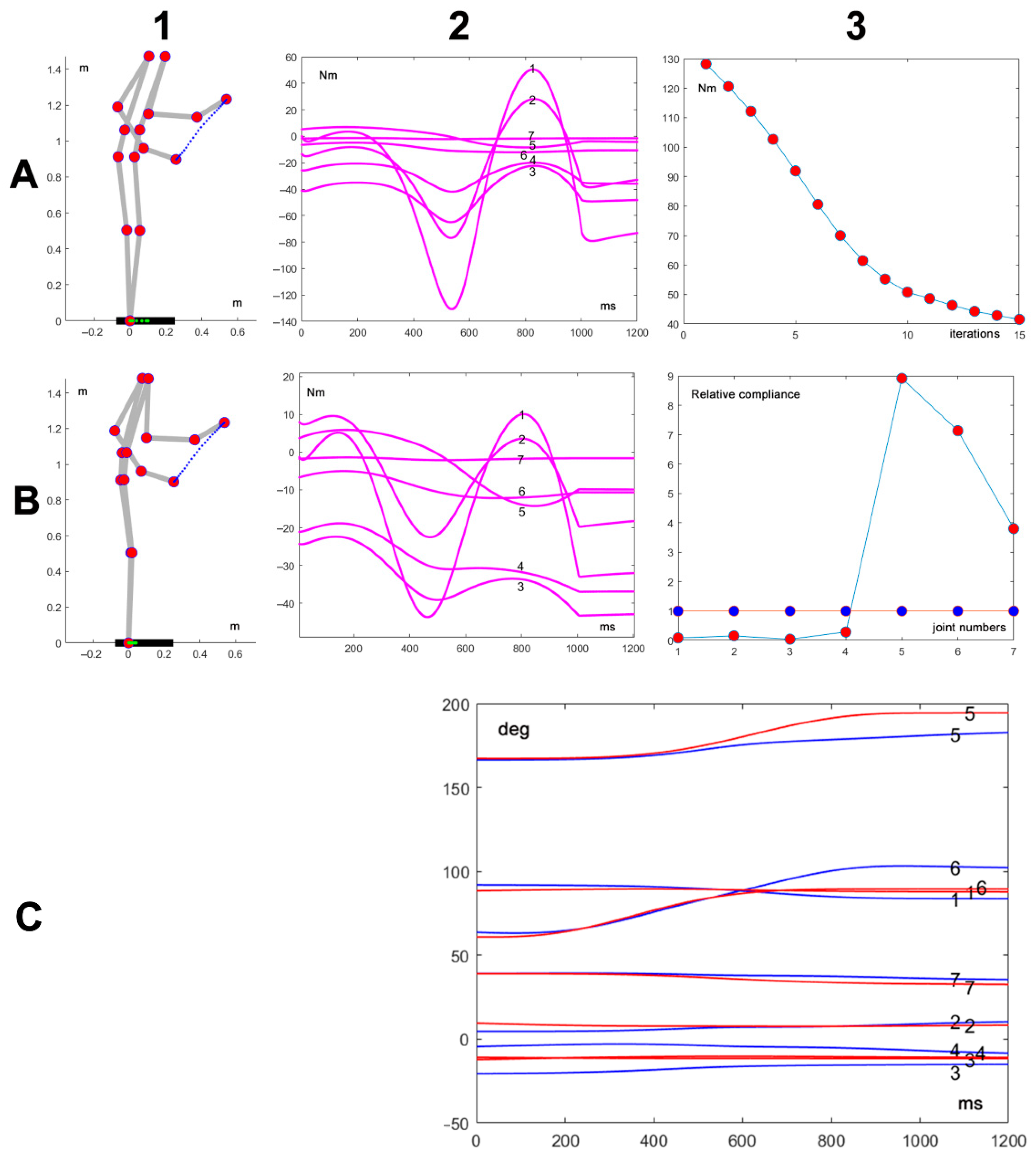
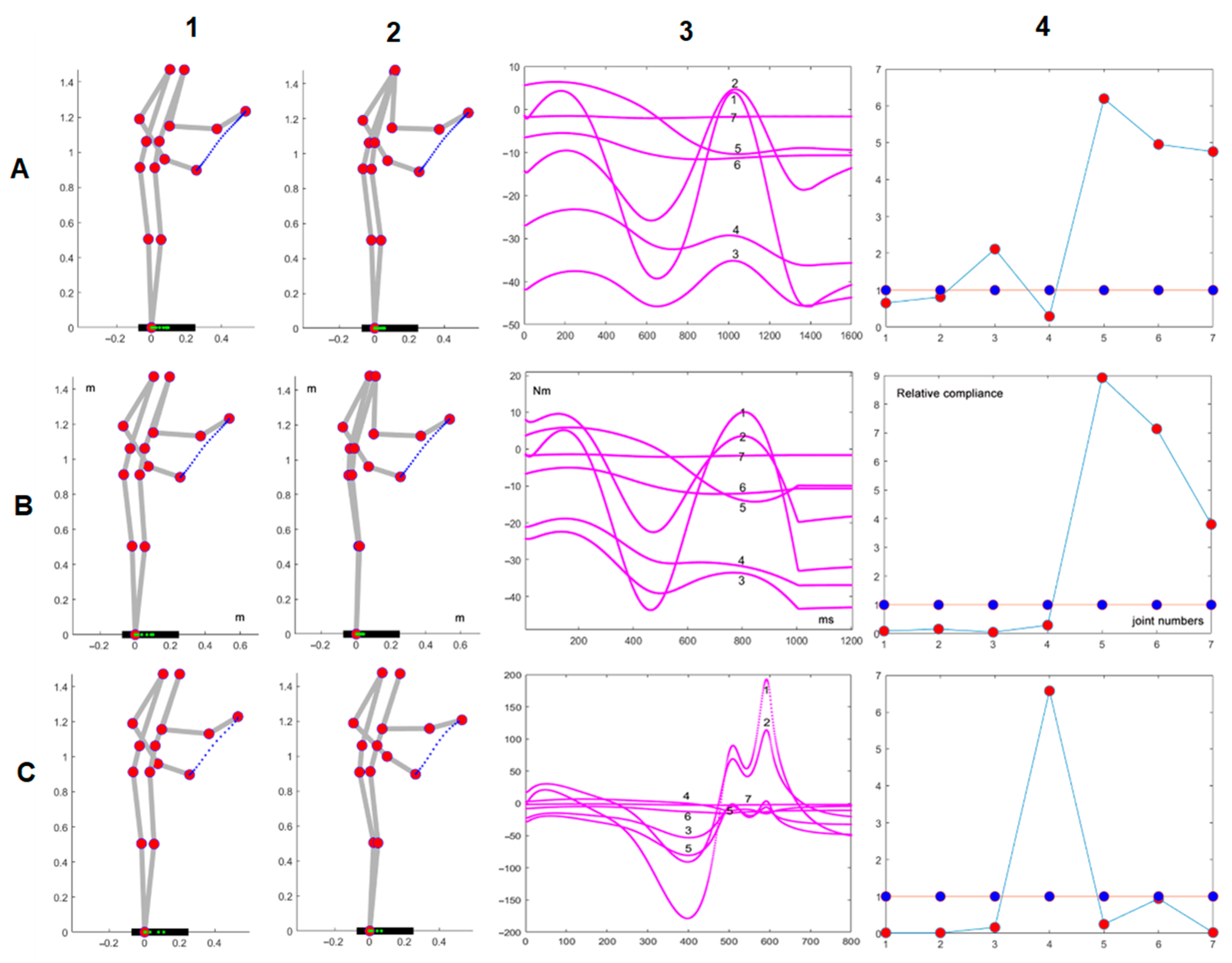
Figure 3 shows an example of the simulation of the model described in the previous section. The parameters of the simulated action are as follows: initial posture $q_0=\left[78.1 30.1-17.7-24.1-160 77.9 20\right]deg$, duration of 1 s, distance of the target of 0.43 m, no load, and the default configuration of the compliance vector $C_{vec}=\left[1 1 1 1 1 1 1\right]$. Panel A1 shows the initial and final posture of the movement, together with the plotted trajectory of the end effector (in blue) and the trajectory of the projection of the CoM on the support base (in green, on the foot bar). Panel A2 is the corresponding plot of the torques of each DOF (identified numerically from 1 to 7). Panel B1 is related to the same action performed at the end of the C-matrix adaptation process, with the same initial posture, the same final target, the same movement duration, no load, and a different configuration of the compliance vector $C_{vec}=\left[0.15 0.25 0.10 0.31 8.8 7.2 3.8\right]$; panel B2 shows the corresponding plot of the torques of each DOF. Panel A3 shows that during the adaptation, which included 15 iteration steps, $Q_{peak}$ is reduced by more than 50%, from an initial value of 130 Nm to a final value of 43 Nm.

Panel B3 shows the initial and final configurations of the compliance vector $C_{vec}$, with blue markers at the beginning and red markers at the end of the optimization procedure; moreover, panel C plots the time course of the joint rotation patterns related to the initial $C_{vec}$ (in blue) and the final adapted $C_{vec}$ (in red). By comparing such rotation patterns and the corresponding torque vectors (panels A2 vs. B2), it is surprising to realize that a rather small modification of kinematics can significantly improve the dynamics, reducing the peak torque by more than 50%. Moreover, it is worth noting that the adaptation process maintains the invariant kinematics of the end-effector, including the speed profile, and satisfies the RoM constraint and the CoM constraint in both cases.

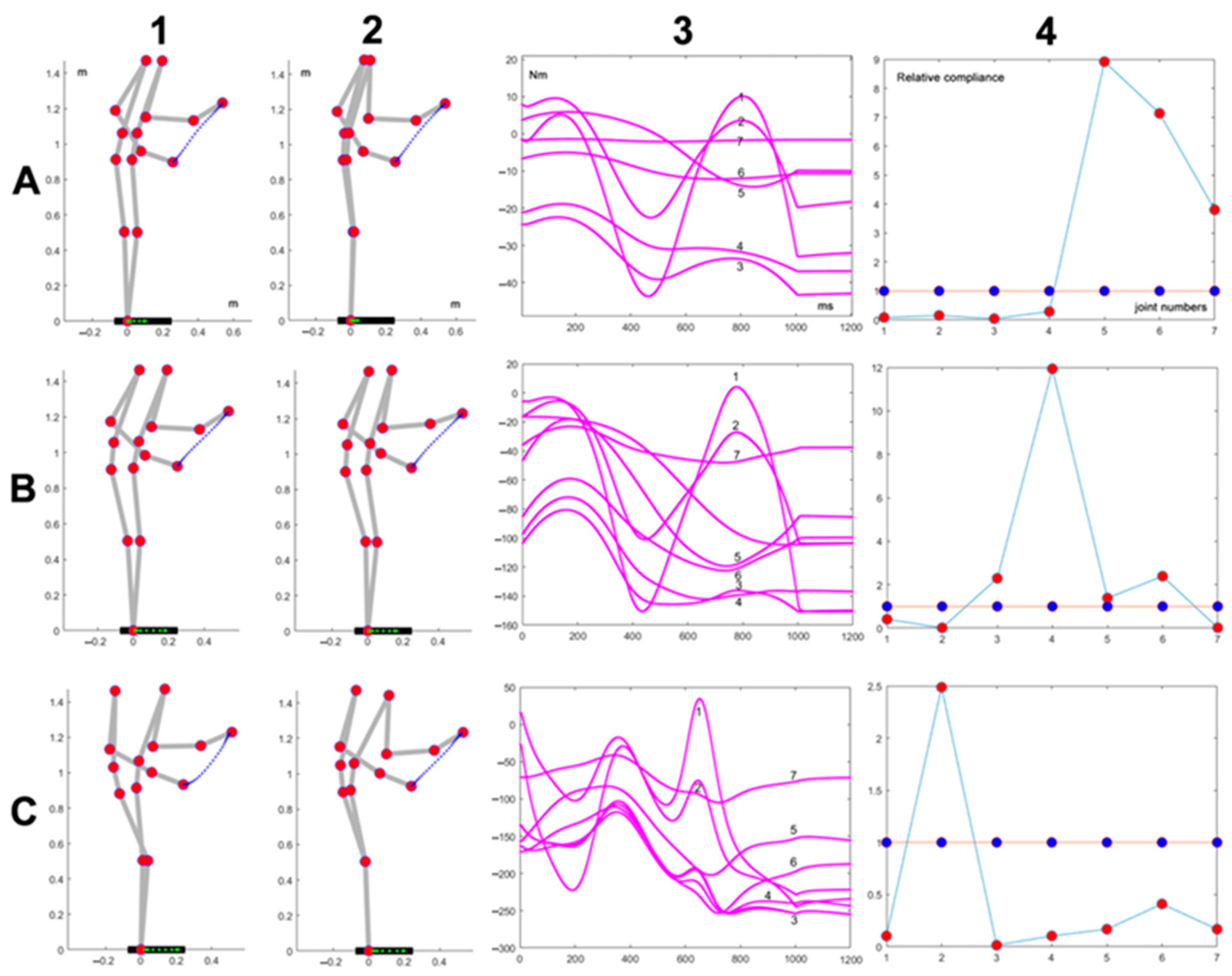
Figure 4 shows the effect of changing the movement direction while keeping the initial posture, the movement duration (1 s) and the absence of load. In all the cases, the adaptation procedure provides a significant reduction in the peak torque, and the corresponding optimized $C_{vec}$ profiles share the shoulder as the prominent DOF while keeping the DOFs of the upper limb at a higher level than the lower limb. The figure also shows that, independent of the $C_{vec}$ profiles, some directions are more challenging for the precision of the kinematic coordination, as is shown by the deviation of the end-effector from the straight path.

Figure 5 shows the effect of changing the load while keeping the same movement direction, distance (0.43 m), and duration (1 s): the load is 0 in panel A, 20 kg in panel B, and 40 kg in panel C. In all the cases, the adaptation procedure provides a significant reduction in the peak torque and the corresponding optimized $C_{vec}$ profiles shift the prominent DOF from the upper part to the lower part of the body as the load increases.

Figure 6 shows the effect of the speed of the movement in relation to a varying duration: 1.4 s, 1 s, 0.6 s. In all the cases, the adaptation procedure provides a significant reduction in the peak torque; the optimized $C_{vec}$ profiles are very similar for slow or very slow movements, as are the required generalized torques. The third simulation (duration 0.6 s) is somewhat different because the kinetic component of the Lagrange function becomes preponderant with respect to the potential component.

The reported simulations show the variability in the torque requirements in relation to similar kinematic coordinated patterns.

4. Discussion

It is generally assumed that the problem of motor redundancy is the central problem of motor control. As observed in the introduction, the early solution, suggested by Nikolai Bernstein one century ago [9], was the “elimination of redundant degrees-of-freedom”, with the assumption that once redundant/unnecessary DOFs have been identified, the neural controller can focus on the essential/nonredundant DOFs straightforwardly. However, this is far from trivial in general, even from the dual point of view of observing multi-joint skilled behavior and attempting to partition the multi-DOF space in controlled and uncontrolled manifolds, according to the uncontrolled manifold concept (UCM) [29]. The opposite process, namely, how to partition the configuration space for generating a purposive, coordinated action, by focusing control on a carefully identified manifold while “leaving alone” the UCM, is much more complicated and reminds us of the difficulty of dealing with inverse kinematics based on our knowledge of direct kinematics. In any case, the UCM concept originated in neurobiology and is quite similar to the null-space concept adopted in industrial robotics, which is the basis for many inversion algorithms.

Traditionally, the industrial robotic approach to inverse kinematics has been formulated as an optimization method, given a kinematic characterization of the task, based on a variety of cost functions: the result is the quest for a complex computational process whose speed and robustness strongly worsen with an increasing degree of redundancy. This is why the “anguish/agony” of motor redundancy resolution through explicit mathematical optimization methods has been challenged by an emphasis on the “bliss” of motor abundance [30], which is based on an assumption about the numerosity of the DOFs: the more the better. For example, experimental evidence supports the hypothesis that the availability of a large number of DOFs improves humans’ ability to carry out tasks that require taking into account multiple constraints simultaneously with minimal interference among them [31], thus enhancing the flexibility of the performance.

The rationale of the principle of motor abundance is somehow related to the consideration that the dynamics of high-dimensional motor control can be understood only in an “ecological” framework that links brain, body, and environment in the same dynamical process, integrating neurobiological, biomechanical, and physical processes. In particular, this idea is captured by the equilibrium point hypothesis on the strict relationship between posture and movement [32,33,34], by positing that posture is not directly controlled by the brain in a detailed way but is force-field driven, i.e., it is the “biophysical consequence” of equilibrium among muscular and environmental forces: “movement” is viewed as a symmetry-breaking phenomenon, i.e., the transition from an equilibrium state to another one.

The organization/reorganization of the abundant/redundant DOFs of the human body for the production of purposive actions can also be characterized in terms of the principle of minimum interaction [35,36], namely the natural tendency of complex systems, such as the neuromuscular system, to reduce the number and intensity of interactions among the subsystems or components recruited to achieve a desired outcome or maintain a specific state. For example, such interaction parsimony can be achieved by threshold mechanisms so that deviations from the average intended synergy are only corrected when they interfere significantly with the task goals.

At the same time, we should not restrict the range of applications of the general principles summarized above, as the equilibrium point hypothesis, to the area of strict motor control without including embodied motor cognition as well. This is because different forms of a simulation theory of cognition [37,38,39,40,41] clearly show that an essential part of such a theory is the simulation of action being performed by the same neural mechanisms as those typically involved in movement execution and perception. The point is that the mental simulation of actions is an essential component of prospection. It builds upon the mental simulation of actions to evaluate their potential future sensorimotor, environmental, and social effects, thus supporting an informed decision-making process [42,43,44].

The proposed model for the bio-inspired coordination of the motor redundance/abundance of humanoid robots is closely linked to the equilibrium point hypothesis because the PMP, originated as an extension of EPH, is indeed characterized by “muscle synergies and actions without movements” [27]: this means that covert/imagined actions and overt/executed actions are totally equivalent from the ideomotor point of view, except for the specific activation of central pattern generators. Furthermore, in agreement with the principle of kinematic abundance, PMP is not computationally intensive but is characterized by equilibrium-seeking dynamics driven by internal or external force fields. In particular, the main loop of the PMP module can be implemented by coupled neural networks, trained according to self-supervised training and capable of simulating the Jacobian and transpose Jacobian matrices [27]. At the same time, the integration of multiple constraints via the interaction of torque fields in full-dimensional space is the simplest way of exploiting the principle of motor abundance. Moreover, the non-linear repulsive fields that implement the CoM-constraint and the RoM-constraint were conceived to match the principle of minimum interaction: the chosen non-linear profile is equivalent to a threshold activation algorithm that tends to reduce the chance of conflicts between the different components of the constraint satisfaction modules.

In motor neurobiology, motor control and motor cognition are well-separated topics, although closely interrelated. Such a concept also applies to a bio-inspired approach for the design of the motor cognitive architecture of humanoid robots. This explains why the proposed synergy formation model is explicitly focused on motor cognition and cannot be considered a specific controller conceived for specific control issues that are specifically related to the intrinsic features of the actuators and the related micro-controllers, such as the modulation of the system stiffness and/or resistance to vibrations. For example, the compliance vector defined in the proposed model must be used as a key element for the optimal definition of the redundant synergy formation process, not as an element for controlling the system’s stiffness. Along the same line of reasoning, we may consider the issue of energetic efficiency. In neurobiology, the analysis of “biological motion” has revealed the energetic efficiency of human actions, mainly determined by their global smoothness [14], i.e., the kinematic organization of the action. A similar kind of issue has been investigated in relation to robotic motion [15], demonstrating that the smoothness of robot motion induces significant energetic improvements. The proposed model of synergy formation is bio-inspired and based on the global smoothness of the generated synergies. Thus, it is energetically efficient from the kinematic point of view. At the same time, we may assume that on top of a kinematic component of energetic efficiency, there is also a component dependent on the actuator design and micro-control, but this is outside the focus of this study.

The proposed model of coordination for redundant humanoid robots has no direct effects on the global system stiffness or on the resistance to vibrations and mechanical perturbations, despite the crucial role of the compliance vector in shaping the kinematic patterns that distribute the planned action to all the DoFs of the body model. The elements of such a vector express how much a DOF resists an “ideomotor perturbation”, i.e., the intention to move in a given direction with a given speed profile. On the other hand, the system stiffness is a function of the microcrontrollers that activate the actuators of each DOF, including variable stiffness actuators [45]. Moreover, it is possible to integrate the motor cognitive network described in this paper with the motor control mechatronics in such a way as to anticipate the physical interaction of the end-effector with the environment or an object/tool to be manipulated with a specific stiffness ellipsoid [25].