Abstract
In this paper, a new consensus tracking control algorithm is proposed for discrete multi-agent systems under binary communication with noise and a time-varying reference state. Unlike previous studies, the leader’s reference state is time-varying and convergent. Each agent estimates its neighbors’ states using a recursive projection algorithm based on noisy binary-valued information. The controller design incorporates both the error between the current and estimated states and the rate of change of the estimated state, resulting in a proportional–derivative-like algorithm (PD-like algorithm). The algorithm achieves consensus tracking with a convergence rate of under certain conditions. Finally, numerical simulations demonstrate the algorithm’s effectiveness and validate the theoretical results.
1. Introduction
Multi-agent systems (MASs) consist of multiple interacting agents and are widely applied in areas such as autonomous vehicle platooning, multi-UAV systems, microgrid frequency control, and other domains [1,2,3]. The consensus control problem is one of the core issues in MAS, aiming to design distributed controllers to make the states of all agents converge to a consensus. The theoretical study of consensus problems began in [4], where A. Jadbabaie et al. provided a theoretical explanation for the phenomenon observed in the Vicsek model [5] using graph connectivity, thus improving the coordination theory based on the nearest neighbor rule in MASs. In [6], R. Olfati-Saber et al. used the Laplacian matrix to study the consensus problem in MASs, providing a consensus analysis framework based on graph theory. Ref. [7] pointed out that under dynamic interaction topologies, if the union of interaction graphs has spanning trees frequently enough during certain time periods, MASs can asymptotically reach consensus, and the restrictions on weighting factors are relaxed. These laid the theoretical foundation for subsequent research on consensus in MAS.
In the consensus tracking control problem of MASs, leader-following consensus is an important cooperative control strategy. Ref. [8] studied the problem of achieving finite-time leader-following consensus in second-order multi-agent systems with both fixed and switching topologies. For situations where the leader’s state information cannot be directly obtained, ref. [9] proposed a tracking control protocol based on distributed observers using relative output measurements and information received from neighbors. Ref. [10] combined neighbor-based feedback control laws and dynamic estimation rules with Lyapunov stability analysis to investigate the consensus problem in MASs with an active leader and variable topologies.
With the practical application of MAS, the influence of noise such as sensor noise, channel fading, and electromagnetic interference on measurement and information communication cannot be ignored. Ref. [11] introduced a stochastic approximation algorithm for models with noisy measurements and proposed to combine the decay property of the stochastic Lyapunov function with the so-called invariance direction to achieve convergence analysis. Ref. [12] proposed a new velocity decomposition technique for noisy measurements and time-varying directed topologies and designed a distributed estimation algorithm based on it. Furthermore, with limited communication bandwidth resources, quantized communication has been introduced to improve communication efficiency among MASs. The study of quantized consensus began in [13], where each agent’s state was set as an integer, and a quantized gossip algorithm was proposed for the distributed averaging problem to achieve quantized consensus. Quantized communication has increasingly attracted the interest of researchers. Refs. [14,15,16,17] used different types of quantizers to study consensus problems.
However, there is relatively little research on binary communication, as a special form of quantized communication, in MASs. However, its simplicity, extremely low communication bandwidth requirements, and strong anti-interference ability have attracted many researchers. Refs. [18,19] study system identification problems under binary-valued observations and cyber-attacks. Ref. [20] proposed a two-time-scale consensus protocol for consensus problems with random noise and binary measurements under undirected and fixed topologies. However, the state estimation and control in it are carried out alternately. Inspired by the recursive projection algorithm, refs. [21,22] proposed a new consensus algorithm that can simultaneously perform state estimation and control and update the state in real time, considering noisy measurement and binary quantizers. The convergence rate of this algorithm is , which is faster than that in [20]. Ref. [23] further explored the consensus tracking problem in systems with time-invariant leaders under directed topologies. In this paper, the leader’s state discussed is time-varying, which is more challenging than in [22]. Meanwhile, in [24], the authors separately investigated the cases of a convergent leader and bounded leader. Decaying gains and constant gains in the control algorithms are designed for the two cases, respectively.
In this paper, the state of the leader is time-varying, and the uniform boundedness of the agent’s time-varying state cannot be guaranteed, requiring a reanalysis of its uniform boundedness properties. This increases the difficulty of analysis compared with the constant leader in Reference [23]. Moreover, most of the consensus algorithms with binary-valued communication only use proportional (P-like) control strategies based on the estimated states of neighbors. For consensus tracking problems with accurate information of neighbors, PD-like algorithms were designed in [25,26]. In this paper, a PD-like algorithm is introduced, taking into account the rate of change of the estimated state of the agents’ neighbors. How to analyze the influence of the derivative term on consensus error is more challenging.
The contributions of this paper are as follows:
- This paper proposes a novel online algorithm consisting of estimation and control for the consensus tracking problem with a time-varying reference state and binary-valued communication. In the estimation part, the recursive projection algorithm (RPA) is used to deal with binary-valued observations. In the control part, a differential term is added to track the varying of neighbors in addition to a proportional term, which results in a PD-like algorithm.
- Due to the introduction of differential terms, the PD-like algorithm increases the complexity of convergence analysis. The differential terms describe an estimate of the rate of change of the neighbors. Using the properties of the estimation algorithm, the differential term can be handled using the rate of change of the leader. If the state of the leader is convergent, it is proved that the followers can asymptotically track the leader using a dual Lyapunov function analysis framework constructed based on the estimation and tracking control.
- The PD-like algorithm has significant advantages in terms of convergence speed. It introduces the difference in state estimation in the control input and integrates the recursive projection estimation and differential feedback mechanisms, compensating for the loss of quantized information and enhancing the system’s adaptability to dynamic leaders. This enables the system to adjust its own state quickly and accelerate the convergence speed towards the leader’s state. Moreover, through theoretical analysis, it can be seen that the convergence rate of the algorithm depends on the rate of change of the leader. Compared with algorithms that only use proportional control strategies in [24], the convergence rate of this algorithm is faster, which ensures that the multi-agent system can quickly achieve consensus tracking with binary-valued communication.
The remainder of this paper is structured as follows. Nomenclature summarizes some important symbols. Section 2 describes the consensus tracking control problem with binary-valued communication. Section 3 presents the consensus tracking control algorithm. Section 4 provides the main conclusions of the algorithm, including convergence and the convergence rate. Section 5 verifies the effectiveness of the theory through simulation. Section 6 summarizes this paper and looks ahead to future work.
2. Problem Formulation
Consider a discrete-time multi-agent system consisting of n agents:
where represents the state of agent i at time t, and is the corresponding control input. This system also includes a leader agent , whose state is and is expressed as follows:
where is the rate of change of the leader’s state. The remaining n agents are called followers. So, the vector update equation of this system is as follows:
with . Let and .
Consider that the multi-agent system is represented by a directed topological network structure , where is the set of nodes, and each node corresponds to an agent. is the set of edges, which represent the channels for information interaction among agents. Matrix is the adjacency matrix of topology G. If there is an edge from agent j to agent i, which means that agent i can directly obtain information from agent j, then , and agent j is called a neighbor of agent i, denoted as ; otherwise, , and agent j is not a neighbor of agent i. is the degree matrix, where represents the number of neighbors of agent i. Specifically, since the leader cannot receive feedback from any follower, for adjacency matrix A, we have , , and . The Laplacian matrix of the directed graph is .
When agent i receives information from its neighbor agent j, it is affected by random noise, and its observed value is as follows:
where is the set of all neighbors of agent i, is the state of agent j at time t, is the communication noise, is the unmeasurable output, C is the binary sensor threshold, and is the binary information obtained by agent i from neighbor agent j. is an indicative function, defined as
Assumption 1.
Network structure G is connected and is a directed spanning tree with the leader as the root node.
Remark 1.
Let L be the Laplacian matrix of directed graph G. It has eigenvalues with non-negative real parts and has a unique eigenvalue of 0. The corresponding eigenvector has all elements equal to 1.
Remark 2.
According to the condition of Assumption 1, there exists a matrix that satisfies the following conditions:
Let an invertible matrix , with and , where all eigenvalues of matrix are the non-zero eigenvalues of matrix L with positive real parts. And matrix is a Jordan matrix.
Assumption 2.
In Equation (4), the noise follows a normal distribution with a mean of 0 and is independent of i, j, and t. Its distribution function is , and its probability density function is .
Remark 3.
We assume that the distribution of this noise is known from prior knowledge.
The reference state considered in this paper is time-varying and convergent, which is described by the following assumption.
Assumption 3.
There exists a constant such that
From Assumption 3, the following lemma can be derived.
Lemma 1.
The rate of change of the leader satisfies that is convergent [24].
The main task of the algorithm is to design the control so that the followers can track the leader’s state through binary communication, that is,
3. Control Algorithm
We use the recursive projection algorithm (RPA) in [21] to estimate the states of neighbors, where the step size decays over time. An attenuation gain and an estimated differential term are introduced into the control law. The consensus algorithm and the control law are as follows:
- Initialization: The initial state of each agent and its estimations of the initial states of its neighbors are as follows:for , , and . Here, , which is a known boundary for the states.
- Observation: Each agent observes the binary information of its neighbors, as shown in Equation (4).
- Estimation: Each agent uses the observed binary information to calculate the estimation of its neighbors through the RPA algorithm:where is a coefficient in the step size of estimation, and is a projection operator defined as follows:
- Update: Each agent designs a controller to update its own state based on the estimation of its neighbors.where is a constant. The proportional (P) term and the derivative (D) term are and , respectively. By designing the controller, the state of agent i is updated as follows:
- Repeat: .
Remark 4.
According to the recursive projection operator, it can be known that the states estimated by the agents for their neighbors are bounded.
Proposition 1.
The states of all the followers updated using (9) satisfy
where , is the number of agent i’s neighbors, γ is the control parameter, , and β is the coefficient of estimation.
Proof of Proposition 1.
By updating the state of (9), we can obtain
The change rate of the neighbor’s estimated state can be obtained using projection algorithm (7):
Then, we can obtain the following using (10):
Here, in order to further determine the upper bound of , let . Since and are fixed parameters related to the agents, choosing this specific time point is helpful for facilitating subsequent derivations in combination with the previous inequalities and initial conditions.
Then, we have
Since the initial state of agent i and the estimates of the neighbors’ states are bounded, agent i’s state will be bounded through updating with a finite step. So, there exists a constant such that . Hence,
Assuming that
we can obtain the following inequality:
According to mathematical induction, we have
Let
It follows that
Due to , we have
□
In order to analyze the impact of the difference between the estimated value and the true value on the system, we define error vectors . They combine the estimation errors of each agent for the states of their neighbors. Hence, let . Define the error vectors as follows:
with . For any error vector , we define the following -dimensional vectors and as the starting point and the ending point, respectively:
for . Place and in the order of the error vector , and the following two matrices are obtained:
4. Main Result
In this section, the tracking error and the estimation error are first defined, and the conditional inequalities they satisfy are given. Finally, the convergence and convergence rates of the tracking error and the estimation error are obtained.
For a discrete multi-agent system, when Equation (6) is satisfied, it indicates that the system has reached a consensus. In Remark 2, is the left eigenvector corresponding to eigenvalue 0 of Laplacian matrix L, and it satisfies . Define a new convergence index:
where . Since , we can conclude that
where . Since , we can obtain
Define and . We have
and
Thus, we can deduce that . And to enable the system to achieve consensus tracking, we can prove that , where for any random variable x.
Matrix is a Hurwitz matrix. There exists a positive definite symmetric matrix that satisfies the following equation:
Due to , we have
where and are the minimum and maximum eigenvalues of matrix K respectively.
Define and , which represent the tracking error and the estimation error in the mean square sense, respectively.
In comparison to state updating [24] using the P-like control algorithm, parameter and item are added to state updating Equation (16) with the PD-like control algorithm. The parameter is constant, and we can obtain the property of item with (11) as follows:
We have the following lemmas on and .
Lemma 2.
Under Assumptions 1 and 2, tracking error satisfies the error of estimates
where , is the maximum eigenvalue of matrix , and is a constant.
Lemma 3.
Under Assumptions 1 and 2, estimate error satisfies
as , where , W is the bound of the projection of estimation, , , , , and is a constant.
Due to Equation (20), the proofs of Lemmas 2 and 3 are similar to the proofs of Lemmas 2 and 3 in [24].
To prove the convergence of the algorithm, we give a lemma as follows.
Lemma 4
(Theorem 1.2.23, [27]). If satisfies the iterative equation
where , converges, then
By Lemmas 1–4, we can obtain the convergence and convergence rate of the algorithm as follows.
Theorem 1
(Convergence). For the algorithm with Assumptions 1–3, if the coefficient β in estimate satisfies
where , and are the same as those in Lemmas 2 and 3, we can obtain
for and
for .
Proof of Theorem 1.
Let . Then, . We utilize the symmetric property of matrix .
Then, we can obtain
Then, we can obtain
Hence,
where is the minimum eigenvalue of matrix . Due to , we have, by Lemma 4,
Thus,
which implies the theorem. □
Theorem 2
(Convergence rate). Let the changing of the leader be . For the PD-like algorithm with Assumptions 1–3, we can obtain
and
for , where
and are the same as those in Lemmas 2 and 3.
Proof of Theorem 2.
The proof of the theorem is similar to that in Theorem 2 of [24]. □
Remark 5.
Theorem 2 indicates that the convergence rate of the PD-like algorithm depends on (the communication topology) and ε (the rate of change of the leader).
5. Simulation
The simulation consisted of a multi-agent system with the network topology illustrated in Figure 1. The system included four follower agents and one leader agent, where agent 5 was designated as the leader.
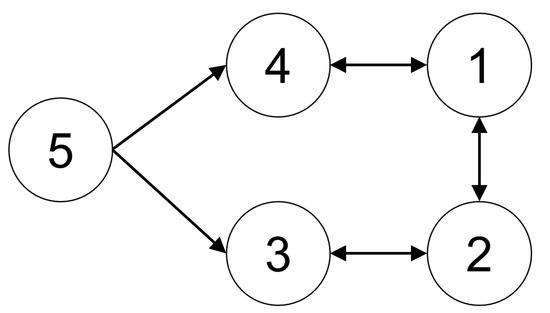
Figure 1.
Network topology of multi-agent system.
Each follower agent can obtain information from its respective neighbors, with the neighbor sets defined as follows: , where is the set of agent i’s neighbors. In contrast, agent 5, as the leader, does not receive information from any other agents. Laplacian matrix L corresponding to this topology is defined as .
The Jordan canonical form of Laplacian matrix L is . The corresponding transformation matrices are , and .
Based on , matrix K is obtained as . Then, based on related definitions of Lemma 2 and Lemma 3, we can calculate and .
Let the initial values for the states of the agents be , and the initial estimates of the neighbors’ states for each agent be . The threshold is given as , and the state boundary conditions are defined as . The noise follows a normal distribution , and can be computed as .
The state of the leader is convergent, and its state update formula is given by
where , which satisfies . In the simulation, the experimental parameters were set as and . The symbol l defined in Theorem 2 can be computed as = 203.0038. Choosing satisfies , and the trajectories of the agent states and their estimates are shown in Figure 2 and Figure 3, respectively. Figure 4 and Figure 5 present the tracking error and estimation error, respectively. The results demonstrate that the followers converge to the leader’s state, confirming the theoretical findings in Theorem 1. Figure 6 shows the relationship between the tracking error and the rate of change of the leader. The faster the leader changes, the slower the tracking error converges, which is consistent with Theorem 2. Figure 7 shows the state–time curves of agents under the P-like algorithm. It can be seen that the convergence to consensus is slower than that of the PD-like algorithm. At the same time, Figure 8 compares the tracking errors of the two algorithms. The red line represents the PD-like algorithm, and the blue line represents the P-like algorithm. It can also be seen that the PD-like algorithm converges faster.
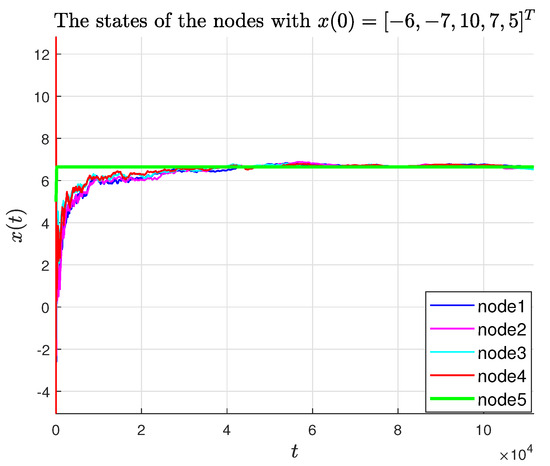
Figure 2.
The state-time curves of agents under the PD-like algorithm.
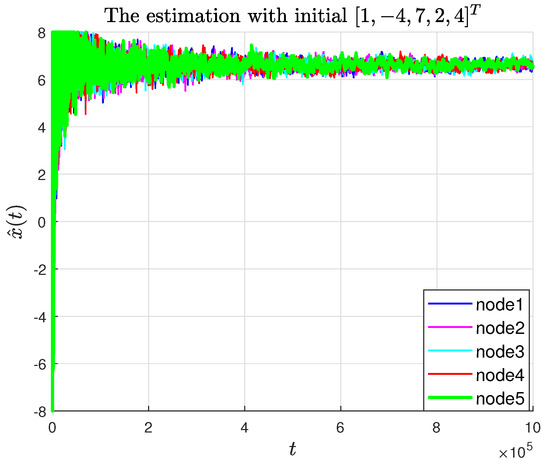
Figure 3.
The estimation-time curves of agents under the PD-like algorithm.
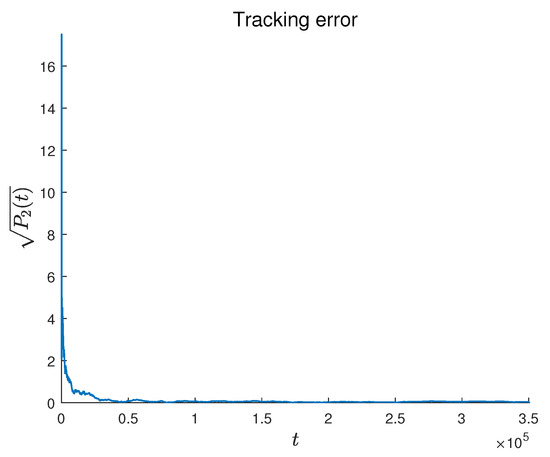
Figure 4.
The tracking error curve between the followers and the leader under the PD-like algorithm.
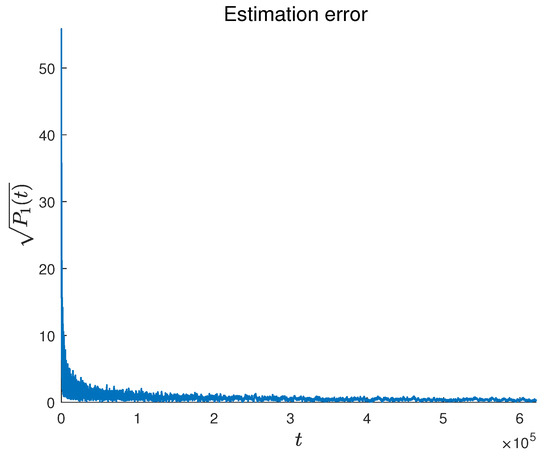
Figure 5.
The estimation error curve between the agents’ estimated values and the true states under the PD-like algorithm.
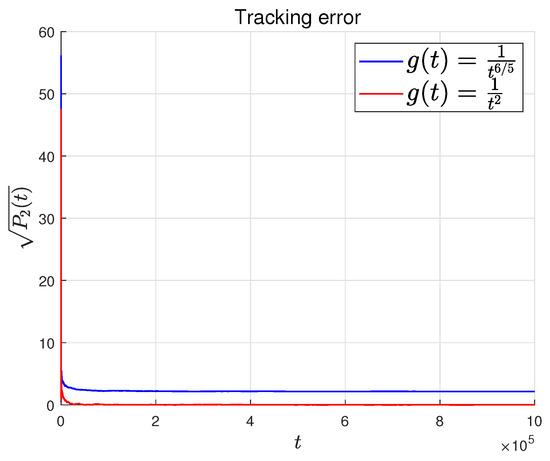
Figure 6.
Tracking error curves and under the PD-like algorithm.
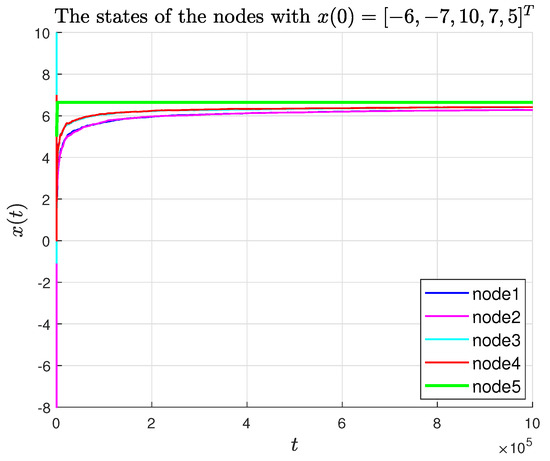
Figure 7.
The state-time curves of agents under the P-like algorithm.
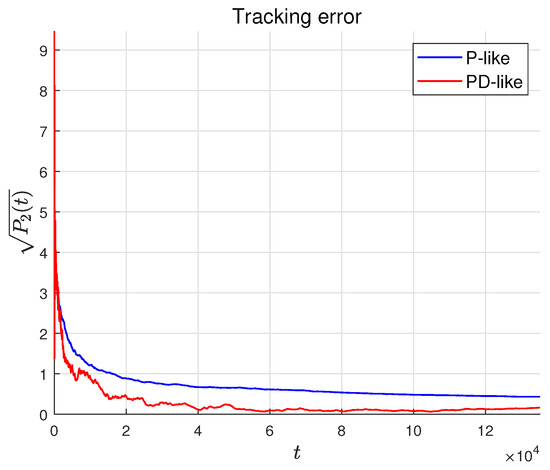
Figure 8.
Tracking error comparison of P-like and PD-like algorithms.
6. Conclusions
This paper presents a consensus tracking algorithm for discrete-time multi-agent systems under binary-valued communication, considering measurement noise and a time-varying reference state. Each agent estimates the states of its neighbors using RPA and designs a controller to update its state. An estimated differential term is introduced into the controller. Subsequently, the agents can converge to the leader’s reference state, and the convergence speed is closely related to the rate of change of the leader’s state and the system parameters.
There is a lot of work that deserves attention in the future. Presently, the academic community is actively engaged in developing safer and more efficient control algorithms. Notable examples include the design of cooperative control protocols for nonlinear multi-agent systems against different attacks [28,29], and the integration of event-triggered mechanisms into multi-agent consensus tracking problems to significantly reduce system resource consumption while maintaining tracking performance—all of which represent cutting-edge research frontiers [30]. Nevertheless, in practical applications (such as the collective behavior of mobile robots [31]), agents often encounter complex non-matching input constraints, nonlinear dynamic characteristics, and unknown time-varying disturbances. Addressing these challenges by designing robust and adaptive control strategies remains a critical hurdle that demands urgent breakthroughs.
Author Contributions
Conceptualization, T.W.; methodology, T.W.; software, Y.W.; validation, X.S.; formal analysis, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, J.W.; supervision, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the National Natural Science Foundation of China (Grants No. 62473040 and 62473042).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Notation | Meaning |
| The set of real numbers | |
| The Euclidean norm | |
| The state of the i-th agent at time t | |
| The state of leader with time variation | |
| The leader’s state change rate | |
| The control input of the i-th agent at time t | |
| The estimated value of the state of neighbor j at time t by agent i | |
| The error vectors | |
| The coefficient in the estimation step size | |
| The constant in the control law | |
| The eigenvalues of matrix U |
References
- Wang, X.; Li, Y.; Huang, L.; Huang, X.; Zhao, H.; Han, X.; Xiang, J.; Wang, H. Cooperative Control for Connected Automated Vehicle Platoon with C-V2X PC5 Interface. In Proceedings of the 2023 IEEE International Conference on Unmanned Systems (ICUS), Hefei, China, 13–15 October 2023; pp. 635–640. [Google Scholar]
- Yang, H.; Jiang, B.; Yang, H. Fault Tolerant Cooperative Control for Heterogeneous Multiple UAVs. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; pp. 1–6. [Google Scholar]
- Bidram, A.; Lewis, F.L.; Davoudi, A.; Qu, Z. Frequency control of electric power microgrids using distributed cooperative control of multi-agent systems. In Proceedings of the 2013 IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, Nanjing, China, 26–29 May 2013; pp. 223–228. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef] [PubMed]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Guan, Z.H.; Sun, F.L.; Wang, Y.W.; Li, T. Finite-Time Consensus for Leader-Following Second-Order Multi-Agent Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2646–2654. [Google Scholar] [CrossRef]
- Hajshirmohamadi, S.; Sheikholeslam, F.; Meskin, N.; Ghommam, J. Observer-Based Leader-Following Consensus for Linear Multiagent Systems with a Leader of Unknown Input. IEEE Syst. J. 2021, 15, 95–104. [Google Scholar] [CrossRef]
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
- Huang, M.; Manton, J.H. Stochastic Lyapunov Analysis for Consensus Algorithms with Noisy Measurements. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 1419–1424. [Google Scholar]
- Hu, J.; Feng, G. Distributed tracking control of leader–follower multi-agent systems under noisy measurement. Automatica 2010, 46, 1382–1387. [Google Scholar] [CrossRef]
- Kashyap, A.; Başar, T.; Srikant, R. Quantized consensus. Automatica 2007, 43, 1192–1203. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Z.; Ji, H. Distributed output consensus of heterogeneous linear multi-agent systems with dynamic quantization. Int. J. Robust Nonlinear Control 2024, 34, 10251–10275. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, B. Quantized Consensus by the ADMM: Probabilistic Versus Deterministic Quantizers. IEEE Trans. Signal Process. 2016, 64, 1700–1713. [Google Scholar] [CrossRef]
- Ma, J.; Ji, H.; Sun, D.; Feng, G. An approach to quantized consensus of continuous-time linear multi-agent systems. Automatica 2018, 91, 98–104. [Google Scholar] [CrossRef]
- Liu, H.; Cao, M.; De Persis, C. Quantization effects on synchronized motion of teams of mobile agents with second-order dynamics. Syst. Control Lett. 2012, 61, 1157–1167. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Q.; Zhao, Y. Identification of FIR Systems with binary-valued observations under replay attacks. Automatica 2025, 172, 112001. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Xue, W.; Zhao, Y. System Identification With Binary-Valued Observations Under Data Tampering Attacks. IEEE Trans. Autom. Control 2021, 66, 3825–3832. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, T.; Bi, W. Consensus Protocol for Multiagent Systems With Undirected Topologies and Binary-Valued Communications. IEEE Transactions on Automatic Control 2019, 64, 206–221. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Y. Recursive projection algorithm on FIR system identification with binary-valued observations. Automatica 2013, 49, 3396–3401. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Zhao, Y. Consensus of Multi-Agent Systems Under Binary-Valued Measurements and Recursive Projection Algorithm. IEEE Trans. Autom. Control 2020, 65, 2678–2685. [Google Scholar] [CrossRef]
- Qiu, Z.; Ren, Z.; Wang, T. Consensus Tracking Algorithm for Multi-Agent Systems with Binary-Valued Measurements. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 4030–4035. [Google Scholar]
- Wang, T.; Qiu, Z.; Lu, X.; Zhao, Y. Consensus Tracking Control of Multi-agent Systems with A Time-varying Reference State under Binary-valued Communication. arXiv 2025, arXiv:2503.15955. [Google Scholar]
- Ren, W. Multi-vehicle consensus with a time-varying reference state. Syst. Control Lett. 2007, 56, 474–483. [Google Scholar] [CrossRef]
- Cao, Y.; Ren, W.; Li, Y. Distributed discrete-time coordinated tracking with a time-varying reference state and limited communication. Automatica 2009, 45, 1299–1305. [Google Scholar] [CrossRef]
- Guo, L. Time-Varying Stochastic Systems: Stability, Estimation and Control; Jilin Science and Technology Press: Changchun, China, 1993. [Google Scholar]
- Liu, G.; Sun, Q.; Su, H.; Wang, M. Adaptive Cooperative Fault-Tolerant Control for Output-Constrained Nonlinear Multi-Agent Systems Under Stochastic FDI Attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 1–12. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Q.; Su, H.; Hu, Z. Adaptive Tracking Control for Uncertain Nonlinear Multi-Agent Systems With Partially Sensor Attack. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6270–6279. [Google Scholar] [CrossRef]
- Lu, X.; Wang, T.; Zhao, Y.; Zhang, J.F. Consensus of multi-agent systems under binary-valued measurements: An event-triggered coordination approach. Automatica 2025, 176, 112255. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Zuo, Z.; Jin, J.; Zheng, J. Collective Behaviors of Mobile Robots Beyond the Nearest Neighbor Rules With Switching Topology. IEEE Trans. Cybern. 2018, 48, 1577–1590. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).