Design and Basic Performance Analysis of a Bionic Finger Soft Actuator with a Dual-Chamber Composite Structure
Abstract
1. Introduction
2. Design of Soft Actuators
2.1. Biomimetic Principles
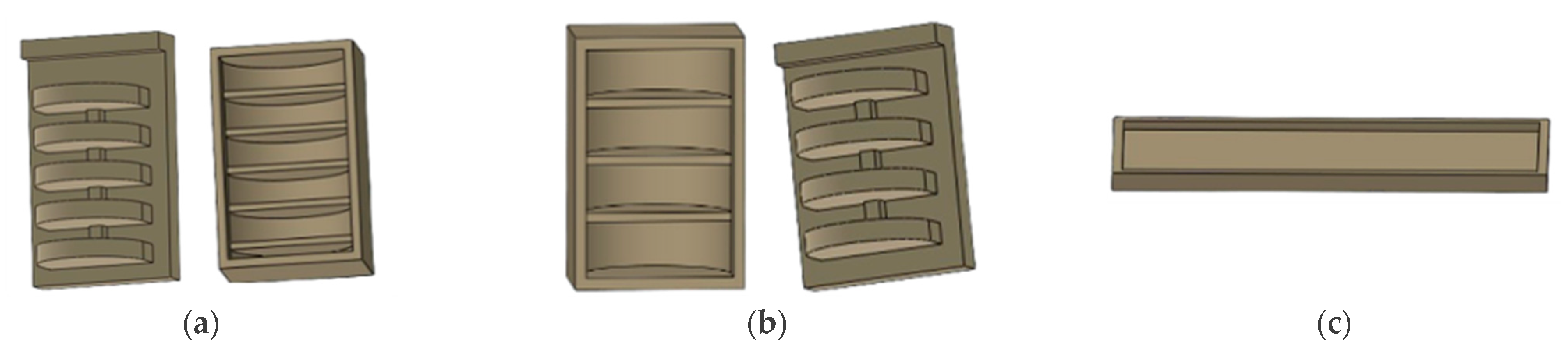
2.2. Structural Design
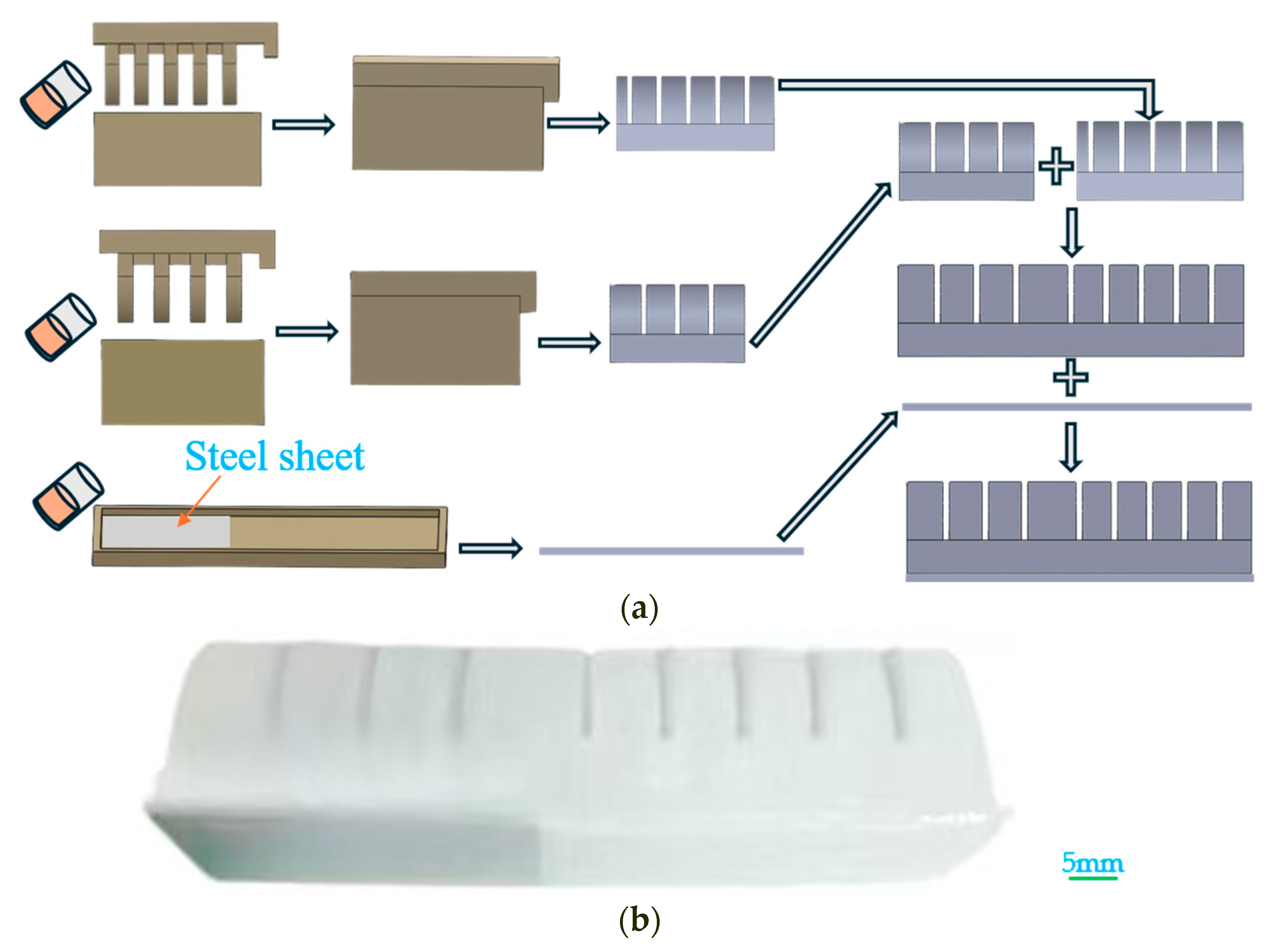
2.3. Manufacturing of Soft Fingers
3. Establishment of Theoretical Model of Soft Finger Bending
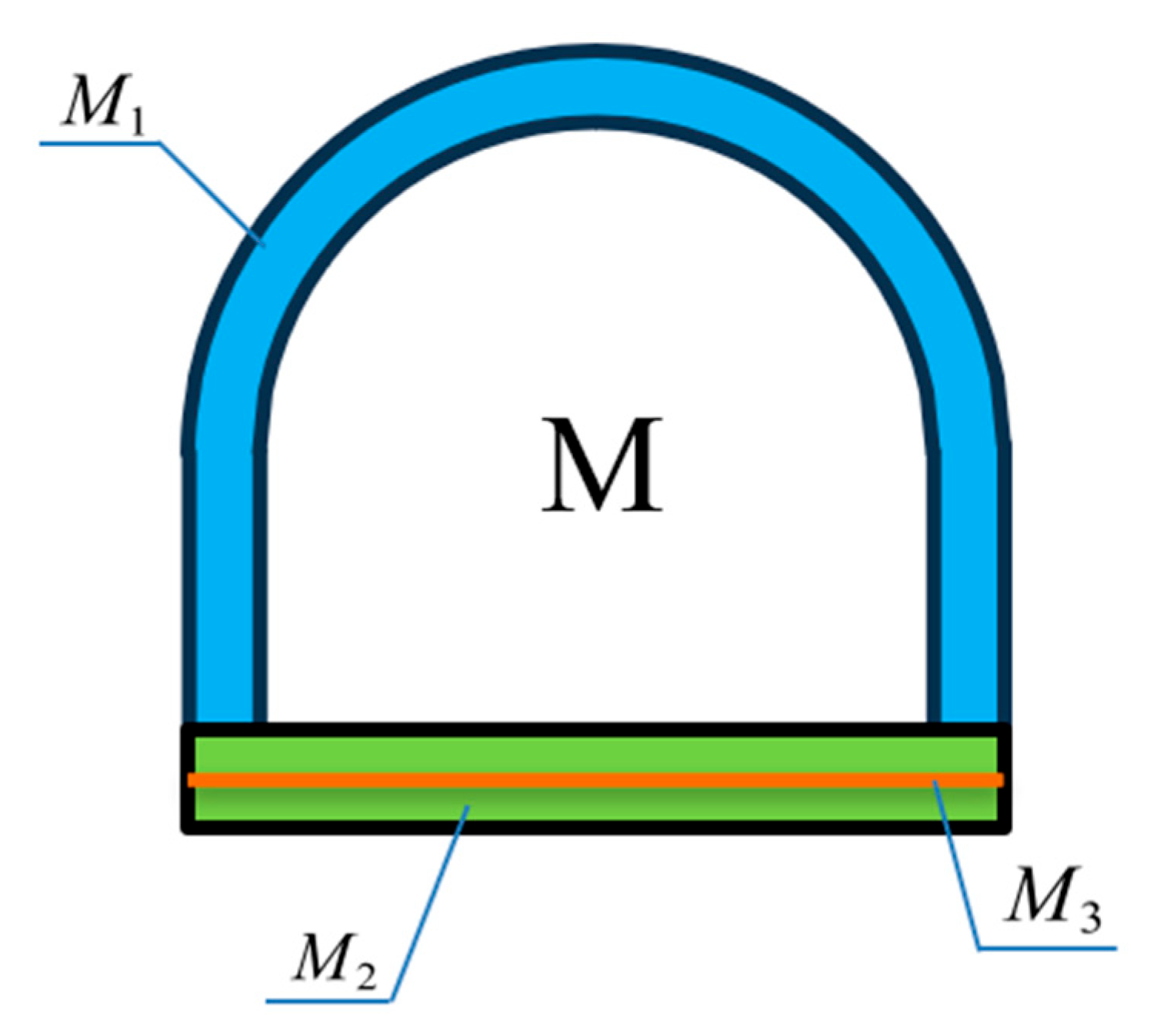
3.1. Selection of Constitutive Model
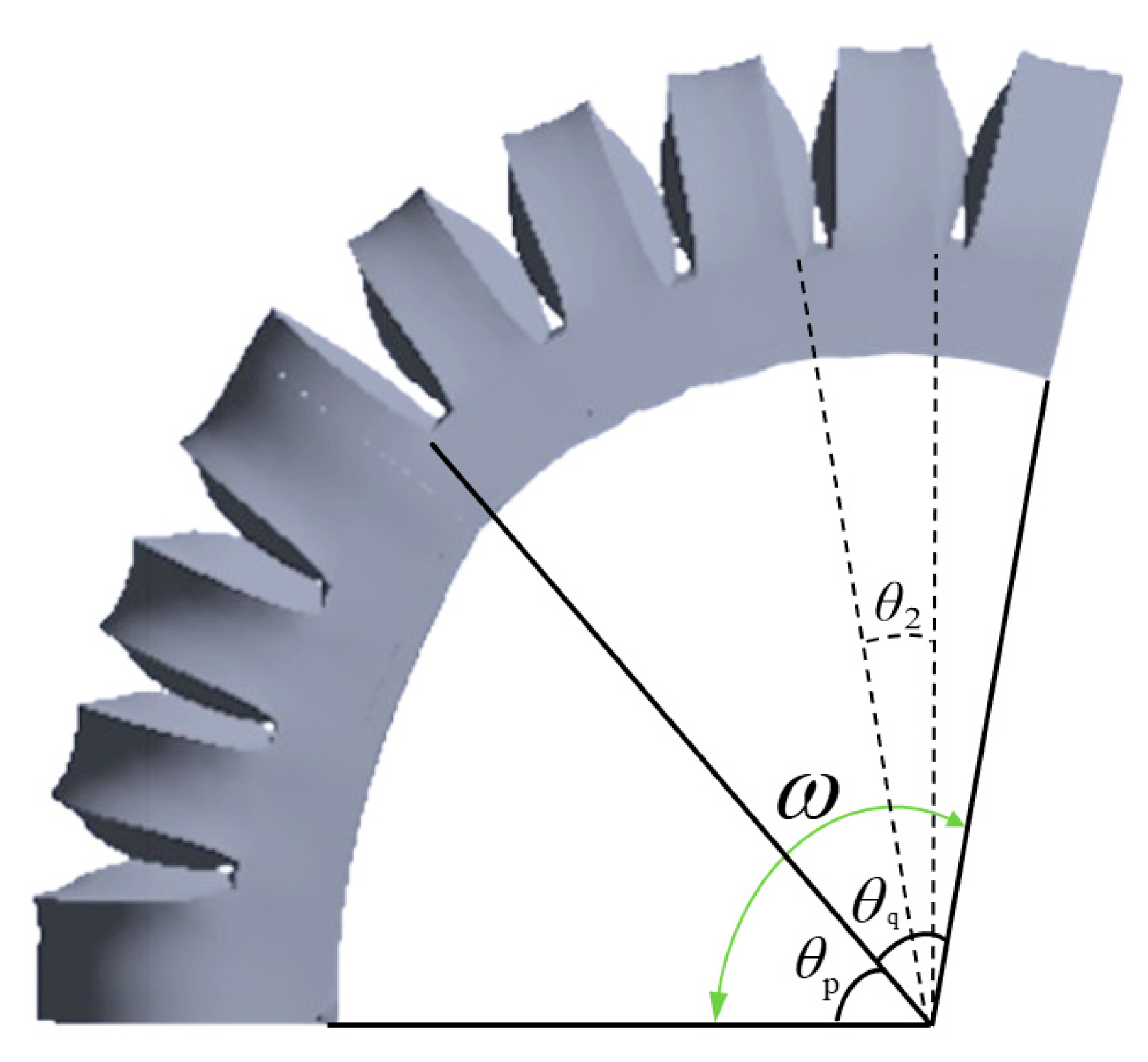
3.2. Bending Model of Fingertip Actuator
3.3. Finger Root Actuator Bending Model
3.4. Analysis of the Overall Bending Angle of the Finger
4. Finite Element Simulation Analysis
4.1. Analysis Steps
- (1)
- Model the soft finger components in SolidWorks 2018 and save them in Parasolid format (.x_ t) for abaqus import.
- (2)
- Define material properties: the constitutive model is the Yeoh model, with the coefficient set to , . The steel sheet is an elastic material with a Young’s modulus of E = 193 GPa and a Poisson’s ratio of ν = 0.3. The density of the silica gel material is 1100 kg/m3.
- (3)
- Assemble the components.
- (4)
- Create a gravity load: the load type is gravity. The load direction is the negative direction of the Z-axis. The parameter “component 3” is −9810 mm/s2.
- (5)
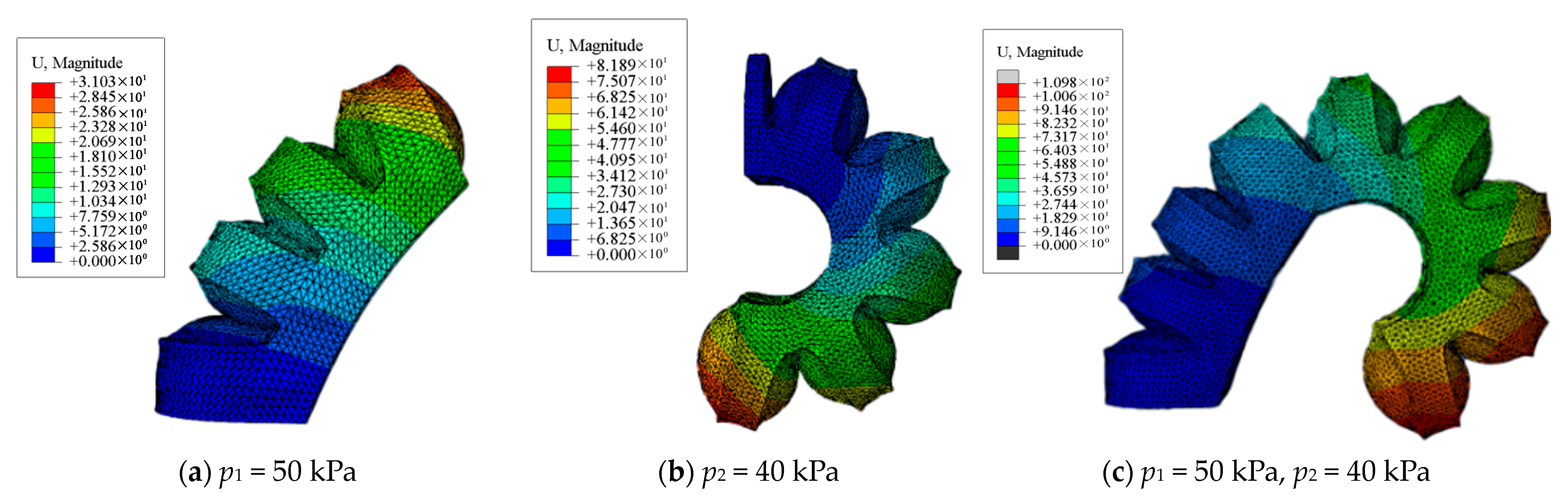
- Define loads and boundary conditions: fix the end and apply internal pressure, as shown in Figure 9a.
- (6)
- Create self-contact interactions.
- (7)
- Set tangential and normal contact properties for the expansion wall surface.
- (8)
- Mesh with C3D10H elements, as shown in Figure 9b.
- (9)
- Create and submit the job for analysis.

4.2. Simulation Analysis of Key Parameters of Soft Finger
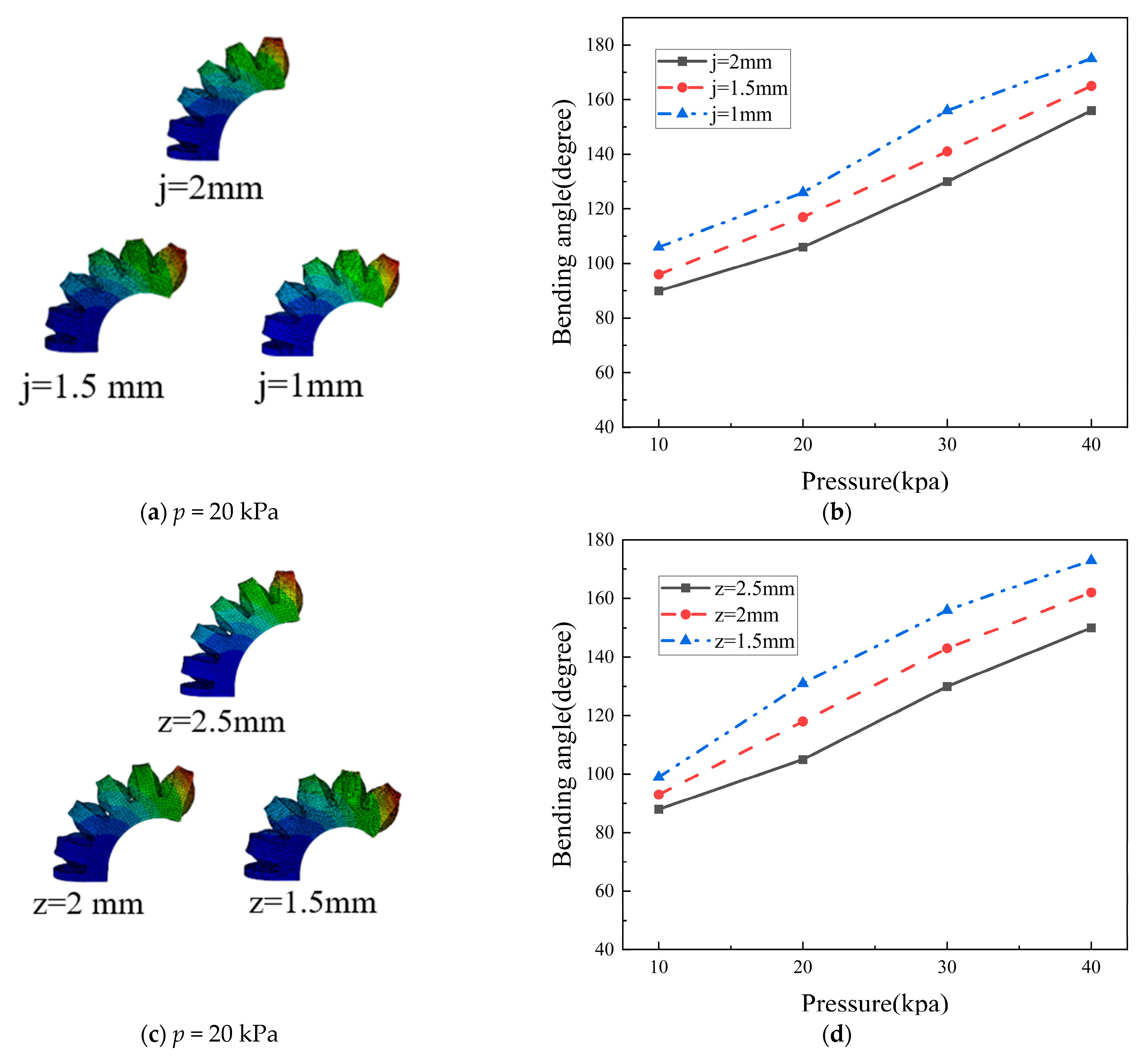
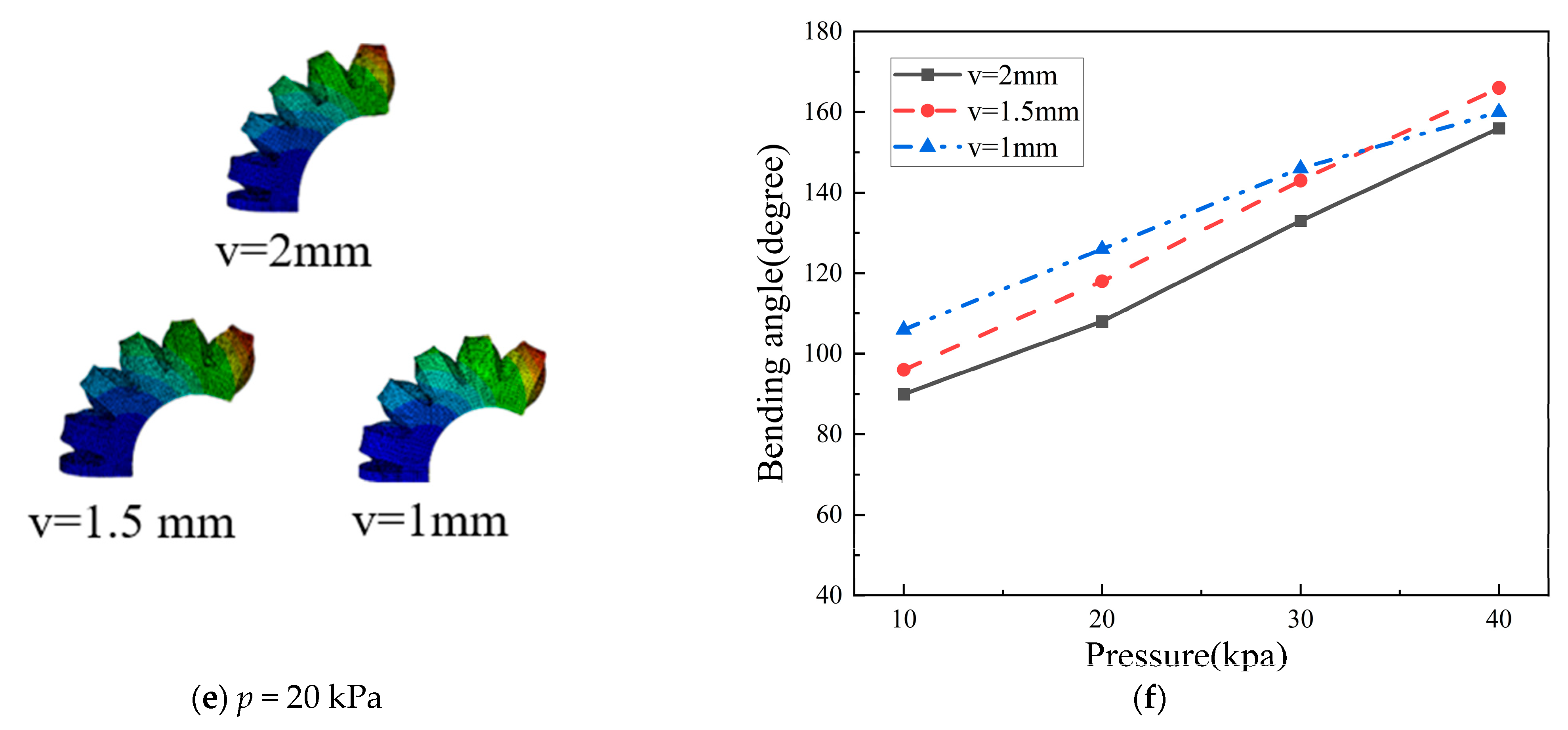
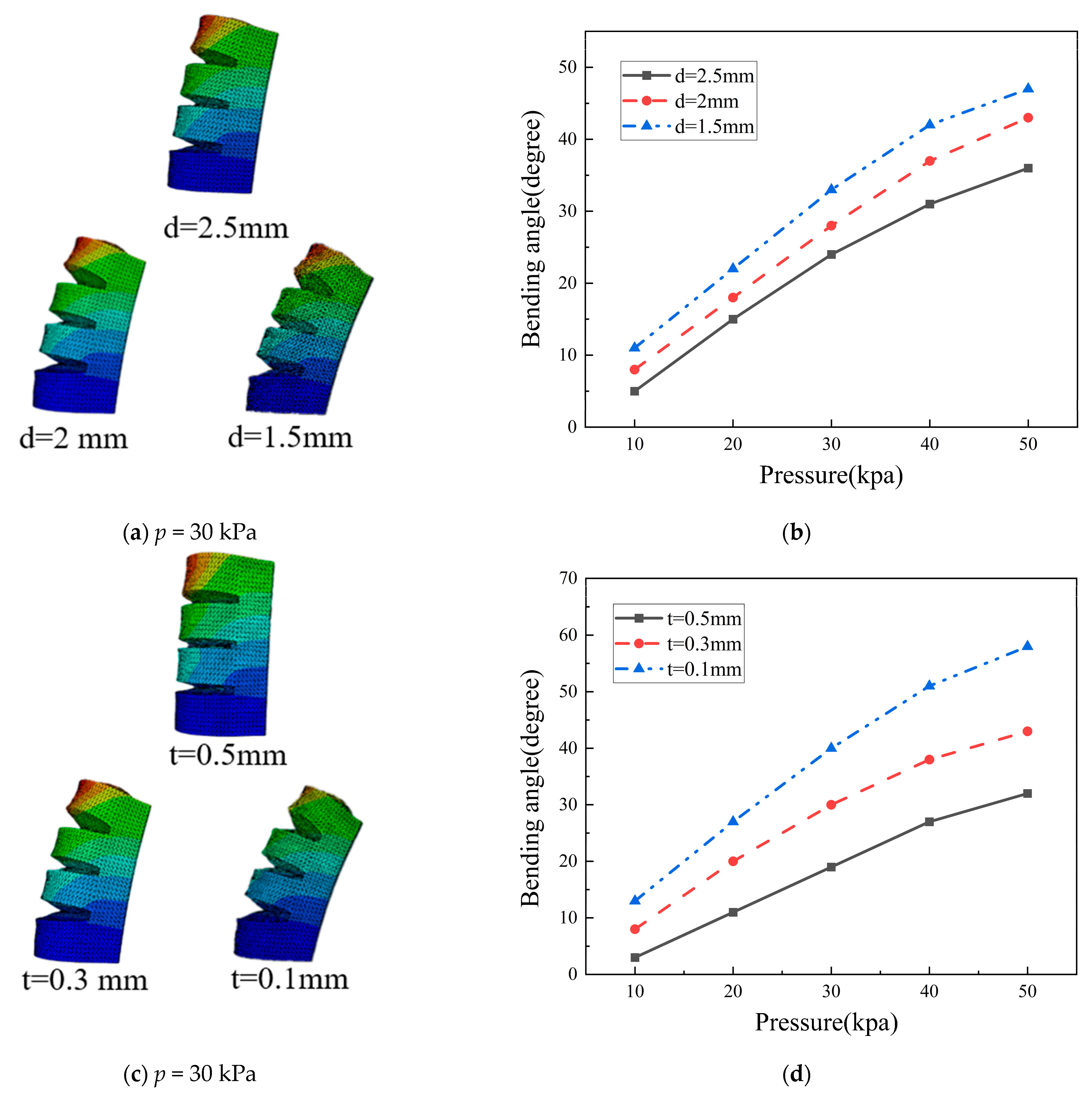
4.2.1. Parameter Analysis of the Tip Actuator
4.2.2. Parameter Analysis of the Finger Root Actuator
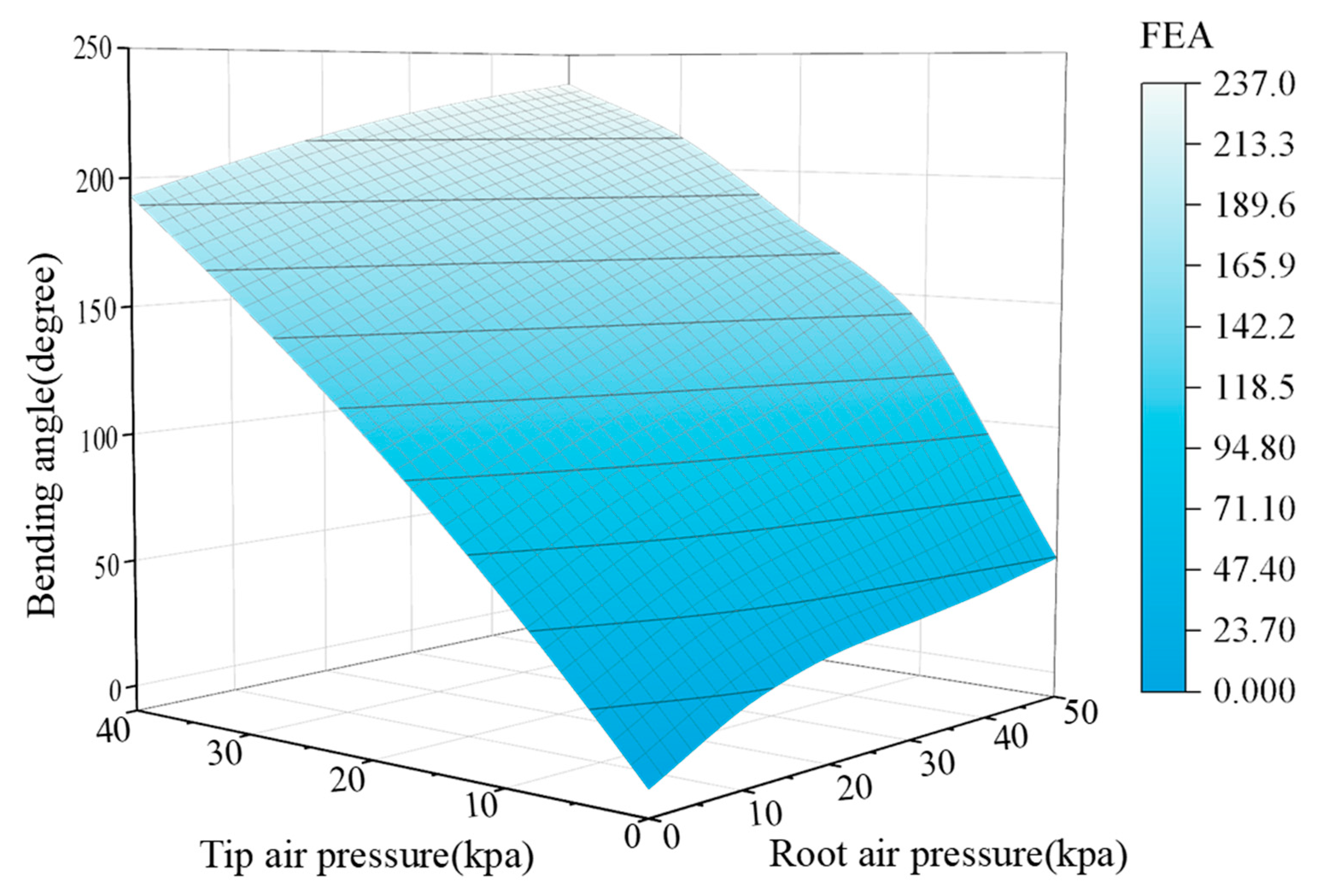
4.3. Simulation Analysis of the Overall Deformation of the Finger
5. Experimental Testing and Analysis
5.1. Bending Deformation Capability Testing of the Soft Finger
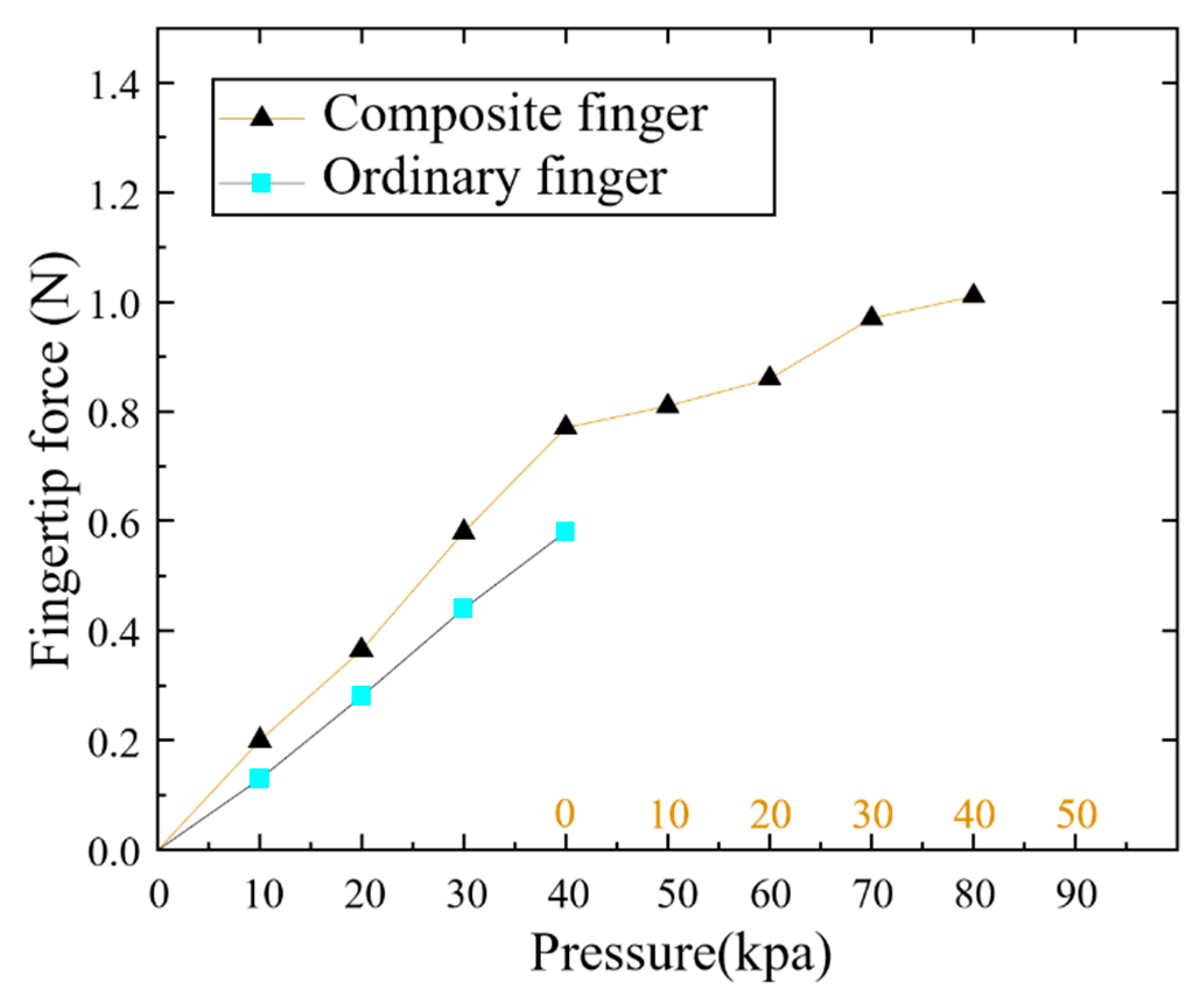
5.2. Fingertip Force Testing of the Soft Robotic Finger
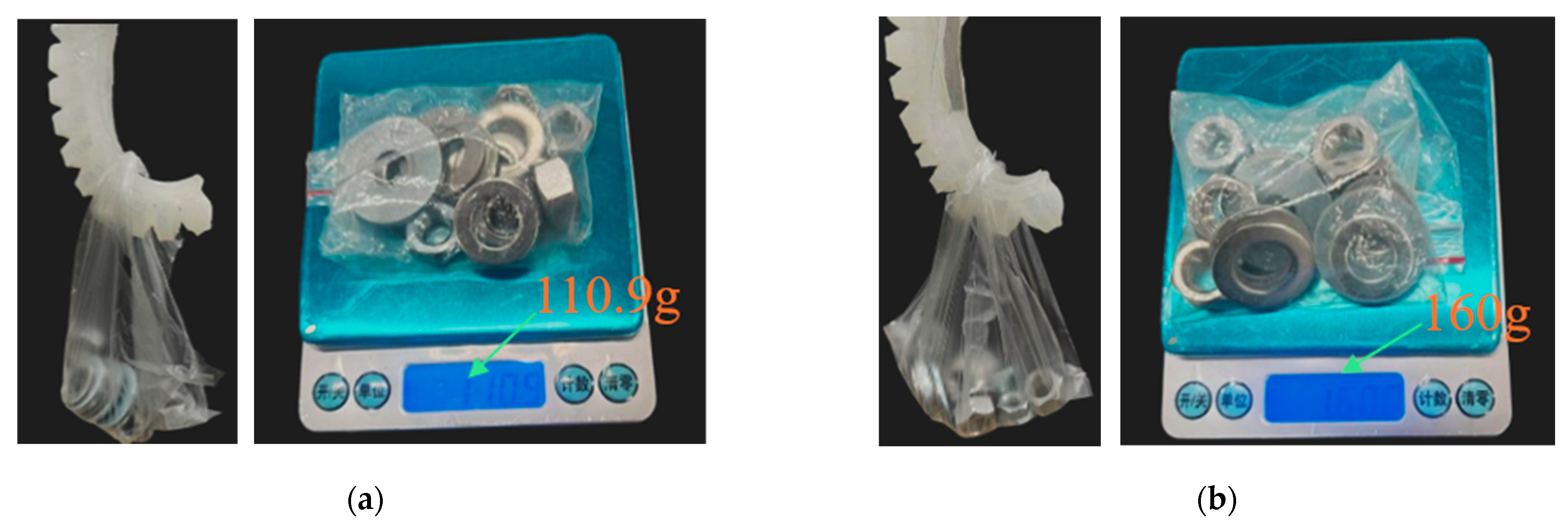
5.3. Hook Quality Test
6. Performance Test of Soft Manipulator
6.1. Construction of the Experimental Platform
6.2. Gripping Diameter Test
6.3. Gripping Force Testing
6.4. Physical Object Grasping Applications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flesher, S.N.; Downey, J.E.; Weiss, J.M.; Hughes, C.L.; Herrera, A.J.; Tyler-Kabara, E.C.; Boninger, M.L.; Collinger, J.L.; Gaunt, R.A. A brain-computer interface that evokes tactile sensations improves robotic arm control. Science 2021, 372, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ndou, W.S.; Ng, N.; Gaston, P.; Simpson, P.M.; Macpherson, G.J.; Patton, J.T.; Clement, N.D. Robotic-arm assisted total knee arthroplasty is associated with improved accuracy and patient reported outcomes: A systematic review and meta-analysis. Knee Surg. Sports Traumatol. Arthrosc. 2022, 30, 2677–2695. [Google Scholar] [CrossRef] [PubMed]
- Khalid, M.Y.; Arif, Z.U.; Ahmed, W.; Umer, R.; Zolfagharian, A.; Bodaghi, M. 4D printing: Technological developments in robotics applications. Sensor. Actuat. A Phys. 2022, 343, 113670. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, S.; Fang, B.; Sun, F.; Liu, H.; Li, H. A review of smart materials for the boost of soft actuators, soft sensors, and robotics applications. Chin. J. Mech. Eng. 2022, 35, 37. [Google Scholar] [CrossRef]
- Goh, G.D.; Goh, G.L.; Lyu, Z.; Ariffin, M.Z.; Yeong, W.Y.; Lum, G.Z.; Campolo, D.; Han, B.S.; Wong, H.Y.A. 3D printing of robotic soft grippers: Toward smart actuation and sensing. Adv. Mater. Technol. 2022, 7, 2101672. [Google Scholar] [CrossRef]
- Sparrman, B.; Du Pasquier, C.; Thomsen, C.; Darbari, S.; Rustom, R.; Laucks, J.; Shea, K.; Tibbits, S. Printed silicone pneumatic actuators for soft robotics. Addit. Manuf. 2021, 40, 101860. [Google Scholar] [CrossRef]
- Yap, Y.L.; Sing, S.L.; Yeong, W.Y. A review of 3D printing processes and materials for soft robotics. Rapid Prototyp. J. 2020, 26, 1345–1361. [Google Scholar] [CrossRef]
- Filippova, O.V.; Maksimkin, A.V.; Dayyoub, T.; Larionov, D.I.; Telyshev, D.V. Sustainable Elastomers for Actuators: “Green” Synthetic Approaches and Material Properties. Polymers 2023, 15, 2755. [Google Scholar] [CrossRef]
- Kim, M.S.; Heo, J.K.; Rodrigue, H.; Lee, H.T.; Pané, S.; Han, M.W.; Ahn, S.H. Shape memory alloy (SMA) actuators: The role of material, form, and scaling effects. Adv. Mater. Technol. 2023, 35, 2208517. [Google Scholar] [CrossRef]
- Chen, R.; Wu, L.; Sun, Y.; Chen, J.-Q.; Guo, J.-L. Variable stiffness soft pneumatic grippers augmented with active vacuum adhesion. Smart Mater. Struct. 2020, 29, 105028. [Google Scholar] [CrossRef]
- Silva, A.B.; Murcia, M.; Mohseni, O.; Takahashi, R.; Forner-Cordero, A.; Seyfarth, A.; Hosoda, K.; Sharbafi, M.A. Design of Low-Cost Modular Bio-Inspired Electric–Pneumatic Actuator (EPA)-Driven Legged Robots. Biomimetics 2024, 9, 164. [Google Scholar] [CrossRef] [PubMed]
- Han, P.; Lauder, G.V.; Dong, H. Hydrodynamics of median-fin interactions in fish-like locomotion: Effects of fin shape and movement. Phys. Fluids 2020, 32, 011902. [Google Scholar] [CrossRef]
- Zuo, Q.; Xu, Y.; Xie, F.; Fang, H.; He, K.; Zhong, Y.; Li, Z. Dynamic modeling of a novel kind of rigid-soft coupling biomimetic robotic fish. J. Intell. Robot. Syst. 2022, 105, 41. [Google Scholar] [CrossRef]
- Joyee, E.B.; Pan, Y. A fully three-dimensional printed inchworm-inspired soft robot with magnetic actuation. Soft Robot. 2019, 6, 333–345. [Google Scholar] [CrossRef]
- Zhai, Y.; De Boer, A.; Yan, J.; Shih, B.; Faber, M.; Speros, J.; Gupta, R.; Tolley, M.T. Desktop fabrication of monolithic soft robotic devices with embedded fluidic control circuits. Sci. Robot. 2023, 8, eadg3792. [Google Scholar] [CrossRef]
- Merces, L.; Ferro, L.M.M.; Thomas, A.; Karnaushenko, D.D.; Luo, Y.; Egunov, A.I.; Zhang, W.; Bandari, V.K.; Lee, Y.; McCaskill, J.S.; et al. Bio-Inspired Dynamically Morphing Microelectronics toward High-Density Energy Applications and Intelligent Biomedical Implants. Adv. Mater. 2024, 36, 2313327. [Google Scholar] [CrossRef]
- Zhang, M.; Pal, A.; Zheng, Z.; Gardi, G.; Yildiz, E.; Sitti, M. Hydrogel muscles powering reconfigurable micro-metastructures with wide-spectrum programmability. Nat. Mater. 2023, 22, 1243–1252. [Google Scholar] [CrossRef]
- Bezha, K.; Ito, K. Soft manipulator inspired by octopi: Object grasping in all anatomical planes using a tendon-driven continuum arm. Artif. Life Robot. 2023, 28, 96–105. [Google Scholar] [CrossRef]
- Pi, J.; Liu, J.; Zhou, K.; Qian, M. An octopus-inspired bionic flexible gripper for apple grasping. Agriculture 2021, 11, 1014. [Google Scholar] [CrossRef]
- An, S.-Q.; Li, W.-H.; Li, J.-H.; Zou, H.-L.; Deng, Z.-C. Tuning stiffness with granular chain structures for versatile soft robots. Soft Robot. 2023, 10, 493–503. [Google Scholar] [CrossRef]
- Li, X.; Zheng, T.; Sui, D.; Lin, N.; Zhang, Q.; Zhao, J.; Zhu, Y. A 3D printed variable cross-section pneumatic soft manipulator with high-precision positioning capability: Design and control implementation. Sens. Actuators A Phys. 2022, 342, 113644. [Google Scholar] [CrossRef]
- Li, J.; Luan, Z.; Wang, Y.; Huang, M.; Yan, J.; Wang, Y. Analysis modeling and experiment of bionic winding soft actuator inspired by plant tendrils. Smart Mater. Struct. 2023, 32, 035023. [Google Scholar] [CrossRef]
- Xiao, W.; Hu, D.; Yang, G.; Jiang, C. Modeling and analysis of soft robotic surfaces actuated by pneumatic network bending actuators. Smart Mater. Struct. 2022, 31, 055001. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, W.; Tang, B. Design and feasibility tests of a lightweight soft gripper for compliant and flexible envelope grasping. Soft Robot. 2022, 9, 376–385. [Google Scholar] [CrossRef]
- Dunai, L.; Novak, M.; García Espert, C. Human hand anatomy-based prosthetic hand. Sensors 2020, 21, 137. [Google Scholar] [CrossRef]
- Tan, H.W.; Choong, Y.Y.C.; Kuo, C.N.; Low, H.Y.; Chua, C.K. 3D printed electronics: Processes, materials and future trends. Prog. Mater. Sci. 2022, 127, 100945. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Overvelde, J.T.; Galloway, K.C.; Wood, R.J.; Bertoldi, K.; Walsh, C.J. Modeling of soft fiber-reinforced bending actuators. IEEE Trans. Robot. 2015, 31, 778–789. [Google Scholar] [CrossRef]
- Polygerinos, P.; Lyne, S.; Wang, Z.; Nicolini, L.F.; Mosadegh, B.; Whitesides, G.M.; Walsh, C.J. Towards a soft pneumatic glove for hand rehabilitation. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1512–1517. [Google Scholar]
- Qin, G.; Ji, A.; Cheng, Y.; Zhao, W.; Pan, H.; Shi, S.; Song, Y. A snake-inspired layer-driven continuum robot. Soft Rob. 2022, 9, 788–797. [Google Scholar] [CrossRef]
- Shan, Y.; Zhao, Y.; Yu, H.; Pei, C.; Jin, Z.; Sun, Y. Design and grasping force modeling for a soft robotic gripper with multi-stem twining. J. Bionic Eng. 2023, 20, 2123–2134. [Google Scholar] [CrossRef]


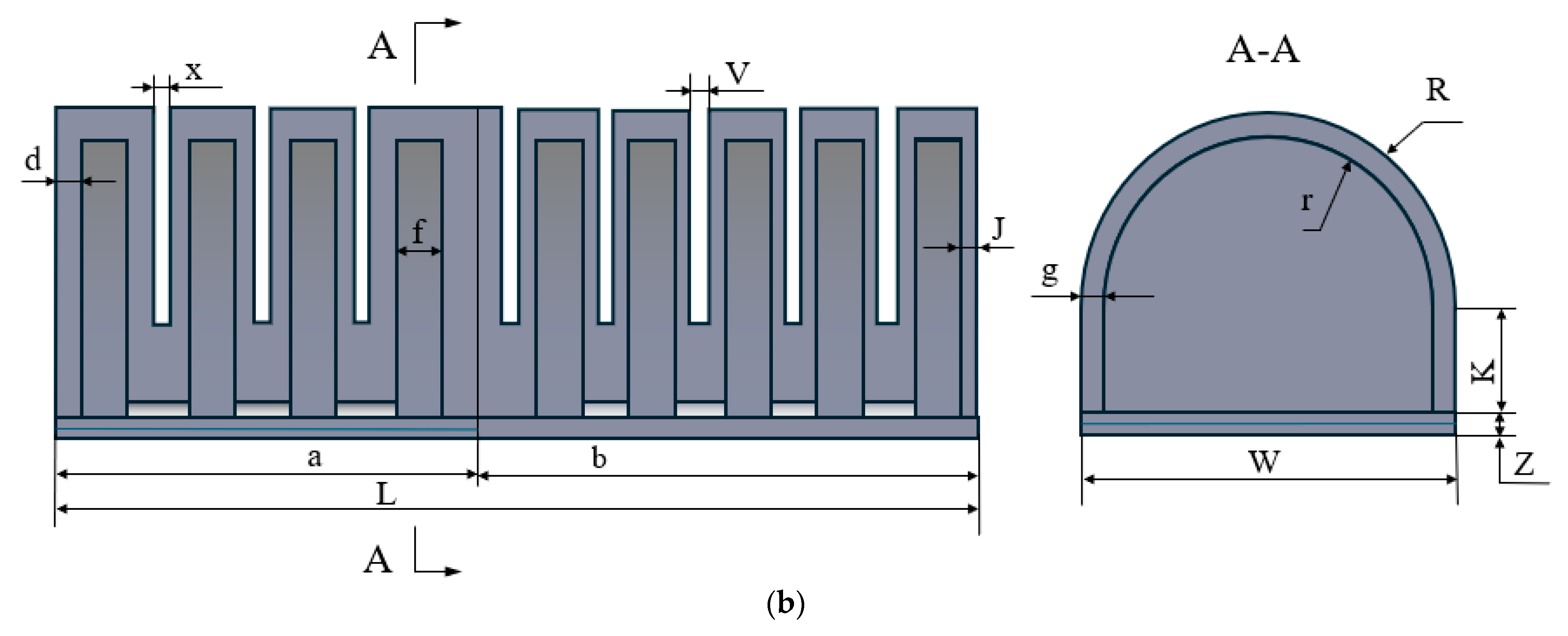

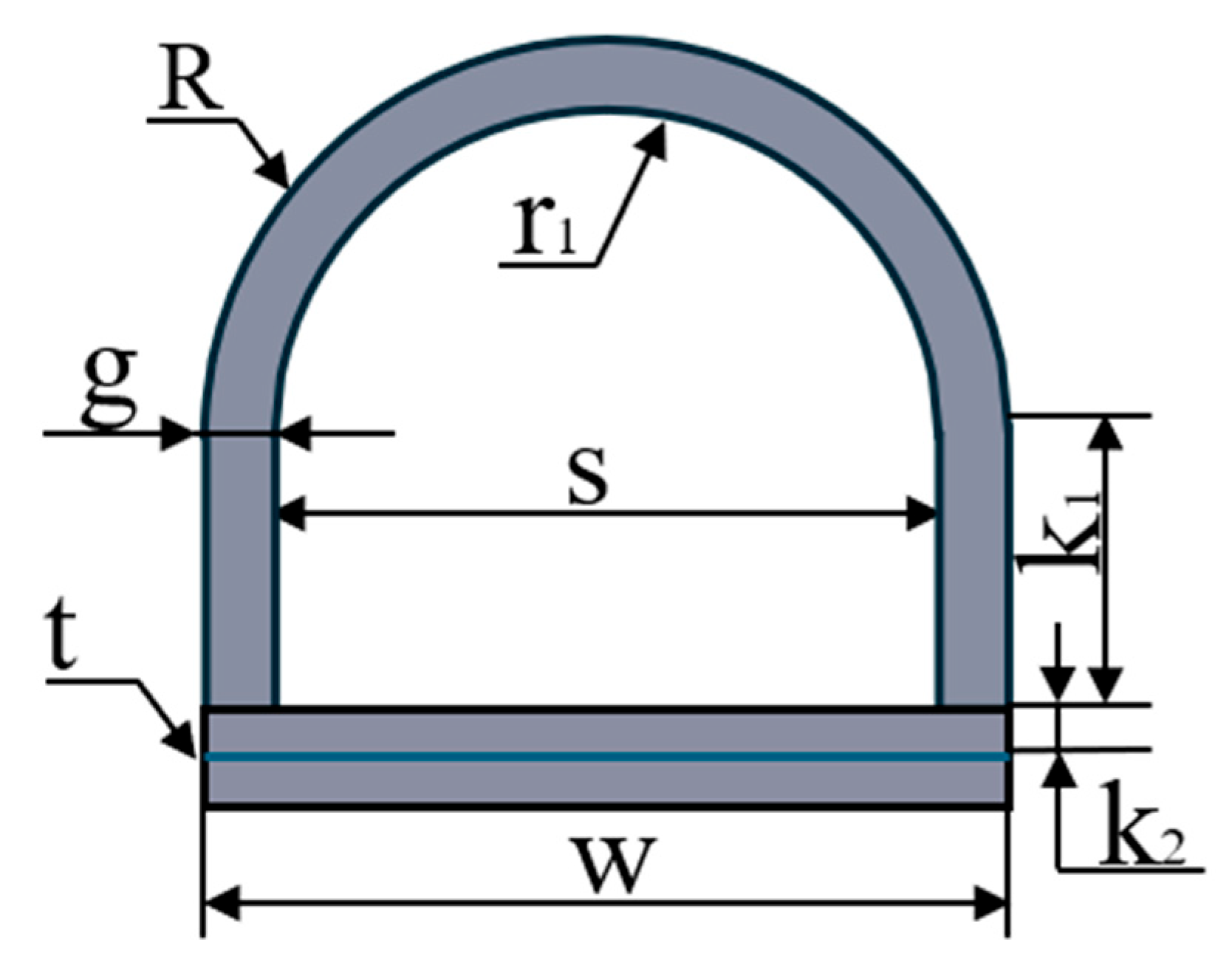
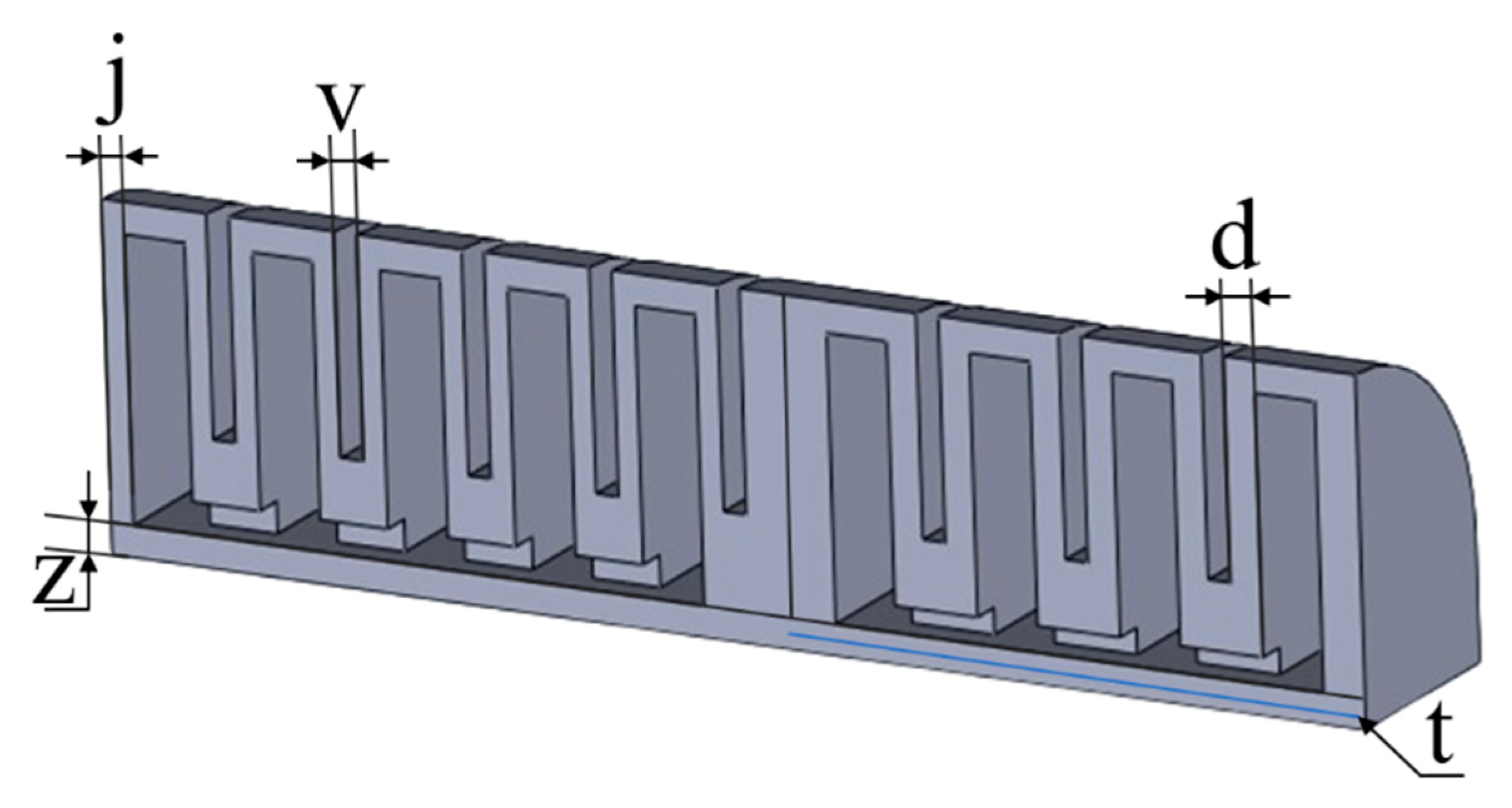









| Notation | Structural Parameters | Value (mm) |
|---|---|---|
| L | Soft finger length | 83.5 |
| a | Finger root actuator length | 38 |
| b | Fingertip actuator length | 45.5 |
| W | The width of a finger | 28 |
| Z + K + R | Soft finger height | 22 |
| f | Chamber length | 4 |
| 2r | Chamber width | 24 |
| K + r | Chamber height | 18 |
| d | Finger root actuator expansion wall thickness | 2 |
| j | Fingertip actuator expansion wall thickness | 1.5 |
| Z | Strain restriction layer thickness | 2 |
| v | Fingertip cavity spacing | 1.5 |
| x | Finger root cavity spacing | 2 |
| g | Actuator radial wall thickness | 2 |
| t | Flexible steel sheet thickness | 0.3 |
| Name | Weight (g) | Grabbing Success Rate (%) |
|---|---|---|
| Remote Control | 110 | 96.7% |
| Sunglasses | 27 | 95.7% |
| Mineral Water | 406 | 98.3% |
| Hand Cream | 66 | 95.5% |
| Orange | 116 | 95.3% |
| Tennis Ball | 60 | 96.3% |
| Wine Bottle | 143 | 95.4% |
| Turbine Blade | 788 | 96.4% |
| Syringe | 26 | 97.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Liu, S.; Wang, D.; Huang, S.; Zhang, D.; Shi, M.; Dai, W.; Wang, S. Design and Basic Performance Analysis of a Bionic Finger Soft Actuator with a Dual-Chamber Composite Structure. Actuators 2025, 14, 268. https://doi.org/10.3390/act14060268
Cai Y, Liu S, Wang D, Huang S, Zhang D, Shi M, Dai W, Wang S. Design and Basic Performance Analysis of a Bionic Finger Soft Actuator with a Dual-Chamber Composite Structure. Actuators. 2025; 14(6):268. https://doi.org/10.3390/act14060268
Chicago/Turabian StyleCai, Yu, Sheng Liu, Dazhong Wang, Shuai Huang, Dong Zhang, Mengyao Shi, Wenqing Dai, and Shang Wang. 2025. "Design and Basic Performance Analysis of a Bionic Finger Soft Actuator with a Dual-Chamber Composite Structure" Actuators 14, no. 6: 268. https://doi.org/10.3390/act14060268
APA StyleCai, Y., Liu, S., Wang, D., Huang, S., Zhang, D., Shi, M., Dai, W., & Wang, S. (2025). Design and Basic Performance Analysis of a Bionic Finger Soft Actuator with a Dual-Chamber Composite Structure. Actuators, 14(6), 268. https://doi.org/10.3390/act14060268







