Dynamic Mechanistic–Data-Driven Hybrid Modeling of the Main Distributing Valve in a Hydroturbine Governor
Abstract
1. Introduction
- (1)
- Based on the structural characteristics and working mechanism of the MDV, a modular modeling strategy is adopted to construct a mechanism-based model (MBM) framework covering electromechanical-hydraulic multi-domain coupling. By accurately mapping the physical interaction relationships of each module, the physical interpretability of the model is fundamentally ensured.
- (2)
- A Bayesian optimization-enhanced Light Gradient Boosting Machine (BO-LightGBM) model is developed, aiming to efficiently learn the complex dynamic characteristics and system uncertainties that cannot be explained by the MBM.
- (3)
- The MBM serves as the physical backbone of the entire system, reducing the BO-LightGBM model’s dependence on learning full-scale physical features. The effective integration of mechanism knowledge and data information is achieved through a cascade–additive approach, making up for the deficiency of the MBM in describing complex nonlinear factors.
- (4)
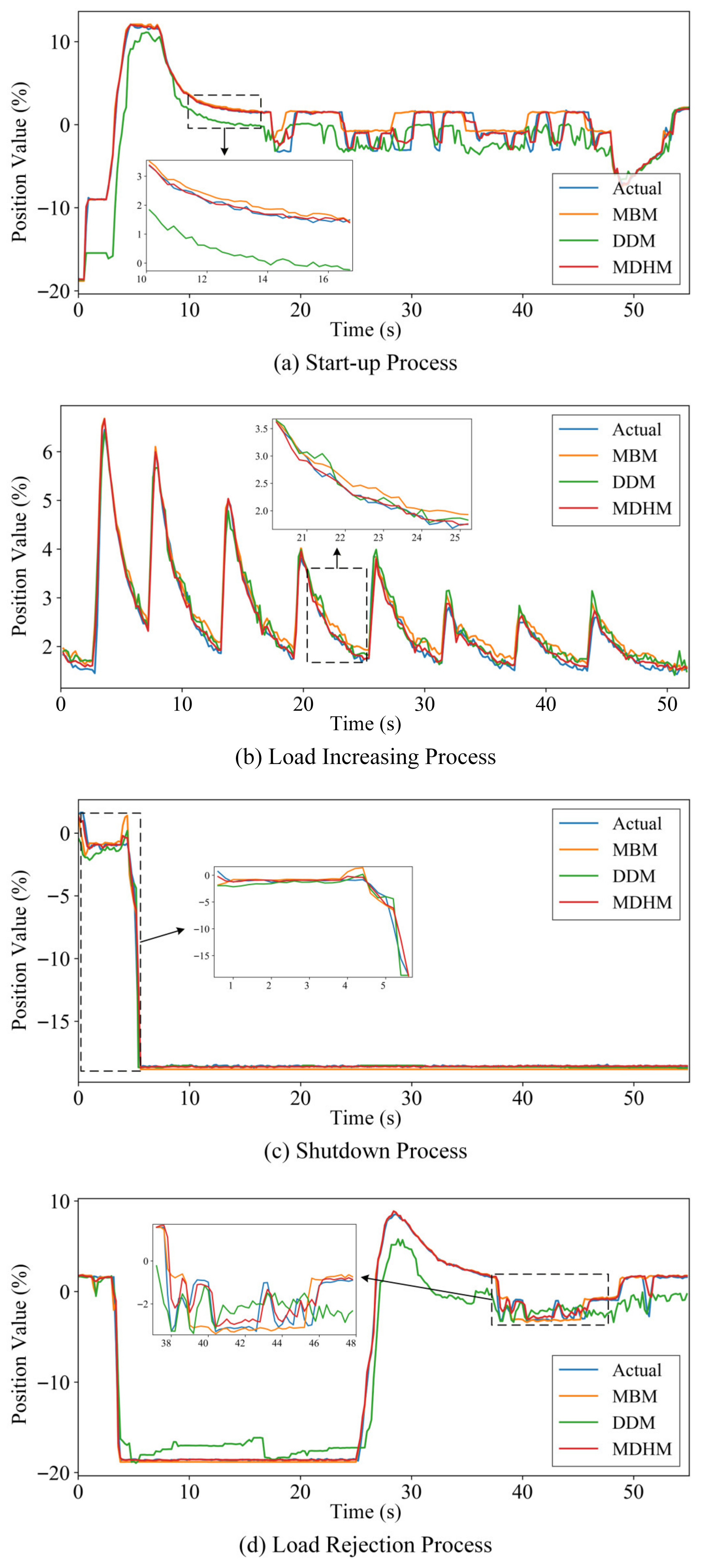
- Based on the actual operating dataset of the governor, comparative experiments are conducted under 4 typical dynamic processes—start-up, load increasing, shutdown, and load rejection—to verify the simulation accuracy and adaptability of the proposed modeling method in practical engineering scenarios.
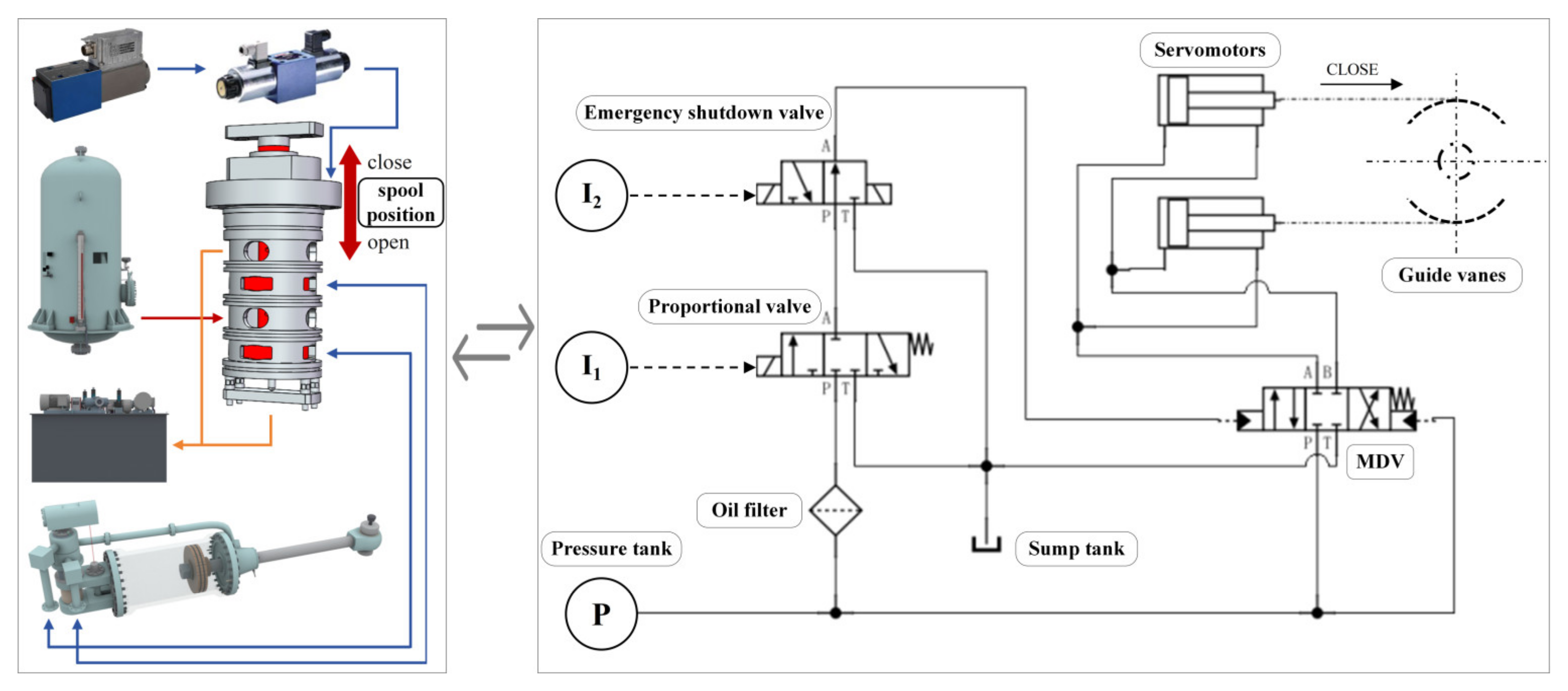
2. Modular Modeling Method Based on the Mechanism of the MDV
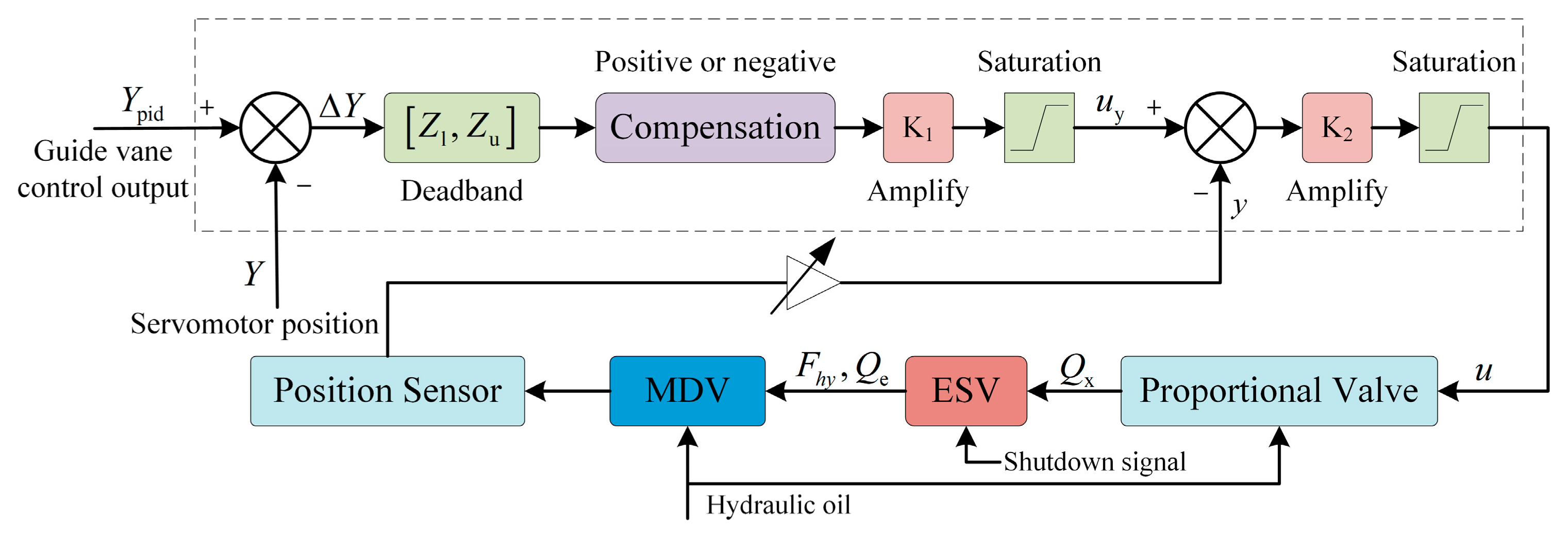
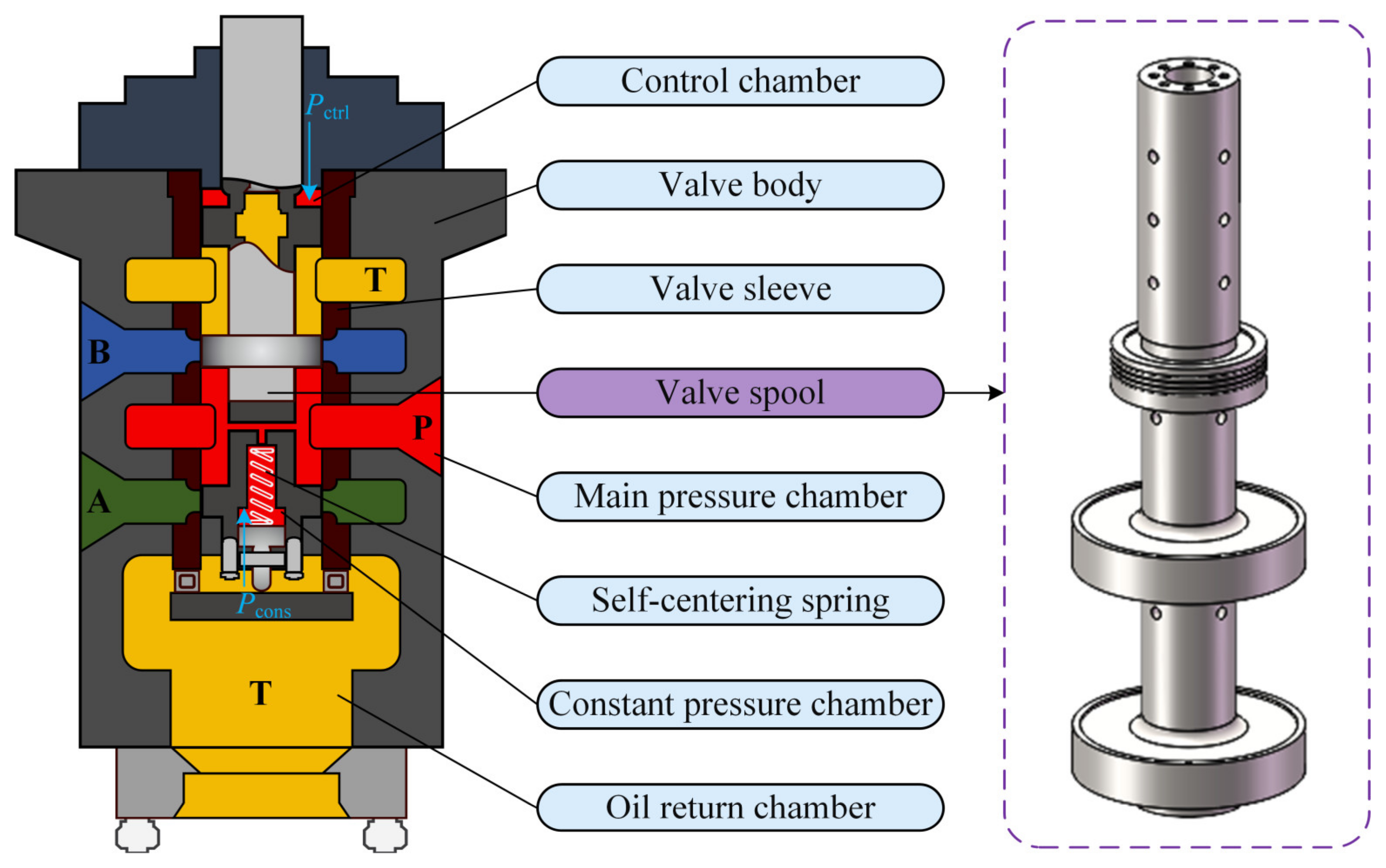
2.1. Structure and Control Principle of the Servo System
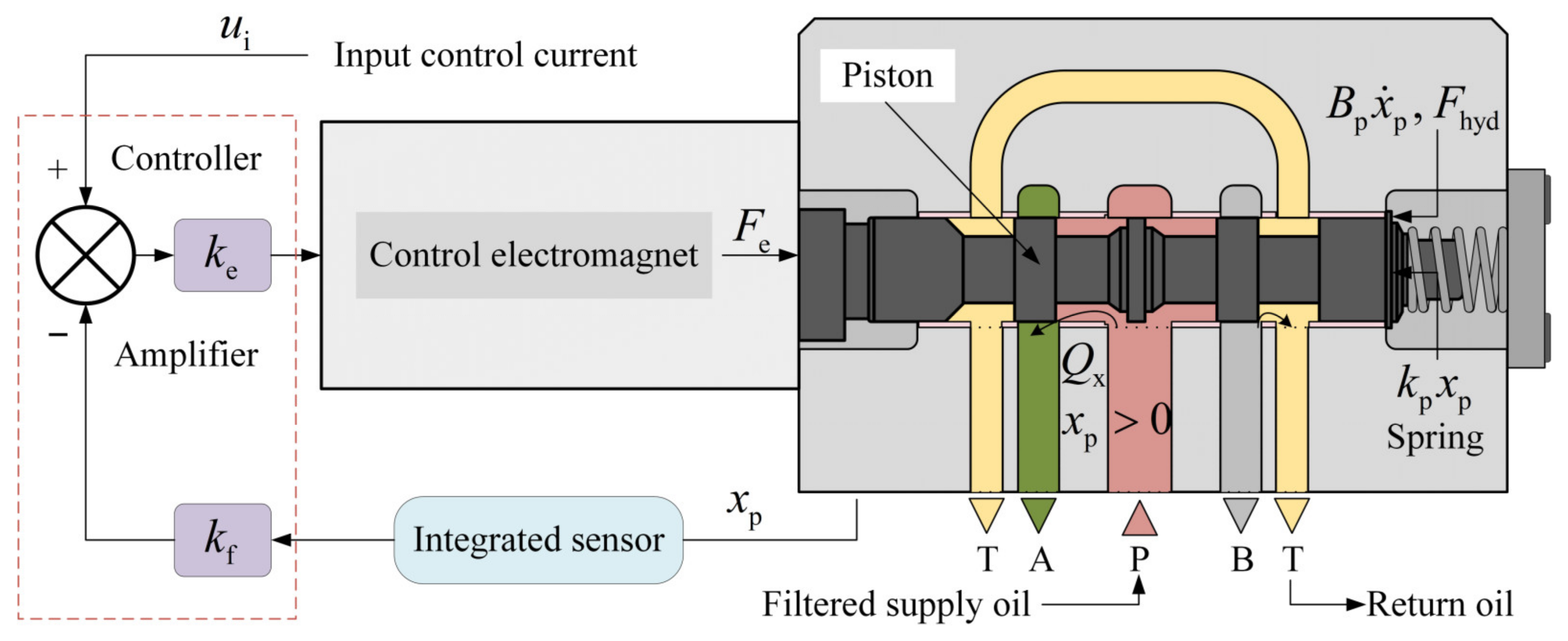
2.2. Mechanism Modeling of the Proportional Valve
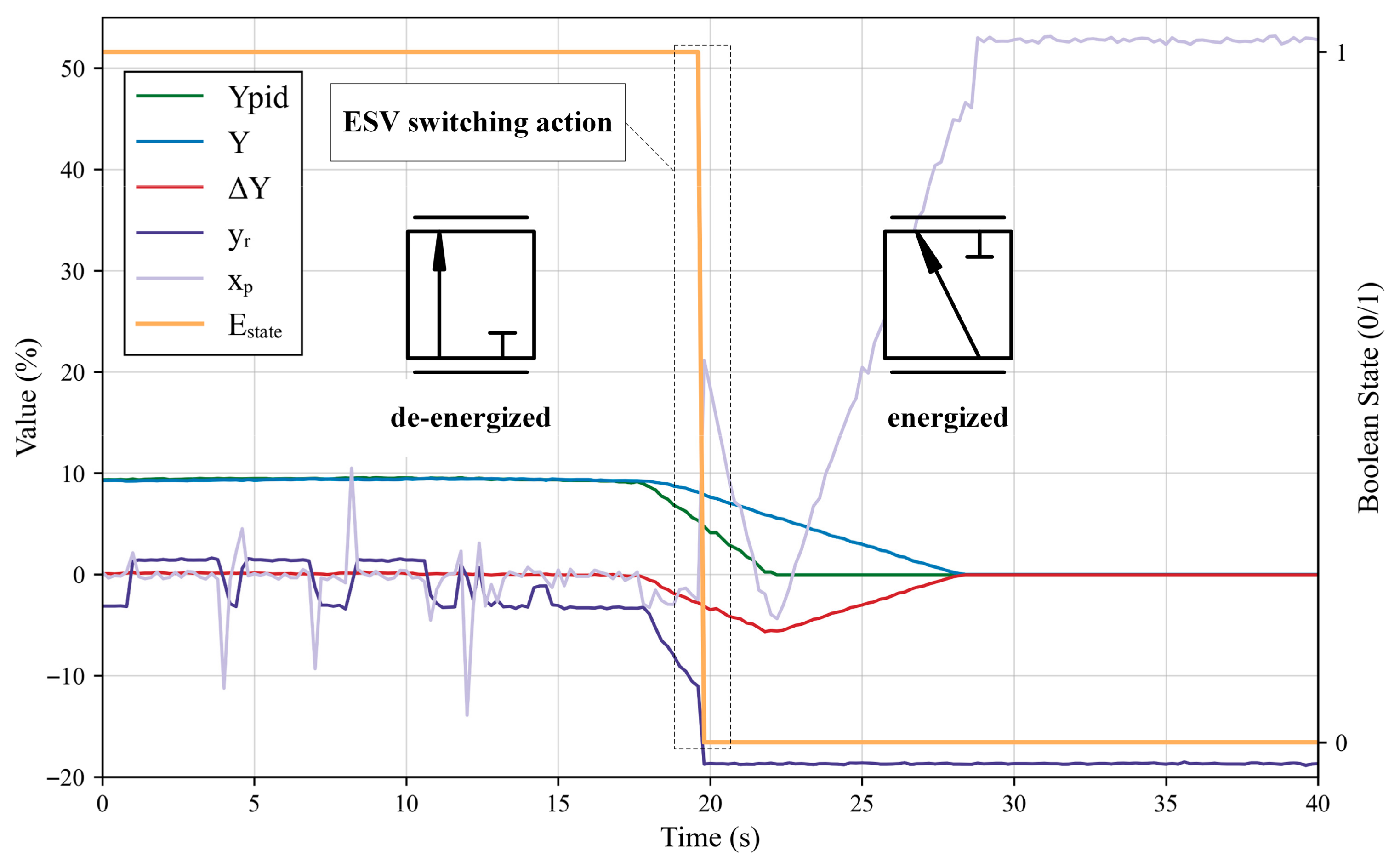
2.3. Mechanism Modeling of the Emergency Shutdown Valve
2.4. Mechanism Modeling of the MDV
3. Data-Driven Modeling Method and Model Hybridization Strategy
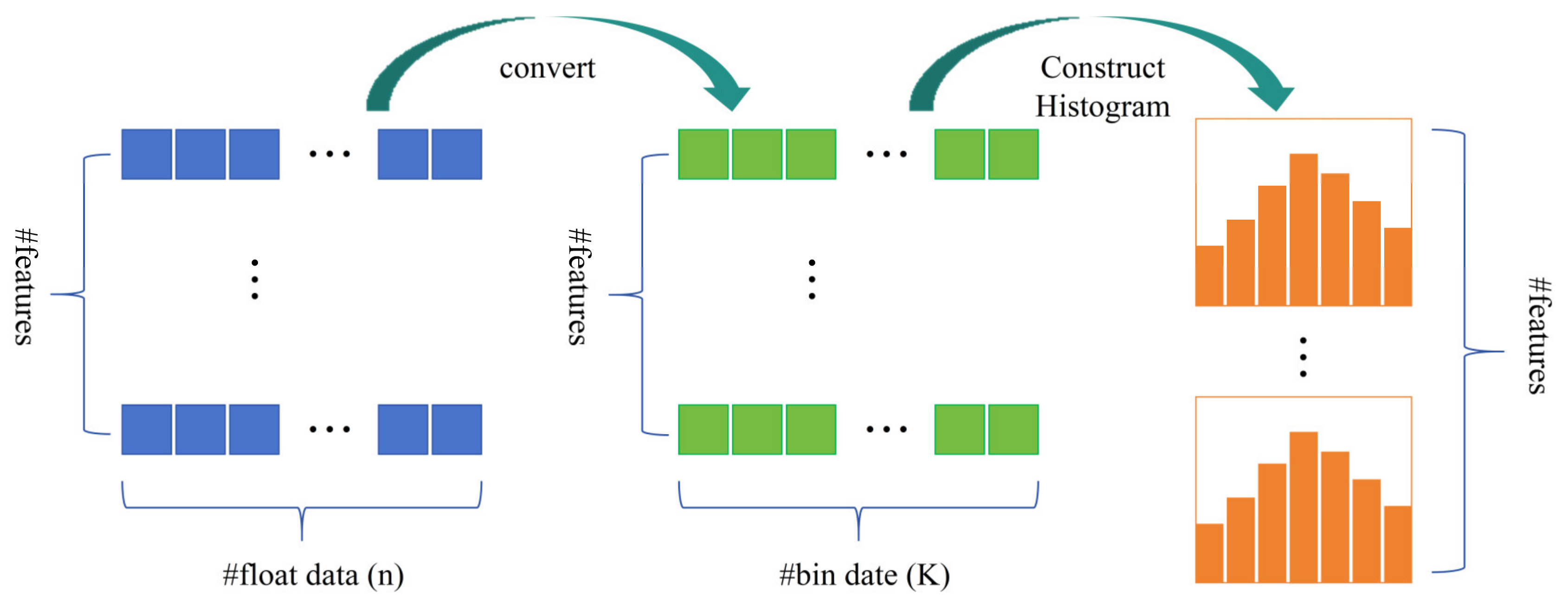
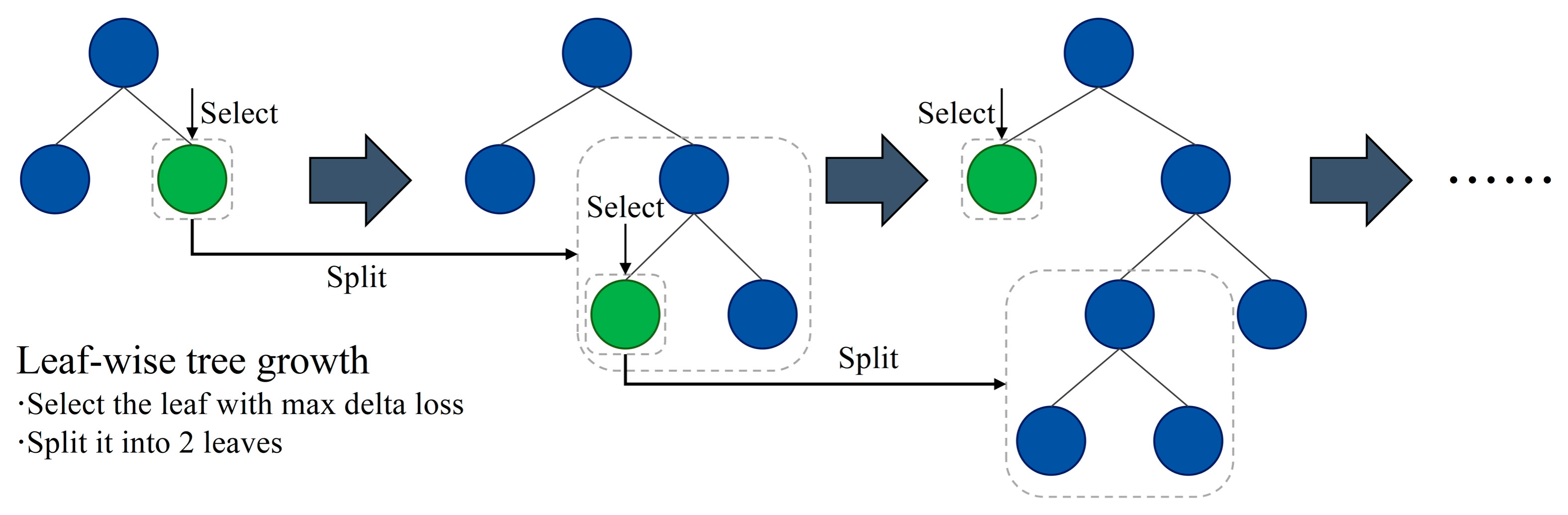
3.1. Lightweight Gradient Boosting Machine
- 1.
- Histogram Algorithm
- 2.
- Leaf-wise Strategy
- 3.
- Gradient-based One-Side Sampling (GOSS)
- 4.
- Exclusive Feature Bundling (EFB)
3.2. Bayesian Optimization
- 1.
- Surrogate Model
- 2.
- Acquisition Function
- 3.
- Iterative Update
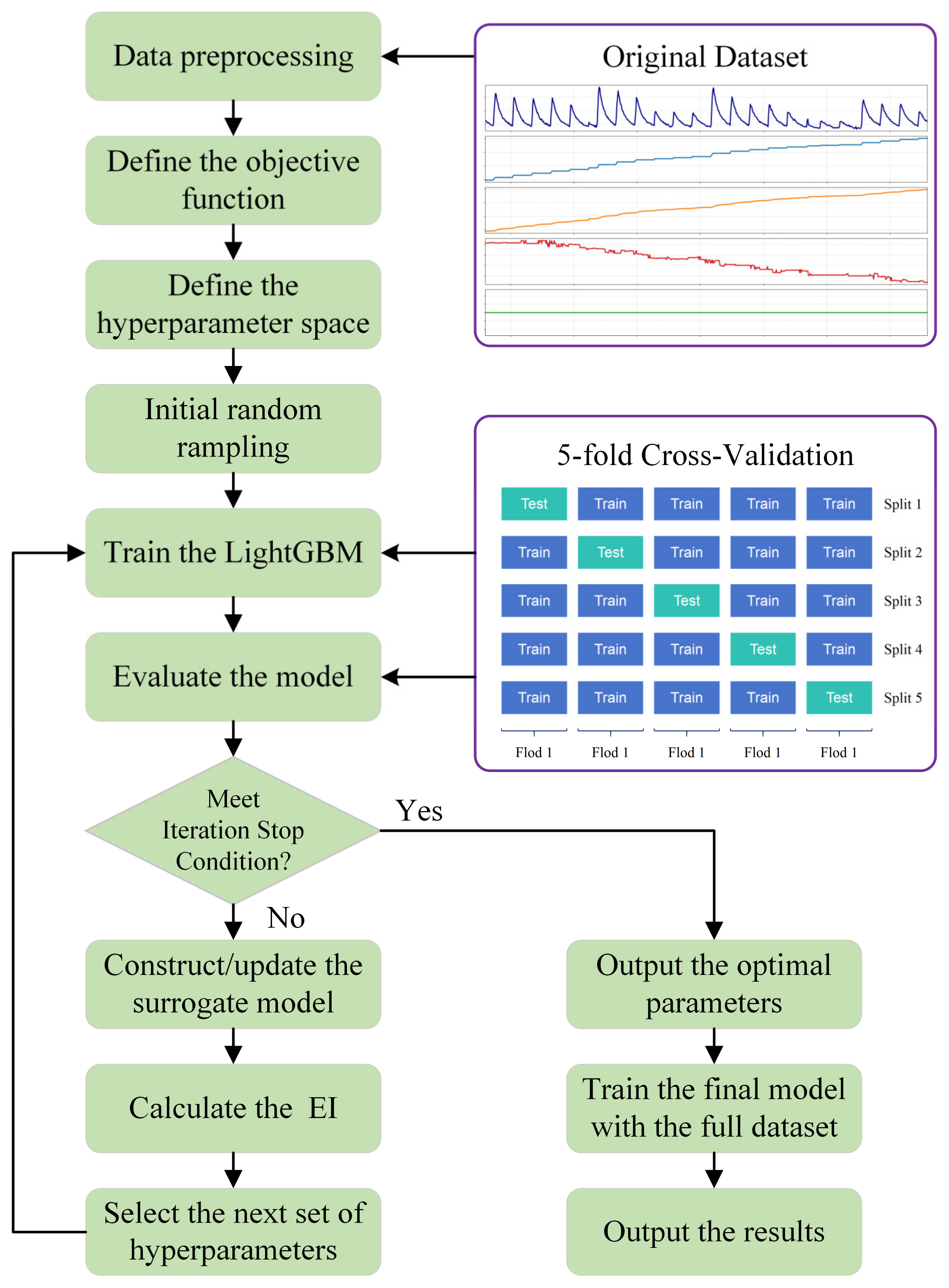
3.3. BO-LightGBM Data-Driven Model
- (1)
- First, clean the original data to handle missing values, outliers, and duplicate values in the data; divide the cleaned dataset into a training set and a test set according to the characteristics of time series; construct effective features based on industrial mechanisms as the input variables of the model.
- (2)
- Based on the characteristics of industrial data and the requirements for model robustness, select the L1 loss as the objective function. The model is validated using 5-Fold Time Series Cross-Validation to simulate real-world application scenarios and avoid evaluation bias caused by data leakage.
- (3)
- Define the search space for the core hyperparameters of LightGBM, including learning_rate, max_depth, num_leaves, etc.
- (4)
- Train the LightGBM model based on the hyperparameters generated by initial random sampling to provide initial data for the subsequent construction of the surrogate model.
- (5)
- Use MAE (Mean Absolute Error) as the core evaluation metric to evaluate the performance of the LightGBM model corresponding to each group of hyperparameters on the validation set. Record the MAE value of the validation set corresponding to each group of hyperparameters to form a historical evaluation dataset of “hyperparameters-performance”.
- (6)
- Construct/update the surrogate model based on historical evaluation results. Select the next group of hyperparameters that are most likely to improve performance through the EI, and use this group of hyperparameters to train a new LightGBM model.
- (7)
- Repeat steps 5–6 until the preset stopping condition is met (reaching the maximum number of iterations or convergence of model performance). After terminating the iteration process, output the optimal parameters.
- (8)
- Retrain the model on the full training set using the optimal parameters to form the final model.
3.4. Cascade–Additive Hybrid Model
4. Case Study and Result Analysis
4.1. Data Preparation and Model Parameterization
4.1.1. Data Preparation
4.1.2. Parameter Configuration of the MBM
4.1.3. Hyperparameter Optimization of the BO-LightGBM
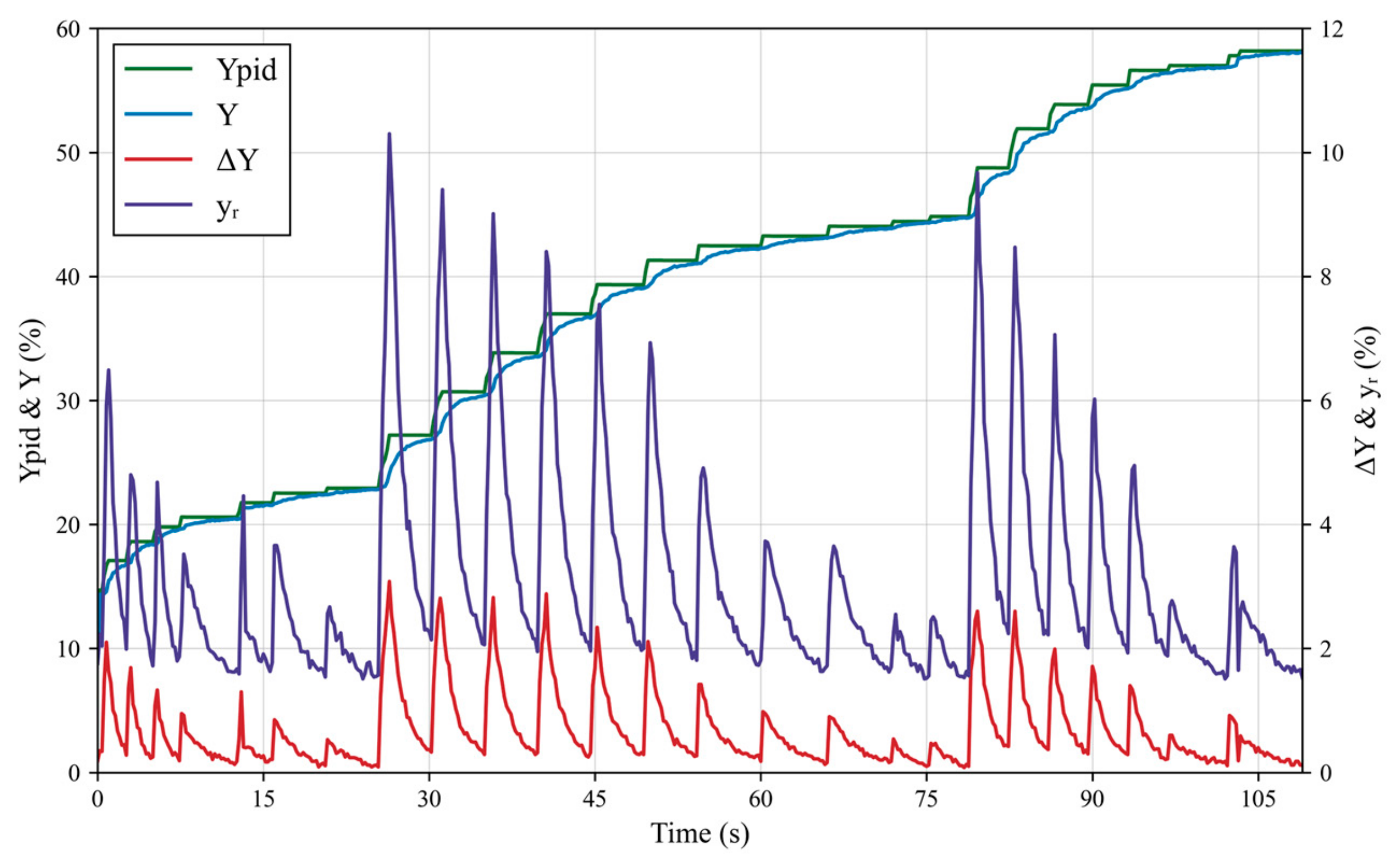
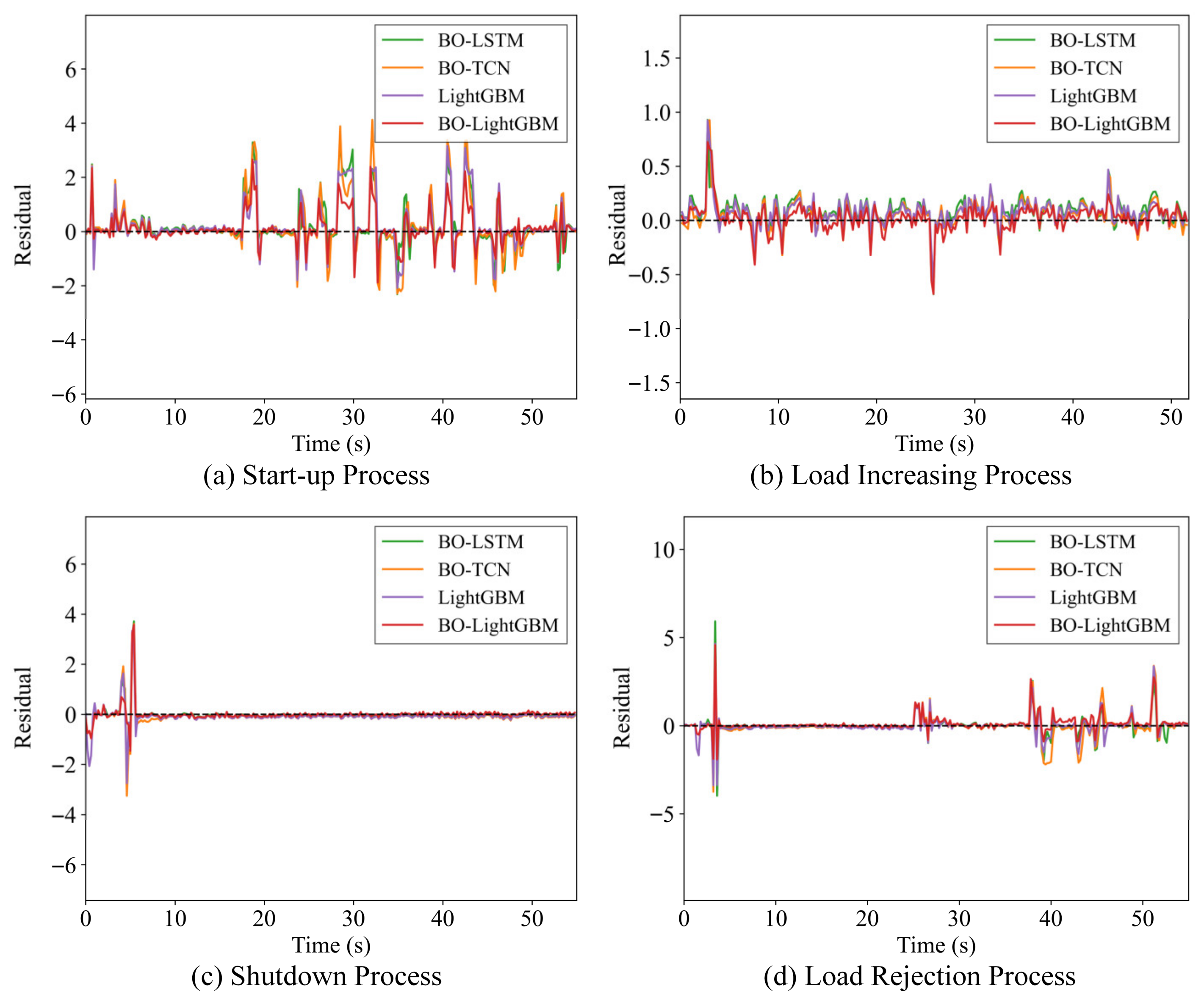
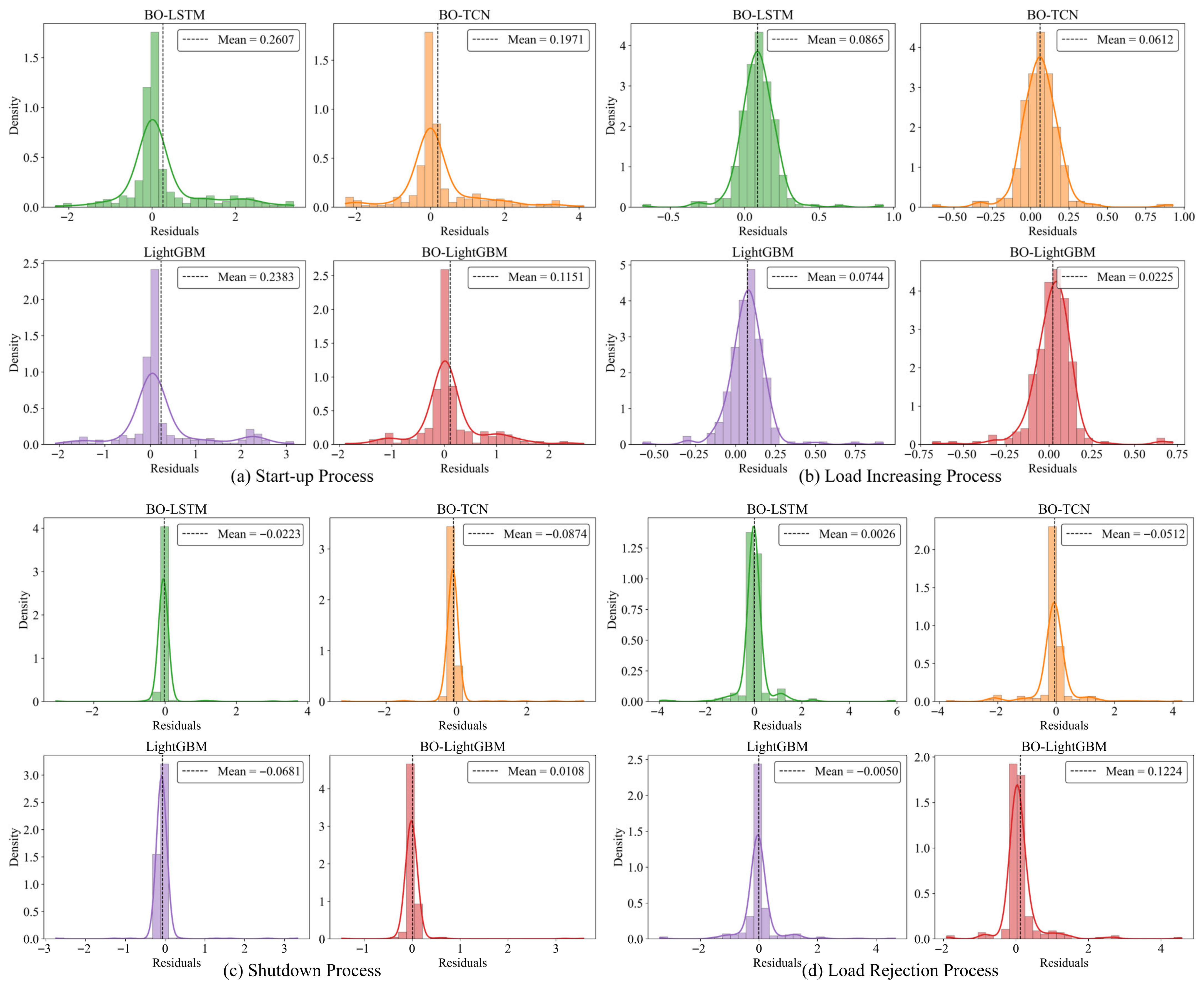
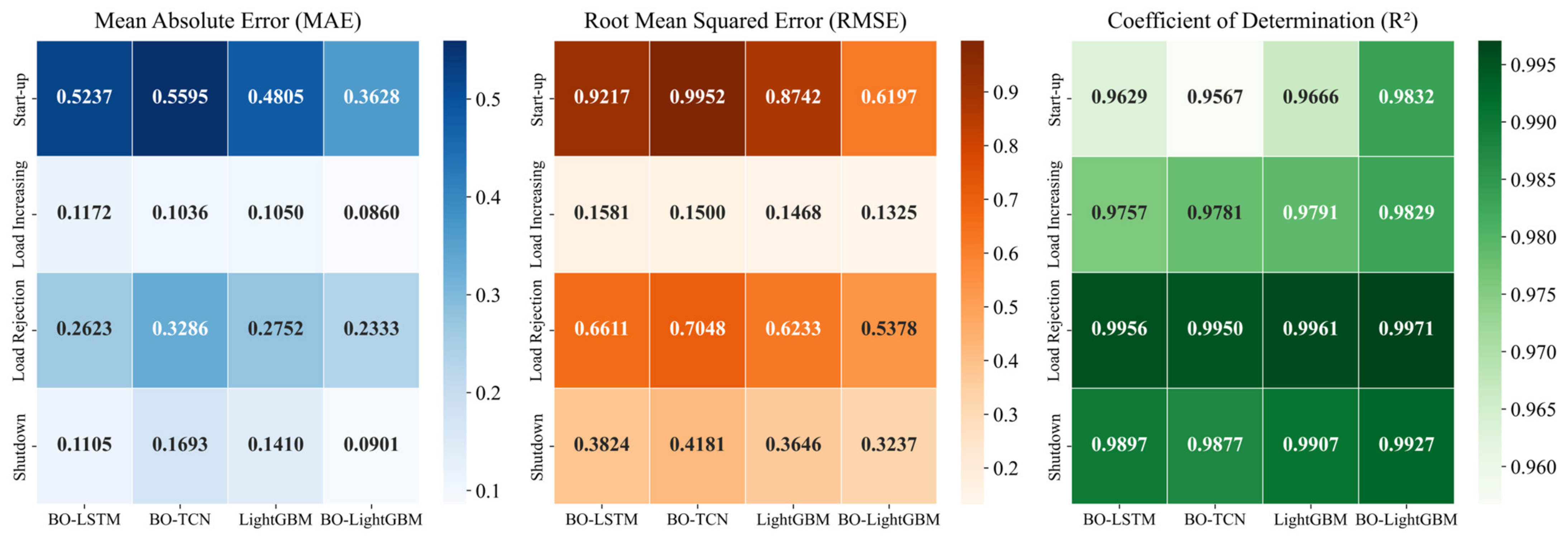
4.2. Results and Discussion
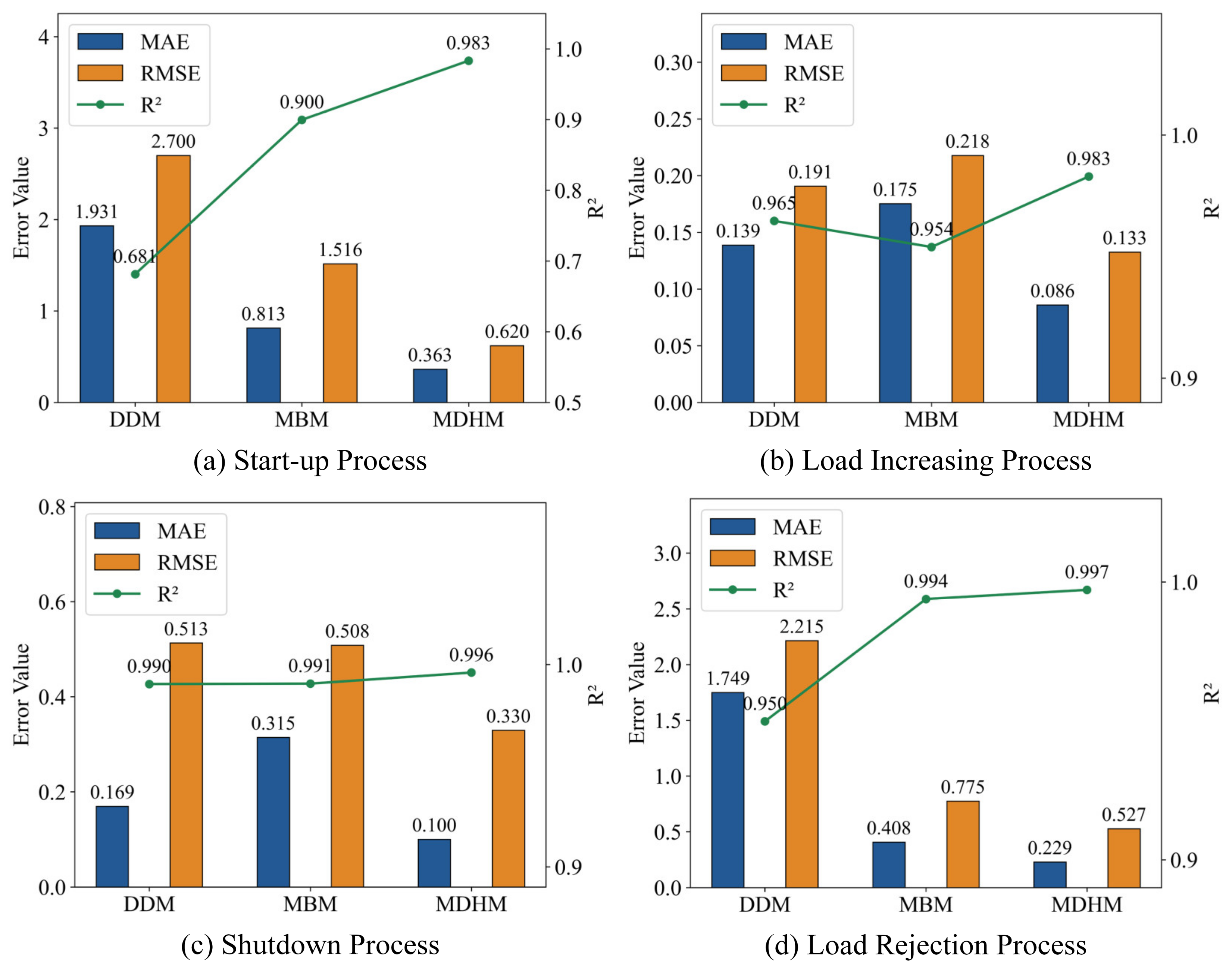
4.3. Verification of the Superiority of the BO-LightGBM
5. Conclusions and Future Work
- (1)
- By in-depth exploration of the internal operating principles of the governor’s servo system, a nonlinear MBM was constructed. This model comprehensively characterizes the spool’s key motion features and dynamic response behavior, demonstrating good stability under complex dynamic conditions and providing a solid physical foundation for subsequent hybrid modeling.
- (2)
- A BO-LightGBM model was proposed to specifically learn the complex behaviors and uncertainties that cannot be captured by the MBM. Through a cascade–additive hybrid framework, the method achieves complementary advantages between physical prior knowledge and data-driven learning capability, significantly improving prediction accuracy without compromising physical interpretability.
- (3)
- The effectiveness and superiority of the proposed hybrid model were validated through comparative experiments under multiple operating conditions. The hybrid model demonstrated the best performance across the three tested typical dynamic processes and one extreme condition, achieving maximum MAE reductions of 68.3% and 86.9% compared with the mechanism-based and data-driven models, respectively. Further comparison results indicate that employing BO-LightGBM as the data-driven module in the hybrid framework yields higher accuracy and stability in simulating the MDV position.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDV | Main distributing valve |
| HTGS | Hydro-turbine governing system |
| ESV | Emergency shutdown valve |
| MBM | Mechanism-based model |
| DDM | Data-driven model |
| MDHM | Mechanistic–data-driven hybrid model |
| LightGBM | Lightweight Gradient Boosting Machine |
| GBDT | Gradient Boosting Decision Tree |
| GOSS | Gradient-based One-Side Sampling |
| EFB | Exclusive Feature Bundling |
| BO | Bayesian optimization |
| GP | Gaussian Process |
| EI | Expected Improvement |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| R2 | Coefficient of Determination |
| BO-LightGBM | Bayesian optimization-enhanced Lightweight Gradient Boosting Machine |
| BO-LSTM | Bayesian optimization-based Long Short-Term Memory network |
| BO-TCN | Bayesian optimization-based Temporal Convolutional Network |
| KDE | Kernel density estimation |
| Std | Standard deviation |
References
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Shu, Y.; Chen, G.; He, J.; Zhang, F. Building a New Electric Power System Based on New Energy Sources. Strateg. Study CAE 2021, 23, 61–69. [Google Scholar] [CrossRef]
- Xu, B.B.; Zhang, J.J.; Egusquiza, M.; Chen, D.Y.; Li, F.; Behrens, P.; Egusquiza, E. A review of dynamic models and stability analysis for a hydro-turbine governing system. Renew. Sustain. Energy Rev. 2021, 144, 110880. [Google Scholar] [CrossRef]
- Yang, W.J.; Norrlund, P.; Bladh, J.; Yang, J.D.; Lundin, U. Hydraulic damping mechanism of low frequency oscillations in power systems: Quantitative analysis using a nonlinear model of hydropower plants. Appl. Energy 2018, 212, 1138–1152. [Google Scholar] [CrossRef]
- Mitchell, C. Momentum is increasing towards a flexible electricity system based on renewables. Nat. Energy 2016, 1, 6. [Google Scholar] [CrossRef]
- Chang, M.K.; Eichman, J.D.; Mueller, F.; Samuelsen, S. Buffering intermittent renewable power with hydroelectric generation: A case study in California. Appl. Energy 2013, 112, 1–11. [Google Scholar] [CrossRef]
- Kumari, R.; Prabhakaran, K.K.; Desingu, K.; Chelliah, T.R.; Sarma, S.V.A. Improved Hydroturbine Control and Future Prospects of Variable Speed Hydropower Plant. IEEE Trans. Ind. Appl. 2021, 57, 941–952. [Google Scholar] [CrossRef]
- Zhang, N. Study on Nonlinear Model Parameter Identification and Control Optimization of Pumped Storage Unit Governing System. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Wu, J.; Zhou, B.; Li, Z.; He, L.; Xu, D. Static Characteristic Simulations of Giant Main Distributing Valve. Hydropower Pumped Storage 2012, 36, 24–26. [Google Scholar]
- Liu, H.; Chang, Z.; Lu, Z.; Pi, C.; Yang, G. Technical Modification of Displacement Sensor for Main Distribution Valve of Governor in Xiangjiaba Hydropower Plant. China Rural Water Hydropower 2020, 138–142. Available online: https://irrigate.whu.edu.cn/EN/Y2020/V0/I2/138 (accessed on 25 September 2025).
- Tu, Y.; Zhang, Q. Research on intelligent diagnosis method of governor hydraulic tracking fault. Yangtze River 2022, 53, 184–187. [Google Scholar] [CrossRef]
- Calinoiu, C.; Vasiliu, D.; Radu, P.; Vasiliu, N.; Cristinel, I.P. Sizing and tuning speed governors for turbines by AMESIM. In Proceedings of the European Simulation and Modelling Conference (ESM 2013), Lancaster University, Lancaster, UK, 23–25 October 2013; pp. 220–226. [Google Scholar]
- Fang, H.Q.; Chen, L.; Dlakavu, N.; Shen, Z.Y. Basic Modeling and simulation tool for analysis of hydraulic transients in hydroelectric power plants. IEEE Trans. Energy Convers. 2008, 23, 834–841. [Google Scholar] [CrossRef]
- Tian, Y.Q.; Wang, B.; Chen, P.; Yang, Y. Finite-time Takagi-Sugeno fuzzy controller design for hydraulic turbine governing systems with mechanical time delays. Renew. Energy 2021, 173, 614–624. [Google Scholar] [CrossRef]
- Li, C.S.; Zhou, J.Z.; Xiao, J.; Xiao, H. Hydraulic turbine governing system identification using T S fuzzy model optimized by chaotic gravitational search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 2073–2082. [Google Scholar] [CrossRef]
- Lu, X.D.; Li, C.S.; Chang, H.; Wang, H.; Zhu, Z.W.; Liu, D.; Tan, X.Q.; Xu, R.L. Primary frequency regulation performance in hydropower systems: Precise quantification and holistic enhancement under wide-range operation. Appl. Energy 2025, 389, 21. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, W.; Wang, G.; Xia, C.; Li, Z.; Yu, D.; Ma, C. Source-grid Coordination of Hydraulic Turbine Governing System. Power Syst. Technol. 2021, 45, 1852–1861. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, J.; Shao, B. Main Distributing Valve Linear Modeling and Performance Analysis. Water Sci. Eng. Technol. 2014, 25–27. [Google Scholar] [CrossRef]
- Wu, J.; Su, Y.; Zhang, J.; Zhu, R.; Yu, H. Simulation on the Response Speed of Main Distributing Valve. Hydraul. Pneum. Seals 2013, 33, 30–32. [Google Scholar] [CrossRef]
- Xia, L.; Wang, Y.; Liu, M.; Jie, S. Simulation and analysis of faults in the electro-hydraulic servo system of hydraulic turbine governor based on SimHydraulics. China Meas. Test 2022, 48, 105–112. [Google Scholar]
- Yan, N.; Feng, C.; Huang, C. Modeling and Identification Method of Electro-hydraulic Servo System for Hydro Turbine Governor. Water Resour. Power 2019, 37, 166–169+82. [Google Scholar] [CrossRef]
- Milic, V.; Situm, Z.; Essert, M. Robust H∞ position control synthesis of an electro-hydraulic servo system. ISA Trans. 2010, 49, 535–542. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Ivannikova, V.; Maskeliunaite, L. The impact of mechanical vibrations on pressure pulsation, considering the nonlinearity of the hydraulic valve. J. Low Freq. Noise Vib. Act. Control 2025, 44, 706–719. [Google Scholar] [CrossRef]
- Wu, W.; Wei, C.H.; Zhou, J.J.; Hu, J.B.; Yuan, S.H. Numerical and experimental nonlinear dynamics of a proportional pressure-regulating valve. Nonlinear Dyn. 2021, 103, 1415–1425. [Google Scholar] [CrossRef]
- Yao, J.Y. Model-based nonlinear control of hydraulic servo systems: Challenges, developments and perspectives. Front. Mech. Eng. 2018, 13, 179–210. [Google Scholar] [CrossRef]
- Wang, Q.; Li, F.; Tang, Y.; Xu, Y. Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 2019, 34, 4557–4568. [Google Scholar] [CrossRef]
- Song, H.D.; Liu, X.J.; Song, M.Q. Comparative study of data-driven and model-driven approaches in prediction of nuclear power plants operating parameters. Appl. Energy 2023, 341, 14. [Google Scholar] [CrossRef]
- Luo, W.C.; Hu, T.L.; Ye, Y.X.; Zhang, C.R.; Wei, Y.L. A hybrid predictive maintenance approach for CNC machine tool driven by Digital Twin. Robot. Comput.-Integr. Manuf. 2020, 65, 16. [Google Scholar] [CrossRef]
- Guo, Y.H.; Wang, N.B.; Shao, S.Q.; Huang, C.Q.; Zhang, Z.T.; Li, X.Q.; Wang, Y.D. A review on hybrid physics and data-driven modeling methods applied in air source heat pump systems for energy efficiency improvement. Renew. Sustain. Energy Rev. 2024, 204, 14. [Google Scholar] [CrossRef]
- Li, F.; Wang, Q.; Hu, J.; Tang, Y. Combined Data-driven and Knowledge-driven Methodology Research Advances and Its Applied Prospect in Power Systems. Proc. CSEE 2021, 41, 4377–4390. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Wang, H.; Tang, M.; Zhang, J.; Hu, X.H. Hybrid mechanism and data driven approach for high-precision modeling of gas flow regulation systems of VFDR. Complex Intell. Syst. 2025, 11, 23. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, H.R.; Liu, C.Y.; Chen, J.; Wu, Q.W.; Terzija, V. A dual-driven linear modeling approach for multiple energy flow calculation in electricity-heat system. Appl. Energy 2022, 314, 16. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, T.; Chen, Z.; Xi, B.; Jia, X. Design of mechanical structure and hydraulic system of tubular turbine governor. Chin. J. Eng. Des. 2020, 27, 753–764. [Google Scholar] [CrossRef]
- Kosek, M.; Downar, D.; Sliwinski, P. Hydraulic valve design methodology for hydro turbine control system. Flow Meas. Instrum. 2024, 100, 14. [Google Scholar] [CrossRef]
- Kosek, M.; Sliwinski, P. Shaping the flow characteristics of a proportional directional valve. Sci. Rep. 2025, 15, 24. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhang, C.; Jin, B.; Yuan, T.B. Simulation and experimental research on steady flow force compensation for a servo proportional valve. Flow Meas. Instrum. 2023, 94, 102457. [Google Scholar] [CrossRef]
- Li, R.C.; Sun, Y.H.; Wu, X.W.; Zhang, P.; Li, D.F.; Lin, J.H.; Xia, Y.H.; Sun, Q.Y. Review of the Research on and Optimization of the Flow Force of Hydraulic Spool Valves. Processes 2023, 11, 2183. [Google Scholar] [CrossRef]
- Cristofori, D.; Vacca, A. The Modeling of Electrohydraulic Proportional Valves. J. Dyn. Syst. Meas. Control-Trans. Asme 2012, 134, 021008. [Google Scholar] [CrossRef]
- Ke, G.L.; Meng, Q.; Finley, T.; Wang, T.F.; Chen, W.; Ma, W.D.; Ye, Q.W.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. Advances in Neural Information Processing Systems 30 (NIPS 2017). [Google Scholar]
- González, S.; García, S.; Del Ser, J.; Rokach, L.; Herrera, F. A practical tutorial on bagging and boosting based ensembles for machine learning: Algorithms, software tools, performance study, practical perspectives and opportunities. Inf. Fusion 2020, 64, 205–237. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgo, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.Y.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Cheng, C.H.; Huang, K.K.; Zhou, C.; Li, Y.G. Series Dynamic Hybrid Model Based on Material Conservation and Neural Networks for Oxidation Leaching Process. In Proceedings of the IEEE International Conference on Recent Advances in Systems Science and Engineering (RASSE), Shanghai University, Shanghai, China, 12–14 December 2021. [Google Scholar]
- Hu, J.; Tang, Y.; Li, F.; Wang, Q.; Zhao, X. Performance Analysis on Parallel Mode of Data-Physical Fusion Model in Power System. Autom. Electr. Power Syst. 2022, 46, 15–24. [Google Scholar]
- Zhang, H.Y.; Jiang, S.L.; Gao, D.F.; Sun, Y.W.; Bai, W.X. A Review of Physics-Based, Data-Driven, and Hybrid Models for Tool Wear Monitoring. Machines 2024, 12, 833. [Google Scholar] [CrossRef]

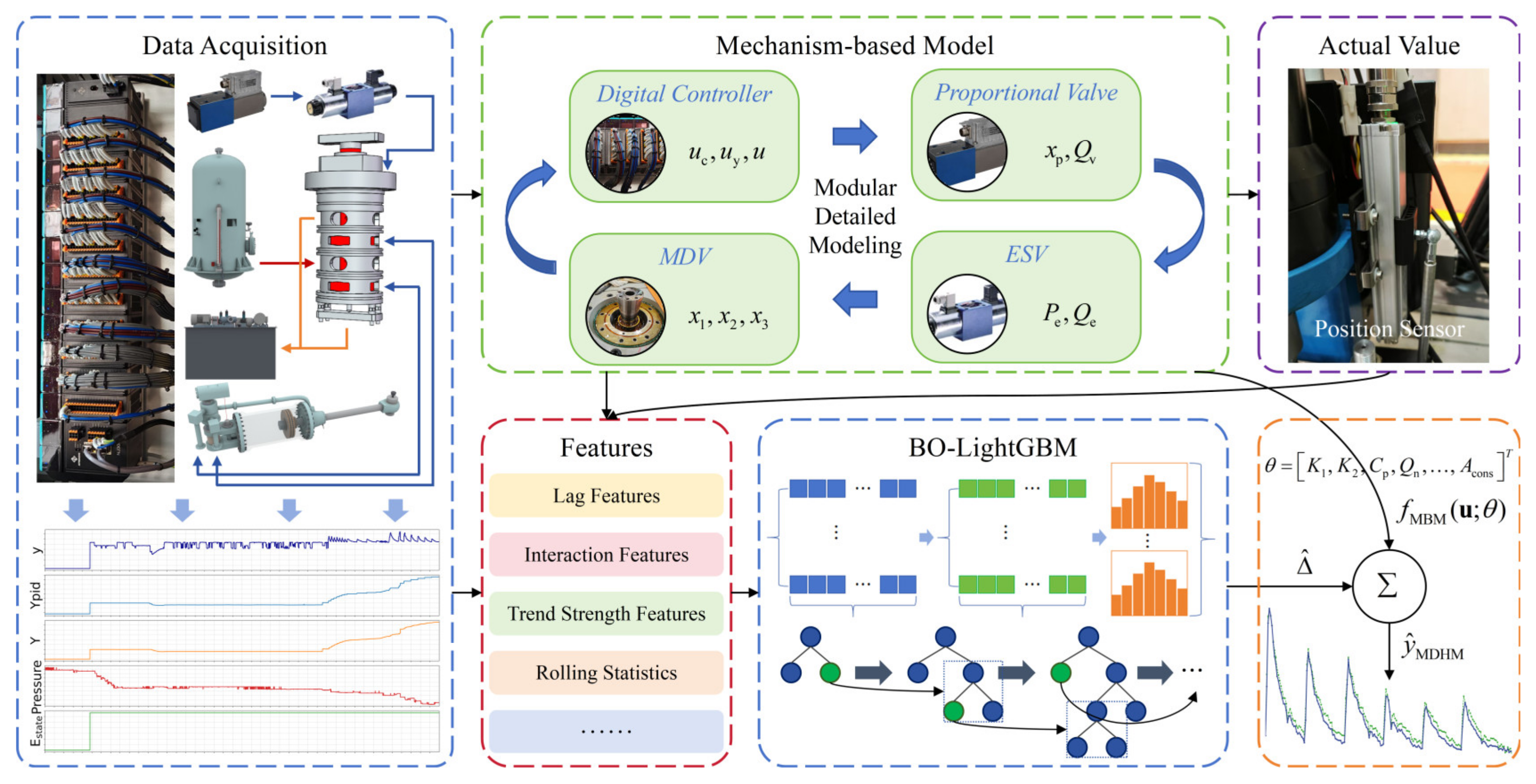
| Feature Type | Feature Name |
|---|---|
| Original features | Pressure of the pressure tank |
| Guide vane control output | |
| Guide Vane Opening | |
| ESV state | |
| MBM output | MBM-simulated position |
| Interaction features | Opening deviation |
| Lag features | Opening deviation-lag |
| MBM-simulated position-lag | |
| MBM simulation deviation-lag | |
| Trend strength features | Opening deviation-trend strength |
| MBM-simulated position-trend strength | |
| Rolling mean | Opening deviation-rolling mean |
| MBM-simulated position-rolling mean | |
| MBM simulation deviation-rolling mean | |
| Rolling maximum | Opening deviation-rolling max |
| MBM-simulated position-rolling max | |
| MBM simulation deviation-rolling max | |
| Rolling standard deviation | Opening deviation-rolling Std |
| MBM-simulated position-rolling Std | |
| MBM simulation deviation-rolling Std |
| Parameter | Symbol | Value | Description |
|---|---|---|---|
| Large-loop gain coefficient | 3 | Tuning value | |
| Small-loop gain coefficient | 0.3 | Tuning value | |
| Positive compensation coefficient | - | Confidential | |
| Negative compensation coefficient | - | Confidential | |
| Gain coefficient (second-order system) | 1 | Derived from the Bode diagram | |
| Natural frequency (second-order system) | 326.7 rad/s | Derived from the Bode diagram | |
| Damping ratio (second-order system) | 0.6 | Derived from the Bode diagram | |
| Return oil pressure | 5 bar | Empirical value | |
| Rated flow of the proportional valve | 40 min/L | Obtained from the product manual | |
| Density of hydraulic oil | 880 kg/m3 | Typical density of No. 46 hydraulic oil | |
| Bulk modulus of hydraulic oil | 1500 Mpa | Selected from the typical range | |
| Mass of the MDV spool | - | Confidential | |
| Self-centering spring stiffness | 7453 N/m | Experimentally measured | |
| Viscous damping coefficient | 5000 N·s/m | Selected from the typical range | |
| Lower limit of MDV spool position | −18.80% | Normalized with respect to rated value | |
| Upper limit of MDV spool position | 12.05% | Normalized with respect to rated value | |
| Control chamber area | - | Confidential | |
| Constant-pressure chamber area | - | Confidential |
| Hyperparameter | Description | Search Range | Optimal Value |
|---|---|---|---|
| learning_rate | Step size shrinkage | 0.001–0.1 | 0.022 |
| num_leaves | Maximum number of leaves in one tree | 20–300 | 161 |
| max_depth | Maximum depth of a tree | 3–25 | 17 |
| min_data_in_leaf | Minimum number of data points in a leaf | 10–100 | 33 |
| lambda_l1 | L1 regularization coefficient | 0–10 | 10 |
| lambda_l2 | L2 regularization coefficient | 0–10 | 3.475 |
| feature_fraction | Fraction of features used for each tree | 0.5–1 | 0.642 |
| bagging_fraction | Fraction of data used for each iteration | 0.5–1 | 1 |
| bagging_freq | Frequency of performing bagging | 0–10 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Z.; Guo, J.; Wu, S.; Wei, Z.; Lyu, J.; Zhang, K. Dynamic Mechanistic–Data-Driven Hybrid Modeling of the Main Distributing Valve in a Hydroturbine Governor. Actuators 2025, 14, 572. https://doi.org/10.3390/act14120572
Lyu Z, Guo J, Wu S, Wei Z, Lyu J, Zhang K. Dynamic Mechanistic–Data-Driven Hybrid Modeling of the Main Distributing Valve in a Hydroturbine Governor. Actuators. 2025; 14(12):572. https://doi.org/10.3390/act14120572
Chicago/Turabian StyleLyu, Zhuofan, Jiang Guo, Shang Wu, Zhuo Wei, Jiaxuan Lyu, and Kefei Zhang. 2025. "Dynamic Mechanistic–Data-Driven Hybrid Modeling of the Main Distributing Valve in a Hydroturbine Governor" Actuators 14, no. 12: 572. https://doi.org/10.3390/act14120572
APA StyleLyu, Z., Guo, J., Wu, S., Wei, Z., Lyu, J., & Zhang, K. (2025). Dynamic Mechanistic–Data-Driven Hybrid Modeling of the Main Distributing Valve in a Hydroturbine Governor. Actuators, 14(12), 572. https://doi.org/10.3390/act14120572






