Hysteresis Modeling of a Magnetic Shape Memory Alloy Actuator Using a NARMAX Model and a Long Short-Term Memory Neural Network

Abstract

Hysteresis primarily affects the positioning accuracy of the magnetic shape memory alloy-based actuator (M-SMAA). This paper proposes the use of the nonlinear autoregressive moving average with an exogenous input (NARMAX) model to describe the complex dynamic hysteresis of M-SMAA. First, an improved Prandtl–Ishlinskii operator is proposed as the exogenous variable function for the NARMAX model, using a hyperbolic tangent function as the input to the exogenous variable function, to better capture and represent the multivalued mapping hysteresis in M-SMAA. Then, a long short-term memory neural network is introduced to construct the NARMAX model, further optimizing its performance. Finally, the experimental results verify the effectiveness of the model.

1. Introduction

The magnetic shape memory alloy-based actuator (M-SMAA) is a new type of smart material actuator that utilizes the coupling effect between the characteristics of a shape memory alloy and an applied magnetic field to achieve actuation [1,2,3]. Compared to conventional electrically or thermally driven SMA actuators, the M-SMAA has the advantages of fast response, high control precision, and strong load-carrying capacity, enabling precise displacement control at the micro-nano scale. The M-SMAA also has the characteristics of a small-volume, lightweight, and simple structure, exhibiting broad application prospects in the fields of micro-robotics, micro-manipulation, and micro-positioning [4,5]. However, the intricate hysteresis in the M-SMAA significantly impacts not only the positioning accuracy of the actuator but also the controllability of the system, potentially causing system instability. Figure 1 presents the input–output curves of the M-SMAA. As shown in the figure, a pronounced hysteresis exists between the input current and the output displacement. Moreover, this hysteresis behavior exhibits a clear rate-dependent property. This limitation hinders its widespread application in precision positioning and actuation. Therefore, studying the complex hysteresis characteristics of the M-SMAA and establishing an accurate hysteresis model is significant for improving its positioning accuracy and promoting its application research.

Currently, hysteresis has been found in many actual systems. Since the hysteresis exhibited by different systems varies, the methods for describing hysteresis are also diverse. Based on different modeling principles, hysteresis modeling methods can be roughly divided into three categories: modeling methods based on physical properties, modeling methods based on hysteresis phenomena, and other modeling methods.

The modeling method based on physical properties aims to represent hysteresis by exploring the underlying mechanism of its generation, leveraging the physical properties of the plant. This type of modeling method can not only intuitively reflect the physical properties of the plant, but also reveal the inherent relationship between the hysteresis characteristics and the physical parameters of the plant [6,7]. However, the modeling method based on physical properties has the disadvantages of a low modeling accuracy, many unknown parameters, complex calculation processes, and inconvenient physical parameter measurement. Therefore, the most commonly used is the modeling method based on the hysteresis phenomena.

The hysteresis model based on the hysteresis phenomena can be divided into an operator-based hysteresis model and a differential equation-based hysteresis model. The operator-based hysteresis model is a mathematical model established based on the hysteresis phenomenon reflected by the plant. The operator-based model realizes the description of the hysteresis through the accumulation of basic hysteresis operators. Common operator-based hysteresis models include the Preisach model [8,9,10,11], the Prandtl–Ishlinskii (PI) model [12,13,14,15], and the Krasnosel’skii–Pokrovskii model [16,17,18]. Since the operator-based model can ignore the physical characteristics of the material itself and has higher modeling accuracy, it has been widely applied. However, the operator-based hysteresis model often involves complex mathematical expressions and multiple parameters, requiring a large amount of experimental data to determine the appropriate parameters. This increases the difficulty and computational cost of modeling. Another commonly used hysteresis model is the differential equation-based hysteresis model, which describes the hysteresis in the form of differential equations. Common differential equation-based hysteresis models include the Duhem model [19,20] and the Bouc-Wen model [21,22,23]. However, due to certain limitations of the differential equation-based hysteresis model in describing the hysteresis loop with high saturation and high asymmetry, it is not suitable for describing the complex dynamic hysteresis of the M-SMAA.

In recent years, the nonlinear autoregressive moving average model with the exogenous input (NARMAX) model has become a research hotspot in hysteresis modeling. Yu et al. combined the improved fractional-order method with NARMAX to describe the hysteresis of the M-SMAA, but the established model has poor adaptability, and its performance needs to be improved when dealing with complex nonlinearity [24,25] combined the neural network with the NARMAX model and introduced an exogenous variable function to deal with rate hysteresis. The established model can effectively describe the rate-dependent hysteresis, but the model is complex, and its real-time performance needs to be improved.

Although the classic NARMAX model has achieved satisfactory results in the field of nonlinear system modeling, there are still some obvious limitations in describing system with multi-valued mapping hysteresis. Firstly, the inherent complexity of a nonlinear system often requires the NARMAX model to construct an extremely large and complex parameter system to achieve an accurate description. This not only significantly increases the computational burden but also greatly enhances the complexity of model parameter identification, thereby affecting the modeling accuracy. Secondly, the multi-valued mapping hysteresis poses a significant challenge for the NARMAX model. It is difficult to deeply and accurately capture the dynamic change of the hysteresis behavior. Furthermore, the construction of an effective NARMAX model usually relies on a deep understanding of the prior knowledge of the system, to appropriately select the input variables and determine the model structure. However, for hysteresis systems with strong nonlinearity and multi-valued mapping characteristics, obtaining accurate and useful prior knowledge is not an easy task, which largely limits the application effectiveness and practicality of the NARMAX model in the hysteresis system. Furthermore, constructing hybrid hysteresis models using multiple models is an effective approach to describing complex hysteresis. However, existing hybrid models still fail to simultaneously capture the multi-valued, rate-dependent, and asymmetric hysteresis behaviors of the M-SMAA. To address this issue, an improved NARMAX framework combined with an LSTMNN and a tanh-based PI operator is developed in this work.

In this paper, to enhance the ability of the NARMAX model to describe the hysteresis, an improved PI operator is adopted as the exogenous variable function of the NARMAX model, which improves the model’s ability to capture and represent the hysteresis with multi-valued mapping. Furthermore, to further optimize the model performance, a neural network (NN) is introduced to construct the NARMAX model. The established model can more accurately describe the dynamic hysteresis behavior of the M-SMAA, effectively improving the fitting capability of the model. The contributions of this work are summarized as follows:

1. The improved PI operator with a hyperbolic tangent function as input is used as the exogenous variable function of the NARMAX model, which effectively enhances the ability of the NARMAX model to describe the hysteresis with multi-valued mapping.

2. The long short-term memory neural network (LSTMNN) is introduced to construct the NARMAX model, further optimizing the model performance and enabling it to more accurately describe the dynamic hysteresis of the M-SMAA.

The arrangement of this paper is as follows: Section 2 introduces the modeling method, Section 3 validates the model performance, and Section 4 summarizes the paper.

2. Modeling Method

The NARMAX model can effectively capture the nonlinear, time-varying, and complex dynamic characteristics of the system. It combines the influences of auto-regression, moving average and exogenous input, thus enabling a more accurate description of the behavior of the system. By selecting the appropriate model order and the parameter estimation method, the NARMAX model can provide accurate modeling and prediction for various complex systems, providing strong support and a decision-making basis for solving practical problems. The classical discrete NARMAX model can be written in the following form:

$$\begin{array}{cc}\hfill y_m\left(k\right)=& t_0+t_{1}v(k-1)+\dots +t_{r}y\left(k-h_y\right)+\hfill \\ \hfill & t_{11}{v}^2(k-1)+t_{12}v(k-1)v(k-2)+\dots +\hfill \\ \hfill & t_{rr}{y}^2\left(k-h_y\right)+t_{111}{v}^3(k-1)+\hfill \\ \hfill & t_{112}{v}^2(k-1)v(k-2)+\dots +\hfill \\ \hfill & {\theta }_{rrr}{y}^3\left(k-h_y\right)+\dots \hfill \\ \hfill =& t_0+\sum _{j_1=1}^r{t}_{j_1}{a}_{j_1}+\sum _{j_1=1}^r\sum _{j_2=j_1}^r{t}_{j_1{j}_2}{a}_{j_1}{a}_{j_2}+\dots +\hfill \\ \hfill & \sum _{j_1=1}^r\dots ·\sum _{j_q=j_{q-1}}^r{t}_{j_1\dots j_q}{a}_{j_1}...a_{j_q}\hfill \end{array}$$

(1)

where q represents the order of the model, and a represents the combination of model input v, output y, and exogenous variable function n. t is the coefficient term corresponding to a. $h_{(.)}$ denotes the lag of v, n, and y.

The expression of the improved PI operator is

$$\begin{array}{c}\hfill n\left(k\right)=max\left\{tanh\right(v\left(k\right))-\mathsf{\Theta },min\{tanh\left(v\right(k\left)\right),n\left(k\right)\left\}\right\}\end{array}$$

(2)

where $\mathsf{\Theta }$ is the threshold of the operator.

The hyperbolic tangent function possesses a more diverse range of nonlinear properties, enabling it to capture the complex nonlinear of the system more effectively. By substituting the PI operator’s input with the hyperbolic tangent function and exploiting the function’s distinctive features, the model’s capability to capture complex nonlinear relationships has been strengthened, enhancing the modeling accuracy.

The NARMAX model effectively characterizes the hysteresis of the M-SMAA, but it has limitations in capturing its complex dynamic hysteresis. Specifically, the model cannot be updated in real time, hindering its ability to adapt and optimize based on changes in the actuator’s operating conditions and performance. Furthermore, the model’s inability to fully utilize the latest data to update and improve itself leads to a decrease in its accuracy and precision over time. Considering the limitations of the NARMAX model, the neural network-based NARMAX model has gained significant attention as a more effective approach to describe the complex dynamic hysteresis of the M-SMAA. Among various neural network architectures, the LSTMNN has emerged as the ideal choice due to its unique advantages [26,27]. The LSTMNN can handle time series data excellently, effectively capture complex hysteresis, and enable real-time adjustment and optimization for model parameters. Currently, there are few studies on the hysteresis modeling of the M-SMAA using an LSTMNN. In our previous work [28], the U model based on the LSTMNN is used to describe the hysteresis of the M-SMAA, but the neural network is not optimized for the characteristics of hysteresis. In this paper, the improved hysteresis operator is used as the input of the LSTMNN, which effectively improves the performance of the model.

Figure 2 shows the block diagram of the LSTMNN-based NARMAX model. The LSTMNN architecture comprises an input layer, a hidden layer, and an output layer. The NN’s input ${\gamma }_j$ is the autoregressive moving average terms of the NARMAX model. The hidden layer, using its unique cell state and hidden state mechanism, can effectively capture both the long-term and short-term dependencies in the time series data. The LSTM cell consists of an input gate ${\wp }_i$, a forget gate $f_i$, and an output gate ${\mathsf{\Omega }}_i$. The input gate governs how much of the current input information is stored in the cell state; the forget gate dictates how much of the past information is discarded; and the output gate determines how much of the cell state information is output. The model proposed in this paper takes the LSTM cell as the core, processes long-term and short-term dependencies, memorizes historical information through a three-gate mechanism, and optimizes the parameters through backpropagation learning. With the real-time dynamic update mechanism of the LSTMNN, this model can automatically adjust and optimize the parameters according to the changes of the input signal, accurately describe the hysteresis behavior of the M-SMAA, effectively capture its complex dynamic hysteresis characteristics, and has a high degree of adaptability.

The expression of the LSTMNN is as follows:

$$\left\{\begin{array}{cc}\hfill {\lambda }_i\left(k\right)& =\sum _{j=1}^z{W}_{ij}{\gamma }_j\left(k\right)\hfill \\ \hfill {\wp }_i\left(k\right)& =\mathsf{\Phi }\left(W_{\wp i}{\lambda }_i\left(k\right)+{\mathsf{\Gamma }}_{\wp i}{\partial }_i(k-1)+{\delta }_{\wp i}\right)\hfill \\ \hfill f_i\left(k\right)& =\mathsf{\Phi }\left(W_{Fi}{\lambda }_i\left(k\right)+{\mathsf{\Gamma }}_{fi}{\partial }_i(k-1)+{\delta }_{fi}\right)\hfill \\ \hfill {\mathsf{\Omega }}_i\left(k\right)& =\mathsf{\Phi }\left(W_{\mathsf{\Omega }i}{\lambda }_i\left(k\right)+{\mathsf{\Gamma }}_{\mathsf{\Omega }i}{\partial }_i(k-1)+{\delta }_{\mathsf{\Omega }i}\right)\hfill \\ \hfill {\partial }_i\left(k\right)& ={\mathsf{\Omega }}_i\left(k\right)\times tanh\left(R_i\left(k\right)\right)\hfill \\ \hfill {\widehat{R}}_i\left(k\right)& =tanh\left(W_{Ri}{\lambda }_i\left(k\right)+{\mathsf{\Gamma }}_{Ri}\partial (k-1)+{\delta }_{Ri}\right)\hfill \\ \hfill R_i\left(k\right)& ={\wp }_i\left(k\right)\times {\widehat{R}}_i\left(k\right)+f_i\left(k\right)\times R_i(k-1)\hfill \\ \hfill O\left(k\right)& =\sum _{i=1}^m{W}_{\partial i}{\partial }_i\left(k\right)+{\delta }_O\hfill \end{array}\right.$$

(3)

where $\gamma$ and O denote the input and output of the LSTMNN. $f_i$, ${\wp }_i$, $R_i$, and ${\omega }_i$ represent the cell state, forget gate, input gate, and output gate of the LSTM cell, respectively. In addition, $\mathsf{\Phi }$ represents the sigmoid activation function, and ${\partial }_i$ denotes the hidden state. $\mathbf{W}={[W_{ij},W_{\wp i},W_{Fi},W_{\mathsf{\Omega }i},W_{Ri},W_{hi},{\mathsf{\Gamma }}_{\wp i},{\mathsf{\Gamma }}_{Fi},{\mathsf{\Gamma }}_{\mathsf{\Omega }i},{\mathsf{\Gamma }}_{Ri},{\delta }_{\wp i},{\delta }_{Fi},{\delta }_{\mathsf{\Omega }i},{\delta }_{Ri},{\delta }_O]}^T$ are the weights and biases in the LSTM.

The parameters of the NN are updated by the gradient descent algorithm:

$$\left\{\begin{array}{c}{E}_m\left(k\right)={\displaystyle \frac{1}{2}}{\left(y\left(k\right)-y_m\left(k\right)\right)}^2\\ \\ \mathbf{W}(k+1)=\mathbf{W}\left(k\right)-{\eta }_1{\displaystyle \frac{\partial E_m\left(k\right)}{\partial \mathbf{W}\left(k\right)}}\end{array}\right.$$

(4)

where $\mathbf{W}$ and $y_m$ denote the NN paramenter and model output, respectively. $E_m$ is a function of the error, and ${\eta }_1$ is the learning rate of the NN.

Considering the parameter selection method and principle in [28], NN parameters are selected as follows by comprehensively considering modeling accuracy and computational complexity, i.e., the NN is structured in three layers, each containing 55, 7, and 1 neurons, respectively. $h_v$ = 2, $h_n$ = 2, $h_y$ = 1, r = 5, $\eta$ = 0.6, q = 3.

3. Experimental Results and Analysis

Figure 3a,b show the experimental platform and the schematic diagram of the device connections, respectively. The experimental system includes a computer, a data acquisition card, programmable DC power, the M-SMAA, a displacement sensor (LVDT), and a temperature sensor. The computer communicates with other experimental devices through the data acquisition card, which is responsible for data acquisition and analysis. Specifically, the MATLAB software on the computer generates a driving signal, which is converted to an analog signal via the data acquisition card and sent to the programmable DC power. The programmable DC power outputs an adjustable current based on the driving signal, which serves as the excitation current for the M-SMAA. Under the drive of input current, the M-SMAA generates output displacement. The displacement sensor collects this signal and feeds it back to the computer via the data acquisition card. The MATLAB software can analyze and process the real-time displacement response data collected. Meanwhile, the temperature sensor collects the real-time working temperature of the M-SMAA to ensure safe and stable operation.

To validate the effectiveness of the proposed modeling method, a series of experiments are conducted under various conditions, including different sinusoidal input frequencies, loads, and complex harmonic signal (CHS) and triangular wave signal (TWS). Furthermore, the experimental results were compared with the models in [29] (denoted as M1) and the literature [16] (denoted as M2) to demonstrate the superior performance of the proposed method. The experimental results indicate that the proposed model (denoted as M2) accurately captures the hysteresis of the M-SMAA across various conditions. Specifically:

Figure 4 presents the modeling results for sinusoidal signals at different frequencies. Under 1, 3, and 6 Hz sinusoidal input signals, the proposed model exhibits good modeling accuracy, reflecting its ability to approximate the rate-dependent hysteresis. This is attributed to the powerful nonlinear approximation capability of the NN, which can effectively describe the influence of input frequency changes on the hysteresis output.

Figure 5 illustrates the modeling results for a 2 Hz sinusoidal input with loads of 100, 200, and 300 g. Experimental results indicate that the proposed model accurately fits the force-dependent hysteresis of the M-SMAA. This demonstrates the model’s strong adaptability, allowing it to adjust to varying loads that influence hysteresis characteristics.

Figure 6 and Figure 7 present modeling results for CHS and TWS with 0 g and 100 g loads, respectively. The results indicate that the proposed model accurately captures M-SMAA hysteresis under both complex harmonic and triangular signal excitations, regardless of load conditions. This proves that the model can not only approximate the major hysteresis loop but also capture the minor hysteresis loop, and has an advantage in handling various input signals in complex hysteresis modeling.

Table 1. RMSE (μm), MAXE (%), MAE (μm), and ATC (s) of the proposed model and the comparison model.

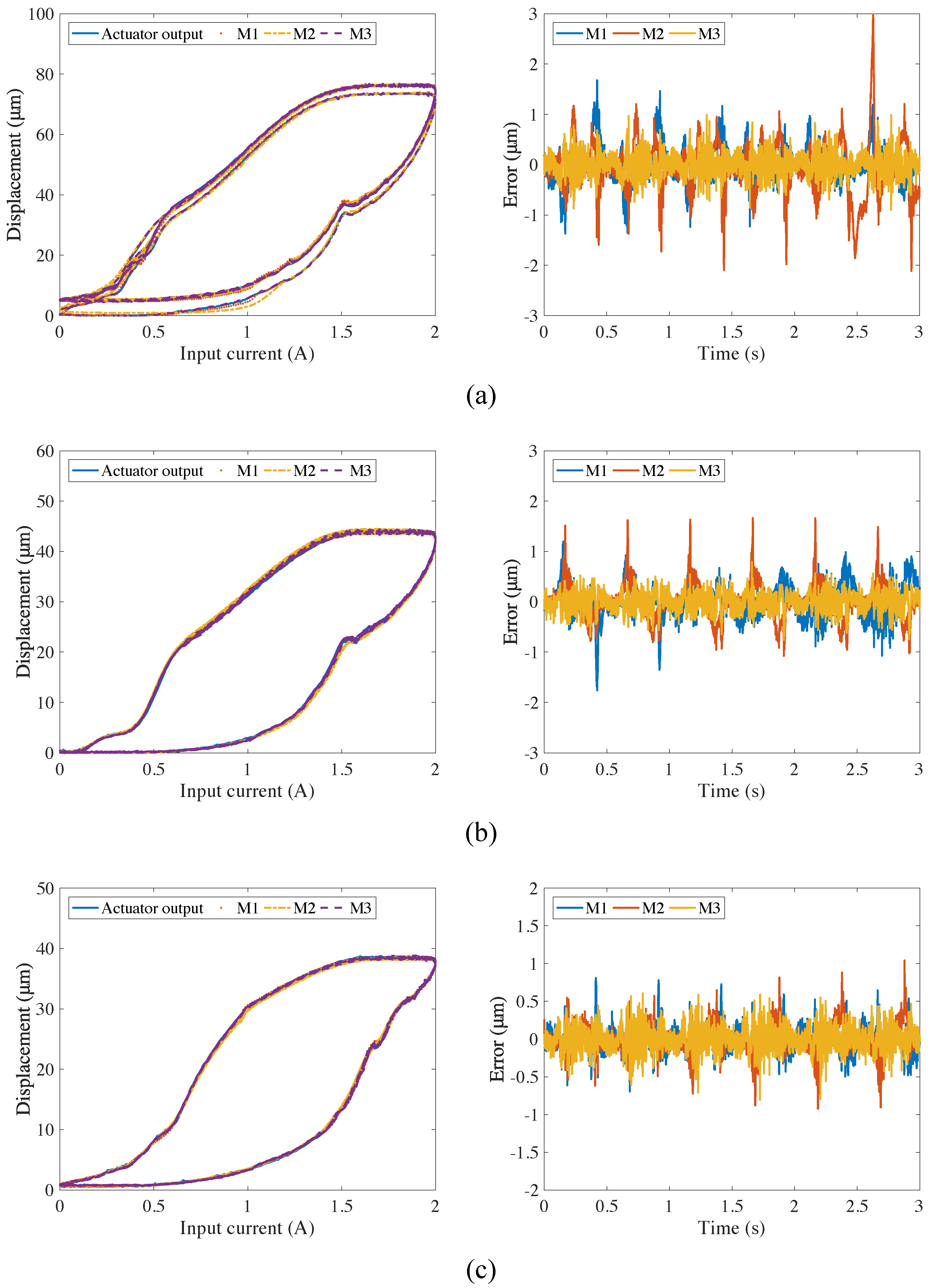
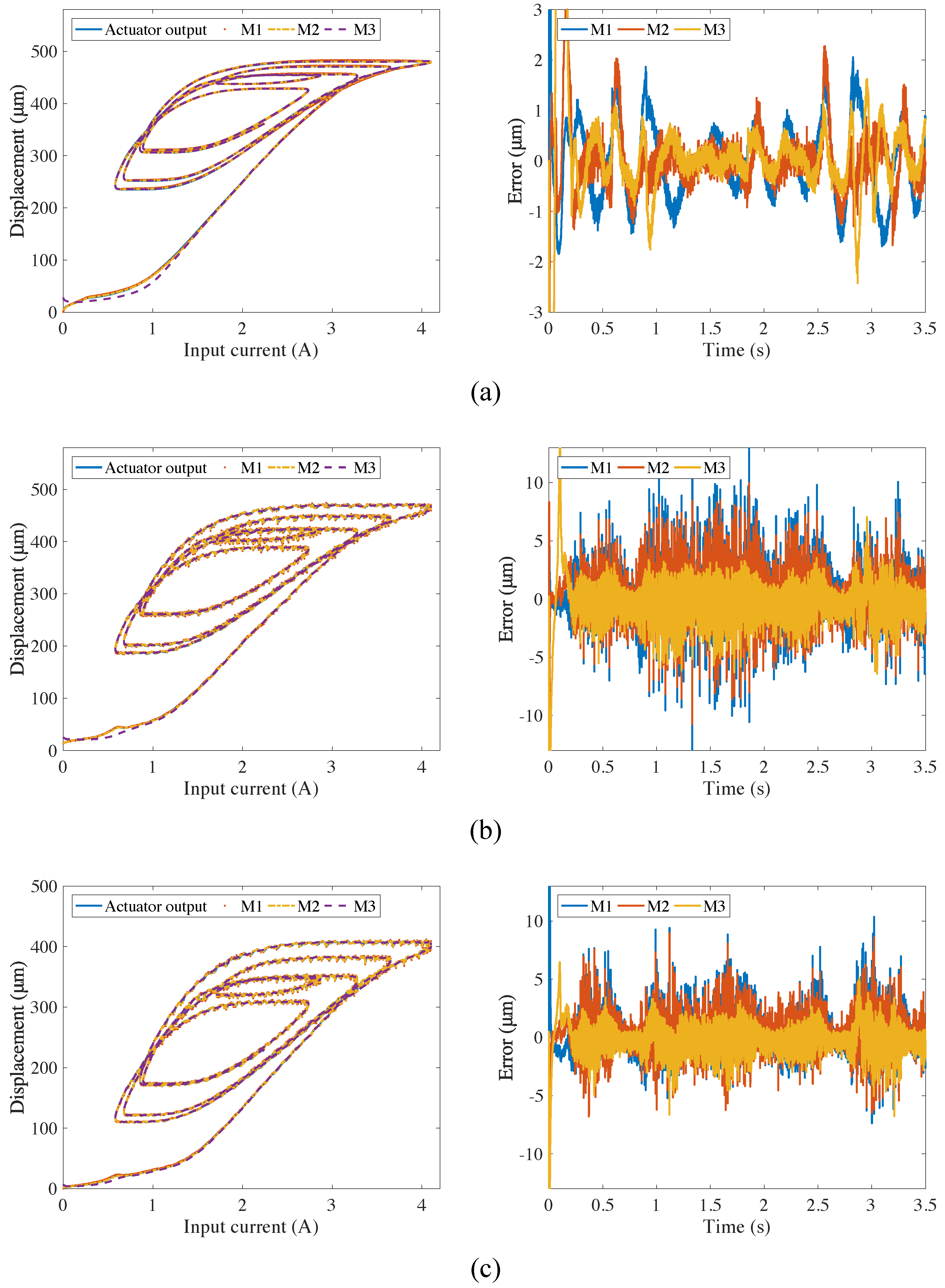
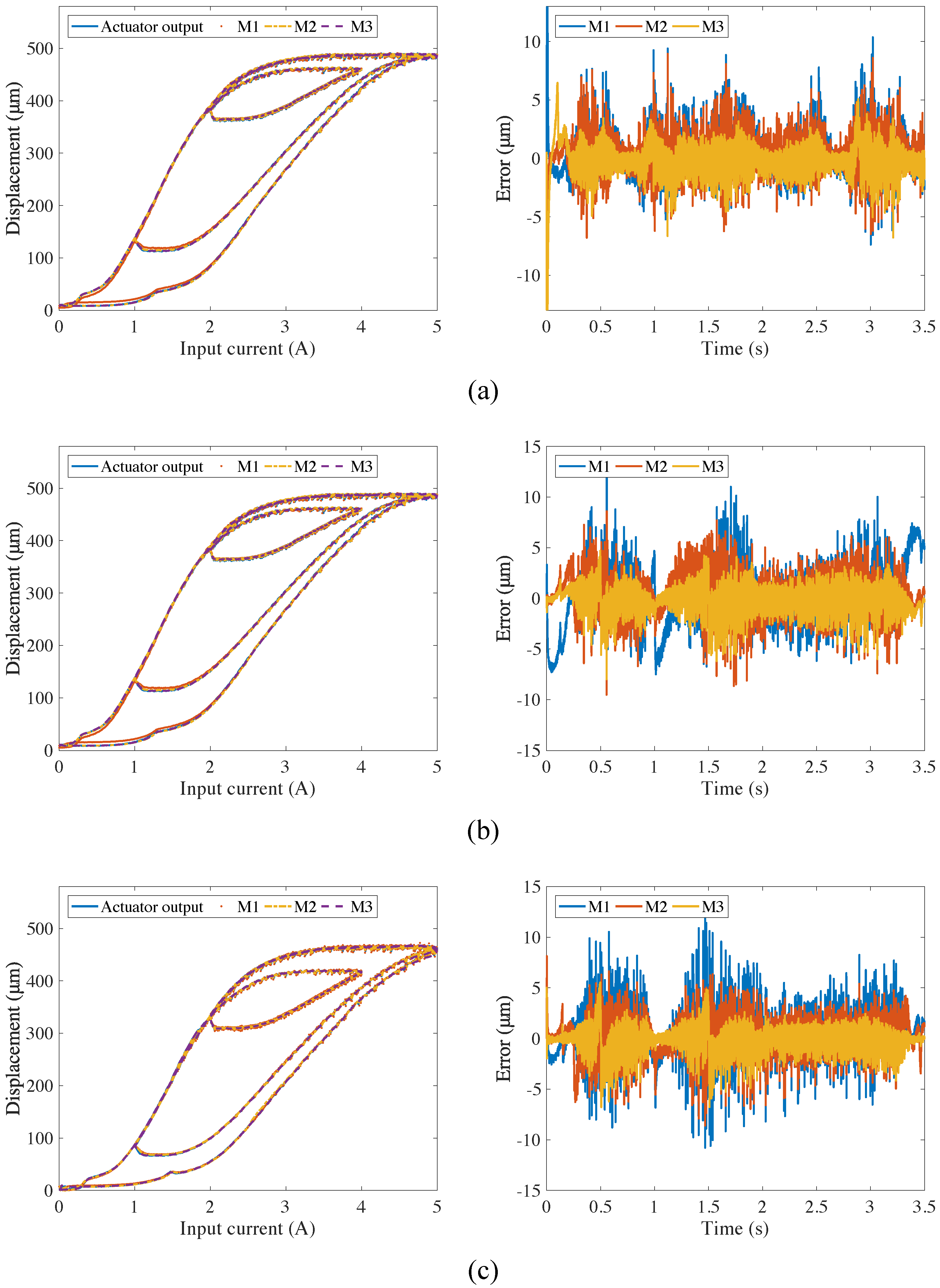
Input Signal	M1	M2	M3
1 Hz, 0 g	0.5783/1.03/0.39/1.39	0.4334/0.97/0.35/4.97	0.2434/0.67/0.21/2.56
3 Hz, 0 g	0.5982/1.43/0.42/1.02	0.4625/1.22/0.37/3.34	0.3334/0.83/0.27/1.95
6 Hz, 0 g	1.9974/1.99/1.40/0.33	1.6357/1.79/1.31/2.58	0.4438/1.21/0.36/0.85
2 Hz, 100 g	0.2758/3.87/0.23/1.03	0.2047/3.06/0.16/5.32	0.1602/1.37/0.13/2.57
2 Hz, 200 g	0.4893/3.94/0.39/1.47	0.3609/3.62/0.29/4.77	0.1880/1.72/0.15/2.50
2 Hz, 300 g	0.6803/4.74/0.57/1.29	0.5584/4.20/0.45/5.01	0.2242/1.79/0.18/2.63
CHS, 0 g	0.6439/0.57/0.51/0.97	0.5222/0.49/0.42/4.58	0.4904/0.35/0.39/1.99
CHS, 100 g	1.7074/1.61/1.43/1.12	1.6734/1.52/1.34/4.21	1.2342/1.10/0.99/2.21
CHS, 200 g	2.3904/2.26/1.80/0.99	2.1751/2.16/1.74/4.02	1.5525/1.94/1.24/2.17
TWS, 0 g	2.0087/1.49/1.51/1.22	1.8241/1.37/1.46/5.35	1.4327/1.09/1.15/2.86
TWS, 100 g	2.4744/1.63/1.69/1.07	1.9943/1.53/1.60/5.01	1.6233/1.14/1.30/2.95
TWS, 200 g	2.8943/1.83/1.72/1.23	2.0180/1.77/1.61/5.27	1.7259/1.55/1.38/2.88

summarizes the root mean square error (RMSE), maximum error (MAXE), mean absolute error (MAE), and average time consumption (ATC) for both the proposed and comparison models. The experimental data show that, when the frequency rises, the error of the comparison model increases significantly. However, the error of the model in this paper increases to a lower extent. When the load changes, an increase in load will cause the error of the comparison model to increase obviously, while the error increase range of the model in this paper is relatively small. For different types of input signals, whether it is a complex harmonic signal or a triangular wave signal, the model in this paper performs well under different loads, and the error is relatively small. The error-index and ATC show that the proposed model maintains a smaller modeling error range compared to existing methods, effectively describing M-SMAA hysteresis and demonstrating superior performance.

In conclusion, the experimental results and error analysis indicate that the proposed model exhibits excellent accuracy across various input conditions, effectively capturing both rate-dependent and force-dependent hysteresis of the M-SMAA, providing a reliable modeling solution for the practical application of M-SMAA.

4. Conclusions

This study developed an LSTMNN-based NARMAX model to describe the complex dynamic hysteresis of the M-SMAA. Experimental results show that the proposed model outperforms the comparison model in terms of modeling performance. This is because the hysteresis characteristics of the M-SMAA are typically time-dependent, and the LSTMNN has a stronger capability in processing time-series data, effectively capturing the dependencies and temporal dynamics in long sequences, and better memorizing historical information, thereby providing more accurate predictions of future outputs. Although the proposed model achieves high accuracy under different operating conditions, its performance may still be influenced by temperature variations and dataset dependence, which will be further investigated in future work.